1 Introduction

The quantum correlation for a quantum state contain entanglement and other type of nonclassical correlations. It is known that the quantum correlations are more comprehensive than entanglement [1, 2]. Quantum discord(QD) [3, 4] is a measure of nonclassical correlations which include not only quantum correlations with entanglement but also entanglement-free quantum correlations that may occur in separable states. QD captures the nonclassical correlations, more general than entanglement, that can exist between parts of a quantum system even if the corresponding quantum entanglement does vanish. QD is considered to be a more general resource of quantum advantage than quantum entanglement in quantum information processing [5–13]. QD has been investigated in a wider context [14–24] including entanglement-free quantum computation [5], quantum communication [12, 15–17], and quantum phase transitions in many-body physics [18–25].

As the natural candidates for the realization of the correlation, spin chains have demonstrated some substantial advantages compared with the other physical systems [26–29]. They not only have useful applications, but also display rich correlation features [30, 32, 33]. The simplest spin chain, Heisenberg chain has been used to construct a quantum computer and quantum dots [31]. In addition, by suitable coding, the Heisenberg interaction alone can be used for quantum computation. Therefore, it is very interesting and necessary to study the quantum correlation in spin model. In this paper, several interesting results are obtained based on the behaviors of the QD and C about the effects of external field parameter B, D and the coupling coefficient J, where many of them are in contrast to the behavior of the entanglement.

In this paper, the quantum correlation behaviors of a two-qubit anisotropic Heisenberg XYZ chain with environmental decoherence under an uniformly inhomogeneous magnetic field and the strength of DM interaction have been investigated. In Section 2, we introduce the Hamiltonian of the system and give the master equation which provides the evolution of an open system. In Section 3, briefly review the definitions concurrence C and QD, and the werner state as the initial state. In Section 4, the quantum correlation behaviors of this spin system and the difference between concurrence with QD are investigated. Conclusions are finally drawn in Section 5.

2 Description of the Model and the Master Equation

We consider the Hamiltonian H for the anisotropic two-qubit Heisenberg XYZ chain in an external magnetic field B(along the z axis) and in the presence of the Dzyaloshinski-Moriya(DM) anisotropic antisymmrtric interaction.

$$\begin{array}{@{}rcl@{}} H&=&B({S_{1}^{z}}+{S_{2}^{z}})+J(S_{1}^{+}S_{2}^{-}+S_{1}^{-}S_{2}^{+}) \\ &&+\frac{J_{z}}{2}{\sigma_{1}^{z}}{\sigma_{2}^{z}}+\frac{D}{2}({\sigma_{1}^{x}}{\sigma_{2}^{y}}-{\sigma_{1}^{y}}{\sigma_{2}^{x}}), \end{array} $$
(1)

where J and J z are the real coupling coefficients, the model is called antiferromagnetic for J>0 and ferromagnetic for J<0. \(S_{n}^{\alpha }=\frac {1}{2}\sigma _{n}^{\alpha }\) (α = x,y,z), and \(\sigma _{n}^{\alpha }\) are the local spin \(-\frac {1}{2}\) operators and Pauli operators, respectively, at site n, \(\hbar =1\), and the periodic boundary condition S n+1 = S 1 applies. The parameter D is the DM interaction.

Decoherence of the quantum system due to interacting with its surrounding is the important difficulty to perform quantum computation tasks. Therefore, it is inevitable to specify the dynamical properties of quantum correlations for preserve the protocol to against decoherence. Many investigation have been paid to dynamics of quantum correlations both theoretically and experimentally in the Markovian [35] and non-Markovian [36] environment. For instance, there are many investigations on decoherence due to spin environment [36], like single qubit coupled to the environment and two qubits coupled to the environment. The master equation describing the environmental decoherence under Markovian approximation [34] is given

$$\begin{array}{@{}rcl@{}} \frac{d\rho}{dt}=-i[H,\rho]+\gamma\sum\limits_{j=1,2}[\sigma_{j}^{-}\rho \sigma_{j}^{-\dag}-\frac{1}{2}\{\sigma_{j}^{-\dag}\sigma_{j}^{-},\rho\}], \end{array} $$
(2)

where { } means anticommutator and γ is the environmental decoherence rate. With knowing the master equation, the explict forms of the evolution state ρ(t) can be derived by solving the master equation with ρ(0) as the initial condition. And then, we will use two measures of quantum correlation (the entanglement and QD) to study the quantum correlation properties of two spins, and study the difference between the two measures.

3 The Definitions of Entanglement and QD and the Introduction of the Initial State

By knowing the master equation, the explicit forms of the evolution state ρ t can be derived by solving the master equation with ρ 0 as the initial condition. For a two-qubit system, we know that the density matrix contains nonzero elements usually along the main diagonal and anti-diagonal, which is prepared in an initial quantum state determined by the X-state form initial density matrix ρ 0, after some time the evolution state density matrix ρ t remain preserve the X structure. C denotes the concurrence which is defined as

$$\begin{array}{@{}rcl@{}} \mathrm{C}=\max(\lambda_{1}-\lambda_{2}-\lambda_{3}-\lambda_{4},\ \ 0). \end{array} $$
(3)

where λ k (k=1,2,3,4) are the square roots of eigenvalues in decreasing order of magnitude of the ”spin-flipped” density matrix operator R = ρ(σ y⊗σ y)ρ ∗(σ y⊗σ y), where the asterisk indicates complex conjugation. The concurrence C ranges from 0 to 1, if C=0 or 1, the system is in an unentangled or a maximally entangled state, else it corresponds to a partial entangled state.

In classical information theory, the total correlations in a bipartite quantum system are measured by the total quantum mutual information rho A B defined as

$$\begin{array}{@{}rcl@{}} I(\rho_{AB})=S(\rho_{A})+S(\rho_{B})-S(\rho_{AB}), \end{array} $$
(4)

where S(ρ)=−Tr(ρlog2ρ) is the Von Neumann entropy of density matrix, ρ A and ρ B are the reduced density matrices of the subsystem A and B, respectively; The quantum mutual information is usually used as a measure of total correlations that include quantum and classical ones. The classical correlation \(\mathcal {C}(\rho _{AB})\) is defined as the maximum information about one subsystem ρ i , which is usually depends on the type of measurement performed on the other subsystem. In this paper, we limit ourselves to projective measurement π k =|k〉〈k| (k=± ) performed only on the subsystem B, the two orthogonal states |+〉 and |−〉 can be represented as a unitary vector on the Bloch sphere |+〉= cos𝜃|1〉 + e iϕ sin𝜃|0〉 and |−〉 = e −iϕ sin𝜃|1〉− cos𝜃|0〉 with 0 ≤ 𝜃 ≤ π/2 and 0 ≤ ϕ ≤ 2π. Then the classical correlation can be defined as

$$\begin{array}{@{}rcl@{}} \mathcal{C}(\rho_{AB})=S(\rho_{A})-\min_{\{{\Pi}_{k}\}}[\sum\limits_{k}p_{k}S(\rho^{(k)}_{A})], \end{array} $$
(5)

the minimum is taken over the complete set of orthogonal projectors π k , where \(\rho ^{(k)}_{A}=\frac {1}{p_{k}}\text {Tr}_{B}[(\mathrm {I}_{A}\otimes {\Pi }_{k})\rho _{AB}(\mathrm {I}_{A}\otimes {\Pi }_{k})]\) is the reduced matrix of subsystem A after obtaining the measurement outcome k, where p k =Tr A B [(I A ⊗π k )ρ A B (I A ⊗π k )]. Then the difference between the total correlations and the classical correlations can be defined as

$$\begin{array}{@{}rcl@{}} \mathrm{D}(\rho_{AB})= I(\rho_{AB})-\mathcal{C}(\rho_{AB}), \end{array} $$
(6)

which is the so-called quantum discord(QD ). Usually, QD is somewhat difficult to calculate and we cannot get the analytical solutions. While for the X-structure density matrix, if we define

$$\begin{array}{@{}rcl@{}} \mathrm{Q}_{j}=H(\rho_{11}+\rho_{33})+\sum\limits^{4}_{i=1}\lambda_{i}\log_{2}\lambda_{i}+D_{j}, \end{array} $$
(7)

with λ i being the eigenvalues of ρ A B , then we can obtain the exact expression of quantum discord as [38]

$$\begin{array}{@{}rcl@{}} \mathrm{D}(\rho_{AB})=\min(\mathrm{Q}_{1}, \mathrm{Q}_{2}) \end{array} $$
(8)

where D 1 = H(τ) and D 2=−Σ i ρ i i log2ρ i i −H(ρ 11 + ρ 33), with \(\tau =(1+\sqrt {[1-2(\rho _{33}+\rho _{44})]^{2}+4(|\rho _{14}|+|\rho _{23}|)^{2}})/2\), and H(τ)=−τlog2τ−(1−τ)log2(1−τ). With knowing about these, in the following, we study the dynamical characters about the quantum correlation of this two-qubits system prepared in different initial states by using concurrence C and QD.

Here we chose the initial state as the well-known Werner state [37], which is formed by a mixture of the maximally entangled state and the separable maximally mixed state,

$$\begin{array}{@{}rcl@{}} \rho_{0}=r|\varphi\rangle\langle\varphi|+\frac{1-r}{d^{2}}I_{1}\otimes I_{2}. \end{array} $$
(9)

where

$$\begin{array}{@{}rcl@{}} |\varphi\rangle=\frac{1}{\sqrt{d}}\sum\limits_{i=1}^{d}|i\rangle_{1}|i\rangle_{2}. \end{array} $$
(10)

is the maximally entangled state in d-dimensional Hilbert space and I denotes the identity operator. The parameter r(0 ≤ r ≤ 1) is the probability of the maximally entangled state in the mixture. The less the r, the larger the mixed degree. The Werner state is entangled if r>1/(1 + d).

In this paper, we choose the two-qubit system of interest initially in Werner state,

$$\begin{array}{@{}rcl@{}} \rho_{0}=r|\varphi\rangle\langle\varphi|+\frac{1-r}{4}I_{1}\otimes I_{2}. \end{array} $$
(11)

When 1/3<r ≤ 1, the two qubits are entangled.

4 The Properties of Entanglement and QD

In the standard basis, { |00〉,|01〉,|10〉,|11〉}, the density matrix |ρ(t)〉 of the system reads

$$\begin{array}{@{}rcl@{}} \rho(t)= \begin{array}{cccc} \rho_{11} & 0 & 0 & 0\\ 0 & \rho_{22} & \rho_{23} & 0\\ 0 & \rho_{32} & \rho_{33} & 0\\ 0 & 0 & 0 & \rho_{44} \end{array} \end{array} $$
(12)

where

$$\begin{array}{@{}rcl@{}} \rho_{11}&=&\frac{1-r}{4}e^{-2\gamma t}, \\ \rho_{22}&=&\frac{1}{2}e^{-\gamma t}-\rho_{11}+\frac{2rD}{\alpha}e^{-\gamma t}\sin\frac{t\alpha}{2}, \\ \rho_{33}&=&\frac{1}{2}e^{-\gamma t}-\rho_{11}-\frac{2rD}{\alpha}e^{-\gamma t}\sin\frac{t\alpha}{2}, \\ \rho_{23}&=&\rho^{\ast}_{32}=\frac{r}{2}e^{-\gamma t}\frac{4D\cos\frac{t\alpha}{2}+iJ}{4D+iJ}, \\ \rho_{14}&=&1+\rho_{11}-e^{-\gamma t}, \end{array} $$
(13)

where \(\alpha =\sqrt {16D^{2}+J^{2}}\). By knowing the density matrix and the definitions of concurrence and QD, it is convenient for us to obtain the quantum correlation properties. Based on the results given in(3,11), the concurrence for the mixed state is

$$\begin{array}{@{}rcl@{}} \mathrm{C}=\max(2(\sqrt{\rho_{22}\rho_{33}}-\sqrt{\rho_{11}\rho_{44}}),\ \ 0). \end{array} $$
(14)

Since the explicit expressions of concurrence and QD are very complicated, here we skip the details and give our results in terms of figures

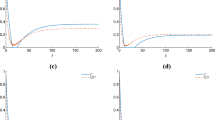
From (13) we know that the entanglement state is independent on external magnetic field B and the coupling coefficient J z , so the parameters B and J z has no influence on the concurrence and QD. The time evolution of QD and concurrence is plotted in Fig. 1. The pictures show that, the concurrence and QD both exhibit osillatory behaviors starting with an maximum value as expected for a maximally entangled initial state. One could see that if the two qubits are not entangled initially, i.e., r=1/3, there exists quantum correlation but no entanglement, as shown in Fig. 1a. This indicates that QD is more robust than the entanglement in this sense. For r=1/2, we can see that the entanglement decays more faster than QD, and the initial value of the QD is bigger than the initial value of concurrence. However, for r=3/4, the concurrence and QD both change periodicity, the phenomenon of entanglement sudden death and birth appears periodicity and the initial value of QD is smaller than the initial value of the concurrence. Which indicate that the initial values of the concurrence and QD are different with same value of r, the relative magnitude of the initial values of the concurrence and QD is not sure with the increasing of r and the initial values of the concurrence and QD both increase with the increasing of r. Particularly, when r=1, the initial state takes the form \(|\varphi \rangle =\frac {1}{\sqrt {2}}(|01\rangle +|10\rangle )\), which is a pure Bell state. It is clearly seen from Fig. 1d, the concurrence change periodicity from the maximum value 1 to a minimum value close to 0, but the QD vanish. This is different with the conclusion that QD is more general than entanglement.

Fig. 1
figure 1

Graphs of concurrence (solid line) and QD (dashed line) with respect to the time t for (a) r=1/3; (b) r=1/2; (c) r=3/4; (d) r=1, at fixed J=1; γ=1; D=2

Full size image

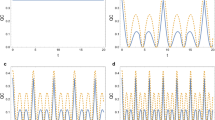
Following, we devote to investigate the influence of the parameters D and J on the time evolution of the concurrence and the QD when r=0.8. Where r is constant, so the initial state is a fixed state. In Fig. 2, we plot the concurrence and QD as functions of time and DM interaction at J=2,γ=1. These curves also show that the concurrence and QD change periodicity with the time evolution, the amplitude of the oscillation decreases and finally it will tend to zero when time increase, but the frequency of the concurrence and QD is dependent on the DM interaction. With the increasing of the DM interaction, the frequency of the oscillation of the concurrence and QD increases. The oscillation properties of the concurrence and QD on the DM interaction also can be seen from [13]. Comparing Fig. 2a with b, we noticed that the initial values of the concurrence and the QD are constant with the increasing of D, which means that the DM interaction has no influence on the quantum corralation of the initial state. What’s more, the interesting thing is that the initial value of concurrence is bigger than QD. Secondly, we examine the effect of the real coupling coefficient J on the QD and the concurrence and the results are given in Fig. 3. The concurrence and the QD change periodicity with the time evolution, and the frequency of the oscillation is also dependent on J. The lager the J is, the lager the frequency is. Any more, the variations of the concurrence and QD on J are also periodicity. The initial values of the concurrence and QD is fixed with the change of coupling coefficient J, which means that J have no influence on the initial values of the concurrence and QD. At the same time, we could see that the initial value of concurrence is larger than the initial value of QD.

Fig. 2
figure 2

Concurrence and QD versus time t and D are respectively plotted at fixed r=0.8; γ=1; J=1

Full size image
Fig. 3
figure 3

Concurrence and QD versus time t and J are respectively plotted at fixed r=0.8; γ=1; D=2

Full size image

5 Conclusion

In summary, we have investigated the quantum correlation properties under decoherence environment on two qubits that are initially in entangled Werner state. We firstly discussed the influence of mixture degree r on the dynamics. There are some difference between the time evolution behaviors of these two correlation measures with different value of r. For 0<r ≤ 1/3, there exists quantum correlation but no entanglement, which indicates that QD is more robust than the entanglement in this sense. For 1/3<r ≤ 1, the phenomenon of entanglement sudden death and birth appears periodicity with the increasing of r, but not in the QD. For r=1, the initial state will be a pure Bell state, there is one interesting thing that the concurrence decays from 1 to a minimum value close to 0 but the QD vanish. Moreover, we also have investigated the influence of the different parameters on the dynamics of concurrence and QD. The results imply that the external magnetic field B and the coupling coefficient J z have no influence on the concurrence and QD. The time evolution of the concurrence and QD both show the oscillation property, and the frequency of the oscillation depend on the DM interaction and the coupling coefficient J. With the increasing of the D or J, the frequency increase. The variation of the concurrence and QD on the DM interaction also show the oscillation property with the increasing of D or J.