1 Introduction

Einstein–Podolsky–Rosen steering, the phenomenon that was first discussed by Schrodinger and afterward considered as a notion of quantum nonlocality, has gained significant attention in recent days [1,2,3,4]. This quantum phenomenon, which has no classical analogue, is observed if one of two distant observers, sharing an entangled state, can remotely steer the particle of the other distant observer by performing measurements on his/her particle only. The experimental criteria for analyzing the presence of bipartite steering, first investigated in [5], were formalized in ref where the authors generalized this concept for arbitrary systems [6]. Till date there has been a lot of analysis regarding various features of steering nonlocality such as methods of detection [7] and quantification of steering [8, 9], steering of continuous variable systems [10], loophole-free demonstration of steering [11], applications as a resource of nonlocal correlations in the field of quantum information protocols, exploiting the relation of steering with incompatibility of quantum measurements [12, 13] and its ability to detect bound entanglement [14]. Apart from its foundational richness, EPR steering do have multifaceted applications in practical tasks such as semi-device independent scenario [15] where only one party can trust his or her apparatus but the other party’s apparatus is not trusted. In that situation the presence of steerable state provides a better chance to allow secure key distribution [16]. Even for some other tasks such as randomness certification [17], entanglement-assisted sub-channel discrimination [18], and secure teleportation through continuous-variables steerable states [19] are found to be useful.

Being a notion of nonlocality, there exists a hierarchy according to which steering is defined as a form of quantum inseparability, intermediate in between entanglement and Bell nonlocality. Considering pure quantum states these three notions are equivalent, whereas in general they are inequivalent in case of mixed states [20]. However in the context of comparison of steering nonlocality with that of Bell nonlocality, it is interesting to mention that analogous to hidden nonlocality [21, 22], existence of hidden steering has been proved in [20] for bipartite scenario. Just as in the case of exploiting nonlocality beyond Bell scenarios via the notion of hidden nonlocality [21, 22], hidden steering refers to revelation of steering nonlocality under suitable sequential measurements. In this context, an obvious interest grows regarding analysis of the same for multipartite scenario.

Due to increase in complexity as one shifts from bipartite to multipartite system, till date there has been limited attempts to understand the feature of multipartite steering phenomenon. Analogous to both entanglement and Bell nonlocality, the concept of genuine steering has been established in recent days. In this context, it may be mentioned that unlike Bell nonlocality and entanglement, due to asymmetric nature of steering nonlocality the notion of genuine steering nonlocality lacks uniqueness. However, genuine steering was first introduced in [23] where the authors provided the criteria for detecting genuineness in steering scenario for both continuous as well as discrete variable systems. Later two other notions of genuine steering were introduced in [24] mainly for tripartite framework where two parties measurements are fully specified, i.e., one party can control remaining. In this context, the author has also designed genuine steering inequalities to detect genuine tripartite steering. Now speaking of genuine steering nonlocality, it may be interesting to explore the possibility of exploiting the same via some suitable sequential measurement protocol.

To be precise, our present topic of discussion will continue in the direction of analyzing hidden genuine tripartite steering nonlocality in the framework introduced in [24]. For present topic of discussion, we will follow terms and terminologies used in [24]. We will design a protocol involving a sequence of measurements such that initially starting from tripartite states which may not be genuinely steerable, the protocol may generate a genuinely steerable state. Interestingly, the initial states which will be used in the protocol do have a bi-local model [25,26,27].

The paper has organized as follows. In Sect. 2, we have introduced the notion of steering both in bipartite as well as genuine multipartite scenario. Then, in Sect. 3, we have presented suitable sequential operations to achieve the final state. Section 4 contains our main results then discussion.

2 Background

In this section, we are basically going to include a brief detailing of the mathematical tools that will be used in our work.

2.1 Genuine tripartite steering

Firstly, we discuss the criteria of detecting genuine steering [24]. It is true that there are lots of definitions are available in the literature about Genuine steering, we choose one of them.

2.1.1 Formal definition

Correlations P(a, b, c|x, y, z) shared between three parties, say Alice, Bob and Charlie are obtained by performing the measurements x, y, z by Alice, Bob and Charlie, respectively, having outcomes a, b, c. Correlations P(a, b, c|x, y, z) are said to be genuinely steerable [24] from one party, say Charlie to remaining two parties Alice and Bob, if those are inexplicable in the following form:

$$\begin{aligned} P(a,b,c|x,y,z)= & {} \sum _{\lambda }q_\lambda \left[ P(a,b|x,y,\rho _{\mathrm{AB}}(\lambda ))\right] P(c|z,\lambda )\nonumber \\&+\sum _{\lambda }p_{\lambda }P\left( a|x,\rho ^\lambda _a\right) P\left( b|y,\rho ^\lambda _b\right) P(c|z,\lambda ). \end{aligned}$$
(1)

where \(P(a,b|x,y,\rho _{\mathrm{AB}}(\lambda ))\) denotes the nonlocal probability distribution arising from two-qubit state \(\rho ^\lambda _{\mathrm{AB}}\), and \(P(a|x, \rho ^\lambda _{\mathrm{A}})\) and \(P(b|y, \rho ^\lambda _{\mathrm{B}})\) are the distributions arising from qubit states \(\rho ^\lambda _{\mathrm{A}}\) and \(\rho ^\lambda _{\mathrm{B}}\). Here, we want to mention that both the terms of right-hand side of the equation are taken over same \(\lambda \) and \(\sum _{\lambda } q_\lambda +\sum _{\lambda } p_\lambda =1\).

Here, Charlie performs uncharacterized measurement, whereas both Alice and Bob have access to qubit measurements. The tripartite correlation will be called genuinely unsteerable if it is explained by (1) where \(\rho _{\mathrm{AB}}(\lambda )\) is called hidden state for Alice and Bob side. In [24], the author designed detection criteria of tripartite genuine steering (Svetlichny steering), based on Svetlichny inequality [28]. The detection criterion is given in the form of a Bell-type inequality:

$$\begin{aligned} \langle {\mathrm{CHSH}}_{\mathrm{AB}}z_1+{\mathrm{CHSH}}^{\prime }_{\mathrm{AB}}z_0\rangle _{2\times 2\times ?}^{\mathrm{NLHS}}\le 2\sqrt{2}. \end{aligned}$$
(2)

where CHSH\(_{\mathrm{AB}}\) and CHSH\(^{\prime }_{\mathrm{AB}}\) stand for two inequivalent facets defining Bell-CHSH polytope for Alice and Bob and \(\{z_0,z_1\}\) are measurements on Charlie’s part. Here, NLHS stands for nonlocal hidden state, whereas \(2\times 2\times ?\) implies that only two parties (Alice and Bob) have access to qubit measurements but Charlie does not trust his measurement devices and hence are uncharacterized. Alice and bob should have orthonormal measurement settings. If correlations arising due to measurements on any given quantum state (\(\rho \)) violate this inequality (Eq. 2), then that guarantees genuinely steerable of \(\rho \) from Charlie to Alice and Bob. Analogously genuine steerability of \(\rho \) from Bob to Charlie and Alice and that from Alice to Charlie and Bob can be guaranteed, respectively, by violation of the following criteria:

$$\begin{aligned} \langle {\mathrm{CHSH}}_{\mathrm{BC}}x_1+{\mathrm{CHSH}}^{\prime }_{\mathrm{BC}}x_0\rangle _{2\times 2\times ?}^{\mathrm{NLHS}}\le & {} 2\sqrt{2}. \end{aligned}$$
(3)
$$\begin{aligned} \langle {\mathrm{CHSH}}_{\mathrm{AC}}y_1+{\mathrm{CHSH}}^{\prime }_{\mathrm{AC}}y_0\rangle _{2\times 2\times ?}^{\mathrm{NLHS}}\le & {} 2\sqrt{2}. \end{aligned}$$
(4)

Terms CHSH\(_{\mathrm{BC}}\), CHSH\(^{\prime }_{\mathrm{BC}}\), CHSH\(_{\mathrm{AC}}\), CHSH\(^{\prime }_{\mathrm{AC}}\) have analogous definitions. Hence, a state is genuinely steerable from one party to the remaining two parties if it can violate atleast one of these three criteria (Eqs. 2, 3, 4). Now this definition of steering is slightly different from the definition given in [23]. Now we shall discuss how this definition is different from previous definition.

2.1.2 Previous definition

According to the definition by He and Reid [23], the tripartite correlation P(a, b, c|x, y, z) detects genuine steering iff it does not have a decomposition as follows:

$$\begin{aligned} P(a,b,c|x, y, z)&= p_1 \sum _{\lambda } r(\lambda ) P(a|x, \lambda ) P(b, c |y, z, \rho _{\mathrm{BC}}(\lambda )) \nonumber \\&\quad + p_2 \sum _{\lambda } s(\lambda ) P(b|y, \lambda ) P(a, c |x, z, \rho _{\mathrm{AC}}(\lambda )) \nonumber \\&\quad + p_3 \sum _{\lambda } t(\lambda ) P(c|z, \lambda ) P(a, b |x, y, \rho _{\mathrm{AB}}(\lambda )), \end{aligned}$$
(5)

where \(p_1 + p_2 + p_3 =1\), \(\sum _{\lambda } r(\lambda ) = 1\), \(\sum _{\lambda } s(\lambda ) = 1\), \(\sum _{\lambda } t(\lambda ) = 1\). Here, \(P(a|x, \lambda )\) denotes an arbitrary probability distributions arising from LHV \(\lambda \) and \(P(b, c |y, z, \rho _{\mathrm{BC}}(\lambda )) \) denotes the quantum probability of obtaining the outcomes b and c, when measurements y and z are performed by Bob and Charlie, respectively, on the bipartite local hidden state (LHS) \(\rho _{\mathrm{BC}}(\lambda )\) shared between Bob and Charlie. The quantum probability distribution \(P_{\mathrm{Q}}(b, c |y, z, \rho _{\mathrm{BC}}(\lambda )) \) may demonstrate quantum nonlocality, or EPR steering. The other terms are defined similarly.

Note that the definition of genuine tripartite steering by [24] is not equivalent to that by He and Reid [23]. In the above definition by He and Reid, Alice, Bob and Charlie are all assumed to perform characterized measurements at some point in the decomposition given by Eq. (5) (i.e., trusted and untrusted parties are not fixed). One the other hand, we have considered a tripartite steering scenario where the trusted and untrusted parties are fixed. (Alice and Bob are trusted parties and Charlie is untrusted party.) The definition by [24] is applicable in such a tripartite steering scenario where the trusted and untrusted parties are fixed. We have, therefore, used the definition of genuine tripartite steering by [24]. We now discuss about some relevant tools for measuring genuine multipartite entanglement and genuine steering.

2.2 Genuine multipartite concurrence

We briefly now describe \(C_{\mathrm{GM}}\), a measure of genuine multipartite entanglement. For pure n-partite states(\(|\psi \rangle \)), this measure is defined as [29] : \(C_{\mathrm{GM}}(|\psi \rangle ):= min _j\sqrt{2 (1-\Pi _j(|\psi \rangle ))}\) where \(\Pi _j(|\psi \rangle )\) is the purity of \(j^{th}\) bipartition of \(|\psi \rangle \). The expression of \(C_{\mathrm{GM}}\) for X states is given in [30]. For tripartite X states,

$$\begin{aligned} C_{\mathrm{GM}}=2\,max _i\{0,|\gamma _i|-w_i\} \end{aligned}$$
(6)

with \(w_i=\sum _{j\ne i}\sqrt{a_jb_j}\) where \(a_j\), \(b_j\) and \(\gamma _j(j=1,2,3,4)\) are the elements of the density matrix of tripartite X state:

$$\begin{aligned} \begin{bmatrix} a_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \gamma _1 \\ 0 &{} a_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} \gamma _2 &{} 0 \\ 0 &{} 0 &{} a_3 &{} 0 &{} 0 &{} \gamma _3 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} a_4 &{} \gamma _4 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}{\gamma _4}^*&{}b_4 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{}{\gamma _3}^*&{}0 &{} &{} b_3 &{} 0 &{} 0 \\ 0 &{}{\gamma _2}^*&{} 0 &{} 0 &{} 0 &{} 0 &{} b_2 &{} 0 \\ {\gamma _1}^*&{} 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 &{} b_1 \\ \end{bmatrix} \end{aligned}$$

2.3 Genuine steering measure

As we have discussed initially, there is no formal definition of genuine steering, but we can propose a formal measure of genuine steering irrespective of the definitions. First, we define genuine steering measure which is analogous to the bipartite steering measure first described in [31]. This measure is given by the following quantity:

$$\begin{aligned} S_{\mathrm{gen}}(\rho )= \max \left\{ 0,\frac{S_n(\rho )-1}{S_n^{\max }-1}\right\} \end{aligned}$$
(7)

where\(S^{\max }_{n}=\max _\rho S_{n}(\rho )\) and \(S_n(\rho )=\max _\eta S_n(\rho ,\eta )\) with the maximization taken over all measurement settings \(\eta \) and \(0\le S_{\mathrm{gen}}(\rho )\le 1\).

After giving a brief detailing of our mathematical tools, we now proceed with our results. To start with, we design the sequential measurement protocol based on which we observe the enhanced revelation of genuine steering.

3 Revealing multipartite genuine steering

The protocol that we propose here is a stochastic local operation and classical communication (SLOCC) protocol which consists of two stages: preparation stage and measurement stage. We name this protocol as sequential measurement protocol. A detailed sketch of the protocol is given below:

3.1 Brief outline of the protocol

Sequential measurement protocol Three spatially separated parties (say, \(A_i;i=1,2,3\)) are involved in this protocol. n number of tripartite quantum states can be distributed among them. None of these states violate genuine steering inequality [24]. As each party holds one particle from each of the n tripartite states hence each of the parties holds n number of particles.

3.1.1 Preparation stage

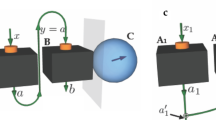
  • In the preparation stage, every party can perform some joint measurement on their respective \(n-1\) particles and then broadcast the results to others (Fig. 1).

  • At the end of measurements by all the three parties, a tripartite quantum state shared among \(A_1\), \(A_2\) and \(A_3\) is generated. Clearly this final state is always prepared depending upon the measurement results obtained by the parties in the previous step.

Fig. 1
figure 1

Schematic diagram for preparation and measurement stage

Full size image

3.1.2 Measurement stage

  • In the measurement stage, all the three parties can perform any projective measurement in arbitrary directions. But in this stage they are not allowed to communicate among themselves.

  • After measurements they can generate a tripartite correlation so that they can verify that this correlation can violate the genuine steering inequality.

We refer to this protocol of sequential measurements by the three parties sharing n states as a sequential measurement protocol (SMP).

Having sketched the protocol we now give examples of some families of tripartite states which when used in this network, reveal genuine steering for some members of these families. Such an observation is supported with an increase in the amount of genuine steering, guaranteed by the measure of steering \(S_{\mathrm{gen}}(\rho )\) (Eq. 7).

Let the three initial states be given by:

$$\begin{aligned} \rho _1 = p_1 |\psi _f\rangle \langle \psi _f|+(1- p_1)|001\rangle \langle 001| \end{aligned}$$
(8)

with \(|\psi _f\rangle =\cos \theta _1|000\rangle +\sin \theta _1|111\rangle \), \(0\le \theta _1\le \frac{\pi }{4}\) and \(0\le p_1\le 1\);

$$\begin{aligned} \rho _2= p_2 |\psi _m\rangle \langle \psi _m|+(1-p_2)|010\rangle \langle 010| \end{aligned}$$
(9)

with \(|\psi _m\rangle =\frac{|000\rangle +|111\rangle }{\sqrt{2}}\) and \(0\le p_2\le 1\);

$$\begin{aligned} \rho _3= p_3 |\psi _l\rangle \langle \psi _l|+(1-p_3)|100\rangle \langle 100| \end{aligned}$$
(10)

with \(|\psi _l\rangle =\sin \theta _3|000\rangle +\cos \theta _3|111\rangle \), \(0\le \theta _1\le \frac{\pi }{4}\) and \(0\le p_1\le 1\). In this context it may be noted that the three initial states have Svetlichny bi-local model under projective measurement for the following restricted range of state parameters:

  • For first state (\(\rho _1\)) : \(p_1 \le \frac{1}{(1 + \sin [2\theta _1])}\);

  • Second state (\(\rho _2\)) : \(p_2 \le \frac{1}{2}\) ;

  • Third state (\(\rho _3\)) : \(p_3 \le \frac{1}{(1 + \sin [2\theta _3])}\).

Each of the three parties \(A_1\), \(A_2\) and \(A_3\) performs Bell basis measurements on their respective particles. Depending on a particular output of all the measurements (here \(|\psi ^{\pm }\rangle =\frac{|01\rangle \pm |10\rangle }{\sqrt{2}}\)), a resultant state \(\rho _4^{\pm }\) is obtained which after correcting the phase term is given by:

$$\begin{aligned} \rho _4 = \frac{p_3 |\phi \rangle \langle \phi | + (1 - p_3)\sin ^2 \theta _1|100\rangle \langle 100|}{\sin ^2 \theta _1+ p_3 \cos 2\theta _1 \sin ^2 \theta _3 } \end{aligned}$$
(11)

where \(|\phi \rangle = \cos \theta _1 \sin \theta _3|000\rangle + \sin \theta _1 \cos \theta _3 |111\rangle \).

Clearly \(\rho _4\) is independent of \(p_1\) and \(p_2\). Interestingly, \(\rho _4\) can also be generated for some other combination of sequential operations on some different arrangement of particles between the parties \(A_i(1,2,3)\) and for different output of Bell measurement. For the initial states \(\rho _i\)\((i = 1, 2, 3)\), the amount of genuine entanglement are given by

$$\begin{aligned} C^{\rho _1}_{\mathrm{GM}}= & {} p_1 \sin 2\theta _1 ,\\ C^{\rho _2}_{\mathrm{GM}}= & {} p_2 \end{aligned}$$

and

$$\begin{aligned} C^{\rho _3}_{\mathrm{GM}} = p_3 \sin 2\theta _3 \end{aligned}$$
(12)

whereas that of \(\rho _4\) is given by

$$\begin{aligned} C^{\rho _4}_{\mathrm{GM}} = \frac{p_3 \sin 2\theta _1\sin 2\theta _3 }{2(\sin ^2 \theta _1+ p_3 \cos 2\theta _1 \sin ^2 \theta _3)}. \end{aligned}$$
(13)

Equation (12) indicates that the initial states \(\rho _i(i=1,2,3)\) are genuinely entangled for any nonzero value of the state parameters .

The maximum value of the genuine steering operators (\(S_i\)) (Eq. 2) under projective measurements, for state \(\rho _i(i=1,2,3)\) is given by:

$$\begin{aligned} S_1= & {} \max \left[ 2\, p_1\sin 2\theta _1, \frac{1}{\sqrt{2}}\sqrt{((1-p_1-p_1 {\mathrm{Cos}}[2 \theta _1])^2+(p_1 {\mathrm{Sin}}[2\theta _1])^2}\right] ,\\ S_2= & {} \max \left[ 2\, p_2, \frac{1}{\sqrt{2}}\sqrt{((1-p_2)^2+(p_2)^2)}\right] \,\,\,\, \end{aligned}$$

and

$$\begin{aligned} S_3 = \max \left[ 2\, p_3\sin 2\theta _3, \frac{1}{\sqrt{2}}\sqrt{((1-p_3+p_3 {\mathrm{Cos}}[2 \theta _3])^2+(p_3 {\mathrm{Sin}}[2\theta _3])^2} )|\right] , \end{aligned}$$
(14)

respectively, whereas that for the final state \(\rho _4\), it is given by

$$\begin{aligned} S_4= & {} \max \left[ \frac{\,p_3 \sin 2\theta _1\sin 2\theta _3}{\sin ^2 \theta _1+ p_3 \cos 2\theta _1 \sin ^2 \theta _3}, \right. \nonumber \\&\left. \frac{\sqrt{2} \sqrt{(1-p_3+p_3 {\mathrm{Cos}}[2 \theta _3]-{\mathrm{Cos}}[2 \theta _1])^2+(p_3 {\mathrm{Sin}}[2 \theta _1] {\mathrm{Sin}}[2\theta _3])^2}}{2-2(1-p_3){\mathrm{Cos}}[2 \theta _1]-p_3{\mathrm{Cos}}[2(\theta _1-\theta _3)]-p_3 {\mathrm{Cos}}[2(\theta _1+\theta _3)]}\right] .\qquad \end{aligned}$$
(15)

3.1.3 Result: observation

It is clear from the maximum value of genuine steering operator (Eqs. 14, 15) and the measure of entanglement (Eqs. 12, 13) of both initial states and final state, that each of them does not violate genuine steering inequalities (Eqs. 2, 3, 4) for \(C^{\rho _i}_{\mathrm{GM}}\le \frac{1}{2}(i=1,2,3,4).\)

Thus to observe genuine steering revelation, there should exist some fixed values of the parameters of the three initial Sveltlichny bi-local states with \(C^{\rho _i}_{\mathrm{GM}}\le \frac{1}{2}\) such that the final state can have \(C^{\rho _4}_{\mathrm{GM}}>\frac{1}{2}\). Interestingly, we get such states from the families of the initial states \(\rho _1\) (Eq. 8), \(\rho _2\) (Eq. 9) and \(\rho _3\) (Eq. 10).

For example, let \(\theta _1=0.1\), \(p_1\le 0.509 \) , \(p_2\le \frac{1}{2}\), \(\theta _3=0.1\) and \(p_3\in [0,0.83426]\). Then, each of the initial states have Svetlichny bi-local model (moreover one can show that these models are \(NS_2\) local [25,26,27]) and \(C^{\rho _i}_{\mathrm{GM}}\le \frac{1}{2}\). Thus, they do not violate genuine steering inequalities (Eqs. 2, 3, 4).

But when used in our protocol (Sect. 3), they can generate a state \(\rho _4\) (with \(C^{\rho _4}_{\mathrm{GM}}>\frac{1}{2}\)) which exhibits genuine steering by violating genuine steering inequalities for \(p_3 \ge 0.33557\). This guarantees revelation of genuine steering for \(p_3 \in [0.33557,0.83426]\). So initially each of these three states are unable to exhibit genuine steering but after the sequential measurements are taken into account they can violate that genuine steering inequality. Now a pertinent question would be whether one can quantify this revelation of genuine steering as observed in our protocol. We deal with this question in the next subsection.

3.2 Result: enhancement of the genuine steering measure

In this part, we show that the prescribed protocol indeed enhances a measure of genuine steering in the resulting state. The amount of genuine steering for the three initial states is:

$$\begin{aligned} S_{\mathrm{gen}}(\rho _1)= & {} \max \{0,2\, p_1\sin 2\theta _1-1\},\nonumber \\ S_{\mathrm{gen}}(\rho _2)= & {} \max \{0,2\, p_2-1\},\nonumber \\ S_{\mathrm{gen}}(\rho _3)= & {} \max \{0,2\, p_3\sin 2\theta _3-1\} \end{aligned}$$
(16)

whereas for the final states the genuine steerable quantity takes the form:

$$\begin{aligned} S_{\mathrm{gen}}(\rho _4)= \max \left\{ 0,\frac{p_3 \sin 2\theta _1\sin 2\theta _3}{\sin ^2 \theta _1+ p_3 \cos 2\theta _1 \sin ^2 \theta _3}-1\right\} \end{aligned}$$
(17)

If we take \(p_1=p_3\) and \(\theta _1=\theta _3\) then for any values of \(p_1\) and \(\theta _1\) the final state is more genuinely steerable than the initial ones.

4 Conclusion

Genuine steering nonlocality, being a weaker notion of genuine nonlocality is considered to be a resource in various practical tasks. So apart from its theoretical importance, revelation of such a resource under any protocol that allows only classical communication and shared randomness is of immense practical importance. Motivated by that we have attempted to design a SLOCC protocol which demonstrates revelation of ‘hidden’ genuine steering. Our discussion in a restricted sense guarantees the fact that under suitable measurements by the parties involved in the network, our protocol is sufficient to show genuine steering even from some quantum states which have bi-local models. However, under our protocol each of the parties having two particles perform Bell basis measurements and the remaining parties perform projective measurements. In brief, this protocol enables one to go beyond the scope of existing witnesses of genuine steering and thus demonstrate genuine steering for a larger class of multipartite states. In this context, it will be interesting to consider more generalized measurement settings by the parties which may be yielding better results.