1 Introduction

Quantum coherence as the most fundamental quantum feature originates from the quantum state superposition principle which is closely related to the other quantum features such as entanglement, quantum discord, quantum non-locality. Recently, quantum coherence has been widely studied in the point of resource theory of view [1,2,3,4,5,6,7]. Roughly speaking, the quantum features could be dominated by the systematic quantum coherence to some extent. However, the superposition in quantum mechanics does not always play the expected role. It could ensure the existence of some quantum feature, while it could also lead to the coherent destruction. The obvious example is the vanishing entanglement for the superposition of two Bell states with equal amplitudes. A mathematically general treatment on the effects of superposition for the quantum entanglement was first addressed in Ref. [8] which shows von Neumann entropy entanglement of a superposition state is well limited by the entanglement of the superposed states. Later, how the entanglement of a superposition state is distributed among its components was studied extensively [9,10,11,12,13,14,15,16,17,18,19,20]. Due to the close relationship between quantum coherence and general quantum features, it is natural to consider how the quantum feature is distributed among the different components of the superposition state or whether we can give a reference evaluation of the quantum feature for the superposition state based on the features of each component.

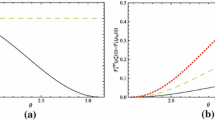
In both classical and quantum physics, the parameter estimation (PE) is a central task . Quantum Fisher information (QFI) as an important quantity in PE [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35] can bound the measurement accuracy for some parameters by the remarkable Cramé r–Rao inequality [21] which shows that the larger QFI means higher sensitivity of the PE. Since the pioneer work [22] showed that the precision of phase estimation can beat the shot-noise limit (standard quantum limit), lots of works aiming to improve the measurement accuracy have been done in different aspects such as the PE based on maximally correlated states [26, 36], N00N states [27,28,29], squeezed states [30, 32], or generalized phase-matching condition [33] , and so on. In particular, enormous effects have been devoted to how to improve the precision of PE in the open systems within the Markovian [34] or non-Markovian regimes [35], especially including various environments [37,38,39,40,41,42,43,44,45,46,47,48]. One of the common implications in the relevant jobs mentioned above is that the quantum features in PE procedure could provide a powerful means to enhancing QFI, which directly leads to the significant consideration that how to effectively exploit the quantum features in quantum metrology [29, 43, 44, 49,50,51,52,53,54,55,56,57]. However, such a research in a relatively general PE process is not so easy due to the practically limited computability, especially in the open systems despite its good definition. Only in some particular cases, the QFI can be easily evaluated. Recently, Escher et al. [31] proposed an upper bound \(C_{Q} \) for the QFI in a general protocol to estimate an unknown parameter depicted in Fig. 1, if one Kraus representation of the quantum channel is provided. Of course, the optimization on all the Kraus representations to the quantum channel could reach the upper bound \(C_Q\) and give another definition of the QFI. Considering the Cramér–Rao inequality, one can find that \(C_Q\) actually contributes to the lower bound of the precision of the PE similar to the QFI. In this sense, within a particular measurement protocol, it can effectively avoid the concrete calculation of QFI and be of great significance to consider \(C_Q\) instead of QFI.

In this paper, we mainly consider the general protocol in Fig. 1 and study how \(C_Q\) for the superposition input state is distributed among its superposed components. It is found that \(C_Q\) of the superposition state is well upper and lower bounded by the \(C_Q\) of the superposed components. As applications, we study distribution of \(C_Q\) by considering a qubit superposition state undergoes the depolarization channel, dephasing channel and the amplitude damping channel, respectively. The numerical results validate our bounds. The paper is organized as follows. In Sect. 2, after a brief introduction of QFI, we present our main result about the bounds on \(C_Q\). In Sect. 4, we consider the case with a qubit undergoing various quantum channels. The conclusion is drawn finally.

Fig. 1
figure 1

Quantum parameter estimation process: 1. the initial state preparation; 2. the parametric process via dynamical evolution; 3. the measurement of quantum state; 4. the parameter estimation

Full size image

2 The parameter estimation and the quantum Fisher information

2.1 The Fisher information

Figure 1 shows a general quantum process to estimate an unknown parameter \(\theta \). In the above scheme, the measurement precision of \(\theta \) is characterized by the uncertainty of the estimated phase \(\theta ^{est}\) defined by

$$\begin{aligned} \delta \theta =\left\langle \left( \frac{\theta ^{est}}{\left| \partial \left\langle \theta ^{est}\right\rangle /\partial \theta \right| } -\theta \right) ^{2}\right\rangle ^{1/2} \end{aligned}$$
(1)

which, for an unbiased estimator, is just the standard deviation [23, 24, 58]. Based on the quantum parameter estimation [23, 24, 58], \(\delta \theta \) is limited by the quantum Cramér–Rao bound as

$$\begin{aligned} \left( \delta \theta \right) ^{2}\ge \frac{1}{NF_{Q}}, \end{aligned}$$
(2)

where \(F_{Q}=\mathrm {Tr}\{\rho _{\theta }L_{\theta }^{2}\}\) is the quantum Fisher information with \(L_{\theta }\) being the symmetric logarithmic derivative defined by [23]

$$\begin{aligned} 2\partial _{\theta }\rho (\theta )=L_{\theta }\rho (\theta )+\rho (\theta )L_{\theta }. \end{aligned}$$
(3)

It was shown in Refs. [23, 24, 58] that this bound can always be reached asymptotically by maximum likelihood estimation and a projective measurement in the eigen basis of the “symmetric logarithmic derivative operator.”

In a closed system, if the preparation of the initial state is a pure state \( \rho _{0}=\left| \varphi \right\rangle \left\langle \varphi \right| \), and the dynamic evolution process is unitary evolution \(\hat{U}(\theta )\), then \(F_{Q}\) can be expressed as [31]

$$\begin{aligned} F_{Q}[\hat{U}(\theta )\rho _{0}\hat{U}^{\dagger }(\theta )]=4\left\langle \varDelta \hat{H}^{2}\right\rangle , \end{aligned}$$
(4)

where

$$\begin{aligned} \left\langle \varDelta \hat{H}^{2}\right\rangle \equiv [\left\langle \varphi \right| \hat{H}^{2}(\theta )\left| \varphi \right\rangle -\left\langle \varphi \right| \hat{H}(\theta )\left| \varphi \right\rangle ^{2}] \end{aligned}$$
(5)

with \(\hat{H}=i(\mathrm{d}\hat{U}^{\dagger }(\theta )/\mathrm{d}\theta )\hat{U}(\theta )\). It is obvious that the Fisher information is equivalent to the variance of \(2 \hat{H}\).

In the open system, namely, the initial state pure state \(\rho _{0}=\left| \varphi \right\rangle \left\langle \varphi \right| \) undergoes the non-unitary evolution governed by the arbitrary Kraus operators \(\hat{\varPi }_{l}(x)\) as \(\rho (\theta )\equiv \sum \limits _{l}\hat{\varPi }_{l}(\theta )\rho _{0}\hat{\varPi }_{l}^{\dagger }(\theta )\), it can be found in [31] that the quantum Fisher information \(F_{Q}\) is upper bounded by \(C_{Q}\) defined as [31]

$$\begin{aligned} C_{Q}(\rho _{0})=4\left[ \left\langle \hat{H}_{1}(\theta )\right\rangle -\left\langle \hat{H}_{2}(\theta )\right\rangle ^{2}\right] , \end{aligned}$$
(6)

with

$$\begin{aligned} \hat{H}_{1}(\theta )= & {} \sum \limits _{l}\frac{\mathrm{d}\hat{\varPi }_{l}^{\dagger }(\theta ) }{\mathrm{d}\theta }\frac{\mathrm{d}\hat{\varPi }_{l}(\theta )}{\mathrm{d}\theta }, \end{aligned}$$
(7)
$$\begin{aligned} \hat{H}_{2}(\theta )= & {} i\sum \limits _{l}\frac{\mathrm{d}\hat{\varPi }_{l}^{\dagger }(\theta ) }{\mathrm{d}\theta }\hat{\varPi }_{l}(\theta ). \end{aligned}$$
(8)

In particular, it is shown that the exact Fisher information in the open system can be obtained by

$$\begin{aligned} F_{Q}[\rho (\theta )]=\min _{\{\hat{\varPi }_{l}(\theta )\}}C_{Q}[\rho _{0},\hat{ \varPi }_{l}(\theta )], \end{aligned}$$
(9)

where the minimization is taken over all possible Kraus representations that achieve \(\rho (\theta )\).

2.2 Bound on Fisher information of superposition

Let us consider the scheme depicted in Fig. 1. For a initial pure state \( \left| \psi \right\rangle \), a parameter x is imposed on the state by a dynamic procedure \(\hat{\varPi }_{l}(x)\); then, the final state can be denoted by \(\rho (x)=\sum \limits _{l}\hat{\varPi }_{l}(x)\left| \psi \right\rangle \left\langle \psi \right| \hat{\varPi }_{l}^{\dagger }(x)\). We can measure some observable to evaluate the parameter x. It is obvious that \(C_{Q}\) for this parameter x is given by

$$\begin{aligned} C_{Q}(\left| \psi \right\rangle )=4[\left\langle \hat{H}_{1}(x)\right\rangle _{\psi }-\left\langle \hat{H}_{2}(x)\right\rangle _{\psi }^{2}], \end{aligned}$$
(10)

where \(\hat{H}_{1}(x)\) and \(\hat{H}_{2}(x)\) are defined as Eqs. (7) and (8) for x instead of \(\theta \) and we use the subscript \( \psi \) to label the initial state. Now we suppose the initial state is a superposition state as \(\left| \psi \right\rangle =\sum _{i=1}^{N}\alpha _i \left| \psi _i\right\rangle \). Then we would like to study how \( C_{Q}\left( \left| \psi \right\rangle \right) \) is distributed among the components \(\left| \psi _i\right\rangle \). Thus we will present our main result in the following rigorous form.

Theorem 1

Let the superposition state \(\left| \psi \right\rangle =\sum \limits _{i=1}^{N}\alpha _{i}\left| \psi _{i}\right\rangle \) with \(\sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}=1\) undergoes the dynamics given in Fig. 1, where x is the parameter to be measured, and then \(C_{Q}\left( \left| \tilde{\psi } \right\rangle \right) \) is bounded by

$$\begin{aligned} B_{-}\le \Vert \left| \psi \right\rangle \Vert ^{2}C_{Q}\left( \left| \tilde{\psi }\right\rangle \right) \le B_{+}, \end{aligned}$$
(11)

where, \(\left| \tilde{\psi }\right\rangle =\frac{\left| \psi \right\rangle }{\Vert \left| \psi \right\rangle \Vert }\) with \(\Vert \left| \psi \right\rangle \Vert \) representing the \(l_{2}\) norm of a vector,

$$\begin{aligned} B_{-}=\max \{0,b_{-}\},B_{+}=b_{+}, \end{aligned}$$
(12)

with

$$\begin{aligned} b_{\pm }= & {} \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}C_{Qi}+E_{\pm }(x)+F(x), \end{aligned}$$
(13)
$$\begin{aligned} E_{\pm }(x)= & {} \pm 8\sum _{i<j}\left| \alpha _{i}\alpha _{j}\right| \sqrt{\left| \left\langle \hat{H}_{1}(x)\right\rangle _{i}\left\langle \hat{H}_{1}(x)\right\rangle _{j}\right| } \nonumber \\&+\frac{4}{\Vert \left| \psi \right\rangle \Vert ^{2}}\left[ \left| \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{ H}_{2}(x)\right\rangle _{i}\right| \right. \nonumber \\&\mp \left. \sum _{i<j}2\left| \alpha _{i}\alpha _{j}\right| \sqrt{ \left| \left\langle \hat{H}_{2}(x)\right\rangle _{i}\left\langle \hat{H} _{2}(x)\right\rangle _{j}\right| }\right] ^{2}, \end{aligned}$$
(14)

and

$$\begin{aligned} F(x)=4\sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H}_{2}(x)\right\rangle _{i}^{2}. \end{aligned}$$
(15)

Proof

According to the definition of \(C_{Q}\), we can write \(C_{Q}\) of the state \(\left| \psi \right\rangle \) as

$$\begin{aligned} C_{Q}(\left| \tilde{\psi }\right\rangle )= & {} 4\left[ \left\langle \hat{H}_{1}(x)\right\rangle _{\tilde{\psi }}-\left\langle \hat{H}_{2}(x)\right\rangle _{\tilde{\psi }}^{2}\right] \nonumber \\= & {} 4\left[ \frac{1}{\Vert \left| \psi \right\rangle \Vert ^{2}}\left\langle \hat{H}_{1}(x)\right\rangle _{\psi }-\frac{1}{\Vert \left| \psi \right\rangle \Vert ^{4}}\left\langle \hat{H}_{2}(x)\right\rangle _{\psi }^{2}\right] , \end{aligned}$$
(16)

or

$$\begin{aligned} \Vert \left| \psi \right\rangle \Vert ^{2}C_{Q}(\left| \tilde{\psi } \right\rangle ) =4\left[ \left\langle \hat{H}_{1}(x)\right\rangle _{\psi }-\frac{1}{\Vert \left| \psi \right\rangle \Vert ^{2}}\left\langle \hat{H}_{2}(x)\right\rangle _{\psi }^{2}\right] . \end{aligned}$$
(17)

The expansion of the two items of \(\left\langle \hat{H}_{1}(x)\right\rangle _{\psi }\) and \(\left\langle \hat{H}_{2}(x)\right\rangle _{\psi }^{2}\) read

$$\begin{aligned} \left\langle \hat{H}_{1}(x)\right\rangle _{\psi } =\sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H}_{1}(x)\right\rangle _{i} +\sum _{i\ne j}\alpha _{i}^{*}\alpha _{j}\left\langle \hat{H} _{1}(x)\right\rangle _{ij}, \end{aligned}$$
(18)

and

$$\begin{aligned} \left\langle \hat{H}_{2}(x)\right\rangle _{\psi }^{2} =\left( \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H}_{2}(x)\right\rangle _{i} +\sum _{i\ne j}\alpha _{i}^{*}\alpha _{j}\left\langle \hat{H} _{2}(x)\right\rangle _{ij}\right) ^{2}. \end{aligned}$$
(19)

where \(\left\langle X\right\rangle _{ij}=\left\langle \psi _{i}\right| X\left| \psi _{j}\right\rangle \) and \(\left\langle X\right\rangle _{i}=\left\langle \psi _{i}\right| X\left| \psi _{i}\right\rangle \) for any X. Substituting Eqs. (18) and (19) into Eq. (17), one can find

$$\begin{aligned} \Vert \left| \psi \right\rangle \Vert ^{2}C_{Q}\left( \left| \tilde{\psi } \right\rangle \right)= & {} 4\left[ \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H}_{1}(x)\right\rangle _{i}+\sum _{i\ne j}\alpha _{i}^{*}\alpha _{j}\left\langle \hat{H}_{1}(x)\right\rangle _{ij} \right. \nonumber \\&\left. -\frac{1}{\Vert \left| \psi \right\rangle \Vert ^{2}}\left( \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H} _{2}(x)\right\rangle _{i}+\sum _{i\ne j}\alpha _{i}^{*}\alpha _{j}\left\langle \hat{H}_{2}(x)\right\rangle _{ij}\right) ^{2}\right] .\nonumber \\ \end{aligned}$$
(20)

Based on the definition of \(C_{Q}\), one can also find

$$\begin{aligned} \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}C_{Qi}=4\sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left[ \left\langle \hat{H}_{1}(x)\right\rangle _{i}-\left\langle \hat{H}_{2}(x)\right\rangle _{i}^{2}\right] . \end{aligned}$$
(21)

Substituting Eq. (21) into Eq. (20), we have

$$\begin{aligned} \Vert \left| \psi \right\rangle \Vert ^{2}C_{Q}\left( \left| \tilde{\psi } \right\rangle \right)= & {} \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}C_{Qi}+\,4\sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H}_{2}(x)\right\rangle _{i}^{2} \nonumber \\&+\,4\sum _{i\ne j}\alpha _{i}^{*}\alpha _{j}\left\langle \hat{H} _{1}(x)\right\rangle _{ij} \nonumber \\&-\,\frac{4}{\Vert \left| \psi \right\rangle \Vert ^{2}}\left[ \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H}_{2}(x)\right\rangle _{i}+\sum _{i\ne j}\alpha _{i}^{*}\alpha _{j}\left\langle \hat{H}_{2}(x)\right\rangle _{ij}\right] ^{2}.\nonumber \\ \end{aligned}$$
(22)

For an observable measurement X, we can always get

$$\begin{aligned} \alpha _{i}^{*}\alpha _{j}\left\langle X\right\rangle _{ij}+\alpha _{i}\alpha _{j}^{*}\left\langle X\right\rangle _{ji}\le 2\left| \alpha _{i}\alpha _{j}\right| \sqrt{\left| \left\langle X\right\rangle _{i}\left\langle X\right\rangle _{j}\right| }, \end{aligned}$$
(23)

which is directly from the absolute value inequality \(\sum a_{i}\le \left| \sum a_{i}\right| \le \sum \left| a_{i}\right| \) and the Cauchy inequality of the number \(a_{i}\). Thus Eq. (22) can be rewritten as

$$\begin{aligned} \Vert \left| \psi \right\rangle \Vert ^{2}C_{Q}\left( \left| \tilde{\psi } \right\rangle \right)\ge & {} \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}C_{Qi}+4\sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H}_{2}(x)\right\rangle _{i}^{2} \nonumber \\&-8\sum _{i<j}\left| \alpha _{i}\alpha _{j}\right| \sqrt{\left| \left\langle \hat{H}_{1}(x)\right\rangle _{i}\left\langle \hat{H} _{1}(x)\right\rangle _{j}\right| }\nonumber \\&+\frac{4}{\Vert \left| \psi \right\rangle \Vert ^{2}}\left[ \left| \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H}_{2}(x)\right\rangle _{i}\right| \right. \nonumber \\&+\left. \sum _{i<j}2\left| \alpha _{i}\alpha _{j}\right| \sqrt{ \left| \left\langle \hat{H}_{2}(x)\right\rangle _{i}\left\langle \hat{H}_{2}(x)\right\rangle _{j}\right| }\right] ^{2}. \end{aligned}$$
(24)

Similarly, based on Eq. (23), one can also find the following inequality holds. That is,

$$\begin{aligned} \Vert \left| \psi \right\rangle \Vert ^{2}C_{Q}\left( \left| \tilde{\psi } \right\rangle \right)\le & {} \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}C_{Qi} \nonumber \\&+\,8\sum _{i<j}\left| \alpha _{i}\alpha _{j}\right| \sqrt{ \left| \left\langle \hat{H}_{1}(x)\right\rangle _{i}\left\langle \hat{H} _{1}(x)\right\rangle _{j}\right| } \nonumber \\&+\,4\sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H}_{2}(x)\right\rangle _{i}^{2}+\frac{4}{\Vert \left| \psi \right\rangle \Vert ^{2}}\left[ \left| \sum \limits _{i=1}^{N}\left| \alpha _{i}\right| ^{2}\left\langle \hat{H}_{2}(x)\right\rangle _{i}\right| \right. \nonumber \\&-\sum _{i<j}\left. 2\left| \alpha _{i}\alpha _{j}\right| \sqrt{ \left| \left\langle \hat{H}_{2}(x)\right\rangle _{i}\left\langle \hat{H}_{2}(x)\right\rangle _{j}\right| }\right] . \end{aligned}$$
(25)

Equations (24) and (25) complete the proof. \(\square \)

3 Applications

In order to demonstrate the validity of the bounds, we will consider the bound on a initial superposition state of a qubit undergoing the dephasing quantum channel, the amplitude damping channel and the depolarization channel, respectively [59].

The initial pure state can be formally given by

$$\begin{aligned} \left| \psi \right\rangle =\alpha \left| \psi _{1}\right\rangle +\beta \left| \psi _{2}\right\rangle , \end{aligned}$$
(26)

with \(\left| \alpha \right| ^{2}+\left| \beta \right| ^{2}=1\) , where \(\left| \psi _{1}\right\rangle \) and \(\left| \psi _{2}\right\rangle \) will be given in the concrete computation. So the final state after going through various channels can be written as \(\rho (P)=\sum \limits _{l}\hat{\varPi }_{l}(P)\left| \psi \right\rangle \left\langle \psi \right| \hat{\varPi }_{l}^{\dagger }(P)\) with P denoting the measured parameter that is imposed by the channels. Thus based on our theorem, one can calculate \(C_{Q}\left( \left| \psi \right\rangle \right) \) and its corresponding two bounds.

Dephasing channel We first consider the dephasing channel which is described by the Kraus operators \(M_{\mu }\) \((\mu =0,1,2)\) as

$$\begin{aligned} M_{0}= & {} \sqrt{1-P}\left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array} \right) ,M_{1}=\sqrt{P}\left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 0 \end{array} \right) , \nonumber \\ M_{2}= & {} \sqrt{P}\left( \begin{array}{cc} 0 &{} 0 \\ 0 &{} 1 \end{array} \right) . \end{aligned}$$
(27)

The initial superposition state is given by

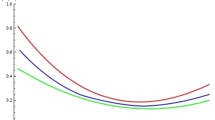
$$\begin{aligned} \left| \psi \right\rangle =\alpha \left| \psi _{1}\right\rangle +\beta \left| \psi _{2}\right\rangle \end{aligned}$$
(28)

with the randomly generated \(\left| \psi _{1}\right\rangle =[0.9838;0.1795]\); \(\left| \psi _{2}\right\rangle =[0.4186;0.9082]\). In addition, we set \(\alpha =-0.3690\) and \(\beta =0.9294\). The final state after the action of the dephasing channel is denoted by \(\rho (P)\). The Fisher information \(F(\rho (P))\) and its upper bound \(C_{Q}\left( \left| \psi \right\rangle \right) \) are plotted in Fig. 2. It can be found that the Fisher information is upper bounded by \(C_Q\). We especially plot the upper and lower bounds of \(C_{Q}\) in Fig. 2. It is shown that \(C_{Q}\) is well restricted by the two bounds, which, at the same time, indicates the two bounds we obtained are valid.

Fig. 2
figure 2

The QFI, \(C_{Q}\) and the bounds \(B_\pm \) versus the estimated parameter P

Full size image

Depolarized channelThe depolarized channel is given by

$$\begin{aligned} M_{0}= & {} \sqrt{1-P}\sigma _{0},M_{1}=\sqrt{\frac{P}{3}}\sigma _{1}, \nonumber \\ M_{2}= & {} \sqrt{\frac{P}{3}}\sigma _{2},M_{3}=\sqrt{\frac{P}{3}}\sigma _{3}. \end{aligned}$$
(29)

The final state after \(\rho _{0}\) undergoing the evolution of quantum channel is given by

$$\begin{aligned} \rho ^{\prime }=M_{0}\rho _{0}M_{0}^{\dagger }+M_{1}\rho _{0}M_{1}^{\dagger }+M_{2}\rho _{0}M_{2}^{\dagger }+M_{3}\rho _{0}M_{3}^{\dagger }. \end{aligned}$$
(30)

Similarly, we consider two initial states \(\left| \psi _1\right\rangle =[0.8301;0.5579]\) and \(\left| \psi _2\right\rangle =[0.9777;0.2101]\) with \(\alpha =-0.3463\) and \(\beta =0.9381\). Thus similar to Fig. 2, we plot various quantities in Fig. 3. We can find that our theorem has provided the good upper and lower bounds.

Fig. 3
figure 3

The QFI, \(C_{Q}\) and the bounds \(B_\pm \) versus the estimated parameter P

Full size image

Amplitude damping quantum channelFinally, we also consider the amplitude damping quantum channels given by

(31)

Here we consider two initial state randomly generated by MATLAB as \(\left| \psi _1\right\rangle =[0.3706;0.9288]\) and \(\left| \psi _2\right\rangle =[0.8951;0.4459]\). The superposition amplitude is randomly chosen as \(\alpha =0.0495+0.0752i\) and \(\beta =-0.9929\). We plot the bounds of \(C_Q\) and Fisher information in Fig. 4. Our good bounds can also be observed from Fig. 4.

Fig. 4
figure 4

The QFI, \(C_{Q}\) and the bounds \(B_\pm \) versus the estimated parameter P

Full size image

Finally, we would like to emphasize that all the considered states and the relevant parameters are produced randomly by MATLAB. The tightness of our bounds depends on these states and parameters \(\alpha \) and \(\beta \). In particular, one can find that in Fig. 4, the lower bound \(B_-\) and the Fisher information \(F_Q\) intersect with each other for some particular P. This phenomenon could appear in all the three kinds of quantum channels if we choose other initial states or different \(\alpha \) and \(\beta \). This does not affect the validity of our two bounds on \(C_Q\). It only indicates that in some cases the lower bound \(B_-\) is not so tight as we expected. In other words, it only shows the state dependence of the bounds and the Fisher information.

4 Discussion and conclusion

In this paper, we consider how the superposition input state affects the quantum Fisher information in a general quantum parameter estimation scheme. We obtain that \(C_{Q}\) for the case with the superposition input state can be well bounded by the \(C_Q\)’s corresponding to the cases with each superposed components as input state. Considering \(C_{Q}\) as the compact bound on quantum Fisher information, the upper and lower bounds on \(C_{Q}\) allow us to better evaluate how quantum Fisher information is distributed among its superposed components, which could help us to predict the bound on the maximum accuracy for a parameter estimation process. How the QFI instead of \(C_Q\) is distributed in a general case is a much more interesting question which deserves us forthcoming efforts.