1 Introduction

The Quantum Information Theory and Quantum Computation are hot topics that are the theoretical basis of Quantum Computers, which are described as computer technology of the future and intended to operate at very high speeds.

Quantum Fisher Information, a version of Fisher Information, developed for quantum systems, has also become a highly studied subject in recent years, as it also measures the sensitivity that systems can provide for phase sensitive tasks [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36, 40, 43, 44].

Quantum Fisher Information (QFI) is a very useful concept for analyzing situations that require phase sensitivity. This feature has attracted attention and extends the classical Fisher Information. Especially for systems with a higher QFI value, the accuracy is more clearly achieved; For example, clock synchronization [41] and quantum frequency standards [42]. Although some of the pure entangled systems may exceed the classical limit, this does not apply to all entangled systems [37]. The interaction between the quantum system and the environment not only reduces entanglement but also reduces the system’s Quantum Fisher Information, in general. So we can say that researching quantum systems on QFI is important for the progress of quantum technologies. In recent studies, a single parameter, χ 2 parameter, phase sensitivity was added to measure only the self-knowledge of the system under investigation [12]. Since a condition of χ 2 < 1 is not provided for a general quantum system, it is understood that the system has multiple entanglement and this system provides better phase accuracy than a separable system. These quantum systems are called “useful” systems in the literature. For two-level N-particle quantumsystems, the Cramer-Rao limit is defined by the following formula [38, 39]:

$$ {\Delta} \phi_{QCB}\equiv \frac{1}{\sqrt {N_{m}F}} $$
(1)

where N m is the number of experiments on the system being measured and F is the Quantum Fisher Information value. We can write 3-dimensional vectors normalized in the nth direction of angular momentum operators, J n , Pauli matrices as follows:

$$ J_{\vec{n}}=\sum\limits_{\alpha =x,y,z} {\frac{1}{2}n_{\alpha} \sigma_{\alpha} } $$
(2)

For J n , the Fisher Information of the ρ quantum system can be expressed in a symmetric matrix C [10]:

$$ F\left( {\rho ,J_{\vec{n}} } \right)=\sum\limits_{i\ne j} {\frac{2\left( {p_{i} -p_{j}} \right)^{2}}{p_{i} +p_{j}} } \left| \left\langle i \right| J_{\vec{n}} \left| j \right\rangle^{2} \right|=\vec{n} C\vec{n}^{T} $$
(3)

where p i and |i〉 represent the eigenvalues and eigenvectors of the ρ system, respectively, and the matrix C is defined as

$$ C_{kl} =\sum\limits_{i\ne j} {\frac{\left( {p_{i} -p_{j}} \right)^{2}}{p_{i} +p_{j}} } \left[ \left\langle i \right| J_{k} \left| j \right\rangle \left\langle j \right| J_{i} \left| i \right\rangle +\left\langle i \right| J_{i} \left| j \right\rangle \left\langle j \right|J_{k} \left| i \right\rangle \right] $$
(4)

The largest F value between the N options is selected and averaged over N particles. The Fisher Information value is calculated as the greatest eigenvalue of the C matrix. This definition is expressed by the equation:

$$ \overline{F}_{\max} =\frac{1}{N}\underset{\vec{{n}}}{\max}~ F(\rho ,J_{\vec{{n}}} )=\frac{\lambda_{\max} } {N}. $$
(5)

2 Quantum State with Arbitrary Relative Phase and Reported Results

In this section, we introduce N qubit systems in decoherence channels. Particularly the system studied is superposition of a W and a GHZ state [7] and,

$$ \left| \boldsymbol{\varphi}^{\boldsymbol{N}} \right\rangle =\boldsymbol{\alpha} \,\boldsymbol{e}^{\boldsymbol{i}\boldsymbol{\mu}}\left| {\boldsymbol{GHZ}^{\boldsymbol{N}}} \right\rangle + \boldsymbol{\beta} \boldsymbol{e}^{\boldsymbol{i\nu}}\left| {\boldsymbol{W}^{\boldsymbol{N}}} \right\rangle +\boldsymbol{\gamma} \left| {\overline{\boldsymbol{W}}^{\boldsymbol{N}}} \right\rangle $$
(6)

Here N is the number of qubits, and α, β and γ are the superposition coefficient. In this work, we consider the case for N = 3,4 a n d 5. Here \(\boldsymbol {\beta } =\sqrt {\mathbf {1}-(\boldsymbol {\alpha } ^{\mathbf {2}}+\boldsymbol {\gamma }^{\mathbf {2}})} \) and \(\overline {\boldsymbol {W}}\) is the W state in which Pauli spin matrix (α X ) is applied to each qubit. The decoherence channels are amplitude damping (ADC), phase damping (PDC) and depolarizing (DPC) respectively. Then we study the QFI of the N qubit systems for different scenarios. As a first scenario, we take the superposition coeffients α = 0.6 and relative phase parameters μ = π and ν = −π/9 and γ is variable in (0, 0.8) interval and we apply ADC to systems |φ 3〉 , |φ 4〉 , and |φ 5〉. In Fig. 1, changes in QFI values per particle for ADC are showed.

Fig. 1
figure 1

Changes in QFI per particle for ADC with changing p values (Red: N = 3, Blue: N = 4, Green: N = 5)

Full size image

In the second scenario, we apply PDC the same system with same values. In Fig. 2, changes in QFI values per particle for PDC are shown.

Fig. 2
figure 2

Changes in QFI per particle for PDC with changing p values (Red: N = 3, Blue: N = 4, Green: N = 5)

Full size image

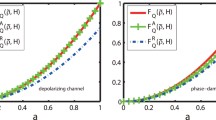
In the third scenario, we apply DPC the same system with same values. In Fig. 3, changes in QFI values per particle for DPC are shown.

Fig. 3
figure 3

Changes in QFI per particle for DPC with changing p values (Red: N = 3, Blue: N = 4, Green: N = 5)

Full size image

In APC scenario, we see minimum points for all N values for value of p =∼ 0.65. Until this point QFI per particle decreases and after it increases. For all N values, even if there is a minimum QFI per particle remains greater than ∼0,15 value. We can say that this quantum system is more resistant to APC noise than the others.

In PDC scenario, the QFI per particle values are always decreasing, the minimum is for p = 1 for each value of N. For the system N = 3, it is significantly more resistant to PDC noise than the systems for values N = 4 and N = 5.

In DPC scenario, the QFI per particle values are always decreasing and surprisingly DPC destroys completely QFI after values p =∼0.8 for each value of N.

In the fourth scenario, we find the QFI per particle as functions of γ and p. Surprisingly the QFI per particle values remains the same when γ values change. This is an important result observed during this study.

In Fig. 4, we show in 3D plot, the changes of QFI per particle values under each decoherence channel for values N = 3, N = 4 and N = 5, respectively.

Fig. 4
figure 4

QFI values as function of γ and p (3D plot)

Full size image

3 Conclusion

We studied the changes in QFI values for a useful quantum system state which is a superposition of W N and GHZ N states where N = 3, 4 and 5. In this work, we extended this problem for the mentioned arbitrary phased system and we observed the changes of QFI values/per particle in amplitude damping, phase damping and depolarizing channels. We showed the changes in QFI depending on noise parameters and superposition coefficient. Surprisingly the QFI per particle values remains the same when γ values change. DPC destroys completely QFI after values p =∼0.8 for each value of N. And studied quantum system is more resistant to APC noise than the others.