1 Introduction

In this paper, we study spontaneous decay of a laser-driven two-level atom which is coupled to the electromagnetic field in the vacuum state. This is a very simple problem with a solution that is universally well known, yet is complex enough that it allows us to make full use of the features a quantum computer provides. This combination gives us the opportunity to assess the performance of the quantum computer on a real-world problem.

The techniques that we use to discretize the quantum stochastic differential equation [15] that describes the interaction between the two-level atom and the laser field are very well known [2, 5, 6, 17, 18, 22]. The discretized model consists of a repeated unitary interaction of the two-level atom with subsequent slices of the field, parametrized by a discretization parameter \(\lambda \). The repeated interaction model easily leads to a quantum stochastic difference equation that has the QSDE we wish to simulate as its limit as \(\lambda \) goes to zero. Note that in the discretized model, the unitarity of the interaction is preserved. This is a very desirable feature: e.g., after every time evolution step, probabilities will always take values between 0 and 1. Furthermore, this unitarity allows us to easily map the interaction on unitary gates in a quantum computer.

The motivation for the work we present here is twofold and aimed at a future in which computers with more and more reliable qubits are accessible:

  1. 1.

    We wish to emphasize that quantum optics might prove to be a very fruitful field of application for early quantum computers. It is well known how to discretize the type of problems that arise in quantum optics and the resulting quantum stochastic difference equations are easily implemented on a quantum computer, using standard quantum gates. Moreover, the field of quantum optics historically contains many interesting problems and techniques that can serve as interesting benchmark problems for early quantum computers.

  2. 2.

    Furthermore, on a quantum computer we can do a fully coherent simulation of a system in interaction with the electromagnetic field. That is, on a large enough quantum computer, we can simulate the complete unitary that describes the interaction between system and field. This puts us past standard analyses using master equations or quantum filtering equations [3, 4, 8, 10] because we also have a complete description of the field to our availability. This could be very useful if we wish to simulate non-Markovian networks of systems interacting at different points with the same field, possibly containing fully coherent feedback loops [11, 12].

The remainder of this paper is organized as follows. Section 2 introduces the QSDE that we wish to simulate on a quantum computer: a laser-driven two-level atom in interaction with the vacuum electromagnetic field. We discuss repeated unitary interaction models, the resulting quantum stochastic difference equations and discuss how to take the limit to obtain quantum stochastic differential equations [2, 5, 6, 18, 22]. Next, we introduce the repeated interaction that leads to the QSDE corresponding to the system under study. Section 3 then describes how we have implemented the repeated interaction model of Sect. 2 on the IBMqx4 Tenerife quantum computer [16].

Section 4 presents the results of our simulations. We compute the reduced dynamics of the two-level atom from the simulation results and compare it to the dynamics given by the theoretical master equation, derived from the underlying discrete model. We also compute the conditional dynamics of the two-level atom conditioned on both counting photons in the field and observing a field quadrature in the field and compare the results to the quantum filtering equations derived from the underlying discrete model [6, 7, 13, 14]. Reproducing the correct quantum filtering equations would give an indication that the quantum computer also reproduces the correlation between the field and the two-level atom correctly.

In Sect. 5, we formulate some conclusions from our results. It should be noted that currently only very limited simulations can be done due to the small number of reliable qubits in the quantum computers that are currently available. In a 5-qubit machine such as the IBMqx4, there are only 4 qubits available to represent the field, severely limiting the simulation capabilities. The work in this paper should be seen through the lens of a hoped-for strong increase in the computing capacity in the near future.

2 Quantum stochastic difference equations

We will now first introduce the problem that we will be studying in this paper. We consider a two-level atom in interaction with an electromagnetic field. We will let the two-level atom be driven by a laser. We will not model the laser by an additional channel in the field that is in an coherent state, but instead will directly introduce the Rabi oscillations induced by the laser field as a Hamiltonian term in the QSDE. We will use the following notation throughout the paper: \(\sigma _x, \sigma _y\) and \(\sigma _z\) are the standard Pauli matrices. Furthermore, \(\sigma _+\) and \(\sigma _-\) are the raising and lowering operator matrices of the two-level atom, respectively. The interaction of the laser-driven two-level atom with the vacuum electromagnetic field is then given by the following quantum stochastic differential equation (QSDE) in the sense of [15]

$$\begin{aligned} \hbox {d}U_t= & {} \left\{ \sqrt{\kappa }\sigma _- \hbox {d}A_t^* - \sqrt{\kappa }\sigma _+ \hbox {d}A_t -\frac{1}{2}\kappa \sigma _+\sigma _- \hbox {d}t - i\omega \sigma _+ \sigma _- \hbox {d}t \right. \nonumber \\&-\left. i\frac{\Omega }{2} \sigma _y \hbox {d}t \right\} U_t, \quad U_0 = I, \end{aligned}$$
(1)

where \(\kappa \) is the decay rate, \(\omega \) is the transition frequency of the two-level atom and \(\Omega \) is the frequency of the Rabi oscillations originating from the interaction of a classical laser field with the atomic spin. We note that a QSDE, such as Eq. (1), allows a very concrete representation in terms of Maassen’s integral–sum kernels [19] on the Guichardet space. We will, however, not follow this approach in this paper and instead refer the interested reader to [20, 23] for more details.

In order to implement Eq. (1) on a quantum computer, we first need to introduce the discrete models (see, e.g., [6] for a detailed introduction) that in a suitable limit will converge to a quantum stochastic differential equation [2, 5, 18, 22] such as Eq. (1). To this end we first define a time interval [0, T]. This time interval is divided into N equal sub-intervals of length T / N. We define \(\lambda := \sqrt{T/N}\), i.e., there are N time slices of length \(\lambda ^2\). With each time slice we associate a two-level quantum system representing the slice of the (truncated) field that interacts with the two-level atom at that moment. In this way we obtain a repeated interaction

$$\begin{aligned} U(l) = \overleftarrow{\prod }_{i = 1}^l M_i = M_l M_{l-1}\ldots M_2M_1, \ \ \ \ 1 \le l \le N. \end{aligned}$$
(2)

Here \(M_i\) is a unitary operator that couples the two-level atom and the ith field slice which is here also represented by a two-level system. Note that for the problem studied in this paper, all \(M_i\)’s are identical apart from the fact that they all act on their own slice of the field. Furthermore, we will let the \(M_i\)’s be a function of \(\lambda \), such that if \(\lambda \) goes to 0 (i.e., N goes to infinity) the individual \(M_i\)’s converge to the identity map I. That is, we will get more and more interactions, each having smaller and smaller effect.

We now introduce linear operators \(M^\pm , M^+, M^-\) and \(M^0\) [6], acting on the two-level atom Hilbert space, in such a way that we have the following decomposition

$$\begin{aligned} M_i - I = M^\pm \otimes \Delta \Lambda (i) + M^+\otimes \Delta A^*(i) + M^- \otimes \Delta A(i) + M^0 \otimes \Delta t(i), \end{aligned}$$
(3)

where the discrete quantum noises (see, e.g., [6]) are given by

$$\begin{aligned} \Delta \Lambda (i):= & {} (\sigma _+ \sigma _-)_i, \quad \Delta A^*(i) := \lambda (\sigma _+)_i, \\ \Delta A(i):= & {} \lambda (\sigma _-)_i,\quad \Delta t(i) := \lambda ^2 I_i. \end{aligned}$$

Note that this decomposition uniquely defines the coefficients \(M^\pm , M^+, M^-\) and \(M^0\). and note that these coefficients are all a function of \(\lambda \). We leave this dependency on \(\lambda \), as well as the tensor products in Eq. (3), implicit in order to keep the notation light.

We can now write Eq. (2) as the following quantum stochastic difference equation (see, e.g., [6])

$$\begin{aligned} \begin{aligned} \Delta U(l)&:= U(l)-U(l-1) \\&= \Big \{M^\pm \Delta \Lambda (l) + M^+\Delta A^*(l) + M^- \Delta A(l) + M^0 \Delta t(l)\Big \}U(l-1), \end{aligned} \end{aligned}$$
(4)

where \(1 \le l \le N\) and \(U(0) = I\). We now have the following theorem due to Parthasarathy [22] (weak convergence), Lindsay and Parthasarathy [18] (weak convergence of the quantum flow) and Attal and Pautrat [2] (strong convergence uniform on compact time intervals). We state the theorem without giving the precise meaning of the mode of convergence of the repeated interaction model to the unitary solution of the QSDE because we would need to introduce further mathematical details that would make us stray too far from the main narrative of this article (see however [2], or [5]).

Theorem 2.1

(Parthasarathy [22], Lindsay and Parthasarathy [18], Attal and Pautrat [2]) Suppose the following limits exist:

$$\begin{aligned} \begin{aligned} S&:= \lim _{\lambda \rightarrow 0} M^\pm + I, \quad L := \lim _{\lambda \rightarrow 0} M^+ \\ L^\dag&:= \lim _{\lambda \rightarrow 0} - M^-S^*, \quad H := \lim _{\lambda \rightarrow 0} i M^0 + \frac{i}{2} L^* L, \end{aligned} \end{aligned}$$
(5)

then it follows that S is unitary, \(L^\dag \) is the adjoint of L, i.e., \(L^* = L^\dag \), H is self-adjoint and \(U([t/\lambda ^2])\) (where the brackets [ ] stand for rounding down to an integer) converges to a unitary \(U_t\) given by the following QSDE

$$\begin{aligned} \hbox {d}U_t = \left\{ (S-I)\hbox {d}\Lambda _t + LdA_t^* - L^*SdA_t - \frac{1}{2}L^*Ldt - iHdt\right\} U_t, \quad U_0 = I.\nonumber \\ \end{aligned}$$
(6)

We proceed by guessing an interaction unitary \(M_i\) in the repeated interaction Eq. (2) and check via Theorem 2.1 that it leads to the correct limit coefficients to reproduce in the limit our system of interest which is given by Eq. (1). Note that there are several choices for \(M_i\) that will lead to the correct limit system. We will take the following \(M_i\) and will show that it indeed leads to Eq. (1) in the limit \(\lambda \rightarrow 0\):

$$\begin{aligned} \begin{aligned}&M_i{ } = \exp \Big (\sqrt{\kappa }\sigma _-\otimes \lambda \sigma _+ - \sqrt{\kappa }\sigma _+\otimes \lambda \sigma _-\Big ) \exp \Big ( -i \omega \sigma _+\sigma _-\otimes \lambda ^2 I_i\Big ) \exp \Big ( -i \frac{\Omega }{2} \sigma _y \otimes \lambda ^2 I_i\Big ) \\&\,= \tiny \begin{pmatrix} e^{ {-}i \omega \lambda ^2}\cos \left( \frac{\Omega \lambda ^2}{2}\right) &{}\qquad {-}e^{ {-}i \omega \lambda ^2}\sin \left( \frac{\Omega \lambda ^2}{2}\right) &{}\qquad 0 &{}\qquad 0 \\ \cos (\sqrt{\kappa }\lambda )\sin \left( \frac{\Omega \lambda ^2}{2}\right) &{}\qquad \cos (\sqrt{\kappa }\lambda )\cos \left( \frac{\Omega \lambda ^2}{2}\right) &{}\qquad e^{ {-}i \omega \lambda ^2} \sin (\sqrt{\kappa }\lambda )\cos \left( \frac{\Omega \lambda ^2}{2}\right) &{}\qquad {-}e^{ {-}i \omega \lambda ^2} \sin (\sqrt{\kappa }\lambda )\sin \left( \frac{\Omega \lambda ^2}{2}\right) \\ {-}\sin (\sqrt{\kappa }\lambda )\sin \left( \frac{\Omega \lambda ^2}{2}\right) &{}\qquad {-}\sin (\sqrt{\kappa }\lambda )\cos \left( \frac{\Omega \lambda ^2}{2}\right) &{}\qquad e^{ {-}i \omega \lambda ^2}\cos (\sqrt{\kappa }\lambda )\cos \left( \frac{\Omega \lambda ^2}{2}\right) &{}\qquad {-}e^{ {-}i \omega \lambda ^2}\cos (\sqrt{\kappa }\lambda )\sin \left( \frac{\Omega \lambda ^2}{2}\right) \\ 0 &{}\qquad 0 &{}\qquad \sin \left( \frac{\Omega \lambda ^2}{2}\right) &{}\qquad \cos \left( \frac{\Omega \lambda ^2}{2}\right) \\ \end{pmatrix}. \end{aligned}\nonumber \\ \end{aligned}$$
(7)

A short calculation then reveals

$$\begin{aligned} \begin{aligned}&M^0 = \begin{pmatrix} \frac{e^{ -i \omega \lambda ^2}\cos (\sqrt{\kappa }\lambda )\cos \left( \frac{\Omega \lambda ^2}{2}\right) -1}{\lambda ^2} &{} \frac{-e^{ -i \omega \lambda ^2}\cos (\sqrt{\kappa }\lambda )\sin \left( \frac{\Omega \lambda ^2}{2}\right) }{\lambda ^2} \\ \frac{ \sin \left( \frac{\Omega \lambda ^2}{2}\right) }{\lambda ^2} &{} \frac{\cos \left( \frac{\Omega \lambda ^2}{2}\right) -1}{\lambda ^2} \\ \end{pmatrix}, \\&M^- = \begin{pmatrix} \frac{-\sin (\sqrt{\kappa }\lambda )\sin \left( \frac{\Omega \lambda ^2}{2}\right) }{\lambda } &{} \frac{-\sin (\sqrt{\kappa }\lambda )\cos \left( \frac{\Omega \lambda ^2}{2}\right) }{\lambda }\\ 0 &{} 0 \end{pmatrix}, \\&M^+ = \begin{pmatrix} 0 &{} 0 \\ \frac{e^{ -i \omega \lambda ^2} \sin (\sqrt{\kappa }\lambda )\cos \left( \frac{\Omega \lambda ^2}{2}\right) }{\lambda } &{} \frac{-e^{ -i \omega \lambda ^2} \sin (\sqrt{\kappa }\lambda )\sin \left( \frac{\Omega \lambda ^2}{2}\right) }{\lambda } \end{pmatrix}, \\&M^\pm = \begin{pmatrix} e^{ -i \omega \lambda ^2}\big (1-\cos (\sqrt{\kappa }\lambda )\big )\cos \left( \frac{\Omega \lambda ^2}{2}\right) &{} e^{ -i \omega \lambda ^2}(\cos (\sqrt{\kappa }\lambda )-1)\sin \left( \frac{\Omega \lambda ^2}{2}\right) \\ (\mathrm{cos}(\sqrt{\kappa }\lambda ) - 1)\sin (\frac{\Omega \lambda ^2}{2}) &{} (\cos (\sqrt{\kappa }\lambda )-1)\cos \left( \frac{\Omega \lambda ^2}{2}\right) \\ \end{pmatrix}. \end{aligned} \end{aligned}$$
(8)

Using the definitions of S, L and H in Eq. (5), we find

$$\begin{aligned}\begin{aligned}&S = I, \ \ \ \ L = \sqrt{\kappa } \sigma _- , \ \ \ \ H = \omega \sigma _+ \sigma _- + \frac{\Omega }{2}\sigma _y. \end{aligned} \end{aligned}$$

That is, we have found a repeated interaction model that converges to the QSDE of Eq. (1).

Note that S converges to the identity I, which means that the gauge term \(\hbox {d}\Lambda _t\) does not survive in the limiting QSDE Eq. (1), which is as it should be. Note, however, that it is possible to start with unitary repeated interaction models in the sense of Eq. (2) that do have a limit with a non-trivial gauge term present. Examples can be found in [2, 5]. Furthermore, note that since the \(M_i\)’s in Eq. (2) are unitary, it is always possible to implement them with a quantum circuit [21] (i.e., also in the case when we would have non-trivial gauge terms).

Fig. 1
figure 1

Calculated expectation values for the Pauli spin operators for the two-level atom, using parameters \(\kappa =1\), \(\omega =0\) and \(\Omega =12\). Results are plotted for the master equation Eq. (9), and calculations on the actual IBMqx4 Tenerife quantum computer. The results of the master equation are obtained using a time step \(\lambda ^2=0.01\). The IBMqx4 curve consists of collected results of experiments with time steps \(\lambda ^2=0.16\), 0.14, and 0.10, each averaged over 10,240 runs

Full size image
Fig. 2
figure 2

Time evolution of the expectation value of the Pauli \(\sigma _z\) operator of the two-level atom, in the homodyne detection scheme, for the four trajectories that have accumulated the most statistics. The trajectory is given by the title above the plots, which shows \(\Delta Y\). The filter equation results are from Eqn (11). The IBMqx4 results are averaged over 10,240 runs. The simulator results are obtained from the IBM Qiskit simulator, using the same quantum assembly code that was used on the IBMqx4 Tenerife computer, and are averaged over 102,400 runs

Full size image
Fig. 3
figure 3

As Fig. 2, for the \(\sigma _x\) operator

Full size image
Fig. 4
figure 4

As Fig. 2, for the \(\sigma _y\) operator

Full size image
Fig. 5
figure 5

Time evolution of the expectation value of the Pauli \(\sigma _z\) operator of the two-level atom, in the photon counting scheme, for the case where no photons were detected (0000), and where a single photon was detected after the fourth (0001), third (0010), second (0100) and first (1000) time step. The filter equation results are from Eq. (12). The IBMqx4 results are averaged over 10,240 runs. The simulator results are obtained from the IBM Qiskit simulator, using the same quantum assembly code that was used on the IBMqx4 Tenerife computer, and are averaged over 102,400 runs

Full size image
Fig. 6
figure 6

As Fig. 5, for the \(\sigma _x\) operator

Full size image
Fig. 7
figure 7

As Fig. 5, for the \(\sigma _y\) operator

Full size image

3 The quantum circuit

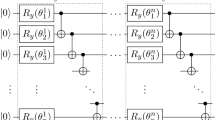
The various contributions to the interaction between the atom and the field, given in Eq. (7), can easily be mapped to elementary quantum gates. The following quantum circuit [21] implements this interaction for a single time slice:

figure a

The Open QASM [9] code implementing this circuit on the IBMqx4 Tenerife quantum computer is given by:

figure b

In this code, the atom state is stored in qubit 2, and the state of the electromagnetic field slice in qubit 0.

For modeling multiple time slices, different qubits are used to describe the field at different times, and coupled to the atom qubit. Currently, this limits the simulation to a maximum of four time slices on the IBMqx4 computer. If operations based on classical bits were enabled, we could reuse the same qubit for the field by measuring this qubit, and rotating it back to its \(| 0\rangle \) state when the outcome is 1. Unfortunately, this is currently only implemented in simulators and not in real hardware.

At the end of the simulation, all qubits (both field and atom) were measured. The atom was measured in the x, y, and z basis, whereas the field qubits were measured in the x and z basis. The calculations were executed on both the IBMqx4 Tenerife quantum computer and the IBM Qiskit [1] simulator. Statistics were collected over 10,240 runs for each combination of measurement directions of atom and field on the IBMqx4 quantum computer, and over 102,400 runs in the simulator.

In all simulations we performed, the transition frequency \(\omega \) was taken to be zero for simplicity.

4 Results

4.1 Master equation

The repeated interaction model given by Eq. (7) leads to the following discrete time master equation [6, Eqn 4.3, p. 265] for the state \(\rho _l\) of the two-level atom:

$$\begin{aligned} \Delta \rho _l := \rho _l - \rho _{l-1} =\mathcal {L}(\rho _{l-1})\lambda ^2,\ \ \ \ \rho _0 = \begin{pmatrix} 0 &{} 0 \\ 0 &{} 1\end{pmatrix}, \end{aligned}$$
(9)

where the discretized Lindblad operator is given by [6, Eqn 4.4, p. 265]

$$\begin{aligned} \mathcal {L}(\rho ) := M^+ \rho {M^+}^* + \lambda ^2 M^0 \rho {M^0}^* + M^0\rho + \rho {M^0}^*. \end{aligned}$$
(10)

Here \(M^+\) and \(M^0\) are given by Eq. (8). Figure 1 compares the theoretical results given by the master equation Eq. (9) and the results obtained with the IBMqx4 Tenerife quantum computer.

4.2 Homodyne quantum filter

We now turn to the situation where we are not simply tracing over the field, but condition on observations made in the field. Suppose that for \(l = 1,2,3,4\), we have observed \(\lambda *\sigma _x\) in the field:

$$\begin{aligned} \Delta Y(l) := \lambda * \hbox {``the outcome of the\ } \sigma _x \text{-measurement } \text{ of } \text{ the } l\hbox {th field qubit''}. \end{aligned}$$

Physically, this corresponds to the case where we observe the field with a homodyne detection setup after the interaction with the two-level atom. We can condition the time evolution of the density matrix on an observed homodyne photo current detection record. The conditioned density matrix obeys the following discrete quantum filtering equation for homodyne detection [6, Section 5.2, p. 274]

$$\begin{aligned} \Delta \rho _l= & {} \mathcal {L}(\rho _{l-1})\lambda ^2 + \frac{\mathcal {J}(\rho _{l-1})- \text{ tr }[\mathcal {J}(\rho _{l-1})] \Big ( \rho _{l-1}+\lambda ^2\mathcal {L}(\rho _{l-1})\Big )}{1-\lambda ^2 \text{ tr }[\mathcal {J}(\rho _{l-1})]^2} \nonumber \\&\times \Big (\Delta Y(l) -\, \text{ tr }[\mathcal {J}(\rho _{l-1})]\lambda ^2\Big ), \end{aligned}$$
(11)

where \(\mathcal {L}\) is given by Eq. (10) and \(\mathcal {J}\) and the initial state \(\rho _0\) are given by

$$\begin{aligned} \mathcal {J}(\rho ) := M^+\rho + \rho {M^+}^* + \lambda ^2M^+\rho {M^0}^* + \lambda ^2M^0 \rho {M^+}^*, \quad \rho _0= \begin{pmatrix} 0 &{}\quad 0 \\ 0 &{}\quad 1\end{pmatrix}, \end{aligned}$$

Here \(M^+\) and \(M^0\) are given by Eq. (8). Figures 2, 3 and 4 compare the theoretical results given by the quantum filter equation Eq. (11) and the results obtained with the IBM Qiskit simulator and the IBMqx4 Tenerife quantum computer.

4.3 Counting quantum filter

Finally, we turn to the situation where we condition on having observed \(\sigma _+\sigma _-\) in the field for \(l=1,2,3,4\). That is, we have the following observations:

$$\begin{aligned} \Delta Y(l) = \frac{1 + \hbox {``the outcome of the\ } \sigma _z \text{-measurement } \text{ of } \text{ the } l\hbox {th field qubit''}}{2}. \end{aligned}$$

Physically, this corresponds to the case where we observe the field with a photo detector after the interaction with the two-level atom. We can condition the time evolution of the density matrix on an observed photo detection record. The conditioned density matrix obeys the following discrete quantum filtering equation for photon counting [6, Section 5.3, p. 276]

$$\begin{aligned} \begin{aligned} \Delta \rho _l{ }&= \mathcal {L}(\rho _{l-1})\lambda ^2 + \frac{\frac{M^+\rho _{l-1}{M^+}^*}{\text{ tr }[\rho _{l-1} {M^+}^* M^+]} - \rho _{l-1}-\lambda ^2\mathcal {L}(\rho _{l-1})}{1-\lambda ^2 \text{ tr }[\rho _{l-1} {M^+}^* M^+]} \\&\quad \times \Big (\Delta Y(l) - \text{ tr }[\rho _{l-1} {M^+}^* M^+]\lambda ^2\Big ), \\ \rho _0{ }&= \begin{pmatrix} 0 &{}\quad 0 \\ 0 &{}\quad 1\end{pmatrix}. \end{aligned} \end{aligned}$$
(12)

Here \(M^+\) is given by Eq. (8). Figures 5, 6 and 7 compare the theoretical results given by the quantum filter equation Eq. (12) and the results obtained with the IBM Qiskit simulator and the IBMqx4 Tenerife quantum computer.

5 Conclusion

In this paper we have shown that it is fairly straightforward to implement quantum stochastic differential equations on a quantum computer. The mathematical theory [2, 5, 6, 17, 18, 22] behind the necessary discretization of the equations is well worked out and easily translated into a quantum circuit. Even with the very limited capacity of the currently available quantum computers, it is possible to simulate some simple quantum optical features described by a QSDE (e.g., a Rabi oscillation).

We have also seen that the filter equations are to a large extent correctly reproduced on the IBMqx4 Tenerife quantum computer, although agreement becomes progressively worse as the number of quantum gates increases. This provides confidence that the (quantum) correlations between the atom and the field are accounted for correctly. This opens the door to fully coherent simulations of systems that interact with the field at different points, even including fully coherent feedback loops [11, 12]. Naturally, this is only feasible when quantum computers are available with more and more reliable qubits.

As can be seen in Figures 5 and 6, the time evolution between counts in the photon counting scheme seems to be accounted for correctly; however, the jump operation does not seem to be accurate to the theory. This can be understood though: there are relatively few jumps and there is already quite a bit of noise on the results when the field is in the vacuum state. This means there is an identity component in the jump operator that leads to a deviation from the theory. Note that in principle, it is possible to incorporate the additional noise into a phenomenological model of the computer.

With respect to the discrete quantum filtering equations [6], we note that they completely coincide with the IBM Qiskit simulator results. However, they are much less computationally intensive and could still be used if the number of qubits is larger than the simulator can deal with. Note, however, that in the simulator it is also possible to recycle the field qubits after they have been measured. This is currently not yet possible on the real IBMQ hardware.

As a final note, we would like to remark that in this paper we have only considered gate-based quantum computation with super conducting qubits as made available through the cloud by IBMQ. Master equations and filtering equations (stochastic Schrödinger equations) have also been used to study other platforms such as quantum annealing, see, e.g., [24].

It will be interesting to see future quantum computers simulate more complex benchmark problems originating from quantum optics.