1 Introduction

In order to prevent the contents of messages exchanged in group communications from revealing, some form of encryption must be used. Therefore, the communicating parties should first agree upon a shared secret key which can then be used to implement a classical private key cryptosystem and communicate securely. One approach to establish such a shared key is through a key distribution (KD) protocol where one of the participants, usually called the key distribution center (KDC), determines the key alone and distributes it securely among others. This approach might appear efficient and practical; however, the security in a KD protocol might be circumvented by a KDC who, out of some malicious grounds (such as commercial, political, or military benefit) might send a faulty key to some parties. Even a fully trusted KDC may impose serious issues: It introduces a single point of failure, a performance bottleneck, and is an attractive target for adversaries. Moreover, it might be simply unacceptable for a single party to generate the group key. For example, each party may need assurance that the resulting group key is fresh and random. Centralized key distribution may not even be a feasible choice for environments with no hierarchy of trust, for example, a group composed of members in competing organizations or countries. All in all, assuming a fixed distribution center is a poor assumption for highly dynamic environments [1]. Therefore, we might require the involvement of all group members for constructing the secret key. The cryptographic primitive which allows a group of participants to cooperatively derive a common secret key is called a key agreement (KA) protocol. Although the security of KA protocols is no longer jeopardized by a malicious chairperson sending fake values, they still suffer from other insider attacks. Here, a malicious group member may try to exclude honest participants from the group by sending faulty messages in such a way that victim members obtain flawed keys. In this regard, it is essential for any KA protocol to withstand participants attacks and ensure that such malicious attempts would not go unnoticed. The first classical KA was introduced by Deffie and Hellman in 1976 [2] to enable two users to interact with each other and jointly contribute to a negotiating key. The security of this scheme is based on the intractability of what is called the discrete logarithm (DL) problem. Since then lots of KA protocols have appeared in the literature with the same security assumptions. However, along with growing computing power and development of quantum computers, classical KA protocols are facing severe challenges. For the special case of DLP-based schemes, in 1997, Shor introduced polynomial-time quantum algorithms for discrete logarithm [3] and prime factorization problems. These two quantum algorithms clearly established that neither the RSA protocol nor the DH-based KA protocols would remain secure if a scalable quantum computer is built. Unlike the classic case, the security of quantum versions of KD and KA protocols, known, respectively, as quantum key distribution (QKD) and quantum key agreement (QKA) is simply based on physical principles such as Heisenberg uncertainty principle and quantum no-cloning theorem. The first QKA scheme was introduced by Zhou et al. in 2004 [4] using quantum teleportation. However, in 2009, Tsai and Hwang [5] showed that this quantum teleportation-based protocol suffers from a weakness. They showed that a particular user can completely determine the final (shared) key without being detected. In [6,7,8,9], one can find other examples of QKA protocols, all limited to the two-party case.

Recently, Sun et al. [10] proposed an innovative and efficient multiparty QKA based on commutative encryption which can be applied for arbitrary number of participants. They compared their protocol with [11,12,13] and showed that it is more efficient in terms of the number of used qubits. The novelty of Sun et al.’s protocol mostly lies in the fact that it does not need any entangled states or unitary operation and that the (highly efficient) rotation operation is used to implement commutative encryption. Each participant uses secret private angles for encrypting his photons, and at the end, all participants determine the shared secret key simultaneously. As for security, the authors of [10] first show that their scheme withstands outside attacks. They claim that no malicious participant can influence the final shared key so that their scheme is secure against inside attacks. The goal of this paper is to show that this claim is not true. We prove that any participant can prohibit legitimate parties from obtaining the final shared key and remain completely unnoticed.

The rest of this paper is organized as follows: The QKA scheme of Sun et al. is reviewed in Sect. 2 and its cryptanalysis is explained in Sect. 3. Section 4 explains our proposed improvement to guard against the attack. Finally, concluding remarks are provided in Sect. 5.

2 Review of the Sun et al.’s multiparty quantum key agreement protocol

In this section, we use the following notations to briefly review Sun et al.’s scheme.

N:

The number of participants

\({P_0}\ldots {P_{N - 1}}\) :

The participants

K:

The final shared key

n:

The bit-length of the shared secret key

\({K_i} = ({k_{i,1}}\ldots {k_{i,n}}),0 \le i < N\) :

The main secret key of participant i

\({\theta _i} = (\theta _1^i,\ldots ,\theta _n^i),0 \le \theta _j^i < \pi \) :

The axillary secret key of participant i

\(\left| {{K_i}} \right\rangle = \left| {{k_{i,1}}} \right\rangle \left| {{k_{i,2}}} \right\rangle \ldots \left| {{k_{i,n}}} \right\rangle \) :

Encoding \(K_i\) into n photon

\({E_{k}}[\left| \psi \right\rangle ]\) :

Encryption of state \(\left| \psi \right\rangle \) with key k

\({D_{k}}[C]\) :

Decryption of C with key k

\(EXor_{{K_j}}[\left| {{K_i}} \right\rangle ] = \left| {{K_i} \oplus {K_j}} \right\rangle \) :

See Remark in this section

\(ins\_d(\left| {{K_i}} \right\rangle )\) :

Inserting decoy states randomly in \(\left| {{K_i}} \right\rangle \)

annc(i):

The announcement of \(P_i\)

\(M[\left| \psi \right\rangle ]\) :

Measuring state \(\left| \psi \right\rangle \) in basis \(\{ \left| 0 \right\rangle ,\left| 1 \right\rangle \} \)

Let \(P = \{ {P_0},{P_1},\ldots ,{P_{N - 1}}\} \) be the set of participants who want to run the protocol and generate a secret shared key. The participants are arranged on a ring such that \({P_{i - 1}}\) and \({P_{i+1}}\) are the left and right neighbors of \({P_{i}}\), respectively, \(\{ 0 \le i < N\} \). All indices through this paper are computed mod N, i.e., \({P_{i \pm N}} = {P_i}\) for all \(\{ 0 \le i < N\} \). The members of P want to derive the secret shared key K as the XOR of their individual secret keys, i.e., \(K = {K_0} \oplus \ldots \oplus {K_{N - 1}}\).

In this protocol, the commutative encryption of Reference [14] is used to protect participant’s keys. Note that binary data can be encoded by using horizontal and vertical polarization (i.e., the horizontally polarized photon \(\left| 0 \right\rangle \) represents zero in a binary representation and the vertically polarized photon \(\left| 1 \right\rangle \) represents one). Now, to encrypt these polarized photons, rotation operation is used which has a commutative property. The encryption key is a set of angles \(k = \{ {\theta _i}:0 \le {\theta _i} < \pi ,i = 1,2,\ldots ,n\} \) for an n-bit message, where the subscript indicates the position in the message where the encryption with angle \({\theta _i}\) is applied. The encryption of some state \(\left| \psi \right\rangle \) with a secret key \(k = \{ \theta \} \) is \({E_k}[\left| \psi \right\rangle ] = R(\theta )\left| \psi \right\rangle \) where \(R(\theta )\) is the following matrix:

$$\begin{aligned} R(\theta ) = \left( {\begin{array}{*{20}{c}} {\cos (\theta )}&{}{\sin (\theta )}\\ { - \sin (\theta )}&{}{\cos (\theta )} \end{array}} \right) \end{aligned}$$

For decrypting the cipher photon, rotation operation by angle \(\theta \) in the opposite direction is applied, i.e., \({D_k}[{E_k}[\left| \psi \right\rangle ]] = R( - \theta )({E_k}[\left| \psi \right\rangle ])\).

Remark

The classic XOR operation can be applied on qubits by the following scenario.

Rotating the encrypted photon by 90 degree changes the photon where as rotation by 0 degree does not. In other words, we have \({E_{\frac{\pi }{2}}}\left| 0 \right\rangle = \left| 1 \right\rangle \), \({E_{\frac{\pi }{2}}}\left| 1 \right\rangle = \left| 0 \right\rangle \), \({E_0}\left| 0 \right\rangle = \left| 0 \right\rangle \) and \({E_0}\left| 1 \right\rangle = \left| 1 \right\rangle \). The notation \(EXo{r_k}[\left| \psi \right\rangle ]\) is used in this paper to describe this operation.

An algorithmic description of Sun et al.’s protocol is given below.

figure a

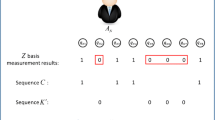
Fig. 1 (cited from [13]) is a graphical representation of Sun et al.’s protocol process.

Fig. 1
figure 1

Graphical representation of the Sun et al.’s protocol ([13])

Full size image

The protocol requires all parties, one after another, to check eavesdroppers, and only if all transmitted photons are secure, they encode their secret key on these photons.

3 Cryptanalysis of Sun et al.’s protocol against participant attack

Sun et al. considered the security of their scheme against outsiders first. As for insider attack (which is the main focus of our paper), i.e., participant’s attack, they made the assumption that participants are not of mutual trust. Sun et al. then claimed that their delayed message encoding strategy can prohibit any dishonest party from influencing the final key as her wish.

In this section, we show that Sun et al.’s scheme suffers from a security problem. More precisely, under the assumption of no mutual trust between participants, we show that a malicious participant can deprive legitimate parties from obtaining the same shared key and remain completely unnoticed. Although all parties obtain ”a” final shared key simultaneously, but this final key can be manipulated by the malicious participant and is no longer the Xor of the individual secret keys. This is described in detail in the following theorem. Recall that according to Sun et al.’s scheme, the final shared key should be \(K = {K_0} \oplus \ldots \oplus {K_i} \oplus \ldots \oplus {K_{N - 1}}\) where \({K_i}\) is the main secret key of participant \(i(0 \le i < N)\).

Theorem 1

Consider Sun et al.’s scheme reviewed in Sect. 2. Assume that \({P_i}\) is a dishonest participant. Then \({P_i}\), without being detected, can interrupt the creation of the final shared key in the sense that some honest participant computes \(K' \ne K\) as the shared key. Moreover, at the end of protocol \({P_i}\) knows the value of both K and \(K'\).

Proof

\({P_i}\) receives the sequence \(S_j^{i - 1}\) from \(P_{i-1}\). Then, \(P_{i-1}\) and \(P_i\) execute the eavesdropping checking by using decoy states as described in previous section. If there is no eavesdropper, \(P_i\) obtains \(\left| {K_j^{i - 1}} \right\rangle = EXo{r_{{K_{i - 1}}}}[EXo{r_{{K_{i - 2}}}}\ldots [\left| {{E_{{\theta _j}}}[\left| {{K_j}} \right\rangle ]} \right\rangle ]]\). Assume that \(P_i\)’s intention is to fool \(P_j\). For computing \(\left| {K_j^i} \right\rangle \), \(P_i\) proceeds as follows:

  1. 1.

    Generates a random bit string \(K'_i\) of length n.

  2. 2.

    Computes \(K''_i = {K_i} \oplus K'_i\).

  3. 3.

    Performs commutative encryption on \(\left| {K_j^{i - 1}} \right\rangle \) according to \(K''_i\), i.e. \(\left| {K_j^i} \right\rangle = EXo{r_{K''_i}}\Big [EXo{r_{{K_{i - 1}}}}\ldots \left[ \Big | {{E_{{\theta _j}}}[\Big | {{K_j}} \Big \rangle \Big ]} \Big \rangle \Big ]\right] \).

  4. 4.

    Sends \(S_j^i = ins\_d\left( \left| {K_j^i} \right\rangle \right) \) to \(P_i+1\).

The parties \({P_{i + 1}},\ldots ,{P_{j - 1}}\) sequentially perform eavesdropping check and the commutative encryption processes. \({P_{j - 1}}\) sends the sequence \(S_j^{j - 1}\) to \({P_j}\). They do eavesdropping check. In the absence of the eavesdropper, \({P_j}\) obtains \({E_{\theta j}}[\left| {K_{j - 1}} \oplus \ldots \oplus K''_i\right. \left. \oplus \ldots \oplus {K_{j + 1}} \oplus {K_j} \right\rangle ]\). He decrypts it with his secret key \({\theta _j}\), \({D_{\theta j}}[{E_{\theta j}}[\left| {K_{j - 1}} \oplus \ldots \oplus \right. \left. K''_i \oplus \ldots \oplus {K_{j + 1}} \oplus {K_j} \right\rangle ]] = \left| {{K_{j - 1}} \oplus \ldots \oplus K''_i\oplus \ldots \oplus {K_{j + 1}} \oplus {K_j}} \right\rangle \). At the end of protocol, the result of \({P_j}\)’s measurement on \(\left| {{K_{j - 1}} \oplus \ldots \oplus K''_i \oplus \ldots \oplus {K_{j + 1}} \oplus {K_j}} \right\rangle \) is the fake key \({K'} = {K_0} \oplus \ldots \oplus K''_i \oplus \ldots \oplus {K_{N - 1}}\), while the result of the other participants is \(K = {K_0} \oplus \ldots \oplus {K_i} \oplus \ldots \oplus {K_{N - 1}}\) because \(P_i\) has done commutative encryption on photons \(\left| {K_t^{i - 1}} \right\rangle ,0 \le t < N,t \ne j\) according to his main secret key \({K_i}\). The malicious participant \({P_i}\) can obtain the value of \({P_j}\)’s fake key by exclusive-OR of \(K'_i\) and K. It is easy to show that \({K'} = K \oplus K'_i\). According to the procedure of the protocol, the malicious party will be undetected. \(\square \)

4 Improvement to Sun et al.’s QKA protocol

The attack described in previous section can be launched against any KA (circular or not) in which the data provided by participants are not somehow verified, i.e., participants are not forced to commit to the information they broadcast. The aim of this section is to propose an improvement to fix this problem. Note that due to the nature of Sun et al.’s proposed protocol (its circularity and performing the measurement at the end of the protocol), there is no way to detect the cheating party. Fortunately, this does not mean that the protocol is useless. One of the advantages of Sun et al.’s approach is its efficiency in using qubits which is achieved because of the circularity. The point of our paper is that this QKA protocol should be used in situations where participants are all trusted and efficiency is of prime importance. In the case where each party’s key is just a random bit string and privacy (as described in Reference [13]) is not the main concern, we propose a solution which can prohibit the dishonest party from the above attack. In the proposed improvement each party basically sends his (encrypted) share to others. Therefore, we bind each party to his contribution of the final secret key and make it possible to detect the cheating member.

In the following, we first provide the details of our proposed improvement and then elaborate on the associated costs and merits.

figure b

We now proceed to show that although the cost of the aforementioned solution is using more qubits but still using rotation operation will preserve the merits of the protocol. We use the Cabello [15] qubit efficiency, which is given as

$$\begin{aligned} \eta = \frac{c}{{q + b}} \end{aligned}$$

where c denotes the length of the transmitted bits, q is the number of the used qubits, and b is the number of classical bits exchanged for decoding of the message.

In order to generate n bits of shared key, in our improvement to Sun et. al’s protocol, each party has to prepare \( (N-1).n \) single photons. As stated in [10] for QKA, c is the length of the shared key generated by the protocol. Hence, the qubit efficiency of our improvement to Sun et al.’s protocol can be computed by

$$\begin{aligned} \eta = \frac{n}{{(\kappa .n+n)N(N - 1)}} = \frac{1}{{(\kappa +1)(N - 1)N}} \end{aligned}$$

where \( \kappa \) is the detection rate (i.e., \( \kappa \) represents the number of detection qubits when one qubit is need to be sent)[16].

This is quite acceptable compared to recent existing QKA in the literature. As an example, the qubit efficiency of the scheme of [16] is similar to our scheme. As another example, the QKA of [11] achieves \( {\textstyle {2 \over {(\kappa + 1)N}}} \) as its qubit efficiency. However, both of these protocols use multipartite entangled states which are much more difficult to prepare and more fragile in practice [17]. Although in [11] cluster states are used and these states are more stable than GHZ states employed in [16], they still suffer from decoherence which can be viewed as the loss of information from a system into the environment [18].

On the other hand, our proposed improvement uses rotation operation. This is a great advantage since this operation can be realized by current technologies. The photon is linearly polarized by a polarizing apparatus called linear polarizer, and the direction can be determined by the orientation of the polarizer. In order to rotate the polarized photon, the photon is passed through a Faraday effect modulator. The rotation angle is controlled by the strength of the magnetic field parallel to the light beam. The output polarization from the Faraday effect modulator can be rotated by the desired angle. Therefore, in view of the difficulty in creating and maintaining multiparty entangled states, our proposed improvement is more efficient and practical. The results are summarized in Table 1.

Table 1 Comparison between previously proposed multiparty QKA protocols and our proposed improvement
Full size table

5 Conclusion

In this paper, we consider the security of the multiparty quantum key agreement of [10]. It is claimed that the protocol is secure against both outside and inside adversaries. We propose an attack that rejects this claim for inside attackers. We show that a malicious participant can provide fake values such that group members compute different final shared keys and at the same time his malicious behavior will not be detected. Although all participants retrieve the final share key simultaneously, there is no guarantee that they all obtain the same key as expected. We further demonstrate how to fix this problem at an acceptable cost.