1 Introduction

Quantum metrology [1, 2] is an important ingredient of quantum technologies. It is aimed to provide parameter estimation with high measurement precision. Parameter estimation, an important milestone of quantum technology, has developed new techniques in measurement of parameter sensitivity during recent years yielding remarkable scientific breakthroughs. In classical parameter estimation theory, the Craḿer-Rao bound (CRB) expresses a lower bound on the variance of an unbiased estimator [3,4,5]. Its quantum counterpart “the quantum Cramer-Rao bound (QCRB)” that accounts for all (unbiased) measurement techniques allowed by quantum mechanics is discussed in Refs. [6, 7]. There exists an optimal quantum measurement whose classical Fisher information, obtained from the measurement outcomes, achieves the quantum Fisher information (QFI) [8]. Quantum Fisher information can be used to estimate the value of an unknown parameter. It is an abstract quantity that measures the maximum information about a parameter that can be extracted from a given measurement procedure. In other words, it is a measure of how fast a given state changes under a given evolution. It can also be used as a pointer that how useful a quantum state is for quantum metrology [9,10,11]. A larger QFI implies that the parameter can be estimated with a higher precision. In this work, we use the symmetric logarithmic derivative (SLD) operator-based method to quantify QFI, because it has tremendous physical properties, such as convexity and invariance under unitary processes. Recently, QFI is found to be a sensitive probe to the quantum phase transitions [12, 13]. It has also been proposed as a measure for macroscopicity of quantum systems [14, 15]. Time evolution of the QFI of a system whose dynamics is described by the phase-damped model has been studied by Berrada et al. [16]. The QFI in phase estimation for a qubit placed under the influence of a non-Markovian environment is investigated recently [17]. It has also been extended for the case of two-mode Gaussian states: The mode-mixed thermal states and the squeezed thermal states by Paulina and Tudo [18]. Moreover, a new emphasis has emerged in this context where QFI is related to the properties of interacting many-body quantum systems.

The study of atom-field interaction lies at the heart of quantum optics. One of the most simplest example is a two-level atom coupled to a single-mode quantized radiation field in an optical cavity which represents the well-known Jaynes–Cummings model (JCM) [19, 20]. The JCM is the simplest quantum mechanical model which describes a formalism for a two-level atom interacting with a quantized radiation field in the rotating wave approximation (RWA). Various generalizations of this model have been proposed so far [21,22,23,24,25,26,27,28,29,30,31,32]. For instance, a general formalism for a \(\Lambda \)-type three-level atom interacting with a correlated two-mode field is presented by Abdel-Aty et al. [33]. Dynamics of entanglement and other nonclassical properties of a V- and a \(\Lambda \)-type three-level atom interacting with a single-mode field in a Kerr medium with intensity-dependent coupling and in the presence of the detuning parameters have been studied by Faghihi and Tavassoly [34]. The dynamic behaviour of the JCM beyond the RWA has been investigated where the effect of the counter-rotating terms on some nonclassical features has been examined [35]. A model with moving atoms undergoing one-photon and two-photon transitions in a two-mode coherent-state field has been studied by Joshi and Schlicher [36, 37]. Furthermore, the dynamics of entanglement for a higher-level atoms interacting with a single-mode cavity field has been investigated by different authors [38,39,40]. Recently, the geometric phase of a two-level atomic system driven by a phase noise laser under non-Markovian dynamics has been studied by Abdel-Khalek [41].

Assuming that the system does not evolve continuously, Milburn [42] has proposed a simple model of intrinsic decoherence based on an assumption that on sufficiently short time steps the system does not evolve continuously under unitary evolution but rather in a stochastic sequence of identical unitary transformations. This model has been applied to the study of decoherence effects in Jayne–Cummings model [43,44,45] in open quantum systems [46] in a two-level system coupled to a photon field [47]. In this direction, the effect of intrinsic decoherence on the entropy squeezing of coupled field-superconducting charge qubit [48]. Also, the intrinsic decoherence of tripartite states Bell-nonlocality has been investigated [49]. It has been shown that the multipartite Bell-inequality violations can be destroyed infinite time in the system.

The main focus of this work is to investigate the time evolution of QFI and von Neumann entropy under intrinsic decoherence for phase shift estimator parameter of a moving and non-moving N-level atomic system. We consider the examples of three-, four- and five-level atomic system interacting with a coherent field under rotating wave approximations. It is seen that both the intrinsic decoherence and phase shift parameter play an important role during the time evolution of the N-level atomic system. There is a monotonic relation between the atomic quantum Fisher information and entanglement in the absence of atomic motion. On the other hand, atomic quantum Fisher information and entanglement exhibit an opposite behaviour during its time evolution in the presence of atomic motion. Time evolution of the entanglement is found to be very sensitive in the presence of intrinsic decoherence. Dramatic changes take place in the degree of entanglement when we increase the intrinsic decoherence parameter. Larger value of intrinsic decoherence leads to sudden death of entanglement. However, the damping behaviour of entanglement is independent of the system dimensions for larger timescales. Furthermore, we compare our results with the existing literature and found it consistent with the previous studies.

The paper is organized as follows. In Sect. 2, we present the basic definition of quantum Fisher Information and von Neumann entropy and its formalism for numerical calculations. The model Hamiltonian and interaction dynamics of coherent field with moving N-level atomic system in terms of phase shift estimator parameter and intrinsic decoherence are presented in Sect. 3. In Sect. 4, numerical results and discussions are presented. In Sect. 5, we conclude our results.

2 The quantum Fisher information

The classical Fisher information for a given process with a single unknown parameter \(\theta \) is defined as

$$\begin{aligned} F_{\theta }=\sum _{i}p_{i}(\theta )\left[ \frac{\partial }{\partial \theta }\ln p_{i}(\theta )\right] ^{2}, \end{aligned}$$
(1)

where \(p_{i}(\theta )\) is the probability density conditioned on the fixed parameter with measurement outcome \(\{x_{i}\}\) for a discrete observable X. The classical Fisher information characterizes the inverse variance of the asymptotic normality of a maximum-likelihood estimator. The quantum Fisher information of a parameterized quantum states \(\rho (\theta )\) can be defined by extending it to quantum regime

$$\begin{aligned} F_{\theta }=\text {Tr}[\rho (\theta )L^{2}], \end{aligned}$$
(2)

where \(\theta \) is the parameter to be measured, and L is the symmetric logarithmic derivative (SLD) determined by

$$\begin{aligned} \frac{\text {d}\rho (\theta )}{\text {d}\theta }=\frac{1}{2}[\rho (\theta )L+L\rho (\theta )], \end{aligned}$$
(3)

Here, we consider N-dimensional system (N can be infinite) with the density operator \(\rho (\theta ).\) The spectral decomposition of the density matrix can be written as

$$\begin{aligned} \rho _{\theta }=\sum _{K}\lambda _{K}|k\rangle \langle k|, \end{aligned}$$
(4)

The QFI with respect to \(\theta \) for such a density matrix is given by [50,51,52]

$$\begin{aligned} F_{\theta }=\sum _{k}\frac{(\partial _{\theta }\lambda _{k})^{2}}{\lambda _{k} }+2\sum _{k,k^{^{\prime }}}\frac{(\lambda _{k}-\lambda _{k^{^{\prime }}})}{ (\lambda _{k}+\lambda _{k^{\prime }})}|\langle k|\partial _{\theta }k^{^{\prime }}\rangle |^{2} \end{aligned}$$
(5)

where \(\lambda _{k}>0\) and \(\lambda _{k}+\lambda _{k^{\prime }}>0.\) The first term in Eq. (5) is classical Fisher information, and the second term represents its quantum counterpart. In this fashion, we can define the atomic quantum Fisher information of a bipartite density operator \(\rho _{AB.}\) in terms of \(\theta \) as [53]

$$\begin{aligned} I_{QF}(t)=I_{AB}(\theta ,t)=\text {Tr}[\rho _{AB}(\theta ,t)\{L(\theta ,t)\}^{2}] \end{aligned}$$
(6)

where \(L(\theta ,t)\) is the quantum score [54] (the symmetric logarithmic derivative) which can be found as

$$\begin{aligned} \frac{\partial \rho _{AB}(\theta ,t)}{\partial \theta }=\frac{1}{2}[L(\theta ,t)\rho _{AB}(\theta ,t)+\rho _{AB}(\theta ,t)L(\theta ,t)] \end{aligned}$$
(7)

Similarly, the von Neumann entropy can be defined as

$$\begin{aligned} S_{A}=-\text {Tr(}\rho _{A}\ln \rho _{A}\text {)}=-\sum _{i}r_{i}\ln r_{i} \end{aligned}$$
(8)

where \(r_{i}\) are the eigenvalues of the atomic density matrix \(\rho _{A}= \hbox {Tr}_{B}(\rho _{AB})\).

3 The intrinsic decoherence model for N-level atomic system

Milburn has proposed a simple model of intrinsic decoherence by giving a modification of standard quantum mechanics. He assumed that on a sufficiently small timescale \(\tau ,\) the state of the system changes by

(9)

with a probability of p(t). The master equation describing the intrinsic decoherence under the Markovian approximations is given by

$$\begin{aligned} \frac{\text {d}\rho (t)}{\text {d}t}=-i[H,\rho (t)]-\frac{\gamma }{2}[H,[H,\rho (t)]] \end{aligned}$$
(10)

where \(\gamma \) is the intrinsic decoherence parameter. The formal solution of the above master equation can be expressed as

$$\begin{aligned} \rho (t)=\sum _{k=0}^{\infty }\frac{(t)^{k}}{k!}M^{k}\rho (0)M^{\dagger k} \end{aligned}$$
(11)

where \(\rho (0)\) is the density operator of the initial state and \(M^{k}\) is defined by

$$\begin{aligned} M^{k}=H^{k}e^{-iHt}e^{-\frac{t}{2}H^{2}} \end{aligned}$$
(12)

The dynamics of a density operator for a system under intrinsic decoherence can be governed by the formalism given below. For our particular case, we consider the model consisting of moving N-level atoms interacting with a single-mode cavity field. The field mode is described by the creation (annihilation) operator \(\hat{a}^{\dag }\hat{a}\) and frequency \(\Omega \) . The total Hamiltonian \(\hat{H}_{\text {Tot}}\) in the rotating wave approximation for the given system can be written as [55]

$$\begin{aligned} \hat{H}_{\text {Tot}}=\hat{H}_{\text {Atom-Field}}+\hat{H}_{\text {Int}}. \end{aligned}$$
(13)
Fig. 1
figure 1

(Colour online) Atomic quantum Fisher information (upper panel) and von Neumann entropy (lower panel) as a function of time for three-level atomic system for \(\alpha \) = 6 and the phase shift estimator parameter \(\phi =0\) (left panel) and \(\pi /4\) (right panel). The atomic motion parameter p is neglected

Full size image
Fig. 2
figure 2

(Colour online) Atomic quantum Fisher information (upper panel) and von Neumann entropy (lower panel) as a function of time for four-level atomic system for \(\alpha \) = 6 and the phase shift estimator parameter \( \phi =0\) (left panel) and \(\pi /4\) (right panel). The atomic motion parameter p is neglected

Full size image
Fig. 3
figure 3

(Colour online) Atomic quantum Fisher information (upper panel) and von Neumann entropy (lower panel) as a function of time for five-level atomic system for \(\alpha \) = 6 and the phase shift estimator parameter \( \phi =0\) (left panel) and \(\pi /4\) (right panel). The atomic motion parameter p is neglected

Full size image
Fig. 4
figure 4

(Colour online) Atomic quantum Fisher information (upper panel) and von Neumann entropy (lower panel) as a function of time for three-level atomic system for \(\alpha \) = 6 and the phase shift estimator parameter \(\phi =0\) (left panel) and \(\pi /4\) (right panel) in the presence of atomic motion for \(p=1\)

Full size image
Fig. 5
figure 5

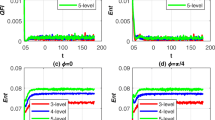
(Colour online) Atomic quantum Fisher information (upper panel) and von Neumann entropy (lower panel) as a function of time for four-level atomic system for \(\alpha \) = 6 and the phase shift estimator parameter \( \phi =0\) (left panel) and \(\pi /4\) (right panel) in the presence of atomic motion for \(p=1\)

Full size image
Fig. 6
figure 6

(Colour online) Atomic quantum Fisher information (upper panel) and von Neumann entropy (lower panel) as a function of time for five-level atomic system for \(\alpha \) = 6 and the phase shift estimator parameter \( \phi =0\) (left panel) and \(\pi /4\) (right panel) in the presence of atomic motion for \(p=1\)

Full size image
Fig. 7
figure 7

(Colour online) Comparison of intrinsic decoherence on QFI (upper panel) and von Neumann entropy (lower panel) of a three-level atomic system, b five-level atomic system without atomic motion for \(\phi =0\)

Full size image
Fig. 8
figure 8

(Colour online) Comparison of intrinsic decoherence on QFI (upper panel) and von Neumann entropy (lower panel) of a three-level atomic system, b five-level atomic system without atomic motion for \(\phi =\pi /4 \)

Full size image
Fig. 9
figure 9

(Colour online) 3D viewgraphs of QFI (left panel) and von Neumann entropy (right panel) for a five-level atomic system (a, b) with atomic motion (c, d) without atomic motion for \(\gamma =0.01.\)

Full size image

Where \(\hat{H}_{\text {Atom-Field}}\) is the Hamiltonian for the non-interacting atom and field, and the interaction part is \(\hat{H}_{\text {Int}}\). We can define \(\hat{H }_{\text {Atom-Field}}\) as

$$\begin{aligned} \hat{H}_{\text {Atom-Field}}=\sum \limits _{j}\omega _{j}\hat{\sigma }_{j,j}+\Omega \hat{a}^{\dag }\hat{a} , \end{aligned}$$
(14)

where \(\hat{\sigma }_{j\text {,}j}=\left| j\right\rangle \left\langle j\right| \) are known as population operators for the j th level. The interaction Hamiltonian for the non-resonant case is given by [56, 57]

$$\begin{aligned} \hat{H}_{\text {Int}}=\sum _{s=1}^{N}\Omega (t)\left[ \hat{a}e^{-i\Delta _{s}t}\hat{ \sigma }_{s\text {,}s+1}+\left( \hat{a}e^{-i\Delta _{s}t}\hat{\sigma }_{s\text {, }s+1}\right) ^{\dagger }\right] \text {.} \end{aligned}$$
(15)

We can define detuning parameter as

$$\begin{aligned} \Delta _{s}=\Omega +\omega _{s+1}-\omega _{s}\text {,} \end{aligned}$$
(16)

and the coupling constant for atom and field is g, \(\Omega (t)\) represents the shape function of the cavity field mode [58, 59] and the atomic motion is along z-axis. A realization of particular interest is

$$\begin{aligned} \Omega (t)= & {} g \sin \text {(}p\pi vt\text {/}L) \text { in the presence of atomic motion , }p\ne 0 \nonumber \\ \Omega (t)= & {} g\text { in the absence of atomic motion }p=0 \end{aligned}$$
(17)

where v denotes the atomic motion velocity and p stands for the number of half wavelengths of the mode in the cavity and L represents the cavity length in z-direction. Let us now consider the atomic motion velocity as \( v=\lambda L\) /T which leads to

$$\begin{aligned} \Omega _{1}(t)= & {} \int _{0}^{t}\Omega (\tau )\text {d}\tau =\frac{1}{p}(1-\cos (p\pi vt/L)\text { for }p\ne 0 \end{aligned}$$
(18)
$$\begin{aligned}= & {} gt\text { for }p=0 \end{aligned}$$
(19)

In order to find the phase shift parameter as precisely as possible, we consider the optimal input state as

$$\begin{aligned} |\Psi (0)\rangle _{\text {Opt}}=\frac{1}{\sqrt{2}}(|1\rangle +|0\rangle )\otimes |\alpha \rangle \end{aligned}$$
(20)

where j describes the state of atom and \(\alpha \) is the coherent state of the input field as given below

$$\begin{aligned} |\alpha \rangle =\sum _{m=0}^{\infty }\alpha ^{m}\sqrt{e^{-|\alpha |^{2}}/m!} |m\rangle \end{aligned}$$
(21)

In order to introduce the phase shift parameter \(\phi \), we consider a single-atom phase gate which introduces the phase shift as

$$\begin{aligned} \hat{U}_{\phi }=|1\rangle \langle 1|+e^{i\phi }|0\rangle \langle |0|, \end{aligned}$$
(22)

\(|\Psi (0)\rangle \) is obtained from the operation of the single-atom phase gate on \(|\Psi (0)\rangle _{\text {Opt}}\)

$$\begin{aligned} \hat{U}_{\phi }|\Psi (0)\rangle _{\text {Opt}}= & {} |\Psi (0)\rangle \end{aligned}$$
(23)
$$\begin{aligned}= & {} \frac{1}{\sqrt{2}}(|1\rangle +e^{i\phi }|0\rangle )\otimes |\alpha \rangle \end{aligned}$$
(24)

After the phase gate operation, the system will have the interaction with a field. The precision of the estimation is strongly affected by the characteristics of the interaction between the field and moving N-level atomic system.

Now, we can write the state \(|\Psi (0)\rangle \) as

$$\begin{aligned} |\Psi (0)\rangle =\frac{1}{\sqrt{2}}(|1,m+1\rangle +e^{i\phi }|0,m\rangle ) \end{aligned}$$
(25)

where \(|1,m+1\rangle \) and \(|0,m\rangle \) are allowable atom-field states. The state in which number of photons are consistent with the atomic level are known as allowable atom-field states. If m photons are present in 0 level than \(m+1\) photons will be present in level 1. \(m+2\) with level 1 or 0 is not allowed. It will be allowed with level 2. For our N-level atomic system, the allowable basis are given by

$$\begin{aligned} |0,m\rangle ,|1,m+1\rangle ,|2,m+2\rangle ,........|N-2,(m+N-2)\rangle ,|N-1,(m+N-1)\rangle \quad \end{aligned}$$
(26)

where m are number of photons initially present in the cavity and \(N{-}1\) are the number of levels in an atom. 0 and \(N{-}1\) represent the excited and ground state of the atom.

Let us consider the time-independent case, characterized by the transformation matrix \(\hat{U}\left( t\right) \). The wave function

$$\begin{aligned} |\Psi (t)\rangle =\hat{U}\left( t\right) |\Psi (0)\rangle , \end{aligned}$$
(27)

and U(t) is given by

$$\begin{aligned} U(t)=\sum _{z=1}^{N}\exp \left( \frac{-\gamma }{2}t-E_{z}t\right) |\varphi _{z}(t)\rangle \langle \varphi _{z}(t)|, \end{aligned}$$
(28)

where \(|\varphi _{z}(t)\rangle \) and \(E_{z}(t)\) are eigenvectors and eigenvalues of the Hamiltonian \(H_{\text {Int}}\), respectively, and \(\gamma \) is the intrinsic decoherence parameter. The quantum Fisher information is calculated numerically for the atom-field density matrix given below

$$\begin{aligned} \hat{\rho }(t)=\hat{U}\left( t\right) \rho (0)\hat{U}^{^{\dagger }}\left( t\right) . \end{aligned}$$
(29)

Now, the influence of the parameters \(\gamma ,\) \(\phi \) and p on the evolution of the atomic QFI and von Neumann entropy is presented in the next section.

4 Numerical results and discussions

In this section, we present the main results for the evolution of atomic quantum Fisher information and von Neumann entropy for N-level atomic system influenced by intrinsic decoherence. We set the mean photon number n =\(|\alpha |^{2}=\) 36 for our convenience and the time t has been scaled, i.e. one unit of time is given by the inverse of the coupling constant g. Our main interest in this case is to investigate the dynamical behaviour of atomic QFI and von Neumann entropy under intrinsic decoherence and the phase shift estimator parameter \(\phi \) in the presence and absence of the atomic motion. In Fig. 1, we plot the atomic quantum Fisher information and von Neumann entropy for a three-level atomic system as a function of time for \(\alpha \) = 6 and the phase shift estimator parameter \(\phi =0\) and \(\pi /4\) in the absence of atomic motion. In Figs. 2 and 3, the atomic quantum Fisher information and von Neumann entropy for four- and five-level atomic systems are plotted as a function of time for \(\alpha \) = 6 and the phase shift estimator parameter \(\phi =0\) and \(\pi /4\) in the absence of atomic motion. It is shown that there is a monotonic relation between the atomic quantum Fisher information and entanglement in the case of non-moving atoms. It is seen that the intrinsic decoherence causes the decay of entanglement and Fisher information of the N-level atomic system. It is also seen that the local maximum values at the revival time of both QFI and \(S_{A}\) decreases gradually during the time evolution. The local maximum value at the revival time decreases more rapidly in case of four- and five-level atoms as compared to the three-level atoms.

We use the similar approach as adopted in Ref. [60] for our calculations, whereas Obada and Khalek used the probability amplitude approach to study the atomic quantum Fisher information [61]. When we compare our results with the existing literature, a correlation between the quantum entanglement and quantum Fisher information is observed. A decrease in quantum entanglement corresponds to the negative QFI flow and the positive QFI corresponds to the growth of the quantum entanglement. It is also seen that the QFI slowly decay to the minimal value and then rise again after long time similar to Ref. [60]. In this case, the system has a long-time-interval separable state or in other words the disappearing of entanglement. From this result, it is clear that the considered case leads to the maximization of QFI during the time evolution. However, the variations of the QFI correspond to the negative and positive values of QFI flow within certain intervals of the time. QFI decreases as the time goes on corresponds to the systematic loss of coherence of the radiation field as discussed in Ref. [62]. The argument presented by Khalek et al. [62] that the amplitude of QFI due to increase of \({<}n{>}\) is justified. The same happens due to statistical properties of the Poissonian photon number distribution of the coherent field.

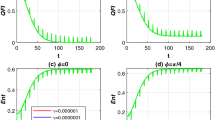
In Figs. 4, 5 and 6, the atomic quantum Fisher information and von Neumann entropy for three-, four- and five-level atomic systems are plotted as a function of time for \(\alpha \) = 6 and the phase shift estimator parameter \(\phi =0\) and \(\pi /4\) in the presence of atomic motion, i.e. \(p=1\). We find that the atomic quantum Fisher information and entanglement exhibit an opposite behaviour during the time evolution in the presence of atomic motion. It is shown that the atomic motion destroys the monotonic correlation between QFI and \(S_{A}.\) In Figs. 7 and 8, we compare the effect of intrinsic decoherence on QFI and von Neumann entropy for three- and five-level atomic systems without atomic motion for \(\phi =0\) and \( \phi =\pi /4\), respectively. It is seen that the evolution of the entropy is very sensitive to the degree of intrinsic decoherence. Our results show that the effect of intrinsic decoherence decreases the degree of entanglement between the atom and the field. In other words, the intrinsic decoherence in the atom-field interaction suppresses the non-classical effects of the atomic system. Drastic change has been observed when we increase the value of intrinsic decoherence parameter \(\gamma \) from 0.1 to 0.01. The value of entanglement and Fisher information saturate to its lower level for longer times. A further increase in the value of intrinsic decoherence leads to sudden death of entanglement.

In Fig. 9, we present 3D viewgraphs of QFI (left panel) and von Neumann entropy (right panel) for a five-level atomic system (a and b) with atomic motion (c and d) without atomic motion for \(\gamma =0.01.\) A damping behaviour of entanglement is seen in the presence of intrinsic decoherence. It can be seen that the damping behaviour of entanglement is independent of the system dimensions for larger timescales. The phase shift parameter is helpful to distinguish the system dimensions in case of higher-dimensional systems. Furthermore, the periodic behaviour of QFI becomes more prominent for higher-dimensional systems in the presence of atomic motion.

5 Conclusions

We consider a rather more general approach for quantification of entanglement to be quantified through von Neumann entropy for N-level atomic system. Different examples have been investigated in order to study the dynamics of QFI and von Neumann entropy under intrinsic decoherence for moving and non-moving N-level atoms such as three-, four- and five-level atomic systems. The QFI and von Neumann entropy are calculated numerically for all the cases under consideration. The phase shift estimator parameter, intrinsic decoherence and the atomic motion play a very important role during the time evolution of the atomic systems. It is shown that there is a monotonic relation between the atomic quantum Fisher information and entanglement in the absence of atomic motion. It is seen that the local maximum values at the revival time of both QFI and \(S_{A}\) decrease gradually during its time evolution. The local maximum value at the revival time decreases more rapidly in case of four- and five-level atoms as compared to the three-level atoms. The periodic behaviour of QFI is observed and becomes more prominent for higher-dimensional moving systems. Furthermore, atomic quantum Fisher information and entanglement exhibit an opposite behaviour during its time evolution in the presence of atomic motion. It has also been observed that the atomic motion destroys the monotonic correlation between QFI and \(S_{A}.\) Time evolution of entanglement is found to be very sensitive to the degree of intrinsic decoherence. Dramatic change takes place in the degree of entanglement when we increase the value of intrinsic decoherence. Intrinsic decoherence in the atom-field interaction suppresses the non-classical effects of the atomic systems. The entanglement and Fisher information saturate to its lower level for longer times at larger values of intrinsic decoherence. A further increase in the value of intrinsic decoherence parameter leads to sudden death of entanglement. However, the damping behaviour of entanglement is independent of the system dimensions for larger timescales.