1 Introduction

Since the first quantum key distribution (QKD) was proposed in 1984 [1], quantum communication has received much attention for its unconditional security, which is guaranteed by physical principles. Many progresses in QKD [2,3,4] and quantum secure direct communication (QSDC) [5,6,7] have been made. In fact, most of these works can be treated as basic two-party communication. With the rapid development of quantum networks, the communication demand will become more complex. Beyond two-party communication, multi-party communication is naturally in the spotlight for expanding quantum communication. Quantum secret sharing (QSS) [8] is one of typical applications, which combines classical secret sharing and quantum information science. In QSS, a dealer worries about there might be a liar player, so it encodes a secret into multiple shares and distributes them to different players. Every player cannot obtain any information on the secret from its own share. Only if all players cooperate can they restructure the secret.

In a conventional sense, QSS is a cryptographic protocol that prevents malicious players from damaging a secret. From the perspective of communication, QSS is also a type of secure one-to-many communication mode, in which a sender transmits a message to multiple receivers and all receivers cooperate to receive the message. The receivers in QSS form a coordinated group in a sense, which is similar to coordinated multi-point (CoMP) communication in a LTE-A (long-term evolution—advanced) cellular network [9]. As we know, CoMP communication is a rising technology, and it aims to jointly coordinate base stations to provide services for cell users, which will greatly improve the quality of service. It is noteworthy that both QSS and CoMP need coordinated work of nodes as a common requirement of communication.

In order to extend the communication mode of quantum networks, we attempt to flexibly organize a coordinated group and performs coordinated multi-point communication, in which nodes cooperate to realize one-to-many communication just like QSS, as well as many-to-one communication. Considering the requirements of multi-point communication, the expensive cost of quantum resource and the characteristic of quantum channel, a desired quantum coordinated multi-point (QCoMP) communication scheme should meet the following requirements as far as possible: (1) Confidentiality. When there are multiple senders, only a receiver can obtain messages from all senders, and senders cannot get messages from each other; (2) Resource-saving. Organization of coordinated group and message transmission should consume the quantum resources available, which will not lead to a large number of additional resource consumption; (3) Flexibility. A coordinated group should be organized flexibly and the number of coordinated group members can be adjusted flexibly.

Quantum entanglement is the inherent physical property of quantum mechanics, which plays an important role in quantum information science, including quantum communication and quantum computing. Furthermore, entanglement swapping is a common technology, which allows two non-interacting quantum particles to be entangled by means of joint measurement. Particularly, the state of a newly born entangled pair has specific relevance with previous joint measurement, i.e., the state of a newly born entangled pair can be deduced from the outcomes of joint measurement on previous two particles. This specific relevance is very useful for the design of quantum protocols in many fields. In addition, entanglement swapping features simple process and low cost and can establish connection between remote parties.

Inspired by the virtues of entanglement swapping, we propose a quantum coordinated multi-point (QCoMP) communication scheme based on entanglement swapping, which uses EPR pairs to flexibly organize a coordinated group and encodes message. In brief, the QCoMP communication scheme transmits messages by means of multi-party entanglement swapping so that no quantum particles are transmitted directly. It can realize one-to-many communication, many-to-one communication, and one-to-some communication.

The main contributions of our work are:

  1. 1.

    One-to-many mode for QCoMP communication was designed from the idea of QSS. By virtue of entanglement swapping, one sender can encode its messages on local particles, and all receivers coordinate to obtain messages from the sender. Furthermore, the only sender can detect whether there is a liar in the coordinated network thus it can prevent liars from damaging the communication.

  2. 2.

    Also, many-to-one mode for QCoMP communication was designed. In the many-to-one mode, all senders encode their own messages on local particles and coordinate to perform multi-party entanglement swapping to send their messages to one receiver. To protect the security of messages, senders messages are privacy for each other and all messages can be only obtained by the only receiver. Moreover, the one-to-some mode is an extension following the many-to-one mode to help spread messages to desired parties, which can provide more efficient communication performance than the one-to-many mode.

2 Related works

2.1 Multi-party entanglement swapping

Entanglement swapping is widely used in many fields such as quantum secret sharing [10,11,12], quantum secure direct communication [13, 14], and quantum signature [15].

Before introducing entanglement swapping, we agree on four Bell states as follows:

$$\begin{aligned} \left| {{\phi ^ \pm }} \right\rangle \mathrm{{ = }}\frac{1}{{\sqrt{2} }}\left( {\left| {00} \right\rangle \pm \left| {11} \right\rangle } \right) ,\left| {{\psi ^ \pm }} \right\rangle \mathrm{{ = }}\frac{1}{{\sqrt{2} }}\left( {\left| {01} \right\rangle \pm \left| {10} \right\rangle } \right) \end{aligned}$$
(1)

We introduce a simple two-party entanglement swapping at first.

Assume there are two EPR pairs, which are in the state of \({\left| {{\phi ^\mathrm{{ + }}}} \right\rangle _{12}} \otimes {\left| {{\phi ^\mathrm{{ + }}}} \right\rangle _{34}}\), where the subscript denotes the particle number, \({\left| {{\phi ^\mathrm{{ + }}}} \right\rangle _{12}}\) denotes that the particles 1 and 2 are in the entangled state of \(\left| {{\phi ^\mathrm{{ + }}}} \right\rangle \), and \({\left| {{\phi ^\mathrm{{ + }}}} \right\rangle _{34}}\) denotes that the particles 3 and 4 are in the entangled state of \(\left| {{\phi ^\mathrm{{ + }}}} \right\rangle \).

When the particles 1 and 3 are held by party A, the particles 2 and 4 are held by party B, entanglement swapping can begin. A performs a Bell measurement on the particles 1 and 3, so the system state can be rewritten as:

$$\begin{aligned} \ {\left| {{\phi ^ + }} \right\rangle _{12}} \otimes {\left| {{\phi ^ + }} \right\rangle _{34}}= & {} \frac{1}{2}{\left( {\left| {00} \right\rangle + \left| {11} \right\rangle } \right) _{12}} \otimes {\left( {\left| {00} \right\rangle + \left| {11} \right\rangle } \right) _{34}} \nonumber \\= & {} \frac{1}{2}{\left( {\left| {0000} \right\rangle \mathrm{{ + }}\left| {0101} \right\rangle \mathrm{{ + }}\left| {1010} \right\rangle \mathrm{{ + }}\left| {1111} \right\rangle } \right) _{1324}} \nonumber \\= & {} \frac{1}{2}{\left( {\left| {{\phi ^ + }} \right\rangle \left| {{\phi ^ + }} \right\rangle + \left| {{\phi ^ - }} \right\rangle \left| {{\phi ^ - }} \right\rangle + \left| {{\psi ^ + }} \right\rangle \left| {{\psi ^ + }} \right\rangle + \left| {{\psi ^ - }} \right\rangle \left| {{\psi ^ - }} \right\rangle } \right) _{1324}}\qquad \end{aligned}$$
(2)

From Eq. (2), we can see that entanglement swapping leads to two results: One is the Bell measurement on the particles 1 and 3 makes two non-interacting particles 2 and 4 entangled, which is like “swapping” the entanglement from 1–2 and 3–4 to 2–4. The other result is the state of the newly born entangled pair \({\left| \Phi \right\rangle _{24}}\) has specific relevance with the measurement outcome of \({\left| \Phi \right\rangle _{13}}\), e.g., if the measurement outcome of the particles 1 and 3 is \({\left| {{\psi ^ + }} \right\rangle _{13}} \), then according to Eq. (2), the newly born entangled state \({\left| \Phi \right\rangle _{24}}\) must be in the state of \({\left| {{\psi ^ + }} \right\rangle _{24}}\).

Based on the above discussion of two parties, we can extend to three parties or more parties.

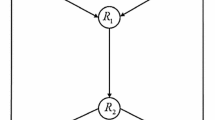
Consider the case shown in Fig. 1, there are three parties A, B, and C. A owns particles 1 and 6, B owns particles 2 and 3, while C owns particles 4 and 5. The dotted line represents entanglement between particles, i.e., particles 1 and 2; 3 and 4; 5 and 6 are in an entangled state, respectively. The solid-line box represents performing a Bell statement.

Assume that the original quantum system state in Fig. 1 is:

$$\begin{aligned}&{\left| {{\phi ^ - }} \right\rangle _{12}} \otimes {\left| {{\psi ^ + }} \right\rangle _{34}} \otimes {\left| {{\psi ^ - }} \right\rangle _{56}} = \frac{1}{{\sqrt{2} }}{\left( {\left| {00} \right\rangle - \left| {11} \right\rangle } \right) _{12}}\nonumber \\&\quad \otimes \frac{1}{{\sqrt{2} }}{\left( {\left| {01} \right\rangle + \left| {10} \right\rangle } \right) _{34}} \otimes \frac{1}{{\sqrt{2} }}{\left( {\left| {01} \right\rangle - \left| {10} \right\rangle } \right) _{56}} \end{aligned}$$
(3)
Fig. 1
figure 1

Entanglement swapping for three parties

Full size image

After A, B, and C perform a Bell measurement on their own two particles, respectively, i.e., A performs a Bell measurement on the particles 1 and 6, while B performs a Bell measurement on the particles 2 and 3, C performs a Bell measurement on the particles 4 and 5, the quantum system can be rewritten as:

$$\begin{aligned} \begin{array}{l} \ {\left| {{\phi ^ - }} \right\rangle _{12}} \otimes {\left| {{\psi ^ + }} \right\rangle _{34}} \otimes {\left| {{\psi ^ - }} \right\rangle _{56}} \mathrm{{ = }}\frac{1}{4}\bigg ({\left| {{\psi ^ + }} \right\rangle _{16}}{\left| {{\phi ^ + }} \right\rangle _{23}}{\left| {{\psi ^ + }} \right\rangle _{45}} - {\left| {{\psi ^ + }} \right\rangle _{16}}{\left| {{\phi ^ - }} \right\rangle _{23}}{\left| {{\psi ^ - }} \right\rangle _{45}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ...... \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ - {\left| {{\phi ^ + }} \right\rangle _{16}}{\left| {{\psi ^ + }} \right\rangle _{23}}{\left| {{\psi ^ + }} \right\rangle _{45}} - {\left| {{\phi ^\mathrm{{ + }}}} \right\rangle _{16}}{\left| {{\psi ^ - }} \right\rangle _{23}}{\left| {{\psi ^ - }} \right\rangle _{45}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ - {\left| {{\phi ^ - }} \right\rangle _{16}}{\left| {{\psi ^ + }} \right\rangle _{23}}{\left| {{\psi ^ - }} \right\rangle _{45}} - {\left| {{\phi ^ - }} \right\rangle _{16}}{\left| {{\psi ^ - }} \right\rangle _{23}}{\left| {{\psi ^ + }} \right\rangle _{45}}\bigg ) \\ \end{array} \end{aligned}$$
(4)

In order to summarize the law of entanglement swapping, we agree on each Bell state corresponding to two bits:

$$\begin{aligned} \left| {{\phi ^\mathrm{{ + }}}} \right\rangle \rightarrow 00,\mathrm{{ }}\left| {{\phi ^ - }} \right\rangle \rightarrow 01,\mathrm{{ }}\left| {{\psi ^\mathrm{{ + }}}} \right\rangle \rightarrow 10,\mathrm{{ }}\left| {{\psi ^ - }} \right\rangle \rightarrow 11 \end{aligned}$$
(5)

A universal law can be extracted from Eq. (4), although it is not much obvious:

$$\begin{aligned} {M_{16}} \oplus {M_{23}} \oplus {M_{45}} = {O_{12}} \oplus {O_{34}} \oplus {O_{56}} \end{aligned}$$
(6)

where the subscript denotes the order number of a particle, M denotes measurement outcome, and O denotes the original state of an entangled pair. For example, \({M_{16}}\) denotes the outcome of a Bell measurement on the particles 1 and 6, and \({O_{12}}\) denotes the original state of an entangled pair consisting of the particles 1 and 2. Through Eq. (4), we can find that each possible case of three-party entanglement swapping will satisfy the law in Eq. (6). For example, if the measurement outcomes of three parties are \({M_{16}}\mathrm{{ = }}{\left| {{\psi ^ + }} \right\rangle _{16}},{M_{23}}\mathrm{{ = }}{\left| {{\phi ^ + }} \right\rangle _{23}},{M_{45}}\mathrm{{ = }}{\left| {{\psi ^ + }} \right\rangle _{45}}\), then we can get:

$$\begin{aligned}&{M_{16}} \oplus {M_{23}} \oplus {M_{45}} = 10 \oplus 00 \oplus 10 = 00 \end{aligned}$$
(7)
$$\begin{aligned}&{O_{12}} \oplus {O_{34}} \oplus {O_{56}} = 01 \oplus 10 \oplus 11\mathrm{{ = }}00 \end{aligned}$$
(8)

Obviously, Eqs. (7) and (8) satisfy the law in Eq. (6).

Shi et.al [16] studied how entanglement swapping extends to any more parties and found that the law still works, so the law in multi-party entanglement swapping can be summarized:

$$\begin{aligned} {M_{1(2n)}} \oplus {M_{23}} \oplus {M_{45}} \oplus \cdots \oplus {M_{(2n - 2)(2n - 1)}} = {O_{12}} \oplus {O_{34}} \oplus \cdots \oplus {O_{(2n - 1)(2n)}}\qquad \end{aligned}$$
(9)

The measurement outcomes of multi-party entanglement swapping satisfy the law in Eq. (9), but the establishment of multi-party entanglement swapping has two requirements: (1) Parties form a closed loop node by node, i.e., each party has a previous neighbor and a next neighbor. (2) Adjacent parties have a shared EPR pair, which is the foundation of entanglement swapping.

2.2 Message transmission based on entanglement swapping

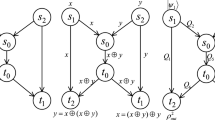
As an important usage, entanglement swapping can be used to transmit a message by utilizing the specific relevance among measurement outcomes. We make an example to show how it works with three-party entanglement swapping in Fig. 1. We assume that A is a sender, B and C are receivers. In order to send a message, we agree on four unitary operators for encoding, each operator corresponds to two bits as its subscript:

$$\begin{aligned} {U_{00}} = \left[ {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}1 \end{array}} \right] \mathrm{{ }}{U_{01}} = \left[ {\begin{array}{*{20}{c}} 0&{}1\\ 1&{}0 \end{array}} \right] \mathrm{{ }}{U_{10}} = \left[ {\begin{array}{*{20}{c}} 0&{}{ - 1}\\ 1&{}0 \end{array}} \right] \mathrm{{ }}{U_{11}} = \left[ {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}{ - 1} \end{array}} \right] \end{aligned}$$
(10)

If A wants to send a message “11”, then it will perform a unitary operator \({U_{11}}\) on the particle 1. After that, three nodes perform a Bell measurement on their own two particles, and then they publish measurement outcomes, respectively. For example, their outcomes are \({M_{16}}\mathrm{{ = }}{\left| {{\psi ^ - }} \right\rangle _{16}},{M_{23}}\mathrm{{ = }}{\left| {{\phi ^ + }} \right\rangle _{23}},{M_{45}}\mathrm{{ = }}{\left| {{\psi ^ + }} \right\rangle _{45}}\). Note that A performs an encoding operator in the particle 1, so \({M_{16}}\mathrm{{ = }}{\left| {{\psi ^ - }} \right\rangle _{16}}\) is the outcome after encoding. According to the law of entanglement swapping, the outcome before encoding \({M'_{16}}\) can be obtained:

$$\begin{aligned} {M'_{16}} \oplus {M_{23}} \oplus {M_{45}} = {O_{12}} \oplus {O_{34}} \oplus {O_{56}} \end{aligned}$$
(11)

We assume that all of the original EPR states O are known to three parties, so B and C can obtain \({M'_{16}}\mathrm{{ = }}{\left| {{\psi ^ + }} \right\rangle _{16}}\) from Eq. (11).

Then B and C can get the encoding operator \({U_X}\) A performed by comparing \({M_{16}}\) and \({M'_{16}}\):

$$\begin{aligned} {M_{16}} = {U_X}{M'_{16}} \end{aligned}$$
(12)

The operator \({U_X}\) A performed can be deduced to be \({U_X} = {U_{11}}\), so A’s message “11” is decoded by B and C.

3 Quantum coordinated multi-point communication scheme

In a quantum network, nodes are usually equipped with EPR pairs for teleportation so that the assignment of EPR resources is a worthy topic and has been studied a lot in a quantum network [17, 18]. Classical communication is also often used as an auxiliary method by virtue of its low cost and technical maturity. Considering the general conditions of a quantum network, we propose a quantum coordinated multi-point (QCoMP) communication scheme based on entanglement swapping. The objective of our scheme is to flexibly organize a coordinated group and efficiently transmit messages among it. EPR pairs between nodes are utilized to organize a coordinated group, messages are encoded on local particles and transmitted by entanglement swapping, and no quantum states are directly transmitted via quantum channels. To meet different communication requirements, the scheme can work in different modes.

The proposed QCoMP communication scheme is described as follows:

Step 1 Group organizing

Nodes are organized to form a coordinated group, in which adjacent nodes share EPR pairs and all nodes form a closed loop.

Step 2 Mode choosing

According to communication needs, nodes decide to choose a work mode such as one-to-many or many-to-one for communication.

Step 3 Communication executing

Depending on work mode, the different procedures are executed as described in the following part.

Fig. 2
figure 2

One-to-many mode

Full size image

3.1 One-to-many mode

In the one-to-many mode, one node will be selected to be a sender who sends a message to the rest of nodes, which is common in communication networks. Without loss of generality, as shown in Fig. 2, we assume the number of receivers are m, which are represented by \(Ri\mathrm{{(1}} \le i \le m\mathrm{{)}}\), while the only sender is represented by S.

Step 3 Message encoding

(3.1) Assume that S wants to send a message with the length of 2l bits, it publishes the number l to all groups over classical channels, and then each node in a group prepares l EPR particles entangled with two adjacent nodes, respectively, i.e., l particles are entangled with previous node’s particles, and other l particles are entangled with next node’s particles. Then the whole quantum system can be described as:

$$\begin{aligned} \left| \Phi \right\rangle = \prod \limits _{j = 1}^l {{{\left| \Phi \right\rangle }^j}} = \prod \limits _{j = 1}^l {\left( O_{_{{S_2}R{1_1}}}^j \otimes O_{_{R{1_2}R{2_1}}}^j \otimes \cdots \otimes O_{_{R{{(m - 1)}_2}R{m_1}}}^j \otimes O_{_{R{m_2}{S_1}}}^j\right) } \end{aligned}$$
(13)

where the superscript \(j(1 \le j \le l)\) denotes an index from 1 to l, the subscripts 1 and 2 denote the local particles 1 and 2, respectively. Each local particle 2 is entangled with next node’s particle 1, while each local particle 1 is entangled with previous node’ particle 2. For example, \(O_{_{{S_2}R{1_1}}}^j\) denotes the original state of an EPR pair with the index j, which consists of S’s particle 2 and R1’s particle 1.

(3.2) S divides the \(2l-bit\) message into l parts, and each part is two bits, and then it encodes each two bits on its particles \(\left| \Phi \right\rangle _{_{{S_1}}}^j(1 \le j \le l)\), respectively, and each encoding operator corresponds 2 bits, and specific encoding operators are listed as follows:

$$\begin{aligned} {U_{00}} = \left[ {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}1 \end{array}} \right] ,\mathrm{{ }}{U_{01}} = \left[ {\begin{array}{*{20}{c}} 0&{}1\\ 1&{}0 \end{array}} \right] ,\mathrm{{ }}{U_{10}} = \left[ {\begin{array}{*{20}{c}} 0&{}{ - 1}\\ 1&{}0 \end{array}} \right] ,\mathrm{{ }}{U_{11}} = \left[ {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}{ - 1} \end{array}} \right] \end{aligned}$$
(14)

For example, assume that \(S's\) message is “101101...”, and then it will perform \({U_{10}}\) on the particle \(\left| \Phi \right\rangle _{_{{S_1}}}^1\), perform \({U_{11}}\) on the particle \(\left| \Phi \right\rangle _{_{{S_1}}}^2\), perform \({U_{01}}\) on the particle \(\left| \Phi \right\rangle _{_{{S_1}}}^3\)...

Step 4 Measurement publishing

Receivers perform multi-party entanglement swapping, i.e., every receiver \({Ri}(1 \le i \le m)\) performs a Bell measurement on all its own particles \(\left| \Phi \right\rangle _{_{R{i_1}R{i_2}}}^j(1 \le j \le l)\), respectively, thus obtains l outcomes \(M_{_{R{i_1}R{i_2}}}^j(1 \le j \le l)\), then Ri combines its all measurement outcomes \(M_{_{R{i_1}R{i_2}}}^j(1 \le j \le l)\) as a sequence \({M_{Ri}}\), whose structure is shown in Fig. 3 and its length is 2l.

Fig. 3
figure 3

Combination of measurement outcomes

Full size image

Then every Ri publishes its combinational measurement outcome \({M_{Ri}}\).

Step 5 Security ensuring

After all receivers Ri publish their outcomes \({M_{R{i}}}\), S needs to detect if there exists a liar in a group or an external attack on EPR channels.

(5.1) S performs a Bell measurement on its particles \({\left| \Phi \right\rangle _{{S_1}{S_2}}^j(1 \le j \le l)}\), respectively, and obtains l outcomes \(M_{{S_1}{S_2}}^j(1 \le j \le l)\), then it combines them as \({M_S}\) in the same way as Ri does. Because S has encoded a message on its particles in Step 3 Message encoding, \({M_S}\) is the outcome after encoding. To perform security ensuring, S should recover \({M_S}\) to \({M'_S}\), which is the outcome without being encoded. For example, if S performs an encoding operator \({U_{01}}\) on a certain particle \(\left| \Phi \right\rangle _{{S_1}}^j(1 \le j \le l)\), the measurement outcome of \(M_{{S_1}{S_2}}^j\) is \(\left| {{\psi ^ - }} \right\rangle \) corresponding to 11, so \(M'^j_{{S_1}{S_2}}\) can be obtained according to \(M_{{S_1}{S_2}}^j = {U_{01}}M'^j_{{S_1}{S_2}}\) by \(M'^j_{{S_1}{S_2}} = 11 \oplus 01 = 10\). In this way, S can get all \(M'^j_{{S_1}{S_2}}(1 \le j \le l)\) and combine them as \({M'_S}\).

(5.2) According to the law of multi-party entanglement swapping, for a certain \(j(1 \le j \le l)\), the following equation should be satisfied:

$$\begin{aligned} {{M'}_{{S_1}{S_2}}^j} \oplus M_{R{1_1}R{1_2}}^j \oplus M_{R{2_1}R{2_2}}^j... \oplus M_{R{m_1}R{m_2}}^j = O_{{S_2}R{1_1}}^j \oplus O_{R{1_2}R{2_1}}^j \oplus O_{R{2_2}R{3_1}}^j \oplus \cdots \oplus O_{R{m_2}{S_1}}^j \end{aligned}$$
(15)

We assume that the original state O of all EPR pairs is in the state of \(\left| {{\phi ^ + }} \right\rangle \), which corresponds to “00”, so in Eq. (15), \(O_{{S_2}R{1_1}}^j = O_{R{1_2}R{2_1}}^j = \cdots = O_{R{m_2}{S_1}}^j = 00\). For convenient description, we denote \({O_{k}}\) as a sequence that consists of k “0”, so Eq. (15) can be rewritten as:

$$\begin{aligned} {M'}_{{S_1}{S_2}}^j \oplus M_{R{1_1}R{1_2}}^j \oplus M_{R{2_1}R{2_2}}^j... \oplus M_{R{m_1}R{m_2}}^j = {O_2} \oplus {O_2} \oplus \cdots \oplus {O_2}\mathrm{{ = }}{O_2} \end{aligned}$$
(16)

Similarly, for combinatorial measurement outcomes, we can get:

$$\begin{aligned} {M'_S} \oplus {M_{R1}} \oplus {M_{R2}} \oplus \cdots \oplus {M_{Rm}} = {O_{2l}} \oplus {O_{2l}} \oplus \cdots \oplus {O_{2l}} = {O_{2l}} \end{aligned}$$
(17)

Where \({O_{2l}}\) is a sequence of 2l “0”.

(5.3) S checks Eq. (17). If Eq. (17) works, it means measurement outcomes satisfy the law, so S publishes \({M_S}\). Otherwise, there may be a liar or an external attack, so the scheme terminates.

Step 6 Message decoding

Since all receivers’ outcomes \({M_{R{i}}}\) and the sender’s outcome \({M_S}\) are published, all receivers \({Ri}(1 \le i \le m)\) can decode the message from S by:

$$\begin{aligned} {M'_S} = {M_{R1}} \oplus {M_{R2}} \oplus \cdots \oplus {M_{Rm}} \oplus {O_{2l}} \end{aligned}$$
(18)
$$\begin{aligned} {M_S} = {({U_X})^{ \otimes l}}{M'_S} \end{aligned}$$
(19)

According to Eq. (18), \({M'_S}\), which is the outcome of S without encoding, can be obtained. Then l encoding operators \({U_X}\) can be obtained by comparing \({M_S}\) and \({M'_S}\) and each \({U_X}\) corresponds to 2 bits, so a \(2l-bit\) message is obtained by all receivers, the one-to-many mode completes.

3.2 Many-to-one mode

In the many-to-one mode, one node will be selected to be a receiver and receive messages from the rest of nodes, which are senders. It is also common in communication networks. For example, a node needs to collect some information from the rest of nodes, or some nodes have information needed to converge to one central node. Without loss of generality, as shown in Fig. 4, we assume the number of senders is m. Senders are represented by \({Si}(1 \le i \le m)\), while the only receiver is represented by R.

Fig. 4
figure 4

Many-to-one mode

Full size image

Step 3 Message encoding

In the many-to-one mode, we assume each sender \({Si}(1 \le i \le m)\) has its own message with the length of 2l to send, so each node in a coordinated group prepares ml EPR particles entangled with two adjacent nodes, respectively, i.e., ml particles are entangled with next adjacent node’s particles, and other ml particles are entangled with previous adjacent node’s particles. The whole quantum system can be described as:

$$\begin{aligned} \left| \Phi \right\rangle = \prod \limits _{j = 1}^{ml} {{{\left| \Phi \right\rangle }^j}} = \prod \limits _{j = 1}^{ml} {\left( O_{_{{R_2}S{1_1}}}^j \otimes O_{_{S{1_2}S{2_1}}}^j \otimes \cdots \otimes O_{_{S{{(m - 1)}_2}S{{m}_1}}}^j \otimes O_{_{S{m_2}{R_1}}}^j\right) }\qquad \end{aligned}$$
(20)

(3.1) Each sender Si has a \(2l-bit\) message to send. One encoding operator can encode a two-bit message, and each sender needs l particles to encode a message. Consider the particles index of this mode is from 1 to ml, each Si can encode its \(2l-bit\) message on l particles, which are \(\left| \Phi \right\rangle _{S{i_1}}^j((i - 1)l + 1 \le j \le il)\), i.e., sender S1 encodes its message on \(\left| \Phi \right\rangle _{S{1_1}}^j(1 \le j \le l)\), sender S2 encodes its message on \(\left| \Phi \right\rangle _{S{2_1}}^j((l + 1) \le j \le 2l)\)..., encoding operator is the same as Eq. (10).

(3.2) After encoding, senders perform multi-party entanglement swapping, i.e., each sender \(Si(1 \le i \le m)\) performs a Bell measurement on its own particles \(\left| \Phi \right\rangle _{S{i_1}S{i_2}}^j(1 \le j \le ml)\), respectively, and thus get ml outcomes \(M_{S{i_1}S{i_2}}^j(1 \le j \le ml)\). Then Si combines them as \({M_{Si}}\) and publishes it.

Step 4 Message decoding

(4.1) After all \({M_{Si}}(1 \le i \le m)\) are published, R performs a Bell measurement on the particles \(\left| \Phi \right\rangle _{{R_1}{R_2}}^j(1 \le j \le ml)\), respectively, and gets ml outcomes \(M_{{R_1}R_2^{}}^j(1 \le j \le ml)\), then it combines them as \({M_R}\).

(4.2) For sender \({S_1}\), it encodes a \(2l-bit\) message on l particles \(\left| \Phi \right\rangle _{S{1_1}}^j(1 \le j \le l)\), according to the law of multi-party entanglement swapping, the following formula works from the first number to 2lth number:

$$\begin{aligned} {M_R} \oplus {M'_{S1}} \oplus {M_{S2}} \oplus \cdots \oplus {M_{Sm}} = {O_{2ml}} \oplus {O_{2ml}} \oplus \cdots \oplus {O_{2ml}}={O_{2ml}} \end{aligned}$$
(21)

where \({M'_{S1}}\) is the measurement outcome of \({S_1}\) without encoding, and \({O_{2ml}}\) is a sequence with 2ml 0. From Eq. (21), \({M'_{S1}}\) can be obtained by:

$$\begin{aligned} {M'_{S1}} = {M_R} \oplus {M_{S2}} \oplus \cdots \oplus {M_{Sm}} \end{aligned}$$
(22)

Equation (22) also only works from the first number to the 2lth number. Note that S1 encodes its \(2l-bit\) message on \(\left| \Phi \right\rangle _{S{1_1}}^j(1 \le j \le l)\), 2l number is enough to decode \(S1's\) message.

By comparing \(S1's\) measurement outcome \({M_{S1}}\) after encoding and outcome \({M'_{S1}}\) without encoding from the first number to the 2lth number, R can obtain l encoding operators \({U_X}\):

$$\begin{aligned} {M_{S1}} = {({U_X})^{ \otimes l}}{M'_{S1}} \end{aligned}$$
(23)

Each \({U_X}\) corresponds to 2 bits, so R can obtain a \(2l-bit\) message from S1.

Similarly, for each Si, Eq. (24) works from the \((2\left( {i - 1} \right) l + 1)\)th number to the (2il)th number:

$$\begin{aligned} {M'_{Si}}= & {} {M_R} \oplus {M_{S1}} \oplus \cdots \oplus {M_{Sm}}(except\mathrm{{ }}{M_{Si}}) \end{aligned}$$
(24)
$$\begin{aligned} {M_{Si}}= & {} {({U_X})^{ \otimes l}}{M'_{Si}} \end{aligned}$$
(25)

According to Eq. (25), R compares \({M_{Si}}\) and \({M'_{Si}}\) from the \((2\left( {i - 1} \right) l + 1)\)th number to the (2il)th number to get l \({U_X}\), thus obtains a \(2l-bit\) message from Si. When R obtains messages from all \(Si(1 \le i \le m)\), the many-to-one mode completes.

3.3 Extension of many-to-one mode: one-to-some mode

In the many-to-one mode, a receiver obtains all messages from senders, then the only receiver R may wish these messages are again sent to some nodes in a coordinated group, which is called one-to-some mode.

Compared with the one-to-many mode, the one-to-some mode realizes more efficient communication by means of using the owned measurement outcomes. Note that in the many-to-one mode, senders cannot get a message from each other for the reason that they do not know the measurement outcome \({M_R}\) of R, so they cannot decode a message from other senders. Based on above analysis, if R wants to send these messages to some nodes, it just needs to send the outcome \({M_R}\) to them, then they can decode messages. We define the nodes that R wants to send messages to as node D, and \(D \in \left\{ {S1,S2,\ldots ,{S_m}} \right\} \).

According to the existence of EPR channel between R and D, there are two cases for the one-to-some mode following the process of the many-to-one mode:

Case 1 D has a direct EPR channel with R.

Step 5 R will send \({M_R}\) to D by teleportation. Concretely, they agree on two orthogonal states corresponding to a classical bit, such as \(\{ \left| 0 \right\rangle \rightarrow 0,\left| 1 \right\rangle \rightarrow 1\} \), and then R prepares qubits that represent \({M_R}\) and sends them to D by teleportation.

Step 6 After D gets \({M_R}\) from R, considering \({M_R}\), all \({M_{S_i}}\), and the law of multi-party entanglement swapping, D can obtain messages from all \({S_i}\) as R does.

Case 2 D has no direct EPR channels with R.

In a quantum network, it is common that a node needs to transmit a message to a remote node without direct EPR channels. To solve this problem, quantum routing establishment can be applied. Concretely, a routing path is chosen and some intermediate nodes are assigned to be assistants. Intermediate nodes consume their EPR resources, but know nothing about messages, they are just assistants who can help a sender transmit qubits to receivers. Quantum routing establishment has been well studied[17, 18], which can be applied to send \({M_R}\) from R to D.

Step 5 R prepares qubits that represents \({M_R}\) and send them to D by quantum routing establishment.

Step 6 After receiving \({M_R}\) from R, D can obtain messages from all \({S_i}\) as R does.

4 Performance analysis

4.1 Full group sharing

In the many-to-one mode, the only receiver R can get a message from a certain sender \(S_i(1 \le i \le m)\) by:

$$\begin{aligned} {M'_{Si}}= & {} {M_R} \oplus {M_{S1}} \oplus {M_{S2}}... \oplus {M_{Sm}} (except{M_{Si}}) \end{aligned}$$
(26)
$$\begin{aligned} {M_{Si}}= & {} {({U_X})^{ \otimes l}}{M'_{Si}} \end{aligned}$$
(27)

For each Si, Eqs. (26) and (27) work from the \((2(i - 1)l + 1)\)th number to the 2ilth number, R can get l \({U_X}\), thus get a \(2l-bit\) message from each Si.

Note that R does not publish its own measurement outcome \({M_R}\), without which senders cannot read out messages from each other.

After the many-to-one mode finishes, R may want these messages to be obtained by some Si in a group, so it will send \({M_R}\) to those Si, which is the case of one to some.

Note that in the one-to-some mode, we define nodes that R wants to send messages to as a node set D, and \(D \in \left\{ {S1,S2,\ldots ,{S_m}} \right\} \). When transmitting \({M_R}\), intermediate nodes may be needed if there are no direct EPR channels, we allow each node’s transmission to be a unit load and define the whole transmission load as T.

Fig. 5
figure 5

Transmission load

Full size image

Through the analysis of transmission load T under different situations with D, we summarize two following theorems:

Theorem 1

For a certain D, the whole transmission load T meets , where denotes the nearest integer not less than it.

Proof

If D and R have a direct EPR channel, just as S1 in the left part of Fig. 5, then R can transmit \({M_R}\) to D directly by teleportation, which only costs one load for R, in this best condition, \(T=1\). Consider a worst condition, if D is in the farthest position away from R, i.e., D is in the middle of all Si, just as Sp in the left part of Fig. 5. In this condition, it needs a half of nodes, S1, S2,..., \(S(p-1)\) to be intermediate nodes to assist R to transmit \({M_R}\), it needs nodes’ transmission, so . From the above analysis, the whole transmission load T for a certain D meets . \(\square \)

Theorem 2

If R wants every \({R_i}\) to obtain all messages, i.e., the number of D is equal to m, then the whole transmission load T meets \(T = m\).

Proof

If the number of D is m, R wants to send messages to all Ri, which is also a common requirement that messages are shared to a whole group. We know that Ri can get all messages only if they can get \({M_R}\). Consider all Ri are D and there are EPR channels between adjacent nodes, R just needs to send \({M_R}\) to its adjacent node, namely S1 and Sm, by teleportation, which cost 2 loads, then S1 and Sm sends \({M_R}\) to S2 and \(S(m-1)\), which cost 1 load, respectively, and S2 and \(S(m-1)\)...., which is shown in the right part of Fig. 5. Finally, when \({M_R}\) is sent to Sp, all Si get \({M_R}\). In this condition, each transmission occurs directly by teleportation between adjacent nodes, it cost 1 load for each node, so the whole transmission load is \(T = m\). \(\square \)

4.2 Resource consumption

The resources our scheme consumes are EPR pairs for entanglement swapping and classical bits for measurement outcome publishing. Since EPR resource is more expensive, we only consider it rather than classical bits.

In our scheme, EPR resource is used for two purposes. One is used for coordinated transmission based on multi-party entanglement swapping in the one-to-many mode or the many-to-one mode, and the other is used for constructing a routing path to teleport \({M_R}\) to node D in the one-to-some mode.

In order to describe the resource consumption more clearly, we define G as the efficiency of EPR resource:

$$\begin{aligned} G = \frac{M}{R} \end{aligned}$$
(28)

where M is the total amount of messages that all receivers obtain, R is the EPR amount that whole group consumes, and G depicts the efficiency of EPR resource to evaluate how many messages to be transmitted each EPR pair achieves. Note that there are \((m+1)\) nodes in a coordinated group, including sender and receiver, and each sender’s message length is 2l. The detailed resource consumption is listed in Table 1.

Table 1 Resource consumption and efficiency
Full size table

From Table 1, we can know that the efficiency in the one-to-many mode is \(\frac{2m}{{m + 1}}\), while the efficiency in the many-to-one mode is \( \frac{2m}{{{{(m + 1)}^2}}}\). In the many-to-one mode, all senders coordinate to send messages to the only receiver, but each sender encodes its message only on l EPR particles, which results in lower efficiency. In the extended mode of the many-to-one mode, namely the one-to-some mode for full group sharing, EPR pairs are used to teleport \({M_R}\), which helps decode all senders and achieve the efficiency of \(G=2m\). Obviously, each performance item of the one-to-some mode is better than that of the one-to-many mode.

EPR pair plays an important role in our QCoMP communication scheme. It is not only the organization foundation of a coordinated group, but also the carrier for encoding a message. Firstly, our scheme is based on quantum multi-party entanglement swapping. To perform multi-party entanglement swapping, an organized group must meet two requirements: (1) Nodes form a closed loop node by node, i.e., each node has a previous neighbor and a next neighbor. (2) Adjacent nodes have shared EPR pairs. All of the above organization of a coordinated group needs EPR channels. Secondly, EPR pairs are carriers that encode messages. Concretely, whether in the one-to-many mode or the many-to-one mode, a message is encoded on a sender’s own particles, which is the local particle 1 entangled with the previous adjacent node’s particle 2, and each particle 1 can perform one of four unitary operators corresponding to a 2-bit message. Receivers can decode messages from published measurement outcomes according to the specific law of multi-party entanglement swapping. Meanwhile, the QCoMP communication scheme is designed to organize a coordinated group and realize multi-point transmission. In fact, EPR pairs are previously arranged among nodes in a quantum network, so there is a high probability of existing shared pairs between neighbor nodes. As a result, nodes can flexibly organize a coordinated group as long as they have communication desire and can form a closed loop without limitation to a specific number. However, there may occur a bad case that sometimes nodes cannot form a closed loop of EPR channels during the process of organizing a group, i.e., there is a lack of EPR channels between some nodes which may be far away between each other. In this case, a group can invite another node to join the group to fill up the lack of EPR channels, then the group can form a closed loop with new nodes.

5 Security analysis

Our scheme aims to realize coordinated transmission in a quantum network. Concretely, receivers coordinate to receive a message from one sender (in the one-to-many mode), or senders coordinate to send their messages to one receiver (in the many-to-one mode).

Coordinated transmission is the purpose and highlight of our scheme. Because multiple parties are involved in coordinated networks, our scheme is exposed to more security threats. Attackers may try to perform various attacks to damage communication and obtain messages. Our scheme faces different security challenges in the one-to-many mode and the many-to-one mode, so the security analysis will organized from these two aspects.

5.1 Under one-to-many mode

5.1.1 Intercept–resend attack

Our scheme assumes that adjacent nodes initially share EPR pairs, which can be used for multi-party entanglement swapping. Practically, the shared EPR pair is prepared in one party, then it holds one particle of the EPR pair and transmits the other particle to next party, thus they can share an EPR channel. During the process of EPR pair distribution, the transmitted particle is easily and frequently attacked by an external attacker. An external attacker may intercept the transmitted particle and resend a fake particle prepared by itself to the corresponding receiver, which is called intercept–resend attack.

Fig. 6
figure 6

Security of one-to-many mode

Full size image

Without loss of generality, we take an example of four-party coordinated networks to analyze this type of attack. As shown in left subgraph of Fig. 6, E is an external attacker who launches an intercept–resend attack, it intercepts the transmitted particle from S to R1 (particle 1 inside E), then it prepares an EPR pair (particle \(1'\) inside E and particle 1 inside R1) and sends one particle of the pair to R1. Similarly, E intercepts the transmitted particle from R1 (particle \(2'\) inside E), then it prepares another EPR pair (particle 2 inside E and particle 1 inside R2) and sends one particle of the pair to R2. As a result, E has shared EPR channels with S, R1 and R2. In fact, it successfully takes the place of R1 in the coordinated network, whereas the other normal nodes are not aware of that situation. If the communication continues without discovering E, E can obtain messages from the Bell measurement outcomes of all other parties and its measurement outcome on its particles 1 and 2:

$$\begin{aligned} {M'_{{S_1}{S_2}}}= & {} {M_{{E_1}{E_2}}} \oplus {M_{R{2_1}R{2_2}}} \oplus {M_{R{3_1}}}{M_{R{3_2}}} \end{aligned}$$
(29)
$$\begin{aligned} {M_{{S_1}{S_2}}}= & {} {U_X}{M'_{{S_1}{S_2}}} \end{aligned}$$
(30)

As described in Step 5 Security ensuring, the one-to-many mode can detect such attack. Only if the attacker E passes the checking step, can it obtain messages from R in subsequent steps. In the checking step, R will take all receivers’ measurement outcomes, i.e., R1, R2, R3, into consideration to examine whether they meet the law of multi-party entanglement swapping:

$$\begin{aligned} {M'_{{S_1}{S_2}}} = {M_{R{1_1}R{1_2}}} \oplus {M_{R{2_1}R{2_2}}} \oplus {M_{R{3_1}R{3_2}}} \end{aligned}$$
(31)

Since the outcome \({M_{R{1_1}R{1_2}}}\) is not relevant with other outcomes, which is replaced by \({M_{{E_1}{E_2}}}\), the relationship should be:

$$\begin{aligned} {M'_{{S_1}{S_2}}} = {M_{{E_1}{E_2}}} \oplus {M_{R{2_1}R{2_2}}} \oplus {M_{R{3_1}}}{M_{R{3_2}}} \end{aligned}$$
(32)

The security check (31) can be passed only if \({M_{R{1_1}R{1_2}}}={M_{{E_1}{E_2}}}\). Because of the randomness of Bell measurement, the probability of \({M_{R{1_1}R{1_2}}}={M_{{E_1}{E_2}}}\) is 25%. In the one-to-many mode, each round of multi-party entanglement swapping encodes two-bit messages of a sender. Assume that the length of a sender’s message is l bits, then the probability for attacker E to pass the checking is \({\left( {25\% } \right) ^{\frac{l}{2}}}\), while l is large enough, the probability that E can pass the checking is approximately 0.

5.1.2 Noisy channel attack

The security analysis above is based on an ideal channel. However, in reality, due to the fluctuation of the birefringence in optical fiber, transmitted quantum particles will suffer from noises over the channel. An external attacker E may hide its attack under the noise of quantum channel. In a noisy quantum channel, we assume that the quantum bit error rate (QBER) caused by channel noise is \(\delta \) and \(\delta \approx 5.4\mathrm{{\% }}\)[19]. The attacker E can hide its attack under the noise if QBER introduced by it is smaller than \(\delta \). Comparatively, in the one-to-many mode, QBER introduced by E is 75%, which is far larger than \(\delta \). Therefore the attacker will be detected for reason of high QBER it brings.

5.1.3 Collusion attack

Our scheme is based on the cooperation of all participants. It is inevitable that some small group may try to deceive. For example, in the one-to-many mode, some receivers may collude and launch an internal attack to obtain correct messages from a sender, while other receivers obtain incorrect messages, which is called collusion attack. We also take an example of four-party coordinated networks to analyze this attack. As shown in right subgraph of Fig. 6, R1 and R2 are dishonest receivers and they may take strategies to deceive, their goal is to obtain correct messages from S while letting R3 obtain incorrect messages. So they publish incorrect Bell measurement outcomes as their strategies.

There are two feasible strategies:

(1) Only one of them publishes the incorrect measurement outcomes.

Here we assume that a liar is R1, it publishes the incorrect outcome \(M_{R{1_1}R{1_2}}^\mathrm{{*}}\), while the correct one is \({M_{R{1_1}R{1_2}}}\). A sender S will launch security checking in Step 5 Security ensuring after all receivers publish their measurement outcomes:

$$\begin{aligned} {M'_{{S_1}{S_2}}} = {M_{R{1_1}R{1_2}}} \oplus {M_{R{2_1}R{2_2}}} \oplus {M_{R{3_1}R{3_2}}} \end{aligned}$$
(33)

The checking equation (33) fails due to \(M_{R{1_1}R{1_2}}^* \ne {M_{R{1_1}R{1_2}}}\), then S will terminate the scheme.

(2) Both of them publish the incorrect measurement outcomes.

R1 and R2 may collude to lie about their measurement outcomes \(M_{R{1_1}R{1_2}}^*\) and \(M_{R{2_1}R{2_2}}^*\), while the correct ones are \(M_{R{1_1}R{1_2}}\) and \(M_{R{2_1}R{2_2}}\). If \(M_{R{1_1}R{1_2}}^* \oplus M_{R{2_1}R{2_2}}^\mathrm{{*}} \ne {M_{R{1_1}R{1_2}}} \oplus {M_{R{2_1}R{2_2}}}\), security checking will fail. In order to pass security checking, R1 and R2 may discuss and make the fake measurement outcomes meet \(M_{R{1_1}R{1_2}}^* \oplus M_{R{2_1}R{2_2}}^\mathrm{{*}}\mathrm{{ = }}{M_{R{1_1}R{1_2}}} \oplus {M_{R{2_1}R{2_2}}}\). Then security checking can be passed. However, in this case, R3 can still obtain correct messages because

$$\begin{aligned} {M'_{{S_1}{S_2}}} = M_{R{1_1}R{1_2}}^\mathrm{{*}} \oplus M_{R{2_1}R{2_2}}^\mathrm{{*}} \oplus {M_{R{3_1}R{3_2}}}\mathrm{{ = }}{M_{R{1_1}R{1_2}}} \oplus {M_{R{2_1}R{2_2}}} \oplus {M_{R{3_1}R{3_2}}}\qquad \end{aligned}$$
(34)

Therefore by collusion attack, R1 and R2 cannot achieve their goal that they obtain a correct message while R3 obtains an incorrect one.

5.2 Under many-to-one mode

5.2.1 Privacy for each other

The many-to-one mode aims to realize a message transmission from multiple senders to one receiver, which meets specific demands of quantum networks. This mode relies on the cooperation of all involved senders. There is an important security requirement of this mode that a sender \(Si(1 \le i \le m)\) cannot obtain messages from other senders \(Sq(1 \le q \le m,q \ne i)\), that is, the message is privacy for each other. All messages from senders can only be obtained by receiver R. The following analyzes how our scheme meets this requirement.

In the many-to-one mode, the EPR pairs between nodes are divided into various subsequences according to particle index, each sender \(Si(1 \le i \le m)\) is allowed to encode his own 2l-bit message on particles with specific index of range \(\left| \Phi \right\rangle _{S{i_1}}^j((i - 1)l + 1 \le j \le il)\).

All \({M_{Si}}\) are measurement outcomes after being encoded, and each sender Si encodes his messages on different index ranges of the outcomes, so for a certain index range from \((2\left( {i - 1} \right) l + 1)\) to (2il), R can decode a message from a corresponding sender \(Si(1 \le i \le m)\) by:

$$\begin{aligned} {M'_{Si}}= & {} {M_R} \oplus {M_{S1}} \oplus \cdots \oplus {M_{Sm}(except {M_{Si}})} \end{aligned}$$
(35)
$$\begin{aligned} {M_{Si}}= & {} {({U_X})^{ \otimes l}}{M'_{Si}} \end{aligned}$$
(36)

Equation (35) can get the \({M'_{Si}}\), which is outcome before being encoding. By comparing \({M'_{Si}}\) and \({M_{Si}}\), R gets l encoding operators \({U_X}\), thus gets a \(2l-\)bit message from Si. Note that R does not publish its outcome \({M_R}\). Lacking of \({M_R}\), all Ri cannot decode other senders’ messages, so the requirement of the many-to-one mode is satisfied.

5.2.2 Discussion

The many-to-one mode relies heavily on cooperation of nodes, which is the foundation of the communication and security. In the many-to-one mode, each sender Si encodes its message on particles with a certain index range \(\left| \Phi \right\rangle _{S{i_1}}^j((i - 1)l + 1 \le j \le il)\), the measurement outcome \(M_{Ri}\) it publishes is not only used for transmitting its message to R, but also used for helping other senders to transmit their message. If a sender Si deceives scheme and tells a lie about its measurement outcomes \({M_{Si}}\), then all messages will be decoded incorrectly by receiver R due to the wrong outcome \({M_{Si}}\). Unfortunately, our scheme has no checking step to detect a internal liar in the many-to-one mode.

To enhance the security of the many-to-one mode, some extra checking steps can be introduced into the scheme, e.g., after decoding all messages, R may randomly choose several senders and send decoded messages by teleportation to them to ensure whether the decoded messages are correct or not. If messages are decoded correctly, the chosen nodes will send back an acknowledgment message to R, then R knows messages are decoded correctly and there is no a liar among senders.

6 Conclusion

This paper proposed a quantum coordinated multi-point (QCoMP) communication scheme based on entanglement swapping. It realizes the one-to-many mode, where many receivers coordinate to receive a message from one sender, as well as the many-to-one mode, where many senders coordinate to send messages to one receiver. In the QCoMP communication scheme, EPR pairs provide the foundation of coordinated group organization and also the carrier that encodes messages. As a result, our scheme can flexibly organize a coordinated group and make good use of EPR resources. As for security, one-to-many mode has a detecting step to detect an external attack or an internal liar, but the many-to-one mode needs the coordination of a group to ensure security. As long as nodes coordinate to work, flexible group organization and different communication modes will bring convenience and extension to quantum networks. Furthermore, security enhancement of many-to-one communication can be considered in future work.