1 Introduction

It is well known that the security of quantum communication is assured by physical principles such as Heisenberg uncertainty principle and quantum no-cloning theorem. However, quite a few effective attack strategies have been proposed, such as intercept-resend attack, entanglement-swapping attack, teleportation attack, dense-coding attack, channel-loss attack, denial-of-service attack, correlation-extractability attack, Trojan-horse attack, and participant attack. As the study of quantum cryptography develops, a few branches of quantum cryptography have been studied in recent years, including quantum key distribution (QKD), quantum secret sharing (QSS), quantum secure direct communication (QSDC), quantum encryption algorithm (QEA), quantum identification (QI), and quantum signature (QS). Quantum cryptography is based on the physical characteristics, e.g., eavesdropping can be detected by means of the collapse of a quantum state during the measurement, which combines quantum theory with classical cryptography and utilize quantum effect for achieving unconditional security.

Quantum signature that concerns about the authenticity and non-repudiation of messages on insecure quantum channels is an important research topic in quantum cryptography. So far, a few quantum signature schemes have been proposed. In 2001, Gottesman and Chuang [1] proposed the first quantum signature scheme based on quantum one-way functions and quantum swap test. In this scheme, the public key can only be used once for signing merely one bit of message each time. In 2002, Zeng and Keitel [2] proposed a pioneering arbitrated quantum signature (AQS) protocol which can be used to sign both classical message and quantum one. This scheme uses the correlation of Greenberger–Horne–Zeilinger (GHZ) triplet states and quantum one-time pads to ensure the security. To verify the validity of a signature, as a necessary and important technique, probabilistic comparison of two unknown quantum states was also introduced. This work provides an elementary model to sign a quantum message. Although it was mentioned that both known and unknown quantum states could be signed, there were some corresponding comments about whether it is suitable for unknown messages [3, 4]. Then, a variety of quantum signature schemes based on AQS have been proposed. Lee et al. [5] proposed two quantum signature schemes with message recovery. One scheme used a public board and the other did not, but his schemes rely on the availability of an arbitrator and can be signed only by one user. Wang et al. [6] proposed an arbitrated quantum signature scheme with single photons. Zeng et al. [7] proposed a true quantum signature algorithm based on continuous-variable entangled state. A key pair, i.e., private signature key and public verification key, is generated based on a one-way function. In these arbitrated signature schemes, the arbitrator can have access to the contents of the messages, and therefore, the security of most arbitrated signature schemes depends heavily on the trustworthiness of the arbitrator. Furthermore, the existence of an arbitrator can reduce the communication efficiency of the whole system. In 2007, Wen and Liu [8] proposed a quantum signature scheme without an arbitrator. Their scheme can be used to sign general quantum superposition states. However, by claiming that the signing key was lost or stolen, a signer in a quantum signature scheme without an arbitrator can later deny sending a signature. Li et al. [9] found that in the Zeng’s scheme, the arbitrator is unnecessary to be entangled, and thus, the GHZ states can be replaced by Bell states and presented a Bell-state-based AQS protocol. His scheme simplified Zeng’s protocol and provided higher efficiency in transmission. Zou et al. [10] further achieved AQS without entangled state. Yang and Wen [11, 12] proposed a pioneering work in arbitrated quantum signature of classical messages resistant to collective amplitude damping noises. By using the technique of decoherence-free (DF) subspaces to protect quantum computation and transmission, their scheme works over such a noisy quantum channel. Later, Chong et al. [13] pointed out a security flaw in Yang and Wen’s scheme, in which a legitimate but malicious user can perform Trojan-horse attacks to reveal the other party’s secret key without being detected. Based on Yang and Wen’s idea, Hwang et al. [14] proposed a new arbitrated quantum signature of classical messages against collective amplitude damping noise to prevent Chong et al.’s Trojan-horse attacks. Moreover, he further pointed out that in Yang and Wen’s scheme, the arbitrator may not be able to solve the dispute between two users even if Trojan-horse attacks are not performed, i.e., if the signer denies his/her signature, or the verifier denies his/her verification, the arbitrator cannot do anything at all to solve the dispute. To protect the privacy of message owners, Wen et al. [15] proposed the first quantum group signature scheme by using quantum teleportation. Xu et al. [16] proposed a quantum group blind signature scheme by combining the properties of group signature and blind signature. Recently, Shi et al. [17] proposed a quantum communication scheme for blind signature based on two-particle entangled quantum system to create a novel systemetrical quantum cryptosystem. All the messages are encrypted by the private key of the sender Alice during the communication and the authenticity verification of signatures, and an arbitrator’s batch efficient proxy signature is applied.

In order to authenticate the identity of data source in a network, homomorphic signature scheme [18] is considerably paid attention to instead of standard signature schemes in classical cryptography. However, homomorphic signature schemes of classical information are inapplicable in quantum networks. It is believed that homomorphic signature of quantum information is more meaningful and difficult than its counterpart in classical cryptography. Particularly, homomorphic signature in form of quantum states is desired for quantum networks. On one hand, the main problem is how to design a signature operation for quantum states. On the other hand, the authentication of different data sources is also a very hard problem for classical networks, so it is necessary to explore whether it is a hard problem for quantum networks or not. If quantum homomorphic signature scheme is feasible, it will be very helpful to enhance the security of quantum networks. However, a solution to quantum homomorphic signature still remains open. It is crucial to find an equivalent quantum homomorphic operation to realize signature computing in form of quantum states. Until now, there is no obvious way to combine two quantum signatures (e.g., \({{S}_{1}}\) and \({{S}_{2}}\)) from the senders to realize a homomorphic operation due to the properties of quantum mechanics.

Inspired by entanglement swapping [19], we first propose a new quantum homomorphic signature scheme which can be used to authenticate data packets of multiple streams for quantum networks. After combining two quantum signatures by entanglement swapping, it can generate a new homomorphic signature at the intermediate node. The proposed quantum signature scheme can effectively guarantee the security of secret key and verify the identity of different data sources in a quantum network.

The main contributions of our work are as follows:

(1) A homomorphic operation for quantum states is first found The homomorphic operation is the key part of quantum homomorphic signature. We delicately utilize entanglement swapping for the homomorphic operation which satisfies homomorphic property for the operation of quantum states.

(2) Quantum homomorphic signature scheme is first proposed The property of quantum homomorphic signature scheme is derived. It contributes to the signature operation in the bottleneck nodes of quantum network. It also contributes to the authentication of multi-source unicast stream or single-source multicast stream. Our scheme provides a convenient model to combine authentication into quantum networks, which would be significant to enhance the security of quantum communication.

This paper is structured as follows. In Sect. 2, we introduce the related works, including homomorphic signature and entanglement swapping. Section 3 mainly focuses on the quantum homomorphic signature scheme. Then, we give a detailed security analysis in Sect. 4 and discuss the network scenario of quantum homomorphic signature for different streams in Sect. 5. Section 6 is our conclusion.

2 Related works

2.1 Homomorphic signature

Homomorphism can be divided into two types: additive homomorphism and multiplicative homomorphism [20]. Given variables \({{X}_{1}}\) and \({{X}_{2}}\), a function \(\phi \) is additively homomorphic if there exists a function \(f\) satisfying \(\phi \left( {{X}_{1}}+{{X}_{2}} \right) =f\left( \phi \left( {{X}_{1}} \right) ,\phi \left( {{X}_{2}} \right) \right) \). Similarly, \(\phi \) is multiplicative homomorphic if there exists a function \(f\) satisfying \(\phi \left( {{X}_{1}}\times {{X}_{2}} \right) =f\left( \phi \left( {{X}_{1}} \right) ,\phi \left( {{X}_{2}} \right) \right) \). Homomorphic signature scheme is based on homomorphic algorithm. Assume that a node receives messages \(( {{E}_{1}},{{E}_{2}},\ldots ,{{E}_{n}} )\) and corresponding signatures \(( \phi ( {{E}_{1}} ),\phi ( {{E}_{2}} ), \ldots ,\phi ( {{E}_{n}} ) )\), where \(\phi \) is additively homomorphic. If this node wants to generate a signature on \({{a}_{1}}{{E}_{1}}+{{a}_{2}}{{E}_{2}},\ldots , +{{a}_{n}}{{E}_{n}}\), it can obtain the signature by means of \(S=f( \phi ( {{E}_{1}} ),\phi ({{E}_{2}} ),\ldots , \phi ( {{E}_{n}} ) )\) equal to \(\phi ( {{a}_{1}}{{E}_{1}}+{{a}_{2}}{{E}_{2}},\cdot \cdot \cdot +{{a}_{n}}{{E}_{n}} )\). A concrete example of homomorphic signature scheme BFKW was given by Boneh et al. [21]. Hence, homomorphic signature scheme can generate a new signature on its message without the private keys of data sources, which is very important to distributed networks and can be used to generate new signatures at intermediate nodes through directly manipulating the original signatures of received messages without encryption operation.

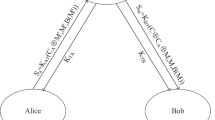
A general quantum signature model is conjectured just as shown in Fig. 1. By sharing an EPR pair (denoted as \({\left| \psi \right\rangle }_{12}\)) with a verifier \(V\), a signer \(A\) can sign on its classical information \(X\) by means of performing a corresponding unitary operation on its particle 2. For the aggregation of multiple signatures, it is the most straight idea to guarantee that each signer shares an EPR pair with the aggregator \(C\), then the aggregator generates a new signature. Just as described in Fig. 1, the key is to generate a new homomorphic signature \({{S}_{3}}=U\left( {{X}_{1}}\oplus {{X}_{2}} \right) \cdot {{\left| \psi \right\rangle }_{4}}\) at the aggregator \(C\) according to two signatures \({{S}_{1}}\) and \({{S}_{2}}\). As far as we know, no quantum signature schemes have been proposed to combine homomorphic algorithm till now. The existing quantum signature schemes are also not suitable for quantum network just as described in Introduction. Hence, it is significant to investigate the design of quantum homomorphic signature for the authentication of data sources in quantum networks.

Fig. 1
figure 1

Quantum signature model

Full size image

2.2 Entanglement swapping

Entanglement swapping [19] is a miracle property of quantum entanglement. The key idea of entanglement swapping is that two non-entangled particles (1, 3) become an entangled state by measurement as shown in Fig. 2. Assume the original states of these particles are:

$$\begin{aligned} {{\left| {{\phi }^{+}} \right\rangle }_{12}}&= \frac{1}{\sqrt{2}}\left( {{\left| 00 \right\rangle }_{12}}+{{\left| 11 \right\rangle }_{12}} \right) ,\\ {{\left| {{\psi }^{+}} \right\rangle }_{34}}&= \frac{1}{\sqrt{2}}\left( {{\left| 01 \right\rangle }_{34}}+{{\left| 10 \right\rangle }_{34}} \right) . \end{aligned}$$
Fig. 2
figure 2

Entanglement swapping

Full size image

Then,

$$\begin{aligned}&{{\left| {{\phi }^{+}} \right\rangle }_{12}}\otimes {{\left| {{\psi }^{+}} \right\rangle }_{34}} \nonumber \\&\quad =\frac{1}{2}\left( {{\left| 0001 \right\rangle }_{1234}}+{{\left| 0010 \right\rangle }_{1234}}+{{\left| 1101 \right\rangle }_{1234}}+{{\left| 1110 \right\rangle }_{1234}} \right) \nonumber \\&\quad =\frac{1}{2}\left( {{\left| 0001 \right\rangle }_{1324}}+{{\left| 0100 \right\rangle }_{1324}}+{{\left| 1011 \right\rangle }_{1324}}+{{\left| 1110 \right\rangle }_{1324}} \right) \nonumber \\&\quad =\frac{1}{4}\left[ \left( {{\left| {{\phi }^{+}} \right\rangle }_{13}}+{{\left| {{\phi }^{-}} \right\rangle }_{13}} \right) \right. \left( {{\left| {{\psi }^{+}} \right\rangle }_{24}}+{{\left| {{\psi }^{-}} \right\rangle }_{24}} \right) +\left( {{\left| {{\psi }^{+}} \right\rangle }_{13}}+{{\left| {{\psi }^{-}} \right\rangle }_{13}} \right) \nonumber \\&\left( {{\left| {{\phi }^{+}} \right\rangle }_{24}}-{{\left| {{\phi }^{-}} \right\rangle }_{24}} \right) +\left( {{\left| {{\psi }^{+}} \right\rangle }_{13}}-{{\left| {{\psi }^{-}} \right\rangle }_{13}} \right) \left( {{\left| {{\phi }^{+}} \right\rangle }_{24}}+{{\left| {{\phi }^{-}} \right\rangle }_{24}} \right) \nonumber \\&\quad \quad \left. +\left( {{\left| {{\phi }^{+}} \right\rangle }_{13}}-{{\left| {{\phi }^{-}} \right\rangle }_{13}} \right) \left( {{\left| {{\psi }^{+}} \right\rangle }_{24}}-{{\left| {{\psi }^{-}} \right\rangle }_{24}} \right) \right] \nonumber \\&\quad =\frac{1}{2}\left( {{\left| {{\phi }^{+}} \right\rangle }_{13}}{{\left| {{\psi }^{+}} \right\rangle }_{24}}+{{\left| {{\phi }^{-}} \right\rangle }_{13}}{{\left| {{\psi }^{-}} \right\rangle }_{24}}+{{\left| {{\psi }^{+}} \right\rangle }_{13}}{{\left| {{\phi }^{+}} \right\rangle }_{24}} \right. \nonumber \\&\quad \quad \left. +{{\left| {{\psi }^{-}} \right\rangle }_{13}}{{\left| {{\phi }^{-}} \right\rangle }_{24}}\right) \end{aligned}$$
(1)

According to Eq. (1), if we perform a Bell-state measurement on the particles 1 and 3, the particles 2 and 4 would collapse to another entangled state. For instance, if the measurement result of the particles 1 and 3 is \({{\left| {{\phi }^{+}} \right\rangle }_{13}}\), then the state of the particles 2 and 4 would be \({{\left| {{\psi }^{+}} \right\rangle }_{24}}\).

In other cases, the states of particles after entanglement swapping are shown in Table 1.

Table 1 States of particles after entanglement swapping
Full size table

Note that if we treat the particles 2 and 4 as two signatures, we can transform these two signatures into an entangled state without original data by means of entanglement swapping. Then in the new entangled state, the particle 4 can be treated as a new signature. Here, we take a simple example for illustration. Firstly four operators are defined as follows for convenience:

$$\begin{aligned} {U(00)}&= I=\left| 0 \right\rangle \left\langle 0 \right| +\left| 1 \right\rangle \left\langle 1 \right| =\left( \begin{matrix} 1 &{} 0 \\ 0 &{} 1 \\ \end{matrix} \right) \\ {U(01)}&= {{\sigma }_{x}}=\left| 1 \right\rangle \left\langle 0 \right| +\left| 0 \right\rangle \left\langle 1 \right| =\left( \begin{matrix} 0 &{} 1 \\ 1 &{} 0 \\ \end{matrix} \right) \\ {U(10)}&= {{\sigma }_{z}}=\left| 0 \right\rangle \left\langle 0 \right| -\left| 1 \right\rangle \left\langle 1 \right| =\left( \begin{matrix} 1 &{} 0 \\ 0 &{} -1 \\ \end{matrix} \right) \\ {U(11)}&= -i{{\sigma }_{y}}=\left| 0 \right\rangle \left\langle 1 \right| -\left| 1 \right\rangle \left\langle 0 \right| =\left( \begin{matrix} 0 &{} 1 \\ -1 &{} 0 \\ \end{matrix} \right) . \end{aligned}$$

Assume the signatures are \({{S}_{1}}=U\left( 01 \right) {{\left| \psi \right\rangle }_{2}}={{\sigma }_{x}}{{\left| \psi \right\rangle }_{2}}\) and \({{S}_{2}}=U\left( 10 \right) {{\left| \psi \right\rangle }_{4}}={{\sigma }_{z}}{{\left| \psi \right\rangle }_{4}}\), the state of all particles would be \({{\left| {{\psi }'} \right\rangle }_{12}}\otimes {{\left| {{\psi }'} \right\rangle }_{34}}={{\sigma }_{x}}^{(2)}{{\left| {{\phi }^{+}} \right\rangle }_{12}}\otimes {{\sigma }_{z}}^{(4)}{{\left| {{\phi }^{+}} \right\rangle }_{34}}\), here the superscript (i) means performing an operation on the particle i. After entanglement swapping, the particles 2 and 4 would collapse to an entangled state. Without loss of generality, we assume that the measurement result of the particles 1 and 3 is \({{\left| {{\phi }^{+}} \right\rangle }_{13}}\). Hence according to Table 1, the state of the particles 2 and 4 would be \({{\left| {{\psi }^{-}} \right\rangle }_{24}}\). In comparison with the original resulting state of \({{\left| {{\phi }^{+}} \right\rangle }_{24}}\) after entanglement swapping without signature, we obtain \({{\left| {{\psi }^{-}} \right\rangle }_{24}}=-i{{\sigma }_{y}}{{\left| {{\phi }^{+}} \right\rangle }_{24}}=U\left( 01\oplus 10 \right) {{\left| {{\phi }^{+}} \right\rangle }_{24}}\). This result gives an important hint of relationship between entanglement swapping and homomorphic operation. The key to the design of homomorphic operation is to make the particle 4 become the homomorphic signature result of combining two original signatures. Hence, entanglement swapping provides the possibility of homomorphic operation for quantum signature.

3 Quantum homomorphic signature scheme

Inspired by the idea of entanglement swapping, we propose a quantum homomorphic signature scheme based on entanglement swapping. Assume that the object of a signature is classical information, and the carrier of a signature is quantum information, a signer sends the data of classical bits \({{X}_{1}} ({{X}_{2}})\) with the signature of quantum states to a verifier. Quantum homomorphic signature model is shown in Fig. 3. \({{A}_{1}} ({{A}_{2}})\) are the signers, \({{M}_{1}}\) is the aggregator who aggregates the received signatures to generate a new signature according to original signatures, and \({{M}_{2}}\) is the verifier.

Fig. 3
figure 3

Quantum homomorphic signature model

Full size image

Our signature scheme is defined by a tuple of algorithms (Setup, Sign, Combine, Verify) such that:

  1. (1)

    Setup

Step 1: Quantum key distribution. \({{A}_{1}}({{A}_{2}})\) chooses two classical bits (denoted as \({{Y}_{1}}({{Y}_{2}})\)) as its secret key and shares this key with \({M}_{2}\) by quantum key distribution protocol, such as an improved BB84 protocol with authentication [22] which can defend against middle-man attack, here \({{Y}_{1}},{{Y}_{2}}\in \left\{ 00,01,10,11\right\} \).

Step 2: EPR pair distribution. \({{M}_{1}}\) firstly prepares two pairs of entanglement:

$$\begin{aligned} {{\left| {{\phi }^{+}} \right\rangle }_{12}}&=\frac{1}{\sqrt{2}}\left( \left| {{0}_{1}}{{0}_{2}} \right\rangle +\left| {{1}_{1}}{{1}_{2}} \right\rangle \right) \\ {{\left| {{\phi }^{+}} \right\rangle }_{34}}&=\frac{1}{\sqrt{2}}\left( \left| {{0}_{3}}{{0}_{4}} \right\rangle +\left| {{1}_{3}}{{1}_{4}} \right\rangle \right) . \end{aligned}$$

\({{M}_{1}}\) sends its particles 2 and 4 (denoted as \({{\left| \psi \right\rangle }_{2}}, \ \ {{\left| \psi \right\rangle }_{4}}\)) to \({{A}_{1}}\) and \({{A}_{2}}\), respectively.

  1. (2)

    Sign

After receiving the particle from \({{M}_{1}},\, {{A}_{1}}({{A}_{2}})\) chooses a unitary operator according to the exclusive OR result of its classical bits \({{X}_{1}}({{X}_{2}})\) and key \({{Y}_{1}}({{Y}_{2}})\) and performs a corresponding operation on the particle 2(4).

Note that \({{\left| {{\psi }^{\prime }} \right\rangle }_{12}}=U({X}_{1}\oplus {Y}_{1})^{(2)}{\left| {{\psi }} \right\rangle }_{12}\). Although the particles 1 and 2 belongs to one entangled pair, we view the resulting state of the particle 2(4), namely \({{\left| {{\psi }^{\prime }} \right\rangle }_{2}}({{\left| {{\psi }^{\prime }} \right\rangle }_{4}})\), as the signature of \({{A}_{1}}({{A}_{2}})\) just for convenient description. In fact, the particle 2(4) is in an entangled state and thus has no pure state representation on its own.

Here, the unitary operator corresponding to the classical bits \({{X}_{i}}\) and the key \({{Y}_{i}}\) is chosen as follows:

$$\begin{aligned}&{{X}_{i}}\oplus {{Y}_{i}}=00\rightarrow I=\left( \begin{matrix} 1 &{} 0 \\ 0 &{} 1 \\ \end{matrix} \right) \nonumber \\&{{X}_{i}}\oplus {{Y}_{i}}=01\rightarrow \ {{\sigma }_{x}}\ =\left( \begin{matrix} 0 &{} 1 \\ 1 &{} 0 \\ \end{matrix} \right) \\&{{X}_{i}}\oplus {{Y}_{i}}=10\rightarrow {{\sigma }_{z}}=\left( \begin{matrix} 1 &{} 0 \\ 0 &{} -1 \\ \end{matrix} \right) \nonumber \\&{{X}_{i}}\oplus {{Y}_{i}}=11\rightarrow -i{{\sigma }_{y}}=\left( \begin{matrix} 0 &{} -1 \\ 1 &{} 0 \\ \end{matrix} \right) \nonumber \end{aligned}$$
(2)

Hence after signing phase, the state of the two EPR pairs would be \({{\left| {{\psi }'} \right\rangle }_{12}}=U{{\left( {{X}_{1}}\oplus {{Y}_{1}} \right) }^{(2)}}\cdot {{\left| {{\phi }^{+}} \right\rangle }_{12}},\, {{\left| {{\psi }'} \right\rangle }_{34}}=U{{\left( {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}}\cdot {{\left| {{\phi }^{+}} \right\rangle }_{34}}\).

  1. (3)

    Combine

Step 1: \({{A}_{1}} ({{A}_{2}})\) sends the transformed particle 2(4), namely \({{\left| {{\psi }^{\prime }} \right\rangle }_{2}}({{\left| {{\psi }^{\prime }} \right\rangle }_{4}})\), and the classical bits \({{X}_{1}}\oplus {{Y}_{1}} ({{X}_{2}}\oplus {{Y}_{2}})\) to \({{M}_{1}}\).

Step 2: \({{M}_{1}}\) performs a Bell-state measurement on the particles 1 and 3. Here, we denote \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{13}}\) as the state of the particles 1 and 3 after measurement. Then according to entanglement swapping, the particles 2 and 4 would collapse to the Bell state which can be denoted as \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{24}}\). \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{4}}\) would be the signature of \({{M}_{1}}\), i.e., \({{\left| S \right\rangle }_{{{M}_{1}}}}={{\left| {{\psi }''} \right\rangle }_{4}}\).

Step 3: \({{M}_{1}}\) sends the classical information \({{\left( {{X}_{1}}\oplus {Y}_{1} \right) }}\oplus \left( {{X}_{2}}\oplus {{Y}_{2}} \right) \) and the particles (1, 2, 3, 4) (i.e., \({{\left| {{\psi }''} \right\rangle }_{13}}\otimes {{\left| {{\psi }''} \right\rangle }_{24}}\)) to \({{M}_{2}}\).

  1. (4)

    Verify

After receiving the classical information and the particles from \({{M}_{1}},\, {{M}_{2}}\) can verify the signature as follows:

Step 1: \({{M}_{2}}\) performs a Bell-state measurement on the particles 1 and 3, and obtains \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{13}}\). Note that \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{13}}\) falls to one of the four Bell states according to Table 1. Hence, the Bell-state measurement on the particles 1 and 3 from \({{M}_{2}}\) would be non-destructive.

Step 2: \({{M}_{2}}\) performs a Bell-state measurement on the particles 2 and 4, and obtains \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{24}}\).

Step 3: According to Table 1, \({{M}_{2}}\) compares \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{24}}\) with \({{\left| \psi \right\rangle }_{24}}\), and obtains an operator which satisfies \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{24}}=c\left( Z \right) U{{\left( Z \right) }^{(4)}}\cdot {{\left| \psi \right\rangle }_{24}}\). Here, the superscript (4) means performing an operation on the particle 4, and \(\left| c\left( Z \right) \right| =1\). Consider the resulting state of the original particles after entanglement swapping. If the measurement result of the original particles 1 and 3 satisfies \({{\left| {{\psi }} \right\rangle }_{13}}={{\left| {{\psi }''} \right\rangle }_{13}}\), then we denote \({{\left| {{\psi }} \right\rangle }_{24}}\) as the resulting state of the original particles 2 and 4 after entanglement swapping.

Step 4: \({{M}_{2}}\) compares \({{X}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{1}}\oplus {{Y}_{2}}\) with \(Z\). If \({{X}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{1}}\oplus {{Y}_{2}}=Z,\, {{M}_{2}}\) would confirm that \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{4}}\) is the signature of \({{M}_{1}}\). Then, \({{M}_{2}}\) can calculate \({{X}_{1}}\oplus {{X}_{2}}\) by its keys \({{Y}_{1}}\) and \({{Y}_{2}}\) (which are prior shared with the senders as described in the process of signature). Otherwise \({{M}_{2}}\) would deny the signature.

We take an example to illuminate this scheme more clearly.

Example 1

Assume \({{X}_{1}=00},\, {{Y}_{1}=01},\, {{X}_{2}=01}\) and \({{Y}_{2}=11}\). Then, the signatures of \({A}_{1}\) and \({A}_{2}\) are \({{S}_{1}}=U\left( 00\oplus 01 \right) {{\left| \psi \right\rangle }_{2}}={{\sigma }_{x}}{{\left| \psi \right\rangle }_{2}},\, {{S}_{2}}=U( 01\oplus 11 ){{\left| \psi \right\rangle }_{4}}={{\sigma }_{z}}{{\left| \psi \right\rangle }_{4}}\), respectively. After signing phase, the state of the particles (1, 2, 3, 4) becomes:

$$\begin{aligned} {{\left| {{\phi }^{+}} \right\rangle }_{12}}\rightarrow {{\left| {{\psi }'} \right\rangle }_{12}}&={{\sigma }_{x}}^{(2)}{{\left| {{\phi }^{+}} \right\rangle }_{12}}={{\left| {{\psi }^{+}} \right\rangle }_{34}}\\ {{\left| {{\phi }^{+}} \right\rangle }_{34}}\rightarrow {{\left| {{\psi }'} \right\rangle }_{34}}&={{\sigma }_{z}}^{(4)}{{\left| {{\phi }^{+}} \right\rangle }_{34}}={{\left| {{\phi }^{-}} \right\rangle }_{34}}. \end{aligned}$$

After combining phase, the particles 1(2) and 3(4) would collapse to a Bell state according to entanglement swapping. Here, we assume that \({{\left| {{\psi }''} \right\rangle }_{13}}={{\left| {{\psi }^{+}} \right\rangle }_{13}}\). After receiving the information and signatures (the particles), \({{M}_{2}}\) would obtain that \({{\left| {{\psi }''} \right\rangle }_{24}}={{\left| {{\phi }^{-}} \right\rangle }_{24}}\) by measurement. Then, \({{M}_{2}}\) compares \({{\left| {{\phi }^{-}} \right\rangle }_{24}}\) with the corresponding original state of \({{\left| \psi \right\rangle }_{24}}\) (which equals to \({{\left| {{\psi }^{+}} \right\rangle }_{24}}\) as shown in Table 1). Without modification from attackers, \({{M}_{2}}\) will obtain that \({{\left| {{\psi }''} \right\rangle }_{24}}={{\left| {{\phi }^{-}} \right\rangle }_{24}}=-U{{\left( 11 \right) }^{(4)}}{{\left| \psi \right\rangle }_{24}}=-U{{\left( 11 \right) }^{(4)}}{{\left| {{\psi }^{+}} \right\rangle }_{24}}\), i.e., \({Z=11}\). By verifying whether \(Z\) equals to \({{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}}\) (=11) or not, \({{M}_{2}}\) can confirm that the resulting data \({{X}_{1}}\oplus {{X}_{2}}\) are surely from the senders \({A}_{1}\) and \({A}_{2}\).

4 Scheme analysis

In this section, we give the analysis of the above quantum homomorphic signature scheme.

To prove the homomorphism of our quantum signature scheme, we give two lemmas as follows:

Lemma 1

\(U({{X}_{1}})U({{X}_{2}})\left| \varphi \right\rangle =c( {{X}_{1}},{{X}_{2}} )U( {{X}_{1}}\oplus {{X}_{2}} )\left| \varphi \right\rangle \), where \({{X}_{1}}\), \({{X}_{2}} \in \{00,10,01,11\},\, \left| c\left( {{X}_{1}},{{X}_{2}} \right) \right| =1\).

Proof

Since \(c( {{X}_{1}},{{X}_{2}} )\) depends on \({X}_{1}\) and \({X}_{2}\), its value equals to -1 or 1. Hence, when \(\left| c\left( {{X}_{1}},{{X}_{2}} \right) \right| =1\), the above lemma can be easily proved.

Lemma 2

\({{U}_{1}}^{(1)}\cdot {{U}_{2}}^{(2)}\cdot {{\left| \psi \right\rangle }_{12}}={{c}_{x}}\cdot {{\left( {{U}_{1}}\cdot {{U}_{2}} \right) }^{(2)}}{{\left| \psi \right\rangle }_{12}},\, \left| {{c}_{x}} \right| =1\), where the superscript (i) means performing an operation on the particle i, \({{U}_{1}},{{U}_{2}}\in \left\{ I,{{\sigma }_{x}},{{\sigma }_{z}},-i{{\sigma }_{y}} \right\} ,\, {{\left| \psi \right\rangle }_{12}}\in \left\{ \left| {{\phi }^{+}} \right\rangle ,\left| {{\phi }^{-}} \right\rangle ,\left| {{\psi }^{+}} \right\rangle ,\left| {{\psi }^{-}} \right\rangle \right\} \).

Proof

Assume that \({{U}_{1}}=\left( \begin{matrix} {{x}_{1}} &{} {{x}_{2}} \\ {{x}_{3}} &{} {{x}_{4}} \\ \end{matrix} \right) ,\, {{U}_{2}}=\left( \begin{matrix} {{y}_{1}} &{} {{y}_{2}} \\ {{y}_{3}} &{} {{y}_{4}} \\ \end{matrix} \right) \). Considering \({{U}_{1}},{{U}_{2}}\in \left\{ I,{{\sigma }_{x}},{{\sigma }_{z}},-i{{\sigma }_{y}} \right\} \), we can obtain that

$$\begin{aligned} \left| {{x}_{1}} \right|&=\left| {{x}_{4}} \right| \ \left| {{x}_{2}} \right| =\left| {{x}_{3}} \right| \ \ {{x}_{1}}\cdot {{x}_{2}}=0 \nonumber \\ \left| {{y}_{1}} \right|&=\left| {{y}_{4}} \right| \ \ \left| {{y}_{2}} \right| =\left| {{y}_{3}} \right| \ {{y}_{1}}\cdot {{y}_{2}}=0. \end{aligned}$$
(3)

Take \({{\left| \psi \right\rangle }_{12}}={{\left| {{\phi }^{+}} \right\rangle }_{12}}\) as an example, we obtain that

$$\begin{aligned}&{{U}_{1}}^{(1)}\cdot {{U}_{2}}^{(2)}\cdot {{\left| \psi \right\rangle }_{12}} \\&\quad =\frac{1}{\sqrt{2}}\left\{ \left[ \left( \begin{matrix} {{x}_{1}} &{} {{x}_{2}} \\ {{x}_{3}} &{} {{x}_{4}} \\ \end{matrix} \right) \cdot \left( \begin{matrix} 1 \\ 0 \\ \end{matrix} \right) \right] \otimes \left[ \left( \begin{matrix} {{y}_{1}} &{} {{y}_{2}} \\ {{y}_{3}} &{} {{y}_{4}} \\ \end{matrix} \right) \cdot \left( \begin{matrix} 1 \\ 0 \\ \end{matrix} \right) \right] \right. \\&\qquad + \left. \left[ \left( \begin{matrix} {{x}_{1}} &{} {{x}_{2}} \\ {{x}_{3}} &{} {{x}_{4}} \\ \end{matrix} \right) \cdot \left( \begin{matrix} 0 \\ 1 \\ \end{matrix} \right) \right] \otimes \left[ \left( \begin{matrix} {{y}_{1}} &{} {{y}_{2}} \\ {{y}_{3}} &{} {{y}_{4}} \\ \end{matrix} \right) \cdot \left( \begin{matrix} 0 \\ 1 \\ \end{matrix} \right) \right] \right\} \\&\quad =\frac{1}{\sqrt{2}}\left[ \left( \begin{matrix} {{x}_{1}} \\ {{x}_{3}} \\ \end{matrix} \right) \otimes \left( \begin{matrix} {{y}_{1}} \\ {{y}_{3}} \\ \end{matrix} \right) +\left( \begin{matrix} {{x}_{2}} \\ {{x}_{4}} \\ \end{matrix} \right) \otimes \left( \begin{matrix} {{y}_{2}} \\ {{y}_{4}} \\ \end{matrix} \right) \right] \\&\quad =\frac{1}{\sqrt{2}}\left( \begin{matrix} {{x}_{1}}{{y}_{1}}+{{x}_{2}}{{y}_{2}} \\ {{x}_{1}}{{y}_{3}}+{{x}_{2}}{{y}_{4}} \\ {{x}_{3}}{{y}_{1}}+{{x}_{4}}{{y}_{2}} \\ {{x}_{3}}{{y}_{3}}+{{x}_{4}}{{y}_{4}} \\ \end{matrix} \right) \\ \\&{{\left( {{U}_{1}}\cdot {{U}_{2}} \right) }^{(2)}}{{\left| \psi \right\rangle }_{12}} \\&\quad =\frac{1}{\sqrt{2}}\left( \begin{matrix} 1 \\ 0 \\ \end{matrix} \right) \otimes \left[ \left( \begin{matrix} {{x}_{1}}{{y}_{1}}+{{x}_{2}}{{y}_{3}} &{} {{x}_{1}}{{y}_{2}}+{{x}_{2}}{{y}_{4}} \\ {{x}_{3}}{{y}_{1}}+{{x}_{4}}{{y}_{3}} &{} {{x}_{3}}{{y}_{2}}+{{x}_{4}}{{y}_{4}} \\ \end{matrix} \right) \cdot \left( \begin{matrix} 1 \\ 0 \\ \end{matrix} \right) \right] \\&\qquad + \frac{1}{\sqrt{2}}\left( \begin{matrix} 0 \\ 1 \\ \end{matrix} \right) \otimes \left[ \left( \begin{matrix} {{x}_{1}}{{y}_{1}}+{{x}_{2}}{{y}_{3}} &{} {{x}_{1}}{{y}_{2}}+{{x}_{2}}{{y}_{4}} \\ {{x}_{3}}{{y}_{1}}+{{x}_{4}}{{y}_{3}} &{} {{x}_{3}}{{y}_{2}}+{{x}_{4}}{{y}_{4}} \\ \end{matrix} \right) \cdot \left( \begin{matrix} 0 \\ 1 \\ \end{matrix} \right) \right] \\&\quad =\frac{1}{\sqrt{2}}\left( \begin{matrix} {{x}_{1}}{{y}_{1}}+{{x}_{2}}{{y}_{3}} \\ {{x}_{3}}{{y}_{1}}+{{x}_{4}}{{y}_{3}} \\ {{x}_{1}}{{y}_{2}}+{{x}_{2}}{{y}_{4}} \\ {{x}_{3}}{{y}_{2}}+{{x}_{4}}{{y}_{4}} \\ \end{matrix} \right) \end{aligned}$$

In consideration of Eq. (3), we obtain that

$$\begin{aligned}&{{x}_{1}}=1={{y}_{1}}\rightarrow {{U}_{1}}^{(1)}\cdot {{U}_{2}}^{(2)}\cdot {{\left| \psi \right\rangle }_{12}} \\&\quad =\frac{1}{\sqrt{2}}\left( \begin{matrix} {{x}_{1}}{{y}_{1}}+{{x}_{2}}{{y}_{2}} \\ {{x}_{1}}{{y}_{3}}+{{x}_{2}}{{y}_{4}} \\ {{x}_{3}}{{y}_{1}}+{{x}_{4}}{{y}_{2}} \\ {{x}_{3}}{{y}_{3}}+{{x}_{4}}{{y}_{4}} \\ \end{matrix} \right) =\frac{1}{\sqrt{2}}\left( \begin{matrix} {{x}_{1}}{{y}_{1}} \\ 0 \\ 0 \\ {{x}_{4}}{{y}_{4}} \\ \end{matrix} \right) \\&\quad =\frac{1}{\sqrt{2}}\left( \begin{matrix} {{x}_{1}}{{y}_{1}}+{{x}_{2}}{{y}_{3}} \\ {{x}_{3}}{{y}_{1}}+{{x}_{4}}{{y}_{3}} \\ {{x}_{1}}{{y}_{2}}+{{x}_{2}}{{y}_{4}} \\ {{x}_{3}}{{y}_{2}}+{{x}_{4}}{{y}_{4}} \\ \end{matrix} \right) ={{\left( {{U}_{1}}\cdot {{U}_{2}} \right) }^{(2)}}{{\left| \psi \right\rangle }_{12}} \end{aligned}$$

In other cases, the same conclusion can be drawn. Hence, Lemma 2 is proved.

Property 1

The proposed quantum signature scheme is additively homomorphic.

Proof

According to this scheme, the signature of \({{A}_{i}}\) is \({{\left| {{\psi }^{\prime }} \right\rangle }_{2i}}=U( {{X}_{i}}\oplus {{Y}_{i}} ){{\left| \psi \right\rangle }_{2i}}\). Then, the state of all particles after \({{A}_{i}}\) generates a signature would be transformed into: \({{\left| {{\phi }^{+}} \right\rangle }_{12}}\otimes {{\left| {{\phi }^{+}} \right\rangle }_{34}}\rightarrow {{\left| {{\psi }^{\prime }} \right\rangle }_{1234}}\).

$$\begin{aligned} {{\left| {{\psi }^{\prime }} \right\rangle }_{1234}}&=U{{\left( {{X}_{1}}\oplus {{Y}_{1}} \right) }^{(2)}}{{\left| {{\phi }^{+}} \right\rangle }_{12}}\otimes U{{\left( {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}}{{\left| {{\phi }^{+}} \right\rangle }_{34}} \\&=\frac{1}{2}U{{\left( {{X}_{1}}\oplus {{Y}_{1}} \right) }^{(2)}}U{{\left( {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}}\left( {{\left| 0000 \right\rangle }_{1234}}+{{\left| 0011 \right\rangle }_{1234}} \right. \\&\quad \left. +\,{{\left| 1100 \right\rangle }_{1234}}+{{\left| 1111 \right\rangle }_{1234}} \right) \\&=\frac{1}{2}U{{\left( {{X}_{1}}\oplus {{Y}_{1}} \right) }^{(2)}}U{{\left( {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}}\left( {{\left| {{\phi }^{+}} \right\rangle }_{13}}{{\left| {{\phi }^{+}} \right\rangle }_{24}} \right. \\&\quad \left. + {{\left| {{\phi }^{-}} \right\rangle }_{13}}{{\left| {{\phi }^{-}} \right\rangle }_{24}}+{{\left| {{\psi }^{+}} \right\rangle }_{13}}{{\left| {{\psi }^{+}} \right\rangle }_{24}}+{{\left| {{\psi }^{-}} \right\rangle }_{13}}{{\left| {{\psi }^{-}} \right\rangle }_{24}} \right) \end{aligned}$$

It can be rewritten as follows according to Lemmas 1 and 2:

$$\begin{aligned}&{{\left| {{\psi }^{\prime }} \right\rangle }_{1234}} \\&\quad = \frac{1}{2}\left[ \left( {{\left| {{\phi }^{+}} \right\rangle }_{13}}\right) \left( {{c}_{x}}\cdot U{{\left( {{X}_{1}}\oplus {{Y}_{1}} \right) }^{(4)}}U{{\left( {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}}{{\left| {{\phi }^{+}} \right\rangle }_{24}} \right) \right. \\&\quad \quad + \left( {{\left| {{\phi }^{-}} \right\rangle }_{13}} \right) \left( {{c}_{x}}\cdot U{{\left( {{X}_{1}}\oplus {{Y}_{1}} \right) }^{(4)}}U{{\left( {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}}{{\left| {{\phi }^{-}} \right\rangle }_{24}} \right) \\&\quad \quad +\left( {{\left| {{\psi }^{+}} \right\rangle }_{13}} \right) \left( {{c}_{x}}\cdot U{{\left( {{X}_{1}}\oplus {{Y}_{1}} \right) }^{(4)}}U{{\left( {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}}{{\left| {{\psi }^{+}} \right\rangle }_{24}} \right) \\&\quad \quad +\left( {{\left| {{\psi }^{-}} \right\rangle }_{13}} \right) \left. \left( {{c}_{x}}\cdot U{{\left( {{X}_{1}}\oplus {{Y}_{1}} \right) }^{(4)}}U{{\left( {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}}{{\left| {{\psi }^{-}} \right\rangle }_{24}} \right) \right] \\&\quad =\frac{1}{2}\left[ {{\left| {{\phi }^{+}} \right\rangle }_{13}} \left( {{c}_{x}}\cdot c\left( {{U}_{1}},{{U}_{2}} \right) \cdot U{{\left( {{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}} \right. \right. \\&\left. {{\left| {{\phi }^{+}} \right\rangle }_{24}} \right) + {{\left| {{\phi }^{-}} \right\rangle }_{13}} \left( {{c}_{x}}\cdot c\left( {{U}_{1}},{{U}_{2}} \right) \cdot U{{\left( {{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}} \right. \\&\left. {{\left| {{\phi }^{-}} \right\rangle }_{24}} \right) + {{\left| {{\psi }^{+}} \right\rangle }_{13}} \left( {{c}_{x}}\cdot c\left( {{U}_{1}},{{U}_{2}} \right) \cdot U{{\left( {{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}} \right. \\&\left. {{\left| {{\psi }^{+}} \right\rangle }_{24}} \right) + {{\left| {{\psi }^{-}} \right\rangle }_{13}}\left( {{c}_{x}}\cdot c\left( {{U}_{1}},{{U}_{2}} \right) \cdot U{{\left( {{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}} \right. \\&\left. {{\left| {{\psi }^{-}} \right\rangle }_{24}} \right] \end{aligned}$$

After performing a Bell-state measurement on the particles 1 and 3, we obtain that \({{\left| {{\psi }''}\right\rangle }_{24}}=U({X}_{1}\oplus {Y}_{1}\oplus {X}_{2}\oplus {Y}_{2})^{(4)} \left| \psi \right\rangle _{24}\). Note that \(\left| {{c}_{x}}\cdot c\left( {{U}_{1}},{{U}_{2}} \right) \right| =1\) is a phase factor and can be ignored after performing a Bell-state measurement. Compared with the original state \({{\left| {{\phi }^{+}} \right\rangle }_{12}}\otimes {{\left| {{\phi }^{+}} \right\rangle }_{34}}=\frac{1}{2}{{\left| {{\phi }^{+}} \right\rangle }_{13}}{{\left| {{\phi }^{+}} \right\rangle }_{24}}+{{\left| {{\phi }^{-}} \right\rangle }_{13}}{{\left| {{\phi }^{-}} \right\rangle }_{24}}+{{\left| {{\psi }^{+}} \right\rangle }_{13}}{{\left| {{\psi }^{+}} \right\rangle }_{24}}+{{\left| {{\psi }^{-}} \right\rangle }_{13}}{{\left| {{\psi }^{-}} \right\rangle }_{24}},\) we obtain that \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{24}}=c( Z )\cdot U{{( Z )}^{(4)}}\cdot {{\left| \psi \right\rangle }_{24}},\, Z={{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}}\).

Here, we can view the operation of entanglement swapping as a function \(f\) and the operation of signature as a function \({S}_{ign}\). As we know, the function of \(f\) is \({{\left| {{\phi }^{+}} \right\rangle }_{12}}\otimes {{\left| {{\phi }^{+}} \right\rangle }_{34}}\rightarrow {{\left| {{\psi }'} \right\rangle }_{13}}\otimes {{\left| {{\psi }'} \right\rangle }_{24}}\), and the function of \({S}_{ign}\) is \({S}_{ign}\left( X \right) =U{{\left( X\oplus Y \right) }^{(2)}}{{\left| \psi \right\rangle }_{12}}\), here \(Y\) is the secret key corresponding to the information \(X\).

By definition, the aggregator \({{M}_{1}}\) receives the messages \(\left( {{X}_{1}}\oplus {{Y}_{1}},{{X}_{2}}\oplus {{Y}_{2}} \right) \) and the corresponding signatures. Note that different from classical case, we only view the particles 2(4) as the signature \({{S}_{1}}({{S}_{2}})\). Hence, \({{S}_{1}}({{S}_{2}})\) can be generated by \({S}_{ign}( {{X}_{1}} )({S}_{ign}( {{X}_{2}} ))\) as follows:

$$\begin{aligned} {S}_{ign}( {{X}_{1}} )\rightarrow {{S}_{1}}&={{\left| {{\psi }^{\prime }} \right\rangle }_{2}}=U( {{X}_{1}}\oplus {{Y}_{1}} ){{\left| \psi \right\rangle }_{2}},\\ {S}_{ign}( {{X}_{2}} )\rightarrow {{S}_{2}}&={{\left| {{\psi }^{\prime }} \right\rangle }_{4}}=U( {{X}_{2}}\oplus {{Y}_{2}} ){{\left| \psi \right\rangle }_{4}}. \end{aligned}$$

Without the keys \({{Y}_{1}}\) and \({{Y}_{2}},\, {{M}_{1}}\) generates a new signature by entanglement swapping. The whole process can be described as follows:

$$\begin{aligned} f\left( {S}_{ign}\left( {{X}_{1}} \right) ,{S}_{ign}\left( {{X}_{2}} \right) \right)&={{\left| {{\psi }''} \right\rangle }_{13}}\otimes {{\left| {{\psi }''} \right\rangle }_{24}} \\&=U{{\left( {{X}_{1}}\oplus {{Y}_{1}} \right) }^{(2)}}{{\left| \psi \right\rangle }_{12}}\otimes U{{\left( {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}}{{\left| \psi \right\rangle }_{24}} \\&={{\left| \psi \right\rangle }_{13}}\otimes U{{\left( {{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}} \right) }^{(4)}}{{\left| \psi \right\rangle }_{24}}. \end{aligned}$$

Obviously \(f({S}_{ign}( {{X}_{1}} ),{S}_{ign}( {{X}_{2}} ) )\rightarrow {{S}_{{{M}_{1}}}}={{\left| {{\psi }^{\prime \prime }} \right\rangle }_{4}}=U( {{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}} ){{\left| \psi \right\rangle }_{4}}\). If \({{M}_{1}}\) generates its signature according to the information \({{X}_{1}}\oplus {{X}_{2}}\) and the key \({{Y}_{1}}\oplus {{Y}_{2}}\), then \({S}_{ign}\left( {{X}_{1}}\oplus {{X}_{2}} \right) \rightarrow {{S}_{{{M}_{1}}}}=U( {{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}} ){{\left| \psi \right\rangle }_{4}}\). Thus \(f( {S}_{ign}( {{X}_{1}} ),{S}_{ign}( {{X}_{2}} ) )\rightarrow {{S}_{{{M}_{1}}}}={{S}_{{{M}_{1}}}}\leftarrow {S}_{ign}( {{X}_{1}}\oplus {{X}_{2}} )\). Comparing with the definition of classical additive homomorphism \(\phi \left( {{X}_{1}}+{{X}_{2}} \right) =f\left( \phi \left( {{X}_{1}} \right) ,\phi \left( {{X}_{2}} \right) \right) \), our signature scheme satisfies the property of additive homomorphism.

To prove the unforgeability of our scheme, we first give two lemmas as follows:

Lemma 3

The secret key \({{Y}_{i}}\) is shared by \({{M}_{2}}\) and \({{A}_{i}}\) securely.

Proof

Although the BB84 protocol has been proved to be unconditionally secure, it is vulnerable to middle-man attack. Hence, we use an improved BB84 protocol inspired by the literature [22] to distribute the key to defend against middle-man attack.

In this protocol, \({{M}_{2}}\) and \({{A}_{i}}\) share a series of EPR pairs. \({{M}_{2}}\) owns one half of these particles and \({{A}_{i}}\) owns the others. \({{M}_{2}}\) prepares a photon sequence (we called these particles as key particles for convenience), whose particles correspond to the base vector \(\left| + \right\rangle \ \left| - \right\rangle \) or \(\left| 1 \right\rangle \left| 0 \right\rangle \) at random. Firstly, \({{M}_{2}}\) inserts its EPR particles into its photon sequence at random and preserve the sequence number of these EPR particles. Then, \({{M}_{2}}\) sends its photon sequence and the sequence number to \({{A}_{i}}\). \({{A}_{i}}\) performs measurement on the key particles on the basis of \(\left| + \right\rangle \ \left| - \right\rangle \) or \(\left| 0 \right\rangle \ \left| 1 \right\rangle \). And \({{A}_{i}}\) tells \({{M}_{2}}\) the chosen measurement basis. \({{M}_{2}}\) tells \({{A}_{i}}\) the photons that they measured by the same base vectors. Consequently they discard the photons that they measured by the different base vectors. After transforming the remaining key particles to classical bits (called raw key) as follows: \(\left| 1 \right\rangle \rightarrow \ 1,\ \left| 0 \right\rangle \rightarrow 0\ \left| + \right\rangle \rightarrow \ 1,\ \left| - \right\rangle \rightarrow 0\), they choose some bits of the raw key and compare them. Obviously if the unequal bits exceed a certain threshold, they have suffered from wiretapping attack.

In this process, \({{A}_{i}}\) can also detect the middle-man attack by measuring the EPR particles in the photon sequence and its own EPR particles. If a middle-man, Mallory, captures the sequence number of these EPR particles and the photon sequence, forges the EPR particles and sends it to \({{A}_{i}}\). Because \({{A}_{i}}\) can measure the EPR particles by four Bell bases at random, the measurement results of the EPR particles forged by Mallory would be different from the EPR particles of \({{A}_{i}}\). Hence, the middle-man attack would be found. Based on the improved BB84 protocol, this quantum key distribution protocol can defend against any middle-man attack. Hence, we can prove Lemma 3.

Lemma 4

The secret key \({{Y}_{i}}\) is impossibly calculated by means of classical information and its corresponding quantum signature.

Proof

As shown in Fig. 4, any attacker cannot obtain the secret key by capturing classical information and its quantum signature. The details are as follows:

  1. (1)

    If an attacker captures the particle 2i (\(i\in \{1,2\}\)) and the information \({{X}_{i}}\oplus {{Y}_{i}}\) which are sent by \({{A}_{i}}\), he cannot obtain the key \({{Y}_{i}}\).

Assume an attacker obtains the particle 2 and the classical bits \({{X}_{1}}\oplus {{Y}_{1}}\). Without the particle 1, he cannot obtain \({{\left| \psi ^{\prime } \right\rangle }_{12}}\), but the state of the particle 2 (\(\left| + \right\rangle \) or \(\left| - \right\rangle \)) by a corresponding measurement basis, which can prevent him from calculating the unitary operation \(U\left( {{X}_{1}}\oplus {{Y}_{1}} \right) \). Hence, any attacker cannot obtain the key \({{Y}_{i}}\) only by capturing the particle 2i and the information \({{X}_{i}}\oplus {{Y}_{i}}\) sent by \({{A}_{i}}\).

  1. (2)

    If an attacker captures the particles (1, 2, 3, 4) and the information \(\left( {{X}_{1}}\oplus {{Y}_{1}} \right) \oplus \left( {{X}_{2}}\oplus {{Y}_{2}} \right) \) which are sent by the intermediate nodes \({{M}_{1}}\), he cannot obtain the key \({{Y}_{i}}\).

In this case, an attacker can obtain the state of the particles 2 and 4, namely \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{24}}=U{{({{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}})}^{(4)}}{{\left| \psi \right\rangle }_{24}}\) by performing a Bell-state measurement on them. However, the attacker can only obtain the classical bits \({{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}}\) by the unitary operator \(U({{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}})\). But he cannot obtain the keys \({{Y}_{1}}\) and \({{Y}_{2}}\) separately even if he can also captures \({{X}_{1}}\oplus {{Y}_{1}}\) and \({{X}_{2}}\oplus {{Y}_{2}}\).

Fig. 4
figure 4

The security of secret key

Full size image

Property 2

The signature \({{S}_{i}}\) is unforgeable.

Proof

According to our quantum signature scheme, the signature of \({{A}_{i}}\) is \({{S}_{i}}=U\left( {{X}_{i}}\oplus {{Y}_{i}} \right) {{\left| \psi \right\rangle }_{2i}}\). In other words, the key \({{Y}_{i}}\) is necessary to generate a signature. According to Lemmas 3 and 4, any attacker cannot obtain the key \({{Y}_{i}}\) by wiretap attacks. Hence, without the key \({{Y}_{i}}\), any attacker cannot forge a signature corresponding to his data \({{X}_{i}}^{\prime }\).

In a quantum network, quantum channels are secure. In virtue of quantum homomorphic signature scheme, the classical bits would not be falsified. Even if an attacker obtains the classical bits by wiretap, he cannot recover the original quantum states. Furthermore, even if an attacker or malicious node falsifies these classical bits, the receivers would find and filter out these corrupt packets. Hence, our quantum signature scheme can effectively defend against active attacks and wiretap attacks.

Property 3

If two senders use a same secret key, namely \({{Y}_{1}}={{Y}_{2}}\), our quantum signature scheme can verify the identity of a single data source. If two senders use different secret keys, namely \({{Y}_{1}}\ne {{Y}_{2}}\), our quantum signature scheme can verify the identity of different data sources.

Proof

When \({{Y}_{1}}={{Y}_{2}}\), our quantum network model can be viewed as a single-source multicast network. The information sent by \({{A}_{1}}\) and \({{A}_{2}}\) is from a single-source node upstream. Then by verifying the homomorphic signature, we can directly confirm that whether the classical bits \({{X}_{1}}\oplus {{X}_{2}}\) received by \({{M}_{2}}\) are the exclusive OR result of the classical bits \({{X}_{1}}\) and \({{X}_{2}}\) from a certain source node. When \({{Y}_{1}}\ne {{Y}_{2}}\), our quantum network model can be viewed as a multi-source unicast network, where there are two source nodes \({{A}_{1}}\) and \({{A}_{2}}\). The homomorphic signature received by \({{M}_{2}}\) is the combination of signatures from \({{A}_{1}}\) and \({{A}_{2}}\) at the intermediate node \({{M}_{1}}\). Hence, by verifying the signature of \({{M}_{1}}\), we can confirm that whether the classical bits \({{X}_{1}}\oplus {{X}_{2}}\) are from \({{M}_{1}}\). Note that the classical bits of \({{M}_{1}}\) are the exclusive OR result of the classical bits \({{X}_{1}}\) from \({{A}_{1}}\) and \({{X}_{2}}\) from \({{A}_{2}}\). On this basis, we can indirectly authenticate the identity of data source.

5 Discussion

In this section, we will discuss the effect of quantum homomorphic signature on quantum network. For a more complicated and general scenario, there exist more than two source nodes. Thus it is necessary to discuss whether our scheme can be realized to combine more signatures by some adjustment. As shown in Fig. 5, a multi-source model always can be transformed into double-source model. In this model, three source nodes \({{A}_{1}},\, {{A}_{2}}\) and \({{A}_{3}}\) transmit their information to a intermediate node \({{M}_{1}}\). By adding a node \({{D}_{1}}\), we can transform this triple-source model into two double-source model whose source nodes are \({{A}_{1}},\, {{D}_{1}}\) and \({{A}_{2}},\, {{A}_{3}}\), respectively. Obviously our quantum homomorphic signature scheme can be extended to this scenario after transformation. The details are described as follows:

  1. (1)

    Setup

Similarly, we assume that \({{A}_{i}}\) share its key \({{Y}_{i}}\) with \({{M}_{2}}\) by the improved BB84 protocol described in Lemma 3. Furthermore, \({{M}_{1}}\) prepares three pairs of entangled states:

$$\begin{aligned} {{\left| {{\phi }^{+}} \right\rangle }_{12}}&= \frac{1}{\sqrt{2}}\left( \left| {{0}_{1}}{{0}_{2}} \right\rangle +\left| {{1}_{1}}{{1}_{2}} \right\rangle \right) \\ {{\left| {{\phi }^{+}} \right\rangle }_{34}}&= \frac{1}{\sqrt{2}}\left( \left| {{0}_{3}}{{0}_{4}} \right\rangle +\left| {{1}_{3}}{{1}_{4}} \right\rangle \right) \\ {{\left| {{\phi }^{+}} \right\rangle }_{56}}&= \frac{1}{\sqrt{2}}\left( \left| {{0}_{5}}{{0}_{6}} \right\rangle +\left| {{1}_{5}}{{1}_{6}} \right\rangle \right) . \end{aligned}$$

\({{M}_{1}}\) sends its particles 2, 4 and 6 (denoted as \({{\left| \psi \right\rangle }_{2}},\ \ {{\left| \psi \right\rangle }_{4}},\ {{\left| \psi \right\rangle }_{6}}\)) to \({{A}_{1}},\, {{A}_{2}}\) and \({{A}_{3}}\), respectively.

  1. (2)

    Sign

In this phase each source node \({{A}_{i}}\) signs on its particle 2i according to its classical information \({{X}_{i}}\). The method of signature is the same as that in double-source model which is described in Sect. 3. Then, \({{A}_{i}}\) send its particle 2i and classical information \({{X}_{i}\oplus {Y}_{i}}\) to \({{M}_{1}}\). Here, we assume that the state of the particle 2i is \({{\left| {{\psi }'} \right\rangle }_{\left( 2i \right) }}=U\left( {{X}_{i}}\oplus {{Y}_{i}} \right) {{\left| \psi \right\rangle }_{\left( 2i \right) }}\).

  1. (3)

    Combine

After receiving the particles and information from source nodes, \({{M}_{1}}\) first combines the signature of \({{A}_{2}}\) and \({{A}_{3}}\) and obtains a result (which can be viewed as the signature of the added node \({{D}_{1}}\) in Fig. 5). Then, \({{M}_{1}}\) combines the result and the signature of \({{A}_{1}}\). The detailed process is described as follows:

Step 1: \({{M}_{1}}\) performs a Bell-state measurement on the particles 3 and 5 and obtains the result \({{\left| {{\psi }''} \right\rangle }_{35}}\). Obviously, the state of the particles 4 and 6 would be \({{\left| {{\psi }''} \right\rangle }_{46}}={{c}_{1}}\cdot U{{\left( {{X}_{2}}\oplus {{Y}_{2}}\oplus {{X}_{3}}\oplus {{Y}_{3}} \right) }^{\left( 6 \right) }}{{\left| \psi \right\rangle }_{46}}\) according to the Property 1. Here, the value of \({{c}_{1}}\) depends on \({{X}_{2}}\oplus {{Y}_{2}}\) and \({{X}_{3}}\oplus {{Y}_{3}}\), which satisfies \(\left| {{c}_{1}} \right| =1\) according to Lemma 1.

Fig. 5
figure 5

Multi-source model

Full size image

Step 2: \({{M}_{1}}\) performs a Bell-state measurement on the particles 1 and 4 and obtains the result \({{\left| {{\psi }''} \right\rangle }_{14}}\). Then, the state of the particles 2 and 6 would be \({{\left| {{\psi }''} \right\rangle }_{26}}={{c}_{1}}\cdot {{c}_{2}}\cdot U{{\left( {{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}}\oplus {{X}_{3}}\oplus {{Y}_{3}} \right) }^{\left( 6 \right) }}{{\left| \psi \right\rangle }_{46}}\). Here, the value of \({{c}_{2}}\) depends on \({{X}_{1}}\oplus {{Y}_{1}}\) and \({{X}_{2}}\oplus {{Y}_{2}}\oplus {{X}_{3}}\oplus {{Y}_{3}}\), which satisfies \(\left| {{c}_{1}} \right| =1\) according to Lemma 1.

Step 3: \({{M}_{1}}\) sends the classical information \({{X}_{1}}\oplus {Y}_{1}\oplus {{X}_{2}}\oplus {Y}_{2}\oplus {{X}_{3}}\oplus {Y}_{3}\) and the particles (1, 2, 3, 4, 5, 6) (i.e., \({{\left| {{\psi }''} \right\rangle }_{35}}\otimes {{\left| {{\psi }''} \right\rangle }_{14}}\otimes {{\left| {{\psi }''} \right\rangle }_{26}}\)) to \({{M}_{2}}\).

  1. (4)

    Verify

After receiving the particles and \({{X}_{1}}\oplus {Y}_{1}\oplus {{X}_{2}}\oplus {Y}_{2}\oplus {{X}_{3}}\oplus {Y}_{3},\, {{M}_{2}}\) can verify the signature as follows:

Step 1: \({{M}_{2}}\) performs the Bell-state measurement on the particles 3, 5 and 1, 4 and obtains \({{\left| {{\psi }''} \right\rangle }_{35}}\) and \({{\left| {{\psi }''} \right\rangle }_{14}}\). According to Table 1, we can find out the value of \({{\left| \psi \right\rangle }_{46}}\) which is the entanglement swapping result of \({{\left| \psi \right\rangle }_{34}}\otimes {{\left| \psi \right\rangle }_{56}}\) when \({{\left| \psi \right\rangle }_{35}}={{\left| {{\psi }''} \right\rangle }_{35}}\). Similarly, with the value of \({{\left| \psi \right\rangle }_{46}}\), we can also calculate the value of \({{\left| \psi \right\rangle }_{26}}\) which is the entanglement swapping result of \({{\left| \psi \right\rangle }_{12}}\otimes {{\left| \psi \right\rangle }_{46}}\) when \({{\left| \psi \right\rangle }_{14}}={{\left| {{\psi }''} \right\rangle }_{14}}\).

Step 2: \({{M}_{2}}\) performs the Bell-state measurement on the particles 2, 6 and obtains \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{26}}\). Then, \({{M}_{2}}\) compares \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{26}}\) with \({{\left| \psi \right\rangle }_{26}}\) and obtains an operator which satisfies \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{26}}=c\left( Z \right) U{{\left( Z \right) }^{(4)}}\cdot {{\left| \psi \right\rangle }_{26}}\). Here, \(\left| c\left( Z \right) \right| =1\).

Step 3: \({{M}_{2}}\) calculates \({{X}_{1}}\oplus {{X}_{2}}\oplus {{X}_{3}}\) by its keys. Furthermore, if \({{X}_{1}}\oplus {{Y}_{1}}\oplus {{X}_{2}}\oplus {{Y}_{2}}\oplus {{X}_{3}}\oplus {{Y}_{3}}=Z,\, {{M}_{2}}\) would confirm that \({{\left| {{\psi }^{\prime \prime }} \right\rangle }_{6}}\) is the signature of \({{M}_{1}}\) and assure that the resulting information \({{X}_{1}}\oplus {{X}_{2}}\oplus {{X}_{3}}\) originates from the source nodes \({{A}_{1}},\, {{A}_{2}}\) and \({{A}_{3}}\). Otherwise, \({{M}_{2}}\) would deny the signature.

According to the above approach, our scheme can be easily extended to multi-source model which may contain n source nodes. Moreover, it can solve the problem of identity authentication of single-source unicast, single-source multicast, multi-source unicast, or multi-source multicast in quantum networks.

Note that our scheme would consume 4 extra particles (two entangled pairs) to generate a homomorphic signature. Obviously, for an n-source node model, it would need 2n particles. Hence, the efficiency and security of EPR pair distribution is very important. An effective distribution scheme would be of great value to the popularization of our scheme in the future. It is worth noting that the particles (1,2,3,4) in our scheme would still fall into the Bell state after homomorphic signature as follows: \({{\left| \varphi \right\rangle }_{12}}\otimes {{\left| \varphi \right\rangle }_{34}}\rightarrow {{\left| \varphi ^\prime \right\rangle }_{13}}\otimes {{\left| \varphi \prime \right\rangle }_{24}}\). This means that the particles can be reused for next signature. Hence, by a reasonable design in the future, the consumed particles for homomorphic signature would be reduced, which could greatly enhance the efficiency of our scheme.

6 Conclusion

To verify the identity of different data sources in the quantum network, we designed a quantum homomorphic signature scheme based on entanglement swapping. In our scheme, any attacker which attempts to falsify the data would be found. Security analysis shows that this scheme can effectively guarantee the security of secret key and verify the identity of different data sources in the quantum network. Of course, for a more general scenario, our signature scheme need to be further extended to combine more signatures.