The enhanced measurement-device-independent quantum key distribution with two-intensity decoy states

Abstract

We put forward a new scheme for implementing the measurement-device-independent quantum key distribution (QKD) with weak coherent source, while using only two different intensities. In the new scheme, we insert a beam splitter and a local detector at both Alice’s and Bob’s side, and then all the triggering and non-triggering signals could be employed to process parameter estimations, resulting in very precise estimations for the two-single-photon contributions. Besides, we compare its behavior with two other often used methods, i.e., the conventional standard three-intensity decoy-state measurement-device-independent QKD and the passive measurement-device-independent QKD. Through numerical simulations, we demonstrate that our new approach can exhibit outstanding characteristics not only in the secure transmission distance, but also in the final key generation rate.

1 Introduction

In the past few decades, the quantum key distribution (QKD) has attracted extensive attention from the scientific world, which is mainly attributed to its theoretical unconditional security ensured by laws of quantum mechanics [1–3]. But unfortunately, practical legitimate users, usually named Alice and Bob, can only possess imperfect devices, e.g., non-ideal single-photon sources, imperfect single-photon detectors and lossy channels. Then a malicious eavesdropper, Eve, who might own the most advance computational power and technology, can carry out corresponding attacks by making use of the loopholes due to imperfections [4–10]. In order to countermeasure the so-called photon-number-splitting (PNS) attack [4–6], the decoy-state method was created [11–16]. Moreover, the measurement-device-independent quantum key distribution (MDI-QKD) [17, 18] has been invented to defeat the more powerful side-channel attacks [7–10]. Hitherto, under current technology the MDI-QKD seems to possess the highest level security among different protocols.

Recently, different schemes of MDI-QKD have been widely studied both theoretically and experimentally. For example, some apply different number of decoy states [19, 20], and others employ either weak coherent states (WCS) [20–22] or heralded single-photon sources (HSPS) [23–25]. However, for those schemes applying decoy states with one, two or three intensities, the performance is poorer than the asymptotic case of using infinite number of decoy states. In this paper, we propose a new method of the decoy-state MDI-QKD that uses a weak coherent source. Although it only needs two intensities, it offers better performance compared with most other existing MDI-QKD methods, e.g., the standard three-intensity decoy-state MDI-QKD and the passive decoy-state MDI-QKD.

Our paper is organized as follows: In Sect. 2, we introduce some basic notations for the configuration of our QKD setups and then describe our new proposed two-intensity decoy-state MDI-QKD step by step. In Sect. 3, we derive a formula giving the lower bound of the counting rate and the upper bound of quantum-bit error rate (QBER) from the two-single-photon pulses. In Sect. 4, we present the corresponding numerical simulations and compare our new proposal with other existing schemes, e.g., the standard three-intensity decoy-state MDI-QKD and the passive MDI-QKD. In Sect. 5, we analyze the finite data size effect in practical implementations. In Sect. 6, a summary and conclusions are given.

2 The new proposed MDI-QKD with two-intensity weak coherent light

Before describing our new two-intensity MDI-QKD protocol, let us first briefly review the local triggering setup [26]. As is illustrated in Fig. 1, denote the two input states of the beam splitter (BS) as $\rho$ and $\sigma$ (Fock diagonal states) , where t is the transmittance of the BS. The two Fock diagonal states ($\rho$ and $\sigma$) can be expressed as:

$$\begin{aligned} \rho = \sum \limits _{n = 0}^\infty {{p_n}} \left| n \right\rangle \left\langle n \right| , \qquad \sigma = \sum \limits _{n = 0}^\infty {{r_n}\left| n \right\rangle } \left\langle n \right| . \end{aligned}$$

(1)

Fig. 1

Local triggering setup: $\rho$ and $\sigma$ (two states which are diagonal in the Fock basis) represent the two input states of a beam splitter (BS); t is the transmittance of the BS; the two output modes of the BS are denoted as a and b, respectively; $\rho _{{\text {out}}}$ represents the output state from mode a, PD the single-photon detector

If we properly select the above two input modes, then we can get a classical correlation between the two outcome signals, which means we can get different photon-number statistics in the signal mode a by conditional detecting the signal in mode b. Here we suppose that the Fock states in the two input ports are both weak coherent sources (WCS), which are generated by attenuated lasers. Hence, they can be written as:

$$\begin{aligned} \rho = {e^{ - {\mu _1}}}\sum \limits _{n = 0}^\infty {\frac{{{\mu _1}^n}}{{n!}}} \left| n \right\rangle \left\langle n \right| , \qquad \sigma = {e^{ - \mu _{2}}}\sum \limits _{n = 0}^\infty {\frac{{{\mu _2}^n}}{{n!}}} \left| n \right\rangle \left\langle n \right| , \end{aligned}$$

(2)

where $\mu _{1}$ and $\mu _{2}$ are the average photon numbers of the two input signals, respectively. The expression for $p_{n,m}$, which is the joint probability of having n photons in mode a and m photons in output mode b, can be expressed:

$$\begin{aligned} {p_{n,m}} = \frac{{{\nu ^{n + m}}{e^\nu }}}{{n!m!}}\frac{1}{{2\pi }}\int _0^{2\pi } {\gamma {{\left( \theta \right) }^n}} {(1 - \gamma \left( \theta \right) )^m}{\hbox {d}}\theta . \end{aligned}$$

(3)

The parameters $\nu$, $\gamma \left( \theta \right)$, and $\zeta$ are defined as follows:

$$\begin{aligned} \nu= & {} {\mu _1} + {\mu _2}, \end{aligned}$$

(4)

$$\begin{aligned} \gamma \left( \theta \right)= & {} \frac{{{\mu _1}t + {\mu _2}(1 - t) + \zeta \cos \theta }}{\nu }, \end{aligned}$$

(5)

$$\begin{aligned} \zeta= & {} 2\sqrt{{\mu _1}{\mu _2}(1 - t)t}. \end{aligned}$$

(6)

Here the parameter t means the transmittance of a beam splitter. If Alice does not consider the measurement result in mode b, then the probability of having n photons in mode a can be given as:

$$\begin{aligned} {p_n}(\nu ) = \sum \limits _{m = 0}^\infty {{p_{n,m}}} = \frac{{{\nu ^n}}}{{n!}}\frac{1}{{2\pi }}\int _0^{2\pi } {\gamma {{\left( \theta \right) }^n}{e^{ - \nu \gamma \left( \theta \right) }}} {\hbox {d}}\theta . \end{aligned}$$

(7)

When considering the detection results of Alice, the joint probability for finding n photons in mode a and no click in Alice’s threshold photon detector can be denoted as $p_n^{\mathop t\limits ^-}$. We can express it as:

$$\begin{aligned} p_n^{\mathop {\mathrm{{ }}t}\limits ^ - }(\nu )= & {} (1 - \varepsilon )\sum \limits _{m = 0}^\infty {{{(1 - {\eta _\mathrm{A}})}^m}} {p_{n,m}} \nonumber \\= & {} (1 - \varepsilon )\frac{{{\nu ^n}{e^{ - {\eta _\mathrm{A}}\nu }}}}{{n!}}\frac{1}{{2\pi }}\int _0^{2\pi } {\gamma {{\left( \theta \right) }^n}} {e^{ - (1 - {\eta _\mathrm{A}})\nu \gamma \left( \theta \right) }}{\hbox {d}}\theta . \end{aligned}$$

(8)

Here $\varepsilon$ refers to the dark count rate and $\eta _\mathrm{A}$ is the detection efficiency of Alice’s threshold detector. In the same way, we can denote another parameter $p^{t}_{n}$, which represents the probability of having n photons in mode a and observing a click in Alice’s threshold detector at the same time. We finally get the following expression:

$$\begin{aligned} p_n^t(\nu ) = p_n(\nu ) - p_n^{\mathop t\limits ^ - }(\nu ). \end{aligned}$$

(9)

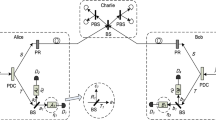
In our new protocol, both Alice and Bob possess this kind of BS devices, separately sending out optical pulses to the untrusted third part (UTP), named Charlie. Charlie who may be controlled by Eve applies a joint measurement on the two-pulse signals from both Alice and Bob and publicly announces the measurement results after all signal transmission is finished. The schematic of our experimental setup is shown in Fig. 2.

Fig. 2

Schematic setup of the new two-intensity decoy-state MDI-QKD. At Alice (Bob)’s side, $\rho$ and $\sigma$ interfere at a BS with a transmittance t. $\mu _{i}$ ($i=1,2$) corresponds to the intensity of the input light; a and b each denotes one of the output modes; $D_{0}$ represents the local threshold single-photon detector, with a detection efficiency $\eta _\mathrm{A}$ ($\eta _\mathrm{B}$) at Alice’s (Bob’s) side. At the UTP’s (Charlie’s) side, pulses from Alice and Bob interfere at a 50:50 BS and then each enters a polarizing beam splitter (PBS); $D_{i}$ ($i=1,2,3,4$) represents the single-photon detector, with a detection efficiency $\eta _\mathrm{C}$; PR represents a polarization rotator

Now let us describe our new proposal step by step by using a polarization coding scheme as an example:

First, both Alice and Bob randomly modulate their pulses in input 1 into two different intensities, $\mu$ and $\mu '$, and interfere it with the local reference beam from input 2 at a BS. The two output modes are denoted as mode a and mode b, respectively. Mode b is used for detection with the local detector ($D_{0}$); Mode a is randomly encoded into one of the four polarization states, i.e., horizontal (H), vertical (V), 45$^\circ$ ($+$) and 135$^\circ$ (−) polarizations, and sent out to the UTP. Meantime, Alice (Bob) sends out a triggering signal whenever $D_{0}$ clicks.

Second, the UTP carries out partial Bell-state projection measurements on the pulses from Alice and Bob, recording all the successful events. Besides, the UTP classifies all the successful events into two species, the triggered and the non-triggered. After all the signal transmission finished, the UTP publicly announces his measurement results.

Third, based on the UTP’s announcement, Alice (Bob) applies post-selection and bit-flip operations on the qubits in her (his) hand, obtaining the raw key.

Fifth, Alice and Bob carry out error correction and a privacy amplification processes to achieve the final key.

It is worth noting that the main differences between our new scheme and the old passive QKD schemes are the following: At both Alice and Bob’s side, light in input 2 ($\sigma$) is fixed with intensity $\mu _2$, and light in input 1 ($\rho$) is randomly modulated into two different intensities, $\mu$ and ${\mu '}$ ($\mu < \mu '$), where $\mu$ refers to the decoy state and ${\mu '}$ represents the signal state. According to Eq. (4), for each $\mu$ and ${\mu '}$, we have corresponding $\nu$ and ${\nu }$ , with $\nu = \mu + \mu _2$, and ${\nu }'= {\mu }'+ \mu _2$ individually. Moreover, we also have relevant values for $p_n$, $p_n^{\mathop t\limits ^ - }$ and $p_n^t$ for each $\mu$ and ${\mu '}$. That is to say, by modulating light (in input 1) into $\mu$ and ${\mu '}$, we can obtain six types of nonzero counting events. By properly choosing two of them, i.e., $p_n^t(\nu )$ and $p_n({\nu '})$, we can denote them as c and $c^{'}$, respectively. Then in the photon-number space, we have

$$\begin{aligned} {\rho _{l}} = \sum \limits _n {l_{n}} \left| n \right\rangle \left\langle n \right| , \quad \ ({l} = c, c^{'}) \end{aligned}$$

(10)

where

$$\begin{aligned} c_{n}(\mu _{i})= & {} p_n(\nu _{i})- p_n^{\mathop t\limits ^-}(\nu _{i}), \nonumber \\ c_{n}^{'}({\mu }_{i}')= & {} p_n({\nu }_{i}'), \end{aligned}$$

(11)

with $i= A,B$.

In order to analyze our new scheme, we firstly assume the following condition holds true for any ${\mu ^{'}} \ge \mu$ and $n \geqslant 2$ [19]:

$$\begin{aligned} \frac{{{c_{n}^{'}}({\mu ^{'}})}}{{{c_{n}}(\mu )}} \ge \frac{{{c_{n-1}^{'}}({\mu ^{'}})}}{{{c_{n-1}}(\mu )}} \ge \frac{{{c_{1}^{'}}({\mu ^{'}})}}{{{c_{1}}(\mu )}}. \end{aligned}$$

(12)

This assumption will be readdressed later on.

3 Derivation of $Y_{11}^{L}$ and $e_{11}^{U}$

In order to calculate the final key generation rate, the counting rate and the QBER of the two-single-photon pluses should first be estimated. Here Alice and Bob randomly modulate their pulses in input 1 into $\mu _{i}$ and $\mu _{i}'$, ($\mu _{i} < \mu '_{i}$, $i = A,B$), individually. For simplicity, we denote the intensity from Alice or Bob as x and y, respectively, where $x \in \{ \mu _\mathrm{A}, \mu '_\mathrm{A} \}$ and $y\in \{ \mu _\mathrm{B}, \mu ' _\mathrm{B} \}$. Then we can calculate the average gain ($S_{x,y}^W$) and average quantum-bit error ($T_{x,y}^W =: E_{x,y}^W S_{x,y}^W$) with the following expressions:

$$\begin{aligned} S_{x,y}^W= & {} \sum \limits _{m,n = 0}^\infty {l_{n}(x)l_{m}(y)Y_{nm}^W}, \end{aligned}$$

(13)

$$\begin{aligned} E_{x,y}^WS_{x,y}^W= & {} \sum \limits _{m,n = 0}^\infty {l_{n}(x)l_{m}(y)e_{nm}^WY_{nm}^W}, \end{aligned}$$

(14)

where W represents the X or Z basis; ${l} = c, c^{'}$; $Y_{nm}^W$ and $e_{nm}^W$ each corresponds to the yield and the QBER when Alice sends out an n-photon pulse and Bob sends out an m-photon pulse; $E_{x,y}^W$ is the average QBER. In the MDI-QKD, two bases (Z and X) have been used for preparing, transmitting and measuring. Usually the Z basis is used for distilling the secure keys, while the X basis is only for error testing. For simplicity, we suppose the MDI-QKD has been implemented with the two bases independently. Hereafter, the superscript W will be omitted without causing any confusion.

With Eq. (13), $S_{ \mu ,\mu }$ and ${S_{ \mu ',\mu ' }}$ can be written as:

$$\begin{aligned} S_{\mu ,\mu }= & {} \tilde{S}_{00}+c_{1}^2(\mu ){Y_{11}} + {c_{1}}(\mu )\sum \limits _{m = 2}^\infty {{c_{m}}(\mu ){Y_{1m}}} \nonumber \\&+ {c_{1}}(\mu )\sum \limits _{n = 2}^\infty {{c_{n}}(\mu ){Y_{n1}}} \nonumber \\&+\sum \limits _{n,m = 2}^\infty {{c_{n} }(\mu ){c_{m} }(\mu ){Y_{nm}}}, \end{aligned}$$

(15)

$$\begin{aligned} {S_{\mu ' ,\mu ' }}= & {} {\tilde{S}' _{00}} + {c_{1}^{'}}^2({\mu ' }){Y_{11}} + {c_{1}^{'}}({\mu ' })\sum \limits _{m = 2}^\infty {{c_{m}^{'}}({\mu ' }){Y_{1m}}} \nonumber \\&+\, {c_{1}^{'}}({\mu ' })\sum \limits _{n = 2}^\infty {{c_{n}^{'}}({\mu ' }){Y_{n1}}} \nonumber \\&+ \sum \limits _{n,m = 2}^\infty {{c_{n}^{'}}({\mu ' }){c_{m}^{'}}({\mu ' }){Y_{nm}}}, \end{aligned}$$

(16)

where $\tilde{S}_{00} = {S_{\mu ,0}} + {S_{0,\mu }} - {S_{0,0}}$, $\tilde{S}' _{00} = {S_{\mu ' ,0}} + {S_{0,\mu ' }} - {S' _{0,0}}$. Denote $\kappa =: \frac{{{c_{1}^{'}}({\mu '}){c_{2}^{'}}({\mu ' })}}{{{c_{1}}(\mu ){c_{2} }(\mu )}}$. By combining Eqs. (15) and (16), we get

$$\begin{aligned} {Y_{11}} = \frac{{\kappa ({S_{\mu ,\mu }} - \tilde{S}_{00}) - ({S_{{\mu '},{\mu ' }}} - \tilde{S}' _{00} ) + \tau }}{{\kappa c_{1}^2 (\mu ) - {c_{1}^{'}}^2({\mu ' })}}, \end{aligned}$$

(17)

where

$$\begin{aligned} \tau= & {} \sum \limits _{m = 2}^\infty {\left[ c_{1}^{'}({\mu ' }){c_{m}^{'}}({\mu '}) - \kappa {c_{1} }(\mu ){c_{m}}(\mu )\right] {Y_{1m}}} \nonumber \\&+ \sum \limits _{n = 2}^\infty {\left[ {c_{1}^{'}}({\mu ' }){c_{n}^{'}}({\mu ' }) - \kappa {c_{1}}(\mu ){c_{n}}(\mu )\right] {Y_{n1}}} \\&+ \sum \limits _{n,m = 2}^\infty {\left[ {c_{n}^{'}}({\mu ' }){c_{m}^{'}}({\mu ' }) - \kappa {c_{n} }(\mu ){c_{m} }(\mu )\right] {Y_{nm}}}. \end{aligned}$$

Below we denote $\tau ={h_1}+{h_2}+{h_3}$. According to Eq. (12), we have $\tau >0$, which follows from

$$\begin{aligned} {h_1}= & {} \sum \limits _{m = 2}^\infty {\left[ {c_{1}^{'}}({\mu ' }){c_{m}^{'}}({\mu '}) - \kappa {c_{1} }(\mu ){c_{m}}(\mu )\right] {Y_{1m}}} \nonumber \\= & {} \sum \limits _{m = 2}^\infty {\frac{{{c_{1}^{'}}({\mu ' })}}{{{c_{2}}(\mu )}}\left[ {c_{2}}(\mu ){c_{m}^{'}}({\mu ' }) - {c_{2}^{'}}({\mu ' }){c_{m} }(\mu )\right] {Y_{1m}} \ge 0}; \nonumber \\ {h_2}= & {} \sum \limits _{n = 2}^\infty {\left[ {c_{1}^{'}}({\mu ' }){c_{n}^{'}}({\mu ' }) - \kappa {c_{1} }(\mu ){c_{n} }(\mu )\right] {Y_{n1}}} \nonumber \\= & {} \sum \limits _{n = 2}^\infty {\frac{{{c_{1}^{'}}({\mu ' })}}{{{c_{2} }(\mu )}}\left[ {c_{2} }(\mu ){c_{n}^{'}}({\mu ' }) - {c_{2}^{'}}({\mu ' }){c_{n}}(\mu )\right] {Y_{n1}} \ge 0}; \nonumber \\ {h_3}= & {} \sum \limits _{m,n = 2}^\infty {\left[ {c_{n}^{'}}({\mu ' }){c_{m}^{'}}({\mu ' }) - \kappa {c_{n} }(\mu ){c_{m} }(\mu )\right] {Y_{nm}}} \nonumber \\\ge & {} \sum \limits _{m,n = 2}^\infty {\frac{{{c_{n} }({\mu }){c_{m}^{'}}({\mu '})}}{{{c_{1} }(\mu ){c_{2} }(\mu )}}\left[ {c_{1} }(\mu ){c_{2}^{'}}({\mu ' }) - {c_{1}^{'}}({\mu ' }){c_{2}}(\mu )\right] {Y_{nm}}} \ge 0. \end{aligned}$$

With the conditions above, we can get the lower bound for the two-single-photon counting rate in the Z basis ($Y_{11}^{Z}$):

$$\begin{aligned} Y_{11}^Z \ge \mathrm{{Y}}_{11}^{Z,L}: = \frac{{{c_1}^\prime (\mu '){c_2}^\prime (\mu ')(S_{\mu ,\mu }^Z - \tilde{S}_{00}^Z)\mathrm{{ }} - {c_1}(\mu ){c_2}(\mu )(S_{\mu ',\mu '}^Z - \widetilde{S}{{_{00}^Z}^\prime })}}{{{c_1}^\prime (\mu '){c_1}(\mu )\Big [ {{c_1}(\mu ){c_2}^\prime (\mu ') - {c_1}^\prime (\mu '){c_2}(\mu )} \Big ]}}. \end{aligned}$$

(18)

Similarly, we can get the upper bound of the QBER for two-single-photon pulses in the X basis ($e^{X}_{11}$):

$$\begin{aligned} e_{11}^X \le {\text {e}}_{11}^{X,U} := \frac{{{E_{\mu ,\mu }^XS_{\mu ,\mu }^X}}-{{E_{\mu ,0 }^XS_{\mu ,0 }^X}}-{{E_{0,\mu }^XS_{0 ,\mu }^X}}+{{E_{0,0 }^XS_{0 ,0 }^X}}}{{c_1^{2}(\mu )Y_{11}^X}}. \end{aligned}$$

(19)

With the formulae above, we can now calculate the final key generation rate with [18, 24]:

$$\begin{aligned} R \ge {{c_{1}^{'}}^2}{( \mu ' )}Y_{11}^Z[1 - {H_2}(e_{11}^X)] - S_{{\mu '},{\mu ' }}^Z f {H_2}(E_{{\mu ' },{\mu '}}^Z), \end{aligned}$$

(20)

where f is a factor for the cost of error correction efficiency, and here we take $f=1.16$. $H_2(x)$ is the binary Shannon information function, given by $H_2(x) = - x{\log _2}(x) - (1 - x){\log _2}(1 - x)$.

4 Numerical simulation for MDI-QKD

We can now numerically calculate the key generation rate and compare the performance of our method with other schemes, e.g., the passive MDI-QKD and the three-intensity MDI-QKD. Here we assume that the UTP is located in the middle of Alice’s and Bob’s transmission link and that the detectors of the UTP are identical, e.g., have the same dark count rate $Y_0$ and detection efficiency $\eta _\mathrm{C}$. Moreover, the detection efficiency $\eta _\mathrm{C}$ does not depend on the incoming signals. The gains and error rates, which can be observed in the experiment, could be estimated with linear model channels. According to the linear model in [24], the state $\left| n \right\rangle \left\langle n\right|$ from Alice can be changed into $\sum \limits _{k = 0}^n {C_n^k{\eta ^k}{{(1 - \eta )}^{n - k}}\left| k \right\rangle \left\langle k \right| }$, when it arrives to the UTP. Here $C_n^k$ is the binomial coefficient, defined as $C_n^k=: {\frac{{n!}}{{k!(n - k)!}}}$; $\eta$ is the transmittance from Alice to the UTP.

Depending on the transmittance distance, we can set the values for $S_{\mu ,\mu }$, $S_{\mu ', \mu '}$, $E_{\mu ,\mu }$ and $E_{\mu ', \mu '}$, which probably would be the observed in real experiments. So after setting the values mentioned above, the parameters of $Y_{11}^Z$ and $e_{11}^X$ can be obtained. Furthermore, we can calculate the key generation rate with the formula in Eq. (20).

For a fair comparison, we use the same the numerical parameters as in [18, 23], with $\alpha =0.2$ dB/km, $\eta _\mathrm{C}=0.145$, $d_C=3\times 10^{-6}$, $e_d=0.015$, ${\eta _i} = 0.75$ and ${d _i} = 10^{-6}$ ($i=A,B$) in our simulations. Moreover, we use the same value of $\mu _{2}$ as in [26], $\mu _{2}=10^{-4}$. Then we do a simulation for the two-single-photon contributions ($Y_{11}$ and $e_{11}$), the optimal intensity for the signal state ($\mu '$) and the final key generation rate by using different methods. The corresponding simulation results are shown in Figs. 3, 4 and 5. Here, we need to stress that during our simulation we have numerically checked that all the parameters used can satisfied the conditions in Eq. (12).

Fig. 3

Comparison for the counting rate (${Y_{11}}$) (a) and the quantum-bit error rate ($e_{11}$) (b) from two-single-photon pulses by using different methods, i.e., the passive MDI-QKD ($W_{1}$), the standard three-intensity decoy-state MDI-QKD ($W_{3}$) and the new proposed two-intensity decoy-state method ($W_{2}$). $W_{0}$ represents the case of using an infinite number of decoy states. Here we reasonably set $\mu =0.1$ for the decoy state in both the new proposed two-intensity decoy-state scheme and the standard three-intensity decoy-state method, and in all the schemes we use the optimal intensity for the signal state ($\mu '$) at each distance

Fig. 4

Comparison of the optimal value of signal state (${\mu }^{'}$) for MDI-QKD in different methods, i.e., the passive MDI-QKD method with WCS ($W_{1}$), the three-intensity MDI-QKD method with WCS ($W_{3}$) and the new method proposed by us ($W_{2}$). Besides, the solid curve ($W_{0}$ ) represents the MDI-QKD method with infinite decoy states

Fig. 5

Comparison of the absolute key generation rate (a) and the relative key generation rate (b) for MDI-QKD between using different methods. In a, from the bottom to the top, each line corresponds to the passive MDI-QKD ($W_{1}$), the three-intensity MDI-QKD ($W_{3}$), the new proposed two-intensity MDI-QKD ($W_{2}$) and the asymptotic case of using infinite decoy states ($W_{0}$). In b, it shows the ratio of the key generation rates between our new scheme and the passive MDI-QKD method in the left axis and displays the ratio of the key generation rates between our scheme and conventional three-intensity decoy state in the right axis. Here we reasonably set $\mu =0.1$ for the decoy state and optimize the value of $\mu '$ for the signal state at each distance in all the methods

In Fig. 3, we compare the estimated values for the counting rate of two-single-photon pulses ($Y_{11}$) (a) and the QBER of two-single-photon pulses ($e_{11}$) (b) by using different methods. $W_{1}$ and $W_{3}$ each represents the passive MDI-QKD ($W_{1}$) and the standard three-intensity decoy-state MDI-QKD ($W_{3}$), respectively. $W_{2}$ corresponds to the new proposed two-intensity MDI-QKD. Moreover, we also plot for the ideal case of using infinite number of decoy states ($W_{0}$) ($W_{0}$ corresponds to the experimental setup in Fig. 2, and it is the same hereafter). In order to give a fair comparison, at each distance we have used the optimal intensity for the signal state (${\mu }^{'}$) in all the above methods and set a reasonable value for the decoy state ($\mu =0.1$) in both the new proposed two-intensity decoy-state scheme and the standard three-intensity decoy-state method. From Fig. 3a, b, we find that all the three practical schemes ($W_{1}$, $W_{2}$ and $W_{3}$) show similar estimation values of $Y_{11}$, while they show drastically different performance for $e_{11}$. Obviously, our new proposed two-intensity scheme ($W_{2}$) exhibits significantly lower estimation value of $e_{11}$ than the other two.

In Fig. 4, we plot the optimal intensity (${\mu }^{'}$) at each distance with different methods. Similar in Fig. 3, $W_{0}$ represents the ideal case of using infinite number of decoy states, $W_{1}$ and $W_{3}$ each corresponds to the result of using the passive decoy-state scheme and the conventional three-intensity decoy-state method, respectively, and $W_{2}$ refers to the result of using our new proposal. From Fig. 4, we find that the optimal intensity (${\mu }^{'}$) in our new method is much higher than in the other two practical methods ($W_{1}$ and $W_{3}$), getting much closer to the asymptotic case of using an infinite number of decoy states ($W_{0}$).

In Fig. 5a, b, we compare either the absolute key generation rate or the relative key generation rate between using different methods. In Fig. 5a, $W_{0}$, $W_{1}$ and $W_{3}$ each corresponds to the asymptotic case of using infinite number of decoy states, the passive decoy-state scheme and the conventional decoy-state method. $W_{2}$ refers to the result of using our new proposal. Obviously, our new method ($W_{2}$) presents a much higher key generation rate than the other two practical methods ($W_{1}$ and $W_{3}$) and approaches the ideal case of using infinite number of decoy states ($W_{0}$) very closely. Moreover, in order to give a vivid comparison between these three practical methods, we plot the ratio of the key generation rate between using our new scheme and other two practical methods ($W_{1}$ and $W_{3}$) in Fig. 5b. Excitingly, our new proposal exhibits more than two times improvement in the key generation rate than conventional three-intensity decoy-state method at longer distance (>150 km), and more than ten times improvement compared to the passive decoy-state scheme at distances longer than 120 km, see the left axis in Fig. 5b. The improvement is on the one hand due to the relatively high optimal intensity used in our new scheme as shown in Fig. 4, and on the other hand, it is attributed to the more precise estimation on the QBER of single-photon pulses ($e_{11}$), see Fig. 3b.

5 Statistical fluctuations

In the practical implementation of QKD, Alice and Bob can only send finite number of pulses within reasonable experimental time, which will inevitably induce statistical fluctuation. Below we will account for the finite data size effect in real-life experiments.

As we know, the statistical fluctuation effect can be calculated by applying the deviation theory, e.g., the Chernoff bound [27]. The measurement outcome of the overall gain and the quantum-bit errors in the W basis satisfies

$$\begin{aligned} N_{x,y}^W\hat{S}_{x,y}^W = N_{x,y}^WS_{x,y}^W + {\delta _{x,y}}, \end{aligned}$$

(21)

$$\begin{aligned} N_{x,y}^W\hat{T}_{x,y}^W = N_{x,y}^WT_{x,y}^W + {\widetilde{\delta } _{x,y}}, \end{aligned}$$

(22)

with probability 1-2${\varepsilon _{x,y}}$, where $T_{x,y}^W: = E_{x,y}^W S_{x,y}^W$, ${\delta _{x,y}} \in [ { - {\Delta _{x,y}},{{\hat{\Delta } }_{x,y}}}]$, ${\widetilde{\delta } _{x,y}} \in [ { - {\Delta _1},{{\hat{\Delta }}_2}}]$, ${\Delta _{x,y}} = g( {N_{x,y}^W\hat{S}_{x,y}^W,{{\varepsilon _{x,y}^4}/{16}}})$, ${\hat{\Delta } _{x,y}} = g( {N_{x,y}^W\hat{S}_{x,y}^W,\varepsilon _{x,y}^{{3/2}}} )$, ${\Delta _1} = g( {N_{x,y }^W\hat{E}_{x,y }^W\hat{S}_{x,y }^W,{{\varepsilon _{x,y }^4}/ {16}}})$, ${\Delta _2} = g( {N_{x,y }^W\hat{E}_{x,y }^W\hat{S}_{x,y }^W,\varepsilon _{x,y }^{{3/2}}})$ and $g( {a,b} ) = \sqrt{2a\ln ( {{b^{ - 1}}})}$. Here ${\varepsilon _{x,y}}$ denotes the following probabilities: $\Pr ( {N_{x,y}^WS_{x,y}^W - N_{x,y}^W\hat{S}_{x,y}^W \ge \Delta _{x,y} }) \le {\varepsilon _{x,y}}$, $\Pr ( {N_{x,y}^W\hat{S}_{x,y}^W - N_{x,y}^WS_{x,y}^W \ge \hat{\Delta } _{x,y} }) \le {\varepsilon _{x,y}}$; $\Pr ( {N_{x,y}^WT_{x,y}^W - N_{x,y}^W\hat{T}_{x,y}^W \ge \Delta _1} ) \le {\varepsilon _{x,y}}$, $\Pr ( {N_{x,y}^W\hat{T}_{x,y}^W - N_{x,y}^WT_{x,y}^W \ge \Delta _2} ) \le {\varepsilon _{x,y}}$ [27]. $N_{x,y}^W$ is the number of pulses in the W basis, with the intensities of x and y sent by Alice and Bob, respectively. According to Eq. (21), we have

$$\begin{aligned} S_{x,y}^W - \frac{{{\Delta _{x,y}}}}{{N_{x,y}^W}} \le \hat{S}_{x,y}^W \le S_{x,y}^W + \frac{{{{\hat{\Delta } }_{x,y}}}}{{N_{x,y}^W}}. \end{aligned}$$

(23)

Then we can obtain the following inequalities

$$\begin{aligned} S_{x,y}^{W} \le \varsigma \left( {S_{x,y}^W} \right) : = \hat{S}_{x,y}^W + \frac{{{\Delta _{x,y}}}}{{N_{x,y}^W}}, \end{aligned}$$

(24)

$$\begin{aligned} S_{x,y}^{W} \ge \widetilde{\varsigma } \left( {S_{x,y}^W} \right) : = \hat{S}_{x,y}^W - \frac{{{{\hat{\Delta }}_{x,y}}}}{{N_{x,y}^W}}, \end{aligned}$$

(25)

$$\begin{aligned} T_{x,y}^{W} \le \xi \left( {T_{x,y}^W} \right) : = \hat{T}_{x,y}^W + \frac{{{\Delta _1}}}{{N_{x,y}^W}}, \end{aligned}$$

(26)

$$\begin{aligned} T_{x,y}^{W} \ge \widetilde{\xi } \left( {T_{x,y}^W} \right) : = \hat{T}_{x,y}^W - \frac{{{\Delta _2}}}{{N_{x,y}^W}}. \end{aligned}$$

(27)

According to Eqs. (18), (24) and (25), we obtain

$$\begin{aligned} Y_{11}^Z \ge \mathrm{{Y}}_{11}^{Z,L}: = \frac{{{c_1}^\prime (\mu '){c_2}^\prime (\mu ')\left[ {\widetilde{\varsigma } \left( {S_{\mu ,\mu }^Z} \right) - {\varsigma } \left( {\tilde{S}_{00}^Z} \right) } \right] - {c_1}(\mu ){c_2}(\mu )\left[ {{\varsigma } \left( {S_{\mu ',\mu '}^Z} \right) - \widetilde{\varsigma } \left( {\tilde{S}{{_{00}^Z}^\prime }} \right) } \right] }}{{\mathrm{{ }}{c_1}^\prime (\mu '){c_1}(\mu )\left[ {{c_1}(\mu ){c_2}^\prime (\mu ') - {c_1}^\prime (\mu '){c_2}(\mu )} \right] }}\mathrm{{ }}. \end{aligned}$$

(28)

Similarly, we can obtain the modified upper bound of single-photon quantum-bit error rate

$$\begin{aligned} e_{11}^X \le e_{11}^{X,U}: = \frac{{\xi \left( {T_{\mu ,\mu }^X} \right) - \widetilde{\xi } \left( {T_{\mu ,0}^X} \right) - \widetilde{\xi } \left( {T_{0,\mu }^X} \right) + \xi \left( {T_{0,0}^X} \right) }}{{c_1^2\left( \mu \right) Y_{11}^{X,L}}} + \Omega \left( {{N^Z}Y_{11}^Z,{N^X}Y_{11}^X,{\varepsilon _e}} \right) , \end{aligned}$$

(29)

where $\Omega \left( {a,b,c} \right) = \sqrt{{{\left( {a + 1} \right) \ln \left( {{c^{ - 1}}} \right) } \big / {\left[ {2b\left( {a + b} \right) } \right] }}}$. Therefore, Eq. (20) can be modified as:

$$\begin{aligned} R&\geqslant { - S_{\mu ',\mu '}^Zf{H_2}( {E_{\mu ','\mu }^Z} ) + {c_1}'{{(\mu ')}^2}Y_{11}^{Z,L}[ {1 - {H_2}( {e_{11}^{X,U}} )} ]} \nonumber \\&-\frac{1}{N_\text {tol}}({\log _2}\frac{8}{{{\epsilon _\text {cor}}}} + 2{\log _2}\frac{2}{{{\varepsilon _1}{\varepsilon _2}}} + 2{\log _2}\frac{1}{{2{\varepsilon _\text {PA}}}}). \end{aligned}$$

(30)

The protocol is $\epsilon _\text {sec}$-secret and $\epsilon _\text {cor}$-correct, where $\epsilon _\text {sec}=2(2\varepsilon _e+\varepsilon _1+\varepsilon _2)+3\varepsilon _{\mu ,\mu }+2\varepsilon _{\mu ' ,\mu ' }+\varepsilon _b+\varepsilon _\text {PA}$ [27]. $N_\text {tol}$ denotes number of total pulses emitted by Alice and Bob. For simplicity, we fix $\epsilon _\text {sec}=10^{-10}$, $\epsilon _\text {cor}=10^{-15}$ and set each error term to a common value $\varepsilon$ , thus $\epsilon _\text {sec}$=$15\varepsilon$. Besides, we suppose that the length of pulses is the same for each pair of intensities of Alice and Bob. Moreover, we have assumed the number of pulses sent by Alice (or Bob) have the proportion: $N_{\mu '}^W:N_\mu ^W = 1:1$.

In practical QKD implementation, the data size usually ranges between ${10^{12}}$ and ${10^{14}}$ [28–30]. We draw out corresponding numerical simulation results for our new proposed two-intensity decoy-state MDI-QKD and the standard three-intensity decoy-state protocols by accounting for statistical fluctuations, see Fig. 6. Obviously, the secure key generation rates will drop down with reducing the total number of pulses. However, it decreases more slowly in our new two-intensity scheme than the three-intensity one, e.g., in our new scheme a quite high key rate can still be obtained at the distance of 170 km with the data size of ${10^{12}}$.

Fig. 6

Key generation rates of MDI-QKD using the new method proposed by us with statistical fluctuation, compared with the finite data case of using the three-intensity MDI-QKD method with WCS . The black solid curve $W_{2}$ ($W_{3}$) refers to the case without statistical fluctuation, and the rest of the curves $W_{2}$-f ($W_{3}$-f) represent the case when taking statistical fluctuation into account

6 Conclusion

In summary, we have presented a practical scheme of implementing two-intensity weak coherent light into the MDI-QKD. In contrast to the conventional three-intensity decoy-state MDI-QKD, in our new proposal we insert a beam splitter and a local detector at both Alice’s and Bob’s side, and then both the triggering and non-triggering signals could be employed to process parameter estimations. While compared with the original passive decoy-state MDI-QKD, the main differences are: Alice (or Bob) randomly modulates her (or his) seeding pulses into two different intensities. By combing with both their triggering and non-triggering characteristics, the detection results at Charlie’s side could be divided into many different events. Therefore, we could obtain more input parameters and achieve more precise estimations for the two-single-photon contributions.

To analyze our proposal, we carry out corresponding numerical simulations. Our simulation results demonstrate that our new scheme exhibits drastically enhanced performance compared with two other existing methods both in the transmission distance and in the final key generation rate, approaching very closely to the asymptotic case of using infinite number of decoy states. Moreover, even when taking statistical fluctuation into account, our scheme can still give a quite high key generation rate at a long transmission distance (>170 km). In addition, our scheme only needs linear optics and can be easily realized with current technology. Therefore, it may have a promising application in the future of the quantum key distribution.