1 Introduction

Uncertainty principle is considered to be one of the most singular characteristics of quantum mechanics. Ever since the first uncertainty relation of position–momentum was proposed by Heisenberg in 1927 [1], many efforts have been made in interpreting the intrinsic meaning of this kind of inequalities. The traditional approach that formulates uncertainty relations is based on the variance of measurement outcomes. The most famous one is due to Robertson [2], who derived the following uncertainty inequality for two observables A and B:

$$\begin{aligned} \Delta _{\rho } A\Delta _{\rho } B\ge \frac{1}{2}|\langle [A,B]\rangle _{\rho }|, \end{aligned}$$
(1)

where \(\Delta _{\rho }\Omega =\sqrt{\langle \Omega ^{2}\rangle _{\rho }-\langle \Omega \rangle _{\rho }^{2}}\) is the standard deviation of an observable \(\Omega \), and \([A,B]=AB-BA\). It is obvious that the above relation is nontrivial for two noncommuting observables when suitable states are measured. That is to say, the lower bound in (1) can be used to capture the noncommutativity of two observables. There also have been many ways to describe uncertainty relations, such as in terms of entropies [3–8] and by means of majorization technique [9–14].

Based on several nice properties such as convexity and additivity, Wigner and Yanase (WY) introduced their skew information. Being a measure for the noncommutativity between a state \(\rho \) and an observable H, the skew information provides a measure of quantum uncertainty of H in the state \(\rho \) and was used by Luo to derive a refinement of Heisenberg’s uncertainty relation for mixed states [16].

On the other hand, the skew information

$$\begin{aligned} I_{\rho }(H)=-\frac{1}{2}\mathrm {Tr}\left( [\sqrt{\rho },H]^{2}\right) =\frac{1}{2}\Vert [\sqrt{\rho },H]\Vert ^{2} \end{aligned}$$

was introduced by Wigner and Yanase in 1963 [15] to quantify the information content of a quantum state \(\rho \) with respect to the observables not commuting with (i.e., skew to) the conserved quantity H. It becomes a useful tool in quantum information theory in recent years, such as characterizing nonclassical correlations [21], being a measure of the H coherence of the state \(\rho \) [22], and quantifying the dynamics of some physical phenomena [23–25].

However, previous works demonstrated that the skew information is not suitable for formulating uncertainty relations: The following relation:

$$\begin{aligned} I_{\rho }(A)I_{\rho }(B)\ge \frac{1}{4}|\langle [A,B]\rangle _{\rho }|^{2} \end{aligned}$$

turned to be false [17–20]. Alternatively, in Ref. [16], Luo defined the quantity \(U_{\rho }(H)\),

$$\begin{aligned} U_{\rho }(H)=\sqrt{(\Delta _{\rho } H)^{4}-[(\Delta _{\rho } H)^{2}-I_{\rho }(H)]^{2}}, \end{aligned}$$

and provided a new Heisenberg-type uncertainty relation:

$$\begin{aligned} U_{\rho }(A)U_{\rho }(B)\ge \frac{1}{4}|\langle [A,B]\rangle _{\rho }|^{2}. \end{aligned}$$
(2)

After that, Furuichi [26] derived a Schrödinger-type uncertainty relation using the quantity \(U_{\rho }(H)\), and a generalization of Schrödinger’s uncertainty relation based on Wigner–Yanase skew information is presented in Ref. [27].

Besides uncertainty relations in the product form, variance-based and standard deviation-based sum uncertainty relations are also attracting considerable attention recently [28–31]. In Ref. [28], the authors derived two variance-based sum uncertainty relations for two incompatible observables. They show that the lower bounds are nontrivial whenever the two observables are incompatible on the state of the system. Thus, the lower bounds of these uncertainty inequalities can be used to capture the incompatibility of the observables. After that, Chen and Fei [29] presented two uncertainty inequalities in terms of the sum of variances and standard deviations for arbitrary N incompatible observables, respectively.

In this paper, we formulate sum uncertainty relations by use of the skew information. We presented several uncertainty inequalities for arbitrary N observables. These lower bounds have explicit physical meaning, i.e., they can be used to capture the noncommutativity of the observables like Heisenberg–Robertson product uncertainty relation (1). Some applications and examples are also provided.

2 Skew information-based sum uncertainty relations for two observables

We first present two skew information-based sum uncertainty inequalities for two observables.

Theorem 1

For two observables A and B, we have

$$\begin{aligned} I_{\rho }(A)+I_{\rho }(B)\ge \frac{1}{2}\max \left\{ I_{\rho }(A+B),I_{\rho }(A-B)\right\} . \end{aligned}$$
(3)

Proof

Consider the parallelogram law in a Hilbert space: \(\Vert u+v\Vert ^{2}+\Vert u-v\Vert ^{2}=2(\Vert u\Vert ^{2}+\Vert v\Vert ^{2})\). Let \(u=[\sqrt{\rho },A],v=[\sqrt{\rho },B]\). Then, we have

$$\begin{aligned} I_{\rho }(A)+I_{\rho }(B)= & {} \frac{1}{2}\left[ I_{\rho }(A+B)+I_{\rho }(A-B)\right] \nonumber \\\ge & {} \frac{1}{2}\max \left\{ I_{\rho }(A+B),I_{\rho }(A-B)\right\} . \end{aligned}$$
(4)

This completes the proof. \(\square \)

If the lower bound in (3) is zero, then we have \([\sqrt{\rho },A+B]=[\sqrt{\rho },A-B]=0\), which implies that \([\sqrt{\rho },A]=[\sqrt{\rho },B]=0\). Further, we can conclude that \([\rho ,A]=[\rho ,B]=0\) and \(\langle [A,B]\rangle _{\rho }=0\). Hence, it is easy to see that if the two observables A and B are noncommutative, the relation (3) is nontrivial. That is to say, skew information can be used to formulate sum uncertainty relations, and the lower bound we derived in (3) is meaningful. In particular, for pure states, we get the uncertainty relations presented in Refs. [28, 32], since in this case, \(I_{\rho }(H)=(\Delta _{\rho } H)^{2}\).

Similar to the standard deviation-based sum uncertainty relations, we provide another uncertainty inequality by using the quantity \(\sqrt{I_{\rho }(H)}\). From the inequality \(\Vert u\pm v\Vert \le \Vert u\Vert +\Vert v\Vert \), we have the following Theorem.

Theorem 2

For two observables A and B, we have

$$\begin{aligned} \sqrt{I_{\rho }(A)}+\sqrt{I_{\rho }(B)}\ge \max \{\sqrt{I_{\rho }(A+B)},\sqrt{I_{\rho }(A-B)}\}. \end{aligned}$$
(5)

It is obvious that the lower bound in (5) is nonzero as long as A and B are noncommutative. Thus, the relation (5) can be used to characterize the noncommutativity of A and B too.

3 Skew information-based sum uncertainty relations for arbitrary N observables

Before generalizing the uncertainty relations (3) and (5) to arbitrary N observables case, let us first improve several uncertainty relations for N observables. Let \(A_{1},\ldots ,A_{N}\) be N observables. Since

$$\begin{aligned} \sqrt{I_{\rho }\left( \sum _{i=1}^{N}A_{i}\right) }= & {} \frac{1}{\sqrt{2}}\left\| \left[ \sqrt{\rho },\sum _{i=1}^{N}A_{i}\right] \right\| \nonumber \\\le & {} \frac{1}{\sqrt{2}}\sum _{i=1}^{N}\Vert [\sqrt{\rho },A_{i}]\Vert \nonumber \\= & {} \sum _{i=1}^{N}\sqrt{I_{\rho }(A_{i})}, \end{aligned}$$
(6)

we get

$$\begin{aligned} \sum _{i=1}^{N}\sqrt{I_{\rho }(A_{i})}\ge \sqrt{I_{\rho }\left( \sum _{i=1}^{N}A_{i}\right) }. \end{aligned}$$
(7)

If \(\rho \) is a pure state, then the relation (7) gives rise to the result presented in Ref. [30]:

$$\begin{aligned} \sum _{i}\Delta _{\rho }(A_{i})\ge \Delta _{\rho }\left( \sum _{i}A_{i}\right) . \end{aligned}$$

Let \(\{A_{i}\}_{i=1}^{N}\) and \(\{B_{j}\}_{j=1}^{N}\) be two sets of noncommuting observables satisfying \([A_{i},B_{j}]=\mathrm {i}\delta _{ij}C\). In Ref. [30], it has been proved that the product of sum of uncertainties in the individual observables satisfies the following inequality:

$$\begin{aligned} \left( \sum _{i=1}^{N}\Delta _{\rho } A_{i}\right) \left( \sum _{i=1}^{N}\Delta _{\rho } B_{j}\right) \ge \frac{N}{2}|\langle C\rangle _{\rho }|. \end{aligned}$$
(8)

By using uncertainty relation (2) and noting that \(\sqrt{U_{\rho }(H)}\le \Delta _{\rho }H\), we have a refined form of (8):

$$\begin{aligned} \left( \sum _{i=1}^{N}\sqrt{U_{\rho }(A_{i})}\right) \left( \sum _{j=1}^{N}\sqrt{U_{\rho }(B_{j})}\right)= & {} \sum _{ij}\sqrt{U_{\rho }(A_{i})U_{\rho }(B_{j})}\nonumber \\\ge & {} \frac{1}{2}\sum _{ij}|\langle [A_{i},B_{j}]\rangle _{\rho }|\nonumber \\= & {} \frac{N}{2}|\langle C\rangle _{\rho }|. \end{aligned}$$
(9)

The above uncertainty relation (8) can be further improved:

Theorem 3

Let \(\{A_{i}\}_{i=1}^{N}\) and \(\{B_{j}\}_{j=1}^{N}\) be two sets of noncommuting observables satisfying \([A_{i},B_{j}]=\mathrm {i}\delta _{ij}C\). Then, we have

$$\begin{aligned} \left( \sum _{i=1}^{N}U_{\rho }(A_{i})\right) \left( \sum _{j=1}^{N}U_{\rho }(B_{j})\right) \ge \frac{N}{4}|\langle C\rangle _{\rho }|^{2}. \end{aligned}$$
(10)

Proof

$$\begin{aligned} \left( \sum _{i=1}^{N}U_{\rho }(A_{i})\right) \left( \sum _{j=1}^{N}U_{\rho }(B_{j})\right)= & {} \sum _{ij}U_{\rho }(A_{i})U_{\rho }(B_{j})\nonumber \\\ge & {} \frac{1}{4}\sum _{ij}|\langle [A_{i},B_{j}]\rangle _{\rho }|^{2}\nonumber \\= & {} \frac{N}{4}|\langle C\rangle _{\rho }|^{2}. \end{aligned}$$
(11)

To show that the uncertainty relation (10) is stronger than (9), one only need to note that \(\left( \sum _{i=1}^{N}\sqrt{U_{\rho }(\Omega _{i})}\right) ^{2}\ge \left( \sum _{i=1}^{N}U_{\rho }(\Omega _{i})\right) \), \(\Omega =A,B\). \(\square \)

Let us now generalize the uncertainty relation (3) to arbitrary N observables.

Theorem 4

For arbitrary N observables \(A_{1}\), \(A_{2}\), \(\ldots \), \(A_{N}\), we have

$$\begin{aligned} \sum _{i=1}^{N}I_{\rho }(A_{i})\ge & {} \frac{1}{N-2}\left[ \sum _{1\le i<j\le N}I_{\rho }(A_{i}+A_{j}) -\frac{1}{(N-1)^{2}}\right. \nonumber \\&\left. \left( \sum _{1\le i<j\le N}\sqrt{I_{\rho }(A_{i}+A_{j})}\right) ^{2}\right] . \end{aligned}$$
(12)

If \(A_{i}s\) are mutually noncommutative, then the lower bound in (12) is nonzero.

Proof

Consider the following inequality in a Hilbert space [29]:

$$\begin{aligned} \sum _{i=1}^{N}\Vert u_{i}\Vert ^{2}\ge & {} \frac{1}{N-2}\left[ \sum _{1\le i<j\le N}\Vert u_{i}+u_{j}\Vert ^{2} -\frac{1}{(N-1)^{2}}\left( \sum _{1\le i<j\le N}\Vert u_{i}+u_{j}\Vert \right) ^{2}\right] \nonumber \\\ge & {} \frac{1}{2(N-1)}\sum _{1\le i<j\le N}\Vert u_{i}+u_{j}\Vert ^{2}. \end{aligned}$$
(13)

Let \(u_{i}=[\sqrt{\rho },A_{i}]\). We obtain (12) directly. Moreover, if the lower bound (12) is zero, then each \(I_{\rho }(A_{i}+A_{j})\) is equal to zero, which implies that \(I_{\rho }(A_{i})=0,\forall i\). Thus, we have \(\langle [A_{i},A_{j}]\rangle _{\rho }=0\). That is to say, for N noncommuting observables, the relation (12) is nontrivial. \(\square \)

Remark

From (3), one may also trivially derive an uncertainty relation for N observables by adding the skew information of every pair of the observables. Nevertheless, it can be seen from (13) that the lower bound in (12) is tighter than the one trivially derived from (3) in such way.

We now generalize uncertainty relation (5) to arbitrary N observables case.

Theorem 5

For arbitrary N observables \(A_{1}\), \(A_{2}\), \(\ldots \), \(A_{N}\), we have

$$\begin{aligned} \sum _{i=1}^{N}\sqrt{I_{\rho }(A_{i})}\ge \frac{1}{N-2}\left[ \sum _{1\le i<j\le N}\sqrt{I_{\rho }(A_{i}+A_{j})} -\sqrt{I_{\rho }\left( \sum _{i=1}^{N}A_{i}\right) }\right] . \end{aligned}$$
(14)

If \(A_{i}s\) are mutually noncommutative, then the lower bound in (14) is nonzero.

Proof

Using the following inequality [29, 33, 34],

$$\begin{aligned} \sum _{i=1}^{N}\Vert u_{i}\Vert\ge & {} \frac{1}{N-2}\left( \sum _{1\le i<j\le N}\Vert u_{i}+u_{j}\Vert -\left\| \sum _{i=1}^{N}u_{i}\right\| \right) \nonumber \\\ge & {} \left\| \sum _{i=1}^{N}u_{i}\right\| , \end{aligned}$$
(15)

and setting \(u_{i}=[\sqrt{\rho },A_{i}]\), we get (14). If the lower bound in (14) is zero, so is (7), and all \(I_{\rho }(A_{i}+A_{j})\) are equal to zero. In this case, we have \(I_{\rho }(A_{i})=0,\forall i\), and \(\langle [A_{i},A_{j}]\rangle _{\rho }=0\). Thus, as long as \(A_{i}s\) are mutually noncommutative, the relation (14) is nontrivial. \(\square \)

It can be verified from (15) that the inequality (14) is tighter than (7). In the following, we provide a new skew information-based sum uncertainty relation.

Theorem 6

Let \(A_{1}\), \(A_{2}\), \(\ldots \), \(A_{N}\) be N observables, \(\rho \) a quantum state such that \(I_{\rho }(A_{i})\ne 0, \forall i\). Let G be an \(N\times N\) matrix with entries \(G_{ij}=\mathrm {Tr}(X_{i}X_{j})\), where \(X_{i}=\mathrm {i}[\sqrt{\rho },A_{i}]/\Vert [\sqrt{\rho },A_{i}]\Vert , \mathrm {i}=\sqrt{-1}, \forall i\). Then, we have

$$\begin{aligned} \sum _{i=1}^{N}I_{\rho }(A_{i})\ge \frac{1}{\lambda _{\max }(G)}I_{\rho }\left( \sum _{i=1}^{N}A_{i}\right) , \end{aligned}$$
(16)

where \(\lambda _{\max }(G)\) denotes the maximal eigenvalue of G.

Proof

Since \(X_{i}s\) are Hermitian matrices, G is also Hermitian. Further, G is a positive semi-definite matrix, since \(\sum _{i,j}x_{i}^{*}G_{ij}x_{j}=\sum _{i,j}x_{i}^{*}\mathrm {Tr}(X_{i}X_{j})x_{j}=\Vert \sum _{i}x_{i}X_{i}\Vert ^{2}\ge 0\). Thus, all eigenvalues of G are nonnegative numbers. Note that

$$\begin{aligned} I_{\rho }\left( \sum _{i}A_{i}\right)= & {} -\frac{1}{2}\mathrm {Tr}\left( \left[ \sqrt{\rho },\sum _{i}A_{i}\right] ^{2}\right) \nonumber \\= & {} \frac{1}{2}\sum _{i,j}\mathrm {Tr}\left[ (\mathrm {i}[\sqrt{\rho },A_{i}])(\mathrm {i}[\sqrt{\rho },A_{j}])\right] \nonumber \\= & {} \frac{1}{2}\sum _{i,j}\Vert [\sqrt{\rho },A_{i}]\Vert G_{ij}\Vert [\sqrt{\rho },A_{j}]\Vert \nonumber \\= & {} \sum _{i,j}\sqrt{I_{\rho }(A_{i})}G_{ij}\sqrt{I_{\rho }(A_{j})}\nonumber \\\le & {} \lambda _{\max }(G)\sum _{i}I_{\rho }(A_{i}), \end{aligned}$$
(17)

we get (16). \(\square \)

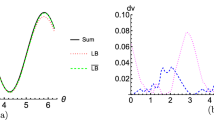
As an example, let us consider three observables case, the Pauli matrices \(\sigma _{1}=|0\rangle \langle 1|+|1\rangle \langle 0|\), \(\sigma _{2}=-i|0\rangle \langle 1|+i|1\rangle \langle 0|\), and \(\sigma _{3}=|0\rangle \langle 0|-|1\rangle \langle 1|\). Let the measured states be given with Bloch vector \(\overrightarrow{r}=(\frac{\sqrt{3}}{2}\cos \theta ,\frac{\sqrt{3}}{2}\sin \theta ,0)\). Then, we have \(I_{\rho }(\sigma _{1})=\frac{1}{2}\sin ^{2}\theta \), \(I_{\rho }(\sigma _{2})=\frac{1}{2}\cos ^{2}\theta \), \(I_{\rho }(\sigma _{3})=\frac{1}{2}\), \(\lambda _{\max }(G)=2\), \(I_{\rho }(\sigma _{1}+\sigma _{2})=\frac{1}{2}(1-\sin 2\theta )\), \(I_{\rho }(\sigma _{2}+\sigma _{3})=\frac{1}{4}(3+\cos 2\theta )\), \(I_{\rho }(\sigma _{1}+\sigma _{3})=\frac{1}{4}(3-\cos 2\theta )\), \(I_{\rho }(\sigma _{1}+\sigma _{2}+\sigma _{3})=1-\frac{1}{2}\sin 2\theta \). The comparison between the lower bounds (12) and (16) is given in Fig 1.

Fig. 1
figure 1

Horizontal line is the sum of the skew information \(I_{\rho }(\sigma _{1})+I_{\rho }(\sigma _{2})+I_{\rho }(\sigma _{3})\). The dot-dashed line is the bound (12). The dashed line is the bound (16)

Full size image

One can see that (16) is stronger than (12) in some cases. Therefore, we have the following skew information-based sum uncertainty relation:

Theorem 7

$$\begin{aligned} \sum _{i=1}^{N}I_{\rho }(A_{i})\ge \max \{(lb1),(lb2)\}, \end{aligned}$$
(18)

where (lb1) and (lb2) stand for the lower bounds in (12) and (16), respectively.

4 Conclusion

Skew information is an important quantity in the theory of quantum information and plays significant roles in many quantum information processing tasks. In this paper, we have demonstrated that skew information can be used to formulate sum uncertainty relations for arbitrary N observables. The skew information-based sum uncertainty relations are rather different from the variance-based ones like in Refs. [28, 29, 32]. First, the physical meaning of skew information is quite different to the variances of measurement outcomes, although they are numerically equal when the physical system is in a pure quantum state. On the other hand, uncertainty relations based on skew information and variances have their own advantages. The lower bounds of variance-based sum uncertainty relations in Refs. [28, 29, 32] capture the incompatibility of the observables, i.e., the lower bound is nonzero as long as the quantum states are not the common eigenstates of the observables, while the lower bounds of skew information-based uncertainty relations we derived in this paper capture the noncommutativity of the observables, i.e., the inequalities are nontrivial when the observables are noncommutative with respect to the measured states. For pure states, some of these skew information-based inequalities are reduced to the variance-based ones [28, 29, 32]. We hope that these results may shed lights on further investigations on skew information-based uncertainty relations.