1 Introduction

Given an undirected graph \(G = (V ,E)\) with a set V of even number of vertices and a set E of unweighted edges, two graph bisection problems will be considered in the paper: the max-bisection problem and the min-bisection problem. The goal of the max-bisection problem is to divide V into two subsets A and B of the same size so as to maximize the number of edges between A and B, while the goal of the min-bisection problem is to minimize the number of edges between A and B. In theory, both bisection problems are NP-hard for general graphs [9, 14].

These classical combinatorial optimization problems are special cases of graph partitioning [13]. The graph partitioning has many applications, for example divide-and-conquer algorithms [24], compiler optimization [21], VLSI circuit layout [5], load balancing [17], image processing [30], computer vision [22], distributed computing [25] and route planning [7]. In practice, there are many general-purpose heuristics for graph partitioning, e.g., [18, 31, 32] that handle particular graph classes, such as [6, 26, 32]. There are also many practical exact algorithms for graph bisection that use the branch-and-bound approach [8, 23]. These approaches make expensive usage of time and space to obtain lower bounds [1, 2, 8, 16].

On conventional computers, approximation algorithms have gained much attention to tackle the max-bisection and the min-bisection problems. The max-bisection problem, for example, has an approximation ratio of 0.7028 due to [10] which is known to be the best approximation ratio for a long time by introducing the RPR\(^2\) rounding technique into semidefinite programming (SDP) relaxation. In [12], a poly-time algorithm is proposed that given a graph admitting a bisection cutting, a fraction \(1-\varepsilon \) of edges finds a bisection cutting an \((1-g(\varepsilon ))\) fraction of edges where \(g(\varepsilon ) \rightarrow 0\) as \(\varepsilon \rightarrow 0\). A 0.85-approximation algorithm for the max-bisection is obtained in [28]. In [33], the SDP relaxation and the RPR\(^2\) technique of [10] have been used to obtain a performance curve as a function of the ratio of the optimal SDP value over the total weight through finer analysis under the assumption of convexity of the RPR\(^2\) function. For the min-bisection problem, the best-known approximation ratio is \(O(\log \,n)\) [27] with some limited graph classes have known polynomial-time solutions such as grids without holes [11] and graphs with bounded tree width [20].

The aim of the paper was to propose an algorithm that represents the two bisection problems as Boolean constraint satisfaction problems where the set of edges are represented as set of constraints. The algorithm prepares a superposition of all possible graph bisections using an amplitude amplification technique, then evaluates the set of constraints for all possible bisections simultaneously and then amplifies the amplitudes of the best bisections that achieve the maximum/minimum satisfaction to the set of constraints using a novel amplitude amplification technique that applies an iterative partial negation and partial measurement. The proposed algorithm targets a general graph where it runs in \(O(m^2)\) for a graph with m edges and in the worst case runs in \(O(n^4)\) for a dense graph with number edges close to \(m = {\textstyle {{n(n - 1)} \over 2}}\) with n vertices to achieve an arbitrary high probability of success of \(1-\epsilon \) for small \(\epsilon >0\) using a polynomial space resources.

The paper is organized as follows: Sect. 2 shows the data structure used to represent a graph bisection problem as a Boolean constraint satisfaction problem. Section 3 presents the proposed algorithm with analysis on time and space requirements. Section 4 concludes the paper.

2 Data structures and graph representation

Several optimization problems, such as the max-bisection and the min-bisection problems, can be formulated as Boolean constraint satisfaction problems [3, 4] where a feasible solution is a solution with as many variables set to 0 as variables set to 1, i.e., balanced assignment, as follows: For a graph G with n vertices and m edges, consider n Boolean variables \(v_0, \ldots , v_{n-1}\) and m constraints by associating with each edge \((a, b) \in E\) the constraint \(c_l=v_a\oplus v_b\), with \(l=0,1,\ldots ,m-1\), then the max-bisection is the problem that consists of finding a balanced assignment to maximize the number of constraints equal to logic-1 from the m constraints, while the min-bisection is the problem that consists of finding a balanced assignment to maximize the number of constraints equal to logic-0 from the m constraints, such that if a Boolean variable is set to 0, then the associated vertex belongs to the first partition, and if a Boolean variable is set to 1, then the associated vertex belongs to the second partition.

Fig. 1
figure 1

a A random graph with 8 vertices and 12 edges, b a max-bisection instance for the graph in a with 10 edges connecting the two subsets, and c. b A min-bisection instance for the graph in a with 3 edges connecting the two subsets

Full size image

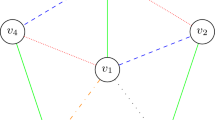
For example, consider the graph G shown in Fig. 1a. Let \(G = (V ,E)\), where,

$$\begin{aligned} \begin{array}{l} V=\{0,1,2,3,4,5,6,7\},\\ E=\{(0,1),(0,2),(0,3),\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1,2),(1,7),(2,3),\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3,4),(3,6),(4,5),\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(4,6),(5,7),(6,7)\}.\\ \end{array} \end{aligned}$$
(1)

Assume that each vertex \(a \in V\) is associated with a Boolean variable \(v_a\), then the set of vertices V can be represented as a vector X of Boolean variables as follows,

$$\begin{aligned} X=(v_0,v_1,v_2,v_3,v_4,v_5,v_6,v_7), \end{aligned}$$
(2)

and if each edge \((a, b) \in E\) is associated with a constraint \(c_l=v_a\oplus v_b\), then the set of edges E can be represented as a vector Z of constraints as follows,

$$\begin{aligned} Z=(c_0,c_1,c_2,c_3,c_4,c_5,c_6,c_7,c_8,c_9,c_{10},c_{11}), \end{aligned}$$
(3)

such that,

$$\begin{aligned} c_0= & {} (v_0\oplus v_1), c_1= (v_0\oplus v_2), c_2= (v_0\oplus v_3),\nonumber \\ c_3= & {} (v_1\oplus v_2), c_4= (v_1\oplus v_7), c_5= (v_2\oplus v_3), \nonumber \\ c_6= & {} (v_3\oplus v_4), c_7= (v_3\oplus v_6), c_8= (v_4\oplus v_5), \nonumber \\ c_9= & {} (v_4\oplus v_6), c_{10}= (v_5 \oplus v_7), c_{11}= (v_6\oplus v_7). \end{aligned}$$
(4)

In general, a bisection \(G_P\) for the graph G can be represented as \(G_p = (x ,z(x))\) such that each vector \(x \in \{0,1\}^n \) of variable assignments is associated with a vector \(z(x)\in \{0,1\}^m\) of constraints evaluated as functions of the variable assignment x. In the max-bisection and the min-bisection problems, the vector x of variable assignments is restricted to be balanced so there are \(M = \left( {\begin{array}{ll} n \\ {{\textstyle {n \over 2}}} \\ \end{array}} \right) \) possible variable assignments among the \(N=2^n\) possible variable assignments, and the solution of the max-bisection problem is to find the variable assignment that is associated with a vector of constraints that contains the maximum number of 1’s, and the solution for the min-bisection problem is to find the variable assignment that is associated with a vector of constraints that contains the maximum number of 0’s. For example, for the graph G shown in Fig. 1a, a max-bisection for G is ((0, 1, 0, 1, 0, 1, 1, 0), (1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1)) with 10 edges connecting the two partitions as shown in Fig. 1b, and a min-bisection for G is ((0, 0, 0, 0, 1, 1, 1, 1), (0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0)) with 3 edges connecting the two partitions as shown in Fig. 1c. It is important to notice that a variable assignment \(x= (0,1,0,1,0,1,1,0)\) is equivalent to \(\overline{x}= (1,0,1,0,1,0,0,1)\), where \(\overline{x}\) is the bit-wise negation of x.

3 The algorithm

Given a graph G with n vertices and m edges, the proposed algorithm is divided into three stages: The first stage prepares a superposition of all balanced assignments for the n variables. The second stage evaluates the m constraints associated with the m edges for every balanced assignment and stores the values of constraints in constraint vectors entangled with the corresponding balanced assignments in the superposition. The third stage amplifies the constraint vector with maximum (minimum) number of satisfied constraints using a partial negation and iterative measurement technique.

3.1 Balanced assignments preparation

To prepare a superposition of all balanced assignments of n qubits, the proposed algorithm can use any amplitude amplification technique, e.g., [15, 34, 35]. An extra step should be added after the amplitude amplification to create an entanglement between the matched items and an auxiliary qubit \(\left| {ax_1 } \right\rangle \), so that the correctness of the items in the superposition can be verified by applying measurement on \(\left| {ax_1 } \right\rangle \) without having to examine the superposition itself. So, if \(\left| {ax_1 } \right\rangle = \left| {1 } \right\rangle \) at the end of this stage, then the superposition contains the correct items, i.e., the balanced assignments, otherwise, repeat the preparation stage until \(\left| {ax_1 } \right\rangle = \left| {1 } \right\rangle \). This is useful for not having to proceed to the next stages until the preparation stage succeeds.

The preparation stage to have a superposition of all balanced assignments of n qubits will use the amplitude amplification technique shown in [35] since it achieves the highest known probability of success using fixed operators and it can be summarized as follows, prepare a superposition of \(2^n\) states by initializing n qubits to state \(\left| {0} \right\rangle \) and apply \(H^{\otimes n}\) on the n qubits

$$\begin{aligned} \left| {\Psi _0 } \right\rangle= & {} \left( {H^{ \otimes n}} \right) \left| 0 \right\rangle ^{ \otimes n} \nonumber \\= & {} \frac{1}{{\sqrt{N} }}\sum \limits _{j = 0}^{N - 1} {\left| j \right\rangle }, \end{aligned}$$
(5)

where H is the Hadamard gate and \(N=2^n\). Assume that the system \(\left| {\Psi _0 } \right\rangle \) is rewritten as follows,

$$\begin{aligned} \left| \Psi _0\right\rangle = \frac{1}{{\sqrt{N} }} {\mathop {\mathop {\sum }\limits _{j = 0}}\limits _{j \in X_T}^{N - 1}} {\left| j \right\rangle } + \frac{1}{{\sqrt{N} }} \mathop {\mathop {\sum }\limits _{j = 0}}\limits _{j \in X_F}^{N-1} {\left| j \right\rangle }, \end{aligned}$$
(6)

where \(X_T\) is the set of all balanced assignments of n bits and \(X_F\) is the set of all unbalanced assignments. Let \(M=\left( {\begin{array}{ll} n \\ {{\textstyle {n \over 2}}} \\ \end{array}} \right) \) be the number of balanced assignments among the \(2^n\) possible assignments, \(\sin (\theta ) = \sqrt{{M / N}}\) and \(0 < \theta \le \pi /2\), then the system can be rewritten as follows,

$$\begin{aligned} \left| \Psi _0\right\rangle = \sin (\theta )\left| {\psi _1 } \right\rangle + \cos (\theta )\left| {\psi _0 } \right\rangle , \end{aligned}$$
(7)

where \(\left| {\psi _1 } \right\rangle = \left| {\tau } \right\rangle \) represents the balanced assignments subspace and \(\left| {\psi _0 } \right\rangle \) represents the unbalanced assignments subspace.

Let \(D=WR_0 \left( \phi \right) W^\dag R_\tau \left( \phi \right) , R_0 \left( \phi \right) = I - (1 - e^{i\phi } )\left| 0 \right\rangle \left\langle 0 \right| , R_\tau \left( \phi \right) = I - (1 - e^{i\phi } )\left| \tau \right\rangle \left\langle \tau \right| \), where \(W=H^{\otimes n}\) is the Walsh–Hadamard transform [19]. Iterate the operator D on \(\left| \Psi _0\right\rangle \) for q times to get,

$$\begin{aligned} \left| {\Psi _1 } \right\rangle = D^{q}\left| {\Psi _0 } \right\rangle = a_q \left| {\psi _1 } \right\rangle + b_q \left| {\psi _0 } \right\rangle , \end{aligned}$$
(8)

such that,

$$\begin{aligned} a_q= & {} \sin (\theta )\left( {e^{iq\phi } U_q \left( y \right) + e^{i(q - 1)\phi } U_{q - 1} \left( y \right) } \right) , \end{aligned}$$
(9)
$$\begin{aligned} b_q= & {} \cos (\theta )e^{i(q - 1)\phi } \left( {U_q \left( y \right) + U_{q - 1} \left( y \right) } \right) , \end{aligned}$$
(10)

where \(y=cos(\delta ), \cos \left( \delta \right) = 2\sin ^2 (\theta )\sin ^2 ({\textstyle {\phi \over 2}}) - 1, 0<\theta \le \pi /2\), and \(U_q\) is the Chebyshev polynomial of the second kind [29] defined as follows,

$$\begin{aligned} U_q \left( y \right) = \frac{{\sin \left( {\left( {q + 1} \right) \delta } \right) }}{{\sin \left( \delta \right) }}. \end{aligned}$$
(11)

Setting \(\phi =6.02193\approx 1.9168\pi , M=\left( {\begin{array}{ll} n \\ {{\textstyle {n \over 2}}} \\ \end{array}} \right) , N=2^n\) and, \(q = \left\lfloor {{\textstyle {\phi \over {\sin (\theta )}}}} \right\rfloor \), then \(\left| {a_q } \right| ^2 \ge 0.9975\) [35]. The upper bound for the required number of iterations q to reach the maximum probability of success is,

$$\begin{aligned} q = \left\lfloor {{\textstyle {\phi \over {\sin (\theta )}}}} \right\rfloor \le 1.9168\pi \sqrt{\frac{N}{M}}, \end{aligned}$$
(12)

and using Stirling’s approximation,

$$\begin{aligned} n! \approx \sqrt{2\pi n} \left( {\frac{n}{e}} \right) ^n, \end{aligned}$$
(13)

then, the upper bound for required number of iterations q to prepare the superposition of all balanced assignments is,

$$\begin{aligned} q \approx 1.9168\root 4 \of {{\frac{{\pi ^5 }}{{2 }}n}} = O\left( \root 4 \of {n} \right) . \end{aligned}$$
(14)

It is required to preserve the states in \(\left| {\psi _1 } \right\rangle \) for further processing in the next stage. This can be done by adding an auxiliary qubit \(\left| {ax_1 } \right\rangle \) initialized to state \(\left| {0} \right\rangle \) and have the states of the balanced assignments entangled with \(\left| {ax_1 } \right\rangle = \left| {1} \right\rangle \), so that, the correctness of the items in the superposition can be verified by applying measurement on \(\left| {ax_1 } \right\rangle \) without having to examine the superposition itself. So, if \(\left| {ax_1 } \right\rangle = \left| {1 } \right\rangle \), then the superposition contains the balanced assignments, otherwise, repeat the preparation stage until \(\left| {ax_1 } \right\rangle = \left| {1 } \right\rangle \). This is useful to be able to proceed to the next stage when the preparation stage succeeds. To prepare the entanglement, let

$$\begin{aligned} \left| {\Psi _2 } \right\rangle= & {} \left| {\Psi _1 } \right\rangle \otimes \left| {0 } \right\rangle \nonumber \\= & {} a_q \left| {\psi _1 } \right\rangle \otimes \left| {0 } \right\rangle + b_q \left| {\psi _0 } \right\rangle \otimes \left| {0 } \right\rangle , \end{aligned}$$
(15)

and apply a quantum Boolean operator \(U_f\) on \(\left| {\Psi _2 } \right\rangle \), where \(U_f\) is defined as follows,

$$\begin{aligned} U_f \left| {x,0} \right\rangle = \left\{ {\begin{array}{ll} {\left| {x ,0} \right\rangle ,\quad \mathrm{if }\quad \left| x\right\rangle \in \left| \psi _0\right\rangle ,} \\ {\left| {x ,1} \right\rangle ,\quad \mathrm{if }\quad \left| x\right\rangle \in \left| \psi _1\right\rangle ,} \\ \end{array}} \right. \end{aligned}$$
(16)

and \(f:\left\{ {0,1} \right\} ^n \rightarrow \{ 0,1\}\) is an n inputs single output Boolean function that evaluates to true for any \(x \in X_T\) and evaluates to false for any \(x \in X_F\); then,

$$\begin{aligned} \left| {\Psi _3 } \right\rangle= & {} U_f \left| {\Psi _2 } \right\rangle \nonumber \\= & {} a_q \left| {\psi _1 } \right\rangle \otimes \left| {1 } \right\rangle + b_q \left| {\psi _0 } \right\rangle \otimes \left| {0 } \right\rangle . \end{aligned}$$
(17)

Apply measurement \(M_1\) on the auxiliary qubit \(\left| {ax_1 } \right\rangle \) as shown in Fig. 2. The probability of finding \(\left| {ax_1 } \right\rangle =\left| {1} \right\rangle \) is,

$$\begin{aligned} \hbox {Pr}{(M_1 = 1)} = \left| {a_q } \right| ^2 \ge 0.9975, \end{aligned}$$
(18)

and the system will collapse to,

$$\begin{aligned} \left| \Psi _3^{(M_1 = 1)}\right\rangle = \left| {\psi _1 } \right\rangle \otimes \left| {1 } \right\rangle . \end{aligned}$$
(19)

3.2 Evaluation of constraints

There are M states in the superposition \(\left| \Psi _3^{(M_1 = 1)}\right\rangle \), each state has an amplitude \({\textstyle {1 \over {\sqrt{M} }}}\), and then let \(\left| \Psi _4\right\rangle \) be the system after the balanced assignment preparation stage as follows,

$$\begin{aligned} \left| \Psi _4\right\rangle = \alpha \sum \limits _{k = 0}^{M - 1} {\left| x_k \right\rangle }, \end{aligned}$$
(20)

where \(\left| ax_1\right\rangle \) is dropped from the system for simplicity and \(\alpha = {\textstyle {1 \over {\sqrt{M} }}}\). For a graph G with n vertices and m edges, every edge (a, b ) connecting vertcies \(a,b \in V\) is associated with a constraint \(c_l=v_a\oplus v_b\), where \(v_a\) and \(v_b\) are the corresponding qubits for vertices a and b in \(\left| \Psi _4\right\rangle \), respectively, such that \(0 \le l < m, 0 \le m \le {\textstyle {{n(n - 1)} \over 2}}, 0 \le a,b \le n-1\) and \(a \ne b\), where \({\textstyle {{n(n - 1)} \over 2}}\) is the maximum number of edges in a graph with n vertices.

To evaluate the m constraints associated with the edges, add m qubits initialized to state \(\left| 0\right\rangle \),

$$\begin{aligned} \left| \Psi _5\right\rangle= & {} \left| \Psi _4\right\rangle \otimes \left| 0\right\rangle ^{\otimes m}\nonumber \\= & {} \alpha \sum \limits _{k = 0}^{M - 1} { {\left| x_k \right\rangle \otimes \left| 0 \right\rangle ^{\otimes m} } }. \end{aligned}$$
(21)

For every constraint \(c_l=v_a \oplus v_b\), apply two \(Cont\_\sigma _X\) gates, \(Cont\_\sigma _X(v_a,c_l)\) and \(Cont\_\sigma _X(v_b,c_l)\), so that \(\left| c_l\right\rangle =\left| v_a\oplus v_b\right\rangle \). The collection of all \(Cont\_\sigma _X\) gates applied to evaluate the m constraints is denoted \(C_v\) in Fig. 2, and then the system is transformed to,

$$\begin{aligned} \left| {\Psi _6 } \right\rangle = \alpha \sum \limits _{k = 0}^{M - 1} {\left( {\left| x_k \right\rangle \otimes \left| {c_0^k c_1^k \ldots c_{m-1}^k } \right\rangle } \right) }, \end{aligned}$$
(22)

where \(\sigma _X\) is the Pauli-X gate which is the quantum equivalent to the NOT gate. It can be seen as a rotation of the Bloch Sphere around the X-axis by \(\pi \) radians as follows,

$$\begin{aligned} \sigma _X = \left[ {\begin{array}{ll} 0 &{} 1 \\ 1 &{} 0 \\ \end{array}} \right] , \end{aligned}$$
(23)

and \(Cont\_U(v,c)\) gate is a controlled gate with control qubit \(\left| v\right\rangle \) and target qubit \(\left| c\right\rangle \) that applies a single qubit unitary operator U on \(\left| c\right\rangle \) only if \(\left| v\right\rangle =\left| 1\right\rangle \), so every qubit \(\left| c_l^k\right\rangle \) carries a value of the constraint \(c_l\) based on the values of \(v_a\) and \(v_b\) in the balanced assignment \(\left| x_k \right\rangle \), i.e., the values of \(v_a^k\) and \(v_b^k\), respectively. Let \(\left| z_k \right\rangle =\left| {c_0^k c_1^k \ldots c_{m-1}^k }\right\rangle \), then the system can be rewritten as follows,

$$\begin{aligned} \left| {\Psi _6 } \right\rangle = \alpha \sum \limits _{k = 0}^{M - 1} {\left( {\left| x_k \right\rangle \otimes \left| {z_k} \right\rangle } \right) }, \end{aligned}$$
(24)

where every \(\left| x_k \right\rangle \) is entangled with the corresponding \(\left| z_k \right\rangle \). The aim of the next stage is to find \(\left| z_k \right\rangle \) with the maximum number of \(\left| 1 \right\rangle \)’s for the max-bisection problem or to find \(\left| z_k \right\rangle \) with the minimum number of \(\left| 1 \right\rangle \)’s for the min-bisection problem.

Fig. 2
figure 2

A quantum circuit for the proposed algorithm

Full size image

3.3 Maximization of the satisfied constraints

Let \(\left| {\psi _c } \right\rangle \) be a superposition on M states as follows,

$$\begin{aligned} \left| {\psi _c } \right\rangle = \alpha \sum \limits _{k = 0}^{M - 1} { \left| {z_k } \right\rangle }, \end{aligned}$$
(25)

where each \(\left| {z_k } \right\rangle \) is an m-qubit state and let \(d_k=\left\langle {z_k } \right\rangle \) be the number of 1’s in state \(\left| {z_k } \right\rangle \) such that \(\left| {z_k } \right\rangle \ne \left| {0 } \right\rangle ^{\otimes m}\), i.e., \(d_k \ne 0\). This will be referred to as the 1-distance of \(\left| {z_k } \right\rangle \).

The max-bisection graph \(\left| {x_{\max }} \right\rangle \) is equivalent to find the state \(\left| {z_{\max }} \right\rangle \) with \(d_{\max }=\max \{d_k,\,0\le k \le M-1\}\) and the state \(\left| {z_{\min } } \right\rangle \) with \(d_{\min }=\min \{d_k,\,0\le k \le M-1\}\) is equivalent to the min-bisection graph \(\left| {x_{\min }} \right\rangle \). Finding the state \(\left| {z_{\min } } \right\rangle \) with the minimum number of 1’s is equivalent to finding the state with the maximum number of 0’s, so, to clear ambiguity, let \(d_{\max 1}=d_{\max }\) be the maximum number of 1’s and \(d_{\max 0}=d_{\min }\) be the maximum number of 0’s, where the number of 0’s in \(\left| {z_k } \right\rangle \) will be referred to as the 0-distance of \(\left| {z_k } \right\rangle \).

To find either \(\left| {z_{\max } } \right\rangle \) or \(\left| {z_{\min } } \right\rangle \), when \(\left| {\psi _c } \right\rangle \) is measured, add an auxiliary qubit \(\left| {ax_2 } \right\rangle \) initialized to state \(\left| 0 \right\rangle \) to the system \(\left| {\psi _c } \right\rangle \) as follows,

$$\begin{aligned} \left| {\psi _m } \right\rangle= & {} \left| {\psi _c } \right\rangle \otimes \left| 0 \right\rangle \nonumber \\= & {} \alpha \sum \limits _{k = 0}^{M - 1} { \left| {z_k } \right\rangle } \otimes \left| 0 \right\rangle . \end{aligned}$$
(26)

The main idea to find \(\left| {z_{\max } } \right\rangle \) is to apply partial negation on the state of \(\left| {ax_2 } \right\rangle \) entangled with \(\left| {z_k } \right\rangle \) based on the number of 1’s in \(\left| {z_k } \right\rangle \), i.e., more 1’s in \(\left| {z_k } \right\rangle \), gives more negation to the state of \(\left| {ax_2 } \right\rangle \) entangled with \(\left| {z_k } \right\rangle \). If the number of 1’s in \(\left| {z_k } \right\rangle \) is m, then the entangled state of \(\left| {ax_2 } \right\rangle \) will be fully negated. The mth partial negation operator is the mth root of \(\sigma _X\) and can be calculated using diagonalization as follows,

$$\begin{aligned} V=\root m \of {\sigma _X} = \frac{1}{2}\left[ {\begin{array}{ll} {1 + t} &{} {1 - t} \\ {1 - t} &{} {1 + t} \\ \end{array}} \right] , \end{aligned}$$
(27)

where \(t={\root m \of {{ - 1}}}\), and applying V for d times on a qubit is equivalent to the operator,

$$\begin{aligned} V^d = \frac{1}{2}\left[ {\begin{array}{ll} {1 + t^d } &{} {1 - t^d } \\ {1 - t^d } &{} {1 + t^d } \\ \end{array}} \right] , \end{aligned}$$
(28)

such that if \(d=m\), then \(V^m=\sigma _X\). To amplify the amplitude of the state \(\left| {z_{\max } } \right\rangle \), apply the operator MAX on \(\left| {\psi _m } \right\rangle \) as will be shown later, where MAX is an operator on \(m+1\) qubits register that applies V conditionally for m times on \(\left| ax_2 \right\rangle \) based on the number of 1’s in \(\left| {c_0 c_1 \ldots c_{m-1} } \right\rangle \) as follows (as shown in Fig. 3a),

$$\begin{aligned} \hbox {MAX} = Cont\_V(c_0 ,ax_2 )Cont\_V(c_1 ,ax_2 ) \ldots Cont\_V(c_{m - 1} ,ax_2), \end{aligned}$$
(29)

so, if \(d_1\) is the number of \(c_l=1\) in \(\left| {c_0 c_1 \ldots c_{m-1} } \right\rangle \), then,

$$\begin{aligned} \hbox {MAX}\left( {\left| {c_0 c_1 ...c_{m - 1} } \right\rangle \otimes \left| 0 \right\rangle } \right) = \left| {c_0 c_1 ...c_{m - 1} } \right\rangle \otimes \left( {\frac{{1 + t^{d_1} }}{2}\left| 0 \right\rangle + \frac{{1 - t^{d_1} }}{2}\left| 1 \right\rangle } \right) . \end{aligned}$$
(30)
Fig. 3
figure 3

Quantum circuits for a the MAX operator and b the MIN operator, followed by a partial measurement then a negation to reset the auxiliary qubit \(\left| {ax_2 } \right\rangle \)

Full size image

Amplifying the amplitude of the state \(\left| {z_{\min } } \right\rangle \) with the minimum number of 1’s is equivalent to amplifying the amplitude of the state with the maximum number of 0’s. To find \(\left| {z_{\min } } \right\rangle \), apply the operator MIN on \(\left| {\psi _m } \right\rangle \) as will be shown later, where MIN is an operator on \(m+1\) qubits register that applies V conditionally for m times on \(\left| ax_2 \right\rangle \) based on the number of 0’s in \(\left| {c_0 c_1 \ldots c_{m-1} } \right\rangle \) as follows (as shown in Fig. 3b),

$$\begin{aligned} \hbox {MIN} = Cont\_V(\overline{c_0} ,ax_2 )Cont\_V(\overline{c_1} ,ax_2 ) \ldots Cont\_V(\overline{c_{m-1}} ,ax_2), \end{aligned}$$
(31)

where \(\overline{c_l}\) is a temporary negation of \(c_l\) before and after the application of \(Cont\_V(c_l ,ax_2)\) as shown in Fig. 3, so, if \(d_0\) is the number of \(c_l=0\) in \(\left| {c_0 c_1 \ldots c_{m-1} } \right\rangle \) then,

$$\begin{aligned} \hbox {MIN}\left( {\left| {c_0 c_1 ...c_{m - 1} } \right\rangle \otimes \left| 0 \right\rangle } \right) = \left| {c_0 c_1 ...c_{m - 1} } \right\rangle \otimes \left( {\frac{{1 + t^{d_0} }}{2}\left| 0 \right\rangle + \frac{{1 - t^{d_0} }}{2}\left| 1 \right\rangle } \right) . \end{aligned}$$
(32)

For the sake of simplicity and to avoid duplication, the operator Q will denote either the operator MAX or the operator MIN, d will denote either \(d_1\) or \(d_0, \left| {z_s } \right\rangle \) will denote either \(\left| {z_{\max } } \right\rangle \) or \(\left| {z_{\min } } \right\rangle \), and \(d_s\) will denote either \(d_{\max 1}\) or \(d_{\max 0}\), so,

$$\begin{aligned} Q\left( {\left| {c_0 c_1 ...c_{m - 1} } \right\rangle \otimes \left| 0 \right\rangle } \right) = \left| {c_0 c_1 ...c_{m - 1} } \right\rangle \otimes \left( {\frac{{1 + t^{d} }}{2}\left| 0 \right\rangle + \frac{{1 - t^{d} }}{2}\left| 1 \right\rangle } \right) , \end{aligned}$$
(33)

and the probabilities of finding the auxiliary qubit \(\left| ax_2 \right\rangle \) in state \({\left| 0 \right\rangle }\) or \({\left| 1 \right\rangle }\) when measured is, respectively, as follows,

$$\begin{aligned} \hbox {Pr}{(ax_2 = 0)}= & {} \left| {\frac{{1 + t^d }}{2}} \right| ^2 = \cos ^2 \left( {\frac{{d\pi }}{{2m}}} \right) , \nonumber \\ \hbox {Pr}{(ax_2 = 1)}= & {} \left| {\frac{{1 - t^d }}{2}} \right| ^2 = \sin ^2 \left( {\frac{{d\pi }}{{2m}}} \right) . \end{aligned}$$
(34)

To find the state \({\left| z_s \right\rangle }\) in \(\left| {\psi _m } \right\rangle \), the proposed algorithm is as follows, as shown in Fig. 3:

  1. 1-

    Let \(\left| {\psi _r } \right\rangle = \left| {\psi _m } \right\rangle \).

  2. 2-

    Repeat the following steps for r times,

    1. i-

      Apply the operator Q on \(\left| {\psi _r } \right\rangle \).

    2. ii-

      Measure \(\left| ax_2 \right\rangle \), if \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \), then let the system post-measurement is \(\left| {\psi _r } \right\rangle \), apply \(\sigma _X\) on \(\left| ax_2 \right\rangle \) to reset to \(\left| 0 \right\rangle \) for the next iteration and then go to Step (i), otherwise restart the stage and go to Step (1).

  3. 3-

    Measure the first m qubits in \(\left| {\psi _r } \right\rangle \) to read \(\left| z_s \right\rangle \).

For simplicity and without loss of generality, assume that a single \(\left| z_s \right\rangle \) exists in \(\left| \psi _v \right\rangle \), although such states will exist in couples since each \(\left| z_s \right\rangle \) is entangled with a variable assignment \(\left| x_s \right\rangle \) and each \(\left| x_s \right\rangle \) is equivalent to \(\left| \overline{x_s} \right\rangle \); moreover, different variable assignments might give rise to constraint vectors with maximum distance, but such information is not known in advance.

Assuming that the algorithm finds \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \) for r times in a row, then the probability of finding \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \) after Step (2-i) in the first iteration, i.e., \(r=1\) is given by,

$$\begin{aligned} \hbox {Pr}^{(1)}{(ax_2 = 1)} = \alpha ^2 \sum \limits _{k = 0}^{M - 1} {\sin ^2 \left( {\frac{{d_k \pi }}{{2m}}} \right) }. \end{aligned}$$
(35)

The probability of finding \(\left| \psi _r \right\rangle =\left| z_s \right\rangle \) after Step (2-i) in the first iteration, i.e., \(r=1\) is given by,

$$\begin{aligned} \hbox {Pr}^{(1)}{(\psi _{r} = z_s)} = \alpha ^2 {\sin ^2 \left( {\frac{{d_s \pi }}{{2m}}} \right) } . \end{aligned}$$
(36)

The probability of finding \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \) after Step (2-i) in the rth iteration, i.e., \(r>1\) is given by,

$$\begin{aligned} \hbox {Pr}^{(r)}{(ax_2 = 1)} = \frac{{\sum \nolimits _{k = 0}^{M - 1} {\sin ^{2r} \left( {\frac{{d_k \pi }}{{2m}}} \right) } }}{{\sum \nolimits _{k = 0}^{M - 1} {\sin ^{2(r - 1)} \left( {\frac{{d_k \pi }}{{2m}}} \right) } }}. \end{aligned}$$
(37)

The probability of finding \(\left| \psi _r \right\rangle =\left| z_s \right\rangle \) after Step (2-i) in the rth iteration, i.e., \(r>1\) is given by,

$$\begin{aligned} \hbox {Pr}^{(r)}{(\psi _{r} = z_s)} = \frac{{{\sin ^{2r} \left( {\frac{{d_s \pi }}{{2m}}} \right) } }}{{\sum \nolimits _{k = 0}^{M - 1} {\sin ^{2(r - 1)} \left( {\frac{{d_k \pi }}{{2m}}} \right) } }}. \end{aligned}$$
(38)

To get the highest probability of success for \(\hbox {Pr}{(\psi _{r} = z_s)}\), Step (2) should be repeated until, \(\left| \hbox {Pr}^{(r)}{(ax_2 = 1)} - \hbox {Pr}^{(r)}{(\psi _r = z_s)} \right| \le \epsilon \) for small \(\epsilon \ge 0\) as shown in Fig. 4. This happens when \(\sum \nolimits _{k = 0,k\ne s}^{M - 1} {\sin ^{2r} \left( {{\textstyle {{d_k \pi } \over {2m}}}} \right) } \le \epsilon \). Since the Sine function is a decreasing function then for sufficient large r,

$$\begin{aligned} \sum \limits _{k = 0,k\ne s}^{M - 1} {\sin ^{2r} \left( {\frac{{d_k \pi }}{{2m}}} \right) } \approx \sin ^{2r} \left( {\frac{{d_{ns} \pi }}{{2m}}} \right) , \end{aligned}$$
(39)

where \(d_{ns}\) is the next maximum distance less than \(d_s\). The values of \(d_s\) and \(d_{ns}\) are unknown in advance, so let \(d_s=m\) be the number of edges, then in the worst case when \(d_s=m, d_{ns}=m-1\) and \(m=n(n-1)/2\), the required number of iterations r for \(\epsilon = 10^{ - \lambda }\) and \(\lambda >0\) can be calculated using the formula,

$$\begin{aligned} 0< & {} \sin ^{2r} \left( {\frac{{(m-1) \pi }}{{2m}}} \right) \le \epsilon , \end{aligned}$$
(40)
$$\begin{aligned} r\ge & {} \frac{{\log \left( \epsilon \right) }}{{2\log \left( {\sin \left( {\frac{{\left( {m - 1} \right) \pi }}{{2m}}} \right) } \right) }} \nonumber \\= & {} \frac{{\log \left( {10^{ - \lambda } } \right) }}{{2\log \left( {\cos \left( {\frac{\pi }{{2m}}} \right) } \right) }} \nonumber \\\ge & {} \lambda \left( {\frac{{2m}}{\pi }} \right) ^2 \nonumber \\= & {} O\left( {m^2 } \right) , \end{aligned}$$
(41)

where \(0 \le m \le {\textstyle {{n(n - 1)} \over 2}}\). For a complete graph where \(m={\textstyle {{n(n - 1)} \over 2}}\), then the upper bound for the required number of iterations r is \(O\left( {n^4 } \right) \). Assuming that a single \(\left| z_s \right\rangle \) exists in the superposition will increase the required number of iterations, so it is important to notice here that the probability of success will not be over-cooked by increasing the required number of iteration r similar to the common amplitude amplification techniques.

Fig. 4
figure 4

The probability of success for a max-bisection instance of the graph shown in Fig. 1 with \(n=8\) and \(m=12\) where the probability of success of \(\left| ax_2\right\rangle \) is 0.6091 after the first iteration and with probability of success of 0.7939 after iterating the algorithm where the probability of success of \(\left| z_{\max }\right\rangle \), is amplified to reach the probability of success of \(\left| ax_2\right\rangle \)

Full size image

3.4 Adjustments on the proposed algorithm

During the above discussion, two problems will arise during the implementation of the proposed algorithm. The first one is to finding \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \) for r times in a row which a critical issue in the success of the proposed algorithm to terminate in polynomial time. The second problem is that the value of \(d_s\) is not known in advance, where the value of \(\hbox {Pr}^{(1)}{(ax_2 = 1)}\) shown in Eq. 35 plays an important role in the success of finding \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \) in the next iterations, this value depends heavily on the density of 1’s, i.e., the ratio \({\textstyle {{d_s } \over m}}\).

Consider the case of a complete graph with even number of vertices, where the number of egdes \(m = {\textstyle {{n(n - 1)} \over 2}}\) and all \(\left| z_k \right\rangle \)’s are equivalent and each can be taken as \(\left| z_s \right\rangle \) then,

$$\begin{aligned} \hbox {Pr}^{(1)}{(ax_2 = 1)} = M \alpha ^2 {\sin ^2 \left( {\frac{{d_s\pi }}{{2m}}} \right) }. \end{aligned}$$
(42)

This case is an easy case where setting \(m=d_s\) in mth root of \(\sigma _X\) will lead to a probability of success of certainty after a single iteration. Assuming a blind approach where \(d_{s}\) is not known, then this case represents the worst ratio \({\textstyle {{d_s } \over m}}\) where the probability of success will be \(\approx 0.5\) for sufficient large graph. Iterating the algorithm will not lead to any increase in the probability of both \(\left| z_s \right\rangle \) and \(\left| ax_2 \right\rangle \).

In the following, adjustments on the proposed algorithm for the max-bisection and the min-bisection graph will be presented to overcome these problems, i.e., to be able to find \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \) after the first iteration with the highest probability of success without a priori knowledge of \(d_s\).

3.4.1 Adjustment for the max-bisection problem

In an arbitrary graph, the density of 1’s will be \({\textstyle {{d_{\max 1} } \over m}}\). In the case of a complete graph, there are M states with 1-distance (\(d_k\)) equals to \({\textstyle {{n^2} \over 4}}\). This case represents the worst density of 1’s where the density will be \({\textstyle {{n^2 } \over {2n(n - 1)}}}\) slightly greater than 0.5 for arbitrary large n. Iterating the proposed algorithm will not amplify the amplitudes after arbitrary number of iterations. To overcome this problem, add \(\mu _{\max }\) temporary qubits initialized to state \(\left| 1 \right\rangle \) to the register \(\left| {c_0 c_1 ...c_{m - 1} } \right\rangle \) as follows,

$$\begin{aligned} \left| {c_0 c_1 ...c_{m - 1} } \right\rangle \rightarrow \left| {c_0 c_1 \ldots c_{m - 1}c_{m}c_{m+1}\ldots c_{m+\mu _{\max }-1} } \right\rangle , \end{aligned}$$
(43)

so that the extended number of edges \(m_{ext}\) will be \(m_{ext}=m+\mu _{\max }\) and \(V=\root m_{ext} \of {{\sigma _X }}\) will be used instead of \(V=\root m \of {{\sigma _X }}\) in the MAX operator, then the density of 1’s will be \({\textstyle {{n^2 + 4\mu _{\max } } \over {2n(n - 1) + 4\mu _{\max } }}}\). To get a probability of success \(\hbox {Pr}_{\max }\) to find \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \) after the first iteration,

$$\begin{aligned} \hbox {Pr}^{(1)} {\left( {ax_2 = 1} \right) } = M \alpha ^2 \sin ^2 \left( {\frac{{\pi \left( {{\textstyle {{n^2 } \over 4}} + \mu _{\max } } \right) }}{{2\left( {{\textstyle {{n(n - 1)} \over 2}} + \mu _{\max } } \right) }}} \right) \ge \hbox {Pr}_{\max }, \end{aligned}$$
(44)

then the required number of temporary qubits \(\mu _{\max }\) is calculated as follows,

$$\begin{aligned} \mu _{\max } \ge \frac{1}{{1 - \omega }}\left( {\frac{{n^2 }}{2}\left( {2\omega - 1} \right) - \frac{n}{2}\omega } \right) , \end{aligned}$$
(45)

where \(\omega = {\textstyle {2 \over \pi }}\sin ^{ - 1} \left( {\sqrt{{{{\hbox {Pr}_{\max } } \over {M\alpha ^2 }}}} } \right) \) and \(\hbox {Pr}_{\max } < {\textstyle {{M \alpha ^2 }}}\), with \(M\alpha ^2=1\) so let \(\hbox {Pr}_{\max } = \delta {\textstyle {{M \alpha ^2 } }}\) such that \(0<\delta <1\). For example, if \(\delta =0.9\), then \(\hbox {Pr} ^{(1)} \left( {ax_2 = 1} \right) \) will be at least 90 % as shown in Fig. 5. To conclude, the problem of low density of 1’s can be solved with a polynomial increase in the number of qubits to get the solution \(\left| z_{\max } \right\rangle \) in \(O\left( m_{ext}^2\right) =O\left( {n^4 } \right) \) iterations with arbitrary high probability \(\delta <1\) to terminate in poly-time, i.e., to read \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \) for r times in a row.

Fig. 5
figure 5

The probability of success for a max-bisection instance of the graph shown in Fig. 1 with \(n=8, m=12, \mu _{\max }=31\) and \(\delta =0.9\), where the probability of success of \(\left| ax_2\right\rangle \) is 0.9305 after the first iteration and with probability of success of 0.9662 after iterating the algorithm where the probability of success of \(\left| z_{\max }\right\rangle \) is amplified to reach the probability of success of \(\left| ax_2\right\rangle \)

Full size image

3.4.2 Adjustment for the min-bisection problem

Similar to the above approach, in an arbitrary graph, the density of 0’s will be \({\textstyle {{d_{\max 0} } \over m}}\). In the case of a complete graph, there are M states with 0-distance (\(d_k\)) equals to \({\textstyle {{n(n - 1)} \over 2}}-{\textstyle {{n^2} \over 4}}\). This case represents the worst density of 0’s where the density will be \({\textstyle {{n-2 } \over {2(n - 1)}}}\) slightly less than 0.5 for arbitrary large n. Iterating the proposed algorithm will not lead to any amplification after arbitrary number of iterations. To overcome this problem, add \(\mu _{\min }\) temporary qubits initialized to state \(\left| 0 \right\rangle \) to the register \(\left| {c_0 c_1 ...c_{m - 1} } \right\rangle \) as follows,

$$\begin{aligned} \left| {c_0 c_1 ...c_{m - 1} } \right\rangle \rightarrow \left| {c_0 c_1 \ldots c_{m - 1}c_{m}c_{m+1}\ldots c_{m+\mu _{\min }-1} } \right\rangle , \end{aligned}$$
(46)

so that the extended number of edges \(m_{ext}\) will be \(m_{ext}=m+\mu _{\min }\) and \(V=\root m_{ext} \of {{\sigma _X }}\) will be used instead of \(V=\root m \of {{\sigma _X }}\) in the MIN operator, then the density of 0’s will be \({\textstyle {{n^2 -2n + 4\mu _{\min } } \over {2n(n - 1) + 4\mu _{\min } }}}\). To get a probability of success \(\hbox {Pr}_{\max }\) to find \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \) after the first iteration,

$$\begin{aligned} \hbox {Pr} ^{(1)} \left( {ax_2 = 1} \right) = M \alpha ^2 \sin ^2 \left( {\frac{{\pi \left( {{\textstyle {{n(n - 1)} \over 2}} - {\textstyle {{n^2 } \over 4}} + \mu _{\min } } \right) }}{{2\left( {{\textstyle {{n(n - 1)} \over 2}} + \mu _{\min } } \right) }}} \right) \ge \hbox {Pr}_{\max }, \end{aligned}$$
(47)

then the required number of temporary qubits \(\mu _{\min }\) is calculated as follows,

$$\begin{aligned} \mu _{\min } \ge \frac{{n^2 }}{4}\left( {\frac{{2\omega - 1}}{{1 - \omega }}} \right) + \frac{n}{2}, \end{aligned}$$
(48)

where \(\omega = {\textstyle {2 \over \pi }}\sin ^{ - 1} \left( {\sqrt{{{{\hbox {Pr}_{\max } } \over {M\alpha ^2 }}}} } \right) \) and \(\hbox {Pr}_{\max } < {\textstyle {{M \alpha ^2 }}}\), with \(M\alpha ^2=1\) so let \(\hbox {Pr}_{\max } = \delta {\textstyle {{M \alpha ^2 } }}\) such that \(0<\delta <1\). For example, if \(\delta =0.9\), then \(\hbox {Pr} ^{(1)} \left( {ax_2 = 1} \right) \) will be at least 90 %. To conclude similar to the case of the max-bisection graph, the problem of low density of 0’s can be solved with a polynomial increase in the number of qubits, larger than the case of the max-bisection graph, to get the solution \(\left| z_{\min } \right\rangle \) in \(O\left( m_{ext}^2\right) =O\left( {n^4 } \right) \) iterations with arbitrary high probability \(\delta <1\) to terminate in poly-time, i.e., to read \(\left| ax_2 \right\rangle =\left| 1 \right\rangle \) for r times in a row.

4 Conclusion

Given an undirected graph G with even number of vertices n and m unweighted edges, the paper proposed a bounded-error quantum polynomial-time (BQP) algorithm to solve the max-bisection problem and the min-bisection problem, where a general graph is considered for both problems.

The proposed algorithm uses a representation of the two problems as a Boolean constraint satisfaction problem, where the set of edges of a graph are represented as a set of constraints. The algorithm is divided into three stages: The first stage prepares a superposition of all possible equally sized graph partitions in \(O\left( {\root 4 \of {n}} \right) \) using an amplitude amplification technique that runs in \(O\left( {\sqrt{{\textstyle {N \over M}}} } \right) \), for \(N=2^n\) and M is the number of possible graph partitions. The algorithm, in the second stage, evaluates the set of constraints for all possible graph partitions. In the third stage, the algorithm amplifies the amplitudes of the best graph bisection that achieves maximum/minimum satisfaction to the set of constraints using an amplitude amplification technique that applies an iterative partial negation where more negation is given to the set of constrains with more satisfied constrains and a partial measurement to amplify the set of constraints with more negation. The third stage runs in \(O(m^2)\) and in the worst case runs in \(O(n^4)\) for a dense graph. It is shown that the proposed algorithm achieves an arbitrary high probability of success of \(1-\epsilon \) for small \(\epsilon >0\) using a polynomial increase in the space resources by adding dummy constraints with predefined values to give more negation to the best graph bisection.