On the quantum discord of general X states

Abstract

Quantum discord Q is a function of density matrix elements. The domain of such a function in the case of two-qubit system with X density matrix may consist of three subdomains at most: two ones where the quantum discord is expressed in closed analytical forms ($Q_{\pi /2}$ and $Q_0$) and an intermediate subdomain for which, to extract the quantum discord $Q_{\theta }$, it is required to solve numerically a one-dimensional minimization problem to find the optimal measurement angle $\theta \in (0,\pi /2)$. Hence, the quantum discord is given by a piecewise analytical–numerical formula $Q=\min \{Q_{\pi /2},Q_{\theta },Q_0\}$. It is shown that the boundaries between the subdomains consist of bifurcation points. The $Q_{\theta }$ subdomains are discovered in the dynamical phase flip channel model, in the anisotropic spin systems at thermal equilibrium, and in the heteronuclear dimers in an external magnetic field. We found that the transitions between $Q_{\theta }$ subdomain and $Q_{\pi /2}$ and $Q_0$ ones occur suddenly, but continuously and smoothly, i.e., nonanalyticity is hidden and can be observed in higher order derivatives of discord function.

1 Introduction

At present, we have a situation where further miniaturization of electronics will inevitably lead to molecular size components. Designing such components requires application of the laws of quantum mechanics. This is expected to lead to a technological breakthrough which will be achieved through employing the holy of holies of the quantum theory—so-called quantum correlations.

Initially, the entanglement has been considered as a quantum correlation [1, 2]. Quantum entanglement is able to bind different parts of systems, even in the case when there is no interaction between those parts (the Einstein–Podolsky–Rosen effect). By this, a change in the state of one subsystem can lead to a change in the state of the other subsystem. Later, this unusual property of quantum entangled states was proved in different experiments.

Quantum entanglement exists only in nonseparable states of bi- and multipartite systems. However, it appears in the last years that there are quantum correlations more general and more fundamental than entanglement. In particular, they can be present in certain separable states, i.e., when the quantum entanglement is absent. As a measure of total purely quantum correlations in bipartite systems, the quantum discord is employed now [3–5]. The basis for the discord conception is the idea of measurements performed on a system and maximum amount of classical information being extracted with their help.

Due to the fact that it is necessary to solve the optimization problem, the evaluation of quantum correlations, especially discord, is extremely hard [6]. If for the two-qubit systems the quantum entanglement of formation has been obtained for the arbitrary density matrices [7–10], the analytical formulas for the quantum discord were proposed for X states [11–16]. In an X matrix, nonzero entries may belong only to the main diagonal and anti-diagonal [17–19]. Notice that the sum and product of X matrices are again the X matrix (i.e., a set of X matrices is algebraically closed).

However, it was found later that the formulas [12–15] are incorrect in general. The reason is that the authors [12–15] believed (and this was their error) that optimal measurements are achieved only in the limiting points, i.e., at the angles $\theta =0$ or $\pi /2$. But on the explicit examples [20–22] of X density matrices, it was proved that the optimal measurements can take place at the intermediate angles in the interval $(0,\pi /2)$. Unfortunately, these examples with density matrices are specific and do not clarify the general situation.

In the present paper, we show that the domain of intermediate optimal angles can arise in the vicinity of transition from the domain with optimal measurement angle $\theta =\pi /2$ to the domain with optimal angle $\theta =0$ (or inversely). The equations for the boundaries between these domains are discussed, and their solutions are investigated for different models. In particular, the boundaries can coincide or be absent at all, and then, the quantum discord is given in the total domain of definition by closed analytical formulas.

In the following sections, the general seven-parameters X density matrix is reduced to the five-parameter form by using local unitary transformations, the existence of intermediate subdomains with the optimal anglers $\theta \not =0, \pi /2$ is proved, and the equations for boundaries between different subdomains are presented and then applied to various physical systems. Finally, in the last section, a brief conclusion is given.

2 Real nonnegative form for the X density matrices and the domain of definition for their entries

In the most general case, the X density matrix of two-qubit (A and B or 1 and 2) system has seven real parameters. The quantum entanglement and quantum discord are invariant under the local unitary transformations of density matrices [1–5]. Owing to this property, one can with the help of such transformations reduce the seven-parameters density matrix to the real, nonnegative five-parameters X form [22–25]. After this, the X density matrix takes the form

$$\begin{aligned} \rho _{AB} =\left( \begin{array}{cccc} a&{}\quad 0&{}\quad 0&{}\quad u\\ 0&{}\quad b&{}\quad v&{}\quad 0\\ 0&{}\quad v&{}\quad c&{}\quad 0\\ u&{}\quad 0&{}\quad 0&{}\quad d \end{array} \right) , \end{aligned}$$

(1)

or, to emphasize explicitly that the off-diagonal elements are nonnegative, and we write

$$\begin{aligned} \rho _{AB} =\left( \begin{array}{cccc} a&{}\quad 0&{}\quad 0&{}\quad |u|\\ 0&{}\quad b&{}\quad |v|&{}\quad 0\\ 0&{}\quad |v|&{}\quad c&{}\quad 0\\ |u|&{}\quad 0&{}\quad 0&{}\quad d \end{array} \right) . \end{aligned}$$

(2)

Thus, one can now consider the density matrices (1) with restrictions (which follow from the normalization condition and nonnegativity definition of any density operator)

$$\begin{aligned} a, b, c, d, u, v\ge 0,\quad a+b+c+d=1, \quad ad\ge u^2, \quad bc\ge v^2. \end{aligned}$$

(3)

These relations define the domain $\mathcal{D}$ of X density matrix in the space of its entries.

We can rewrite the density matrix (1) in the equivalent form

$$\begin{aligned} \rho _{AB} =\frac{1}{4}\!\left( \begin{array}{cccc} 1+s_1+s_2+c_3&{}0&{}0&{}c_1-c_2\\ 0&{}1+s_1-s_2-c_3&{}c_1+c_2&{}0\\ 0&{}c_1+c_2&{}1-s_1+s_2-c_3&{}0\\ c_1-c_2&{}0&{}0&{}1-s_1-s_2+c_3 \end{array} \right) , \end{aligned}$$

(4)

where

$$\begin{aligned}&s_1=a+b-c-d,\quad s_2=a-b+c-d, \nonumber \\&c_1=2(v+u),\quad c_2=2(v-u),\quad c_3=a-b-c+d. \end{aligned}$$

(5)

Decomposition of this matrix on the Pauli matrices $\sigma _\alpha$ ($\alpha =x,y,z$) leads to its Bloch form

$$\begin{aligned} \rho _{AB}=\frac{1}{4}(1 + s_1\sigma _z\otimes 1 + s_21\otimes \sigma _z + c_1\sigma _x\otimes \sigma _x + c_2\sigma _y\otimes \sigma _y + c_3\sigma _z\otimes \sigma _z). \end{aligned}$$

(6)

The expansion coefficients are the unary and binary correlation functions, and therefore, five parameters of density matrix are expressed through the five different correlators,

$$\begin{aligned}&s_1=\langle \sigma ^1_z\rangle =\mathrm{Tr}(\rho _{AB}\sigma _z\otimes 1),\quad s_2=\langle \sigma ^2_z\rangle =\mathrm{Tr}(\rho _{AB}1\otimes \sigma _z), \nonumber \\&c_1=\langle \sigma ^1_x\sigma ^2_x\rangle =\mathrm{Tr}(\rho _{AB}\sigma _x\otimes \sigma _x),\quad c_2=\langle \sigma ^1_y\sigma ^2_y\rangle =\mathrm{Tr}(\rho _{AB}\sigma _y\otimes \sigma _y),\\&c_3=\langle \sigma ^1_z\sigma ^2_z\rangle =\mathrm{Tr}(\rho _{AB}\sigma _z\otimes \sigma _z). \nonumber \end{aligned}$$

(7)

It is clear that

$$\begin{aligned} -1\le s_1, s_2, c_1, c_2, c_3\le 1. \end{aligned}$$

(8)

The domain of definition, $\mathcal{D}$, in the space $(s_1, s_2, c_1, c_2, c_3)$ is formed, according to Eqs. (3) and (5), by conditions (see also [21, 26])

$$\begin{aligned} (1 - c_3)^2\ge (s_1 - s_2)^2 + (c_1 + c_2)^2,\quad (1 + c_3)^2\ge (s_1 + s_2)^2 + (c_1 - c_2)^2.\quad \end{aligned}$$

(9)

The solid $\mathcal{D}$ is finite and lies in the five-dimensional hypercube (8). Numerical calculations show that the volume of $\mathcal{D}$ is 8 % of the hypercube one.

The domain $\mathcal{D}$ is bounded by two quadratic hypersurfaces

$$\begin{aligned} (s_1 - s_2)^2 + (c_1 + c_2)^2 - (c_3-1)^2 = 0 \end{aligned}$$

(10)

and

$$\begin{aligned} (s_1 + s_2)^2 + (c_1 - c_2)^2 - (c_3+1)^2 = 0. \end{aligned}$$

(11)

Rotation by the angle $\pi /4$ around the $c_3$ axis transforms these hyperquadrics to the forms

$$\begin{aligned} (s_2^\prime )^2 + (c_1^\prime )^2 - \frac{(c_3-1)^2}{2} = 0 \end{aligned}$$

(12)

and

$$\begin{aligned} (s_1^\prime )^2 + (c_2^\prime )^2 - \frac{(c_3+1)^2}{2} = 0, \end{aligned}$$

(13)

where

$$\begin{aligned} s_{1,2}^\prime = (\pm s_1+s_2)/\sqrt{2},\quad c_{1,2}^\prime = (\pm c_1+c_2)/\sqrt{2}. \end{aligned}$$

(14)

Thus, the five-dimensional domain $\mathcal{D}$ results from an intersection of two conic hypercylinders (12) and (13).

3 Three alternatives for the quantum discord

As mentioned above, the measurement operations lie in the ground of discord notion. Following the founders of discord conception [27, 28] and their adherents [11–15], we will only consider here the orthogonal projective measurements, i.e., the von Neumann measurements.¹ Such measurements can be reduced to the projections which are characterized by the polar ($\theta$) and azimuthal ($\phi$) angles relative to the z axis [13, 15, 23]. It is important to note that the optimal measurements in the case of real X density matrix with an additional condition $uv\ge 0$ are achieved by $\cos 2\phi =1$ [22, 23]. Since the sign of off-diagonal elements are changed by the local unitary transformations, we can always satisfy the above condition.

In the general nonsymmetrical case ($s_1\ne s_2$ or $b\ne c$), quantum discord depends on a subsystem (A or B) where the measurements are performed. For definiteness and without loss of generality, let the measured subsystem be B. (If measured subsystem is A, we simply should replace everywhere $s_1\rightleftharpoons s_2$ or $b\rightleftharpoons c$.) Then the quantum discord is given as [3–5]

$$\begin{aligned} Q=S(\rho _B)-S(\rho _{AB})+\min _\theta S_\mathrm{cond}(\theta ), \end{aligned}$$

(15)

where $\rho _B=\mathrm{Tr}_A\rho _{AB}$ is the reduced density matrix and $S(\rho )=-\mathrm{Tr}\rho \ln \rho$ is the von Neumann entropy for the corresponding state $\rho$ (Here the entropy is in nats; to transform it, e.g., in bits, one should divide it by $\ln 2$). Simple calculations with (1) lead to

$$\begin{aligned} S(\rho _B)=-(a+c)\ln (a+c)-(b+d)\ln (b+d), \end{aligned}$$

(16)

$S(\rho _{AB})=S$, where

$$\begin{aligned} S= & {} -\frac{a+d+\sqrt{(a-d)^2+4u^2}}{2}\ln \frac{a+d +\sqrt{(a-d)^2+4u^2}}{2} \nonumber \\&-\frac{a+d-\sqrt{(a-d)^2+4u^2}}{2}\ln \frac{a+d-\sqrt{(a-d)^2+4u^2}}{2} \nonumber \\&-\frac{b+c+\sqrt{(b-c)^2+4v^2}}{2}\ln \frac{b+c+\sqrt{(b-c)^2+4v^2}}{2} \nonumber \\&-\frac{b+c-\sqrt{(b-c)^2+4v^2}}{2}\ln \frac{b+c-\sqrt{(b-c)^2+4v^2}}{2}. \end{aligned}$$

(17)

The quantum average conditional entropy of subsystem A is given as [22]

$$\begin{aligned} S_{cond}(\theta )=\varLambda _1\ln \varLambda _1+\varLambda _2\ln \varLambda _2 -\sum _{i=1}^4\lambda _i\ln \lambda _i, \end{aligned}$$

(18)

where

$$\begin{aligned} \varLambda _{1,2}= & {} \frac{1}{4}[1\pm (a-b+c-d)\cos \theta ], \end{aligned}$$

(19)

$$\begin{aligned} \lambda _{1,2}= & {} \frac{1}{4}[\![1+(a-b+c-d)\cos \theta \nonumber \\&\quad \pm \{[a+b-c-d+(a-b-c+d)\cos \theta ]^2+4w^2\sin ^2\theta \}^{1/2}]\!], \end{aligned}$$

(20)

$$\begin{aligned} \lambda _{3,4}= & {} \frac{1}{4}[\![1-(a-b+c-d)\cos \theta \nonumber \\&\quad \pm \{[a+b-c-d-(a-b-c+d)\cos \theta ]^2+4w^2\sin ^2\theta \}^{1/2}]\!], \qquad \end{aligned}$$

(21)

$$\begin{aligned} w= & {} |u|+|v|. \end{aligned}$$

(22)

Thus, $S_\mathrm{cond}$ depends in fact on four parameters because u and v enter via the combination (22). The conditional entropy $S_\mathrm{cond}(\theta )$ is a differentiable function of its argument $\theta$.

Expressions (16)–(22) allow to define the measurement-dependent discord as [4]

$$\begin{aligned} Q(\theta )=S(\rho _B)-S(\rho _{AB})+S_\mathrm{cond}(\theta ), \end{aligned}$$

(23)

where $\theta \in [0,\pi /2]$. It is obvious that the absolute minimum of this discord can be either on the bounds ($\theta =0,\pi /2$) or at the intermediate point $\theta \in (0,\pi /2)$. As a result, there is a choice from three possibilities for the quantum discord

$$\begin{aligned} Q=\min \{Q_0, Q_\theta , Q_{\pi /2}\}. \end{aligned}$$

(24)

This equation generalizes the one proposed earlier for the quantum discord [11–15]

$$\begin{aligned} \tilde{Q}=\min \{Q_0, Q_{\pi /2}\}, \end{aligned}$$

(25)

i.e., it was assumed that the optimal observable can be either $\sigma _z$ or $\sigma _x$. In Fig. 1, we schematically illustrate the parameter domain of a system with three possible subdomains for the discord.

Fig. 1

A fragment of phase diagram with three possible subdomains for the X-state quantum discord

From Eqs. (16)–(23), we have for the discord branch $Q_0\equiv Q(0)$:

$$\begin{aligned} Q_0=-S-a\ln a-b\ln b-c\ln c -d\ln d. \end{aligned}$$

(26)

For $\theta =\pi /2$, we obtain

$$\begin{aligned} Q_{\frac{\pi }{2}}= & {} -S-(a+c)\ln (a+c)-(b+d)\ln (b+d) \nonumber \\&-\frac{1+\sqrt{(a+b-c-d)^2+4w^2}}{2}\ln \frac{1+\sqrt{(a +b-c-d)^2+4w^2}}{2} \nonumber \\&-\frac{1-\sqrt{(a+b-c-d)^2+4w^2}}{2}\ln \frac{1-\sqrt{(a +b-c-d)^2+4w^2}}{2}.\qquad \end{aligned}$$

(27)

Thus, the branches $Q_0$ and $Q_{\pi /2}$ are expressed analytically, and the branch $Q_\theta =\min \nolimits _{\theta \in (0,\pi /2)} Q(\theta )$, if the intermediate minimum exists, should be found from the numerical solution of one-dimensional minimization problem or from the transcendental equation

$$\begin{aligned} S^\prime _\mathrm{cond}(\theta )=0. \end{aligned}$$

(28)

In the latter case, we should choose among all solutions the point which corresponds to the global minimum. The first derivative of conditional entropy with respect to $\theta$ is equal to

$$\begin{aligned} S^\prime _\mathrm{cond}(\theta )=\varLambda ^\prime _1(1+\ln \varLambda _1) +\varLambda ^\prime _2(1+\ln \varLambda _2) -\sum _{i=1}^4\lambda ^\prime _i(1+\ln \lambda _i) \end{aligned}$$

(29)

with

$$\begin{aligned} \varLambda ^\prime _{1,2}= & {} \mp \frac{1}{2}(a-b+c-d)\sin \theta , \end{aligned}$$

(30)

$$\begin{aligned} \lambda ^\prime _{1,2}= & {} \frac{1}{4}\bigg [-(a-b+c-d)\sin \theta \nonumber \\&\pm \frac{[a\!+b-c\!-\!d\!+(a\!-b-c\!+d)\cos \theta ][-(a\!-b-c\!+\!d)\sin \theta ]\!+2w^2\sin 2\theta }{\sqrt{[a\!+b-\!c\!-d\!+\!(a\!-b\!-c\!+\!d)\cos \theta ]^2\!+\!4w^2\sin ^2\theta }}\bigg ], \nonumber \\\end{aligned}$$

(31)

$$\begin{aligned} \lambda ^\prime _{3,4}= & {} \frac{1}{4}\bigg [(a-b+c-d)\sin \theta \nonumber \\&\pm \frac{[a\!+b\!-c\!-d-(a\!-b-c\!+d)\cos \theta ](a\!-b\!-c\!+\!d)\sin \theta \!+\!2w^2\sin 2\theta }{\sqrt{[a\!+b-c\!-d\!-(a\!-b-c\!+d)\cos \theta ]^2\!+\!4w^2\sin ^2\theta }}\bigg ].\nonumber \\ \end{aligned}$$

(32)

All three possible variants for the quantum discord ($Q_0$, $Q_{\pi /2}$, and $Q_\theta$) can really exist in physical systems. In the case when $a=b$ and $b=c$ (or $s_1=s_2=0$), the conditional entropy minimum is always achieved at one of two bound points [11]. However, this is wrong for the more general X states; global minimum can take place at inner points of the interval $(0,\pi /2)$.

Indeed, following the authors [20], let us consider the state

$$\begin{aligned} \rho =\left( \begin{array}{cccc} 0.0783&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0.125&{}\quad 0.100&{}\quad 0\\ 0&{}\quad 0.100&{}\quad 0.125&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0.6717 \end{array} \right) . \end{aligned}$$

(33)

Using Eqs. (18)–(22), we have computed the function $S_\mathrm{cond}(\theta )$ for this state. Its behavior is shown in Fig. 2.

Fig. 2

Quantum conditional entropy $S_\mathrm{cond}$ as a function of measured angle $\theta$ for the state (33)

From the figure, we conclude that the conditional entropy minimum is situated in the intermediate region, namely at the angle $\theta =0.4883\approx 28^\circ$. Two other similar numerical examples of quantum states are given in Ref. [22].

These examples clearly show that the optimal measurement angles can really be in the intermediate region $(0,\pi /2)$, i.e., the optimal observables for quantum discord can be not only the $\sigma _x$ or $\sigma _z$, but also their superposition.

For the real X state with constraint $|u+v|\ge |u-v|$ (i.e., $uv\ge 0$ or $\mathrm{sign}u=\mathrm{sign}v$), the authors [21] have proved a theorem which guarantees that the optimal observable is $\sigma _z$ if

$$\begin{aligned} (|u|+|v|)^2\le (a-b)(d-c) \end{aligned}$$

(34)

and $\sigma _x$ if

$$\begin{aligned} |u|+|v|\ge |\sqrt{ad}-\sqrt{bc}|. \end{aligned}$$

(35)

The theorem states nothing for the region lying between these bounds. But in the case

$$\begin{aligned} ac=bd \end{aligned}$$

(36)

the inequalities (34) and (35) lead to absence of the intermediate region [35].

4 Equations for the boundaries

Let us start with a heuristic example. Consider a two-parameter family of X states [21, 36]

$$\begin{aligned} \rho =\left( \begin{array}{cccc} \epsilon /2&{}\quad 0&{}\quad 0&{}\quad \epsilon /2\\ 0&{}\quad (1-\epsilon )m&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad (1-\epsilon )(1-m)&{}\quad 0\\ \epsilon /2&{}\quad 0&{}\quad 0&{}\quad \epsilon /2 \end{array} \right) \end{aligned}$$

(37)

or

$$\begin{aligned} \rho= & {} \frac{1}{4}[1 + (1-\epsilon )(2m-1)(\sigma _1^z - \sigma _2^z) + \epsilon (\sigma _1^x\sigma _2^x - \sigma _1^y\sigma _2^y) + (2\epsilon -1)\sigma _1^z\sigma _2^z] \nonumber \\= & {} \epsilon |\Phi ^+\rangle \langle \Phi ^+| +(1-\epsilon )m|01\rangle \langle 01|+(1-\epsilon )(1-m)|10\rangle \langle 10|, \end{aligned}$$

(38)

where $|\Phi ^+\rangle =(|00\rangle +|11\rangle )/\sqrt{2}$. The given density matrix $\rho$ represents the generalized Horodecki states [26].

Simple calculation yields $Q_0=\epsilon$ (in bits). Sufficient conditions (34) and (35) for the $Q_0$ and $Q_{\pi /2}$ subdomains give [21]

$$\begin{aligned} \epsilon \le \frac{2m(1-m)}{1+2m(1-m)} \end{aligned}$$

(39)

and

$$\begin{aligned} \epsilon \ge \frac{\sqrt{m(1-m)}}{1+\sqrt{m(1-m)}}, \end{aligned}$$

(40)

respectively. But in the region

$$\begin{aligned} \frac{2m(1-m)}{1+2m(1-m)}<\epsilon <\frac{\sqrt{m(1-m)}}{1+\sqrt{m(1-m)}} \end{aligned}$$

(41)

the above theorem does not say anything.

Let us now find the lines on the plane $(m, \epsilon )$ which are defined by the condition

$$\begin{aligned} Q_0(m,\epsilon )=Q_{\pi /2}(m,\epsilon ). \end{aligned}$$

(42)

Then we will study the changes of curves $S_\mathrm{cond}(\theta )$ in the neighborhood to those lines.

Using Eqs. (17), (26), and (27), we have numerically solved the transcendental equation (42). The solution is only one. The results are plotted in Fig. 3 by dotted line.

Fig. 3

Subdomains $Q_{\pi /2}$, $Q_0$, and (between them) $Q_\theta$ for the state (37). Dotted line corresponds to the condition $Q_{\pi /2}=Q_0$. Solid lines 1 and 2 are the $\pi /2$- and 0-boundaries, respectively

Consider in detail a particular case. Let the $\epsilon$ is held fixed and equal, for example, to $\epsilon =0.228$ (see Fig. 3). Then the equality $Q_0=Q_{\pi /2}$ is satisfied at the crossing point $m_\times =0.101\,234$. Study now the behavior of $S_\mathrm{cond}(\theta )$ when the parameter m varies. Inequalities (39) and (40) guarantee that when $m<0.096\,545$, the discord equals $Q=Q_{\pi /2}$ and $Q=Q_0$ when $m>0.180\,107$. If $m=0.1015$, the minimum of $S_\mathrm{cond}(\theta )$ is at $\theta =0$ (see Fig. 4a). Moreover, the angle $\theta =0$ is optimal for all larger values of m. When the m decreases, the minimum on the curve $S_\mathrm{cond}(\theta )$ inside the interval between 0 and $\pi /2$ appears. The minimum is clearly seen when $m=0.1014$ (Fig. 4b). Near the point $m=0.101\,234$, the minimum achieves large depth. By further decreasing m, the minimum moves to the bound $\theta =\pi /2$, and then, it disappears at all. Optimal measurements undergo to the angle $\theta =\pi /2$.

Fig. 4

Appearance and disappearance of an intermediate minimum on the conditional entropy curve by transition from $Q_0$ to $Q_{\pi /2}$ subdomain. Here, $S_\mathrm{cond}(\theta )$ corresponds to the state (37) at the fixed value of $\epsilon =0.228$ and $m=0.1015$ (a), 0.1014 (b), $0.101\,234$ (c), 0.1011 (d), and 0.1008 (e)

We argue now that both lower and upper boundaries of the interval where the optimal angles lie between 0 and $\pi /2$ are exact, i.e., the intermediate minimum of $S_\mathrm{cond}(\theta )$ suddenly appears and suddenly disappears. Above all, we note that the first derivative of function $S_\mathrm{cond}(\theta )$ at $\theta =0$ and $\pi /2$ equals zero in general case: $S^{\prime }_\mathrm{cond}(0)\equiv S^{\prime }_\mathrm{cond}(\pi /2)\equiv 0$. This is easy to check by direct calculations using Eqs. (29)–(32). Let us turn now again to the Fig. 4. By fixed value of parameter $\epsilon$ and for each value of m, one can say at any moment the inside minimum exists or it is absent. For instance, when $m=0.1015$ ($\epsilon =0.228$), the function $S_\mathrm{cond}(\theta )$ is concave at the point $\theta =0$ and therefore its second derivative $S^{\prime \prime }_\mathrm{cond}(0)>0$. But when $m=0.1014$, the conditional entropy has a local maximum at the same bound point $\theta =0$ and therefore $S^{\prime \prime }_\mathrm{cond}(0)<0$. Hence, the bifurcation point (in the sense that two extrema arise from one) [37] is determined by the condition

$$\begin{aligned} S^{\prime \prime }_\mathrm{cond}(0)=0. \end{aligned}$$

(43)

Similarly, we have for the other bound point $\theta =\pi /2$,

$$\begin{aligned} S^{\prime \prime }_\mathrm{cond}(\pi /2)=0. \end{aligned}$$

(44)

Using Eqs. (18)–(21), we get the second derivatives at limiting points:

$$\begin{aligned} S^{\prime \prime }_\mathrm{cond}(0)= & {} \frac{1}{4}(a-b+c-d)\biggl (2\ln \frac{b+d}{a+c}+\ln \frac{ac}{bd}\biggr ) \nonumber \\&+\,\frac{1}{4}(a-b-c+d)\ln \frac{ad}{bc}-\frac{1}{2}w^2\biggl (\frac{1}{a-c}\ln \frac{a}{c} +\frac{1}{b-d}\ln \frac{b}{d}\biggr )\quad \end{aligned}$$

(45)

and

$$\begin{aligned} S^{\prime \prime }_\mathrm{cond}(\pi /2)= & {} \frac{8w^2}{r^3}[(a-c)(b-d)+w^2]\ln \frac{1+r}{1-r}+(a-b+c-d)^2 \nonumber \\&-\,\frac{1}{2(1+r)}\bigl [a-b+c-d+\frac{1}{r}(a+b-c-d)(a-b-c+d)\bigl ]^2 \nonumber \\&-\,\frac{1}{2(1-r)}\bigl [a-b+c-d-\frac{1}{r}(a+b-c-d)(a-b-c+d)\bigl ]^2,\nonumber \\ \end{aligned}$$

(46)

where

$$\begin{aligned} r=[(a+b-c-d)^2+4w^2]^{1/2} \end{aligned}$$

(47)

and w is given by Eq. (22). The relations (43)–(47) are the boundary equations for the crossover zone $Q_\theta$. Thus, the boundaries consist of bifurcation points. Notice that the equations for the boundaries between three different phases of quantum discord have been obtained for the first time by the author [24, 25] and later by Maldonado-Trapp et al. [38].

If the solutions of Eqs. (43) and (44) are the same, the intermediate subdomain $Q_\theta$ is absent and the quantum discord is given by analytical expressions. On the other hand, instead of rough conditions (34) and (35), the inequalities $S^{\prime \prime }_\mathrm{cond}(0)\le 0$ and $S^{\prime \prime }_\mathrm{cond}(\pi /2)\le 0$ define now the complete subdomains $Q_0$ and $Q_{\pi /2}$, respectively.

Numerical solution of Eqs. (43)–(47) for the state (37) shows that the boundaries are the lines going approximately parallel to the dotted lines (see the lines 1 and 2 in Fig. 3). As a result, the subdomain appears within which the optimal angles should be found numerically. Out of this subdomain, we have analytical expressions for the quantum discord. By $\epsilon =0.228$, the value for m of $\pi /2$-boundary equals $m_{\pi /2}=0.100\,997$, and for the 0-boundary, it is $m_0=0.101\,474$. The middle of this interval equals 0.101 236 which is near the point $m_\times =0.101\,234$.

Consider the discord behavior by a transition from the subdomain $Q_{\pi /2}$ to $Q_0$ one (Fig. 5). One can see that down to crossing point $m_\times =0.101\,234$, the discord ${\tilde{Q}}$, according to Refs. [12–14], equals $Q_{\pi /2}$, and above the point $m_\times$, it equals $Q_0$ (see Fig. 5). If this was valid, the discord ${\tilde{Q}}=\min \{Q_{\pi /2},Q_0\}$ would not be differentiable at the intersection point $m_\times$. However, in fact, the true discord $Q=\min \{Q_{\pi /2},Q_\theta ,Q_0\}$ is smooth. This follows from the numerical solution of the task in the intermediate domain. The results are shown again in Fig. 5 by solid line. It is clearly seen that smoothness occurs. We may say that, instead a fracture at $m_\times$, two hidden transitions occur at the $\pi /2$- and 0-boundaries.

Fig. 5

Dependencies of the false discord $\tilde{Q}=\min \{Q_{\pi /2},Q_0\}$ (dotted line) and the corrected quantum discord $Q=\min \{Q_{\pi /2},Q_\theta ,Q_0\}$ (solid line) for the state (37) with parameter $\epsilon =0.228$ Longer bars mark the exact boundaries $m_{\pi /2}=0.100\,997$ and $m_0=0.101\,474$. Subdomains $m\le m_{\pi /2}$, $m_{\pi /2}<m<m_0$, and $m\ge m_0$ correspond to the discord branches $Q_{\pi /2}$, $Q_\theta$, and $Q_0$, respectively

Notice that the conditions (39) and (40) are rough too and lead to the bounds which lie far beyond the region of Fig. 3.

5 Bell-diagonal states

The case $a=d$ and $b=c$ or $s_1=s_2=0$ corresponds to the Bell-diagonal states. Domain of definition for the physical states, $\mathcal{D}$, lies now in the three-dimensional cube defined by $c_1, c_2, c_3\in [-1,1]$. Two second-order hypersurfaces (10) and (11) are transformed to the two first-order surfaces

$$\begin{aligned} \pm |c_1+c_2|+c_3-1=0 \end{aligned}$$

(48)

and

$$\begin{aligned} \pm |c_1-c_2|+c_3+1=0 . \end{aligned}$$

(49)

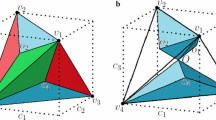
The former consists of two semi-planes with a $\wedge$-shaped cross section, and the latter is similar to it but has a $\vee$-shaped cross section. The angle between semi-planes equals $\arccos (1/3)\approx 78^\circ$. These semi-plane surfaces put bounds to the domain $\mathcal{D}$ that is reduced, as shown in Fig. 6, to a tetrahedron with vertices [39]

$$\begin{aligned} v_1=(-1,1,1),\quad v_2=(1,-1,1),\quad v_3=(1,1,-1),\quad v_4=(-1,-1,-1);\quad \end{aligned}$$

(50)

these vertices lie in octants II $(-,+,+)$, IV $(+,-,+)$, V $(+,+,-)$, and VII $(-,-,-)$, respectively. The centers of tetrahedron facets are

$$\begin{aligned}&o_1=(1/3,1/3,1/3),\quad o_2=(-1/3,-1/3,1/3), \nonumber \\&o_3=(-1/3,1/3,-1/3),\quad o_4=(1/3,-1/3,-1/3). \end{aligned}$$

(51)

Tetrahedron volume equals a third (i.e., about 33.3 %) of the cube one. Notice that the tetrahedron vertices are the states with maximal value of discord (which equals one in bit units).

Fig. 6

Tetrahedron with vertices $v_1, v_2, v_3$ and $v_4$ is the domain for the total Bell-diagonal states. Two regions $(O,v_1,v_2,o_1,o_2)$ and $(O,v_3,v_4,o_3,o_4)$ correspond to the physical states with $Q_0$ discord

It is known [40] that the states with zero discord are negligible in the whole Hilbert space. In particular, it has been proved [41, 42] that, when $s_1=s_2=0$, the zero-discord states have at most one nonzero component of vector $(c_1,c_2,c_3)$, i.e., all classical-only correlated states lie on the Cartesian axes $Oc_1, Oc_2$ or $Oc_3$. (This corresponds to the so-called “Ising spins” introduced as a matter of fact by his adviser W. Lenz in 1920 [43, 44].)

In the case of Bell-diagonal states, both boundary equations (43)–(47) are reduced to a relation

$$\begin{aligned} (a-b)^2=(|u|+|v|)^2, \end{aligned}$$

(52)

so that

$$\begin{aligned} 2|c_3|=|c_1+c_2|+|c_1-c_2|. \end{aligned}$$

(53)

Thus, the $\pi /2$- and 0-boundaries are coincident, the $Q_\theta$ subdomain is absent here, and the quantum discord is given by the explicit analytical formula $Q=\min \{Q_0,Q_{\pi /2}\}$ which is in full agreement with Luo’s results [11].

From Eq. (53), four equations follow

$$\begin{aligned} c_3=\pm c_1\qquad c_3=\pm c_2. \end{aligned}$$

(54)

These planes divide the tetrahedron into subdomains $Q_0$ and $Q_{\pi /2}$, where the quantum discord takes the values $Q_0$ or $Q_{\pi /2}$. $Q_0$ subdomain consists of two hexahedrons $(O,v_1,v_2,o_1,o_2)$ and $(O,v_3,v_4,o_3,o_4)$; they are shown in Fig. 6. The remaining volume of a tetrahedron belongs to the $Q_{\pi /2}$ states. It is in two times larger than the volume of $Q_0$ states.

The behavior of quantum discord for the Bell-diagonal states along different trajectories is illustrated in Fig. 7 by solid lines. Figure 7a shows the discord as a function of $c_3\in [-0.95, 0.45]$ by fixed values of $c_1=0.3$ and $c_2=0.25$. The curve is continuous but has the fractures at $c_3=\pm 0.3$. They happen when the trajectory crosses the planes dividing the $Q_0$ and $Q_{\pi /2}$ subdomains (see Fig. 6). In this case, the optimal measurement angle $\theta$ varies discontinuously; namely, it jumps from $\theta =0$ to $\theta =\pi /2$ or inversely. In the vicinity of cross points, the conditional entropy $S_\mathrm{cond}(\theta )$ changes its form going through a straight line (where any angle $\theta \in [0,\pi /2]$ is optimal). Such a regime of conditional entropy behavior is shown in Fig. 8.

Fig. 7

Quantum discord for the Bell-diagonal states: (a), $Q=\min \{Q_0,Q_{\pi /2}\}$ versus $c_3$ by $c_1=0.3$ and $c_2=0.25$, longer bars mark the positions of fracture points at $c_3=\pm 0.3$; (b), $Q=Q_{\pi /2}$ (solid line) and $Q_0$ (dotted line) versus $c_2$ when $c_1=0.25$ and $c_3=0$

Fig. 8

Transition between $Q_{\pi /2}$ and $Q_0$ subdomains via a straight line for the conditional entropy. Here, $S_\mathrm{cond}(\theta )$ is at and near the fracture point $c_3=0.3$ on the quantum discord curve in Fig. 7a. The curves 1, 2, and 3 correspond to $c_3=0.29$, 0.3, and 0.31, respectively

Figure 7b shows the behavior of branches $Q_0$ and $Q_{\pi /2}$ as functions of $c_2$ by fixed values of other two parameters, $c_1=0.25$ and $c_3=0$. Since here $Q_{\pi /2}<Q_0$, the quantum discord Q equals $Q_{\pi /2}$. The curve $Q_{\pi /2}$ has two fractures. This means that the branch $Q_{\pi /2}$ is a piecewise analytic function. In this case, however, the optimal measurement angle does not change its value $\theta =\pi /2$, and therefore, the position of conditional entropy minimum remains immutable.

6 Physical systems with the $Q_\theta$ subdomains

We are interested now in the systems with $Q_\theta$ phases. As it was seen from the previous section, such regions do not exist in the Bell-diagonal states. Therefore, in this section, we will consider the systems with nonzero values of $s_1, s_2$.

6.1 Phase flip channels

Let us consider the dynamics of quantum discord under decoherence (for a recent review, see, e.g, [45] and references therein). The authors [14] have considered such a dynamics in the phase flip channel.

The problem is to calculate the quantum discord for the X matrix

$$\begin{aligned} \varepsilon= & {} \frac{1}{4}[ 1 + s_1\sigma _z\otimes 1 + s_21\otimes \sigma _z + (1-p)^2c_1\sigma _x\otimes \sigma _x \nonumber \\&+ \,(1-p)^2c_2\sigma _y\otimes \sigma _y + c_3\sigma _z\otimes \sigma _z]. \end{aligned}$$

(55)

Here, the parametrized time $p=1-\exp (-\gamma t)$, where t is the time and $\gamma$ is the phase damping rate. The authors [14] restricted themselves to the case where

$$\begin{aligned} c_2=-c_3c_1,\qquad s_2=c_3s_1,\qquad -1\le c_3\le 1,\qquad -1\le s_1\le 1 . \end{aligned}$$

(56)

Expansion coefficients in Eq. (55) are related to the corresponding X matrix elements as

$$\begin{aligned}&a=(1+s_1+s_2+c_3)/4,\quad b=(1+s_1-s_2-c_3)/4, \nonumber \\&c=(1-s_1+s_2-c_3)/4,\quad d=(1-s_1-s_2+c_3)/4,\\&u=(1-p)^2(c_1-c_2)/4,\quad v=(1-p)^2(c_1+c_2)/4 . \nonumber \end{aligned}$$

(57)

Owing to the relation $s_2=c_3s_1$, the matrix elements a, b, c, and d satisfy the condition (36), and hence, the $Q_\theta$ domain is absent here; conditional entropy behaves similar to that as shown in Fig. 8. Thus, nonzero values of $s_1$ and $s_2$ are the necessary but not sufficient condition for existence of $Q_\theta$ phase.

Consider a different initial state. For example, let us take $s_1=s_2=0.65, c_1=c_2=0.249$, and $c_3=0.5$. As can see from Fig. 9, the curves $Q_0(p)$ and $Q_{\pi /2}(p)$ cross at $p_\times \simeq 0.3158$. An additional study shows that the transition $Q_{\pi /2}\rightarrow Q_0$ goes through the appearance of single minimum on the $S_\mathrm{cond}(\theta )$ curves inside the interval between 0 and $\pi /2$ (similarly to the curves on Fig. 4).

Fig. 9

$Q_0$ (solid line) and $Q_{\pi /2}$ (dotted line) in bits versus p for the phase flip channel with parameters $s_1=s_2=0.65$, $c_1=c_2=0.249$, and $c_3=0.5$. Crossing point of the lines is at $p_\times =0.315\,789\ldots$

Solution of equations for the boundaries, Eqs. (43)–(47), shows that the $\pi /2$- and 0-boundaries do not coincide now, and therefore, the $Q_\theta$ region exists here (see Fig. 10).

Fig. 10

Dependencies of the false discord $\tilde{Q}=\min \{Q_{\pi /2},Q_0\}$ (dotted line) and the corrected quantum discord $Q=\min \{Q_{\pi /2},Q_\theta ,Q_0\}$ (solid line) versus p for the phase flip channel with parameters $s_1=s_2=0.65$, $c_1=c_2=0.249$, and $c_3=0.5$. Longer solid bars mark the boundaries $p_{\pi /2}=0.314\,949$ and $p_0=0.316\,637$. Longer dotted bar marks the position of a fracture, $p_\times =0.315\,789$, on the curve $\tilde{Q}(p)$

6.2 Thermal discord

We now discuss systems at the thermal equilibrium. Discord in such systems is important for applications to various magnetic materials [4, 5]. Let us consider the XYZ spin Hamiltonian

$$\begin{aligned} \mathcal{H} = -\frac{1}{2}(J_x\sigma _1^x\sigma _2^x + J_y\sigma _1^y\sigma _2^y + J_z\sigma _1^z\sigma _2^z + B_1\sigma _1^z + B_2\sigma _2^z). \end{aligned}$$

(58)

This Hamiltonian contains five independent parameters $J_x,J_y,J_z,B_1,B_2\in (-\infty ,\infty )$ (i.e., in $\mathcal{R}^5$) and is the most general real symmetric traceless X matrix. The corresponding Gibbs density matrix is given as

$$\begin{aligned} \rho _{AB}=\frac{1}{Z}e^{-\beta \mathcal{H}} \end{aligned}$$

(59)

(here $\beta =1/T$, T is the temperature in energy units, Z is the partition function) and has also the five-parameter real X structure. Thus, the map $( B_1/T, B_2/T, J_x/T, J_y/T, J_z/T)\leftrightarrow (s_1, s_2, c_1, c_2, c_3)$ (that is $\mathcal{R}^5\leftrightarrow \mathcal{D}$) allows in general to change the density matrix language on a picture of interactions in the XYZ dimer in inhomogeneous fields $B_1$ and $B_2$.

Having solved eigenproblem for the Hamiltonian (58), we then find expressions for the thermal density matrix elements (see also, e.g., [46])

$$\begin{aligned}&a=\frac{1}{2}\frac{\cosh (\beta R_1/2)+[(B_1+B_2)/R_1]\sinh (\beta R_1/2)}{\cosh (\beta R_1/2)+\exp (-\beta J_z)\cosh (\beta R_2/2)}, \nonumber \\&b=\frac{1}{2}\frac{\cosh (\beta R_2/2)+[(B_1-B_2)/R_2]\sinh (\beta R_2/2)}{\exp (\beta J_z)\cosh (\beta R_1/2)+\cosh (\beta R_2/2)}, \nonumber \\&c=\frac{1}{2}\frac{\cosh (\beta R_2/2)-[(B_1-B_2)/R_2]\sinh (\beta R_2/2)}{\exp (\beta J_z)\cosh (\beta R_1/2)+\cosh (\beta R_2/2)},\\&d=\frac{1}{2}\frac{\cosh (\beta R_1/2)-[(B_1+B_2)/R_1]\sinh (\beta R_1/2)}{\cosh (\beta R_1/2)+\exp (-\beta J_z)\cosh (\beta R_2/2)}, \nonumber \\&u=\frac{1}{2}\frac{[(J_x-J_y)/R_1]\sinh (\beta R_1/2)}{\cosh (\beta R_1/2)+\exp (-\beta J_z)\cosh (\beta R_2/2)}, \nonumber \\&v=\frac{1}{2}\frac{[(J_x+J_y)/R_2]\sinh (\beta R_2/2)}{\exp (\beta J_z)\cosh (\beta R_1/2)+\cosh (\beta R_2/2)}, \nonumber \end{aligned}$$

(60)

where

$$\begin{aligned} R_1=[(B_1+B_2)^2+(J_x-J_y)^2]^{1/2},\quad R_2=[(B_1-B_2)^2+(J_x+J_y)^2]^{1/2}.\nonumber \\ \end{aligned}$$

(61)

For the correlations functions (5), we have, respectively,

$$\begin{aligned}&c_{1,2}=\frac{2}{Z}[\![\pm [(J_x-J_y)/R_1]e^{\beta J_z/2}\sinh (\beta R_1/2) \nonumber \\&\quad \quad \quad +\,[(J_x+J_y)/R_2]e^{-\beta J_z/2}\sinh (\beta R_2/2)]\!], \nonumber \\&c_3=\frac{2}{Z}[e^{\beta J_z/2}\cosh (\beta R_1/2)-e^{-\beta J_z/2}\cosh (\beta R_2/2)],\\&s_{1,2}=\frac{2}{Z}[\![[(B_1+B_2)/R_1]e^{\beta J_z/2}\sinh (\beta R_1/2) \nonumber \\&\quad \quad \quad \pm [(B_1-B_2)/R_2]e^{-\beta J_z/2}\sinh (\beta R_2/2)]\!], \nonumber \end{aligned}$$

(62)

where the partition function equals

$$\begin{aligned} Z=2[e^{\beta J_z/2}\cosh (\beta R_1/2)+e^{-\beta J_z/2}\cosh (\beta R_2/2)] \end{aligned}$$

(63)

and $R_1$ and $R_2$ are given again by Eq. (61).

For each choice of interaction constants $J_x, J_y, J_z$ and external fields $B_1$ and $B_2$, we will find the points where the condition $Q_0=Q_{\pi /2}$ is satisfied. After this, we will again study the changes of curves $S_\mathrm{cond}(\theta )$ in the neighborhood of points found.

Taking, for example, a dimer with parameters $J_x=J_y=J=1, J_z=1.02$, and $B_1=B_2=B=1$ (that is the XXZ dimer in an uniform field), we consider the thermal discord behavior by a transition from the subdomain $Q_{\pi /2}$ to $Q_0$ one (Fig. 11). From the figure, one can see that down to the crossing point $T_\times =0.81296$, the discord ${\tilde{Q}}$, according to Refs. [12–14], equals $Q_{\pi /2}$, and above the point $T_\times$, it equals $Q_0$. If this was valid, the discord ${\tilde{Q}}=\min \{Q_0,Q_{\pi /2}\}$ would have a fracture at the intersection point $T_\times$. However, in fact, the true discord Q is a smooth function (at least, it is a function of differentiability class $C^1$). This follows from the numerical solution of the task in the intermediate domain, where the $S_\mathrm{cond}(\theta )$ curves change similar as in Fig. 4. Results for the quantum discord are shown again in Fig. 11. At the bifurcations points $T_{\pi /2}=0.76106$ and $T_0=0.85361$, the higher derivatives of quantum discord $Q=\min \{Q_{\pi /2},Q_\theta ,Q_0\}$ exhibit a discontinuous behavior.

Fig. 11

Dependencies of the false discord $\tilde{Q}=\min \{Q_{\pi /2},Q_0\}$ (dotted line) and the correct quantum discord $Q=\min \{Q_{\pi /2},Q_\theta ,Q_0\}$ (solid line) for the XXZ dimer with parameters $J=1$, $J_z=1.02$ and $B=1$. Longer bars mark the temperatures $T_{\pi /2}=0.76106$ and $T_0=0.85361$. Domains $T\le T_{\pi /2}$, $T_{\pi /2}<T<T_0$, and $T\ge T_0$ correspond to the discord branches $Q_{\pi /2}$, $Q_\theta$, and $Q_0$, respectively

6.3 Heteronuclear systems with dipolar coupling

Let us consider the system (58) with parameters $J_x=J_y=-D$ and $J_z=2D$. Such a model corresponds to a dipolar coupled dimer which is stretched along the z axis [47]

$$\begin{aligned} \mathcal{H} = \frac{1}{2}D(\sigma _1^x\sigma _2^x + \sigma _1^y\sigma _2^y - 2\sigma _1^z\sigma _2^z) - \frac{1}{2}(B_1\sigma _1^z + B_2\sigma _2^z). \end{aligned}$$

(64)

Here the dipolar coupling constant (in frequency units) equals

$$\begin{aligned} D = \frac{\mu _0}{4\pi }\frac{\gamma _1\gamma _2\hbar }{2r_0^3}, \end{aligned}$$

(65)

where $\mu _0$ is the magnetic permeability of free space, $\gamma _1$ and $\gamma _2$ are the gyromagnetic ratios of particles in the dimer, and $r_0$ is the distance between those particles. Normalized fields $B_1$ and $B_2$ in Eq. (65) are

$$\begin{aligned} B_1 = \gamma _1 B_0, \qquad B_2=\gamma _2 B_0, \end{aligned}$$

(66)

where $B_0$ is the external magnetic field induction.

We have performed necessary calculations (according to our approach developed in the previous sections) and found the subdomains of quantum discord in the plane $(B_1/D,B_2/D)$. The results are shown at the normalized temperature $T/D=1$ in Fig. 12. From this figure, one can see that such a system has the $Q_\theta$ regions between the 1, 2 and $1^\prime ,2^\prime$ lines. Notice that the phase diagram (Fig. 12) is not symmetric with respect to the bisection line $B_1/D=B_2/D$ because the quantum discord is not symmetric under the exchange of the subsystems. The $Q_\theta$ regions can be reached by varying the external magnetic field $B_0$. Two possible trajectories are shown in Fig. 12 by dotted lines, $B_2=4B_1$ and $B_2=B_1/4$. (The value $\gamma _2/\gamma _1=4$ approximately corresponds to the quotient of gyromagnetic ratios for the nucleus of $^1\!$H and $^{13}$C.)

Fig. 12

Subdomains $Q_{\pi /2}$, $Q_0$, and (between the lines 1,2 and $1^\prime ,2^\prime$) $Q_\theta$ for the spin dimer (64) at the normalized temperature $T/D=1$. Dotted lines 3 and 4 correspond to $B_2=4B_1$ and $B_2=B_1/4$, respectively

We found also that in the $Q_\theta$ subdomain, the conditional entropy $S_\mathrm{cond}(\theta )$ has only one minimum that is located in the interval $(0,\pi /2)$. The picture is qualitatively similar to that is shown in Fig. 4.

So, the $Q_\theta$ region and corresponding sudden changes of quantum correlation behavior at their boundaries can be observed in solid materials with nuclear dimers.

7 Results and perspectives

In the light of the above, the calculation of quantum discord of any X states can be achieved by following steps. First, the density matrix is transformed to a real form. Second, it is also well to solve the equation $Q_0=Q_{\pi /2}$, determine possible crossing points of branches $Q_0$ and $Q_{\pi /2}$, and study the behavior of $S_\mathrm{cond}(\theta )$ near the crossing points found. Then the equations $S_\mathrm{cond}^{\prime \prime }(0)=0$ and $S_\mathrm{cond}^{\prime \prime }(\pi /2)=0$ are solved to find the boundaries for the intermediate subdomain $Q_{\theta }$. After this, one should numerically find the optimal measurement angle $\theta \in (0,\pi /2)$ and compute $Q_{\theta }=Q(\theta )$. As a result, the quantum discord is given by $Q=\min \{Q_0, Q_\theta , Q_{\pi /2}\}$.

So, the quantum discord of X states is represented analytically if the $Q_\theta$ region is absent. Then the quantum discord is given by the closed form $Q=\min \{Q_{\pi /2},Q_0\}$ and by $Q=Q_{\pi /2}=Q_0$ in the fully isotropic case [48]. The discord is continuous, but generally speaking it is a piecewise smooth function. In particular, this is valid for a special class of X states, namely for the Bell-diagonal states. For them, we found the $Q_0$ and $Q_{\pi /2}$ regions in the total domain of their definition (Fig. 6). It would be interesting to find the subdomains $Q_0$, $Q_\theta$, and $Q_{\pi /2}$ in the five-dimensional domain $\mathcal{D}$ making, e.g., an atlas of maps.

Also, we have shown in this paper that the boundaries for the transition subdomain from $Q_0$ to $Q_{\pi /2}$ or reversely are exactly defined. They consist of nonanalyticity points which are bifurcation ones. The boundaries may coincide, and then, the quantum discord is evaluated analytically in the total domain of definition. The regions $Q_\theta$ with the optimal intermediate angles $\theta \in (0,\pi /2)$ have been found for a number of physical systems including the phase flip channels, spin dimers at the thermal equilibrium, and heteronuclear systems with dipolar interaction. The transitions $Q_{\pi /2}\leftrightarrow Q_\theta \leftrightarrow Q_0$ occur continuously and smoothly. This is a new type of transitions for the quantum discord.

The examples considered show that $Q_\theta$ phases are interesting physical phenomena rather not a mathematical exotic.

We have found only two regimes for the average conditional entropy change by above transitions: (i) via the birth of one intermediate minimum (as shown in Fig. 4) and (ii) via the straight line (as shown in Fig. 8), when arbitrary angle $\theta \in [0,\pi /2]$ is optimal, but any infinitesimal perturbations of model parameters lead to a jump of optimal measurement angle to zero or $\pi /2$. It is hoped that our observations will be rigorously proofed and, maybe, generalized in the future.

At present, the attempts are made to obtain analytical formulas for the super quantum discord of X states with nonzero Bloch vectors [49, 50]. In this connection, one should note that the authors do not take into account a possibility of intermediate optimal angles for the weak measurements which are a generalization of ordinary projective ones.