1 Introduction

Quantum entanglement plays an important role in quantum information processing (QIP). However, quantum entanglement itself is fragile, and it inevitably suffers from various noise in a practical transmission or storage process. The degraded entanglement will decrease the success probability and the security of QIP. Generally speaking, the decoherence effect would decrease the fidelity of entanglement or make the maximally entangled state become to less-entangled one. Therefore, quantum repeaters are required in long-distance quantum communication and distributed quantum computation. Meanwhile, entanglement purification and entanglement concentration provide two powerful ways of depressing the effect of decoherence on the entangled quantum systems.

Entanglement purification is introduced to extract some high-fidelity maximally entangled states from a mixed entangled ensemble, which has been widely studied since Bennett et al. [1] proposed the first entanglement purification protocol for purifying two-particle systems in a Werner state. Compared with entanglement purification, entanglement concentration focuses on a set of systems in a less-entangled pure state, which is more efficient for remote parties to obtain some maximally entangled states [2]. In 1996, Bennett et al. [3] proposed the first entanglement concentration protocol (ECP) based on the Schmidt projection method. In 1999, Bose et al. [4] presented an ECP resorting to entanglement swapping. For entangled photon systems, Yamamoto et al. [5] and Zhao et al. [6] proposed two similar ECPs with linear optics, independently. These two protocols had been experimentally demonstrated [7, 8]. In 2008, Sheng et al. [9] proposed an efficient nonlocal ECP for less-entangled photon pairs using cross-Kerr nonlinearities, which has inspired a lot of theoretical improvements [10–15]. Among them, an important ECP for N-photon systems in a known less-entangled pure state was proposed by Deng [13] in 2012, resorting to the projection measurement on an additional photon. Compared with previous ECPs, this protocol does not depend on a pair of systems in a less-entangled state in each round of concentration, just each system itself and some additional single photons, which can reach an optimal total success probability from the view of efficiency and decrease the difficulty for its implementation in experiment. Recently, Ren et al. [16] introduced an interesting ECP for two-photon four-qubit hyperentangled state with the parameter-splitting method. They also investigated the general hyper-ECP for photon systems [17]. In addition, entanglement concentration has also been widely studied for solid systems, such as conduction electrons [18–20], single atoms [21, 22], quantum dots [23], atomic ensemble [24], and so on.

The nitrogen-vacancy (NV) defect centers in diamond coupled to microresonator is a novel solid-state cavity quantum electrodynamics (QED) system, and a promising candidate for QIP. The NV center consists of nearest neighbor pair of a nitrogen atom substituted for a carbon atom and a lattice vacancy, which has good optical controllability [25] and electron spin coherence even at room temperature [26, 27]. The electron spin can be rapidly read out via quantum logic with nuclear spin ancillary [28]. By coupling to photonic crystal cavities, the resonant zero phonon line (ZPL) relevant to the emitted photons from NV centers can be significantly enhanced [29]. The quantum non-demolition (QND) measurement of the electronic spin state was also sketched [30] and experimentally demonstrated [31]. Based on these properties, the NV center has attracted much attention, and much theoretical and experimental effort has been devoted to QIP using the NV center and microresonator coupled systems [32–37].

In 2008, Dayan et al. [38] demonstrated the single-photon input–output process of a microtoroidal resonator (MTR) coupling to an atom in experiment. Although the MTR allows for an ultrahigh Q factor, the Q factor can be surely degraded when the MTR couples to a tapered fiber, which enables the efficient input–output process of flying photons. The experiment also indicates that the single-atom within the microresonator can dynamically control the cavity output. Hence, based on the MTR-like devices, the entanglement generation [39] and quantum gate operations [40] between distant atoms can be realized via a flying photon passing through different resonators. In 2011, Chen et al. [41] proposed a potentially practical idea to entangle separate NV centers in a scalable fashion by coupling to MTRs. After that, many QIP proposals have emerged using the NV center and MTR (NV–MTR) coupled systems, such as quantum entanglement generation [42–44], universal quantum gates [45–47], QIP in decoherence-free subspace [48, 49], and so on. As the NV–MTR coupled system can serve as an efficient quantum node and connecting the nodes with optical fiber may pioneer a new route for constructing a large-scaled quantum network, it is an essential requirement to investigate the entanglement purification [50] and entanglement concentration [51, 52] for such systems.

In this work, we propose an efficient multipartite ECP for separate NV centers, resorting to the single-photon input–output process of the NV–MTR coupled system. In the present ECP, with the assistance of an ancillary single-photon, maximally entangled state between the NV centers can be obtained with a certain success probability. This process does not destroy the solid-qubit entanglement and thus can be iterated several rounds to obtain an optimal total success probability. Compared with ECPs in Ref. [51, 52], our scheme exhibits some advantages. For example, it exhibits the same success probability as the protocol described in Ref. [51], but does not depend on two copies of the initial state or additional NV centers, just the entangled system itself and some ancillary single photons. In each round of concentration, the single-photon passes through the hybrid quantum circuit composed of only one microcavity and some linear-optical elements, which is helpful in increasing the efficiency under the imperfect cavities. Also the protocol has a high experimental feasibility by considering the current technologies. The future technical advances such as in improving the coupling strength, reducing the photon loss, extending the coherence time and lowering the experimental imperfection will further improve the experimental feasibility.

2 Single-photon input–output process of the NV center and MTR coupled system

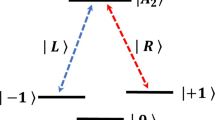
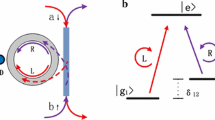
We first introduce the model of single-photon input–output process of the NV–MTR coupled system. The configuration of the system is schematically shown in Fig. 1a, in which a negatively charged NV center fixed on the exterior surface of a MTR is coupled by the evanescent field of the MTR modeled as a single-sided cavity. The relevant electron level structure of the NV center and the transition coupling with the input polarized photon is shown in Fig. 1b. Here we encode the qubits as \(\left| {{}^3A,{m_s} = - 1} \right\rangle = \left| 0 \right\rangle \) and \(\left| {{}^3A,{m_s} = + 1} \right\rangle = \left| 1 \right\rangle \) in the electron ground state spins which facilitates the quantum information storage and further applications. The excited state sub-level \(\left| {{A_2}} \right\rangle = \frac{1}{{\sqrt{2} }}(\left| {{E_ - }} \right\rangle \left| {{m_s} = + 1} \right\rangle + \left| {{E_ + }} \right\rangle \left| {{m_s} = - 1} \right\rangle )\) is employed as the ancillary to provide the optical \(\Lambda \)-type three-level system in the NV center [33, 37], where \(\left| {{E_ \pm }} \right\rangle \) are orbital states with angular momentum projection \({ \pm 1}\) along the NV axis. The level transition between \(\left| 0 \right\rangle \) (\(\left| 1 \right\rangle \)) and \(\left| e \right\rangle \) is resonantly coupled to the \(\left| L \right\rangle \) (\(\left| R \right\rangle \)) circularly polarized photon. When we consider a single-photon pulse with frequency \({\omega _p}\) input in the MTR (see Fig. 1a), the interaction between the MTR field and the NV center is generalized by the Jaynes-Cummings (JC) model with respect to a \(\Lambda \)-type atom. By assuming the NV center is initially prepared in the ground state, we can adiabatically solved the quantum Langevin equations and obtain the reflection coefficient of the input pulse as [39]:

$$\begin{aligned} {r_{L,R}}({\omega _p}) = \frac{{\left[ i({\omega _c} - {\omega _p}) - \frac{\kappa }{2}\right] \left[ i({\omega _0} - {\omega _p}) + \frac{\gamma }{2}\right] + {g^2}}}{{\left[ i({\omega _c} - {\omega _p}) + \frac{\kappa }{2}\right] \left[ i({\omega _0} - {\omega _p}) + \frac{\gamma }{2}\right] + {g^2}}}, \end{aligned}$$
(1)

here \({\omega _c}\) is the MTR mode frequency, \({\omega _0}\) is the transition frequency between the energy level \(\left| 0 \right\rangle \) (\(\left| 1 \right\rangle \)) and \(\left| e \right\rangle \). \(\kappa \) and \(\gamma \) are the cavity decay rate and NV center dipole decay rate, respectively. \(g\) is the coupling strength between the cavity and the NV center. On the other hand, in the case of \(g = 0\) when the input photon encounters the NV center in a mismatched level, the reflection coefficient can be described as:

$$\begin{aligned} r_{L,R}^0({\omega _P}) = \frac{{i({\omega _c} - {\omega _p}) - \frac{\kappa }{2}}}{{i({\omega _c} - {\omega _p}) + \frac{\kappa }{2}}}, \end{aligned}$$
(2)

Under the resonant condition \({\omega _0} = {\omega _c} = {\omega _p}\), we have \(r_{L,R}^0({\omega _P}) = -1\) and Eq. (1) can be rewritten as:

$$\begin{aligned} {r_{L,R}}({\omega _p}) = \frac{{ - \kappa \gamma + 4{g^2}}}{{\kappa \gamma + 4{g^2}}}. \end{aligned}$$
(3)

If we set the coupling strength \(g \ge 5\sqrt{\kappa \gamma }\), the reflection coefficient \(r({\omega _p})\) is nearly unity. Then the single-photon input–output process of the NV–MTR coupled system can be described as:

$$\begin{aligned} \left| L \right\rangle \left| 0 \right\rangle&\rightarrow \left| L \right\rangle \left| 0 \right\rangle ,\left| R \right\rangle \left| 0 \right\rangle \rightarrow - \left| R \right\rangle \left| 0 \right\rangle , \nonumber \\ \left| L \right\rangle \left| 1 \right\rangle&\rightarrow - \left| L \right\rangle \left| 1 \right\rangle ,\left| R \right\rangle \left| 1 \right\rangle \rightarrow \left| R \right\rangle \left| 1 \right\rangle . \end{aligned}$$
(4)
Fig. 1
figure 1

The configuration of the single-photon input–output process of the NV–MTR coupled system. a An NV center fixed on the exterior surface of a MTR is coupled by the evanescent field of the MTR modeled as a single-sided cavity. A single-photon pulse is introduced to interact with the NV center via the cavity input–output process. b The relevant electron energy level structure of the NV center and the transition coupling with the input polarized photon

Full size image

3 Efficient multipartite entanglement concentration protocol for separate NV centers

Based on the single-photon input–output process of the NV–MTR coupled system, the principle of our ECP for separate NV centers in a less-entangled state can be shown in Fig. 2. Here we take the two-particle Bell-like entanglement as an example. Suppose two NV centers shared by remote parties, say Alice and Bob, are initially in a less-entangled pure state

$$\begin{aligned} {\left| \Phi \right\rangle _{ab}} = \alpha {\left| 0 \right\rangle _a}{\left| 0 \right\rangle _b} + \beta {\left| 1 \right\rangle _a}{\left| 1 \right\rangle _b}, \end{aligned}$$
(5)

where the subscripts \(a\) and \(b\) represent the NV centers owned by Alice and Bob, respectively. The coefficients \(\alpha \) and \(\beta \) satisfy the relation \({\left| \alpha \right| ^2} + {\left| \beta \right| ^2} = 1\). Here we assume that Alice knows the two coefficients beforehand. For recovering the maximally entangled state between the two NV centers, Alice first prepares an ancillary single-photon in the state \(\left| R \right\rangle \), and lets it pass through the hybrid quantum circuit as shown in Fig. 2. Here, the half-wave plates (HWPs) are used to perform Hadamard operation on the polarization states of photon. The circular polarization beam splitters (CPBSs) are exploited to transmit the \(\left| R \right\rangle \) photon and reflect the \(\left| L \right\rangle \) photon. If the parameters in the single-photon input–output process of the NV–MTR coupled system satisfy \({\omega _0}={\omega _c}={\omega _p}\) and \(g \ge 5\sqrt{\kappa \gamma }\) as we have discussed above and after the photon passes through the hybrid quantum circuit, the whole state composed of the two NV centers and the ancillary photon becomes to a three-particle hybrid entangled state

$$\begin{aligned} \left| \chi \right\rangle = \alpha {\left| 0 \right\rangle _a}{\left| 0 \right\rangle _b}\left| R \right\rangle + \beta {\left| 1 \right\rangle _a}{\left| 1 \right\rangle _b}\left| L \right\rangle . \end{aligned}$$
(6)

Then a wave plate \({R_\theta }\) is used to rotate the polarization states of the photon on Alice’s side as:

$$\begin{aligned} \left| R \right\rangle&\rightarrow \alpha \left| R \right\rangle + \beta \left| L \right\rangle \nonumber \\ \left| L \right\rangle&\rightarrow \alpha \left| L \right\rangle - \beta \left| R \right\rangle , \end{aligned}$$
(7)

and the whole state becomes

$$\begin{aligned} {\left| \Psi \right\rangle }&= {\left( {\alpha ^2}{{\left| 0 \right\rangle }_a}{{\left| 0 \right\rangle }_b} - {\beta ^2}{{\left| 1 \right\rangle }_a}{{\left| 1 \right\rangle }_b}\right) \left| R \right\rangle }\nonumber \\&+\, \sqrt{2} \alpha \beta \cdot \frac{1}{{\sqrt{2} }}\left( {{\left| 0 \right\rangle }_a}{{\left| 0 \right\rangle }_b} + {{\left| 1 \right\rangle }_a}{{\left| 1 \right\rangle }_b}\right) \left| L \right\rangle . \end{aligned}$$
(8)

Finally, Alice uses CPBS\(_3\) and two photon detectors \(D_1\) and \(D_2\) to measure the photon using the basis \(\{ \left| R \right\rangle \),\(\left| L \right\rangle \}\). If the detector \(D_1\) is triggered with the measurement result of \(\left| L \right\rangle \), the two NV centers are projected to the maximally entangled Bell state \(\left| {{\phi ^ + }} \right\rangle = \frac{1}{{\sqrt{2} }}({\left| 0 \right\rangle _a}{\left| 0 \right\rangle _b} + {\left| 1 \right\rangle _a}{\left| 1 \right\rangle _b})\), which takes place with a success probability of \(2{\alpha ^2}{\beta ^2}\). Then the entanglement concentration process can be finished. On the contrary, if the detector \(D_2\) is triggered with the measurement result of \(\left| R \right\rangle \), the two NV centers are in another less-entangled pure state

$$\begin{aligned} {\left| \Phi \right\rangle _{ab}}' = \frac{1}{{\sqrt{{\alpha ^4} + {\beta ^4}} }} \left( {\alpha ^2}{\left| 0 \right\rangle _a}{\left| 0 \right\rangle _b} - {\beta ^2}{\left| 1 \right\rangle _a}{\left| 1 \right\rangle _b}\right) , \end{aligned}$$
(9)

which takes place with a probability of \(1 - 2{\alpha ^2}{\beta ^2}\).

Fig. 2
figure 2

Schematic setup of the present ECP for separate NV centers in a less-entangled Bell-like state. NV\(_a\) represents the NV center owned by Alice, which is coupled to the MTR as shown in Fig. 1a. HWPs are half-wave plates, CPBSs are circular polarization beam splitter, DL is delay lines, \(D_1\) and \(D_2\) are two photon detectors. The wave plate \({R_\theta }\) is used to rotate the polarization state of the single photon

Full size image

One can see that the process does not destroy the solid-qubit entanglement and thus the less-entangled pure state \({\left| \Phi \right\rangle _{ab}}'\) can be used for the second-round concentration. If we rewrite the coefficients in Eq. (9) as \(\alpha ' = \frac{{{\alpha ^2}}}{{\sqrt{{\alpha ^4} + {\beta ^4}} }}\) and \(\beta ' = - \frac{{{\beta ^2}}}{{\sqrt{{\alpha ^4} + {\beta ^4}} }}\), the state \({\left| \Phi \right\rangle _{ab}}'\) would have the same form as the state \({\left| \Phi \right\rangle _{ab}}\). Thus, Alice can prepare another ancillary single-photon \(\left| R \right\rangle \) and let it pass though the same hybrid quantum circuit as in Fig. 2, but replace the wave plate \({R_\theta }\) with \({R_\theta '}\), which rotates the polarization states of the photon as:

$$\begin{aligned} \left| R \right\rangle&\rightarrow \frac{1}{{\sqrt{{\alpha ^4} + {\beta ^4}} }}\left( {\alpha ^2}\left| R \right\rangle - {\beta ^2}\left| L \right\rangle \right) \!,\nonumber \\ \left| L \right\rangle&\rightarrow \frac{1}{{\sqrt{{\alpha ^4} + {\beta ^4}} }}\left( {\alpha ^2}\left| L \right\rangle + {\beta ^2}\left| R \right\rangle \right) \!. \end{aligned}$$
(10)

The evolution of the whole state can be described as:

$$\begin{aligned} {{{\left| \Phi \right\rangle }_{ab}}' \otimes \left| R \right\rangle }&= {\left( \alpha '{{\left| 0 \right\rangle }_a}{{\left| 0 \right\rangle }_b} + \beta '{{\left| 1 \right\rangle }_a}{{\left| 1 \right\rangle }_b}\right) \otimes \left| R \right\rangle }\nonumber \\&{ \rightarrow (\alpha {'^2}{{\left| 0 \right\rangle }_a}{{\left| 0 \right\rangle }_b} - \beta {'^2}{{\left| 1 \right\rangle }_a}{{\left| 1 \right\rangle }_b})\left| R \right\rangle }\nonumber \\&{ +\, \sqrt{2} \alpha '\beta ' \cdot \frac{1}{{\sqrt{2} }}\left( {{\left| 0 \right\rangle }_a}{{\left| 0 \right\rangle }_b} + {{\left| 1 \right\rangle }_a}{{\left| 1 \right\rangle }_b}\right) \left| L \right\rangle }. \end{aligned}$$
(11)

Obviously, Alice and Bob can obtain the maximally entangled state \(\left| {{\phi ^ + }} \right\rangle \) from the state \({\left| \Phi \right\rangle _{ab}}'\) with a success probability of \(2\alpha {'^2}\beta {'^2}\). Moreover, even though the second round is failure, the resulting less-entangled state can also be recovered to the maximally entangled state in the next round. In this way, the entanglement concentration process can be iterated until success, and the total success probability \(P\) of the present ECP after iterating the concentration process \(n\) rounds is

$$\begin{aligned} P&= 2\left[ {\alpha ^2}{\beta ^2} + \frac{{{\alpha ^4}{\beta ^4}}}{{{\alpha ^4} + {\beta ^4}}} + \frac{{{\alpha ^8}{\beta ^8}}}{{\left( {\alpha ^4} + {\beta ^4}\right) \left( {\alpha ^8} + {\beta ^8}\right) }}\right. \nonumber \\&\left. + \cdots + \frac{{{\alpha ^{2n}}{\beta ^{2n}}}}{{\left( {\alpha ^4} + {\beta ^4}\right) \left( {\alpha ^8} + {\beta ^8}\right) \cdots \left( {\alpha ^{2n}} + {\beta ^{2n}}\right) }}\right] . \end{aligned}$$
(12)

Here in this study, we numerically calculated the total success probability \(P\) as a function of the initial coefficient \(\alpha ^2\) after iterating the concentration process \(n\) (\(n=1,2,3,4\)) rounds in Fig. 3. By iterating the concentration process more rounds, the remote parties can obtain a higher total success probability.

Fig. 3
figure 3

The total success probability \(P\) of the present ECP as a function of the initial coefficient \(\alpha ^2\) after iterating the entanglement concentration process \(n=1,2,3,4\) rounds, respectively

Full size image

It is straightforward to generalize the ECP to obtain maximally entangled GHZ states from less-entangled GHZ-class states on separate NV centers. Suppose the NV centers are initially in \(N\)-particle less-entangled GHZ state

$$\begin{aligned} {\left| \Phi \right\rangle _N} = \alpha {\left| 0 \right\rangle _a}{\left| 0 \right\rangle _b} \cdots {\left| 0 \right\rangle _z} + \beta {\left| 1 \right\rangle _a}{\left| 1 \right\rangle _b} \cdots {\left| 1 \right\rangle _z}, \end{aligned}$$
(13)

where \({\left| \alpha \right| ^2} + {\left| \beta \right| ^2} = 1\), the subscripts represent the NV centers owned by Alice, Bob, ..., and Zach, respectively. If we rewrite \({\left| 0 \right\rangle _{N - 1}} = {\left| 0 \right\rangle _b}{\left| 0 \right\rangle _c} \cdots {\left| 0 \right\rangle _z}\) and \({\left| 1 \right\rangle _{N - 1}} = {\left| 1 \right\rangle _b}{\left| 1 \right\rangle _c} \cdots {\left| 1 \right\rangle _z}\), the state \({\left| \Phi \right\rangle _N}\) can be described as

$$\begin{aligned} {\left| \Phi \right\rangle _N} = \alpha {\left| 0 \right\rangle _a}{\left| 0 \right\rangle _{N - 1}} + \beta {\left| 1 \right\rangle _a}{\left| 1 \right\rangle _{N - 1}}. \end{aligned}$$
(14)

So a maximally entangled GHZ state between these NV centers can be obtained with the same total success probability \(P\) following the same principle as described above.

4 Discussion and summary

So far, we have fully described our ECP for separate NV centers. The key point in the realization of the protocol is the single-photon input–output process of the NV–MTR coupled system. In the discussion above, we focus on the parameters \(g \ge 5\sqrt{\kappa \gamma }\) under the resonant condition \({\omega _0} = {\omega _c} = {\omega _p}\). The physics behind which is the giant optical Faraday rotation near the resonance regime. In Fig. 4a, we numerically calculated the reflectance of the input photon pulse against \(\frac{g}{{\sqrt{\kappa \gamma } }}\) under the resonant condition. We also show the reflectance as a function of \(\frac{g}{\kappa }\) for different \(\gamma \) in Fig. 4b. One can see that the reflectance \({r_{L,R}}({\omega _p}) \ge 0.95\) can be achieved with the coupling strength \(g \ge 3\sqrt{\kappa \gamma }\) even when \(g < 0.1\kappa \), which implies the NV–MTR coupled system does not essentially need to work in the stringent high-Q and strong coupling conditions [53]. In each round of concentration, one of the remote parties first prepares a single-photon and let it pass through the hybrid quantum circuit to produce a (\(N\)+1)-particle (\(N \ge 2\)) hybrid entangled state. The hybrid quantum circuit functions as a hybrid controlled-NOT (CNOT) gate, in which the NV center is the control qubit and the photon is the target qubit. The fidelity \(F\) of the hybrid CNOT gate under the resonant condition can be numerically calculated under perfect linear-optical operations. The results against \(\frac{g}{\kappa }\) for different \(\gamma \) can be found in Fig. 4c. The fidelity increases with the increase of \(\frac{g}{\kappa }\) as expected. For the realistic NV center and microcavity system, the decay rate \({\gamma _{total}}\) approaches to \(2\pi \times 15\) MHz because of the dipolar transitions [37]. The rate \(\gamma \) within the ZPL rage is 3–4 % of \({\gamma _\mathrm{{total}}}\) [54]. Provided the Q factor of the MTR is \(Q = \frac{c}{{\lambda \kappa }} \sim {10^4}\) with \(c\) denotes the speed of light and the transition wavelength \(\lambda = 637\) nm between the states \(\left| 0 \right\rangle \) (\(\left| 1 \right\rangle \)) and \(\left| e \right\rangle \) [37], in order to reach \({r_{L,R}}\left( {{\omega _p}} \right) \simeq 1\), the coupling strength \(g\) should be on the order of hundreds of megahertz, which can be achieved with current technologies. The strong coupling between the NV centers and the whispering-gallery mode (WGM) has been realized in experiments, such as using microspheres [55, 56], diamond-GaP microdisks [57], and SiN photonic crystals [58]. Recently, the large coupling between NV centers and photonic crystal nanocavities has also been realized [59]. Considering a set of efficient parameters \([g,\kappa ,{\gamma _\mathrm{{total}}},{\gamma _\mathrm{{ZPL}}}] = [0.3,26,0.013,0.0004] \times 2\pi \) GHz [57], we have \(\gamma \approx 1.5 \times {10^{ - 5}}\kappa \) and \(g \approx 3\sqrt{\kappa \gamma }\), and the fidelity of the hybrid CNOT gate can exceed 0.95 under the resonant condition. Therefore, the protocol has a high experimental feasibility.

Fig. 4
figure 4

a The reflectance of the input photon pulse against \(\frac{g}{{\sqrt{\kappa \gamma } }}\). b The reflectance as a function of \(\frac{g}{\kappa }\) for different \(\gamma \). c The fidelity of the hybrid CNOT gate against \(\frac{g}{\kappa }\) for different \(\gamma \). All these results are calculated under the resonant condition \({\omega _0} = {\omega _c} = {\omega _p}\)

Full size image

However, there are some experimental challenges in the realization of our ECP that should be noted. For example, though the concentration process can be iterated several rounds, the spin decoherence of NV centers may limit the iteration number. Fortunately, the electron spin relaxation time and the dephasing time of NV centers are proved to be long, which are \(\sim \)ms at room temperature and \(\sim \)s at low temperature [26, 27]. Our protocol involving the ancillary excited state may work well at cryogenic temperatures, though the room-temperature coherent manipulation of the electron spin in a single NV center has been achieved [60–62]. We also noticed that the dynamics decoupling processes of the NV centers were introduced in Ref. [63]. The nonideal photon loss would bring inefficiencies to the protocol as the successful operation is heralded by triggering the photon detector. Nevertheless, the hybrid CNOT gate used in the present protocol is composed of only one microcavity and some linear-optical elements, which is simpler than the parity-check gate (PCG) used in [51] constructed with two microcavity and is helpful in increasing the efficiency if the cavity is imperfect. Moreover, the current fabrication techniques can suppress the photon leakage and make it negligible compared with the main cavity decay into the input–output modes [64]. Highly efficient single-photon source and single-photon detector can also be employed in a realistic application [65]. Therefore, the future technical advances such as in improving the coupling strength, reducing the photon loss, extending the coherence time and lowering the experimental imperfection will further improve the experimental feasibility of the ECP.

In summary, we have proposed an efficient multipartite ECP on separate NV centers, resorting to the single-photon input–output process of the NV–MTR coupled system. In the present ECP, one of the remote parties first prepares an ancillary single-photon and lets it pass through a hybrid quantum circuit to produce a (\(N\)+1)-particle (\(N \ge 2\)) hybrid entangled state, and then by projecting the photon with a suitable orthogonal basis to obtain the \(N\)-particle maximally entangled state between the NV centers. This process can be iterated several rounds to obtain an optimal total success probability. Compared to previous works, the present work exhibits the following distinct features: (1) It does not require two copies of the initial state or additional NV centers; (2) the concentration process does not destroy the solid-qubit entanglement and thus can be iterated several rounds to obtain an optimal total success probability; (3) the hybrid quantum circuit is composed of only one NV-MTR coupled system and some linear-optical elements, and the coupled system can work efficient without the stringent requirement for strong coupling and high-Q cavities. By considering the currently available technologies, such as the possibility of a \(\Lambda \)-type scheme of orthogonally polarized optical photons at 637 nm in a NV center system, the considerable enhancement of the resonant zero phonon line (ZPL) by embedding NV centers in cavities, and the single-photon input–output process with the microtoroidal resonator (MTR) coupling to an atom, the protocol has a high experimental feasibility. Considering the current technologies and the future technical advances, we believe that the protocol is useful in the future applications of long-distance quantum communication and distributed quantum computation.