1 Introduction

Among various kinds of qubits such as atoms, atomic ensembles, trapped ions and photons, the nitrogen-vacancy (NV) center consisting of a substitutional nitrogen atom and an adjacent vacancy has emerged as a promising solid-state qubit for quantum information processing (QIP) [1–4]. This solid-state qubit has many distinctive advantages such as the capability for coherent manipulation in an optical fashion [5] and long coherence time even at room temperature [6]. Importantly, the NV center also provides a Λ-type three-level system [7–9], which can be used for various quantum engineering applications. A promising approach for these applications is to use hybrid photonic quantum devices based on NV centers. Prominent examples include coupling NV centers to microcavities [10], tapered optical fibers [11], and nanomechanical resonators [12, 13]. In these systems, strong interaction between a NV center and a whispering-gallery mode (WGM) of a microcavity provides a prospective platform to entangle distant NV centers. Many entanglement generation and quantum state transfer [14, 15] schemes have been proposed by means of this hybrid quantum system. Implementation of an one-step conditional phase gate with three individual NV centers coupled to a WGM microresonator was investigated [16]. Generation of the W-type and GHZ-type entangled states of distant NV centers coupled to a common microresonator via the WGM were also proposed [14, 17, 18]. NV centers coupled to WGM microresonators are considered as the natural candidates for quantum nodes, and these nodes can be connected by coupling the two cavities via either one flying photon or an optical fiber-taper waveguide [19, 20].

Recently, based on achievements in the strong coupling between NV centers and the modes of photonic crystals cavities (PCCs), Yang et al. have demonstrated another route for building a distributed QIP architecture [21], where each PCC-NV unit acts as a quantum node, and quantum information is transferred and processed in and between the NV centers at spatially different locations. In this work, we propose a protocol capable of an efficient and fast quantum phase gate for two spatially separated NV centers embedded in two separated single-mode PCCs. The key point of our proposal is that we introduce another transition within the ground states strongly driven by a microwave field except the optical transitions driven by the cavity mode and optical laser. With the driven of the optical laser, the decoherence from the excited states of the NV centers can be effectively suppressed by virtue of the Raman transition in the dispersive regime. With the driven of the microwave field, fast operation can be achieved. Meanwhile, the effective coupling rate between the NV centers and the cavity modes can be adjusted by changing the geometrical parameters of the defects or changing the Rabi frequency of the laser pulse. Besides, the cavity-cavity hopping strength can be tuned by the distance between the two PCCs.

2 Theoretical Model and the Solutions

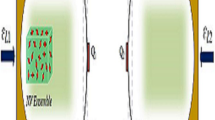
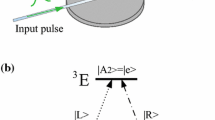
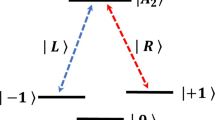
As sketched in Fig. 1(a), we study a hybrid system which consists of two distant coherently driven NV centers located in two directly coupled single-mode nanocavities. Each cavity is formed by a point defect created in photonic crystals, and the cavity frequency can be tuned by changing the geometrical parameters of the defects. In Fig. 1(b), the energy level configuration of a NV center, and its coupling with the cavity mode and driving fields are shown. The electronic ground state of a NV center is spin triplet and labeled as 3 A, with the levels m s = ±1 nearly degenerated and a zero-field splitting (D gs /2π = 2.88GHz) between the states m s = 0 and m s = ±1 [22]. The degeneracy of the levels |3 A, m s = ±1〉 can be lifted by employing an external magnetic field along the quantized symmetry axis of the NV center, which induces a level splitting D eg [22]. The two ground-state spin-triplet sublevels (|3 A, m s = −1〉 and |3 A, m s = +1〉) are used to encode the qubit. We denote these states |0〉 and |1〉. The Λ system could be realized in the NV center if the excited state |e〉 is chosen as \(|A_{2}\rangle =(|E_{-},m_{s}=+1\rangle +|E_{+},m_{s}=-1\rangle )/\sqrt {2}\), where E ± are orbital states with angular momentum projection ±1 along the NV axis [8, 15, 20, 21]. In our scheme, the cavity mode with frequency ω c is far-off resonant from the transition \(|0\rangle \Leftrightarrow |e\rangle \) (with the frequency ω e0), the transition \(|1\rangle \Leftrightarrow |e\rangle \) (with the frequency ω e1) is coupled by a largely detuned laser with frequency ω L and polarization σ +, and the microwave driven field with frequency ω m is resonant with the transition \(|0\rangle \Leftrightarrow |1\rangle \) (with the frequency ω 10). Using both optical and microwave radiation to control an electron spin associated with the NV center in diamond is experimentally accessible [18, 23, 24]. The total Hamiltonian is

$$\begin{array}{@{}rcl@{}} H=H_{NV}+H_{c}+H_{NVc}+H_{NVL}. \end{array} $$
(1)

The Hamiltonian H NV which describes NV centers reads

$$\begin{array}{@{}rcl@{}} H_{NV}=\sum\limits_{j}\omega_{e,j}|e\rangle_{j}\langle e|+\omega_{10,j}|1\rangle_{j}\langle1|. \end{array} $$
(2)

H c describes photons in coupled cavities as

$$\begin{array}{@{}rcl@{}} H_{c}=\sum\limits_{j}\omega_{c}a^{\dagger}_{j}a_{j}+T\left( a^{\dagger}_{j}a_{j+1}+h.c.\right), \end{array} $$
(3)

where ω c is the frequency of photons, \(a_{j} (a^{\dagger }_{j})\) annihilates (creates) a photon in cavity j, and T is the cavity-cavity hopping strength, which can be efficiently modulated by the distance between the two PCCs. This photon tunneling can be realized by the evanescent fields of the two cavities overlapped through the cavity dissipation, or by quantum channels, e.g., conventional optical fibers [25] or PC waveguides [26]. H NVc represents the coupling between NV centers and cavity modes as

$$\begin{array}{@{}rcl@{}} H_{NVc}=\sum\limits_{j}(g_{j}a_{j}|e\rangle_{j}\langle0|+h.c.), \end{array} $$
(4)

where g j is the coupling strength between jth NV center and jth cavity mode. While H NVL describes the coupling between NV centers and driving fields

$$\begin{array}{@{}rcl@{}} H_{NVL}=\sum\limits_{j}\left[{\Omega}_{L,j}e^{-i\omega_{L,j}}|e\rangle_{j}\langle1|+ {\Omega}_{j}e^{-i\omega_{m,j}}|1\rangle_{j}\langle0|+h.c.\right], \end{array} $$
(5)

where Ω L, j and Ω j is the coupling strength between jth NV center and optical laser and microwave driven field, respectively.

Fig. 1
figure 1

(Color online) (a) Schematic diagram of NV centers in coupled PCCs array, where two identical NV centers in diamond nanocrystals are located in two spatially separated nanocavities. (b) Level diagram for a NV center, Levels |0〉, |1〉 and |e〉 have the energy values 0, ω 10 and ω e , respectively. Each NV center interacts with a single mode cavity and two external driving fields

Full size image

Assuming that the detuning Δ j is sufficiently larger than the coupling strength g j and Ω L, j , the excited state |e〉 can be adiabatically eliminated. Meanwhile, the microwave driven field is resonant with the transition frequency ω 10 for each NV center. Using the rotating-wave approximation (RWA), the interaction Hamiltonian in the interaction picture can be written as [18, 27]

$$\begin{array}{@{}rcl@{}} H_{I}&=&T\left( a_{1}^{\dag}a_{2}+a_{1}a_{2}^{\dag}\right)+\sum\limits_{j=1}^{2}\frac{{\Omega}_{j}}{2}S_{x_{j}}\\ &&+\sum\limits_{j=1}^{2}\eta_{j}\left[a^{\dagger}_{j}S^{-}_{j}e^{-i\delta_{j}t}+a_{j}S^{+}_{j}e^{i\delta_{j}t}\right], \end{array} $$
(6)

where \(S^{+}_{j}=|1\rangle _{j}\langle 0|\), \(S^{-}_{j}=|0\rangle _{j}\langle 1|\), and \(\eta _{j}=g_{j}{\Omega }_{L,j}(\frac {1}{{\Delta }_{j}+\delta _{j}}+\frac {1}{{\Delta }_{j}})\) with Δ j = ω e0, j −ω c and δ j = ω c −ω 10, j −ω L, j .

It is convenient to rewrite the NV center-PCC interaction in terms of the hybrid cavity modes P 1 and P 2, which are symmetric and antisymmetric superposition of the localized cavity annihilation operators,

$$\begin{array}{@{}rcl@{}} P_{1}=\frac{1}{\sqrt{2}}(a_{1}+a_{2}), P_{2}=\frac{1}{\sqrt{2}}(a_{1}-a_{2}). \end{array} $$
(7)

Then, we have

$$\begin{array}{@{}rcl@{}} H_{I}&=&T\left( P_{1}^{\dag}P_{1}-P_{2}^{\dag}P_{2}\right)+\sum\limits_{j=1}^{2}\frac{{\Omega}_{j}}{2}S_{x_{j}} +\left[\frac{1}{\sqrt{2}}\eta_{1}(P_{1}+P_{2})\right.\\ &&\left.\times~ S^{+}_{1}e^{i\delta_{1}t}+\frac{1}{\sqrt{2}}\eta_{2}(P_{1}-P_{2})S^{+}_{2}e^{i\delta_{2}t}+h.c.\right]. \end{array} $$
(8)

In the interaction picture with the unitary transformation \(e^{-iH_{fr}t}\) for the free Hamiltonian \(H_{fr}=T(P_{1}^{\dag }P_{1}-P_{2}^{\dag }P_{2})+{\sum }_{j=1}^{2}\frac {{\Omega }_{j}}{2}S_{x_{j}}\), the interaction Hamiltonian under the new basis, \(|+\rangle _{j}=\frac {1}{\sqrt {2}}(|0\rangle _{j}+|1\rangle _{j})\) and \(|-\rangle _{j}=\frac {1}{\sqrt {2}}(|0\rangle _{j}-|1\rangle _{j})\), becomes

$$\begin{array}{@{}rcl@{}} H_{I}&=&\frac{1}{\sqrt{2}}\eta_{1}\left( P_{1}e^{-i(\delta_{1}+T)t}+P_{2}e^{-i(\delta_{2}-T)t}\right)\\&&\times~\left( \tilde{S}_{z_{1}}+\frac{1}{2}\tilde{S}_{+_{1}}e^{i{\Omega}_{1}t}-\frac{1}{2}\tilde{S}_{-_{1}}e^{-i{\Omega}_{1}t}\right)\\&& +\frac{1}{\sqrt{2}}\eta_{2}\left( P_{1}e^{-i(\delta_{1}+T)t}-P_{2}e^{-i(\delta_{2}-T)t}\right)\\&&\times~\left( \tilde{S}_{z_{2}}+\frac{1}{2}\tilde{S}_{+_{2}}e^{i{\Omega}_{2}t}-\frac{1}{2}\tilde{S}_{-_{2}}e^{-i{\Omega}_{2}t}\right)+H.c.. \end{array} $$
(9)

where \(\tilde {S}_{z_{j}}=|+\rangle _{j}\langle +|-|-\rangle _{j}\langle -|)\), \(\tilde {S}_{+_{j}}=|+\rangle _{j}\langle -|\) and \(\tilde {S}_{-_{j}}=|-\rangle _{j}\langle +|\). Suppose Ω i >>{δ i , η i , T}, we further change the Hamiltonian under the rotating-wave approximation,

$$\begin{array}{@{}rcl@{}} H_{eff}=&&\frac{1}{2\sqrt{2}}\left[\left( {\eta^{1}_{1}}S_{x_{1}}+{\eta^{1}_{2}}S_{x_{2}}\right)\left( P_{1}e^{-i(\delta_{1}+T)t}+P^{\dag}_{1}e^{i(\delta_{1}+T)t}\right)\right. \\&&\left.+~\left( {\eta^{2}_{1}}S_{x_{1}}+{\eta^{2}_{2}}S_{x_{2}}\right)\left( P_{2}e^{-i(\delta_{2}-T)t}+P^{\dag}_{2}e^{i(\delta_{2}-T)t}\right)\right], \end{array} $$
(10)

where \({\eta ^{1}_{1}}={\eta ^{2}_{1}}=\eta _{1}\), \({\eta ^{1}_{2}}=-{\eta ^{2}_{2}}=\eta _{2}\). The discarded terms consisting of S z terms and S y terms could reduce the fidelity of the generated state. However, one can use the spin-echo technique to eliminate the infidelity from S z terms, and can accurately control the duration of classical microwave field to fulfill \({\Omega }_{j}\tau = 4n^{\prime }\pi \) (\(n^{\prime }\) is an arbitrary integer) so that the effect of the S y terms vanishes.

The time evolution operator related to the above Hamiltonian can be formally written as [28–30]

$$\begin{array}{@{}rcl@{}} U_{I}(t)=U_{P_{1}}(t)U_{P_{2}}(t), \end{array} $$
(11)

where

$$\begin{array}{@{}rcl@{}} U_{P_{i}}(t)&=&\prod\limits_{j\neq j^{\prime}}\exp\left[-iA^{i}_{jj^{\prime}}(t)S_{x_{j}}S_{x_{j^{\prime}}}\right] \\&&\times\prod\limits_{j}\exp\left\{-i\left[{C^{i}_{j}}(t)P_{i}S_{x_{j}}+C^{i\ast}_{j}(t)P_{i}^{\dag}S_{x_{j}}\right]\right\}, \end{array} $$
(12)

with the parameters determined by

$$\begin{array}{@{}rcl@{}} A^{i}_{jj^{\prime}}(t)=\frac{{\eta^{i}_{j}}\eta^{i}_{j^{\prime}}}{8\triangle^{\prime}_{i}}\left\{t-\frac{1}{i\triangle^{\prime}_{i}}\left[\exp(i\triangle^{\prime}_{i}t)-1\right]\right\}, \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} {C^{i}_{j}}(t)=\frac{i{\eta^{i}_{j}}}{2\sqrt{2}\triangle^{\prime}_{i}}\left[\exp(-i\triangle^{\prime}_{i}t)-1\right], \end{array} $$
(14)

and \(A^{i}_{jj^{\prime }}(0)={C^{i}_{j}}(0)=0\) with \(\triangle ^{\prime }_{1}=\delta _{1}+T\), \(\triangle ^{\prime }_{2}=\delta _{2}-T\).

It is obvious that \({C^{i}_{j}}(t)\) is a periodic function and vanishes at \(\tau =2l_{i}\pi /\triangle ^{\prime }_{i}\) for integer l i . At these instants of time, the NV centers are decoupled from cavities. Setting δ 1 = δ 2 = δ>η i , T and δ = ξT (ξ is an arbitrary odd integer), at the time τ = 2nπ/T, the time evolution operator reduces to a simple form

$$\begin{array}{@{}rcl@{}} U_{I}(\tau)=\exp\left\{i\tau\left[\frac{\eta_{1}\eta_{2}T}{4(\delta+T)(\delta-T)}S_{x_{1}}S_{x_{2}} \right]\right\}. \end{array} $$
(15)

We note that there is a theoretical work on realization of controlled phase gate based on the operator U I (τ) with transmon qubits coupled to a superconducting transmission line resonator [31]. For example, choosing \(\tau [\frac {\eta _{1}\eta _{2}T}{4(\delta +T)(\delta -T)}]=\frac {\pi }{2}\) and the initial state of the two NV centers being |ψ〉 i = |00〉 NV , the final state is

$$\begin{array}{@{}rcl@{}} |\psi\rangle_{f}=\frac{1}{\sqrt{2}}(|00\rangle+i|11\rangle). \end{array} $$
(16)

If we chose n = 1, δ = 3T, η 1 = η 2 = η =\(2\sqrt {2}T\), the final state can be generated at τ = 2π/T. In our scheme, for η = 2π×100MHz, the assumption Ω≫{δ, η, T} with Ωτ = 3×4π and δ≪Δ are well-satisfied, then the entangled state generation time τ≃30ns.

Technological progress in recent years has made it possible to integrate NV centers or quantum dots into PCCs [32–34]. In real situations, there are various decoherence processes such as spontaneous emission of excited states of NV centers, dephase of the electron spins and photon leakage out of cavity. We now estimate effects of these decoherence processes to the implementation of phase gates. For δ≪Δ, η≃2gΩ L /Δ = 2π×100 MHz, with Ω L = 2π×1 GHz, Δ = 2π×20 GHz, and g = 2π×1 GHz [32]. The effective qubit spontaneous decay rate from the state |1〉 to |0〉 could be estimated as \({\Gamma }_{0}{\Omega }_{L}g/{\Delta }^{2}\simeq 2\pi \times 0.0325\) MHz [35] with the spontaneous decay rate for the excited state Γ0 = 2π×13MHz [5]. In current experiments, the relaxation time of the NV spin triplet ranging from milliseconds [3] at room temperature to several seconds [36] at low temperature has been reported. In addition, the dephasing time more than 600 μs has been demonstrated [37], and can be raised to about 2 ms with an isotopically pure diamond sample [6]. These imply that the influences from the spontaneous emission of excited states and intrinsic damping and dephasing of the NV centers are possibly negligible in the present system.

Taking account of the cavity decay, we can use a master equation which include relaxation due to the interaction between each cavity and a reservoir to characterize the time evolution

$$\begin{array}{@{}rcl@{}} \dot{\rho}(t)=-i[H_{eff},\rho(t)]+L_{c}\rho(t), \end{array} $$
(17)

where L c represents the decoherence of the cavity

$$\begin{array}{@{}rcl@{}} L_{c}\rho&=&\frac{\kappa_{a_{1}}}{2}\left( 2a_{1}\rho a^{\dagger}_{1}-a^{\dagger}_{1}a_{1}\rho-\rho a^{\dagger}_{1}a_{1}\right)\\&&+\frac{\kappa_{a_{2}}}{2}\left( 2a_{2}\rho a^{\dagger}_{2}-a^{\dagger}_{2}a_{2}\rho-\rho a^{\dagger}_{2}a_{2}\right). \end{array} $$
(18)

Here, \(\kappa _{a_{i}}\) is the decay rate of the jth cavity. As a conservative estimation, considering \(\kappa _{a_{1}}=\kappa _{a_{2}}=\kappa \), the master (17) reduces to

$$\begin{array}{@{}rcl@{}} \dot{\rho}(t)&=&-i[H_{eff},\rho(t)]+\frac{\kappa}{2}\left( 2P_{1}\rho P^{\dagger}_{1}-P^{\dagger}_{1}P_{1}\rho-\rho P^{\dagger}_{1}P_{1}\right)\\&&+\frac{\kappa}{2}\left( 2P_{2}\rho P^{\dagger}_{2}-P^{\dagger}_{2}P_{2}\rho-\rho P^{\dagger}_{2}P_{2}\right). \end{array} $$
(19)

In order to elegantly solve the above equation, we will introduce an unitary transformation \(U=\exp (-iH_{eff}t)\) so that

$$\begin{array}{@{}rcl@{}} \dot{\rho}(t)=U\tilde{\rho}(t)U^{-1}, \end{array} $$
(20)

then the state \(\tilde {\rho }(t)\) evolves according to the equation

$$\begin{array}{@{}rcl@{}} \dot{\tilde{\rho}}(t)&=&\frac{\kappa}{2}\left( 2\tilde{P}_{1}\tilde{\rho} \tilde{P}^{\dagger}_{1}-\tilde{P}^{\dagger}_{1}\tilde{P}_{1}\tilde{\rho}-\tilde{\rho} \tilde{P}^{\dagger}_{1}\tilde{P}_{1}\right)\\&&+\frac{\kappa}{2}\left( 2\tilde{P}_{2}\tilde{\rho} \tilde{P}^{\dagger}_{2}-\tilde{P}^{\dagger}_{2}\tilde{P}_{2}\tilde{\rho}-\tilde{\rho} \tilde{P}^{\dagger}_{2}\tilde{P}_{2}\right), \end{array} $$
(21)

where

$$\begin{array}{@{}rcl@{}} \tilde{P}_{1}=P_{1}-\frac{e^{i{\Delta}^{\prime}_{1}t}-1}{2\sqrt{2}{\Delta}^{\prime}_{1}}(\eta_{1}S_{x1}+\eta_{2}S_{x2}), \end{array} $$
(22)
$$\begin{array}{@{}rcl@{}} \tilde{P}_{2}=P_{2}-\frac{e^{i{\Delta}^{\prime}_{2}t}-1}{2\sqrt{2}{\Delta}^{\prime}_{2}}(\eta_{1}S_{x1}-\eta_{2}S_{x2}). \end{array} $$
(23)

The density matrix can conveniently expressed in the basis \(\{i\}^{4}_{i=1}=\{|++\rangle , |+-\rangle , |-+\rangle , |--\rangle \}\), and by tracing over the cavity fields states we find the time derivative of the NV centers state operators \(\tilde {\rho }_{ij}=\langle i|\tilde {\rho }|j \rangle \) in the interaction picture for η 1 = η 2 = η

$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{11}^{\cdot}=\tilde{\rho}_{22}^{\cdot}=\tilde{\rho}_{33}^{\cdot}=\tilde{\rho}_{44}^{\cdot}=0, \end{array} $$
(24)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{12}^{\cdot}=\tilde{\rho}_{12}&&\left[-\frac{\kappa \eta^{2}\left( e^{i{\Delta}^{\prime}_{1}t}-1\right)\left( e^{-i{\Delta}^{\prime}_{1}t}-1\right)}{4{\Delta}^{{\prime}2}_{1}}\right.\\&&\left.-\frac{\kappa \eta^{2}\left( e^{i{\Delta}^{\prime}_{2}t}-1\right)\left( e^{-i{\Delta}^{\prime}_{2}t}-1\right)}{4{\Delta}^{{\prime}2}_{2}}\right], \end{array} $$
(25)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{13}^{\cdot}=\tilde{\rho}_{13}&&\left[-\frac{\kappa \eta^{2}\left( e^{i{\Delta}^{\prime}_{1}t}-1\right)\left( e^{-i{\Delta}^{\prime}_{1}t}-1\right)}{4{\Delta}^{{\prime}2}_{1}}\right.\\ &&\left.-\frac{\kappa \eta^{2}\left( e^{i{\Delta}^{\prime}_{2}t}-1\right)\left( e^{-i{\Delta}^{\prime}_{2}t}-1\right)}{4{\Delta}^{{\prime}2}_{2}}\right], \end{array} $$
(26)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{14}^{\cdot}=-\tilde{\rho}_{14}\frac{\kappa \eta^{2}\left( e^{i{\Delta}^{\prime}_{1}t}-1\right)\left( e^{-i{\Delta}^{\prime}_{1}t}-1\right)}{{\Delta}^{{\prime}2}_{1}}, \end{array} $$
(27)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{23}^{\cdot}=-\tilde{\rho}_{23}\frac{\kappa \eta^{2}\left( e^{i{\Delta}^{\prime}_{2}t}-1\right)\left( e^{-i{\Delta}^{\prime}_{2}t}-1\right)}{{\Delta}^{{\prime}2}_{2}}, \end{array} $$
(28)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{24}^{\cdot}=\tilde{\rho}_{24}&&\left[-\frac{\kappa \eta^{2}\left( e^{i{\Delta}^{\prime}_{1}t}-1\right)\left( e^{-i{\Delta}^{\prime}_{1}t}-1\right)}{4{\Delta}^{{\prime}2}_{1}}\right.\\ &&\left.-\frac{\kappa \eta^{2}\left( e^{i{\Delta}^{\prime}_{2}t}-1\right)\left( e^{-i{\Delta}^{\prime}_{2}t}-1\right)}{4{\Delta}^{{\prime}2}_{2}}\right], \end{array} $$
(29)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{34}^{\cdot}=\tilde{\rho}_{34}&&\left[-\frac{\kappa \eta^{2}\left(e^{i{\Delta}^{\prime}_{1}t}-1\right)\left(e^{-i{\Delta}^{\prime}_{1}t}-1\right)}{4{\Delta}^{{\prime}2}_{1}}\right.\\ &&\left.-\frac{\kappa \eta^{2}\left(e^{i{\Delta}^{\prime}_{2}t}-1\right)\left(e^{-i{\Delta}^{\prime}_{2}t}-1\right)}{4{\Delta}^{{\prime}2}_{2}}\right]. \end{array} $$
(30)

These equations are readily integrated, and at times τ = 2nπ/T we get

$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{11}(\tau)=\tilde{\rho}_{11}(0), \end{array} $$
(31)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{22}(\tau)=\tilde{\rho}_{22}(0), \end{array} $$
(32)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{33}(\tau)=\tilde{\rho}_{33}(0), \end{array} $$
(33)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{44}(\tau)=\tilde{\rho}_{44}(0), \end{array} $$
(34)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{12}(\tau)=\tilde{\rho}_{12}(0)\exp\left\{-\frac{\kappa \eta^{2}\tau}{2{\Delta}^{{\prime}2}_{1}}-\frac{\kappa \eta^{2}\tau}{2{\Delta}^{{\prime}2}_{2}}\right\}, \end{array} $$
(35)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{13}(\tau)=\tilde{\rho}_{13}(0)\exp\left\{-\frac{\kappa \eta^{2}\tau}{2{\Delta}^{{\prime}2}_{1}}-\frac{\kappa \eta^{2}\tau}{2{\Delta}^{{\prime}2}_{2}}\right\}, \end{array} $$
(36)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{14}(\tau)=\tilde{\rho}_{14}(0)\exp\left\{-\frac{2\kappa \eta^{2}\tau}{{\Delta}^{{\prime}2}_{1}}\right\}, \end{array} $$
(37)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{23}(\tau)=\tilde{\rho}_{23}(0)\exp\left\{-\frac{2\kappa \eta^{2}\tau}{{\Delta}^{{\prime}2}_{2}}\right\}, \end{array} $$
(38)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{24}(\tau)=\tilde{\rho}_{24}(0)\exp\left\{-\frac{\kappa \eta^{2}\tau}{2{\Delta}^{{\prime}2}_{1}}-\frac{\kappa \eta^{2}\tau}{2{\Delta}^{{\prime}2}_{2}}\right\}, \end{array} $$
(39)
$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{34}(\tau)=\tilde{\rho}_{34}(0)\exp\left\{-\frac{\kappa \eta^{2}\tau}{2{\Delta}^{{\prime}2}_{1}}-\frac{\kappa \eta^{2}\tau}{2{\Delta}^{{\prime}2}_{2}}\right\}. \end{array} $$
(40)

We characterize the entanglement generation process by the conditional fidelity of the quantum state defined by F = 〈ψ f |ρ NV (τ)|ψ f 〉, with ρ NV being the reduced density matrix of the NV centers. The fidelity can be readily evaluated

$$\begin{array}{@{}rcl@{}} F=\frac{1}{2}+\frac{1}{4}\exp\left\{-\frac{2\kappa \eta^{2}\tau}{{\Delta}^{{\prime}2}_{1}}\right\}+\frac{1}{4}\exp\left\{-\frac{2\kappa \eta^{2}\tau}{{\Delta}^{{\prime}2}_{2}}\right\}. \end{array} $$
(41)
Fig. 2
figure 2

The fidelity of entangling the two NV center qubits as a function of κ/T. The parameters are n = 1, δ = 3T, \(\eta =2\sqrt {2}T\)

Full size image

In Fig. 2, we plot the fidelity F as a function of dimensionless parameter κ/T, where we have obtained high fidelity F≃0.93 at κ = 0.01T. Given the cavity quality factor Q = 109 [32], the decay rate of the PC cavity κ = 2π×0.5MHz ≃0.01T.

3 Conclusion

In conclusion, we proposed a potential scheme capable of efficient and fast entangling two distant NV centers using composite PCC-NV architecture. Through adiabatically eliminating the virtually excited states of the NV centers and control of the NV centers under a classical strong driving condition, the entanglement between the two NV center can be generated in the dispersive regime. Our proposal has potentially practical applications for long-distance distributed and scalable QIP based on composite PCC-NV systems with currently available techniques.