Prevention scientists have increasingly turned to integrative data analysis (IDA: Curran & Hussong, 2009) to assess whether findings from multiple studies show consistent preventive intervention effects or consistent etiologic impact of risk or protective processes across a set of studies. A recent special issue of Prevention Science presented 21 papers on this topic (Morgan-López et al., 2023). IDA (also referred to as IPD or individual participant data meta-analysis) combines individual participant-level data from multiple studies of the same topic, allowing us to evaluate an overall summary statistic, such as effect size across randomized trials, to test for and model heterogeneity due to study, population, or contextual characteristics, and to examine mediation. IDA has many advantages over standard meta-analysis. Tests of heterogeneity have much greater statistical power (Dagne et al., 2016; Hussong et al., 2013), and IDA allows for tests of measurement assumptions, including conditional independence and measurement invariance, that are difficult or impossible with meta-analysis (Howe et al., 2019).

Both IDA and meta-analysis assume construct equivalence across studies, defined as the cross-study and cross-measure equivalence of measurement methods used to assess the same construct (Howe et al., 2019). Both often require harmonization of different measures. When measuring a construct such as depression, the goal of harmonization is to create a valid score, or index of a construct state, that has the same meaning for each participant across all studies regardless of which measures they complete. Such scores need to be on the same quantitative scale.

When all studies in an IDA dataset use the same measure or set of measures, we can use item-level data and employ well-established methods such as Item Response Theory (IRT) modeling to create equivalent scores, evaluate whether construct equivalence is compromised due to violations of conditional independence (left-over covariation among indicators in the same measure) or causal invariance (variation in item loadings across samples or studies), and adjust for those violations if necessary (Curran et al., 2008). When different studies use different measures of the same construct; however, information about empirical associations among items can become sparse and indirect, raising questions about the accuracy of estimates from measurement models.

For example, when Brown et al. (2018) combined individual participant data on youth depression from 19 randomized prevention trials, their dataset included item-level data from eight different measures of youth depression from three different types of reporters. One study included three measures, ten included two measures, and six used only one measure. The example in Fig. 1 illustrates several possible patterns of sparseness in the outcome measure of a synthesis dataset combining data from 18 prevention trials. Sparseness is often used to refer to datasets involving categorical items where some categories have very low response frequencies (Bainter, 2017), and sometimes to study-level missing data. Here we use the term sparseness to refer to cases where at least some studies do not use all measures of a construct found in the full set of studies. We use the term measure to refer to sets of indicators, often questionnaire items, that have been validated as a set and are administered together. We use general notation to reference measures (A, B, C, D) here, as this representation can be applied to any construct in a prevention science IDA that is measured in more than one way across combined studies, including outcomes, mediators, moderators, risk factors, or protective factors. In the empirical example we provide later, these include four self-report measures of youth depression.

Fig. 1
figure 1

Example of matrix representation of different patterns of sparseness across 18 trials using four measures of the same construct. Note: Colors distinguish sets of trials that include different combinations of more than one measure. Definitions of direct linkage, indirect linkage, and clique are presented later in the section on graphical representation

Full size image

In this example, patterns 1a and 1f reflect two extremes. In pattern 1a, all trials included all 4 measures of the construct. In 1f, 12 trials employed only measures A and/or B, while 6 trials employed measures C and/or D. Pattern 1a has empirical information concerning the association of each measure and its items with every other measure and items, while pattern 1f has no empirical information concerning the association of items from measure A or B with those from measure C or D. The intermediate patterns have empirical information about the association among every pair of measures, although this information grows increasingly indirect as we move from 1b to 1d. For example, pattern 1b has direct information about the association of items from every pair of measures, and we could calculate correlations among every pair of items both within and across all measures, although those correlations would be based on data from different subsets of studies. Pattern 1e has direct information only for three pairs of measures (A with B, B with D, C with D), and only indirect empirical information about associations among other pairs (A with D indirectly through the association of A with B and B with D).

Judging from the papers presented in the IDA special issue, sparseness appears very common in IDA datasets combining data from multiple studies. Two strategies have been used to harmonize scores across measures in the face of sparseness: Howe and Brown (2023) refer to these as empirical and semantic methods. Empirical methods use statistical modeling based on the entire dataset, and appear tractable as long as all measures have at least indirect information about associations among items. Semantic methods use expert judges to evaluate whether pairs of items have equivalent meaning, even if they use different words and scale anchors, and can be employed when no empirical evidence of cross-measure association is available.

The current study focuses on empirical harmonization. It examines whether and how the sparseness of cross-measure and cross-study associations among items can affect the accuracy of measurement models used to harmonize those measures and achieve construct equivalence across measures and across studies. We first present a framework for describing different patterns of sparseness based on graph theory (Valente, 2008; Wilson, 1996). In the context of IDA, graph theory is useful for characterizing patterns of direct and indirect associations among different measures intended to assess the same construct. We then identify several potential patterns of sparseness, ranging from complete datasets where all studies include all measures to datasets where subsets of measures are found only in some studies but never found in others. Considering sparseness as a missing data problem, we use Monte Carlo methods to simulate datasets based on several different sparseness patterns and evaluate whether and how parameter estimates in three common measurement models become biased as sparseness increases. We then apply lessons from these simulations to an existing dataset having four measures of depression reported by 4146 youth participating in 16 randomized trials of prevention programs (Brown et al., 2018).

Measurement Models

Modern quantitative measurement methods provide a well-established technology for specifying and estimating measurement models using a set of items designed to capture information about the same construct. These include confirmatory factor analysis (CFA) for items with continuous scales and its extension to items with categorical or ordinal scales, often referred to as IRT models. Here we focus on the most common measurement models using reflective indicators, assuming that construct states are latent and unobservable but can be inferred through their causal impact on observable indicators (Bollen & Lennox, 1991).

We can apply common measurement models directly to the analysis of IDA datasets that combine data from multiple studies, referred to as synthesis datasets by Brincks et al. (2018). When all studies use the same measure, we can test measurement assumptions such as conditional independence or measure invariance for the full dataset. With multilevel models, we can also test whether measurement is consistent across different studies (Curran et al., 2014).

The same approaches can be applied to synthesis datasets where all studies use all measures, or where different studies use more than one measure of the same construct (as illustrated in Fig. 1a). These approaches also provide a means of equating latent factor metrics when measures have different scales. For example, when considering measures of youth depression, the Youth Self Report (YSR) scale includes the item “I felt lonely,” with a 3-point rating scale having anchors of “not true (as far as you know),” “somewhat or sometimes true,” “very true or often true,” rated “within the past 6 months.” The Center for Epidemiologic Survey-Depression (CESD) scale includes an item “I felt lonely” with a 4-point rating scale having anchors of “rarely or none of the time,” “some or a little of the time,” “occasionally or a moderate amount of time,” or “most or all of the time,” rated over the past week. Including both items as indicators of a latent variable provides estimates of item loadings and thresholds (item discrimination and item difficulty parameters, in IRT terminology) that allow those items to contribute information to a latent variable with a common metric.

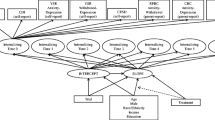
Figure 2 presents three common measurement models that can be used with multiple measures of the same construct. All items from all measures can be considered separate indicators of the same construct in a Single Common Factor Model (Fig. 2a). However, item sets in different measures may be shaped somewhat by unknown nuisance factors such as those due to different modes of administration, leading to measure-level violations of the conditional independence assumption. Hierarchical Models, illustrated in Fig. 2b, can be used to reduce these violations by modeling separate latent variables for each measure. Items from all measures are used as indicators of a higher-order latent variable reflecting the construct they all have in common. Systematic measurement error unique to each measure is modeled in the residual of each measure’s latent variable. Bifactor Models, illustrated in Fig. 2c, present a third more general alternative. These models include a single common latent variable with loadings on all items, and separate latent variables for each measure, all forced to be independent. These models partition item-level residual variation into that unique to each item and that held in common across items within the same measure.

Fig. 2
figure 2

a–c Measurement models

Full size image

Bifactor models reflect the most general case, and include the most loading parameters, as they allow each indicator to load separately and with different strengths on the common factor, as well as on a measure-specific factor. Because of this extra complexity they are often harder to fit, and may require larger sample sizes. Hierarchical models also separate overall common variance from measure-specific variance. However, they include fewer loading parameters as cross-measure associations are modeled through single parameters for loadings of the measure-specific latent variable on the common latent variable, rather than through the association of each item with the common latent variable. This simplifying assumption may not be accurate, although hierarchical models may be the only option for evaluating and adjusting for measure-specific variance when bifactor models fail to converge. Single common factor models ignore measure-specific variation, assuming that all indicators will be independent of one another after accounting for variance due to the common latent variable.

Sparseness as a Missing Data Problem

Although the synthesis dataset illustrated in Fig. 1a includes all measures from all studies, it is common to have missing data within each study and within each measure. Modern quantitative methods allow for using all item information when data are missing at random given covariates (MAR: Enders, 2010). These methods include full information maximum likelihood (FIML), multiple imputation, and Bayesian estimation methods. We can think of these methods as “filling in” the absent data for a variable based on the associations of existing data on that variable with all other observed data, taking into account uncertainty due to missing data.

Turning to the sparser datasets illustrated in Fig. 1, we can consider the measures that are absent for a particular study as a type of missing data. Assuming MAR for missingness of such absent measures, their items, and individual values of these items, these quantitative methods allow us to “fill in” those scores based on the associations of those items with items from other measures in studies where both are used. Assuming MAR, these methods should produce asymptotically unbiased estimates of factor parameters based on only a subset of measures available for each participant, although estimates based on fewer items will have more unsystematic errors. We will see that things get more complicated as sparseness increases. Before addressing this issue, we take up the question of how to characterize patterns of sparseness.

Graphical Representation of Sparseness

We can represent a synthesis dataset that combines data from several studies employing different measures of the same construct in either matrix or graph form. In matrix form, we reference each study as a row and each column as a measure, placing a marker in each cell when a specific measure was used in a particular study. Figure 1 provides examples of matrices for several synthesis datasets from 18 trials with 4 different measures, ranging from a complete dataset (all trials include all measures and items) to a dataset with two isolated subsets (one set of studies uses only measures A and/or B, a second set only measures C and/or D).

Concepts from graph theory (Wilson, 1996) provide another means of summarizing patterns of sparseness in terms of information about empirical associations among measures or item scores. Graphs consist of nodes (also referred to as vertices) and the links between pairs of nodes, referred to as edges. Figure 3 presents graphs for the same synthesis datasets represented in matrix form in Fig. 1. Graphs range from being fully connected (3a: all nodes are linked to all other nodes) to having two isolated subsets (3f: nodes A and B are connected, as are nodes C and D, but there are no cross-subset connections).

Fig. 3
figure 3

a–e Graph representation of forms of sparseness

Full size image

A node in a measurement graph refers to a measure and its associated items for all studies using that measure. For example, the node for measure A in graph 3b subsumes all item data for that measure across trials 1 through 9 (as indicated in matrix 1b). We can pool data from the same measure across studies based on the assumption that the measure operates in the same way across all studies. This assumption is often based on consistency in measurement: measures usually employ a set of instructions common to all items, as well as the same rating scale and anchoring labels. It is also testable using measurement models such as moderated nonlinear factor analysis (Curran et al., 2014).

An edge or line between two nodes refers to cross-measure associations available because two measures are employed in the same study. IDA datasets usually have much less evidence available concerning the association of items across measures. Measurement error in those associations may also be greater because of differences in instruction sets, timeframe for ratings, number of scale points, or scale anchors. Although edges reflect the presence of information about cross-measure cross-item association, the amount of information can vary, depending on how many trials have both measures. For example, the edge connecting measures A and B in graph 3a reflects data from all 18 trials, but the same edge in graph 3b reflects data from only 3 trials. As an added visual guide, we can vary the width of the edge line to reflect differences in the amount of information available. The graphs for datasets in 3a and 3b have identical graph structures, but the latter is based on much sparser data for both the nodes and edges.

Nodes can have both direct and indirect linkages with other nodes. For example, in graph 3c the node A has direct links with nodes B and C, but no direct link with node D. Measure A never occurs in the same study as measure D, so we have no way of estimating how strongly their items are associated based on simple measures of pairwise association. However, measure A is indirectly associated with measure D through three indirect paths: ABD, ACD, and ABCD. Indirect linkages can carry information about the strength of pairwise associations, although the amount of information will depend on the strength of the direct associations making up those indirect links and the number of participants involved. Nodes in graphs 3a and 3b have all possible direct and indirect linkages, while those in graphs 3c, 3d, and 3e have decreasing numbers of direct links and increasing numbers of indirect links. Although information about direct or indirect associations is present in the matrix representation of an IDA dataset, it is more obvious in a graph representation.

A graph’s full set of nodes and edges provides a complete description of all direct and indirect associations among measures and their items. We use the term clique, taken from network models that employ graph theory (Valente, 2008), to describe a set of measures where each measure co-occurs with at least one other measure in the set. That is, all measures within a clique have either a direct or indirect association with all other measures in that clique. Graphs 3a through e all represent single cliques, given that all measures are connected through edges, either directly or indirectly.

Finally, some synthesis datasets involve subsets of nodes that are internally linked but not linked with other subsets, as illustrated in graph 3f. Network models that use graph theory refer to these as separate isolated cliques. Graph 3f illustrates an IDA dataset with two isolated cliques. One clique represents a set of trials that use only measures A and B, while the second clique represents trials that use only measures C and D. There are no direct or indirect links between these cliques, and so there is no information available for empirical estimation of loadings or thresholds, and no way to harmonize within a common metric across these two cliques using empirical evidence, without added assumptions. These situations require other information for harmonizing, such as semantic content, and can require strong assumptions about what constitutes semantic equivalence (Howe & Brown, 2023). Graph 3f reflects an IDA dataset where we may be able to combine empirical harmonization within cliques with semantic harmonization across cliques, an approach we return to later in the Discussion.

The Effects of Sparseness on Measurement Modeling

When a synthesis dataset is complete or all edges are present (Fig. 3a and 3b), we can use standard estimation methods for the three measurement models in Fig. 2, including robust weighted least squares (WLSMV: DiStefano & Morgan, 2014; Flora & Curran, 2004) when item scales are treated as ordinal. However, these estimation methods require information on all associations among all possible pairs of items, and so will no longer be applicable when two measures never co-occur in any study (Fig. 3c through 3e). In those cases, we must use numerical integration algorithms or Markov Chain Monte Carlo algorithms (MCMC) with Bayesian estimators. Although these methods are becoming available for multilevel IRT applications (Huo et al., 2014; Jeon et al., 2014; Mun et al., 2019; Zhang et al., 2023), there are still many uncertainties about their performance with datasets having various forms and levels of sparseness. In one of the few relevant studies, Huo et al. (2014) used a two-stage modeling approach with Bayesian estimation to combine multidimensional alcohol use data from 20 studies with substantial sparseness at both the item and study levels.

We know of no work that systematically evaluates the effects of different patterns of sparseness on analyses that combine multiple measures of the same construct across multiple studies. A central question informs the current study: as we move from a complete graph to graphs with fewer direct and more indirect linkages, what effect will that have on our estimates of a latent general factor as an index of our construct? It will clearly increase unsystematic measurement error, given that the estimates will, by definition, be based on less and less data, but will it also lead to biased estimates? We explore this through simulation. To provide a context, we developed simulations based on prior research on the measurement of youth depression and conducted analyses of an IDA dataset of youth depression measures based on these simulation results.

Monte Carlo Simulation Study

We focused our simulation study on the first five graphs in Fig. 3 (and their matrix representations in Fig. 1), as these provide a logical progression from a complete IDA dataset where all studies include all measures (3a) to IDA datasets with systematic decreases in empirical evidence for direct associations among measures and their items. Pattern 3b has all possible direct associations, but each association is based on only a subset of studies. Patterns 3c, 3d, and 3e have increasingly indirect associations: 3c replicates most of 3b, but has no trials with direct associations between measures A and D (one indirect link). In turn, pattern 3d replicates most of 3c, but has no trials with direct associations between B and C (2 indirect links). Pattern 3e replicates most of 3d, but has no trials with direct associations between A and C. This leads to 3 indirect links: two of these are two-step links (ABD and BDC), but one is now a three-step link (ABCD).

Method

Population Models

We used the Monte Carlo facility in MPLUS Version 8.7 (Muthén & Muthén, 1998–2017) to specify two population models and simulate datasets based on those models. We chose bifactor models as the most general and comprehensive measurement models that included both common factor variance and variance unique to each measure. Both models specified a two-level bifactor structure with 20 ordinal items (as illustrated in Fig. 2c). We used ordinal items given their ubiquity in questionnaire measurement. All items are loaded on a single common factor. Each item also is loaded on one of four secondary factors, resulting in five items assigned to each of four measures. In line with existing measures of youth depression, two measures had items with three ordinal categories, one had items with four ordinal categories, and one had items with five ordinal categories. All five factors (the single common factors and four secondary factors) were forced to be uncorrelated, consistent with the bifactor model, and all factor variances were set to one. Both models were specified as two-level models, with 300 participants clustered within each of the 18 trials. We chose this sample size based on our experience with IDA datasets for prevention trials targeting youth depression. We specified two-level models because study-level conditions may have an impact on measurement models, requiring that standard errors take into account study-level clustering when analyzing IDA data.

One of the population models, termed the strong common factor model, set all loading parameters for the common factor to 1.5 and those on the secondary factors to 0.5. This yielded a model where the common factor accounted for 90% of the explained common variance (Reise et al., 2013), and the secondary factors accounted for only 10%. These values are consistent with those reported in analyses of youth depression measures in IDA datasets (Howe et al., 2019). The second population model, the weak common factor model, reversed these values. The common factor accounted for only 10% of the explained common variance. Item thresholds in both models were set to values from analyses reported in Howe et al. (2019) for four comparable youth depression measures, selecting values from the five items with the strongest loadings. Consistent with studies of youth depression, this led to skewed response frequencies, with the lowest scale point having the largest rates and the highest scale point having relatively few responses.

Simulated Datasets

We simulated 100 datasets for each of the two population models using MPLUS default priors. MPLUS uses Markov Chain Monte Carlo (MCMC) algorithms that repeatedly sample parameter values based on assumptions about the distributions of those values (priors). Each dataset had 300 cases clustered within each of 18 trials, for a total of 5400 cases. Within-cluster distribution priors for factor loadings were set to normal with a mean of zero and standard deviation of 5, as were between-cluster priors for item thresholds, as this weakly informative prior has been shown to help stabilize estimation with little impact on estimates (Muthén et al., 2016, p. 385). Priors for between-level item variances were set to inverse gamma, a noninformative uniform prior. This resulted in 200 simulated datasets, 100 for each of the two population models.

We followed a strategy similar to that employed by Huo et al. (2014) to create sparse datasets. Using the data patterns in Fig. 1, we created datasets with various levels of sparseness based on these simulated datasets for each of five levels of sparseness, reflecting graphs 3a through 3e in Fig. 3. Pattern 3a represented a complete IDA dataset, with every study including every measure and scores for every item. We defined this as the benchmark against which to compare the impact of increasing sparseness, and used the 200 simulated datasets without revision. To create datasets for the one clique/all direct condition (graph 3b, matrix 1b), we took each of the 200 complete datasets and set item values to missing for all measures in trials that had no X in their cells in the respective matrix in Fig. 1. This resulted in datasets with items that had identical values to those in the complete datasets when measures were considered present but had no values for those items when measures were considered absent. We repeated this for each of the three sparseness conditions with increasingly indirect associations. As a result, items in the 200 datasets for each sparseness condition had identical values when measures were present, but values set to missing when measures were absent. This resulted in 1000 datasets (100 datasets for each of 2 population models for each of 5 sparseness conditions). Conditions based on graphs 3b through 3e had missing data for 50%, 54%, 58%, and 62% of scores in the complete dataset.

Analyses

We specified and estimated three models for each of the 1000 simulated datasets, using a graded response model for ordinal dependent variables (Samejima, 1969). The graded response model is one of the most commonly used confirmatory factor models for measures with ordinal items. It uses a logistic framework, assuming that item scale values are categorically different from one another rather than differing on a continuum, but also takes into account their ordering. The factor loading is assumed to be the same across all adjacent pairs of ordered categories, resulting in a single-factor loading estimate on the logit scale for each item, and estimates for k-1 thresholds (where k is the number of scale categories). We used the generalized linear model in MPLUS to estimate factor models based on items with different numbers of ordered categories.

Confirmatory factor analysis with ordinal items often employs weighted least squares estimation, but that is not possible for datasets with indirect associations, as it requires that correlations be calculated for every pair of items. We therefore used Bayesian estimation, which is not constrained by this limitation. We used noninformative or weakly informative priors (normally distributed, with mean of 0 and variance of 5), as we had no pre-existing knowledge about these parameters. We allowed each run to continue until either the potential scale reduction (PSR) factor for all parameters fell below 1.1 (Gelman & Rubin, 1992), or the program completed 1 million iterations. The PSR compares the results of the estimation to that from another randomly initiated chain, and indicates when the chains have converged to a true distribution (see Kadane, 2015 for an excellent introduction to Bayesian methods for prevention science).

We estimated parameters for each dataset three times, using a common factor model (Fig. 2a), a hierarchical model (Fig. 2b), and a bifactor model (Fig. 2c), to assess whether parameter bias might vary depending on type of measurement model. We initially specified each as a two-level model, given that scores based on the population model were clustered within trial. All models converged in the first four sparseness conditions across all datasets, but under the fifth condition (3 indirect linkages) all models failed to converge for most datasets within 1 million iterations. In those cases, we re-specified the analytic models as one-level models, ignoring clustering within trial. The one-level common factor and hierarchical models converged for all 100 datasets; the one-level bifactor model converged for 99 datasets based on a strong common factor and 93 datasets based on the weak common factor. Tables A1–A3 in the online supplementary materials provide annotated MPLUS code for these models.

Parameter Bias

Parameter bias of an estimator is often defined as the simple difference between a population parameter and the central tendency of that parameter estimated over a large number of samples. In this study, we were interested in the difference between average model parameters as estimated from complete datasets and those same parameters as estimated from the same datasets with missing data because not all studies used every measure. The parameters of interest were factor loadings for each item. For ordinal items these factor loadings are log odds.

Simple differences among parameter estimates are not meaningful without some clear metric. We decided to use relative effect size. A common effect size estimate for associations of a continuous X with a categorical Y is the difference in odds of Y at the mean of X compared to odds at 1 standard deviation above that mean. Given that our models set the variance of the latent variable to 1 (and the mean to zero), the factor loading can be interpreted as a log odds ratio comparing these two odds. The comparative bias estimate reflects the percent difference in this effect size, comparing the effect size from the complete dataset to the effect size estimated for each different pattern of sparseness, allowing us to compare how much these effect sizes varied as sparseness increased.

Bias can also be compared to the variation in simulated parameter values. MPLUS provides an estimate of the standard deviation of those values. This standard deviation converges to the population standard error as the number of simulations increases. We used the standard deviation for each loading based on the complete dataset as a benchmark, dividing the raw bias by this value. Given that the simulation drew parameter values from a normal distribution, we can consider raw bias that is outside the range of plus or minus 1.96 as outside the confidence interval for the parameter estimated from complete data. Collins et al. (2001) suggested a more conservative threshold of 0.40, based on experience that bias over this threshold had a negative impact on coverage. We used both thresholds here.

We used the MPLUS Monte Carlo procedure to combine findings across simulated datasets within each of the 30 conditions: these included 3 measurement models (bifactor, hierarchical, single factor) analyzing data based on 2 levels of common factor strength (strong, weak), repeated for datasets having each of the 5 levels of sparseness illustrated in Fig. 3. MPLUS computed average values for each parameter. We then calculated potential parameter bias due to sparseness for each of the four sparseness conditions involving missing data. We subtracted average parameter values based on each sparse dataset from those estimated for the complete datasets and divided that difference by the value from the complete dataset. Loading parameters in the bifactor and single-factor models reflected direct loadings of the common factor with each indicator. However, this was not true of the hierarchical model, where the association is indirect, and involves both the loadings of indicators on each measure factor and the loadings of the measure factor on the higher-order factor. For those models, we also estimated the strength of the indirect path from higher-order factor to each indicator using the product of these loadings, assuming a latent response variable formulation of an unobserved continuous dependent variable (Muthén et al., 2016, pp. 224–225), and estimated bias for these indirect effects.

Results

Posterior predictive checks (comparisons of what the fitted model predicts with the actual data) supported model fit for the bifactor and hierarchical models (PPP values of around 0.5 reflect good model fit, with smaller values reflecting worse fit.) The average posterior predictive p-values (PPP) for these models ranged from 0.494 to 0.515. In contrast, average PPP values for the single-factor model were poor (ranging from 0.000 to 0.141), consistent with the interpretation that this model did not specify measurement error correctly, given that the population models were bifactor models.

Bias Estimates

Table 1 presents estimates of absolute bias as a percentage of effect size in the complete dataset, averaged across all factor loadings for each factor in the three models for both weak and strong common factor datasets. Figures A1 and A2 in the online supplementary materials illustrate how these absolute value bias estimates vary across the sparseness conditions. Specific bias estimates for each factor loading are presented in Tables B1 through B8 in online supplementary materials.

Table 1 Average absolute bias as a percentage of effect size in the complete dataset for each model across sparseness conditions
Full size table

Population Model with Strong Common Factor

Absolute bias as a percentage of effect size remained low in the common factor loadings for the bifactor model and the higher-order factor in the hierarchical model as sparseness increased. Estimates for patterns with one or two indirect linkages were very close to those for the pattern having all direct linkages. The indirect effect estimates in the hierarchical model, which combine information from item loadings on measure factors with that from the loadings of measure factors on the higher-order common factor, very slightly outperformed the loading estimates for the main factor in the bifactor model. The indirect effect estimates also remained low in the loadings for individual measures in the hierarchical model. Two-level models failed to converge when there were three indirect paths, but were estimable when we moved to a simpler one-level model. In that case, the bias estimates remained low and were similar to those for the other sparseness conditions.

We also compared bias estimates to the standard deviation of estimates in the complete data condition (findings are summarized in Table C1 in the online supplementary materials). None of the bias estimates was outside the confidence interval range for the common factor loadings in the bifactor model or for either loadings on individual measures or on the higher-order factor in the hierarchical model. Using the more conservative threshold suggested by Collins et al. (2001), most of the hierarchical model loadings were under the threshold, but almost half of the loadings on the bifactor model was above threshold for the indirect sparseness conditions.

Loadings for the secondary factors in the bifactor model demonstrated increasing bias, and bias became stronger in the datasets with indirect links. Loadings were outside the confidence interval range only for the condition with three indirect links (25%), but almost all loadings were outside the more conservative threshold for the three sparseness conditions.

Absolute bias in the single-factor model was 3 to 5 times higher than that in the hierarchical model or the common factor in the bifactor model, across both direct and indirect sparseness conditions. Fifty to 75% of the single-factor loadings were outside the confidence interval range, and almost all were outside the more conservative threshold.

In summary, when the common factor was strong, increasing sparseness led to little bias in the hierarchical model or in the common factor from the bifactor model, with the hierarchical model performing slightly better. Bias in loadings of the secondary factors in the bifactor model increased with sparseness, but this does not necessarily compromise the bifactor model, as the secondary factors in this case would reflect nuisance variance. The single-factor model had the weakest performance. Two-level models were not tractable when data included 3 indirect linkages.

Population Model with Weak Common Factor

Absolute bias in the common factor was much more pronounced in all models when the common factor in the population model was weak, and the secondary factors were strong. The hierarchical model again performed slightly better than the common factor in the bifactor model in all but the condition with 1 indirect link, and was substantially better in the sparsest condition, although absolute bias for indirect effects was still high (9.5%). Here most of the bias occurred in the loadings of the measures on the higher-order factor, not in the loadings of items on measures, which was low. Bias for loadings in the hierarchical model were never outside of the confidence interval across all sparseness conditions and were above the conservative threshold less than 25% of the time. Raw bias in the common factor loadings of the bifactor model was also always inside the confidence interval for all conditions, but was above the more conservative threshold for 75 to 100% of the loadings. Bias in the secondary factors of the bifactor model was consistently low, and never outside of the confidence intervals, although it did exceed the more conservative threshold in 35 to 80% of the loadings, but with no clear increase across greater sparseness. Absolute bias in the single-factor loadings was very strong, reflecting effect size estimates that were between 2 and 3 times those from the complete dataset. Bias estimates were outside of the confidence interval in 75 to 85% of the loadings, and above the conservative threshold for almost all loadings.

Overall, when the common factor was weak absolute bias was much greater for all common factor loadings regardless of analytic model and was particularly pronounced when datasets included indirect links. The hierarchical model performed slightly better in most conditions, while the single-factor model performed very poorly.

Discussion

These simulations demonstrate that bias in estimating factor loadings is a function of the measurement model, the nature of sparseness, the actual strength of construct loadings, and the presence of common measurement error in specific measures. These findings are based on one set of sparseness patterns for IDA datasets similar to those found in studies of youth depression, so these patterns may not be representative of other IDA datasets.

Based on these findings, we suggest a systematic strategy for exploring possible bias in other IDA datasets: begin by constructing a linkage graph and its associated matrix for the dataset (and include these in any report of findings); if the graph reflects a single clique, specify and estimate a two-level bifactor model for these data as the most general measurement model that evaluates both common and measure-specific variance; if this model appears inestimable, explore a one-level bifactor model or a hierarchical model; once a final model is selected, use parameter estimates to build a population model and Monte Carlo simulation to produce a large number of complete datasets with similar measurement structure and cluster sample sizes; use those complete datasets to create new datasets with the same pattern of sparseness found in the original synthesis dataset; conduct Monte Carlo analyses to produce parameter estimates in the complete and sparse datasets; and use these parameter values to estimate potential bias for this specific pattern of sparseness. We demonstrate this strategy with a synthesis dataset from a recent IDA study.

Example: Youth Depression Study

Sample and Measures

We used a synthesis dataset from an IDA study that combined data on youth depression from 4146 youth who participated in 16 randomized field trials of programs designed to reduce problem behaviors and depression. Details of the samples, trials, and measures were presented in Brown et al. (2018) and Howe et al. (2019). We used item-level data collected at baseline from youth reports of depression symptoms on four measures. This included 27 items from the Child Depression Inventory (CDI: Kovacs, 1992), 20 items from the Center for Epidemiologic Surveys-Depression Scale (CESD: Radloff, 1977), 20 items from the Project Alliance depression scale (PAL: Dishion et al., 2002), and 20 items from the Youth Self Report scale (YSR: Achenbach, 1991). The sparseness pattern found in this dataset, illustrated in Fig. 4, is similar to the “three indirect linkage” pattern used in the simulation study. Direct links were based on data from single studies, and the link between the CDI and the PAL was based on only a subset of participants in one trial.

Fig. 4
figure 4

Sparseness graph for youth depression synthesis dataset. Node sizes reflect relative sample sizes

Full size image

Method

Initial modeling, as well as results of the simulation study for a sparseness graph with 3 indirect linkages, suggested that a one-level hierarchical model would be appropriate for this dataset. We first specified a hierarchical measurement model with items loading on four measure factors. Those factors in turn loaded on a higher-order depression factor. We analyzed these data using a Bayesian estimator with noninformative priors and a convergence criterion of PSR less than 1.1. The model converged without problem. Estimated factor loadings were strong and significant for all items, and for the loadings of the measure factors on the higher-order factor (see Table D1 in supplementary materials).

We then used estimated factor loadings and thresholds from this analysis to create a population model for further simulations. We simulated 100 datasets with complete data clustered within 16 trials with sample sizes identical to those in this synthesis dataset, and with the same number of items having the same number of scale points. We also created 100 datasets that had the same missing data structure as that in the synthesis dataset. We conducted Monte Carlo analyses of these two datasets using a one-level hierarchical model and estimated bias for all parameters (reported in Table D2 in supplementary materials).

Results

As reported in Table 2, average bias in item loadings varied substantially across the four measures. This was also the case for measure loadings on the higher-order factor. However, when we combined these loadings in estimates of indirect effects, a different picture emerged. Bias in these effects was much lower for the CDI, CES-D, and PAL, although still higher for the YSR. These findings suggested that estimates of the higher-order factor based on the actual data would be relatively unbiased when based on the CDI, CES-D, and the PAL, but would lead to underestimates when based on the YSR.

Table 2 Bias estimates from simulation study based on youth depression data
Full size table

To illustrate these effects, we randomly selected one of the simulated datasets and estimated median factor score values for each case for the higher-order factor based on the complete and sparse versions. Figures B1–B4 in the online supplementary materials plot the estimated association between these values for subsets of cases that had data on each measure. Cases that included PAL, CDI, or CES-D scores have estimates that are very close in the upper part of the range but underestimate the factor score in the lower region by up to 1–3%. Cases including the YSR consistently underestimate the factor score by around 3% across the entire range.

Discussion

Our strategy provides evidence that sparseness does not strongly bias factor estimates in a hierarchical measurement model based on this synthesis dataset. However, there appears to be some bias in estimates for those participants with low depression scores, and in scores based on the YSR. These analyses also highlight the importance of evaluating indirect effects in the hierarchical measurement model: here the overestimation bias in item loadings is balanced by the underestimation of measure factor loadings on the higher-order factor.

This strategy does assume that model parameters based on the dataset are at least reasonable ballpark estimates of the strength of loadings for individual measures, and of the association among those measures, allowing us to use these estimates in population models to explore the impact of sparseness given the strength of these associations. The first assumption is bolstered by the substantial sample sizes available for estimating the measurement models for the individual members based on combining data from multiple trials. The second assumption is supported by the presence of subsamples that completed more than one measure (correlations of the CDI factor with factors from the other three measures ranged from 0.52 to 0.87), and to a lesser degree by the presence of indirect associations for those measures that did not co-occur in any sample.

General Discussion and Conclusions

Measurement modeling to achieve construct equivalence across multiple measures of the same construct is an important tool for integrative data analysis, but its application requires careful attention to sparseness in synthesis datasets. Graph theory representations of sparseness patterns provide a systematic way of describing such patterns and exploring their implications for modeling. Results of the simulation study clarified that bias due to sparseness will depend on the strength of the general factor, the nature of the measurement model employed, and the level of indirect linkage among measures in the measurement graph. Given that different synthesis datasets will embody different patterns of sparseness, investigators would do well to use simulation methods to explore the potential for bias given the sparseness pattern they encounter.

This study focused on datasets having systematic violations of conditional independence due to method effects. Measurement models can also be compromised when other assumptions, such as construct invariance, fail to hold. Standard tests of measurement invariance can be extended to IDA datasets to evaluate possible violations of invariance over categorical variables such as age or gender (Howe et al., 2019). More complex methods such as moderated nonlinear factor analysis have been developed to adjust for measure invariance across multiple dimensions (MNLFA: Curran et al., 2014; Gottfredson et al., 2019). However, the impact of sparseness on these methods has yet to be explored.

Future Directions

We followed standard methods for evaluating bias, based on statistical theories of bias. However, these theories focus on individual parameters, while measurement is multivariate and multilevel. When data from multiple measures are combined, bias in one measure may balance out bias in another, leading to a more accurate total score. However, this will not happen whenever studies have data only on one of the two measures; in this case, participants from different studies can have total scores biased in different directions. The field needs to develop and study the performance of methods for evaluating bias at the item, measure, and construct level. This could involve comparing empirical estimates of factor scores across different patterns of sparseness or comparing how sparseness impacts the association of those scores with other constructs.

This study focused on sparseness patterns involving single cliques. When an IDA dataset includes multiple isolated cliques, it may be possible to conduct empirical harmonization within each clique, and then combine findings across cliques. This will require added assumptions: for example, we may need to assume that common factor means and variances are the same across all cliques, as a means of establishing a common metric. Future research will be necessary to evaluate the performance of such extensions.

This study also focused entirely on empirical harmonization. Many recent IDA projects in prevention science have employed semantic harmonization, merging items from different measures based on judgments of their semantic similarity (Cole et al., 2023). Howe and Brown (2023) noted several untested assumptions required for such harmonization, and briefly suggested ways of empirically testing them. Semantic harmonization may be particularly useful when measures form two or more isolated cliques. However, sole reliance on semantic methods can discard substantial empirical information about associations among items both within and between measures. We suggest that the field would profit from exploring methods that integrate semantic and empirical harmonization and evaluating how those methods perform with IDA datasets having various patterns of sparseness.

Most applications of measurement modeling to synthesis datasets used in IDA have also attended to single constructs, as in the current study. However, investigators are often interested in multiple constructs, as when combining studies to evaluate structural equation models involving causal impact or mediation (Huh et al., 2022). Sparseness patterns in the relevant synthesis dataset may be even more complex here, differing for different constructs in the structural model. Other than the work of Huo et al. (2014) on multiple outcome constructs associated hierarchically, we are unaware of attempts to deal with sparseness or to explore how sparseness patterns might bias estimates in models with more than one construct.

It will also be important to determine how we might adjust our analyses to reduce the impact of bias due to sparseness. Our simulation findings suggest that the MAR assumption may not remain tenable as sparseness increases. Exploration of methods for analyzing data that are not missing at random (MNAR) may prove profitable here (Linero & Daniels, 2018).

In conclusion, we recommend that IDA investigators use simulation to explore the potential impact of sparseness whenever data graphs are less than complete. The four-step strategy we employed in the example study is a reasonable way to begin: (1) estimate the measurement model of interest with the actual synthesis dataset; (2) use the estimated parameters from that model as known values in a population model to simulate a large number of datasets with the same structure as that of the synthesis dataset, but with complete data; (3) create a second group of datasets by introducing missingness into the complete datasets to mimic the pattern of sparseness in the synthesis dataset of interest; and (4) conduct Monte Carlo analyses of these two datasets, calculating estimates of bias for each model parameter.