Non-Gaussian Methods for Causal Structure Learning

Abstract

Causal structure learning is one of the most exciting new topics in the fields of machine learning and statistics. In many empirical sciences including prevention science, the causal mechanisms underlying various phenomena need to be studied. Nevertheless, in many cases, classical methods for causal structure learning are not capable of estimating the causal structure of variables. This is because it explicitly or implicitly assumes Gaussianity of data and typically utilizes only the covariance structure. In many applications, however, non-Gaussian data are often obtained, which means that more information may be contained in the data distribution than the covariance matrix is capable of containing. Thus, many new methods have recently been proposed for using the non-Gaussian structure of data and inferring the causal structure of variables. This paper introduces prevention scientists to such causal structure learning methods, particularly those based on the linear, non-Gaussian, acyclic model known as LiNGAM. These non-Gaussian data analysis tools can fully estimate the underlying causal structures of variables under assumptions even in the presence of unobserved common causes. This feature is in contrast to other approaches. A simulated example is also provided.

Introduction

The study of statistical causal reasoning can be roughly divided into two categories. First, if the causal structure of variables is known, the conditions under which the causal effects or intervention effects between variables can be inferred are investigated (Imbens and Rubin 2015; Pearl 2000). Second, if the causal structure is unknown, the conditions under which the causal structure or causal relationships of variables can be inferred are investigated (Spirtes et al. 1993; Shimizu 2014; Zhang and Hyvärinen 2016). The difference between the two tasks is whether the causal structure is known or unknown and reflects different purposes. The second category is called causal discovery or causal structure learning. The two categories are closely related. For example, suppose that the causal structure is unknown based on background causal knowledge. Then, the causal structure is inferred by using causal discovery methods from the latter category, and causal effects that can be inferred are identified based on the inferred causal structure. Causal effects are identified by combining the theories of the two categories as well as background knowledge.

Researchers in various fields, including prevention scientists, have hypothesized about the causal relationships for various phenomena. However, narrowing the candidate hypotheses to one based only on the background theory for a given field is usually difficult. In such cases, multiple candidates need to be compared based on data to determine which is better. Further, if the background theory is not sufficient, developing candidate hypotheses in the first place is difficult. In this case, candidate hypotheses should be generated based on experience or observed data. In either case, causal discovery or causal structure learning methods are useful.

Here is an example where causal discovery is required. People with depression have been reported to tend to have sleep problems. For example, according to an epidemiological survey (Raitakari et al. 2008), the correlation coefficient between depression and the degree of sleep disorder is 0.77 (Rosenström et al. 2012). Epidemiologic researchers may then want to find a causal model to explain this strong correlation. They may consider the following candidate causal models:

• 1. Sleep problems causes depression.

• 2. Depression causes sleep problems.

• 3. There is no direct causal relationship between depression and sleep problems.

These three candidates are graphically represented in Fig. 1. Of course, a fourth candidate is that depression and sleep problems mutually cause each other, i.e., cyclic cases. In this paper, one-way causal relationships are assumed to simplify the illustrative examples. The concept can be further extended to cyclic cases (Lacerda et al. 2008).

Fig. 1

Comparison of three hypotheses regarding the causality direction

If a sleep disorder causes depression, as shown by the causal structure on the left of Fig. 1, then reducing the degree of sleep problems of the subjects would decrease their depression. If the middle structure is the case, then reducing the degree of depression would decrease sleep problems. Lowering the severity of sleep problems would not change the degree of depression. Finally, if the right structure is the case, then depression and sleep problems are not causally related. Then, even if the severity of the sleep problems is lowered, the depression does not change.

By performing randomized experiments, the causal relationship between depression and sleep disturbance can be determined. However, actually performing randomized experiments is not easy. This paper discusses causal discovery methods based on observational data that do not need such randomized experiments to be performed. Note that several assumptions are needed in place of the randomization. Even if some assumptions are needed, they can generate specific causal hypotheses to be verified by further experiments. Therefore, these causal discovery methods do not aim to replace such experiments. Rather, they are intended to help prevention scientists hypothesize good causal model candidates before performing randomized experiments or to do their best when randomized experiments cannot be performed.

Causal structure learning methods aim to discover or infer causal graphs of variables based on data. Causal graphs illustrate the qualitative causal relations of variables. An example is given in Fig. S1 (available online). There are three variables to be analyzed: x₁,x₂, and z₁. There are also two error variables: e₁ and e₂. x₁ and x₂, which are represented by boxes, are observed variables. z₁, which is represented by a dotted circle, is an unobserved variable. The error variables e₁ and e₂ are unobserved, although they are not represented by dotted circles.

In the example graph, all edges between variables are directed. A directed edge starting from a variable and ending with another variable indicates that the former variable directly causes the latter. Based on the terminology of graph theory, the former variable is called a parent of the latter, and the latter variable is called a child of the former. In this causal graph, there is a directed edge from x₁ to x₂. This indicates that x₁ directly causes x₂. Thus, x₁ is a parent of x₂, and x₂ is a child of x₁. If there is no directed edge between two variables, then there is no direct causal relation between the two. The unobserved variable z₁ directly causes both x₁ and x₂. Hence, it is called an unobserved common cause.

In causal structure learning, the objective is to infer the causal graph of variables based on their observed data. Note that this is done without actually intervening on any of the variables. A major topic in this field is understanding the conditions under which the causal graph can be uniquely estimated. This paper first reviews the framework for causal inference, which is also known as the identification of causal effects, and then introduces recent causal discovery methods based on the linear non-Gaussian acyclic model (LiNGAM). Examples of LiNGAM applications include epidemiology (Rosenström et al. 2012), economics (Moneta et al. 2013), finance (Zhang and Chan 2008), and neuroscience (Mills-Finnerty et al. 2014).

Framework of Causal Inference

This section provides a brief review of the causal inference framework based on the structural causal model (SCM) (Pearl 2000). First, structural equation models (SEMs) are introduced for describing data-generating processes (Bollen 1989), which are used to generate values of variables. This framework uses special types of equations known as structural equations to represent how the values of variables are determined.

The structural equations for the case described in Fig. S1 (available online) are given by

$$\begin{array}{@{}rcl@{}} x_{1} &=& f_{1}(z_{1}, e_{1} ) \end{array} $$

(1)

$$\begin{array}{@{}rcl@{}} x_{2} &=& f_{2}(x_{1}, z_{1}, e_{2} ), \end{array} $$

(2)

where the error variable e₁ denotes all factors other than z₁ that can contribute to determining the value of x₁. Similarly, the error variable e₂ denotes all factors other than x₁ and z₁.

Structural equations represent more than a simple mathematical equality. The left-hand sides of the equations are defined by their right-hand sides. For example, in Eq. 1, the value of x₁ on the left-hand side is completely determined by that of z₁ and e₁ through the function f₁.¹

In Eqs. 1 and 2, the value of e₁ is first generated from the probability distribution p(e₁). Then, the value of x₁ is determined by those of z₁ and e₁ through the function f₁. Subsequently, the value of e₂ is generated from the probability distribution p(e₂). Then, the value of x₂ is determined by those of x₁,z₁, and e₂ through the function f₂. The variables z₁,e₁, and e₂ are known as exogenous variables. The values of these exogenous variables are generated outside the model, and their data-generating processes are decided by the modeler to not be further modeled. In contrast, variables whose values are generated inside the model, such as x₁ and x₂, are known as endogenous variables.

Definition of Causality Based on Interventions

Next, causality is defined based on the interventions used in SCMs (Pearl 2000). First, interventions in SEMs are defined. Intervening on the variable x₁ means forcing the value of x₁ to be a constant c regardless of the other variables. This intervention is denoted by do(x = c). In SEMs, this means replacing the function determining x₁ with the constant c, i.e., forcing all individuals in a population to take x = c. Suppose that x₁ is intervened with and forced to take the value of c in the example given in Eqs. 1 and 2. This creates a new SEM denoted by M_{x = c}:

$$\begin{array}{@{}rcl@{}} x_{1} &=& c \end{array} $$

(3)

$$\begin{array}{@{}rcl@{}} x_{2} &=& f_{2}(x_{1}, z_{1}, e_{2} ). \end{array} $$

(4)

As a result, the causal graph shown on the left of Fig. Fig. S2 (available online) changes to that given on the right. The directed edge from the unobserved common cause z₁ to the observed variable x₁ in the causal graph of the original SEM given in Eqs. 1 and 2 disappears because x₁ is forced to be c regardless of the other variables including z₁. Note that the other functions are assumed to not change even if a function is replaced with a constant. Although this may be physically unrealistic in some cases, the revised SEM given in Eqs. 3 and 4 represents a hypothetical population where all individuals in the population are forced to take x = c but the other function f₂ does not change.

Next, the post-intervention distribution is defined. When x₁ is intervened with, the post-intervention distribution of x₂ is defined by the distribution of x₂ in the revised SEM, i.e., M_{x = c}:

$$\begin{array}{@{}rcl@{}} p(x_{2}|do(x_{1}=c)) := p_{M_{x_{1}=c}}(x_{2}). \end{array} $$

(5)

The associated causal graph is shown on the right of Fig. Fig. S2 (available online).

Then, x₁ is a cause of x₂ in this population if there exist two different values c and d such that the post-intervention distributions are different, i.e., if the following holds:

$$\begin{array}{@{}rcl@{}} p(x_{2}|do(x_{1}=d)) \neq p(x_{2}|do(x_{1}=c)). \end{array} $$

(6)

A common method for quantifying the magnitude of causation from x₁ to x₂ is to assess the following average difference (Rubin 1974; Pearl 2000):

$$\begin{array}{@{}rcl@{}} E(x_{2}|do(x_{1}=d)) - E(x_{2}|do(x_{1}=c)). \end{array} $$

(7)

This is called the average causal effect. E denotes the expectation operator and is a shorthand for averaging according to a given distribution. This evaluates to what extent, on average, the value of x₂ would change if the value of x₁ has been changed from c to d. Other quantifying methods include assessing the ratio of the two averages or using the variance or other meaningful statistics that characterize the features of the post-intervention distribution.

As an example, assume that the function f₂ in the SEM of Eqs. 1 and 2 is linear:

$$\begin{array}{@{}rcl@{}} x_{1} &=& \lambda_{11}z_{1} + e_{1} \end{array} $$

(8)

$$\begin{array}{@{}rcl@{}} x_{2} &=& b_{21}x_{1} + \lambda_{21}z_{1} + e_{2}, \end{array} $$

(9)

where b₂₁,λ₁₁, and λ₂₁ are constants. Then, the post-intervened SEM $M_{x_{1}=c}$ takes the form

$$\begin{array}{@{}rcl@{}} x_{1} &=& c \end{array} $$

(10)

$$\begin{array}{@{}rcl@{}} x_{2} &=& b_{21}x_{1} + \lambda_{21}z_{1} + e_{2}. \end{array} $$

(11)

Therefore, the average causal effect of x₁ on x₂ if the value of x₁ has been changed from c to d is given by

$$\begin{array}{@{}rcl@{}} && E(x_{2}|do(x_{1}=d)) - E(x_{2}|do(x_{1}=c)) \end{array} $$

(12)

$$\begin{array}{@{}rcl@{}} & =& E(b_{21}d + \lambda_{21}z_{1} + e_{2}) -E(b_{21}c + \lambda_{21}z_{1} + e_{2}) \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} & =& b_{21}(d-c). \end{array} $$

(14)

The expected average change in x₂ is thus the difference between d and c multiplied by the coefficient b₂₁.

Similarly, the post-intervened model $M_{x_{2}=c}$ shown on the right of Fig. S3 (available online) is written as

$$\begin{array}{@{}rcl@{}} x_{1} &=& \lambda_{21} z_{1} + e_{1} \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}} x_{2} &=& c \end{array} $$

(16)

Then, the average causal effect of x₂ on x₁ when the value of x₂ has been changed from c to d is given by

$$\begin{array}{@{}rcl@{}} &&E(x_{1}|do(x_{2}\,=\,d)) - E(x_{1}|do(x_{2}=c))\\ &=& \lambda_{21}E(z_{1}) + E(e_{1})\\ && -\{ \lambda_{21}E(z_{1}) + E(e_{1}) \} \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}} &=& 0. \end{array} $$

(18)

This is reasonable because x₂ does not contribute to defining x₁ in the original SEM shown in Eqs. 1 and 2 and on the left of Fig. S3 (available online).

Non-Gaussian Methods for Causal Discovery

In causal structure learning, the SCMs introduced above are used to represent model assumptions, including the background knowledge and hypotheses of the modeler. Model assumptions place constraints on the model and restrict the candidate causal structures. Among the structures that satisfy the model assumptions, the causal structure that is most consistent with the data distribution is searched for.

This section explains the basic setup (Pearl 2000; Spirtes et al. 1993) and then introduces the non-Gaussian causal discovery methods based on a model known as LiNGAM (Shimizu et al. 2006; Hoyer et al. 2008; Shimizu 2014). The focus remains on continuous variable cases.

A typical assumption is that the causal relations of variables are acyclic, i.e., there are no directed cycles in the causal graph. Further, the functional relations of the variables are assumed to be linear. The basic model for the continuous observed variables x_i (i = 1,…,p) is therefore formulated as follows:

$$\begin{array}{@{}rcl@{}} x_{i} &=& \underset{j \in \text{pa}(x_{i})}{\sum} b_{ij}x_{j} + e_{i}, \end{array} $$

(19)

where pa(x_i) is the set of parents of x_i in the causal graph, e_i (i = 1,…,p) are error variables, and b_ij (i,j = 1,…,p) are the coefficients that represent the magnitude of direct causation from x_j to x_i.

In the most basic setup, the error variables e_i (i = 1,…,p) are assumed to be independent. The independence assumption between e_i (i = 1,…,p) implies that there are no unobserved common causes. This means that unobserved common causes such as z₁ in the causal graph of Fig. S1 (available online) must be observed. If there is an unobserved common cause, it is not part of the model (19) and generally makes some of the error variables in Eq. 19 dependent. This setup is discussed first. Then, an advanced model with unobserved common causes is presented.

In matrix form, a linear acyclic SCM with no unobserved common cause in Eq. 19 can be written as

$$\begin{array}{@{}rcl@{}} \boldsymbol{x} &=& \mathbf{B} \boldsymbol{x} + \boldsymbol{e}, \end{array} $$

(20)

where the coefficient matrix B collects the magnitudes of direct causation b_ij (i,j = 1,…,p) and the vectors x and e collect the observed variables x_i (i = 1,…,p) and exogenous variables e_i (i = 1,…,p), respectively. The zero/non-zero pattern of b_ij (i,j = 1,…,p) corresponds to the absence/existence pattern of the directed edges. In other words, if the coefficient b_ij≠ 0, there is a directed edge from x_j to x_i. If this is not the case, there is no directed edge from x_j to x_i (i,j = 1,…,p). Because of the acyclicity, the diagonal elements of B are all zeros.

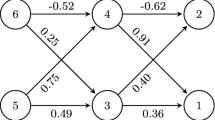
Figure 2 provides an example of causal graphs for representing the linear acyclic SCMs with no unobserved common cause in Eq. 20. The SEM corresponding to the causal graph of the figure is written as

$$\begin{array}{@{}rcl@{}} \left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right] = \left[\begin{array}{ccc} 0 & 0 & 3\\ -5 & 0 & 0\\ 0 & 0 & 0 \end{array} \right] \left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array} \right] + \left[ \begin{array}{c} e_{1}\\ e_{2}\\ e_{3} \end{array} \right]. \end{array} $$

(21)

Fig. 2

Example of causal graphs corresponding to a linear acyclic SEM

The goal of identifying causal structures with this basic setup is to estimate the unknown coefficient matrix B by using the data X. X is assumed to be randomly sampled from a linear acyclic SCM with no unobserved common cause, as represented by Eq. 20 above.

Classical Approach Based on Conditional Independence

Under the causal Markov condition and the faithfulness assumption (Spirtes et al. 1993), conditional independence relations provide a classical way to infer the causal structure of the linear acyclic SCM with no unobserved common causes in Eq. 20.² For any such linear acyclic SCM, the causal Markov condition holds (Pearl and Verma 1991) as follows. Each observed variable x_i is independent of its non-descendants conditional on its parents, i.e., $p(\boldsymbol {x}) = {\Pi }_{i = 1}^{p} p(x_{i}| pa(x_{i}))$. Thus, conditional independence between observed variables provides a clue as to what the underlying causal structure is.

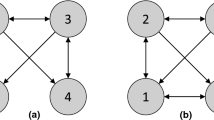
Unfortunately, in many cases, the causal Markov condition is insufficient for uniquely identifying the causal structure of the linear acyclic SCM with no unobserved common causes (Pearl 2000; Spirtes et al. 1993). An example of this is provided in Fig. 3. Suppose that data x are generated from the left causal graph shown in Fig. 3. According to the causal Markov condition, x₂ and x₃ are independent conditional on x₁, and no other conditional independence holds. Therefore, the only information available for estimating the underlying causal structure is the conditional independence of x₂ and x₃. Within the class of linear acyclic SCMs with no unobserved common causes, the three causal graphs give the same conditional independence. In each of these three causal structures, only x₂ and x₃ are conditionally independent. However, only the left causal graph represents the right causal relations, and the other two causal graphs do not. The three causal structures are quite different, and there is no causal direction that is consistent across all three causal graphs. Thus, in this example, the causal Markov condition principle is not capable of uniquely estimating the underlying causal graph.

Fig. 3

Candidate causal structures that give the same conditional independence of variables as the original causal structure on the left

Basic LiNGAM

In this section, the basic LiNGAM is reviewed (Shimizu et al. 2006) before it is extended to cases with unobserved common causes (Hoyer et al. 2008). The assumptions of the basic LiNGAM may appear to be restrictive, and fortunately, they can be relaxed in many ways (Hoyer et al. 2008, 2009; Lacerda et al. 2008; Hyvärinen et al. 2010; Zhang and Hyvärinen 2009).

In Shimizu et al. (2006), a non-Gaussian version of the linear acyclic SCM was proposed with no unobserved common causes in Eq. 19. This is known as a LiNGAM:

$$\begin{array}{@{}rcl@{}} x_{i} = \underset{j \in \text{pa}(x_{i})}{\sum} b_{ij}x_{j} + e_{i}, \end{array} $$

(22)

where the error variables e_i (i = 1,…,p) follow non-Gaussian continuous distributions and are independent. Without loss of generality, their means are assumed to be zeros.

LiNGAMs have been proven to be identifiable (Shimizu et al. 2006), i.e., the coefficients b_ij (i,j = 1,…,d) can be uniquely identified by using the non-Gaussianity of the data. Then, the causal graph can be drawn based on the zero/non-zero pattern of the coefficient matrix B that collects those coefficients b_ij (i,j = 1,…,p). In contrast, the classical approach in the previous subsection only uses the conditional independence of observed variables and does not use the non-Gaussian structure, even when they follow non-Gaussian distributions.

A principle for identifying the causal structure is presented below. First, the Darmois–Skitovitch theorem is referenced (Darmois 1953; Skitovitch 1953):

Theorem 1 (Darmois–Skitovitch theorem)

Define two random variablesy₁andy₂as linear combinations of the independent random variabless_i(i = 1,…,Q):

$$\begin{array}{@{}rcl@{}} y_{1} = \sum\limits_{i = 1}^{Q} \alpha_{i}s_{i}, \quad y_{2} = \sum\limits_{i = 1}^{Q} \beta_{i} s_{i}. \end{array} $$

Then, it can be shown that, ify₁andy₂are independent,all such variabless_ℓfor whichα_ℓβ_ℓ≠ 0 areGaussian.

The contraposition of this theorem therefore shows that, if there exists a non-Gaussian s_j for which α_ℓβ_ℓ≠ 0,y₁ and y₂ are dependent.

To illustrate this, two variable LiNGAM cases are described. The number of observations is assumed to be large enough that estimation errors can be ignored. First, consider the case where x₁ causes x₂:

$$\begin{array}{@{}rcl@{}} x_{1} &=& e_{1} \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} x_{2} &=& b_{21}x_{1} + e_{2}, \end{array} $$

(24)

where b₂₁≠ 0.

By regressing x₂ on x₁,

$$\begin{array}{@{}rcl@{}} {r}_{2}^{(1)} &=& x_{2} - \frac{\text{cov}(x_{2},x_{1})}{\text{var}(x_{1})}x_{1} \end{array} $$

(25)

$$\begin{array}{@{}rcl@{}} &=& x_{2} - b_{21}x_{1} \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} &=& e_{2}. \end{array} $$

(27)

Thus, if x₁(= e₁) is the cause, because e₁ and e₂ are independent, x₁ and ${r}_{2}^{(1)}(=e_{2})$ are also independent.

Next, consider the case where x₂ causes x₁:

$$\begin{array}{@{}rcl@{}} x_{1} &=& b_{12}x_{2} +e_{1} \end{array} $$

(28)

$$\begin{array}{@{}rcl@{}} x_{2} &=& e_{2}, \end{array} $$

(29)

where b₁₂≠ 0. By regressing x₂ on x₁,

$$\begin{array}{@{}rcl@{}} {r}_{2}^{(1)} &=& x_{2} - \frac{\text{cov}(x_{2},x_{1})}{\text{var}(x_{1})}x_{1} \end{array} $$

(30)

$$\begin{array}{@{}rcl@{}} &=& x_{2} - \frac{\text{cov}(x_{2},x_{1})}{\text{var}(x_{1})}(b_{12}x_{2} +e_{1}) \end{array} $$

(31)

$$\begin{array}{@{}rcl@{}} &=& \left\{1 - \frac{b_{12} \text{cov}(x_{2}, x_{1})}{\text{var}(x_{1})}\right\} x_{2} - \frac{\text{cov}(x_{2},x_{1})}{\text{var}(x_{1})} e_{1} \end{array} $$

(32)

$$\begin{array}{@{}rcl@{}} &=& \left\{1-\frac{b_{12}\text{cov}(x_{2},x_{1})}{\text{var}(x_{1})}\right\}e_{2}-\frac{b_{12}\text{var}(x_{2})}{\text{var}(x_{1})}e_{1}. \end{array} $$

(33)

Thus, if x₁ is not the cause, according to the Darmois–Skitovitch theorem, x₁ and ${r}_{2}^{(1)}$ are dependent because e₁ and e₂ are non-Gaussian and independent. Furthermore, the coefficient of e₁ on x₁ and that of e₁ on ${r}_{2}^{(1)}$ are non-zero because b₁₂≠ 0 by definition. Therefore, the causal direction between x₁ and x₂ can be determined by examining the independence between explanatory variables and their residuals (Shimizu et al. 2011).

To evaluate independence, a measure that is not restricted to uncorrelatedness is needed because least-squares regression results in residuals that are always uncorrelated with but not necessarily independent of explanatory variables. For the same reason, non-Gaussianity is required for inferring the causal structure because uncorrelatedness is equivalent to independence for Gaussian variables. Common independence measures include HSIC (Gretton et al. 2005) and mutual information (Bach and Jordan 2002; Kraskov et al. 2004).

LiNGAM with Unobserved Common Causes

An extension of LiNGAM is now described for causal discovery in the presence of unobserved common causes (Hoyer et al. 2008). x₁,…,x_d denotes the observed variables, f₁,…,f_Q denotes the unobserved common causes, and e₁,…,e_d denotes the error variables. All of these variables are continuous. Then, the model is written as follows:

$$\begin{array}{@{}rcl@{}} x_{i} = \underset{j \in \text{pa}(x_{i})}{\sum} b_{ij} x_{j} + \sum\limits_{q = 1}^{Q} \lambda_{iq} f_{q} + e_{i}, \end{array} $$

(34)

where b_ij and λ_iq are constants that represent the magnitudes of direct causation from x_j and f_q to x_i, respectively (i,j = 1,…,p; q = 1,…,Q). The causal relations are assumed to be acyclic. The unobserved common causes f_q (q = 1,…,Q) and error variables e_i (i = 1,…,p) are further assumed to be non-Gaussian and independent. Although the assumption of independence for the unobserved common causes f_q (q = 1,…,Q) looks strong, it can be made without loss of generality under the linearity assumption (Hoyer et al. 2008) because the observed variables are then linear combinations of error variables and hidden common causes.

By using the model in Eq. 34, the following two models with opposite directions of causation can be compared:

$$\begin{array}{@{}rcl@{}} && \text{Model}~1: \left\{\begin{array}{l} x_{1} = {\sum}_{q = 1}^{Q} \lambda_{1q} f_{q} + e_{1} \\ x_{2} = b_{21}x_{1}+{\sum}_{q = 1}^{Q} \lambda_{2q} f_{q} + e_{2} \end{array}\right. \end{array} $$

(35)

$$\begin{array}{@{}rcl@{}} && \text{Model}~2: \left\{\begin{array}{l} x_{1} = b_{12}x_{2}+ {\sum}_{q = 1}^{Q} \lambda_{1q} f_{q} + e_{1}\\ x_{2} = {\sum}_{q = 1}^{Q} \lambda_{2q} f_{q} + e_{2} \end{array} \right.. \end{array} $$

(36)

Figure 4 graphically represents these two models. Note that the number of unobserved common causes Q is assumed to be unknown.

Fig. 4

Models 1 and 2: two models with different causal directions in the presence of three unobserved common causes

In Shimizu and Bollen (2014), the model in Eq. 34 was related to a model with observation-specific intercepts instead of explicitly having unobserved common causes, as shown in Fig. 5. A major advantage of this approach is that neither the number of unobserved common causes Q nor number of coefficients λ_iq (i = 1,…,p; q = 1,…,Q) needs to be estimated. To explain the idea, the model in Eq. 34 for the observation m is rewritten as follows:

$$\begin{array}{@{}rcl@{}} {x}_{i}^{(m)} &=& \sum\limits_{q = 1}^{Q} \lambda_{iq} {f}_{q}^{(m)} + \underset{j \in \text{pa}(x_{i})}{\sum} b_{ij}{x}_{j}^{(m)} + {e}_{i}^{(m)}, \end{array} $$

(37)

where ${x}_{i}^{(m)}, {f}_{q}^{(m)}$, and ${e}_{i}^{(m)}$ denote m-th observations of x_i,f_q, and e_i, respectively (i = 1,…,p; q = 1,…,Q; m = 1,…,n).

Fig. 5

Transforming a LiNGAM with hidden common causes to a LiNGAM with no hidden common causes

Now, the sums of the unobserved common causes can be denoted by ${\mu }_{i}^{(m)}={\sum }_{q = 1}^{Q}\lambda _{iq}{f}_{q}^{(m)}$. Then, the following model is obtained with observation-specific intercepts:

$$\begin{array}{@{}rcl@{}} {x}_{i}^{(m)} &=& \underbrace{{\mu}_{i}^{(m)}}_{{\sum}_{q = 1}^{Q} \lambda_{iq}{f}_{q}^{(m)}} + \underset{j \in \text{pa}(x_{i})}{\sum} b_{ij} {x}_{j}^{(m)} + {e}_{i}^{(m)}, \end{array} $$

(38)

where ${\mu }_{i}^{(m)}$ are observation-specific intercepts. The distributions of ${e}_{i}^{(m)}$ (m = 1,…,n) are assumed to be identical for every m. In this model, the observations are generated from the model with no unobserved common causes, possibly with different parameter values of the intercepts ${\mu }_{i}^{(m)}$. This model has the coefficients b_ij (i,j = 1,…,p) that are common to all observations as well as the observation-specific intercepts ${\mu }_{i}^{(m)}$. This is similar to mixed models (Demidenko 2004). Thus, it is called a mixed-LiNGAM.

Now, the problem of comparing Models 1 and 2 in Eqs. 35 and 36 becomes that of comparing Models 1^′ and 2^′:

$$\begin{array}{@{}rcl@{}} && \text{Model}~1^{\prime}: \left\{\begin{array}{l} {x}_{1}^{(m)} = {\mu}_{1}^{(m)} + {e}_{1}^{(m)}\\ {x}_{2}^{(m)} = {\mu}_{2}^{(m)} + b_{21} {x}_{1}^{(m)}+ {e}_{2}^{(m)} \end{array} \right., \end{array} $$

(39)

$$\begin{array}{@{}rcl@{}} && \text{Model}~2^{\prime}: \left\{\begin{array}{l} {x}_{1}^{(m)} = {\mu}_{1}^{(m)} + b_{12} {x}_{2}^{(m)} + {e}_{1}^{(m)}\\ {x}_{2}^{(m)} = {\mu}_{2}^{(m)} + {e}_{2}^{(m)} \end{array} \right., \end{array} $$

(40)

where ${\mu }_{1}^{(m)} = {\sum }_{q = 1}^{Q}\lambda _{1q}{f}_{q}^{(m)}$ and ${\mu }_{2}^{(m)}={\sum }_{q = 1}^{Q}\lambda _{2q}{f}_{q}^{(m)}$ (m = 1,…,n).

A Bayesian approach is applied to compare Models 1^′ and 2^′ and estimate the possible causal direction between the two observed variables x₁ and x₂. The prior probabilities of the two candidate models are assumed to be uniform. Then, the log-marginal likelihoods of the two models may simply be compared to assess their plausibility. The model with the larger log-marginal likelihood is considered to be closest to the true model (Kass and Raftery 1995). Once the possible causal direction has been estimated, the coefficient b₂₁ or b₁₂ can be checked for its likeliness to be non-zero by examining its posterior distribution.

Error Distributions

The error distributions p(e₁) and p(e₂) can be modeled by using the generalized Gaussian distribution (Hyvärinen et al. 2001) as follows:

$$\begin{array}{@{}rcl@{}} p(e_{i}) &=& \frac{\beta_{i}}{2\alpha_{i} {\Gamma}(1/\beta_{i})} e^{{(-|e_{i}|/\alpha_{i})}^{\beta_{i}}} \quad (i = 1,2). \end{array} $$

(41)

Here, the symbol Γ denotes the Gamma function:

$$\begin{array}{@{}rcl@{}} {\Gamma}(u) = {\int}_{\!\!\!0}^{\infty}e^{-t}t^{u-1}dt, \end{array} $$

where α_i are the scaling parameters, and β_i are the shape parameters (i = 1,2).

The error variances are

$$\begin{array}{@{}rcl@{}} \text{var}(e_{i}) = \frac{{{\alpha}_{i}^{2}}{\Gamma}(3/\beta_{i})}{{\Gamma}(1/\beta_{i})} \quad (i = 1,2). \end{array} $$

Thus, when the standard deviations of the errors are set to h_i (i = 1,2), then the scaling parameters are automatically determined as follows:

$$\begin{array}{@{}rcl@{}} \alpha_{i} = h_{i} \sqrt{\frac{{\Gamma}(1/\beta_{i})}{{\Gamma}(3/\beta_{i})}}. \end{array} $$

Prior Distributions

Next, an informative prior distribution is used for the observation-specific intercepts ${\mu }_{i}^{(m)}$ (i = 1,2;m = 1,…,n). These observation-specific intercepts ${\mu }_{i}^{(m)}$ are the sums of many non-Gaussian independent unobserved common causes ${f}_{q}^{(m)}$ and are dependent. The central limit theorem states that the sum of independent variables becomes increasingly close to the Gaussian (Billingsley 1986). Based on this theorem, the non-Gaussian distributions of the observation-specific intercepts ${\mu }_{i}^{(m)}$ are approximated as the sums of many non-Gaussian independent unobserved common causes by using a bell-shaped curve distribution. The prior distribution of the observation-specific intercepts is modeled by the multivariate t-distribution as follows:

$$\begin{array}{@{}rcl@{}} \left[ \begin{array}{c} {\mu}_{1}^{(m)} \\ {\mu}_{2}^{(m)} \end{array} \right] &=& \text{diag}\left( \left[ \sqrt{\tau_{1}}, \sqrt{\tau_{2}}\right]^{T}\right) \textbf{C}^{-1/2} \boldsymbol{u}, \end{array} $$

(42)

where τ₁ and τ₂ are constants, u ∼ t_ν(0,Σ), and Σ = [σ_ab] is a symmetric scale matrix whose diagonal elements are 1s. C is a diagonal matrix whose diagonal elements give the variance of elements of u, i.e., $\mathbf {C}=\frac {\nu }{\nu -2}\text {diag}(\boldsymbol {{\Sigma }})$ for ν > 2.

Numerical Examples

Experimental results using artificially generated data are presented here.³ The parameters common to all of the observations were the coefficients b₁₂ and b₂₁ and the standard deviations of the error variables e₁ and e₂, which are denoted by h₁ and h₂. Then, the prior distributions of the parameters were modeled as follows:

$$\begin{array}{@{}rcl@{}} b_{12} &\sim& N(0, 0.75^{2}) \end{array} $$

(43)

$$\begin{array}{@{}rcl@{}} b_{21} &\sim& N(0, 0.75^{2}) \end{array} $$

(44)

$$\begin{array}{@{}rcl@{}} h_{1} &\sim& U(0, 1) \end{array} $$

(45)

$$\begin{array}{@{}rcl@{}} h_{2} &\sim& U(0, 1). \end{array} $$

(46)

The observation-specific intercepts ${\mu }_{i}^{(m)}$ (i = 1,2;m = 1,…,n) were generated as follows:

$$\begin{array}{@{}rcl@{}} \left[ \begin{array}{c} {\mu}_{1}^{(m)}\\ {\mu}_{2}^{(m)} \end{array} \right] &=& \left[ \begin{array}{cc} \frac{\tau_{1}}{\text{std}(u_{1})} & 0\\ 0 & \frac{\tau_{2}}{\text{std}(u_{2})} \end{array} \right] \left[ \begin{array}{c} u_{1} \\ u_{2} \end{array} \right], \end{array} $$

(47)

where the random variables u = [u₁,u₂]^T followed the t-distribution with ν degrees of freedom ∼ t_ν(0,Σ). The parameters of the t-distribution Σ are given by the following positive definite matrix:

$$\begin{array}{@{}rcl@{}} \boldsymbol{{\Sigma}}= \left[ \begin{array}{cc} 1 & \sigma_{12}\\ \sigma_{21} & 1 \end{array} \right]. \end{array} $$

(48)

The standard deviations of the intercepts ${\mu }_{1}^{(m)}$ and ${\mu }_{2}^{(m)}$ are τ₁ and τ₂. σ₁₂ determines the magnitude of covariance between the intercepts ${\mu }_{1}^{(m)}$ and ${\mu }_{2}^{(m)}$. The standard deviations of u₁ and u₂, which are denoted by std(u₁) and std(u₂), are $\sqrt {\frac {\nu }{\nu -2}}$ because of the property of the t-distribution.

The hyper-parameters selected with the log-marginal likelihoods are the shape parameters β₁ and β₂ and the parameters of the prior distributions of the observation-specific intercepts ${\mu }_{1}^{(m)}$ and ${\mu }_{2}^{(m)}$, i.e., τ₁,τ₂, and σ₂₁. An empirical Bayesian approach was used to select the hyper-parameters. The following were tested: β₁,β₂ = 0.5,1,2.0,6.0,τ₁,τ₂ = 0.4,0.6,0.8,σ₁₂ = 0 ± 0.3,± 0.5,± 0.7,± 0.9. Then, the set of the hyper-parameters that achieved the largest log-marginal likelihood was selected. The naive Monte Carlo sampling approach was used to compute the log-marginal likelihoods with 10,000 samples for the parameters. The degree of freedom was fixed to eight.

Artificial datasets were generated with a sample size of 100 by using the following LiNGAM with unobserved common causes:

$$\begin{array}{@{}rcl@{}} x_{1} &=& \sum\limits_{q = 1}^{Q} \frac{c}{\sqrt{Q + 1}} f_{q} + e_{1} \end{array} $$

(49)

$$\begin{array}{@{}rcl@{}} x_{2} &=& \sum\limits_{q = 1}^{Q} \frac{c}{\sqrt{Q + 1}} f_{q} + b_{21} x_{1} + e_{2}. \end{array} $$

(50)

The Laplace or uniform distribution was randomly used for the distributions of the error variables e₁ and e₂. Their means were zero, and the standard deviations were $\sqrt {3}$. The distributions of unobserved common causes f_q were randomly selected from the 18 non-Gaussian distributions (Bach and Jordan 2002). The coefficient b₂₁ was selected from the uniform distribution U(− 1.5,1.5). The constant c was 0.5 or 1.0. A larger c indicated a greater causal effect from the unobserved common cause f_q. The number of unobserved common causes Q was 10. In this manner, 100 datasets were generated for every combination of the error distributions and constant c.

Subsequently, the log-marginal likelihoods of Models 1^′ and 2^′ were calculated, and the number of times the causal direction of the model with the largest log-likelihood was the same as that of the model used to generate the dataset was counted.

The Bayes factor was also computed. The Bayes factor of the two models being compared (Models 1^′ and 2^′) is denoted by K. To simplify the notation, K was assumed to be computed so that the larger likelihood was in the numerator and the smaller was in the denominator. Kass and Raftery (Kass and Raftery 1995) proposed that the Bayes factor is negligible if 2log K is 0–2, positive if 2log K is 2–6, strong if 2log K is 6–10, and very strong if 2log K is more than 10.

Overall, as the Bayes factor rose, so did the precision (i.e., the fraction of the number of findings that were successful) in both cases with the magnitudes of the effects of hidden common causes c = 0.5 and 1.0.

In the cases with the smaller magnitude of hidden common causes c = 0.5, for the model comparison indexes 2log K greater than 0 and no more than 2, the precision was 0.51, and the number of findings was 57. For the indexes 2log K greater than 2 and no more than 6, the precision was 0.67, and the number of findings was 96. For the indexes 2log K greater than 6 and no more than 10, the precision was 0.82, and the number of findings was 74. For the indexes 2log K greater than 10 and no more than 10, the precision was 0.82, and number of findings was 74. For the indexes 2log K greater than 10, the precision was 0.97, and number of findings was 173.

In the cases with the larger magnitude of hidden common causes c = 1.0, for the indexes 2log K greater than 0 and no more than 2, the precision was 0.58, and number of findings was 67. For the indexes 2log K greater than 2 and no more than 6, the precision was 0.57, and the number of findings was 131. For the indexes 2log K greater than 6 and no more than 10, the precision was 0.66, and the number of findings was 92. For the indexes 2log K greater than 10, the precision was 0.94, and the number of findings was 109.

This experimental result implies that considering the Bayes factor is useful when selecting a better model with the mixed-LiNGAM method. For the largest Bayes factor cases, the algorithm identified the correct model in more than 90% of the cases with a small sample size of 100.

Discussion

The main assumptions are the linearity and acyclicity of causal relations among observed variables and hidden common causes, non-Gaussian continuous errors, and such many hidden common causes whose sum can be approximated by a bell-shaped curve distribution. The effects of model violations have not yet been extensively studied and should be a good direction of future research. However, it should be possible to extend the proposed method to allow some types of nonlinearity and cyclicity based on the ideas of nonlinear and cyclic extensions (Hoyer et al. 2009; Zhang and Hyvärinen 2009; Lacerda et al. 2008) of basic LiNGAM.

Further, the effects of nonlinearly transforming observed variables should be investigated. Some transformations may make the observed variables more non-Gaussian, but they may also make the functional relations nonlinear. A promising way of modeling such transformations is to use the framework of post nonlinear causal models (Zhang and Hyvärinen 2009). The framework can handle variable-wise nonlinear transformations of observed variables generated from nonlinear and linear acyclic models with no hidden common causes, including the basic LiNGAM. The proposed method would benefit from such theoretical advances.

In the proposed approach, hidden common causes are assumed to be continuous. However, even if the hidden common causes are binary, their sum is approximated well by some bell-shaped curve distribution because of the central limit theorem if the number of hidden common causes is large enough. Therefore, the proposed Bayesian method should work better for more hidden common causes, as long as the noise levels including the magnitudes of effects of hidden common causes and those of error variables do not get too large. A natural way would be to use the Gaussian distributions to approximate the sums of hidden common causes motivated by the central limit theorem. However, in practice, the approximation may be not perfect, and there may be outliers. Thus, the t-distribution with heavier tails than the Gaussian distribution was used in the artificial data experiments in the hope that the inference would become more robust.

Further, in cases that all of the hidden common causes are known and measured, their effects can simply be removed by using regression. When only a smaller subset of the hidden common causes is known and measured, the current Bayesian approach for the two variable cases cannot fully benefit from the observed hidden common causes except when they are the only root variables, i.e., variables that have no parent variables. If they are the only root variables, the other variables only have to be conditioned on the root variables.

This study focused on two variable cases with hidden common causes. This is because analyzing only a smaller subset of observed variables does not lose validity if hidden common causes are allowed. For more than two variables, one approach is to apply the proposed method to every pair of the variables. Then, the estimation results can be combined to infer the entire causal graph.

Conclusion

The utilization of non-Gaussianity to estimate SEMs is useful for causal discovery because non-Gaussian methods are capable of uniquely estimating causal direction even in the presence of unobserved common causes under the model assumptions. Non-Gaussian data are widely encountered (Spirtes and Zhang 2016), and the non-Gaussian approach can be useful in such applications. Download links to papers and codes on this topic are available online: https://sites.google.com/site/sshimizu06/home/lingampapers.