Testing and refining theories of how intervention works to influence outcomes lies at the heart of prevention science. According to the recently updated standards for evidence in research on prevention interventions (Gottfredson et al. 2015), the Society of Prevention Research (SPR) emphasizes that any intervention theory should provide an account of the underlying theoretical mechanism through which an intervention has an effect on the outcome of interest. The “black box” of intervention effects can often be disentangled through decomposing the intervention theory into two core components: an “action theory” that explains how the treatment influences potential mediators and a “conceptual theory” that explains how those mediators are related to the outcome (Chen 1990). Thus, mediation modeling (Baron and Kenny 1986; MacKinnon 2008) can now be seen as a prime method in prevention science because it enables researchers to statistically decompose total treatment effects into direct and indirect effect components. Here, an indirect effect reflects the proposed explanation of why and how the intervention has an effect on the outcome. The direct effect represents a summary of those effects that cannot be explained by the mediator.

Mediation analysis is often considered a (seemingly) intuitive statistical tool to understanding the causal mechanisms of treatment effects. However, in particular, the recent re-conceptualization of total, direct, and indirect effects using the counterfactural (potential outcome) framework of causation (Imai et al. 2010; Pearl 2001) made the exact conditions explicit under which a mediation effect can be interpreted as being causal transparent to researchers. For example, even when a treatment (i.e., the predictor x) is randomized, it is now well understood that the causal effect of a mediator (m) on the outcome (y) cannot be uniquely identified without imposing uncounfoundedness assumptions (so-called ignorability conditions) on the data. These assumptions are similar to those of observational studies. For this reason, blockage- or enhancement designs have been proposed (Imai et al. 2011) with the goal of, in addition to the predictor, experimentally controlling the hypothesized mediator. However, these designs, again, introduce strong assumptions (for details see Bullock et al. 2010).

While research on causal mediation analysis mainly focused on causal effect identification and sensitivity properties under confoundedness, another more subtle assumption received considerably less attention. That is, the assumption of correctness of causal ordering of variable relations that are not under experimental control. For example, in the simple mediation model with randomized treatment, the direction of the mediator-outcome effect, i.e., whether m → y or y → m better approximates the data-generating mechanism, is not uniquely identified and must be determined based on a priori theory alone (Wiedermann and von Eye 2015a, 2016). Here, temporality of mediator-outcome effects is often used as a “remedy.” However, simply measuring the tentative mediator earlier in time than the tentative outcome does not prove causation. Suppose that the “true” mediational mechanism has the form x → y → m. Measuring m at time point t1 (e.g., 3 months after randomization) and y at t2 (6 months later) may, from a purely statistical perspective, support the model x → m1 → y2 although y0, active at an earlier point in time t0, might actually have caused m1 (MacKinnon 2008). Furthermore, spuriousness must also be considered as a possible explanation for the relation of temporally ordered variables (Shrout and Bolger 2002). When mediator and outcome are measured on the same occasion, exploratory approaches are sometimes recommended to evaluate the hypothesized mediation model against plausible alternatives (e.g., Gelfand et al. 2009; Hayes 2013; Iacobucci et al. 2007). Here, different model specifications are examined with the aim of gaining further insights into the data. In other words, the comparison of the mediation effects of x → m → y and x → y → m is assumed to provide empirical guidance to selecting the model that better approximates the data-generating mechanism. Wiedermann and von Eye (2015a) cautioned against such a strategy because alternative model specifications do not provide any further information on the plausibility of a model. This can be explained by the fact that direct and indirect effect estimates depend on the magnitude of pairwise correlations of variables and nothing new is learned from the data that would justify statements about the correctness of a certain mediation model.

When competing conceptual theories about the intervention mechanism exist, statistical methods to evaluate whether one mediation model is superior over an alternative model are desirable. The present work introduces methods of Direction Dependence Analysis (DDA; Wiedermann and von Eye 2015b; Wiedermann and Li 2018) as statistical tools to make such decisions concerning directionally competing models, and applies these methods to the analysis of mediation processes under randomized treatment. The present work extends previous work (Wiedermann and von Eye 2015a, 2016) in three ways: (1) previous studies focused on direction dependence properties of mediation models in purely observational data; we extend DDA for mediation models to situations in which the predictor is under experimental control. (2) DDA has been discussed for cases in which error terms of correctly specified mediation models follow a normal distribution; we discuss methods for errors that are non-normal. (3) Most important, previous studies on DDA in mediation models only considered the two directional explanatory models (in the present context, m → y vs. y → m); we extend DDA to cases in which unconsidered common variables (so-called confounders) are present and show that, by using DDA, all three explanatory models are mutually distinguishable.

In the following sections, we, first, introduce the basic principles of analyzing directional dependence and formally define and review the assumptions of competing mediation models when the treatment is randomized. Then, the two direction dependence components of asymmetry properties of higher-order correlations and asymmetry properties of the independence assumption of explanatory variables and error terms of competing models are introduced. These asymmetry properties can be used to probe the causal precedence of mediator-outcome relations. Significance tests for hypotheses concerning the causal effects of mediator-outcome relations are proposed, and results of a simulation study are presented that evaluates the performance of the tests when selecting the “true” mediation model. A data example is given for illustrative purposes. The article closes with a discussion of possible extensions and empirical requirements of the DDA methodology.

The Direction Dependence Principle

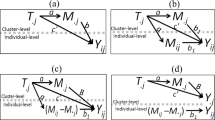
In this section, we focus on the simple linear mediation model, i.e., x denotes the randomized treatment, m is the tentative mediator, and y is the tentative outcome. Note that the presented approach can easily be extended to multiple mediation models (further details are provided in the Discussion section). Mediator and outcome are restricted to be continuous. However, considering that many studies in prevention science make use of composite scores, the presented approach is still applicable to a broad range of research areas. Assuming that mediator and outcome are measured on the same occasion, Fig. 1 conceptually summarizes at least three possible explanations of a mediation effect. For all three explanatory models, we assume that the treatment x affects both, the mediator m and the outcome y, describing a partial mediation process (note that DDA is also applicable in case of full mediation processes). The first model assumes that the mediator causes the outcome (i.e., m → y; Fig. 1a). The second model assumes a reversed causal flow, that is, the outcome causes the mediator (y → m; Fig. 1b). The third model postulates that an unknown common variable u (a confounder) exists that induces a spurious mediator-outcome association (m ← u → y; Fig. 1c). Conventional linear regression-based methods and standard linear structural equation models (SEMs) cannot be used to decide which model best represents the underlying data-generating mechanism. The reason for this is that both methods use data variation up to only second order moments, i.e., variances and covariances. By definition, the covariance is symmetric, i.e., cov(m, y) = cov(y, m), and, thus, no empirical information is available that would help to distinguish cause and effect (von Eye and DeShon 2012). In SEM, this symmetry property is reflected by so-called Markov equivalence classes, i.e., classes of models in which each model has the exact same support by the data in terms of model fit (Stelzl 1986). In contrast, DDA considers data information beyond second order moments (skewness and kurtosis) because asymmetry properties of the Pearson correlation and the related linear model exist under non-normality. These asymmetry properties describe data situations in which variables can no longer be exchanged in their roles as explanatory and outcome variables without leading to systematic violations of model assumptions. In other words, by making use of non-normality of variables, it is possible to identify the model that best approximates the underlying causal mechanism. In the following paragraphs, we define the three mediation models considered in Fig. 1 and introduce two asymmetry properties of the mediator-outcome path under randomized treatment. We also describe significance procedures to test hypotheses compatible with directional dependence. To simplify presentation, we assume that m → y is the “true” confounder-free model and y → m represents the directionally mis-specified model. To simplify notation, we, first, focus on direction dependence in bivariate mediator-outcome relations and ignore the randomized treatment effect. Approaches to adjust for treatment effects will be taken up later.

Fig. 1
figure 1

Conceptual diagrams of three possible explanations of a randomized treatment (x) and a significant mediator-outcome relation. Treatment status is determined at study baseline, m and y are assumed to be measured at the same follow-up measurement occasion. Rectangles represent observed variables, circles represent unobserved variables. Model (a): m causes y, Model (b): y causes m, and Model (c): an unconsidered confounder u is responsible for the m-y relation

Full size image

Competing Mediation Models

Throughout this article, we assume that the data-generating mechanism can validly be described by the linear model. Thus, under randomized treatment x and a causal mechanism of the form m → y, the mediation model can be written as (without loss of generality the intercepts are fixed at zero and continuous variables have zero means and unit variances)

$$ m={b}_{mx}x+{e}_{m(x)} $$
(1)
$$ y={b}_{yx}x+{b}_{ym}m+{e}_{y(xm)} $$
(2)

where byx, and byx + bmxbym represent the direct and total effects of x on y and bmxbym represents the indirect effect of x on y via m (in general, unless otherwise stated, we refer to parameters as population values). Parameter estimates can be obtained using ordinary least squares (OLS) or, in SEMs, maximum likelihood estimation (DDA can be applied under either estimation scheme). The error terms em(x) and ey(xm) are assumed to be independent of the predictors and of each other, i.e., unconfounded variable relations are assumed (here cov(em(x), ey(mx)) = 0 is equivalent to the sequential ignorability assumption in the causal mediation framework; Imai et al. 2010). While the predictor x is assumed to be independent from the error terms due to randomization, independence must be presumed for the mediator. Further, we assume that the error terms are asymmetrically distributed (i.e., non-zero skewnesses), which deviates from the classical mediation model where error normality is usually part of the model definition. It is important to note that the normality assumption is not needed to ensure that OLS point estimates are unbiased, consistent, and (among all linear unbiased estimators) most efficient (Fox 2008). However, statistical inference on regression parameters might be in jeopardy under non-normal errors. Although significance tests are quite robust for large samples, bootstrap techniques can be used as a remedy (cf. Davison and Hinkley 1997). Because em(x) in Eq. (1) is skewed, the continuous mediator (m) will also be skewed and quantified to have non-zero skewness where skewness is defined as \( {\upgamma}_m=E\left[{\left(m-E\left[m\right]\right)}^3\right]/{\upsigma}_m^3 \) (the expected value operator E is shorthand for “average over all subjects”).

The second model that can be entertained is the one that treats y as the mediator and m as the outcome (Fig. 1b). If y → m instead of m → y represents the underlying flow of causation, the mediation model changes to

$$ y={b}_{yx}x+{e}_{y(x)} $$
(3)
$$ m={b}_{mx}x+{b}_{my}y+{e}_{m(xy)}. $$
(4)

Again, x represents the experimentally controlled treatment with bmx, and bmx + byxbmy being the direct and total effects of x on m and byxbmy being the indirect effect of x on m via y. Again, the error terms ey(x) and em(xy) are assumed to be skewed and independent of model-specific predictors and of each other.

Finally, as a third possible explanation, an unconsidered confounder u can induce a spurious mediator-outcome association (Fig. 1c; note that the present approach can also detect partial confounding). In this case, the model can be written as follows:

$$ m={b}_{mx}x+{b}_{mu}u+{e}_{m(xu)} $$
(5)
$$ y={b}_{yx}x+{b}_{yu}u+{e}_{y(xu)}. $$
(6)

Here, the confounder u and/or the two error terms are assumed to be skewed and errors are assumed to be independent of model-specific predictors and of each other. The parameters bmu and byu quantify the magnitude of the confounding effect.

Asymmetric Properties of Higher-Order Correlations

The first direction dependence component considered here makes use of asymmetry properties of higher-order correlations (HOCs) of variables

$$ \mathrm{cor}{\left(m,y\right)}_{ij}=\frac{\operatorname{cov}{\left(m,y\right)}_{ij}}{\upsigma_m^i{\upsigma}_y^j} $$
(7)

with \( \operatorname{cov}{\left(m,y\right)}_{ij}=1/n\sum {\left(m-\overline{m}\right)}^i{\left(y-\overline{y}\right)}^j \) being the higher-order covariance sample estimate and \( {\upsigma}_m^i \) and \( {\upsigma}_y^j \) being the ith and jth power of the standard deviations of m and y. When using the power values i = j = {1, 2}, HOCs of m and y can be expressed as a function of the Pearson correlation of m and y (ρym) and the skewness of the “true” mediator. Specifically, when m → y is the “true” model, one obtains \( \mathrm{cor}{\left(m,y\right)}_{12}={\uprho}_{ym}^2{\upgamma}_m \) and cor(m, y)21 = ρymγm, which implies that

$$ {\uprho}_{ym}=\frac{\mathrm{cor}{\left(m,y\right)}_{12}}{\mathrm{cor}{\left(m,y\right)}_{21}} $$
(8)

(Dodge and Rousson 2000). Because the correlation coefficient is bounded by the interval – 1 ≤ ρym ≤ 1, it follows that (excluding a perfect linear correlation of ∣ρmy∣ = 1 due to practical irrelevance)

$$ \mathrm{cor}{{\left(m,y\right)}^2}_{12}<\mathrm{cor}{{\left(m,y\right)}^2}_{21} $$
(9)

holds whenever m is the “true” mediator and y is the “true” outcome. Similarly, one observes

$$ \mathrm{cor}{{\left(m,y\right)}^2}_{12}>\mathrm{cor}{{\left(m,y\right)}^2}_{21} $$
(10)

under the causally reversed model where y is the “true” mediator and m is the “true” outcome. A bootstrap confidence interval (CI) for the difference in HOC estimates, d = cor(m, y)221 − cor(m, y)212, can be constructed for statistical inference. Here, bootstrap samples of size n are drawn with replacement from the original sample and d is computed for each new sample. This process is repeated B times and those d values that are associated with the α/2 × 100th and (1 – α/2) × 100th percentiles reflect the (1 – α) × 100 CI limits for the desired significance level α. If d is significantly larger than zero, then m → y is more likely to approximate the data-generating mechanism. Conversely, if d is significantly smaller than zero then y → m is more likely to hold.

If a confounder induces the mediator-outcome association, HOCs of m and y are functions of (1) the skewness of the confounder and (2) the pairwise correlations of the confounder with m and y. Specifically, under the model m ← u → y, one obtains \( \mathrm{cor}{\left(m,y\right)}_{12}={\uprho}_{mu}{\uprho}_{yu}^2{\upgamma}_u \) and \( \mathrm{cor}{\left(m,y\right)}_{21}={\uprho}_{mu}^2{\uprho}_{yu}{\upgamma}_u \) (with \( {\upgamma}_u=E\left[{\left(u-E\left[u\right]\right)}^3\right]/{\upsigma}_u^3 \) being the skewness of the confounder) which leads to the ratio

$$ \frac{\mathrm{cor}{\left(m,y\right)}_{12}}{\mathrm{cor}{\left(m,y\right)}_{21}}=\frac{\uprho_{yu}}{\uprho_{mu}}. $$
(11)

In other words, the outcome of the HOC test depends on the magnitude of the ratio of two correlations ρyu and ρmu. When \( {\uprho}_{yu}^2 \) is smaller than \( {\uprho}_{mu}^2 \), it follows that d > 0 and one is more likely to select the model m → y. In contrast, when \( {\uprho}_{yu}^2 \) is larger than \( {\uprho}_{mu}^2 \), then d < 0, which points at the reversed model y → m. Thus, the HOC test assumes unconfoundedness of the “true” model and should be applied with caution whenever confounders are likely to be present. To empirically evaluate the absence/presence of influential confounders, the second DDA component (tests based on independence properties) can be used.

Asymmetric Independence Properties

In linear regression modeling, “independence” refers to the assumption that the magnitude of the error made when predicting the outcome is unrelated to model predictors. Again, let the model in Fig. 1a be the “true” model. Due to randomization, x will be independent of em(x) in Eq. (1) and ey(xm) in Eq. (2). Further, in the absence of confounders, independence will also hold for m and ey(xm). In contrast, non-independence of m and ey(xm) will hold when either a confounder is present (cf. Fig. 1c) or the mediator-outcome path is directionally mis-specified (cf. Fig. 1b). Consider the case in which one erroneously assumes a directional effect from y to m, i.e., the mis-specified bivariate model takes the form m = bmyy + em(y). When inserting the correctly specified bivariate model y = bymm + ey(m), the error term of the mis-specified model can be written as (Shimizu et al. 2011; Wiedermann and von Eye 2015b)

$$ {e}_{m(y)}=\left(1-{\uprho}_{my}^2\right)m-{b}_{my}{e}_{y(m)} $$
(12)

In other words, both, y and em(y), are linear functions of the “true” mediator m and the “true” error term ey(m) from which follows that y and em(y) will be non-independent. Further, for an unconsidered confounder, the independence assumption will be violated in both directionally competing models. This can be seen by expressing the error terms of the two competing bivariate models involving m and y as a function of the true mechanism y = byuu + ey(u) and m = bmuu + em(u) which gives

$$ {\displaystyle \begin{array}{c}{e}_{y(m)}=\left({b}_{yu}-{b}_{ym}{b}_{mu}\right)u-{b}_{ym}{e}_{m(u)}+{e}_{y(u)}\\ {}{e}_{m(y)}=\left({b}_{mu}-{b}_{my}{b}_{yu}\right)u-{b}_{my}{e}_{y(u)}+{e}_{m(u)}.\end{array}} $$
(13)

In other words, m and the error term ey(m) share u and em(u) as common influences and y and em(y) have the common influences u and ey(u). While these two examples serve as intuitive explanations, a rigorous proof of non-independence in directionally mis-specified models of non-normal variables is given in Shimizu et al. (2011) and Wiedermann and von Eye (2015b).

Because OLS residuals and model predictors will always be uncorrelated by construction, significance tests beyond first-order correlations are needed to test independence. Independence tests for (linearly uncorrelated) variables have extensively been discussed in signal processing (Hyvärinen et al. 2001). Here, we focus on so-called non-linear correlation (NLC) tests. In essence, NLC tests make use of the fact that stochastic independence is defined as zero correlation of any continuous unbounded functions of two variables x1 and x2, formally, cov(g(x1), f( x2)) = 0 for any functions f and g. These tests rely on the Pearson correlation test applied to non-linearly transformed variables and are, thus, easy to use. In the present context, squaring residuals is of particular value, because, in the mis-specified model y → m, non-linear covariances then contain information of the skewness of the “true” mediator and the “true” error term (Wiedermann et al. 2017),

$$ \operatorname{cov}\left(y,{e}_{m(y)}^2\right)={\uprho}_{my}{\left(1-{\uprho}_{my}^2\right)}^2{\upgamma}_m+{\uprho}_{my}^2{\upsigma}_{e_{y(m)}}^3{\upgamma}_{e_{y(m)}}. $$
(14)

Thus, the non-linear correlation of y and \( {e}_{m(y)}^2 \) increases with the skewness of m and ey(m). Because independence is assumed in the “true” model m → y, i.e., \( \operatorname{cov}\left(m,{e}_{y(m)}^2\right) \) = 0, the two competing models are asymmetric in their independence properties. For example, if \( \mathrm{cor}\left(y,{e}_{m(y)}^2\right) \) ≠ 0 and \( \mathrm{cor}\left(m,{e}_{y(m)}^2\right) \) = 0 then m → y is more likely to approximate the underlying mechanism. Conversely, if \( \mathrm{cor}\left(y,{e}_{m(y)}^2\right) \) = 0 and \( \mathrm{cor}\left(m,{e}_{y(m)}^2\right) \) ≠ 0 then y → m is more likely to hold. Significance testing can be carried out using Pearson’s correlation test.

Model Selection Guidelines and Adjusting for Treatment Status

So far, we have treated the mediator-outcome association as a bivariate linear model ignoring the treatment effect. To adjust for the treatment effect, we make use of the fact that any multiple linear regression model can be expressed as a partial regression model based on residualized variables. Specifically, DDA can be performed on treatment-residualized variants of the mediator and the outcome to either select m → y, y → m, or m ← u → y. First, one estimates the two auxiliary regression models where y and m are regressed on the treatment x. The extracted residuals of these auxiliary models (i.e., ey(x) for the model x → y and em(x) for the model x → m) represent “purified” measures of y and m adjusted for the treatment effect. Thus, the two adjusted models reflecting m → y and y → m, can also be estimated via

$$ {e}_{y(x)}={a}_{ym}{e}_{m(x)}+{\uptheta}_{y(m)} $$
(15)
$$ {e}_{m(x)}={a}_{my}{e}_{y(x)}+{\uptheta}_{m(y)} $$
(16)

where regression coefficients and error terms are equivalent to those of their multiple variable counterparts in Eq. (2) and (4), i.e., bym = aym, bmy = amy, ey(xm) = θy(m), and em(xy) = θm(y). Performing DDA tests using the models in Eq. (15) and (16) enables one to evaluate the causal direction of the mediator-outcome relation while adjusting for the treatment effect.

The following decision rules can be used to probe the causal precedence of the tentative mediator and tentative outcome (now replacing population parameters with sample estimates):

  • m is more likely to be the mediator and y is more likely to be the outcome, i.e., m → y, when (1) \( d=\mathrm{cor}{{\left({\widehat{e}}_{m(x)},{\widehat{e}}_{y(x)}\right)}^2}_{21}-\mathrm{cor}{{\left({\widehat{e}}_{m(x)},{\widehat{e}}_{y(x)}\right)}^2}_{12} \) is significantly larger than zero and (2) non-linear correlations of \( {\widehat{e}}_{m(x)} \) and \( {\widehat{\uptheta}}_{y(m)} \)do not significantly deviate from zero and, at the same time, non-linear correlations of \( {\widehat{e}}_{y(x)} \) and \( {\widehat{\uptheta}}_{m(y)} \)do significantly deviate from zero (\( {\widehat{e}}_{m(x)} \) and \( {\widehat{e}}_{y(x)} \) refer to the estimated residuals of the two auxiliary regression models described above, and \( {\widehat{\uptheta}}_{y(m)} \) and \( {\widehat{\uptheta}}_{m(y)} \) are the estimated residuals of the models (15) and (16)).

  • y is more likely to be the mediator and m is more likely to be the outcome, i.e., y → m, when (1) \( d=\mathrm{cor}{{\left({\widehat{e}}_{m(x)},{\widehat{e}}_{y(x)}\right)}^2}_{21}-\mathrm{cor}{{\left({\widehat{e}}_{m(x)},{\widehat{e}}_{y(x)}\right)}^2}_{12} \) is significantly smaller than zero and, (2) non-linear correlations of \( {\widehat{e}}_{m(x)} \) and \( {\widehat{\uptheta}}_{y(m)} \)do significantly deviate from zero and, at the same time, non-linear correlations of \( {\widehat{e}}_{y(x)} \) and \( {\widehat{\uptheta}}_{m(y)} \)do not significantly deviate from zero.

  • A confounder u is most likely to be present, when non-linear correlation tests do not allow a clear-cut decision, i.e., when tests of both models are significant/non-significant. The latter emerges from the fact that confounders can decrease the magnitude of non-normality of variables to a degree that renders non-independence no longer detectable. Further, in this case, the difference measure d depends on the magnitude of the correlations of m and y with the confounder u (see above).

Performance of the Model Selection Strategy

In this section, we present the results of a Monte-Carlo simulation study that assessed the performance of model selection using the proposed decision guidelines. Data were simulated according to the true model given in Eq. (1) and (2), i.e., x is a binary treatment variable, m is a continuous mediator, and y is the continuous outcome. We restricted the simulation to the case of equal group sizes. Model intercepts were fixed at zero and regression coefficients were selected to account for small (2% of the variance of the dependent variable), medium (13% of the variance), and large effects (26% of the variance; Cohen 1988). The error terms of the mediation model, em(x) and ey(xm), were generated to exhibit zero means, unit variances, and pre-specified skewness values of 0, 1, and 2 (which is in line with skewness values observed in practice; e.g., Cain et al. 2017). In the zero-skewness case, errors were randomly drawn from the standard normal distribution. Because no directional decisions are possible in the normal case, these scenarios refer to the Type I error behavior of the model selection procedure. Non-zero skewness values were obtained by sampling from the gamma distribution and were used to quantify the empirical power of the tests to identify the “true” model. Sample sizes were n = 200, 500, and 1000. The simulation factors were fully crossed and 1000 samples were generated for each of the 3 (effect size of bmx) × 3 (effect size of byx) × 3 (effect size of bym) × 3 (skewness of em(x)) × 3 (skewness of ey(xm)) × 3 (sample size) = 729 simulation conditions.

For each variable triple, x, m, and y, we, first, regressed m and y on x and extracted the corresponding residuals, \( {\widehat{e}}_{m(x)} \) and \( {\widehat{e}}_{y(x)} \), reflecting the “treatment-purified” mediator and outcome variables. These variables were subsequently analyzed using the two simple linear regression models given in Eq. (15) and (16), that is, reflecting m → y and y → m. One thousand bootstrap samples were used for the HOC test. To evaluate the independence assumption, NLC tests (using the square function for residuals) were separately performed for both models using a significance level of 5%. Model selection was based on the decision guidelines given above.

Results

Table 1 gives the percentages of correctly identifying the causal model m → y in terms of main effects of the simulation conditions (i.e., results for one condition are aggregated across all levels of the remaining conditions). The first four columns show the model selection results for the HOC test and the combined decisions of separate NLC tests in the normal case and when error terms are skewed (see columns labeled with “non-normal case”). Percentages of selecting the “true” model based on the HOC test are close to zero. That is, the procedure is overly conservative in Type I error decisions (note that conservative decisions lead to reduced power which does not invalidate HOC test results per se). In contrast, Type I error rates of the combined NLC tests are close to the nominal significance level of 5% across all simulation conditions. Overall, in the normal case, no distinct decision can be made as expected.

Table 1 Percentages of selecting m → y for HOC and NLC tests as a function of simulation factors when error terms are normally distributed (normal case) and when em(x) is skewed (non-normal case). Values in parentheses give the percentages of selecting the mis-specified model y → m. The last four columns give percentages of combined decisions of the two tests
Full size table

Next, we focus on the non-normal case. As noted above, asymmetry of the mediator is of central importance for both DDA tests. Thus, we focus on cases in which \( {\upgamma}_{e_{m(x)}} \) > 0. Percentages of identifying the “true” model increase with the sample size and the magnitude of the causal effect bym. The power of the NLC procedure increases with the non-normality of both error terms (em(x) and ey(xm)). In contrast, the power of the HOC test increases with the non-normality of em(x) and decreases with the non-normality of ey(xm). Because all tests were adjusted for treatment effects, the magnitudes of the effects involving x (byx and bmx) had virtually no impact on the power of the tests. In general, the HOC test was less powerful than separately evaluating error independence using NLC tests. The last four columns in Table 1 summarize combined decisions of both approaches for \( {\upgamma}_{e_{m(x)}} \) > 0. Percentages in which both approaches correctly identify m → y were close to the observed power curves of the HOC test. Most important, the rates of inconclusive decisions and the rates of erroneously selecting the reverse model y → m are virtually zero. Overall, both procedures show adequate power properties and are able to identify the correct mediation model. Following Cohen’s (1988) 80% power criterion, we arrive at the following conclusions with respect to the most influential factors (bym, \( {\upgamma}_{e_{m(x)}} \), and n): For large bym effects and moderately skewed errors (\( {\upgamma}_{e_{m(x)}} \) = 1), sample sizes n ≥ 500 are needed to achieve acceptable power (for \( {\upgamma}_{e_{m(x)}} \) = 2, even small sample sizes such as n = 200 are sufficient). For medium bym effects and moderately skewed errors large samples (n = 1000) are needed, while small sample sizes are sufficient for highly skewed errors. Finally, for small bym effects, sample sizes beyond n = 1000 would be required even for highly skewed errors (for this scenario, we observe a power of 68.4%).

Data Example: The Impact of Acupuncture on Quality of Life and Chronic Pain

We now illustrate HOC- and NLC-based model selection using a real-world data example with the intention of emphasizing different possible outcomes that can be obtained from DDA (i.e., situations in which one causal model is clearly preferred vs. situation in which confounders are likely to be present). The data come from a randomized controlled trial that evaluates the effectiveness of acupuncture to treat chronic headache in primary care patients (Vickers et al. 2004; Vickers 2006). In total, 401 patients (205 with acupuncture treatment and 196 control patients) between 18 and 65 years of age (M = 45.5, SD = 11.1) completed a daily diary on health-related quality of life (HRQoL; cf. de Wit and Hajos 2013) and headache severity for 4 weeks at baseline, 3 months, and 1 year after randomization. HRQoL was measured using the SF-36 health status questionnaire (Stewart and Ware Jr. 1992), headache severity was measured four times a day and scaled using composite scores of a six-point Likert scale (0 = no headache, …, 5 = intense, incapacitating headache).

Vickers et al. (2004) reported that acupuncture treatment significantly improved headache and HRQoL (specifically for the subscales energy/fatigue and health change). Within the various factors affecting HRQoL, perceived pain is a known mediator (Azizabadi Farahani and Assari 2010). We use follow-up data 1 year after randomization and ask whether the relation of acupuncture, headache severity, and HRQoL can be represented by a mediational mechanism. Specifically, we test the hypothesis that the effect of acupuncture on HRQoL is mediated by headache severity. However, because experimental control was not applicable for headache severity, the reverse causal flow (HRQoL → headache) or the presence of unconsidered confounders cannot be ruled out. Thus, we use DDA tests to empirically confirm a directional relation of the form headache → HRQoL. We use two headache measures (composite scores of headache severity and number of days of headache in 28 days) and two different HRQoL measures (subscales energy/fatigue and health change) from 297 patients who provided valid data 1 year after randomization. Table 2 summarizes descriptive statistics for the considered headache and HRQoL measures. Because outliers can adversely affect the validity of DDA, regression diagnostics were applied in a pre-evaluation phase to detect potentially conspicuous observations (Wiedermann and von Eye 2015b). Based on Cook’s distances, one observation was classified as conspicuous. This observation was omitted from subsequent analyses. In total, four different mediation models were estimated. In all models we adjusted for patients’ age and baseline headache and HRQoL scores.

Table 2 Mean (M), standard deviation (SD), skewness (γ), and excess-kurtosis (κ) for headache and HRQoL measures at baseline and 1-year follow-up
Full size table

Results

Based on bias-corrected accelerated (BCa) nonparametric bootstrapping CIs (with 2000 resamples), we found significant indirect effects for all four mediation models (cf. Table 3) confirming that acupuncture lowers headache severity which, in turn, increases HRQoL. In addition, we obtained significant direct effects for all four models (results not shown) suggesting a partial mediation process of acupuncture, headache, and HRQoL. Next, we evaluated the directionality assumption of the mediator-outcome path inherent to all mediation models. Headache and HRQoL measures significantly deviated from normality (all Shapiro-Wilk p’s < 0.001; skewness estimates ranged from − 0.26 to 1.40 at baseline and from − 0.37 to 1.75 for 1-year follow-up measures; excess-kurtosis estimates ranged from − 0.85 to 1.77 at baseline and from − 0.54 to 3.49 at the 1-year follow-up; cf. Table 2) and, thus, fulfill distributional requirements of DDA. Two thousand bootstrap samples were used to approximate 95% CI limits of the HOC test. The independence assumption was evaluated using NLC tests of squared residuals and untransformed predictors. Results are summarized in Table 3. In general, no distinct decisions are possible based on HOC tests which is line with the observation that rather large sample sizes are needed to achieve acceptable statistical power. Thus, we base direction dependence decisions on independence properties of competing models. NLC tests retain the null hypothesis of independence for all models that posit headache → HRQoL and, at the same time, reject independence in three out of four reversed models (HRQoL → headache; all ps < 0.05). When focusing on headache frequency and perceived health change independence is retained in both models. Making use of the decision guidelines for NLC tests, we have found empirical evidence that headache severity is more likely to causally affect HRQoL than the other way around in three out of four mediation models.

Table 3 Direction dependence results for testing mediation effects of headache and HRQoL under randomized acupuncture treatment among primary care patients. Degrees of freedom of the NLC tests vary due to missing values
Full size table

Robustness of Direction Dependence Results

To complete the analysis, a bootstrapping approach was used to evaluate the robustness of DDA results. For unstable DDA solutions (e.g., due to suboptimal sampling or outliers), one would expect that causal conclusions vary across resamples. The overall percentages how often DDA tests provide evidence for the target model, the causally reversed model, or indicate the presence of common causes can serve as post hoc measures of robustness. For each mediation model, 1000 resamples were generated (i.e., resampling subjects from the original dataset with replacement). For each resample, HOC and NLC tests were performed while adjusting for treatment status, age, and baseline headache and HRQoL scores. Detailed results are given in Table S1 in the online supplement of the article. Overall, the mediation model that involved energy/fatigue and headache severity scores shows the highest stability in DDA decisions. Here, in about 74% of the resamples, the model headache → HRQoL is preferred over the other two possible models (the reversed model was preferred in only 0.5%, and a confounded mediation model was suggested in about 26% of the resamples). In contrast, focusing on perceived health changes and headache frequency, a confounded mediation model is suggested in about 67% of the resamples which is in line with the results in Table 3. Overall, we conclude that the postulated mediation effect of acupuncture on HRQoL through headache can be interpreted as causal when focusing on energy/fatigue levels of patients. However, when focusing on perceived health change, unobserved confounders are likely to bias the mediator-outcome relation and estimated mediation effects should not be endowed with causal meaning.

Discussion

The present article introduced principles of direction dependence to prevention scientists and demonstrated that two tests compatible with DDA can be used to empirically evaluate the conceptual theory of an intervention. Simulations showed that DDA has adequate power to detect the true data-generating mechanism. Because data were simulated according to the model m → y, either the HOC or the NLC test can separately be used. However, because the “true” model is not known a priori when real-world data are analyzed, we recommend using both tests. While NLC tests are essential to test confoundedness, HOC tests evaluate distributional properties of variables reflecting directional assumptions. Non-normality of errors is the key element for model identification (DDA tests can be applied for left- or right-skewed distributions). Estimated model residuals are of central importance for inference concerning directionally competing models. Because error non-normality does not affect the validity of OLS point estimates which are, in turn, used to estimate model residuals, direction dependence tests based on residuals (such as the NLC test) will give unbiased results. Bootstrapping can be used to guarantee valid inference on linear model parameters. Further, to keep matters simple, we focused on a single level simple mediation model with no covariates. However, the presented approach can easily be extended in all three domains.

Covariates (e.g., background or baseline measures) are usually included in regression models to increase precision of estimates and statistical power. In the HOC test, additional covariates can be considered in the same way as when adjusting for treatment status. That is, covariates with causes outside the mediation model (in the sense of an exogenous variable) and known to affect the mediator and/or the outcome can be entered in the two auxiliary regression models that regress y and m on the treatment x. The residuals of these extended auxiliary models then represent “purified” mediator and outcome measures that are adjusted for treatment and covariate effects. While a similar strategy can be applied for non-linear correlation tests in case of categorical covariates (e.g., gender, ethnicity, etc.), covariates that are continuous in nature (e.g., baseline scores, age, etc.) can directly be entered in the regression equations of the mediation model.

Prevention researchers are often confronted with complex nested data structures (e.g., patients are nested in health institutions). While extensions of DDA to multilevel models are currently not available, it is important to realize that several research questions can already be answered using DDA. The reason for this is that several single-level alternatives to multilevel models exist when researchers are primarily interested in subject-level (level 1) hypotheses (Huang 2016). In this case, contextual (level 2) clusters are conceptualized as noise and fixed effects models (i.e., representing J clusters by J—1 dummy variables) or running analyses on demeaned data (i.e., level 2 mean centering dependent and independent variables) can be used to account for clustering effects. From a DDA perspective, fixed effects can again be incorporated using the two-stage auxiliary regression approach described above.

While the simple mediation model given in Eqs. (1) and (2) remains the most frequently estimated model in observational and experimental research, intervention studies in prevention science are often concerned with multiple mediational mechanisms. The presented approach can straightforwardly be applied in the presence of multiple mediators. In case of k mediators, the model in (1) and (2) extends to \( {m}_i={b}_{m_ix}x+{e}_{m_i(x)} \) and \( y={b}_{yx}x+{\sum}_{i=1}^k{b}_{y{m}_i}{m}_i+{e}_{y(xm)} \) for all i = 1, …, k mediators (Hayes 2013). While the treatment effect is again partialled out of all putative mediators and the putative outcome, DDA can be used to evaluate the direction of effect by separately reversing those mediator-outcome paths for which \( {\upgamma}_{e_{m_i(x)}}\ne \) 0. One can proceed in a similar fashion for multiple tentative outcomes.

The DDA tests proposed in this article have several limitations that need to be addressed in future research. First, non-normality is the key element of DDA. While a high prevalence of non-normal variables has repeatedly been reported in empirical data (e.g., Micceri 1989; Cain et al. 2017), it is important to realize that not every form of non-normality makes observed variables eligible for the proposed methods. In general, DDA assumes that non-normality reflects an inherent characteristic of variables under study which implies that non-normality as a result of poor item selection, scaling, ceiling/floor effects, or outliers can lead to biased direction dependence results. Thus, the usage of high-quality measurement instruments and a careful pre-evaluation of variable characteristics are central steps towards meaningful causal statements. In addition, stability of DDA results can be evaluated using nonparametric bootstrapping.

Second, while NLC tests are easy to use, these tests are not rigorous in detecting any form of independence. Because the choice of non-linear functions is almost arbitrary (we focused on the square function due to its relation to the skewness of “true” predictors) and testing all existing non-linear functions is impossible, the current approach introduces additional Type II errors beyond cases of small sample sizes. In other words, even if a zero correlation is observed for a specific non-linear function, one cannot rule out that other functions exist for which non-zero correlations would be obtained. While our simulation study suggests that simple non-linear tests have adequate power (and even outperform HOC tests), more sophisticated independence tests are needed to overcome additional Type II errors. Recently, two promising approaches have been proposed, the Hilbert-Schmidt Independence Criterion (Gretton et al. 2008) and the distance correlation (Székely et al. 2007). Both methods can be shown to detect any form of dependence in the large sample limit. Comparing the performance of various independence measures in the context of DDA constitutes future research material. Similarly, in the present study, direction dependence tests were based on raw residuals (i.e., the discrepancy of observed and fitted outcome values). Alternatively, standardized or studentized residuals may be employed which have the advantage that leverage of data points is considered as well. While differences between raw, standardized, and studentized residuals tend to be small for large sample sizes, making use of standardized or studentized residuals may be useful in cases of small sample sizes. Comparing the performance of different residual estimates is also material for future research.

Third, extensions of DDA when interaction effects are present are needed to allow for testing the direction of effect while accounting for a third variable that modifies the mediator-outcome relation. Similar extensions would enable researchers to apply DDA tests in polynomial regression models (i.e., models that consider higher-order terms, cf. Aiken and West 1991) when non-linear variable relations exist. Here, again, a two-step approach similar to the one used to account for treatment and covariate effects may be used. That is, first, regressing mediator and outcome on products of variables (in case of interaction effects) or higher powers of variables (in case of non-linear relations) and, second, performing DDA on the extracted residuals may allow directional statements with respect to the linear components of variable relations. Evaluating the adequacy of this approach constitutes an important future research endeavor.

Overall, DDA is a powerful tool that can help to uncover the structure of causal effect mechanisms, in particular, in situations in which multiple theories exist of the mechanism through which an intervention affects an outcome. To make the proposed DDA tests accessible to prevention researchers, we provide software implementations of HOC and NLC tests in SPSS (macros and introductory material can be downloaded from http://www.ddaproject.com).