In response to limitations imposed by traditional meta-analysis, an increasingly popular approach for data synthesis is individual participant data (IPD) meta-analysis in which the raw individual-level data for each study are obtained and used for synthesis (Riley et al. 2010). With the raw data on hand, an analyst can adjust for patient-level covariates and take into account repeated measures, missing values, and differential follow-up times. In general, pooling data from multiple studies results in larger sample sizes, increased statistical power, increased variability on important measures, and the capacity to test more sophisticated models (Brown et al. 2016). When the combined samples are more heterogenous than any single trial, IPD meta-analysis may also provide increased confidence in generalization (Perrino et al. 2013).

Another advantage of IPD meta-analysis is increased frequencies of low base-rate behaviors such as suicide or drug use. The frequency of these behaviors may be too low to be modeled in any single study, but may be high enough when aggregated across multiple studies. When multiple longitudinal studies are combined, a much broader developmental period can be considered, given overlapping age ranges across the set of contributing studies (Curran and Hussong 2009). IPD meta-analysis can also substantially increase power to detect moderation. Dagne et al. (2016) found that the power to detect moderator effects for individual-level moderators could be as much as 16 times greater for IPD meta-analysis as compared to standard meta-regression.

IPD meta-analysis has its challenges. In particular, a common situation is when variables of interest are measured differently in different studies. The term harmonization has been coined to describe the procedure of placing variables on the same scale in order to permit pooling of data from a large number of studies (Griffith et al. 2015; Hussong et al. 2013).

There are a number of existing methods for data harmonization which make use of the fact that even if different studies use different outcomes, they are attempting to measure the same construct or constructs of interest. One approach is to treat the unobserved measures as missing data and then replace them with plausible values using multiple imputation (Rubin 1987; Gelman et al. 1998; Resche-Rigon et al. 2013; Siddique et al. 2015; Kline et al. 2015).

With multiple imputation, missing values are replaced with two or more plausible values to create two or more completed data sets. Analyses are then conducted separately on each data set and final estimates are obtained by combining the results from each of the imputed data sets using rules that account for within-imputation and between-imputation variability. See Harel and Zhou (2007) for a review.

In the context of harmonization for IPD meta-analysis, multiple imputation has a number of advantages. Once unmeasured variables have been imputed, analyses and their subsequent inferences are based on existing scales of interest. In addition, after the data set has been filled in, it can be shared with other investigators and can be used for numerous analyses using complete data methods. In fact, once a variable has been multiply imputed, it may be used as an outcome in one analysis and as a covariate in another analysis.

Siddique et al. (2015) describe an imputation-based approach to harmonize outcome measures across five longitudinal depression trials where there is no overlap in outcome measures within trials. They extend previous methods for harmonization by addressing harmonization in a longitudinal setting where different studies have different follow-up times and the relationships between outcomes may change over time. They also discuss practical issues in developing an imputation model including taking into account treatment group and study and develop diagnostics for checking the fit of the imputation model.

In this article, we describe a multiple imputation approach for harmonizing depression measures across 19 longitudinal intervention trials where there is no single outcome measure used by all 19 trials. We use the methods of Siddique et al. (2015) for harmonization in a longitudinal setting in order to account for differential follow-up times between studies and to account for the fact that the relationships between outcome variables may change over time. This paper extends the work of Siddique et al. (2015) by implementing the methods in a more challenging setting with 10 measures sparsely distributed across 19 heterogeneous trials. None of the trials used in Siddique et al. (2015) are among the 19 trials in this paper. We implement our methods using free and easily available software and highlight those conditions where it is not possible to produce accurate imputations, either due to an inability to estimate the parameters in the imputation model or due to an inability to estimate study-specific effects.

This article is organized as follows. In Section 2, we describe the example that motivated this work, a study of 19 randomized trials for the prevention of depression among adolescents. In Section 3, we describe our imputation model and diagnostics for checking the quality of imputations when variables are missing for all participants within a study. Section 4 presents the results of applying our methods to the adolescent data and Section 5 offers discussion and areas for future work.

Motivating Example

Our motivating example is an ongoing IPD meta-analysis investigating moderators of treatment effectiveness for the prevention of depression among adolescents. The project consists of individual participant data from 19 adolescent depression prevention trials. In 9 of the 19 trials, the intervention was intended to specifically target youth depression. In the remaining 10 trials, the focus of the interventions was family-based interventions for behavioral health promotion, and for substance abuse and HIV/AIDS sexual risk behavior prevention. Each trial was an RCT with both an intervention and a control group. More details regarding this project are described in the accompanying article by Brown et al. (2016) in this same issue.

Table 1 lists the 19 trials and various study characteristics. The trials ranged in size from 41 to 697 participants and were roughly half male and half female. Participants were mostly teenagers, with an age range of 7 to 21 years of age. Ten of the 19 studies were longer than 2 years, but for this IPD meta-analysis, we only use data from the first 2 years of each trial. Based on these data, the average number of assessments (including baseline) was four, and trial duration ranged from 6 to 24 months with an average duration of 17 months.

Table 1 Trial names and trial-level descriptive statistics for the 19 adolescent depression trials consisting of 5547 participants
Full size table

The last column in Table 1 lists the number of depression measures used in each trial. While some trials only used one depression measure, most used more than one and the Project Alliance 1 trial used six depression measures.

Table 2 lists the 10 different depression measures used in each of the 19 studies and their average values at baseline. Several important points are worth noting. First, there is no measure that is used by all the trials. Second, some measures are self-reported (denoted by a (S) after the measure), some measures are parent-reported (denoted by a (P)), and one measure is clinician-rated (denoted by a (C)). The third point is that while 10 measures are listed, several of the measures are subscales of a larger measure. The Child Behavior Checklist (CBCL) Anxious/Depressed subscale (CBCL-A), the CBCL Withdrawn/Depressed subscale (CBCL-W) (Achenbach 1991), and the CBCL Depression scale (CBCL-D) (Clarke et al. 1992) are all derived from the CBCL. Hence, all three of these parent-reported subscales are often measured in the same trials. Similarly, the Youth Self Report (YSR) Anxious/Depressed subscale (YSR-A) and the YSR Withdrawn/Depressed subscale (YSR-W) (Ebesutani et al. 2011) are both derived from the YSR and tend to be used in the same trials. Trials that used the YSR also tended to use the Revised Brief Problem Checklist Anxiety/Withdrawl subscale (RBPC) (Quay and Peterson 1996).

Table 2 Baseline means and missing data patterns of the 19 adolescent depression trials. Measures followed by an (S) are self-reported measures. Those followed by a (P) are parent-reported measures. Those followed by a (C) are clinician-rated
Full size table

Table 2 also includes two measures, The Center for Epidemiologic Studies Depression Scale (CESD) (Radloff 1977; 1991; Eaton et al. 2004) and also what is referred to as the CESD10. For some follow-up time points, the CATCH IT trial (trial 18) only used 10 items from the CESD, and we refer to this measure as the CESD10 (Radloff 1977). Since the CESD10 is a subset of the CESD, we are able to calculate the CESD10 for all studies that used the CESD except for the ADEPT trial (trial 10) for which item level CESD data were not available. For those follow-up occasions where the CATCH-IT trial did not use the full CESD, we treat the CESD as missing data while recognizing that the CESD and the CESD10 are highly correlated and that we have four studies that contain both these measures.

Roughly speaking, the 19 trials can be placed into three categories based on which depression measures they used: (1) those trials that use the Children’s Depression Inventory (CDI) (Helsel and Matson 1984; Kovacs 1984) and the CBCL, (2) those that use the YSR, and (3) those that use the CESD and the Children’s Depression Rating Scale (CDRS) (Poznanski et al. 1985; Mayes et al. 2010). Our imputation procedure relies on our ability to estimate the relationship among all these variables. In this regard, trials 8, 10, 84, and 247 are particularly important because they provide connections between the three groups of measures. Trial 8 uses the CBCL and the YSR and trial 84 uses the CDI, CBCL, and the YSR. Together, these two trials link categories 1 and 2. Trial 247 links categories 1 and 3 through the CDI and CESD and Trial 10 links categories 2 and 3 through the CBCL and CESD. Still, as highlighted by the shaded cell entries in Table 2, there is a great deal of sparseness in our data set. If we think of Table 2 as an 19×10 matrix, then only 50 of the 190 cells are filled in. As will be shown, this sparseness will prevent us from filling in all missing cells accurately.

Methods

Our approach for harmonizing the depression data across the multiple trials follows that of Siddique et al. (2015) where the uncollected depression measures are considered missing data and missing observations are multiply imputed. To check the quality of our imputations, we perform diagnostics using the re-imputation strategy of He and Zaslavsky (2012) in which observed data are deleted and then imputed and quantities based on imputed values are compared to the same quantities using observed values.

Set Up

We begin by assembling the data in a vertical (long) format, so that each row represents a single participant at a single point in time. Columns are time, demographics, and the 10 different depression measures used across all trials. To account for skewness in outcomes and non-linear trends over time, all depression measures were transformed using a square root transformation. Imputations were also performed on the original scale. Time, measured as the number of months since baseline, was log-transformed. Once imputation is complete, all depression measures are back-transformed to their original distributions.

Imputation Model

Our imputation model is a multivariate linear mixed-effects regression model as described by Schafer and Yucel (2002) and implemented in the R (R Core Team 2012) package PAN (Zhao and Schafer 2013). This model was used by Siddique et al. (2015) to harmonize multiple depression measures in a IPD setting. Using notation from Schafer and Yucel (2002), let y i denote an n i ×r matrix of multivariate data for participant i, i=1,…,m, where each row of y i is a joint realization of depression measures Y 1,…,Y r , which are measured n i times. We assume that y i follows a multivariate linear mixed-effects model of the form

$$ y_{i} = X_{i}\beta + Z_{i}b_{i} + \varepsilon_{i} $$
(1)

where X i (n i ×p) and Z i (n i ×q) are known covariate matrices, β (p×r) is a matrix of regression coefficients common to all units (the “fixed effects”) and b i (q x r) is a matrix of coefficients specific to unit i (the “random effects”). We assume the n i rows of the error terms ε i are independently normally distributed as N(0,Σ) and the random effects are distributed as vec(b i )∼N(0,Ψ) (where the “vec” operator vectorizes a matrix by stacking its columns). In our model, fixed effects include an intercept term, months since baseline (log-transformed), the square of log-transformed months since baseline, gender, and age. Random effects initially included an intercept term and a random months since baseline term.

Imputations of the missing components of y i are generated by drawing from the posterior predictive distribution of the missing data P(Y m i s |Y o b s ). PAN does this using Markov Chain Monte Carlo (MCMC) (Schafer and Yucel 2002), which requires the specification of prior distributions for the parameters in the imputation model in Eq. 1. Here, we use non-informative priors for both the fixed effects and random effects. Specifically, we assume an improper uniform density for the regression coefficents β and non-informative inverse-Wishart priors for the covariance matrix of the random effects and the error variance with r×2 and r degrees of freedom, respectively, and scale parameters equal to the identity matrix. We assessed convergence of our Markov chains by visual inspection of trace plots and autocorrelation plots as well as by using formal MCMC diagnostics (Cowles and Carlin 1996).

Imputations were performed separately by treatment group so that all of the parameters in Eq. 1 can vary by treatment group. Since both sets of imputations (those based on untransformed values and those based on square root transformed values) assume the data are continuous, once missing values were imputed, we considered two strategies to put imputed values back on an ordinal scale: (1) rounding, where values were rounded to the nearest possible value; and (2) leaving imputed values as continuous which means that negative values remain negative, even though all of the scales in Table 2 are non-negative. Strategy 2 is motivated by research showing that when imputing limited-range variables, it may be best to allow imputed values to remain out of range (Rodwell et al. 2014).

Associations Among the Depression Measures

Fitting the parameters of the model in Eq. 1 requires estimation of the association among all the measures listed in Table 2. That is, for every possible pair of measures, there must be at least one trial in which both measures are given to the same participants. For example, in order to estimate the pairwise association of the CDI with the other variables in Table 2, we can use trials 1, 2, and 84 to estimate most of these associations. More problematic is the CDRS which is used in only three trials and overlaps only with the CESD. So, while we are able to estimate the relationship between the CESD and the CDRS, we cannot estimate the relationship of the CDRS with any of the other depression measures. This will ultimately prevent us from accurately harmonizing the CDRS across all 19 trials. Since the CDRS does not provide any information on the relationship between itself and any other variables besides the CESD, we have dropped the CDRS from our list of variables to be harmonized.

Similarly, the RBPC is either measured by itself (trial 3) or with the YSR. In fact, in trial 3 (Familias Unidas 1), the RBPC is the only measure given to participants. Thus, the only relationship we can measure using the RBPC is the relationship between the RBPC and the YSR. However, most trials that use the RBCP also use the YSR and vice-versa. Furthermore, the YSR itself lacks overlap with most of the other measures. This is evident in Table 3 which displays the correlation matrix of all the depression measures. The numbers in parentheses below the correlations on the diagonal report the number of trials which use each measure. The numbers in parentheses below the correlations on the off-diagonal report the number of trials which use both of the measures listed in the row and column. For example, eight trials use the CDI and one trial uses both the CDI and the CESD whose correlation is 0.81. The shaded cell entries in Table 3 identify those pairs of measures in which there is no overlap. The YSR does not overlap with the CESD in any trial, so that it cannot be harmonized in those four trials that use the CESD and nothing else (trials 18, 49, 50, 61). For this reason, and for the additional reason the RBPC has very low correlation with the YSR, we also drop the RBPC from our list of measures to be harmonized. This has the undesirable consequence of requiring us to also remove trial 3 from the 19 trials we wish to synthesize. A similar decision to drop trial 3 was made by Brown et al. (2016) in the companion paper in this issue.

Table 3 Correlation matrix of all depression measures at baseline across the 19 trials. The number in parentheses under the correlation is the number of trials which used the depression measure (diagonal) or the number of trials using both measures (off-diagonal). Measures followed by an (S) are self-reported measures. Those followed by a (P) are parent-reported measures. Those followed by a (C) are clinician-rated
Full size table

Looking at Table 3, only the CDI emerges as a potential variable for harmonization. The CDI overlaps with all of our remaining measures. The correlations between the CDI and all three CBCL subscales are low, but that is a nature of the two measures, one being self-report, the other parent report. Even if we did have item-level data from the ADEPT Trial (trial 10) which would allow us to calculate the CESD10 for this trial (and thus estimate the association with the CBCL-D and the CESD10), the CBCL-D is not a good target for harmonization due to its low correlation with the CESD. Thus, while we will impute all of the depression measures using the model in Eq. 1, we focus our attention on the CDI since it is the only outcome that has the potential to be imputed accurately.

Besides the large number of NA’s which indicate that the correlation was not estimable because there were no trials which used both measures on the same participants, what is notable about Table 3 is how low the correlations are. While the correlations among subscales of the same measures are moderately high, correlations across different measures are relatively low, especially considering that many of these scales are presumable measuring the same construct. This is likely due to the fact that the measures in Table 3 are a collection of self-reported, parent-reported, and clinican-rated measures. For example, the correlation between the CBCL-D (parent-reported) and CDI (self-reported) and is only 0.28. And the correlation between the CBCL-A (parent-reported) and the YSR-A (self-reported) is 0.18. Most notable, the correlation between the CBCL-D (parent-reported) and the CESD (self-reported) is negative and equal to −0.03. The correlations of the RBPC (parent-reported) with the YSR-A (self-reported) and YSR-W (self-reported) are also low, 0.10 and 0.16, respectively. The only large correlation between two different scales is that of the CDI and CESD which are both self-reported and whose baseline correlation is 0.81.

Each depression measure is imputed based on a regression which conditions on the remaining depression measures. Thus, when imputing the CDI, not only do we need to be able to measure the pairwise association of the CDI with the other depression measures, we must also be able to measure the association of the other depression measures with themselves. This second condition is slightly problematic because, as mentioned before, not all the measures overlap with each other. The CBCL-A and the CBCL-W do not overlap with the CESD. For this reason, we also remove the CBCL-A and the CBCL-W from our measures to be imputed. The YSR-A and the YSR-W also do not overlap with the CESD, but we cannot remove both these measures because they are the only measures used by trials 6, 14, 78, and 98. However, the partial correlation of the CDI and the YRS-W, controlling for the YSR-A is only 0.07 at baseline. Therefore, without much loss of information, we can also remove the YSR-W from our imputation model.

Table 4 is a revised version of Table 3, now only including those five measures and 18 studies in our reduced imputation model. The shaded cell entries are those measures with no overlap and thus inestimable covariances. In our Bayesian set-up, when parameters cannot be identified, their posterior distribution is equal to their prior distribution. Our non-informative inverse-Wishart prior for the covariance matrix sets these covariances to be centered around 0. If the unobserved correlations are small, the non-informative prior will have little effect on the resulting imputations. In the discussion, we describe alternative approaches for handling these inestimable parameters.

Table 4 Correlation matrix of depression measures at baseline
Full size table

Imputation Diagnostics

In our setting, where the amount of missing data is considerable and where we are imputing values for every participant within a trial for some depression measures, it is particularly important to check the imputation model and the quality of its imputations. Here, we use posterior predictive checks using numerical summaries based on test statistics (Gelman et al. 1996). We focus on diagnostics that capture important features of the data that are relevant to our target analyses.

Our approach follows the posterior predictive checking and re-imputation strategy of He and Zaslavsky (2012). We do this by duplicating trials 1, 2, 84, and 247 which contain the CDI and at least one of the other measures in Table 4. Next, we deleted all values of the CDI in these duplicated trials. Finally, we concatenated these deleted data sets with the original 18 trials treating the duplicated trials as if they were four additional trials. Table 5 describes the design of our re-imputation strategy. Note that a limitation of the strategy is that it does not allow us to investigate how well our imputation model imputes the CDI in those trials that do not use the CDI.

Table 5 Design of the duplication and re-imputation strategy. Measures followed by an (S) are self-reported measures. Those followed by a (P) are parent-reported measures
Full size table

Next, we generated imputations using the imputation model described above. Let Y be the observed values of the CDI from the duplicated data prior to deletion and Y imp the imputed version of the CDI in the duplicated data set. To compare observed data to imputed data, we use a test statistic, T(Y,𝜃), some scalar function of the data. Posterior predictive checking consists of comparing T(Y,𝜃) to the distribution of T(Y imp,𝜃) where T(Y imp,𝜃) is the test statistic based on imputed values of Y. Lack of fit of the imputed data to the observed data can be measured by the posterior predictive p-value (ppp), the probability that the imputed data are more extreme than the observed data, as measured by the test quantity (Gelman et al. 1996; Gelman et al. 2004).

A small ppp suggests that the proposed imputation model is not adequate to support the targeted post-imputation analysis (He and Zaslavsky 2012). We investigated three sets of test statistics that capture important relationships linked to our substantive analyses. These test statistics are as follows: (1) the correlation between the CDI and an observed measure at each time point; (2) the means of the CDI at each time point; and (3) the slope of the control group, the treatment group, and the treatment effect from a regression model regressing the CDI values on (log) months since baseline.

Results Based on Application to Adolescent Data

We begin this section by presenting the results of the diagnostics to ensure that our imputations are reasonable and are replicating important relationships relevant to our target analyses. We then analyze the adolescent data using the CDI as our depression outcome of interest. First, we only analyze those eight trials which used the CDI. We then analyze all 18 trials using both observed CDI and imputed CDI data.

MCMC Diagnostics

The first step in evaluating our imputation model is checking the convergence of the Markov chain used to generate the imputations. We assessed convergence of our Markov chains by visual inspection of trace plots and autocorrelation plots. These diagnostics made it very apparent that we were not able to estimate all of the parameters in our imputation model. For many of the measures in Table 4, there was not enough overlap to measure correlations at both the within- and between-participant level. That is, we could not assume both the random effects and the error terms were correlated across measures. This caused us to consider a vastly reduced model in which the covariance matrix Ψ of the random effects vec(b i )∼N(0,Ψ) is block diagonal such that the random effects across outcomes are independent (random effects within an outcome are still correlated). Thus, all the association between measures is via the error covariance. This simplified structure has a number of consequences. First, it assumes that the correlation between two outcomes over time is constant. This is a reasonable assumption as all the measures are presumably measuring the same construct of interest. But due to floor and ceiling effects (see for example (Siddique et al. 2015)), correlations between measures can change as a function of time. The second result is that different outcomes measured on the same participant at different times are assumed to be independent. For example, a participant’s value on the CDI at baseline is independent of their value on the CBCL-D (but not the CDI) at some follow-up time point.

MCMC diagnostics also suggested that our model did not have adequate data to estimate both random intercept and random slope terms for all measures, even with our block diagonal covariance structure. Thus, only random intercept terms were included in our imputation model. This has the result of assuming measure variances are constant over time.

We generated 500,000 parameter draws from our reduced imputation model from a single Markov chain. Trace plots and autocorrelation plots of those parameters associated with the CDI reflected convergence of the chain. Formal diagnostics based on the Geweke Diagnostic (Geweke 1992) and the Gelman-Rubin diagnostic (Gelman and Rubin 1992) based on three parallel chains also suggested convergence. After diagnosing convergence, we ran one of our chains for an additional 500,000 iterations and drew 100 imputations by drawing values from every 5,000 iterations.

Results from Posterior Predictive Checking

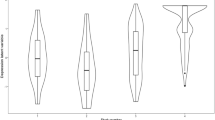
Figures 1 and 2 (available online) display histograms of imputed and observed CDI values from the duplicated data sets. Figure 1 shows imputations based on the imputation model where depression measures were square root transformed prior to entering the imputation model. Imputed values were then squared. The panel on the left of Fig. 1 is a histogram in which imputed values were squared but not rounded to the nearest observed value. As a result, there are a few imputed values greater than 54 which the maximum possible value on the CDI. The middle panel is a histogram in which imputed values were squared and rounded to the nearest observed value such that all values are within the range of the CDI (0 to 54). The panel on the right is a histogram of observed CDI values from the duplicated data.

Figure 2 is an imputation based on the imputation model where depression measures were not transformed prior to entering the imputation model. The panel on the left of Fig. ?? is a histogram in which imputed values were not rounded to the nearest observed value. As a result, there are negative imputed values which are not possible on the CDI. The middle panel is a histogram in which imputed values were rounded to the nearest observed value such that there is a spike at 0 from rounding negative imputed values to 0. The panel on the right is a histogram of observed CDI values from the duplicated data.

Although the imputed values in the middle panel of Fig. 1 appear to best preserve the distribution of the observed data, this is not necessarily the goal of our imputation model. Instead, we wish to preserve important features of the data that are relevant to our target analyses. To this end, we also performed posterior predictive checks of correlations, marginal means, and changes of CDI scores over time. Based on the results of these posterior predictive checks, we selected the imputation model where measures were imputed on their original scale and not rounded. Results from this model are presented below.

Table 6 displays the results of posterior predictive checks (based on 100 imputed data sets) for both control and treatment group participants of the correlation between the CDI and an observed measure in the duplicated trials described in Table 5. In both intervention groups, correlations at baseline and the first two follow-up time points were checked. As mentioned above, our imputation model assumes that partial correlations between any two measures are time-invariant. As a result, imputed analyses do not capture changes in correlations over time. Instead, correlations based on imputed values are averaged over time. For trial 2, the correlation in the duplicated trial (with a deleted and imputed measure) is similar to the observed correlation and the two-sided posterior predictive p values are larger than 0.05. For the remaining trials, the observed correlation and the correlation calculated using the duplicated data set are not similar and the posterior predictive p values are small, sometimes even equal to 0. These results suggest that our imputation model is not preserving all the relationships among the data.

Table 6 Posterior predictive checks of simple correlations at the first three time points in trials 1, 2, 84, and 247. Results are based on imputed CDI values and their correlation with an observed measure. The CDI and CESD are self-reported measures. The CBCL-D is parent-reported
Full size table

Table 7 displays the results for both control and treatment group participants of posterior predictive checks of the mean of the CDI in the duplicated trials at baseline and the first two follow-up time points. In both intervention groups, the results suggest that imputed means are inaccurate. There are two reasons for this inaccuracy. The first is that failing to preserve relationships as demonstrated in Table 6 leads to inaccurate imputations. The second reason is that our model does not incorporate trial-level effects. For example, trials 1, 2, and 84 have similar baseline CBCL-D scores of 4.33, 4.68, and 3.58, respectively. However, their baseline CDI scores are not similar, 5.81, 9.74, and 9.38, respectively. Not accounting for trial-level effects in our imputation model results in pooling observations across trials. The result is that when imputing the CDI in trial 1, the imputed values are skewed toward the CDI values in trials 2 and 84 which are much larger than those in trial 1.

Table 7 Results from posterior predictive checks of CDI means at the first three time points for control and treatment group participants in trials 1, 2, 84, and 247
Full size table

Table 8 displays the results of posterior predictive checks of the fixed coefficients of a random intercept and slope regression model of the imputed depression score as a function of log(number of months since baseline + 1) for each trial in Table 5. Results are for the control group slope, the treatment group slope, and the difference between the two slopes (i.e., the treatment effect). As with the marginal means and correlations, results are attenuated toward the average for all trials. However, because there is less treatment effect heterogeneity in our data (at least for the four duplicated trials), treatment effects based on duplicated data are close to observed treatment effects and all posterior predictive p values are large, the smallest being equal to 0.38. However, this result is not due to an imputation model that fits the data well. Instead, it is a fortunate result of trials 1, 2, 84, and 247 having similar treatment effects.

Table 8 Results from posterior predictive checks of intercept, slope, and difference between slopes in trials 1, 2, 84, and 247
Full size table

Post-Imputation Analysis of Adolescent Trial Data

Despite the findings from the imputation diagnostics, which suggested that our imputation model is not preserving important features of the data, we proceeded to discard the duplicated data and analyze the data from the 18 adolescent trials. We analyzed the CDI scores (both observed and imputed) as a function of treatment and time using the following random intercept and slope regression model. Let CDI i j k be the CDI score for participant i at occasion j,j=1,…,n i in trial k,k=1,…18. And let t i m e i j k be the time since baseline and T i a variable indicating whether participant i was randomized to the intervention or control group. Then, our model is

$$\begin{array}{@{}rcl@{}} \text{CDI}_{ijk} &=& \beta_{0} + \beta_{1}time_{ij} + \beta_{2}(time_{ij}*T_{i}) + b_{0k} \\&&+ b_{0i} + b_{1i}time_{ijk} + \varepsilon_{ijk}. \end{array} $$
(2)

As in our imputation model, time has been transformed as log(months since baseline + 1). We did this so that we could model time linearly in order to simplify the presentation of our analyses and avoid having to include a quadratic effect for time in our model. The term b 0k is a random trial effect with mean 0 and follows a normal distribution. The terms b 0i and b 1i are random intercept and slope terms, respectively, and follow a bivariate normal distribution, again with mean 0. The error term ε i j also follows a normal distribution and is independent of the random effects.

In this model, inference focuses on the regression coefficient β 2, the time by treatment interaction. This term is the difference in slopes between intervention and control groups. Table 9 presents the results of our analysis using only the observed CDI scores as well as using both observed and imputed CDI scores. Focusing on the treatment by time interaction in Table 9, the treatment effect is significant in both CDRS analyses. That is, overall, those who were assigned to one of the eight preventive interventions had more improvement in symptoms than those assigned to the control condition. In terms of effect sizes, at 24 months, the effect size from the analysis which uses the observed data is −0.11. The effect size from the analyses which uses both observed and imputed data is −0.13. For the most part, there is very little difference between the two analyses. This result is not surprising. As was demonstrated, our imputation model was not able to incorporate information from other trials that did not use the CDI. Thus, we see little difference between the two analyses. However, the variance components in the imputed analyses are smaller than those in the observed analyses. This likely reflects the fact that our imputation model did not include these between-person effects. Thus, random effect variances are smaller and residual variance is larger.

Table 9 Observed-only and post-imputation analyses of CDI scores. Observed-only analyses are based on the eight trials that used the CDI (n = 2874 participants). Imputed analyses are based on 100 imputations for all missing CDI scores and include the eigh trials that used the CDI and the 10 trials that did not use the CDI (n = 5289 participants)
Full size table

Discussion

We have described a multiple imputation approach for harmonizing outcomes across multiple longitudinal trials. In our motivating example, we initially sought to harmonize 10 measures across 19 trials. This proved to not be possible using our methodology, because there was not enough overlap across measures to enable us to estimate their joint distribution. We then pursued a more modest goal, dropping one of the trials and attempting to harmonize only the CDI which was already used in 8 of the 18 remaining trials and overlapped with most of the other measures in at least one trial. Based on our imputation diagnostics, this reduced model did not appear to preserve relationships among variables or produce accurate imputations. Performing imputations on the original scale of the outcomes or after square root transformation did not improve our results, nor did rounding or not rounding the imputations. Still, this exercise was informative, because it highlighted those conditions that are necessary for harmonizing measures across multiple trials using multiple imputation. We now summarize each of these conditions.

Trial-Level Variability Should be Incorporated into the Imputation Model

Our imputation model was a two-level hierarchical model where repeated observations were nested within individual. As a result, clustering at the trial level was ignored, and observations on different participants within the same trial were assumed to be independent. See Siddique et al. (2015) for a formal presentation of the assumptions that are made when three-level IPD data is imputed under a two-level imputation model. Ignoring between-trial variability in our imputation model resulted in imputed values which underestimated between-study variability. As a result, imputations of marginal means were attenuated, as our imputation model assumed the conditional means across all trials were the same. Not including random time effects at the trial level assumes that treatment effects are the same across trial. Post-imputation treatment effects were then attenuated toward the overall treatment effect.

At first blush, in a data set which contains 19 trials, incorporating between-trial variability into our imputation model would appear to be feasible. However, in a setting where a depression measure can be missing for every participant within a trial, estimating random-effects at the trial level for each depression measure requires sufficient information to measure the correlation between measures at the trial level which requires that both measures must be used together in three or more trials. As can be seen in Table 3, most pairs of measures overlap in fewer than three trials.

Two sources of between-trial variability in our data set are the various interventions used in the different trials and the various patient populations. When it is not possible to incorporate trial-level variability into the imputation model, one option is to restrict the number of trials to a more homogenous sample with respect to patient population and intervention type. This could potentially remove the need to model trial-level variability at the expense of addressing a different research question.

Relationships Among Variables over Time must be Allowed to Change

Again, due to the sparsity in our data, we were unable to estimate random slope effects at neither the trial nor the participant level in our imputation model. Thus, our models assume that variances of measures are constant over time and that the correlations between measures are time-invariant. However, looking at the observed columns in Table 6, correlations with the CDI appear to change over time. An imputation model that assumes this correlation is the same at all time points will generate inaccurate (or diffuse) imputations. Since our analyses are concerned with measuring change over time, it is essential that our imputed values preserve these relationships over time

Measures to be Harmonized Should be Related to one Another

This last condition seems obvious but it was an issue in our data. Although all studies sought to measure depression, some studies used self ratings, others used parent ratings, and some used clinician ratings. Some subscales sought to measure different components of depression. The result, as seen in Table 3 are ten measures that are for the most part, not highly correlated with one another. This is in contrast with our prior work (Siddique et al. 2015) where we harmonized the CDRS and the Hamilton Depression Rating Scale (HDRS) (Hamilton 1960). In our study, the correlation between the CDRS and the HDRS was as high as 0.85. It is not enough that targets of harmonization putatively be measuring the same construct. The variables themselves need to be highly correlated.

A useful diagnostic in our setting is the fraction of missing information (Rubin 1987) which measures the additional inferential uncertainty in a parameter due to missing data. In some settings, a high rate of missing values for a variable does not automatically translate into high rates of missing information for its marginal parameters because the variable may be highly correlated with other variables that are more fully observed (Schafer, 1997). In those situations, multiple imputation can provide precise and valid inferences. The percentage of missing CDI values in our final set of 18 trials was 65 %. In our analyses of the CDI with observed and imputed data reported in Table 9, the fraction of missing information for the time by treatment interaction term was 61 %. The similarity of these two values suggests that the other depression measures in our data set did not help improve the accuracy of our imputation model and highlights the importance of having variables in the imputation model that are highly correlated with the variables that have missing values.

Conclusion

We sought to harmonize 10 measures across 19 trials and were unable to do so primarily due to the large amount of missing information, the lack of overlap across measures, and the low correlations among many of the measures that did overlap. We pursued harmonization via multiple imputation because, when done correctly, it has the following advantages: variables remain on their original scale, special analytical methods are not required after the data have been imputed, relationships among variables are preserved, and between-trial variability is accounted for. If the analyst is willing to forgo some of these advantages, other approaches may be feasible. The simplest approach is to standardize all measures and treat them as if they were identical on the transformed scale. Standardization can be easily applied in most situations with continuous measures and does not require specialized software. However, standardization does not take into account differences in the measurement properties of different scales and tends to mask heterogeneity between studies. Interpretation can be difficult because the analysis is no longer on the original scale (Griffith et al. 2015).

Latent variable methods which assume a single common factor may be more feasible in our setting but use sophisticated models and require assumptions regarding measurement invariance over time that can be hard to check. This is the approach taken by Brown et al. (2016) in this issue who imposed a two-level latent growth model on the depression measures. Their approach borrows strength across studies by relying on a common single depression factor whose measurement properties are assumed to be constant over the 2 years of data.

A promising approach in our opinion is to bring in additional sources of information. One way to obtain additional information is by drilling down to the item level and linking items across measures. When the same items occur in different measures, an item response theory (IRT) approach can be used (Curran et al. 2008; Curran 2009; Curran and Hussong 2009; Bauer and Hussong 2009). Even if there is no overlap in items across instruments, a bifactor IRT approach can be used to determine a single factor that is shared across all instruments and separate factors that account for differences in instruments. This approach has been investigated on these same data by Howe et al. (2017) who were able to identify invariant items (i.e., showed no differential item functioning) despite extreme sparseness in the overlap of instruments and items.

Another source of (external) information are “bridging studies” that provide overlap on measures when there is no overlap in the data set of interest. These bridging studies can be appended to the data set of interest in order to facilitate harmonization (Siddique et al. 2015). Two other potential approaches are to create synthetic data (Schifeling and Reiter 2015) or use informative priors (Rässler 2003). A careful simulation study investigating properties of the above methods—in addition to imputation—for large scale harmonization would be a useful contribution to the literature. In particular, how these methods perform when faced with the challenges encountered in this paper as follows: little overlap among measures to be harmonized, substantial between-trial variability, and low (and changing over time) correlation among variables.

Increasingly, researchers are collecting data from multiple studies in order to synthesize findings and perform more sophisticated analyes. These projects will continue to grow as federal funding agencies encourage data sharing (National Institutes of Health 2003; National Science Foundation 2011) and more journals require the release of data to accompany manuscripts. Methods that harmonize variables across data sets and facilitate analyses by many researchers are increasingly important in order to make full and efficient use of synthesized data and take advantage of the potential of IPD meta-analysis to address new questions not answerable by a single study.