Bayesian Methods for Prevention Research

Abstract

Bayesian statistics represents a paradigm shift in statistical reasoning and an approach to analysis that is applicable to prevention trials with small samples. This paper introduces the reader to the philosophy behind Bayesian statistics. This introduction is followed by a review of some issues that arise in sampling statistics and how Bayesian methods address them. Finally, the article provides an extended illustration of the application of Bayesian statistics to data from a prevention trial that tested a family-focused intervention.

Charlie goes out on his front porch at 10 p.m. sharp every night and claps his hands three times. His neighbor, Fred, sees him doing this and asks him why he does this. Charlie says, “I’m keeping the elephants away.” Fred replies, “But Charlie, there are no elephants around here.” To which Charlie replies, “you see, it works.”

Bayesian Ideas

Bayesian statistics can be understood as a revision of opinion as the result of observing data. “Opinion” here, before (i.e., prior to) the data, and after (i.e., posterior to) observing the data, is expressed in terms of probability. The revision is accomplished using the Bayes theorem, which is a simple consequence of the definition of conditional probability.

The story of Bayesian statistics begins, I think, with an explanation of the meaning of probability. What does it mean when a weather forecaster says that the probability of rain tomorrow is 30 %? To some, this means that on days when the weather “looks like” tomorrow’s when viewed today, on 30 % of them rain will occur. This is awkward from several points of view. For one, what exactly does looks like mean? Without a careful specification, the probability statement is vacuous. Each specification of looks like is essentially a theory of the weather, which is subjective and differs among forecasters. Adherents of this view, called the frequentist view, claim that it provides an objective basis for probability statements. But this claim has no foundation. In practice, the specification of what looks like means in a particular context is fraught with difficulty.

Another view of probability is more in tune with current Bayesian thought and sees it as a personal statement of how the speaker would bet. If the forecaster would buy or sell a promissory note worth $1 if it rains and nothing if it does not, for thirty cents, then that forecaster’s probability is 30 %. The usual rules of probability can then be derived from the principle that one does not wish to offer bets that make one a sure loser, regardless of whether it does or does not rain. This idea is due to deFinetti (1980). Chapter 1 of Kadane (2011) gives a derivation of the usual rules of probability from this perspective. This approach has some important implications. First, it does not purport to be objective. The bets that one weather forecaster would make are not necessarily those another would make. Thus, probabilities reflect the personal, subjective opinions of the person whose probabilities they are. There is no “the” probability of rain tomorrow. There is only my probability of rain, or yours. Nonetheless, if a Bayesian observes a large number of events judged to be independent and identically distributed, a bet against the relative frequency would lead to sure loss. In this sense, frequentism can be thought of as a special case of the subjective Bayesian view.

A second important consequence of the Bayesian view is that the rules of probability guard only against a certain kind of mistake, of essentially contradicting oneself in the bets you would accept. Thus, probability becomes a kind of language to describe opinions, generally about matters about which one is uncertain. There is no guarantee per se that the opinions are reasonable, deserve serious consideration, or are not entirely out to lunch. A person may put probability one on the proposition that the moon is made of green cheese and do so in a way that obeys the rules of probability. Just as writing a sentence in grammatical English implies nothing about the validity of the thought expressed, so too expressing uncertainty in terms of probability implies nothing about the acceptability to a reader of the uncertainties expressed.

The consequence of this is to write a persuasive work using probabilistic language requires justification of the assumptions made, technically the likelihood function (the distribution of the data given the parameters, viewed as a function of the parameters) and the prior distribution of the parameters. Thus, it becomes a matter of rhetoric, in the traditional sense of an effort to persuade. If the reader judges that the assumptions are reasonably close to her own, she may be willing to continue reading. If not, the results are not very interesting and will probably be skipped. Furthermore, the assumptions have to be justified in terms of the details of the particular applied context and situation. There is not, and cannot be, a canonical analysis of data of a particular type, independent of the context of the gathering of the data and purpose for which the data were collected.

There is another Bayesian view (called “objectivist”) that deemphasizes the subjective nature of the probability statements being made. Often in this line of thought the likelihood is taken to be non-controversial, and the interest centers on choosing priors having various properties thought to represent lack of information. There are several sets of priors variously called “reference,” “ignorance,” “non-informative,” “objective,” etc. Sometimes these priors are “improper,” in that they sum (or integrate) to infinity rather than one. Improper distributions have to be handled with care, as they can lead to paradoxes (see, for example, Dawid et al. (1974)).

Charlie in the anecdote has data: he claps his hands every night, and elephants have not bothered anybody in his neighborhood. But this data does not prove the effectiveness of his treatment. To be persuasive, he needs to establish the counterfactual—what would have happened if he did not clap his hands. The issue in showing the effectiveness of a preventative treatment is exactly the same, showing persuasively what would have happened to these students, or to this village, or whatever, in the absence of the treatment. Sure there are other students or villages without this treatment, but again, what their response would have been had they been given the treatment is not obvious. Thus, the heart of the issue is to persuade the readers about the likely unobserved response of experimental subjects had the other treatment been given. Bayesian statistics offers a language for precisely stating opinions in terms of probabilities, but making them persuasive is the responsibility of the writer, and not something Bayesian statistics per se can address.

Issues of Frequentist Statistics

There are (at least) two special issues that arise in frequentist statistics that Bayesian statistics deals with gracefully. The first is sample size. The emphasis on significance testing in sampling statistics runs up against the following seeming paradox: with a small sample size, null hypotheses are typically not rejected, but with a large sample, null hypothesis typically are rejected. Thus, in a sense, what is being measured is the sample size. And since rhetorical points are won by rejecting hypotheses, investigators are anxious to have a sample size large enough to reject a (typically straw-man) hypothesis. By contrast, a Bayesian analysis with a proper, subjective prior can be done comfortably with samples of any size. What happens is that the spread of posterior distributions (however measured) tends to be smaller if the sample size is large. But the principles apply regardless of sample size. As an extreme example, I once published a statistics paper with no data of the traditional kind. The application was to how long asphalt-concrete roads last before cracking as a function of various covariates like the thickness of the asphalt, etc. Roughly, they last for 25 or 30 years, which is a long time to wait for experimental results. However, we could elicit the opinions of road engineers with 35 or 40 years of experience concerning their probability distributions for how long an asphalt road would last as a function of the covariates. The goal of this paper was to ask questions that a road engineer with little probabilistic training could answer, but that would allow us to give probability distributions describing the road engineer’s opinions, including his or her uncertainties (see Kadane et al. (1980)). Thus, this paper had no traditional sample at all and relied totally on the prior opinions of the road engineers.

A second issue for sampling statistics is called identification of parameters. Suppose the data are represented by x and the parameters by θ. A statistical model (also called the likelihood function) is the probability of the data x given the parameter θ, written p(x|θ). A likelihood is said to be unidentified if there are parameters θ and θ′(θ ≠ θ′) such that p(x|θ) = p(x|θ′) for all data points x. Otherwise, the likelihood is said to be identified. In an unidentified model, it is not possible to distinguish θ from θ′ using only the likelihood. The issue of identification surfaced especially in econometrics (Fisher 1966); it became common practice among frequentists to avoid unidentified likelihoods. For example, suppose there are two independent and normally distributed uncertain quantities, X ₁ and X ₂, with means μ ₁ and μ ₂, respectively, and standard deviation 1, respectively. Suppose only Y = X ₁ + X ₂ can be observed. A frequentist statistician is at a loss to treat data of this kind, since (μ ₁, μ ₂) and (μ ₁ + c, μ ₂ − c) for any constant c will be equally supported by the data Y.

By contrast, a Bayesian with a proper prior distribution on (μ ₁, μ ₂) can use the Bayes theorem to derive a posterior distribution on (μ ₁, μ ₂) given observation Y. Furthermore, the posterior distribution so derived will differ from the prior distribution, so the Bayesian will have learned about μ ₁ and μ ₂ from the data on Y. Lack of identification is not an intrinsic issue for a Bayesian (Lindley and El-Sayyad 1968).

The fact that neither sample size nor identification are issues for Bayesians suggests that the subjective Bayesian viewpoint offers a more flexible and encompassing way to appreciate the import of data.

Application of Bayesian Principles to a Specific Data Set

I have been provided with a data set to illustrate how a Bayesian might analyze prevention data. The origin of the data was described to me as follows:

The larger study was intended by CDC to reduce aggression and prevent violence. The specific mechanism of the targeted intervention was to change population levels of violence by changing parenting and family relationships among youth who were characterized by high aggression combined with high social influence among peers. The evidence from the larger study is that this was to some extent successful. The data set I extracted for [you] is from the targeted sample of youth whose parents were invited to participate in the intervention if their school was randomly assigned to it. I created a data set that is approximately the same size as the data sets gathered in Alaska Native studies, (D. Henry, personal communication, April 16, 2012).

Thus, the analysis given below is more in the nature of a numerical example than a case study. Nonetheless, I can use the data to exemplify how I would think about data of this type. However, because of the somewhat artificial nature of the data, my modeling strategy is to simplify more than I would if I were responsible for drawing substantive conclusions. To be specific, in the modeling to come, I neglect the following, each of which would be a concern in a case study:

• 1. Missing data: I eliminate cases with missing data, rather than model why they are missing.

• 2. I use only the evaluations from the last session, neglecting the pattern of evaluations from previous sessions.

• 3. The priors I use are conventional ignorance priors, not priors elicited from an expert, and are improper.

Each of these can be addressed in the Bayesian framework and would have been in this paper, were it not for the fact that the data were artificially selected for me.

Three measured outcomes of each session are the reports of a interventionist conducting the sessions, a parent, and a youth on the effectiveness of the session. The available covariates include demographic information and positive feelings of the youth and parent toward the interventionist.

The endpoints in the data set, three views of the effects of the program at each session, are not the same as the prevention of violence. Consequently, the relationship between the data endpoints and the prevention of violence is entirely a matter of prior belief.

The next question to consider is how to deal with the fact that different families had differing numbers of sessions, ranging from 2 to 18. There may be any number of reasons. It could be the choice of the family. For example, perhaps families who found the sessions less useful drop out early. Perhaps interventionists decided that families in better shape needed fewer sessions. Perhaps less functional families managed to attend fewer sessions. However, from the viewpoint of the effect of the treatment (whichever it was), I think the ratings of the last session are the most relevant, since that is what the long-term effect on violence would be most affected by. Hence, I concentrate on only the ratings given at the last treatment, with the exception that in a few cases, variables for the last session were missing, in which case the next-to-last session was used.

So the reduced goal of my analysis is to predict the ratings that would have been given about the effect of the unassigned treatment, for each youth/parent(s) unit. Compared to the ratings in fact given, these offer in some sense a measure of the effect of the treatment.

We have data on both the intervention given and the interventionist who delivered the intervention. It is often believed that a necessary condition for the effectiveness of an intervention is a positive connection between the interventionist and the participant. This is a difficult view to examine with data, because it hypothesizes that it is the participant-interventionist interaction, and not the main effects, that are important. In the data at hand, one group of interventionists delivered the basic intervention, while a disjoint group delivered the enhanced intervention. Thus, the interventionist effect is unidentified here. The best we can do is drop “interventionist” as a variable and interpret the treatment variable to be treatment as delivered by the interventionist who delivered it. The data do not allow us to address the question of how effective the same session would have been viewed had the interventionist been instructed to use the alternative methodology. This circumstance may be typical in prevention research. To clarify the language used below, the “enhanced treatment” is referred to as the “treatment;” the un-enhanced treatment is referred to as the control.

To summarize, the goal of this analysis is to compare the reported ratings by the interventionist, parents, and youth actually observed (numbers) to predictions of those reports had the other method (treatment or control, respectively) been used. This approach to causation is championed by Rubin (1974, 2005). Because of the Bayesian perspective used in this paper, these predictions take the form of probability distributions, rather than numbers. The covariates used to do this are the extent of positive feelings toward the interventionist on the part of the youth and parents, respectively, whether there is a male in the household, the gender of the youth, and whether the youth is African-American (Tables 1 and 2).

Table 1 Summary of control variables (n=26)

Table 2 Summary of treatment variables (n = 20)

A Model

While there are many ways to perform such a prediction, my choices here will be to simplify the discussion by choosing conventional (and hopefully familiar) models. Of these, the obvious first choice is the normal regression model.

$$ \mathbf{y} = X\beta + \epsilon ~~\boldsymbol{\epsilon} \sim N(0, \sigma^{2}I) $$

(1)

where y is an n × 1 vector of dependent variables (here, ratings of the effectiveness by the interventionist, parent, and youth). Associated with each y _i is a p × 1 vector of regressors x _i . Then X is an n × p matrix of regressors, with i ^th row $\mathbf {x}^{\prime }_{i}$ and is assumed to be fixed and known. The vector β is the vector of coefficients corresponding to each of the regressors (for this application, positive feelings toward the interventionist, the demographic variables, and a constant). As stated in Eq. 1, the errors are assumed to be normally distributed, independent, with variance σ ². Thus, the parameters here about which we are uncertain are β and σ ².

The intended use of this regression is to apply it to the values of the independent variables of the students in the other treatment group. The difference between the observed value of the dependent variables and the distribution calculated using the regression shows how much difference the treatment made for each variable. The observed rating of the effectiveness of the treatment administered are data, which is considered fixed and known, and has no uncertainty. What is not known with certainty is the counterfactual estimate of what the rating would have been had the other treatment been administered. Since it is not known with certainty, this counterfactual estimate has a distribution, called the posterior predictive distribution.

Suppose the matrix of independent variables for the opposite group is $\widetilde {X}$, having dimensions $\widetilde {n}$ and p. If β and σ ² were known constants, the predictive values $\widetilde {y}$ would have the distribution

$$ \widetilde{y} \sim N(\widetilde{X} \beta, \sigma^{2} I), $$

(2)

which does not depend on the observation y. A frequentist would consider β and σ ² as fixed but unknown and, hence, would not speak of β and σ ² as having distributions. However, we do not know β and σ ². What is distinctly Bayesian in the analysis that follows is to consider the quantities about which we are uncertain, here β and σ ², as having probability distributions. What the observations y then do for us is to inform us about reasonable distributions for β and σ ².

This then requires six regressions, each with six explanatory variables and one (vector) of observations, since there are two scenarios (predict the treatment outcome for each youth in the control condition, predict the control outcome for each youth in the treatment condition) and three outcome variables (the view of effectiveness on the part of the interventionist, the parents, and the youth).

The Bayesian method requires a prior distribution on the parameters, here β and σ ². This is a source of controversy, as the prior represents the opinion of the author and, hence, can be disputed. (The same can be said of the likelihood function, here expressed as Eq. 1).

A convenient class of prior distributions for the likelihood (1) is called the class of conjugate prior distributions (Raiffa and Schlaifer 1961). These have the property that if the prior distribution is in this class, so will the posterior distribution, whatever the data might be. An arbitrary prior distribution can be represented as a weighted mixture of conjugate prior distributions (see Dallal and Hall (1983) and Diaconis and Ylvisaker (1985)), so starting with a single conjugate prior distribution seems reasonable. A discussion of analysis with conjugate prior distributions can be found in Kadane (2011, Chapter 8).

To express the conjugate prior for the likelihood (1), it is convenient to reparameterize using τ = 1/σ ², which is called the precision. Similarly, the inverse of a covariance matrix is called a precision matrix. Thus, Eq. 1 can be rewritten as y|β, τ has a normal distribution with mean X β and precision matrix τ I. The conjugate prior on β and τ can then be stated as follows: β|τ a normal distribution with mean β ₀ and precision matrix τ τ ₁ where τ ₁ is a known p × p matrix, and τ has a gamma distribution with parameters a and b. Here, p = 6, the number of independent variables in each regression (including a constant). While the gamma distribution may be less familiar to many readers than the normal distribution, you can think of it as a generalized chi-square distribution (see Kadane (2011, Section 8.6) for details).

All of this is convenient, provided there are good ways of assessing the parameters of these distributions, namely β ₀, τ ₁, a, and b. One approach to eliciting these quantities is given in Kadane et al. (1980); this method does not require the subject matter expert to understand anything about statistics except what a median is.

In the present application, I am disinclined to use such formal elicitation. I fear that such an exercise would distract too much from the heart of the purpose of this article, which is to convey how I, as a Bayesian, would approach the issue of assessing the relative effectiveness of two treatments.

An alternative is to retreat to so-called non-informative prior distributions, which here means τ ₁ → 0, a → − p/2, b → 0 (β ₀ is irrelevant). Normally, I would advocate pressing hard for the prior information that in many problems is available if one asks. Also, the limiting prior distribution here is improper (meaning it integrates to infinity, not one). This can lead to subtle troubles of various kinds, but those troubles happen not to affect the calculations that follow. Hence, with a bit of reluctance, I adopt the resulting prior, which can be expressed as

$$ p(\boldsymbol{\beta}, \tau) d \boldsymbol{\beta} d \tau \sim d \boldsymbol{\beta} d\tau/\tau. $$

(3)

This implies a uniform distribution for the (six-dimensional) β and a uniform distribution for logτ. The specification of the probability model is now complete. What remains is to explore its consequences.

The choices specified in Eqs. 1, 2, and 3 are conventional. Were I closer to the source of the data, I would want to use a more detailed and sophisticated model that takes advantage of the data from all the sessions a family had with the interventionist, which models missing data, etc. While I certainly agree that those considerations are important, the details of just how to do that would only distract attention from my main objective, which is to show what distinguishes Bayesian from frequentist analysis.

Once specifications of a likelihood and a prior (such as Eqs. 1, 2, and 3 above) are made, the computation of the posterior distribution is a purely technical matter. Every analyst with the same likelihood and prior must come to the same posterior distribution given the data (barring provable error). In the particular case of Eqs. 1, 2, and 3 (and the conjugate nature of those specifications), that technical work is simplified. The details of this bit of math are given in the Appendix. The result is an algorithm that gives samples from the distribution specified in Eq. 2.

Results

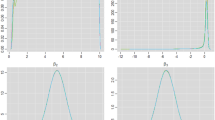
The results are displayed in Figs. 1, 2, and 3. The x-axis is a quantile of a distribution. In the solid line, the intervention has a known effectiveness (data), measured at the time of the intervention. The estimated control is not known, but instead is drawn from its predictive distribution described above. For the dotted line, these roles are reversed. The control has known effectiveness, but the intervention is estimated from its predictive distribution. The y-axis reflects the difference between the two. At zero (there is a horizontal line to mark it), the intervention and control would be regarded as equally good. Positive differences favor the intervention; negative differences favor the control. (There is no particular meaning to a point where the solid and dashed lines meet).

Fig. 1

Interventionist view of effectiveness

Fig. 2

Parent view of effectiveness

Fig. 3

Youth view of effectiveness

There are two interesting aspects of these figures. The treatments were randomly assigned to schools, but not to individuals within schools. Indeed, I have no knowledge of the recruiting methods used within schools. Consequently, there may be omitted covariates that matter to the predictions, for example, age of youth, socio-economic status of the household, presence of violence in the household, food insecurity of the household, etc. One way such omitted covariates might become apparent is in discrepancies between the two lines in each graph. This is particularly noticeable in Fig. 3. Other explanations for the discrepancy include the finiteness of the sample sizes and other deficiencies in the model, such as non-linearity, etc.

Secondly, there is a clear ordering in terms of how effective the different participants rate the advantage of the intervention. The interventionists and parents are enthusiastic about the intervention, the youth not. This is seen as follows: At the median (the 0.5 point on the x-axis), both interventionists and parents are in positive territory in Figs. 1 and 2. Thus, more than half of the probability for both interventionists and parents find the treatment more effective than the control. By contrast, only half of the youth (Fig. 3) lies in positive territory.

This analysis makes several strong assumptions and concentrates solely on estimating whether and to what extent the extended treatment was rated better than the control. In my opinion, however, the major gap is that ratings of intervention sessions are not the same as reducing violence.

Decisions and Costs

The operational question then arises of whether the intervention should be regarded as worth the extra trouble of administering it. This introduces several new considerations. On the cost side, how can one quantify “extra trouble?” For example, suppose that the extra trouble meant that some reduced proportion of the children and families could be offered treatment if the interventions were deemed necessary (holding the budget constant). Then there is the question of efficacy. What difference in the scales that capture the rating of the interventionist, parent, and youth should be regarded as important? Should we take the adults’ view of the matter, or the youth’s? There is a Bayesian decision theory to address the problem of decision-making under uncertainty that would be based on quantitative answers to these questions. For an introduction to this theory, see Lindley (1985).

Conclusion

This paper reviews the fundamentals of Bayesian ideas as they apply to prevention research. While the philosophy of what is random and what is not is crucial for grasping the analysis, the important steps are as follows:

• Recognition that the unobserved counterfactual is the key to establishing the effect of the treatment.

• The only independent variables that can be used are those that vary in both treatment groups (like age of youth, but not identity of interventionist).

• The normal linear model has two sources of uncertainty, σ ² (how well the regression fits the data) and a term reflecting uncertainty in the coefficients β. The latter would not appear in a typical frequentist calculation.

Each of the lines in the figures represents the difference, for a particular youth, between the treatment and the control, only one of which is observed. Consequently, this could be regarded as an unidentified quantity, which would be hard to address from a frequentist viewpoint. However, Bayesian methods permit an informative analysis.

There is a large literature on Bayesian methods in the social sciences. For an alternative analysis of randomized trials, see Gelman and Hill (2006, pp. 167–198). Other sources include Condon (2003, 2005, 2010) Gelman et al. (2013), Geisser (1993), Gill (2007), Jackman (2009), Lancaster (2004), Lindley (2014), and Silver (2012).

The question of what to do as a result of the findings raises a whole new series of issues of costs and benefits. While these are obviously germane to wise decision-making, they suggest an inquiry that goes well beyond (but would be based upon) the analysis of the data.

Appendix

We must calculate an expression for the predictive distribution, that is, the distribution of $\tilde {\mathbf {y}}$ in Eq. 2, taking into account the information in y about β and τ. To begin, we have

$$ p(\tilde{y}| y) = \int p(\tilde{y} | \boldsymbol{\beta}, \tau) p (\boldsymbol{\beta}, \tau | y) d \boldsymbol{\beta} d \tau. $$

(4)

Since $p(\tilde {y} | \boldsymbol {\beta }, \tau )$ is already available in Eq. 2, we concentrate on p(β, τ|y), which is known as the posterior distribution of β and τ. This is a standard Bayesian calculation. The result (see again Section 8.6 of Kadane (2011)) is as follows:

$$ p(\boldsymbol{\beta}, \tau | \mathbf{y}) = p(\boldsymbol{\beta} | \tau, y) p(\tau | y) $$

(5)

where p(β|τ, y) is a normal distribution with mean (X′X)⁻¹ X′y (the usual least squares estimate of β), and precision τ(X′X) (invert this, and you get the usual variance). Also, p(τ|y is a gamma distribution with parameters a′ = (n − p)/2 and $b^{\prime } = (1/2) y^{T} \overline {P}_{X}y$, where $\overline {P}_{X}= I - X(X^{\prime }X)^{-1} X^{\prime }$.

Although the integration suggested by Eq. 4 can be done analytically (the outcome is a multivariate student − t distribution), for our purposes, this integration is unnecessary. We want to use Eq. 4 to create samples of $\tilde {y}$. This can be accomplished as follows:

• (i) Draw a precision τ|y from the specified gamma distribution; suppose the result is τ ^∗.

• (ii) Draw a vector (β|y, τ ^∗) from the specified normal distribution; suppose the result is β ^∗.

• (iii) Draw a vector $\tilde {\mathbf {y}} | \mathbf {y}, \tau ^{*}, \beta ^{*}$ from Eq. 2.

This results in draws from $\tilde {\mathbf {y}}$ that, unlike Eq. 2, do take into account the uncertainty in β and τ. And this algorithm can be repeated as many times as one wishes, to get a sample from the predictive distribution.

Steps (ii) and (iii) can be combined as follows:

$$ f(\tilde{\mathbf{y}} | \mathbf{y}, \sigma^{2}) = \int f_{1}(\tilde{y} | \mathbf{y}, \sigma^{2}, \boldsymbol{\beta}) f_{2}(\boldsymbol{\beta} | \mathbf{y}, \sigma^{2})d \beta, $$

(6)

where f ₁ and f ₂ are both normal distributions, and β enters f ₁ linearly in the mean. Consequently, the distribution of $(\tilde {y} | \mathbf {y}, \sigma ^{2})$ is again normal, with mean

$$\begin{array}{@{}rcl@{}} E[\tilde{y} | \sigma^{2}, y] & = & E[E (\mathbf{y} | \boldsymbol{\beta},\sigma^{2} y | \sigma^{2}y)]\\ & = & E[\tilde{x} \boldsymbol{\beta} | \sigma^{2},y]\\ & = & \tilde{X}(X^{\prime}X)^{-1} X^{\prime}y \end{array} $$

(7)

and variance

$$\begin{array}{@{}rcl@{}} \text{Var} (\tilde{y} | \sigma^{2},y) & = & E[\text{Var}(\tilde{y} | \beta, \sigma^{2},y) | \sigma^{2}, y]\\ &&+ \text{Var}[E(\tilde{y} | \boldsymbol{\beta}, \sigma^{2},y) | \sigma^{2},y]\\ & = & E [\sigma^{2}I_{m}] + \text{Var}[\tilde{X}\boldsymbol{\beta} | \sigma^{2} y]\\ & = & \sigma^{2} [I_{m} + \tilde{X} (X^{\prime} X)^{-1} \tilde{X}^{\prime}] \end{array} $$

(8)

where m is the sample size. (see O’Hagan and Forster (2004, page 325).

Thus, the variance of $\tilde {y} | \sigma ^{2},y$ reflects two sources of uncertainty, σ ² I _m because prediction is inherently uncertain, and $\sigma ^{2}\tilde {X} (X^{\prime }X)^{-1}\tilde {X}$, reflecting uncertainty about β.

Hence, in the algorithm, steps (ii) and (iii) can be replaced by a single draw from a multivariate normal distribution with mean (7) and covariance matrix (8).

This algorithm was run on the data at hand. Observations whose missing data prevented calculation of the predicted ratings were eliminated. A more in-depth treatment would look at whether the very fact that particular data are missing has information about the parameters of interest.

I used the R package to do the computing.