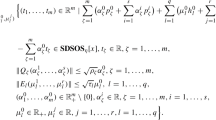On approximate solutions for robust semi-infinite multi-objective convex symmetric cone optimization

Abstract

We present approximate solutions for the robust semi-infinite multi-objective convex symmetric cone programming problem. By using the robust optimization approach, we establish an approximate optimality theorem and approximate duality theorems for approximate solutions in convex symmetric cone optimization problem involving infinitely many constraints to be satisfied and multiple objectives to be optimized simultaneously under the robust characteristic cone constraint qualification. We also give an example to illustrate the obtained results in an important special case, namely the robust semi-infinite multi-objective convex second-order cone program.

1 Introduction

Robust optimization [1,2,3,4] has become a very active methodological approach that is established to deal with optimization problems under uncertainty. The uncertainty means that the entering parameters of those problems are not acknowledged precisely on the time while an answer must be determined. In recent years, many authors have established approximate optimality conditions and duality theorems for approximate solutions ($\epsilon$-solutions) for different classes of optimization problems [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. More specifically, Jeyakumar and Li established strong duality for robust semidefinite linear programming [8], Lee and Jiao established quasi approximate solutions for robust convex programming [9], Lee and Lee established approximate solutions for robust convex programming [11], robust fractional programming [12], robust convex semidefinite programming [14], and robust semi-infinite programming [15]. Lee and Lee also established optimality conditions and duality theorems for robust semi-infinite multi-objective programming [13].

Convex symmetric cone optimization [22,23,24,25,26] problems are a class of convex optimization problems in which we minimize a convex function over the intersection of an affine set with the Cartesian product of symmetric cones. Well-known examples of symmetric cones are the nonnegative orthant cone, the second-order cone, the cone of symmetric positive semidefinite matrices, the cone of complex hermitian positive semidefinite matrices, and the cone of quaternion Hermitian positive semidefinite matrices. Therefore, well-studied special cases of symmetric programming are linear programming, second-order cone programming [27,28,29,30] and semidefinite programming [31,32,33]. Other special cases are optimization problems over complex Hermitian positive semidefinite matrices, and optimization problems over quaternion Hermitian positive semidefinite matrices [22, 23, 25].

To illustrate the modeling potential of conic programming and the extensive applicability of symmetric cone programming, we mention that all convex programming problems can be formulated as conic programs [34], and that almost all real-world applications of conic programming are associated with symmetric cones [27, 28, 31, 32, 34]. There is a strong relationship between symmetric cone programming and Euclidean Jordan algebras. When we optimize over symmetric cones, the importance of Euclidean Jordan algebras stems from the fact that a cone is symmetric if and only if it is the cone of squares of some Euclidean Jordan algebra. Some Jordan algebraic notations, are listed in Table 1. These notations will be used in the sequel. Readers who are unfamiliar with the theory of Jordan algebra are encouraged to read [22, Section 2].

Despite the genuine need for establishing an approximate optimality theorem and approximate duality theorems for convex symmetric cone programming problems, there are no symmetric conicity analogs of these approximate theorems. Inspired by this gap in the literature, in this paper, we establish $\epsilon$-solutions for the robust convex symmetric cone programming problem. Our setting is general in the sense that our convex symmetric cone optimization problem involves infinitely many constraints and multiple objective functions. That is, we establish an $\epsilon$-optimality theorem and $\epsilon$-duality theorems for robust semi-infinite multi-objective convex symmetric cone programming. We also apply our results to an important special case, namely the robust semi-infinite multi-objective convex second-order cone program.

The semi-infinite multi-objective symmetric programming problem is defined as

$$\begin{aligned} (\text {SIMSP}) \left\{ \begin{aligned}&{\text {min}}{} & {} \bigg ( f_1(x),f_2(x),\ldots ,f_K(x)\bigg )\\&\text {s.t.}{} & {} a_0^{(t)} +\sum _{i=1}^m x_i a_i^{(t)}\succeq \; 0,\quad t\in T, \end{aligned}\right. \end{aligned}$$

where $x\in \mathbb {R}^m$, $f_k:\mathbb {R}^m\rightarrow \mathbb {R}, k=1,\ldots ,K$, for $a_i^{(t)} \in \mathcal {J}$ for $i=0,1,\ldots ,m,\;t\in T$, $\mathcal {J}$ is a Jordan algebra with dimension n and rank r, and T is an arbitrary index set that can be infinite.

Table 1 Some Jordan algebraic notations will be used throughout the paper

The semi-infinite multi-objective symmetric programming problem with uncertain data in the constraints is defined as

$$\begin{aligned} (\text {USIMSP}) \left\{ \begin{aligned}&{\text {min}}{} & {} \bigg ( f_1(x),f_2(x),\ldots ,f_K(x)\bigg ) \\&\text {s.t.}{} & {} a_0^{(t)} +\sum _{i=1}^m x_i a_i^{(t)}\succeq 0,\quad t\in T, \end{aligned} \right. \end{aligned}$$

where, for each $i=0,1,\ldots ,m$ and $t\in T$, the element $a_i^{(t)}$ belongs to an uncertainty set $\mathcal {V}_i^{(t)} \subseteq \mathcal {J}$.

The robust counterpart of USIMSP is defined as

$$\begin{aligned} (\text {RSIMSP}) \left\{ \begin{aligned}&{\text {min}}{} & {} \bigg ( f_1(x),f_2(x),\ldots ,f_K(x)\bigg ) \\&\text {s.t.}{} & {} a_0^{(t)} +\displaystyle \sum _{i=1}^m x_ia_i^{(t)} \succeq 0,\quad \forall a_i^{(t)}\in \mathcal {V}_i^{(t)}, \quad i=0,1,\ldots , m,\; t\in T. \end{aligned} \right. \end{aligned}$$

Hence, the robust feasible set $\mathcal {F}_{\mathcal {P}}$ of RSIMSP is given as

$$\begin{aligned} \begin{array}{l} \mathcal {F}_{\mathcal {P}}= \left\{ x \in \mathbb {R}^m : a_0^{(t)} +\sum _{i=1}^m x_i a_i^{(t)}\succeq 0,\; \forall a_i^{(t)}\in \mathcal {V}_i^{(t)},\; t \in T, \;i\in I \right\} , \end{array} \end{aligned}$$

where $I:=\lbrace 0,1,2,\ldots ,m\rbrace$. We make the following assumptions throughout this paper.

Assumption 1.1

For each $t\in T$ and $i\in I$, $\mathcal {V}_i^{(t)}\subseteq \mathcal {J}$ is compact and convex.

Assumption 1.2

The robust feasiblity set $\mathcal {F}_{\mathcal {P}}$ has a nonempty interior.

Assumption 1.1 is necessary to give a characterization and prove properties of the robust characteristic cone which will be given in the next section. Assumption 1.2 is called the Slater condition and is necessary to prove and apply the robust version of Farkas’ lemma.

We use $\mathbb {R}_+^n:= \lbrace (x_1,\ldots ,x_n)\in \mathbb {R}^n: x_i \ge 0, i=1, \ldots , n\rbrace$ to denote the nth dimensional nonnegative orthant cone of $\mathbb {R}^n$. Its interior, $\text {int}\;\mathbb {R}^n_+:= \lbrace (x_1,\ldots ,x_n)\in \mathbb {R}^n: x_i > 0, i=1, \ldots , n\rbrace$, is denoted by $\mathbb {R}_{++}^n$. Let $\epsilon =(\epsilon _1,\ldots ,\epsilon _k)\in {{\mathbb {R}}}^K_+$, we say that $\bar{x}\in \mathcal {F}_{\mathcal {P}}$ is an $\epsilon$-solution of RSIMSP if for any $x\in \mathcal {F}_{\mathcal {P}}$ we have that $f_k(x)\ge f_k(\bar{x})-\epsilon _k$ for each $k=1,\ldots ,K$. Our focus in this paper is to present the approximate solutions ($\epsilon$-solutions) for RSIMSP.

The next pages of the paper are structured as follows: Sect. 2 defines the robust characteristic cone and proves its convexity. The $\epsilon$-optimality condition theorem and the $\epsilon$-duality theorems for robust semi-infinite multi-objective symmetric programming are established in Sects. 3 and 4, respectively. In Sect. 5, we apply our results to an important special case, robust semi-infinite multi-objective second-order cone program.

2 The robust characteristic cone

In this section, we define the robust characteristic cone for our setting and and prove that it is closed and convex. First, we present some preliminaries.

Let $\bar{\mathbb {R}}:=[-\infty ,+\infty ]$ and $f: \mathbb {R}^n \rightarrow \bar{\mathbb {R}}$ be a function. We say f is proper if for all $x\in \mathbb {R}^n,\; f(x) > -\infty$ and there exists $x_0 \in \mathbb {R}^n$ such that $f(x_0)\in \mathbb {R}$. A proper function f is said to be convex if for all $\mu \in [0,1]$, we have

$$\begin{aligned} f((1-\mu )x + \mu y)\le (1-\mu )f(x)+\mu f(y) \end{aligned}$$

for all $x,y \in \mathbb {R}^n$. The domain of f is defined to be the set dom$f:= \lbrace x \in \mathbb {R}^n : f(x) < +\infty \rbrace$. The epigraph of f is defined to be the set $\text {epi} f:=\left\{ (x,r) \in \mathbb {R}^n\times \mathbb {R} : f(x)\le r \right\}$.

The subdifferential of f at $x\in \mathbb {R}^n$ is defined as

$$\begin{aligned} \partial f(x) =\left\{ \begin{array}{lll} \lbrace x^\star \in \mathbb {R}^n: \langle x^\star ,y-x \rangle \le f(y) - f(x) ,\;\forall y\in \mathbb {R}^n\rbrace , &{}&{} \text {if}\; x\in \, \text {dom}\, f, \\ \varnothing ,&{}&{} \text {otherwise}. \end{array} \right. \end{aligned}$$

In general, for any $\epsilon \ge 0$ , the $\epsilon$-subdifferential of f at $x \in \mathbb {R}^n$ is defined by

$$\begin{aligned} \partial _{\epsilon } f(x) =\left\{ \begin{array}{lll} \lbrace x^\star \in \mathbb {R}^n: \langle x^\star ,y-x\rangle \le f(y) - f(x)+\epsilon ,\;\forall y\in \mathbb {R}^n\rbrace , &{}&{} \text {if}\; x\in \, \text {dom}\, f, \\ \varnothing ,&{}&{} \text {otherwise}. \end{array}\right. \end{aligned}$$

A function f is said to be a lower semi-continuous function if lim $\hbox {inf}_ {y\rightarrow x} f (y)\ge f (x)$ for all $x\in \mathbb {R}^n$. The conjugate function of any proper convex function g on $\mathbb {R}^n$ is the function $g^\star :\mathbb {R}^n\rightarrow \mathbb {R}\cup \lbrace +\infty \rbrace$ defined as

$$\begin{aligned} g^\star (x^\star )=\sup \left\{ \langle x^\star , x\rangle - g(x): x\in \mathbb {R}^n\right\} \end{aligned}$$

for any $x^\star \in \mathbb {R}^n$. The following proposition is due to Jeyakumar et al. [35].

Proposition 2.1

Let $f,\;g : \mathbb {R}^n\rightarrow \mathbb {R}\cup \lbrace +\infty \rbrace$ be proper lower semicontinuous convex functions. If one of the functions f and g is continuous, then

$$\begin{aligned} \text {epi}\;(f+g)^\star = \text {epi}\; f^\star + \text {epi}\;g^\star . \end{aligned}$$

For a given set $A \subset \mathbb {R}^n$, we write cl A and co A to denote the closure of A and the convex hull generated by A, respectively. The indicator function $\delta _A$ is defined as

$$\begin{aligned} \delta _A (x) =\left\{ \begin{array}{lll} 0,&{}&{} x\in A, \\ +\infty ,&{}&{} \text {otherwise}. \end{array}\right. \end{aligned}$$

In convex programming, a constrained minimization problem over a closed convex subset C of $\mathbb {R}^n$ can be reformulated as an unconstrained minimization problem by replacing its objective function, say f, with the function $(f+\delta _C)(x)$. The following proposition is due to Hiriart-Urruty and Lemarechal [36].

Proposition 2.2

Let $f: \mathbb {R}^n\rightarrow \mathbb {R}$ be a convex function, C be a closed convex subset of $\mathbb {R}^n$, and $\epsilon \ge 0$. Then

$$\begin{aligned} \partial _{\epsilon } (f+\delta _C)(\bar{x})=\underset{\epsilon _0+ \epsilon _1=\epsilon }{\underset{ \epsilon _0\ge 0,\;\epsilon _1\ge 0,}{\bigcup }} \left\{ \partial _{\epsilon _0}f(\bar{x}) + \partial _{\epsilon _1}\delta _C (\bar{x})\right\} . \end{aligned}$$

We have also the following proposition [37, 38].

Proposition 2.3

Let I is an arbitrary index set, and $g_i: \mathbb {R}^n\rightarrow \mathbb {R}\cup \lbrace \infty \rbrace$ be a proper lower semicontinuous convex function for $i \in I$. Assume that there exists $x_0\in \mathbb {R}^n$ such that $\sup _{i\in I} g_i(x_0) \le +\infty$. Then

$$\begin{aligned} \text {epi}\; \left( \sup _{i\in I} g_i\right) ^\star = \text {cl} \; \left( \text {co} \; \bigcup _{i\in I} \;\text {epi}\;g_i^\star \right) . \end{aligned}$$

Let $\mathcal {D}$ be the robust characteristic cone defined as

$$\begin{aligned} \mathcal {D}:= & {} {\underset{a_i^{(t)}\in \mathcal {V}_i^{(t)},\;i\in I,\;t\in T}{\displaystyle \bigcup }}\\{} & {} \left\{ \displaystyle \sum _{t\in T} \left( z^{(t)}\bullet a_1^{(t)},\;\ldots \;,\; z^{(t)}\bullet a_m^{(t)},\;-z^{(t)}\bullet a_0^{(t)}-r^{(t)} \right) : z^{(t)}\succeq 0, r^{(t)}\ge 0 \right\} . \end{aligned}$$

The following lemma shows that $\mathcal {D}$ is indeed a cone in $\mathbb {R}^{m+1}$ under Assumption 1.1.

Lemma 2.1

The set $\mathcal {D} \subset \mathbb {R}^{m+1}$ is a cone.

Proof

It s clear that $0 \in \mathcal {D}$. To prove the desired result, we need to show that for each $x \in \mathcal {D}$ and $\lambda \in {{\mathbb {R}}}_{++}$, we have $\lambda x \in \mathcal {D}$. Since $x \in \mathcal {D}$, there exist $a_i= (a_i^{(t)})_{t\in T}, i \in I$, $z=(z^{(t)})_{t\in T}$, and $r\in {{\mathbb {R}}}^{(T)}_+$, where $a_i^{(t)} \in \mathcal {V}_i^{(t)}$ and $z^{(t)} \succeq 0$, for all $t\in T$ and $i \in I$, such that $x_i=\sum _{t \in T} (z^{(t)}\bullet a_i^{(t)})$ for $i=1, \ldots , m$, and $x_{m+1}=-\sum _{t \in T}(z^{(t)}\bullet a_0^{(t)}+r^{(t)})$. It follows that $\lambda x_i= \sum _{t \in T} (\lambda z^{(t)}\bullet a_i^{(t)})$ and $\lambda x_{m+1}=-\sum _{t \in T} (\lambda z^{(t)}\bullet a_0^{(t)} + \bar{r})$. Note that $\lambda r^{(t)} \ge 0$, and that $\lambda z^{(t)}\succeq 0$ because $\mathcal {K}_{\mathcal {J}}$ is a cone. Thus, $\lambda x \in \mathcal {D}$. $\square$

The following lemma is due to [21, Lemma 4.2].

Proposition 2.4

Let $\epsilon \in {{\mathbb {R}}}_+$, then $\bar{x}$ is an $\epsilon$-solution of RSIMSP if

$$\begin{aligned} \sum _{k=1}^Kf_k(x)\ge \sum _{k=1}^Kf_k(\bar{x})-\epsilon \end{aligned}$$

for any $x\in \mathcal {F}_{\mathcal {P}}\cap \lbrace x\in \mathbb {R}^m: f_k(x)\ge f_k(\bar{x}), k=1, \ldots , K\rbrace$.

We say that RSIMSP satisfies the convexity condition if for every $t \in T$ we have

$$\begin{aligned} \mathcal {V}_i^{(t)} = \left\{ a_{0}^{(t)}+ \sum _{j=1}^l u_{i_j}^{(t)}a_{j}^{(t)}:\; \left( u_{i_1}^{(t)}, u_{i_2}^{(t)},\ldots ,u_{i_l}^{(t)} \right) \in U_i^{(t)} \right\} , \end{aligned}$$

where $U_i^{(t)}$ is compact convex subset of $\mathbb {R}^l$, $a_{0}^{(t)} \in \mathcal {J}$ and $a_{j}^{(t)}\succeq 0$, for each $t\in T, i\in I$, and $j=1,2,\ldots ,l$. We point out that if the above convexity condition holds, then the uncertainty sets $V^t_i$ includes the box uncertainty sets of linear programming and the spectrahedral uncertainty sets of semidefinite programming as special cases.

The closeness and convexity of the robust characteristic cone $\mathcal {D}$ are necessary for the robust characteristic cone constraint qualification to hold. The following lemma proves the convexity of $\mathcal {D}$ under the convexity condition of RSIMSP (see also [39, Proposition 1]).

Lemma 2.2

If RSIMSP satisfies the convexity condition, the robust characteristic cone $\mathcal {D}$ is convex.

Proof

Let $x,y\in \mathcal {D}$ and let $\lambda \in [0,1]$. We want to show that $\lambda x+(1-\lambda )y\in \mathcal {D}$. From the definition of $\mathcal {D}$, there exist $h_i= (h_i^{(t)})_{t\in T}, c_i= (c_i^{(t)})_{t\in T}, i \in I$, $b=(b^{(t)})_{t\in T},n=(n^{(t)})_{t\in T}$, and $r, s \in {{\mathbb {R}}}^{(T)}_+$, where $h_i^{(t)},c_i^{(t)}\in \mathcal {V}_{t}$, and $b^{(t)},n^{(t)}\succeq 0$, for $i\in I, t\in T$, such that

$$\begin{aligned} \begin{array}{lll} x_i=\displaystyle \sum _{t\in T} \left( b^{(t)}\bullet h_i^{(t)}\right) ,\, i\in I-\lbrace 0\rbrace , &{}&{} x_{m+1}= -\displaystyle \sum _{t\in T} \left( b^{(t)}\bullet h_0^{(t)}+r^{(t)}\right) ,\\ y_i=\displaystyle \sum _{t\in T} \left( n^{(t)}\bullet c_i^{(t)}\right) ,\, i\in I-\lbrace 0\rbrace , &{}&{} y_{m+1}=- \displaystyle \sum _{t\in T} \left( n^{(t)}\bullet c_0^{(t)}+s^{(t)}\right) . \end{array} \end{aligned}$$

Since $h_i^{(t)},c_i^{(t)}\in \mathcal {V}_{t}$, there exist $(u_{i_1}^{(t)},u_{i_2}^{(t)},\ldots ,u_{i_l}^{(t)})\in U_i^{(t)}$ and $(v_{i_1}^{(t)},v_{i_2}^{(t)},\ldots ,v_{i_l}^{(t)}) \in U_i^{(t)}$ such that, for each $i\in I$, we have

$$\begin{aligned} h_i^{(t)}= a_{0}^{(t)}+ \sum _{j=1}^l u_{i_j}^{(t)}a_{j}^{(t)}, \quad \text {and}\quad c^{(t)}_i=a_{0}^{(t)}+ \sum _{j=1}^l v_{i_j}^{(t)}a_{j}^{(t)}. \end{aligned}$$

Fixing an $i\in I-\lbrace 0\rbrace$, we have that

$$\begin{aligned} \lambda x_i+(1-\lambda )y_i= & {} \lambda \displaystyle \sum _{t\in T} \left( b^{(t)}\bullet h_i^{(t)}\right) +(1-\lambda )\displaystyle \sum _{t\in T} \left( n^{(t)} \bullet c_i^{(t)}\right) \\= & {} \displaystyle \sum _{t\in T} \left( \lambda \, b^{(t)}\bullet \left( a_{0}^{(t)}+ \displaystyle \sum _{j=1}^l u_{i_j}^{(t)}a_{j}^{(t)}\right) +(1-\lambda ) \, n^{(t)}\right. \\{} & {} \left. \bullet \left( a_{0}^{(t)}+ \displaystyle \sum _{j=1}^l v_{i_j}^{(t)}a_{j}^{(t)}\right) \right) \\= & {} \displaystyle \sum _{t\in T} \left( a_{j}^{(0)}\bullet \left( \lambda b^{(t)} +(1-\lambda ) n^{(t)} \right) \right. \\{} & {} \left. +\displaystyle \sum _{j=1}^l \left( \lambda u_{i_j}^{(t)}\; b^{(t)} \bullet a_{j}^{(t)} + (1-\lambda ) v_{i_j}^{(t)}\; n^{(t)}\bullet a_{j}^{(t)} \right) \right) . \end{aligned}$$

For $i\in I, t \in T$ and $j=1,2,\ldots ,l$, we define $w_{i_j}^{(t)}$ as

$$\begin{aligned} w_{i_j}^{(t)}=\left\{ \begin{array}{lll} \displaystyle \frac{\lambda u_{i_j}^{(t)}\; b^{(t)} \bullet a_{j}^{(t)} + (1-\lambda ) v_{i_j}^{(t)}\; n^{(t)}\bullet a_{j}^{(t)}}{\left( \lambda b^{(t)} +(1-\lambda ) n^{(t)} \right) \bullet a_{j}^{(t)}}, &{}&{} \text {if}\; \left( \lambda b^{(t)} +(1-\lambda ) n^{(t)} \right) \bullet a_{j}^{(t)} \ne 0, \\ u_{i_j}^{(t)},&{}&{} \text {if}\; \left( \lambda b^{(t)} +(1-\lambda ) n^{(t)} \right) \bullet a_{j}^{(t)} =0. \end{array}\right. \end{aligned}$$

By the convexity of $U_i^{(t)}$, it is clear that $(w_{i_1}^{(t)},w_{i_2}^{(t)}, \ldots ,w_{i_l}^{(t)}) \in U_i^{(t)}$ for $i\in I$. In addition, for each $i\in I-\lbrace 0\rbrace ,\;t\in T$ and $j=1,2,\ldots ,l$, we have that

$$\begin{aligned} w_{i_j}^{(t)} \left( \lambda b^{(t)} +(1-\lambda ) n^{(t)} \right) \bullet a_{j}^{(t)} =u_{i_j}^{(t)}\left( \lambda b^{(t)} \bullet a_{j}^{(t)} \right) + v_{i_j}^{(t)}\left( (1-\lambda ) n^{(t)}\bullet a_{j}^{(t)} \right) . \nonumber \\ \end{aligned}$$

(1)

Note that if $(\lambda b^{(t)}+(1-\lambda )n^{(t)})\bullet a_{j}^{(t)} \ne 0$, the equality in (1) follows trivially. If $(\lambda b^{(t)}+(1-\lambda )n^{(t)})\bullet a_{j}^{(t)} =0$, then $\lambda b^{(t)}\bullet a_{j}^{(t)} =(1-\lambda )n^{(t)} \bullet a_{j}^{(t)}=0$ because $b^{(t)},n^{(t)},a_{j}^{(t)}\succeq 0$, for all $i\in I-\lbrace 0\rbrace , t \in T$ and $j=1,2,\ldots ,l$, and hence the equality in (1) follows in this case as well. It follows immediately that

$$\begin{aligned} \begin{array}{lll} \lambda x_i+(1-\lambda )y_i &{}=&{}\displaystyle \sum _{t\in T} \left( \left( \lambda b^{(t)} +(1-\lambda ) n^{(t)} \right) \bullet a_{0}^{(t)} +\displaystyle \sum _{j=1}^l \left( w_{i_j}^{(t)} \left( \lambda b^{(t)} +(1-\lambda ) n^{(t)} \right) \bullet a_{j}^{(t)} \right) \right) \\ &{}=&{}\displaystyle \sum _{t\in T} \left( \left( \lambda b^{(t)}+(1-\lambda )n^{(t)}\right) \bullet \left( a_{0}^{(t)}+\displaystyle \sum _{j=1}^l w_{i_j}^{(t)}a_{j}^{(t)}\right) \right) , \end{array} \end{aligned}$$

for $i \in I - \{0\}$. Similarly it is also seen that

$$\begin{aligned} \lambda x_{m+1}+(1-\lambda )y_{m+1}= & {} - \displaystyle \sum _{t\in T} \left( \left( \lambda b^{(t)}+(1-\lambda )n^{(t)}\right) \bullet \left( a_{0}^{(t)}+\displaystyle \sum _{j=1}^l w_{0_j}^{(t)}a_{j}^{(t)}\right) \right. \\ {}{} & {} \left. +\left( \lambda r^{(t)}+(1-\lambda )s^{(t)}\right) \right) . \end{aligned}$$

Note that $\lambda r^{(t)} +(1-\lambda )s^{(t)} \ge 0$, $\lambda b^{(t)}+(1-\lambda )n^{(t)}\succeq 0$, and $(w_{i_1}^{(t)},w_{i_2}^{(t)}, \ldots ,w_{i_l}^{(t)}) \in U_i^{(t)}$, for each $i\in I$ and $t \in T$. This implies that $\lambda x+(1-\lambda )y\in \mathcal {D}$, and therefore $\mathcal {D}$ is convex. The proof is complete. $\square$

The following lemma proves the closeness of $\mathcal {D}$ under Assumptions 1.1 and 1.2 (see also [8, Corollary 2.1]).

Lemma 2.3

If the Slater condition holds, the robust characteristic cone $\mathcal {D}$ is closed.

Proof

Let $\lbrace x(k)\rbrace _{k=1}^\infty := \lbrace (x_1(k),x_2(k),\ldots ,x_{m+1}(k)) \rbrace _{k=1}^\infty$ be a sequence in $\mathcal {D}$ that is convergent to the point $x:=(x_1,x_2,\ldots ,x_{m+1}) \in {{\mathbb {R}}}^{m+1}$. To show that $\mathcal {D}$ is closed, we want to show that $x \in \mathcal {D}$. From the definition of $\mathcal {D}$, there exist $a_i(k)= (a_i^{(t)}(k))_{t\in T}, i \in I$, $z(k)=(z^{(t)}(k))_{t\in T}$, and $r(k)\in {{\mathbb {R}}}^{(T)}_+$, where $a_i^{(t)}(k) \in \mathcal {V}_i^{(t)}$ and $z^{(t)}(k) \succeq 0$, for all $t\in T$ and $i \in I$, such that

$$\begin{aligned} x_i(k)=\displaystyle \sum _{t\in T}\left( z^{(t)}(k)\bullet a_{i}^{(t)}(k)\right) , \quad i=1, 2, \ldots , m, \end{aligned}$$

(2)

and

$$\begin{aligned} x_{m+1}(k)=-\displaystyle \sum _{t\in T}\left( z^{(t)}(k)\bullet a_{0}^{(t)}(k)+r^{(t)}(k)\right) . \end{aligned}$$

(3)

Based on Assumption 1.1, the sequence $\lbrace a_{i}^{(t)}(k) \rbrace _{k=1}^\infty$ has a convergent subsequence. Therefore, after passing to a convergent subsequence, if necessary, we may assume that $a_{i}^{(t)}(k)\rightarrow a_i^{(t)}\in \mathcal {V}_i^{(t)}$. Now, we show that $\lbrace \Vert (z^{(t)}(k)\Vert \rbrace$ is a bounded sequence by contradiction. Suppose on the contrary that $\Vert (z^{(t)}(k)\Vert \rightarrow +\infty$. Then, $z^{(t)}(k)/\Vert z^{(t)}(k)\Vert \rightarrow z^{(t)}\in \mathcal {K}_{\mathcal {J}}-\lbrace 0\rbrace$. Dividing both sides of (2) and (3) by $\Vert z^{(t)}(k)\Vert$ and applying the limit, we obtain

$$\begin{aligned} \displaystyle \sum _{t\in T}\left( z^{(t)}\bullet a_i^{(t)}\right)= & {} 0,\; i=1, 2, \ldots , m,\;\quad \text {and}\;\quad -\displaystyle \sum _{t\in T}\left( z^{(t)}\bullet a_0^{(t)}\right) \\= & {} \displaystyle \sum _{t\in T}\underset{k\rightarrow \infty }{\lim }\; \frac{r^{(t)}(k)}{\Vert z^{(t)}(k)\Vert }\ge 0. \end{aligned}$$

Based on Assumption 1.2, there exists $x^{(0)}\in {{\mathbb {R}}}^m$ such that $a_0^{(t)} + \sum _{i=1}^m x^{(0)}_ia_i^{(t)} \succ 0$, for all $a_i^{(t)}\in \mathcal {V}_i^{(t)}$, and

$$\begin{aligned} z^{(t)}\bullet \left( a_0^{(t)} +\displaystyle \sum _{i=1}^m x^{(0)}_ia_i^{(t)} \right) =z^{(t)}\bullet a_0^{(t)}+\displaystyle \sum _{i=1}^m x^{(0)}_i\left( z^{(t)}\bullet a_i^{(t)}\right) \le 0. \end{aligned}$$

This is on one side of the coin, but on the other side, since $z^{(t)}\in \mathcal {K}_{\mathcal {J}}- \lbrace 0\rbrace$, we have $z^{(t)}\bullet (a_0^{(t)} +\sum _{i=1}^m x^{(0)}_ia_i^{(t)})>0$, which is a contradiction. Hence, the sequence $\lbrace \Vert z^{(t)}(k)\Vert \rbrace _{k=1}^\infty$ is bounded. From (3), the sequence $\lbrace r^{(t)}(k)\rbrace _{k=1}^\infty$ is also bounded. Therefore, after passing to a subsequence, if necessary, we can assume that $z^{(t)}(k) \rightarrow \bar{z}^{(t)}$ and $r^{(t)}(k)\rightarrow \bar{r}^{(t)}$. By applying the limit in (2) and (3), we have

$$\begin{aligned} x_i=\displaystyle \sum _{t\in T}\left( \bar{z}^{(t)}\bullet a_i^{(t)}\right) ,\; i=1, 2, \ldots , m, \quad \text {and}\quad x_{m+1}=-\displaystyle \sum _{t\in T}\left( \bar{z}^{(t)}\bullet a_0^{(t)}+\bar{r}^{(t)}\right) . \end{aligned}$$

Thus, $x\in \mathcal {D}$. This completes the proof. $\square$

3 $\epsilon$-Optimality theorem

In this section, we establish the $\epsilon$-optimality theorem for our problem. First, we prove two intermediate lemmas. The next lemma is the robust version of Farkas’ lemma for our setting, and is based on Assumptions 1.2 and 1.1.

Lemma 3.1

Let $(c_k,\alpha _k) \in \mathbb {R}^m \times \mathbb {R}$ for $k=1,\ldots ,K$, then

$$\begin{aligned} \mathcal {F}_{\mathcal {P}}\subset \big \lbrace x\in \mathbb {R}^m :\langle c_k,x\rangle \ge \alpha _k,\;k=1,\dots ,K\big \rbrace \Longleftrightarrow \displaystyle \sum _{K=1}^{K}(c_k,\alpha _k)\in \text {cl co}\; \mathcal {D}. \end{aligned}$$

Proof

Assume that $\mathcal {F}_{\mathcal {P}}\subset \lbrace x\in \mathbb {R}^m :\langle c_k,x\rangle \ge \alpha _k,\;k=1,\dots ,K\rbrace$, and let $\phi _k(x)= \langle c_k,x\rangle - \alpha _k$ for $k=1,2,\ldots ,K$. Then $\mathcal {F}_{\mathcal {P}}\subset \lbrace x\in \mathbb {R}^m :\phi _k(x)\ge 0,\;k=1,\dots ,K\rbrace .$ It follows that $\sum _{k=1}^K\phi _k(x) +\delta _{\mathcal {F}_{\mathcal {P}}}(x)\ge 0$ for all $x\in \mathbb {R}^{m}$. Note that $\phi _k$ is continuous for $k=1,2,\ldots ,K$. Therefore, using Proposition 2.1, we have

$$\begin{aligned} (0,0)\in \text {epi}\;\left( \displaystyle \sum _{k=1}^{K}\phi _k+\delta _{\mathcal {F}_{\mathcal {P}}}\right) ^{\star }= & {} \displaystyle \sum _{k=1}^K \text {epi}\;\phi ^{\star }_k+ \text {epi}\;\delta ^{\star }_{\mathcal {F}_{\mathcal {P}}}\\= & {} \displaystyle \sum _{k=1}^K(c_k,\alpha _k) + \lbrace 0\rbrace \times \mathbb {R}_{+}+ \text {epi}\;\delta ^{\star }_{\mathcal {F}_{\mathcal {P}}}. \end{aligned}$$

Thus,

$$\begin{aligned} \sum _{k=1}^K(c_k,\alpha _k)\in -\text {epi}\;\delta ^{\star }_{\mathcal {F}_{\mathcal {P}}}-\lbrace 0\rbrace \times \mathbb {R}_{+}. \end{aligned}$$

(4)

The desired result is obtained by showing that $\sum _{k=1}^K(c_k,\alpha _k)\in \text {cl co}\; \mathcal {D}$. To prove this, in light of (4), it is enough to show that $\text {epi}\;\delta _{\mathcal {F}_{\mathcal {P}}}^{\star } =-\text {cl co}\; \mathcal {D}$.

Note that, for each $z^{(t)}\succeq 0, a_i^{(t)}\in \mathcal {V}_i^{(t)}$, $i\in I,\;t\in T$ and $\xi \in {{\mathbb {R}}}^m$, we have

$$\begin{aligned}{} & {} \bigg (-z^{(t)}\bullet a_0^{(t)}-\bigg \langle \;\varvec{\cdot }\;,\left( z^{(t)}\bullet a_1^{(t)},\ldots ,z^{(t)}\bullet a_m^{(t)} \right) \bigg \rangle \bigg )^{\star }(\xi )\nonumber \\{} & {} \quad = \underset{x\in {{\mathbb {R}}}^m}{\text {sup}}\left\{ \langle \xi ,x\rangle -\left( -z^{(t)}\bullet a_0^{(t)}-\bigg \langle x,\bigg (z^{(t)}\bullet a_1^{(t)},\ldots ,z^{(t)}\bullet a_m^{(t)}\bigg )\bigg \rangle \right) \right\} \nonumber \\{} & {} \quad = \underset{x\in {{\mathbb {R}}}^m}{\text {sup}} \left\{ \displaystyle \sum _{i=1}^m\xi _ix_i+\displaystyle \sum _{i=1}^m \left( x_i\; z^{(t)}\bullet a_i^{(t)}\right) \right\} +z^{(t)}\bullet a_0^{(t)}\nonumber \\{} & {} \quad =\underset{x\in {{\mathbb {R}}}^m}{\text {sup}}\left\{ \displaystyle \sum _{i=1}^m \left( x_i\left( \xi _i+z^{(t)}\bullet a_i^{(t)}\right) \right) \right\} +z^{(t)}\bullet a_0^{(t)}\nonumber \\{} & {} \quad = \left\{ \begin{array}{lll} z^{(t)}\bullet a_i^{(t)},&{}&{} \text {if}\;\xi _i= -z^{(t)}\bullet a_i^{(t)},\;i=1,\ldots ,m, \\ +\infty ,&{}&{} \text {otherwise}. \end{array}\right. \end{aligned}$$

(5)

Note also that, for any $x\in {{\mathbb {R}}}^m$, we have

$$\begin{aligned} \delta _{\mathcal {F}_{\mathcal {P}}}(x) =\underset{z^{(t)}\succeq 0,\;t\in T}{\underset{a_i^{(t)}\in \mathcal {V}_i^{(t)},\;i\in I,}{\sup }}\left( -z^{(t)}\bullet \left( a_0^{(t)}+\displaystyle \sum _{i=1}^m x_ia_i^{(t)}\right) \right) . \end{aligned}$$

It follows that

$$\begin{aligned} \begin{array}{lll} \text {epi}\;\delta ^{\star }_{\mathcal {F}_{\mathcal {P}}} &{}=\text {epi}\;\left( \underset{z^{(t)}\in \,\,\succeq 0,\;t\in T}{\underset{a_i^{(t)}\in \mathcal {V}_i^{(t)},\;i\in I,}{\sup }} \displaystyle \sum _{t\in T} \bigg ( -z^{(t)}\bullet a_0^{(t)} - \bigg \langle \;\varvec{\cdot }\;, \bigg (z^{(t)}\bullet a_1^{(t)},\ldots ,z^{(t)}\bullet a_m^{(t)}\bigg )\bigg \rangle \bigg )\right) ^{\star }\\ &{}= \text {cl}\;\left( \text {co}\;\underset{z^{(t)}\succeq 0,\;t\in T}{\underset{a_i^{(t)}\in \mathcal {V}_i^{(t)},\;i\in I,}{\displaystyle \bigcup }} \text {epi}\displaystyle \sum _{t\in T} \bigg ( -z^{(t)}\bullet a_0^{(t)} - \bigg \langle \;\varvec{\cdot }\;, \bigg (z^{(t)}\bullet a_1^{(t)},\ldots ,z^{(t)}\bullet a_m^{(t)}\bigg )\bigg \rangle \bigg )^{\star } \right) \\ &{}\quad \text {cl}\;\left( \text {co}\;\underset{}{\underset{a_i^{(t)}\in \mathcal {V}_i^{(t)},\;i\in I,\;t\in T}{\displaystyle \bigcup }} \left\{ \displaystyle \sum _{t\in T} \bigg ( -z^{(t)}\bullet a_1^{(t)},\;\ldots ,\;-z^{(t)}\bullet a_m^{(t)},\;z^{(t)}\bullet a_0^{(t)} +r \bigg ):\right. \right. \\ {} &{}\quad \left. \left. z^{(t)} \succeq 0,\;r^{(t)} \ge 0\right\} \right) = - \text {cl co}\; \mathcal {D}, \end{array} \end{aligned}$$

where the second equality follows from Propositions 2.1 and 2.3 and the third equality follows from (5). The proof is complete. $\square$

The following lemma is also based on Assumption 1.1.

Lemma 3.2

Let $\bar{x}\in \mathcal {F}_{\mathcal {P}}$ and $\epsilon \ge 0$. Let also $f_k:\mathbb {R}^m\rightarrow \mathbb {R}$ be a convex function for $k=1, 2, \ldots , K$. Then $\bar{x}$ is an $\epsilon$-solution of RSIMSP if and only if for each $k=1,2, \ldots , K$ and $t \in T$, there exist $\epsilon _k, \epsilon _t\ge 0$ and $\xi _k\in \partial _{\epsilon _k}f_k(\bar{x})$ such that $\sum _{k=1}^K\epsilon _k +\sum _{t\in T}\epsilon _t=\epsilon$ and

$$\begin{aligned} \left( \displaystyle \sum _{k=1}^K\xi _k,\left\langle \sum _{k=1}^K\xi _k,\bar{x}\right\rangle -\displaystyle \sum _{t\in T}\epsilon _t\right) \in \text {cl co}\;\mathcal {D}. \end{aligned}$$

Proof

Assume that $\bar{x}$ is an $\epsilon$-solution of RSIMSP, where $\epsilon \ge 0$. Then, for any $x\in \mathcal {F}_{\mathcal {P}},\;\sum _{k=1}^{K} f_k(x)\ge \sum _{k=1}^{K}f_k(\bar{x})-\epsilon$. It follows that, for any $x\in \mathbb {R}^m$, we have

$$\begin{aligned} \sum _{k=1}^{K}f_k(x)+\delta _{\mathcal {F}_{\mathcal {P}}}(x)\ge \sum _{k=1}^{K}f_k(\bar{x})+\delta _{\mathcal {F}_{\mathcal {P}}}(\bar{x}) -\epsilon . \end{aligned}$$

Then, according to the definition of $\epsilon$-subdifferentiability, we deduce that $0\in \partial _{\epsilon } (\sum _{k=1}^{K}f_k +\delta _{\mathcal {F}_{\mathcal {P}}})(\bar{x})$, which in view of Proposition 2.2 is equivalent to

$$\begin{aligned} 0\in \sum _{k=1}^{K}\partial _{\epsilon _k} f_k(\bar{x})+\sum _{t\in T}\partial _{\epsilon _t} \delta _{\mathcal {F}_{\mathcal {P}}}(\bar{x}). \end{aligned}$$

Therefore, for each $k=1, \ldots , K$ and $t \in T$, there exist $\epsilon _k, \epsilon _t \ge 0$, $\xi _k\in \partial _{\epsilon _k}f_k(\bar{x})$, and $-\xi _t\in \partial _{\epsilon _t} \delta _{\mathcal {F}_{\mathcal {P}}}(\bar{x})$ such that

$$\begin{aligned} \sum _{k=1}^k\epsilon _k+\sum _{t\in T}\epsilon _t=\epsilon \;\;\;\text {and}\;\;\; \sum _{k=1}^k\xi _k-\sum _{t\in T}\xi _t=0. \end{aligned}$$

Equivalently, for each $k=1, \ldots , K$ and $t \in T$, there exist $\epsilon _k, \epsilon _t\ge 0$ and $\xi _k\in \partial _{\epsilon _k}f_k(\bar{x})$ such that $\langle \xi _k,x\rangle \ge \langle \xi _k,\bar{x}\rangle -\epsilon _t$ for any $x \in \mathcal {F}_{\mathcal {P}}$ and $t \in T$, and hence

$$\begin{aligned} \left\langle \displaystyle \sum _{k=1}^K\xi _k,x\right\rangle \ge \left\langle \sum _{k=1}^K\xi _k,\bar{x}\right\rangle -\displaystyle \sum _{t\in T}\epsilon _t \end{aligned}$$

for any $x\in \mathcal {F}_{\mathcal {P}}$. By Lemma 3.1, we conclude that for each $k=1, \ldots , K$ and $t \in T$, there exist $\epsilon _k,\epsilon _t\ge 0$ and $\xi _k\in \partial _{\epsilon _k}\delta _{\mathcal {F}_{\mathcal {P}}}(\bar{x})$ such that

$$\begin{aligned} \left( \displaystyle \sum _{k=1}^K\xi _k,\left\langle \sum _{k=1}^K\xi _k,\bar{x}\right\rangle -\displaystyle \sum _{t\in T}\epsilon _t\right) \in \text {cl co}\;\mathcal {D}. \end{aligned}$$

The proof is complete. $\square$

In light of Lemmas 3.1 and 3.2, we can obtain the $\epsilon$-optimality theorem under the robust characteristic cone constraint qualification.

Theorem 3.1

(Approximate optimality theorem) Consider the RSIMSP problem, and let $\bar{x}\in \mathcal {F}_{\mathcal {P}}$. Then $\bar{x}$ is an $\epsilon$-solution of RSIMSP if and only if there exist $(\epsilon _t)_{t\in T} \in {{\mathbb {R}}}^{(T)}_+, \epsilon _k \in {{\mathbb {R}}}_+, \xi _k\in \partial _{\epsilon _k}f_k(\bar{x})$, $k=1, 2, \ldots , K$, $\bar{a}_i= (\bar{a}_i^{(t)})_{t\in T}, i \in I$, and $\bar{z}=(\bar{z}^{(t)})_{t\in T}$, where $\bar{a}_i^{(t)} \in \mathcal {V}_i^{(t)}$ and $\bar{z}^{(t)} \succeq 0$, for all $t\in T$ and $i \in I$, such that $\sum _{k=1}^K\epsilon _k+\sum _{t\in T}\epsilon _t=\epsilon$, and

$$\begin{aligned}&\displaystyle \sum _{k=1}^K\xi _k =\displaystyle \sum _{t\in T}\left( \bar{z}^{(t)}\bullet \bar{a}_1^{(t)}, \bar{z}^{(t)}\bullet \bar{a}_2^{(t)}, \ldots ,\bar{z}^{(t)}\bullet \bar{a}_m^{(t)}\right) , \end{aligned}$$

(6)

$$\begin{aligned}&\displaystyle \sum _{t\in T}\epsilon _t \ge \displaystyle \sum _{t\in T} \left( \bar{z}^{(t)}\bullet \left( \bar{a}_0^{(t)}+\displaystyle \sum _{i=1}^m\bar{x}_i\bar{a}_i^{(t)}\right) \right) \ge 0. \end{aligned}$$

(7)

Proof

Assume that $\bar{x}$ is an $\epsilon$-solution of RSIMSP, where $\epsilon \ge 0$. By Lemma 3.2, for each $t \in T$ and $k=1,2, \ldots , K$, there exist $\epsilon _k,\epsilon _t\ge 0$ and $\xi _k\in \partial _{\epsilon _k} f_k(\bar{x})$ such that $\sum _{k=1}^K\epsilon _k+\sum _{t\in T}\epsilon _t= \epsilon$ and

$$\begin{aligned}{} & {} \left( \displaystyle \sum _{k=1}^K\xi _k,\left\langle \displaystyle \sum _{k=1}^K\xi _k,\bar{x}\right\rangle - \displaystyle \sum \limits _{t\in T}\epsilon _t\right) \in \underset{}{\underset{a_i^{(t)}\in \mathcal {V}_i^{(t)},\;i\in I,\;t\in T}{\displaystyle \bigcup }}\\{} & {} \quad \times \left\{ \displaystyle \sum _{t\in T} \bigg (z^{(t)}\bullet a_1^{(t)},\;\ldots ,\;z^{(t)}\bullet a_m^{(t)},\;-z^{(t)}\bullet a_0^{(t)} - r \bigg ): z^{(t)} \succeq 0,\;r^{(t)} \ge 0\right\} . \end{aligned}$$

It follows that

$$\begin{aligned} \begin{array}{ll} &{}\displaystyle \sum _{k=1}^K\xi _k =\displaystyle \sum _{t\in T} \left( \bar{z}^{(t)}\bullet \bar{a}_1^{(t)}, \bar{z}^{(t)}\bullet \bar{a}_2^{(t)}, \ldots ,\bar{z}^{(t)}\bullet \bar{a}_m^{(t)}\right) ,\\ &{}\left\langle \displaystyle \sum _{k=1}^K\xi _k,\bar{x}\right\rangle - \displaystyle \sum \limits _{t\in T}\epsilon _t = -\displaystyle \sum _{t\in T}\left( \bar{z}^{(t)} \bullet \bar{a}_0^{(t)}+\bar{r}^{(t)}\right) , \end{array} \end{aligned}$$

for some $(\bar{r}^{(t)})_{t\in T} \in {{\mathbb {R}}}^{(T)}_+$, $\bar{a}_i= (\bar{a}_i^{(t)})_{t\in T}, i \in I$, and $\bar{z}=(\bar{z}^{(t)})_{t\in T}$, with $\bar{a}_i^{(t)} \in \mathcal {V}_i^{(t)}$ and $\bar{z}^{(t)} \succeq 0$, for all $t\in T$ and $i \in I$.

By combining (3) and (3), we get

$$\begin{aligned} \sum _{t\in T}\epsilon _t\ge \sum _{t\in T} \left( \epsilon _t -\bar{r}^{(t)}\right)= & {} \sum _{t\in T} \left( \bar{z}^{(t)}\bullet \bar{a}_0^{(t)}\right) +\left\langle \displaystyle \sum _{k=1}^K\xi _k,\bar{x}\right\rangle \\= & {} \sum _{t\in T} \left( \bar{z}^{(t)}\bullet \left( \bar{a}_0^{(t)}+\sum _{i=1}^m\bar{x_i}\bar{a}_i^{(t)}\right) \right) \ge 0. \end{aligned}$$

This proves the first direction.

For the second, assume that there exist $(\epsilon _t)_{t\in T} \in {{\mathbb {R}}}^{(T)}_+, \epsilon _k \in {{\mathbb {R}}}_+, \xi _k\in \partial _{\epsilon _k}f_k(\bar{x})$, $k=1, 2, \ldots , K$, $\bar{a}_i= (\bar{a}_i^{(t)})_{t\in T}, i \in I$, and $\bar{z}=(\bar{z}^{(t)})_{t\in T}$, where $\bar{a}_i^{(t)} \in \mathcal {V}_i^{(t)}$ and $\bar{z}^{(t)} \succeq 0$, for all $t\in T$ and $i \in I$, such that the equality $\sum _{k=1}^K\epsilon _k+\sum _{t\in T}\epsilon _t=\epsilon$ holds, and that (6) and (7) hold. By the definition of the $\epsilon$-subdifferentiality of f, for any $x\in \mathbb {R}^m$, we have that

$$\begin{aligned} \displaystyle \sum _{k=1}^{K}f_k(x)- \displaystyle \sum _{k=1}^{K}f_k(\bar{x})\ge & {} \left\langle \displaystyle \sum _{k=1}^{K}\xi _k,x-\bar{x} \right\rangle -\displaystyle \sum _{k=1}^{K}\epsilon _k\\= & {} \left\langle \displaystyle \sum _{t\in T} \left( \bar{z}^{(t)}\bullet \bar{a}_1^{(t)},\ldots ,\bar{z}^{(t)}\bullet \bar{a}_m^{(t)} \right) ,x-\bar{x}\right\rangle -\displaystyle \sum _{k=1}^{K}\epsilon _k\\= & {} \displaystyle \sum _{t\in T} \left( \bar{z}^{(t)}\bullet \left( \displaystyle \sum _{i=1}^m x_i\bar{a}_i^{(t)}\right) - \bar{z}^{(t)}\bullet \left( \displaystyle \sum _{i=1}^m \bar{x}_i\bar{a}_i^{(t)}\right) \right) -\displaystyle \sum _{k=1}^{K}\epsilon _k\\\ge & {} \displaystyle \sum _{t\in T} \left( \bar{z}^{(t)}\bullet \left( \bar{a}_0^{(t)} +\displaystyle \sum _{i=1}^m\bar{x}_i\bar{a}_i^{(t)}\right) \right) -\displaystyle \sum _{k=1}^{K}\epsilon _k -\displaystyle \sum _{t\in T}\epsilon _t\\= & {} \displaystyle \sum _{t\in T} \left( \bar{z}^{(t)}\bullet \left( \bar{a}_0^{(t)} +\displaystyle \sum _{i=1}^m\bar{x}_i\bar{a}_i^{(t)}\right) \right) -\epsilon ~\ge ~ -\epsilon , \end{aligned}$$

where the first equality is obtained from (6), the second and third inequalities follow from (7). Therefore, $\sum _{k=1}^{K}f_k(x) \ge \sum _{k=1}^{K}f_k(\bar{x}) -\epsilon$, for any $x\in \mathcal {F}_{\mathcal {P}}$. Thus, from Proposition 2.4, $\bar{x}$ is an $\epsilon$-solution of RSIMSP. This proves the second direction. The result is established. $\square$

In multi-objective optimization problems, a solution is called Pareto optimal if none of the objective values can be improved without degrading some of the other objective values. The following remark is an immediate corollary of Theorem 3.1.

Remark 3.1

If the vectors $(\epsilon _t)_{t\in T} \in {{\mathbb {R}}}^{(T)}_+$ and $(\epsilon _k)_{1\le k \le K} \in {{\mathbb {R}}}^{K}_+$ in Theorem 3.1 tend to the null vector, we obtain (exact) optimality conditions for Pareto solutions.

4 $\epsilon$-Duality theorems

The (Wolfe-type) dual problem associated with the RSIMSP problem is the problem

$$\begin{aligned}{} & {} (\text {RSIMSD}) \\{} & {} \quad \left\{ \begin{array}{@{}ll} \max &{}\left( f_1(y)- \displaystyle \sum _{t\in T} \left( z^{(t)} \bullet \left( a_0^{(t)}+\displaystyle \sum _{i=1}^m y_ia_i^{(t)}\right) \right) ,\ldots , f_K(y) \right. \\ &{}\quad \left. - \displaystyle \sum _{t\in T} \left( z^{(t)} \bullet \left( a_0^{(t)}+\displaystyle \sum _{i=1}^m y_ia_i^{(t)}\right) \right) \right) \\ \text {s.t.}&{} 0 \in \displaystyle \sum _{k=1}^K \partial _{\epsilon _k}f_k(y)- \displaystyle \sum _{t \in T} \left( z^{(t)}\bullet a_1^{(t)}, z^{(t)}\bullet a_2^{(t)}, \ldots ,z^{(t)}\bullet a_m^{(t)}\right) ,\\ &{}\displaystyle \sum _{k=1}^K \epsilon _k \le \epsilon ,\; \epsilon _k\ge 0,\;z^{(t)} \succeq 0,\; a_i^{(t)}\in \mathcal {V}_i^{(t)},\;t\in T,\;i\in I, \;k=1, 2, \ldots , K. \end{array} \right. \end{aligned}$$

Note that RSIMSD has the feasibility set

$$\begin{aligned} \mathcal {F}_{\mathcal {D}}:= & {} \Bigg \lbrace \left( y,a_0,\dots ,a_m,z\right) :a_i=\left( a_i^{(t)}\right) _{t\in T}, z=\left( z^{(t)}\right) _{t\in T}, \;0 \in \sum _{k=1}^K \partial _{\epsilon _k}f_k(y) \\{} & {} - \sum _{t \in T} \left( z^{(t)}\bullet a_1^{(t)}, \ldots ,z^{(t)}\bullet a_m^{(t)}\right) ,\\{} & {} \sum _{k=1}^K \epsilon _k \le \epsilon , \;\; \epsilon _k\ge 0,\; y \in {{\mathbb {R}}}^m, \; a_i^{(t)} \in \mathcal {V}_i^{(t)}, z^{(t)} \succeq 0,\\{} & {} t\in T, i \in I, k=1, 2, \ldots , K \Bigg \rbrace . \end{aligned}$$

Let $\epsilon \ge 0$. The point $(\bar{x},\bar{a}_0, \dots ,\bar{a}_m, \bar{z})$ is called an $\epsilon$-solution of RSIMSD if for any $(y,a_0,\dots ,a_m, z) \in \mathcal {F}_{\mathcal {D}}$ we have

$$\begin{aligned}{} & {} \displaystyle \sum _{k=1}^K f_k(\bar{x})- \displaystyle \sum _{t \in T} \left( \bar{z}^{(t)}\bullet \left( \bar{a}_0^{(t)} +\sum _{i=1}^m \bar{x}_i \bar{a}_i^{(t)}\right) \right) \\{} & {} \quad \ge \displaystyle \sum _{k=1}^K f_k(y)- \displaystyle \sum _{t \in T}\left( z^{(t)}\bullet \left( a_0^{(t)} +\sum _{i=1}^m y_i a_i^{(t)}\right) \right) -\epsilon . \end{aligned}$$

Now, we are ready to establish the $\epsilon$-weak duality theorem, which holds between the RSIMSP problem and its dual, the RSIMSD problem.

Theorem 4.1

(Approximate weak duality theorem) For any feasible solution x of RSIMSP and any feasible solution $(y,a_0,a_1, \ldots ,a_m,z)$ of RSIMSD, we have

$$\begin{aligned} \displaystyle \sum _{k=1}^K f_k(x) \ge \displaystyle \sum _{k=1}^K f_k(y) -\displaystyle \sum _{t \in T}\left( z^{(t)}\bullet \left( a_0^{(t)} +\sum _{i=1}^m y_i a_i^{(t)}\right) \right) -\epsilon . \end{aligned}$$

Proof

Let x and $(y,a_0,a_1,\ldots ,a_m,z)$ be feasible solutions of RSIMSP and RSIMSD, respectively. Then $a_i= (a_i^{(t)})_{t\in T}$ and $z=(z^{(t)})_{t\in T}$, where $a_i^{(t)} \in \mathcal {V}_i^{(t)}$ and $z^{(t)} \succeq 0$, for all $t\in T$ and $i \in I$, and the inequality $\sum _{t\in T} (z^{(t)}\bullet (a_0^{(t)} + \sum _{i=1}^m x_i a_i^{(t)})) \ge 0$ holds. It follows that, for each $k=1,2, \ldots , K$, there exist $\epsilon _k \ge 0, \xi _k\in \partial _{\epsilon _k}f_k(x)$ such that $\sum _{k=1}^K \xi _k = \sum _{t \in T} \left( z^{(t)}\bullet a_1^{(t)}, z^{(t)}\bullet a_2^{(t)}, \ldots ,z^{(t)}\bullet a_m^{(t)}\right)$ and $\sum _{k=1}^K\epsilon _k \le \epsilon$. Then, by the definition of the $\epsilon$-subdifferentiability, we have that

$$\begin{aligned}{} & {} \displaystyle \sum _{k=1}^K f_k(x)- \left( \displaystyle \sum _{k=1}^K f_k(y)- \displaystyle \sum _{t \in T}\left( z^{(t)}\bullet \left( a_0^{(t)} +\displaystyle \sum _{i=1}^m y_i a_i^{(t)}\right) \right) \right) \\{} & {} \quad \ge \left\langle \displaystyle \sum _{k=1}^K \xi _k,x-y\right\rangle -\displaystyle \sum _{k=1}^K \epsilon _k +\displaystyle \sum _{t \in T} \left( z^{(t)}\bullet \left( a_0^{(t)} +\displaystyle \sum _{i=1}^m y_i a_i^{(t)}\right) \right) \\{} & {} \quad = \left\langle \displaystyle \sum _{t \in T} \left( z^{(t)}\bullet a_1^{(t)}, z^{(t)}\bullet a_2^{(t)}, \ldots ,z^{(t)}\bullet a_m^{(t)}\right) ,x-y\right\rangle -\displaystyle \sum _{k=1}^K\epsilon _k\\{} & {} \qquad +\displaystyle \sum _{t \in T} \left( z^{(t)}\bullet \left( a_0^{(t)} +\displaystyle \sum _{i=1}^m y_i a_i^{(t)}\right) \right) \\{} & {} \quad =\displaystyle \sum _{t \in T} \left( z^{(t)}\bullet \left( a_0^{(t)} +\displaystyle \sum _{i=1}^m x_i a_i^{(t)}\right) \right) -\displaystyle \sum _{k=1}^K \epsilon _k\\{} & {} \quad \ge -\displaystyle \sum _{k=1}^K \epsilon _k ~\ge ~ -\;\epsilon . \end{aligned}$$

The proof is complete. $\square$

Now, we state and prove the $\epsilon$-strong duality, which holds theorem between RSIMSP and RSIMSD under the robust characteristic cone constraint qualification.

Theorem 4.2

(Approximate strong duality theorem) Assume that the robust characteristic cone $\mathcal {D}$ is closed and convex. If $\bar{x}$ is an $\epsilon$-solution of RSIMSP, then there exist $a_i= (a_i^{(t)})_{t\in T}, i \in I$, and $z=(z^{(t)})_{t\in T}$, where $a_i^{(t)} \in \mathcal {V}_i^{(t)}$ and $z^{(t)} \succeq 0$, for all $t\in T$ and $i \in I$, such that $(\bar{x},\bar{a}_0,\bar{a}_1,\ldots ,\bar{a}_m,\bar{z})$ is a $2\epsilon$-solution of RSIMSD.

Proof

Let $\bar{x}$ be an $\epsilon$-solution of RSIMSP, then by using Theorem 3.1, there exist $(\epsilon _t)_{t\in T} \in {{\mathbb {R}}}^{(T)}_+, \epsilon _k \in {{\mathbb {R}}}_+, \xi _k\in \partial _{\epsilon _k}f_k(\bar{x})$, $k=1, 2, \ldots , K$, $\bar{a}_i= (\bar{a}_i^{(t)})_{t\in T}, i \in I$, and $\bar{z}=(\bar{z}^{(t)})_{t\in T}$, where $\bar{a}_i^{(t)} \in \mathcal {V}_i^{(t)}$ and $\bar{z}^{(t)} \succeq 0$, for all $t\in T$ and $i \in I$, such that

$$\begin{aligned} \displaystyle \sum _{k=1}^K\epsilon _k+ \displaystyle \sum _{t\in T}\epsilon _t= & {} \epsilon , \;\; \displaystyle \sum _{k=1}^K\xi _k =\displaystyle \sum _{t\in T}\left( \bar{z}^{(t)}\bullet \bar{a}_1^{(t)}, \bar{z}^{(t)}\bullet \bar{a}_2^{(t)}, \ldots ,\bar{z}^{(t)}\bullet \bar{a}_m^{(t)}\right) ,\\{} & {} \quad \text {and}\;\; \displaystyle \sum _{t\in T}\epsilon _t \ge \displaystyle \sum _{t\in T} \left( \bar{z}^{(t)}\bullet \left( \bar{a}_0^{(t)}+\displaystyle \sum _{i=1}^m\bar{x}_i\bar{a}_i^{(t)}\right) \right) \ge 0. \end{aligned}$$

Therefore, the point ($\bar{x},\bar{a}_0,\bar{a}_1,\ldots ,\bar{a}_m,\bar{z}$) is a feasible solution for RSIMSD. Then, using Theorem 4.1, for any feasible solution $(y,a_0,a_1,\ldots ,a_m,z)$ of RSIMSD, we have that

$$\begin{aligned}{} & {} \displaystyle \sum _{k=1}^K f_k(\bar{x}) - \displaystyle \sum _{t \in T}\left( \bar{z}^{(t)}\bullet \left( \bar{a}_0^{(t)}+\displaystyle \sum _{i=1}^m\bar{x}_i\bar{a}^{(t)}\right) \right) \\ {}{} & {} \qquad - \left( \displaystyle \sum _{k=1}^K f_k(y)-\displaystyle \sum _{t \in T}\left( z^{(t)}\bullet \left( a_0^{(t)}+\sum _{i=1}^m y_ia_i^{(t)}\right) \right) \right) \\{} & {} \quad \ge -\epsilon - \displaystyle \sum _{t \in T} \left( \bar{z}^{(t)}\bullet \left( \bar{a}_0^{(t)}+\displaystyle \sum _{i=1}^m\bar{x_i}\bar{a}_i^{(t)}\right) \right) \\{} & {} \quad \ge -\epsilon - \displaystyle \sum \limits _{t\in T}\epsilon _t\\{} & {} \quad =-\epsilon -\epsilon + \displaystyle \sum \limits _{k=1}^K \epsilon _k ~ \ge ~ -2\epsilon . \end{aligned}$$

This means that $(\bar{x},\bar{a}_0,\bar{a}_1, \ldots ,\bar{a}_m,\bar{z})$ is a $2\epsilon$-solution of RSIMSD. $\square$

Now, we give the $\epsilon$-strong duality between RSIMSP and RSIMSD under the Slater condition and the weakened robust characteristic cone constraint qualification.

Corollary 4.1

Assume that the robust Slater condition holds and that the robust characteristic cone $\mathcal {D}$ is convex. If $\bar{x}$ is an $\epsilon$-solution of RSIMSP, then there exist $a_i= (a_i^{(t)})_{t\in T}, i \in I$, and $z=(z^{(t)})_{t\in T}$, where $a_i^{(t)} \in \mathcal {V}_i^{(t)}$ and $z^{(t)} \succeq 0$, for all $t\in T$ and $i \in I$, such that $(\bar{x},\bar{a}_0,\bar{a}_1,\ldots ,\bar{a}_m,\bar{z})$ is a $2\epsilon$-solution of RSIMSD.

Proof

By Lemma 2.3, the robust characteristic cone $\mathcal {D}$ is closed. The result immediately follows from Theorem 4.2. $\square$

In the remaining part of this paper, we shall demonstrate in an example that the approximate weak and strong duality of a second-order cone program hold true even though the Slater condition fails.

5 An illustrative example

Throughout this section, we use “,” for adjoining vectors and matrices in a row, and use “;” for adjoining them in a column. So, for example, if a, and b are vectors, then $(a^\textsf{T }, b^\textsf{T })^\textsf{T }= (a; b)$.

Let $\mathcal {E}^n$ be the n-dimensional real vector space ${{\mathbb {R}}}\times {{\mathbb {R}}}^{n-1}$ whose elements are indexed from 0. For each vector $x \in \mathcal {E}^n$, we write $\bar{x}$ for the sub-vector consisting of entries 1 through $n-1$; therefore $x = (x_0; \bar{x})$.

The nth-dimensional second-order cone (also known as the quadratic or Lorentz cone) is defined as

$$\begin{aligned} \mathcal {E}^n_+ := \left\{ (x_0; \bar{x} ) \in {{\mathbb {R}}}\times {{\mathbb {R}}}^{n-1} : x_0 \ge \left\Vert \bar{x} \right\Vert \right\} , \end{aligned}$$

where $\left\Vert \,\cdot \, \right\Vert$ denotes the Euclidean norm.

The cone $\mathcal {E}^n_+$ is closed, pointed (i.e., it does not contain a pair of opposite nonzero vectors) and convex with nonempty interior in ${{\mathbb {R}}}^{n}$. It is also known that $\mathcal {E}^n_+$ is self-dual (i.e., it equals its dual cone), and homogeneous (i.e., its automorphism group acts transitively on its interior). Therfore, the cone $\mathcal {E}^n_+$ is symmetric [22, 27]. The graph to the right shows the 3rd-dimensional second-order cone $\mathcal {E}^3_+$.

Table 2 Some notions associated with the Jordan algebra of the second-order cone

Table 2 lists some notions from the Euclidean Jordan algebra associated with the second-order cone.

In this section, we consider the robust semi-infinite multi-objective convex second-order cone programming problem:

$$\begin{aligned} (\text {RSIMSOCP}) \left\{ \begin{array}{lll} \min &{} &{} \left( x_1+x_2^2;\;x_1 \right) \\ \text {s.t.} &{}&{} a_0^{(t)}+x_1a_1^{(t)}+x_2a_2^{(t)}\succeq \;0,\; t\in [0,1],\\ &{}&{} a_i^{(t)}\in \mathcal {V}_i^{(t)}\subseteq \mathcal {E}^3,\;t\in [0,1],i=0,1,2, \end{array} \right. \end{aligned}$$

where $\mathcal {V}_0^{(t)}, \mathcal {V}_1^{(t)}$ and $\mathcal {V}_2^{(t)}$, $t\in [0,1]$, are the uncertainty subsets:

$$\begin{aligned} \begin{array}{lll} \mathcal {V}_0^{(t)} &{}:=&{} \left\{ \left( u_0^{(t)};0;u_0^{(t)}\right) : u_0^{(t)} \in [-t,0] \right\} ,\\ \mathcal {V}_1^{(t)} &{}:=&{} \left\{ \left( 1;u_1^{(t)};1 \right) : u_1^{(t)} \in [-t,t] \right\} ,\\ \mathcal {V}_2^{(t)} &{}:=&{} \left\{ \left( u_2^{(t)};0;u_2^{(t)}\right) : u_2^{(t)}=t \right\} . \end{array} \end{aligned}$$

Now, for any $t\in [0,1]$, we have

$$\begin{aligned} a_0^{(t)}+x_1a_1^{(t)}+x_2a_2^{(t)}= \left[ \begin{array}{c} u_0^{(t)}+x_1+x_2u_2^{(t)} \\ x_1u_1^{(t)}\\ u_0^{(t)}+x_1+x_2u_2^{(t)} \end{array} \right] . \end{aligned}$$

One can see that $\mathcal {F}_{\mathcal {P}}= \lbrace (x_1;x_2): x_1=0,\;x_2\ge 1\rbrace$ is the set of all robust feasible solutions of RSIMSOCP. Let $\epsilon \ge 0$, then $S_{\mathcal {F}_{\mathcal {P}}}=\lbrace (0;x_2): 1\le x_2\le \sqrt{1+\epsilon }\rbrace$ is the set of all $\epsilon$-solutions of RSIMSOCP.

The robust characteristic cone is

$$\begin{aligned} \mathcal {D}= {\underset{a_i^{(t)}\in \mathcal {V}_i^{(t)},i=0,1,2,\;t\in T}{\displaystyle \bigcup }}\left\{ \displaystyle \sum _{t\in T} \left( z^{(t)^\textsf{T }} a_1^{(t)};z^{(t)^\textsf{T }} a_2^{(t)};-z^{(t)^\textsf{T }} a_0^{(t)}-r^{(t)}\right) : z^{(t)}\in \mathcal {E}^3_{+},\;r^{(t)} \ge 0 \right\} . \end{aligned}$$

Note that $z^{(t)}\in \mathcal {E}^3_+$ means that $z_0^{(t)} \ge \left\Vert (z_1^{(t)};z_2^{(t)}) \right\Vert = ((z_1^{(t)})^2+(z_2^{(t)})^2)^{1/2}$. It follows that

$$\begin{aligned} \mathcal {D}= & {} \underset{u_1^{(t)}\in [-t,t],\, t\in T}{\underset{u_0^{(t)}\in [-t,0],\, u_2^{(t)}=t,}{\displaystyle \bigcup }} \Bigg \lbrace \;\displaystyle \sum _{t\in T} \Bigg (z_0^{(t)}+z_1^{(t)}u_1^{(t)}+z_2^{(t)}; \left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)}; \\{} & {} -\left( z_0^{(t)}+z_2^{(t)}\right) u_0^{(t)}-r^{(t)}\Bigg ): z_0^{(t)} \ge \sqrt{\left( z_1^{(t)}\right) ^2+ \left( z_2^{(t)}\right) ^2},r^{(t)} \ge 0\Bigg \rbrace , \end{aligned}$$

which is the set $\mathbb {R}\times \mathbb {R}_+\times \mathbb {R}$, hence $\mathcal {D}$ is closed and convex.

It is clear that $a_0^{(t)}+x_1a_1^{(t)}+x_2a_2^{(t)}$ is on the boundary of the second-order cone for any $(x_1;x_2) \in \mathcal {F}_{\mathcal {P}}$, hence the robust Slater condition fails.

We now formulate the Wolf dual problem, RSIMSOCD, of RSIMSOCP as follows

$$\begin{aligned}{} & {} (\text {RSIMSOCD})\\{} & {} \quad {\left\{ \begin{array}{ll} \text {max} &{}\Bigg ( y_1+y^2_2-\displaystyle \sum _{t\in T}\left( z^{(t)^\textsf{T }} \left( a_0^{(t)}+y_1a_1^{(t)}+y_2a_2^{(t)}\right) \right) ,\\ &{}y_1-\displaystyle \sum _{t\in T}\left( z^{(t)^\textsf{T }} \left( a_0^{(t)}+ y_1a_1^{(t)}+y_2a_2^{(t)}\right) \right) \Bigg )\\ \text {s.t.} &{}0\in \partial _{\epsilon _1}f_1(y) +\partial _{\epsilon _2}f_2(y)-\displaystyle \sum _{t\in T} \left( z^{(t)^\textsf{T }} a_1^{(t)},z^{(t)^\textsf{T }} a_2^{(t)}\right) , \\ &{}\epsilon _1+\epsilon _2\le \epsilon ,\; \epsilon _1\ge 0, \epsilon _2\ge 0,\;z^{(t)}\in \mathcal {E}^3_+,\;a_i^{(t)}\in \mathcal {V}_i^{(t)},\;t\in T,\;i=0,1,2. \end{array}\right. } \end{aligned}$$

Let $\mathcal {U}= [-t,0]\times [-t,t]\times \lbrace t\rbrace$. Then the feasible set $\mathcal {F}_{\mathcal {D}}$ is

$$\begin{aligned} \begin{array}{lll} \mathcal {F}_{\mathcal {D}} &{}=&{}\bigg \lbrace \left( y_1,y_2,a_0^{(t)},a_1^{(t)},a_2^{(t)},z^{(t)}\right) \in \mathbb {R}^2\times \mathcal {U}\times \mathcal {E}^3_+: (0,0)\in \partial _{\epsilon _1}f_1(y_1,y_2) +\partial _{\epsilon _2}f_2(y_1,y_2)\\ &{}&{}- \displaystyle \sum _{t\in T} \left( z^{(t)^\textsf{T }} a_1^{(t)}+z^{(t)^\textsf{T }} a_2^{(t)}\right) ,\\ &{}&{} \epsilon _1+\epsilon _2\le \epsilon , \epsilon _1\ge 0, \epsilon _2\ge 0, a_i^{(t)}\in \mathcal {V}_i^{(t)},\; t\in T,i=0,1,2\bigg \rbrace \\ &{}=&{} \bigg \lbrace \left( y_1,y_2,a_0^{(t)},a_1^{(t)},a_2^{(t)},z^{(t)}\right) \in \mathbb {R}^2\times \mathcal {U}\times \mathcal {E}^3_+:(0,0)\in \lbrace 2\rbrace \\ &{}&{}\times \left[ 2y_2-2\sqrt{\epsilon _1+\epsilon _2},2y_2+2\sqrt{\epsilon _1+\epsilon _2}\right] \\ &{}&{} -\left. \displaystyle \sum _{t\in T}\left( \left( z_0^{(t)}+z_1^{(t)}u_1^{(t)}+z_2^{(t)}\right) ; \left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)} \right) ,\;\epsilon _1+\epsilon _2\le \epsilon ,\epsilon _1\ge 0, \right. \\ &{}&{}\epsilon _2\ge 0,\;a_i^{(t)}\in \mathcal {V}_i^{(t)},\;t\in T,\;i=0,1,2\bigg \rbrace \\ &{}=&{}\bigg \lbrace \left( y_1,y_2,a_0^{(t)},a_1^{(t)}, a_2^{(t)},z^{(t)}\right) \in \mathbb {R}^2\times \mathcal {U}\times \mathcal {E}^3_+:2y_2-2\sqrt{\epsilon _1+\epsilon _2}\\ &{}&{}\le \displaystyle \sum _{t\in T} \left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)}\le 2y_2+2\sqrt{\epsilon _1+\epsilon _2}, \\ &{}&{} \displaystyle \sum _{t\in T} \left( z_0^{(t)}+z_1^{(t)}u_1^{(t)}+z_2^{(t)}\right) =2, \;\epsilon _1+\epsilon _2\le \epsilon , \;\epsilon _1\ge 0, \epsilon _2\ge 0,\;a_i^{(t)}\in \mathcal {V}_i^{(t)},\;t\in T,\;i=0,1,2\bigg \rbrace . \end{array} \end{aligned}$$

Then, for any $(x_1,x_2)\in \mathcal {F}_{\mathcal {P}}$ and any $(y_1,y_2,a_0^{(t)},a_1^{t},a_2^{(t)},z^{(t)}) \in \mathcal {F}_{\mathcal {D}}$, we have, with $x_1=0$ and $x_2\ge y_2$, that

$$\begin{aligned}{} & {} f_1(x_1,x_2)+f_2(x_1,x_2)-\left( f_1(y_1,y_2)+f_2(y_1,y_2)- \displaystyle \sum _{t\in T}\left( z^{(t)^\textsf{T }} \left( a_0^{(t)} + y_1 a_1^{(t)}+y_2 a_2^{(t)}\right) \right) \right) \\{} & {} ~~ =x_2^2-y_1-y_2^2- y_1 +\displaystyle \sum _{t\in T}\left( \left( z_0^{(t)}+z_2^{(t)}\right) u_0^{(t)} +\left( z_0^{(t)}+z_1^{(t)}u_1^{(t)}+z_2^{(t)}\right) y_1 +\left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)}y_2\right) \\{} & {} ~~\ge \left( 2y_2+2\sqrt{\epsilon _1+\epsilon _2}\right) \left( x_2-y_2\right) -\epsilon _1+\left( -2+\displaystyle \sum _{t\in T}\left( z_0^{(t)}+z_1^{(t)}u_1^{(t)}+z_2^{(t)}\right) \right) y_1-\epsilon _2\\{} & {} ~~~~~~+\displaystyle \sum _{t\in T}\bigg (\left( z_0^{(t)}+z_2^{(t)}\right) u_0^{(t)} +\left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)}y_2)\bigg )\\{} & {} ~~\ge \displaystyle \sum _{t\in T}\left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)}\left( x_2-y_2\right) -\epsilon _1-\epsilon _2 +\displaystyle \sum _{t\in T}\left( \left( z_0^{(t)}+z_2^{(t)}\right) u_0^{(t)} +\left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)}y_2\right) \\{} & {} ~~=\displaystyle \sum _{t\in T}\left( z_0^{(t)}+z_2^{(t)}\right) \left( u_2^{(t)}x_2+u_0^{(t)}\right) -\epsilon _1-\epsilon _2\\{} & {} ~~=\displaystyle \sum _{t\in T}\left( z^{(t)^\textsf{T }} \left( a_0^{(t)} +0.a_1^{(t)}+x_2a_2^{(t)}\right) \right) -\epsilon _1-\epsilon _2\\{} & {} ~~\ge -\epsilon _1-\epsilon _2 ~\ge ~ -\;\epsilon . \end{aligned}$$

Also, for any $(x_1,x_2)\in \mathcal {F}_{\mathcal {P}}$ and any $(y_1,y_2,a_0^{(t)},a_1^{t},a_2^{(t)},z^{(t)}) \in \mathcal {F}_{\mathcal {D}}$, we have, with $x_1=0$ and $x_2< y_2$, that

$$\begin{aligned}{} & {} f_1(x_1,x_2)+f_2(x_1,x_2)-\left( f_1(y_1,y_2)+f_2(y_1,y_2)- \displaystyle \sum _{t\in T}\left( z^{(t)^\textsf{T }} \left( a_0^{(t)} + y_1 a_1^{(t)}+y_2 a_2^{(t)}\right) \right) \right) \\{} & {} ~~ =x_2^2-y_1-y_2^2- y_1 +\displaystyle \sum _{t\in T}\left( \left( z_0^{(t)}+z_2^{(t)}\right) u_0^{(t)} +\left( z_0^{(t)}+z_1^{(t)}u_1^{(t)}+z_2^{(t)}\right) y_1 +\left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)}y_2\right) \\{} & {} ~~\ge \left( 2y_2-2\sqrt{\epsilon _1+\epsilon _2}\right) \left( x_2-y_2\right) -\epsilon _1+\left( -2+\displaystyle \sum _{t\in T} \left( z_0^{(t)}+z_1^{(t)}u_1^{(t)}+z_2^{(t)}\right) \right) y_1-\epsilon _2\\{} & {} ~~~~~~+\left. \displaystyle \sum _{t\in T}\bigg (\left( z_0^{(t)}+z_2^{(t)}\right) u_0^{(t)} +\left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)}y_2\right) \bigg )\\{} & {} ~~\ge \displaystyle \sum _{t\in T}\left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)}\left( x_2-y_2\right) -\epsilon _1-\epsilon _2 +\displaystyle \sum _{t\in T}\left( \left( z_0^{(t)}+z_2^{(t)}\right) u_0^{(t)} +\left( z_0^{(t)}+z_2^{(t)}\right) u_2^{(t)}y_2\right) \\{} & {} ~~=\displaystyle \sum _{t\in T}\left( z_0^{(t)}+z_2^{(t)}\right) \left( u_2^{(t)}x_2+u_0^{(t)}\right) -\epsilon _1-\epsilon _2\\{} & {} ~~=\displaystyle \sum _{t\in T}\left( z^{(t)^\textsf{T }} \left( a_0^{(t)} +0.a_1^{(t)}+x_2a_2^{(t)}\right) \right) -\epsilon _1-\epsilon _2\\{} & {} ~~\ge -\epsilon _1-\epsilon _2 ~\ge ~ -\;\epsilon . \end{aligned}$$

This implies that for any $(x_1,x_2)\in \mathcal {F}_{\mathcal {P}}$ and any $(y_1,y_2,a_0^{(t)},a_1^{t},a_2^{(t)},z^{(t)}) \in \mathcal {F}_{\mathcal {D}}$, we have

$$\begin{aligned}{} & {} f_1(x_1,x_2)+f_2(x_1,x_2)-\left( \!\displaystyle f_1(y_1,y_2)+f_2(y_1,y_2)- \displaystyle \sum _{t\in T}\left( z^{(t)^\textsf{T }} \left( a_0^{(t)} + y_1 a_1^{(t)}+ y_2 a_2^{(t)}\right) \!\right) \!\right) \nonumber \\{} & {} \quad \ge - \epsilon . \end{aligned}$$

(8)

Therefore, the approximate weak duality theorem (Theorem 4.1) holds.

For the strong duality, let $(\bar{x}_1,\bar{x}_2)=(0,\sqrt{1+\epsilon })\in S_{\mathcal {F}_{\mathcal {P}}}$, $\epsilon _1+\epsilon _2 =(\sqrt{1+\epsilon }-1)^2$. Let also

$$\begin{aligned}{} & {} \bar{z}^{(t)} =\left[ \begin{array}{c} 2\sqrt{1+\epsilon }-2\sqrt{\epsilon _1+\epsilon _2}\\ 0\\ 0 \end{array}\right] ,\;\; \bar{a}_0^{(t)} =\left[ \begin{array}{c} -1\\ ~~0\\ -1 \end{array}\right] ,\;\; \bar{a}_1^{(t)} =\left[ \begin{array}{c} ~~1\\ -1\\ ~~1 \end{array}\right] ,\;\text {and}\\{} & {} \bar{a}_2^{(t)} =\left[ \begin{array}{c} 1\\ 0\\ 1 \end{array}\right] , \;\;t \in T. \end{aligned}$$

One can see that $(\bar{x}_1,\bar{x}_2,\bar{a}_0^{(t)},\bar{a}_1^{t},\bar{a}_2^{(t)},\bar{z}^{(t)}) \in \mathcal {F}_{\mathcal {D}}$ for $t \in T$. Furthermore, for any $(y_1,y_2,a_0^{(t)},a_1^{t},a_2^{(t)},z^{(t)}) \in \mathcal {F}_{\mathcal {D}}$, we have that

$$\begin{aligned}{} & {} f_1(\bar{x}_1,\bar{x}_2) +f_2(\bar{x}_1,\bar{x}_2) -\displaystyle \sum _{t\in T} \left( \bar{z}^{(t)^\textsf{T }}\left( \bar{a}_0^{(t)}+\bar{x_1}\bar{a}_1^{(t)} +\bar{x_2}\bar{a}_2^{(t)}\right) \right) \\{} & {} \qquad - f_1(y_1,y_2)-f_2(y_1,y_2) +\displaystyle \sum _{t\in T}\left( z^{(t)^\textsf{T }}\left( a_0^{(t)}+ y_1a_1^{(t)}+y_2a_2^{(t)})\right) \right) \\{} & {} \quad \ge -\epsilon - \displaystyle \sum _{t\in T}\left( \bar{z}^{(t)^\textsf{T }} \left( \bar{a}_0^{(t)}+\bar{x}_1\bar{a}_1^{(t)}+\bar{x}_2\bar{a}_2^{(t)}\right) \right) \\{} & {} \quad = -\epsilon -\big (2\sqrt{1+\epsilon }-2\sqrt{\epsilon _1+\epsilon _2}\big ) \big (-1+\sqrt{1+\epsilon }\big )\\{} & {} \quad = -\epsilon -\bigg (\big (\sqrt{1+\epsilon }-\sqrt{\epsilon _1+\epsilon _2}-1\big )^2-\epsilon _1-\epsilon _2+\epsilon \bigg )\\{} & {} \quad = -\epsilon +\epsilon _1+\epsilon _2-\epsilon \ge ~ -2\epsilon , \end{aligned}$$

where we used (8) to obtain the first inequality. Thus, the approximate strong duality theorem (Theorem 4.2) also holds.