Introduction

With the advancement of precision materials science technology, nanostructured composites with an ordered periodic structure have recently been recognized as a distinct class. These structures, which exhibit characteristics of both composites and nanostructures, are called metamaterials. Unconventional physical properties, leading to unique functionalities, can be achieved by carefully designing the structure of these materials. Metamaterials can possess unusual electromagnetic and optical properties, such as negative refractive index [1, 2], unconventional auxetic elastic response with negative Poisson’s ratio, high adsorptive [3], capillary [4], catalytic and photocatalytic [5], and other characteristics. Examples of such metamaterials are porous materials featuring an inverse opal structure.

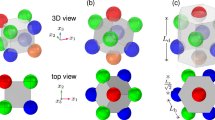
The production of porous nickel material with an inverse opal structure encompasses several stages [6]. Initially, polystyrene spheres are self-assembled onto a designated substrate to form an opal structure through the slow evaporation of a colloidal solution containing these spheres. Then the spheres are incompletely sintered to create bridges between them. In the third stage, nickel is electrodeposited to fill the interstitial spaces between the spheres. Finally, in the fourth stage, the polystyrene is etched away to reveal the inverse opal structure. In some cases, an additional layer of the same or a different material is applied to the structure. The periodic cell of the inverse opal is shown in Fig. 1.

Fig. 1
figure 1

Uncoated (a) and coated (b) periodic cell of inverse opal

Full size image

Inverse opal structures, notable for their unique geometry, have garnered attention in recent years for their versatile applications. One application is wound treatment. Inverse opal hydrogel layers incorporated into hydrogel patches made from medicinal herbs have demonstrated improved mechanical properties [3]. However, the path toward fully implementing the potential of inverse opal structures is fraught with challenges. Research into a camouflage coating produced from biomaterials [7] highlighted limitations in the mechanical properties and environmental resistance of materials with inverse opal structures. In the area of anticounterfeiting, the development of photonic paper using inversion opal structures [8] illustrates how these materials blend optical and mechanical properties. This innovation not only underscores the long life and versatility of these structures but also expands the possibilities for their optical anticounterfeiting applications. Studies of ZnO–Al2O3 inversion opal structures for photocatalysis, reinforced with an atomic layer of amorphous Al2O3, emphasize the importance of strength characteristics and other mechanical properties [5] to promote the self-assembly phenomenon at the tips of optical fibers. In the area of energy storage, inverse opal structures show promise in enhancing the performance of macroporous SnO2 anodes for lithium–ion and sodium–ion batteries. The papers [9, 10] highlight the role of the mechanical properties of porous materials with an inverse opal structure in improving the performance, structural integrity, and capacity of batteries, making a significant advancement in battery technology.

Therefore, the study of inverse opal structures across a wide range of applications—from medical techniques and anticounterfeiting measures to environmental remediation and advanced battery manufacturing processes—emphasizes the need to understand and improve their mechanical properties. The boundary transition from elastic to irreversible plastic deformation is among the most important mechanical characteristics of porous metal materials.

Our objective is to model the transition from elastic to irreversible deformation for materials with an inverse opal structure using the finite element method and determine their effective plastic properties.

Although the pore space structure in inverse opals is rather complex, it can be characterized with just two parameters according to the material production process: the bridge between spherical pores and the thickness of a coating applied to a metal skeleton. In our study, we characterized the structure using the porosity and the thickness of an additionally deposited nickel layer. Nickel serves as the material for both the skeleton and the additional layer in this porous composite [6].

Approaches to Describing the Rigid–Plastic Behavior of Porous Materials

Approaches to determining the loading surface of porous materials can be categorized into two classes: experimental (relying on triaxial load tests) [11, 12] and theoretical (relying on the mechanics of composite materials) [13,14,15]. Contrastingly to full-scale experiments, the theoretical approach allows for a broad variability in loading patterns studied. The micromechanical approach provides a more explicit relationship between the structure and properties of heterogeneous materials, although it involves some idealization of the composite structure. In experimental studies, unique efforts are required for determining and describing the actual structure of a heterogeneous material. In the micromechanical approach, the starting point is typically to set a boundary-value problem for the homogeneous loading of a representative volume that embodies the properties of the entire material and is a plastic matrix with a central round pore. This enables at least a qualitative consideration of the internal parameters that characterize the state and structure of a porous material and a description of its behavior in the transition to irreversible plastic flow, similar to the efforts of Green [13], Gurson [15], et al. Hence, Gurson’ porous plasticity model [15] was developed separately for cylindrical and spherical pores within a repeating elementary volume, where the final results can be presented as the boundary values of the first two invariants of the stress tensor as a function of porosity. However, this model is only accurate for low porosities as it neglects the interaction between pores.

In [16], Tvergaard supplemented Gurson’s model with three additional purely phenomenological parameters. These parameters are not directly related to the structure of a porous material or the rheology of the solid phase but are associated with the effects of pore interaction. This improved version of Gurson’s model, now widely adopted, is referred to in the literature as the Gurson–Tvergaard–Needleman (GTN) model. Further development of the GTN model by various authors is detailed in [17]. An analytical model of porous material flow based on micromechanical averaging was also successfully developed in a series of other studies [13, 18, 19].

In our study, to simplify the analysis of computational modeling results, we adopted an isotropic Mises (two-invariant) model of a material with an arbitrary yield surface in the (p, τ) plane of stress tensor invariants, where

$$p=1/3\sum_{i=1}^{3}{\upsigma }_{ii}; {\tau }^{2}=\sum_{i,j=1}^{3}{\left({\upsigma }_{ij}-p{\delta }_{ij}\right)}^{2}.$$
(1)

These stress tensor invariants are commonly referred to as the mean pressure and tangential stress intensity, respectively [19].

To construct this yield surface, the yield stresses of the inverse opal under various zero single-beam loading paths were found by computational modeling on a representative cell. Each of these boundary stresses provides a point for the yield curve in the (p, τ) plane. Approximation of these points with a curve provides the desired yield surface. However, employing this micromechanically rigid yield surface in an approximated numerical form may be too challenging as it requires introducing the porous inverse opal plasticity model into finite element modeling packages. Therefore, it was decided to approximate the yield curve derived numerically with a simplified material model that is available in finite element modeling packages. Given the specific nature of the metal inverse opal, it was decided, as previously done in [6], to use the Deshpande–Fleck crushed foam model, particularly incorporated in the ABAQUS package.

The Deshpande–Fleck model is purely phenomenological and postulates only the general form of the flow curve F( p, τ) = (3/2) τ2 + α2 p2 – B2 and the flow potential G = (3/2) τ2 + β2 p2 through three arbitrary phenomenological constants: α, β, and B. This model differs from the closed analytical models of porous plasticity by Gurson [15], Shima–Oyane [12], and Stern [19], where the constants are not arbitrary but are determined by porosity.

Micromechanical Averaging of the Stress–Strain State in Inverse Opal

Inverse opal is a microheterogeneous material with a regular periodic structure. For composites of this type, there are well-developed approaches to determining their effective properties [20]. For materials with a periodic structure, micromechanical averaging within a periodic cell—encompassing the scale of inhomogeneity that is smaller than the scale of the averaging length—is sufficient [21]. On the scale of the averaging length, the boundary of a representative cell undergoes distortion close to a linear transformation [22], although this is not the case for an elementary periodic cell [23].

Because of symmetry, when there are no shear components of macroscopic ‘effective’ strains in the XYZ coordinate system shown in Fig. 1, the periodic cell (Fig. 2) of the inverse opal retains a rectangular shape when deformed.

Fig. 2
figure 2

Finite element modeling within a periodic cell: a) finite element grid; b) distribution of tangential stress intensity τ

Full size image

On the other hand, since the effective properties are postulated to be isotropic, the coordinate axes can be aligned with the principal axes of stress and strain tensors. The macroscopic component of the strain tensor \({\varepsilon }_{xx}^{0}\) corresponds to the boundary condition of the fixed normal component of displacements

$${u}_{x}{|}_{x=0}=0; {u}_{x}{|}_{x={h}_{x}}={h}_{x}{\varepsilon }_{xx}^{0}$$
(2)

on the faces perpendicular to the X axis, where hx is the length of the cell along the X axis. In this instance, the tangential components of displacements are not fixed, enabling the face points to slide freely along the face plane resulting in zero tangential stresses. Additionally, for given macroscopic stresses \({\upsigma }_{xx}^{0},\) we have some condition for the equality of the normal components of displacements along the corresponding faces

$${u}_{x}{|}_{x=0}=0; {u}_{x}{|}_{x={h}_{x}}={\widehat{u}}_{x}$$
(3)

along with zero tangential stresses and the condition that the equivalent normal force Px on the faces perpendicular to the X axis is as follows:

$${\text{P}}_{x}{|}_{x=0}=-{\upsigma }_{xx}^{0}{S}_{x}; {\text{P}}_{x}{|}_{x={h}_{x}}={\upsigma }_{xx}^{0}{S}_{x}$$
(4)

(from which we can find \({\widehat{u}}_{x}\)), where Sx = hyhz is the area of the faces perpendicular to the X axis. Similarly, we set boundary conditions for \({\upvarepsilon }_{yy}^{0}, {\upvarepsilon }_{zz}^{0}, {\upsigma }_{yy}^{0},\) and \({\upsigma }_{zz}^{0}\) by replacing the X axis with Y or Z. These boundary conditions for macroscopic stresses and strains are equivalent to the conditional contact of the cell material with some absolutely rigid plate allowing free sliding (zero friction forces) and preventing delamination (even when the plate does not press but pulls the material). Symmetry enabled modeling a quarter of the periodic cell (Fig. 2). It should be noted that the ABAQUS finite element modeling package we used links a specific displacement component for all points in a plane to the displacement of a fixed point. If the magnitude of this displacement is not defined, it will be adjusted to a value that results in zero equivalent force on this plane. This feature is convenient for establishing boundary conditions (3) and (4), corresponding to zero macroscopic stresses.

Effective Plastic Properties for Some Cases of Inverse Opal Structure

We will illustrate the process of determining the yield stress of a porous composite with an inverse opal structure under macroscopic uniaxial compressive loading along the X axis (where \({\upsigma }_{xx}^{0}\) is the only nonzero component in the tensor of macroscopic ‘effective’ stresses). First, we initiate the movement of the \({\widehat{u}}_{x}\) face from Eq. (3) in one direction (loading) and then in the opposite direction to the moment \({\upsigma }_{xx}^{0}=0\) from condition (4), resulting in Px = 0 (unloading). If the skeletal material undergoes irreversible plastic deformation during loading, the macroscopic strains are \({\upvarepsilon }_{xx}^{0}={\upvarepsilon }_{xx}^{\text{res}}\ne 0\) at the moment of complete unloading when \({\upsigma }_{xx}^{0}=0\). This nonzero \({\upvarepsilon }_{xx}^{\text{res}}\) represents the residual macroscopic strains. Following the common engineering criterion of plasticity, we select \({\widehat{u}}_{x}={\widehat{u}}_{x}^{0.002}\) such that \({\upvarepsilon }_{xx}^{\text{res}}=0.002=0.2\%,\) while \({\upsigma }_{xx}^{0}={\upsigma }_{xx}^{0.002}\) corresponding to \({\widehat{u}}_{x}^{0.002}\) is the desired yield stress for uniaxial compression. Note that the residual plastic strain \({\upvarepsilon }_{yy}^{\text{res}}={\upvarepsilon }_{zz}^{\text{res}}\) in the direction transverse to the uniaxial load was also calculated in this modeling process, enabling the calculation of the plastic analog of Poisson’s ratio \({v}_{p}=-{\upvarepsilon }_{yy}^{\text{res}}/{\upvarepsilon }_{xx}^{\text{res}}.\)

Similarly, the yield stresses were determined according to the criterion of 0.2% residual strain for maximum, by modulus, macroscopic strains max \(\left\{\left|{\upvarepsilon }_{xx}^{0}\right|, \left|{\upvarepsilon }_{yy}^{0}\right|, \left|{\upvarepsilon }_{zz}^{0}\right|\right\}=0.002\) and for other single-parameter loading patterns different from uniaxial ones. Knowing the yield stresses, we calculate the boundary values of invariants (p, τ) using Eq. (1) for constructing the yield curve for the inverse opal. The mechanical behavior of nickel, which is the solid phase in the porous composite, was assumed to be elastoplastic with plasticity according to the Mises model, possessing Young’s modulus of 171 GPa, Poisson’s ratio of 0.31, and yield stress under uniaxial loading of 1.98 GPa.

The above method was employed to find a series of yield points in the (p, τ) plane for two cases of opal structure: a highly porous (0.9 porosity) uncoated structure and a structure with 0.57 porosity and an additional coating with relative thickness h/D = 0.065, where D is the diameter of the spherical pores (removed polymer particles). We also analyzed the lateral plastic strain coefficient under uniaxial loading vp , serving as the plastic analog of Poisson’s ratio. In the case of 0.57 porosity, five points for different loading patterns in the (p, τ) plane were found to be sufficient for a suitably smooth approximation of the yield curve (Fig. 3), which are summarized and illustrated in Table 1. For 0.57 porosity, plastic Poisson’s ratio is vp = 0.32 .

Fig. 3
figure 3

Yield curves and potential for 0.57 porosity

Full size image
Table 1 Yield Stress for 0.57 Porosity
Full size table

In the case of 0.9 porosity, the construction of a suitably smooth yield curve (Fig. 4) required two more points in the (p, τ) plane (along with loading patterns), in addition to those provided in Table 1. All analyzed loading patterns for 0.9 porosity are summarized in Table 2. For 0.9 porosity, plastic Poisson’s ratio is vp = 0.416 .

Fig. 4
figure 4

Yield curves and potential for 0.9 porosity

Full size image
Table 2 Yield Stress for 0.9 Porosity
Full size table

Regarding the verification of the phenomenological parameters of the Deshpande–Fleck model, the elliptical Deshpande–Fleck flow surface

$$F\left(p,\tau \right)=\left(3/2\right){\tau }^{2}+{\alpha }^{2}{p}^{2}-{B}^{2}$$

was believed to pass through the points corresponding to the yield stress under pure shear and bulk compression. Accordingly, the only phenomenological parameter of the flow potential G = (3/2) τ2 + β2 p2 , as evident, can be expressed directly through plastic Poisson’s ratio by equation \(\beta =\frac{3}{\sqrt{2}}\sqrt{\frac{1-2{v}_{p}}{1+{v}_{p}}}.\) The parameters of the Deshpande–Fleck model for both porosity values are summarized in Table 3. The yield surface (dashed line) and the yield potential line (bold line) of the Deshpande–Fleck model are illustrated in Figs. 3 and 4.

Table 3 Deshpande–Fleck Model Constants
Full size table

Table 3 shows that parameters α and β for 0.9 porosity differ insignificantly (~10%), while the discrepancy between α and β is quite noticeable, nearly 40%, for 0.57 porosity. This discrepancy suggests an unassociated effective plastic flow of the denser inverse opal in the structure with an additional coating, indicating a significant deviation of the deformation direction (as indicated by the e/γ ratio for the invariants of the strain rate tensor [19]) from the normal to the yield curve. To describe the unassociated plastic flow in the Deshpande–Fleck model, a different flow potential is introduced in addition to the yield curve. However, for highly porous inverse opal structures with thin bridges in the solid phase, we can consider the associated effective plastic flow. Therefore, our assumption concerning the associated nature of the Deshpande–Fleck model (i.e., α = β) made in [6] applies only to highly porous inverse opal structures and may not be entirely correct otherwise. The absolute value of the yield stress for 0.57 porosity is more than an order of magnitude higher than that for 0.9 porosity, as evident from the comparison of the parameter B or the scale in Figs. 3 and 4.

Conclusions

The effective plastic behavior of a porous material with a periodic inverse opal structure under various loading patterns was meticulously modeled using computational micromechanics. These results provided a suitably smooth numerical approximation of the yield curve. To facilitate the use of the plasticity model in finite element modeling packages for optimizing structures with inverse opal elements, the numerical data were approximated with the phenomenological Deshpande–Fleck model.

This approximation proved to be quite accurate, with the shape of the yield curve in the (p, τ) plane closely resembling an ellipse. The effective plastic flow of the inverse opal was found to deviate slightly from the associated plastic flow law in the case of a highly porous inverse opal structure and became significantly unassociated in the case of a structure with medium porosity and an additional coating layer. Despite the nearelliptical shape of the yield curve, the identification of the plastic behavior of inverse opal of unknown structure using a simple uniaxial loading experiment seems to be accurate only at high porosities. In the case of medium porosity, the yield stress under bulk compression predicted upon uniaxial loading experiment differs by almost 30% as shown in Fig. 3.

ARTICLE-LEVEL DECLARATIONS

Conflict of Interest. The authors declare that they have no potential conflict of interest concerning the research findings described in this paper.

Funding. The research was part of P.O. Korobko’s postgraduate effort funded from the postgraduate program of the Frantsevich Institute for Problems of Materials Science, National Academy of Sciences of Ukraine.

Contribution of the Authors. Both authors contributed equally to this work.

Availability of Information. The authors confirm that all data generated or analyzed during the research are included into the published paper.