Representing credal imprecision: from sets of measures to hierarchical Bayesian models

Abstract

The basic Bayesian model of credence states, where each individual’s belief state is represented by a single probability measure, has been criticized as psychologically implausible, unable to represent the intuitive distinction between precise and imprecise probabilities, and normatively unjustifiable due to a need to adopt arbitrary, unmotivated priors. These arguments are often used to motivate a model on which imprecise credal states are represented by sets of probability measures. I connect this debate with recent work in Bayesian cognitive science, where probabilistic models are typically provided with explicit hierarchical structure. Hierarchical Bayesian models are immune to many classic arguments against single-measure models. They represent grades of imprecision in probability assignments automatically, have strong psychological motivation, and can be normatively justified even when certain arbitrary decisions are required. In addition, hierarchical models show much more plausible learning behavior than flat representations in terms of sets of measures, which—on standard assumptions about update—rule out simple cases of learning from a starting point of total ignorance.

1 Introduction

Consider the following two scenarios:

• (1) Two teams, A and B, are about to compete in a soccer game. You’ve seen them compete many times, and you are certain that they are evenly matched. What probability should you assign to the sentence “A will win”?

• (2) Two teams, A and B, are about to compete at soccer. You know nothing at all about these two teams. What probability should you assign to the sentence “A will win”?

If pushed, most people will give the same answers to these questions: “50%”. But our reason for giving these answers is obviously different in (1) and (2). In (1), we have a lot of relevant information to justify making this choice with confidence. In (2), our choice is made in ignorance: we just don’t have any reason at all to favor one team over the other. Obviously, there is an epistemologically relevant difference, and it would be a mistake to represent our information identically in (1) and (2). But the basic Bayesian model of credence states seem not to distinguish our precise, confident opinion in (1) from our imprecise, uncertain opinion in (2)—or so it has been claimed.¹

To fix terminology, call the phenomenon in question “credal (im)precision”. If someone has a definite opinion about some event, perhaps based on rich information—as you might when assigning “A will win” probability .5 in scenario (1)—they are in a state of credal precision with respect to that event. If their probability assignment is highly uncertain and far from definite—as yours would presumably in scenario (2)—they are in a state of credal imprecision with respect to that event.²

This paper considers two formal models of credal precision and imprecision. The first takes ordinary probability to be inadequate as a representation of agents’ credence states, and opts for a richer model using sets of probability measures.³ The second approach tries to explain the possibility of precise or imprecise probability estimates in terms of a probability model that incorporates hierarchical structure—such as that of a Bayesian network (Pearl 1988; Spirtes et al. 1993) or a probabilistic program (Tenenbaum et al. 2011). The need to include hierarchical structure in probabilistic models already enjoys considerable psychological, philosophical, and computational motivation.⁴ There is an obvious gain in theoretical simplicity, then, if we can apply this independently motivated class of models to address objections that have been raised to representing credences by a single measure. I will argue that we can, and that the hierarchical approach is also superior in learning behavior to the flat, set-based representation.

None of this calls directly into doubt whether further phenomena might motivate the use of sets of measures in epistemology or psychological modeling. Nor does it bear on the rather different question of whether these representations are useful in modeling epistemic phenomena that extend beyond the minds of individuals, such as group belief or conversational common ground. My claim is rather that certain phenomena which appear to problematize the basic Bayesian model of individual agents’ informational states, and to support sets-of-measures models, can be given a more illuminating explanation within standard probability models that incorporate explicit hierarchical structure.

2 Credal precision and imprecision

In what I will call the “basic Bayesian model” of credence states, each agent a is associated with a unique probability measure $P_a$—sometimes also called a’s “credence function”. $P_a$ is required to obey the usual laws of probability (non-negativity, normalization, and countable additivity: Kolmogorov 1933). For any proposition C, $P_a(C)$ is a’s degree of belief that C is true.

The basic Bayesian model has many useful features for cognitive modeling and epistemological purposes, and is also subject to many kinds of objections. One well-known objection involves experimental evidence suggesting that ordinary people make systematic errors in probabilistic reasoning (e.g., Tversky and Kahneman 1974; Kahneman et al. 1982). While this kind of critique is surely relevant, I want to set it aside here with a few quick comments. First, there are many additional experiments in which people seem to reason appropriately with probabilities (e.g., Gigerenzer 1991). Second, experiments in which people are asked to reason explicitly about probabilities may be less theoretically revealing than those in which probabilistic reasoning is implicit in the way that uncertainty informs judgment and action (e.g., Griffiths and Tenenbaum 2006; Trommershäuser et al. 2008). The logic is essentially the same as that which motivates cognitive scientists of many persuasions, from linguists to psychophysicists, to give greater weight to people’s unreflective behavior and judgmental processes than to their metalinguistic or metacognitive judgments. Third, recent work has suggested a measure of reconciliation, where at least some errors and biases in probabilistic reasoning may be explicable in terms of performance factors, interactions among cognitive systems, or traces of strategies for efficient approximation (Griffiths et al. 2012; Vul et al. 2014).

The objections that have motivated a rejection of the basic Bayesian model among many epistemologists are primarily of a different kind. Kahneman and Tversky assumed that the basic Bayesian model provides a normatively correct standard for learning and reasoning, and argued that ordinary people’s credence states are defective to the extent that they are not consistent with this model. In contrast, many arguments for rejecting the basic Bayesian model in favor of a sets-of-measures model call into question its normative appropriateness, rather than its descriptive adequacy. These arguments purport to show (a) that it would be normatively inappropriate in many cases for an agent to have a credence state that is well-represented by a single probability measure, and (b) that an accurate psychological model of (normatively appropriate) credence states cannot have the form of a single probability measure. Scenario (2) is a typical example: two teams compete in a game, and you know nothing at all about their relative skills. Joyce (2005, 2010) argues that, in such a scenario, you are making a mistake if you have any precise credence in team A winning. What possible grounds could you have for such “extremely definite beliefs ...and very specific inductive policies”, when “the evidence comes nowhere close to warranting such beliefs and policies” (Joyce 2010, p. 285)? Depending on the teams’ relative skills, the right credence to have might be any value in the range [0, 1]! You don’t know enough to exclude any of these.

This objection is closely related to the problem of insufficient expressiveness that we began with. When asked for a probability estimate in scenarios (1) and (2), I might produce “50%” in both cases—but confidently in (1), and with hesitation and confusion in (2). Similarly, I would immediately reject an uneven bet on either team in (1), but might have a harder time making up my mind in (2). Either way, the basic Bayesian model seems to miss at least two important differences between these judgments: differences in their evidential basis, and in their phenomenology. If a single probability measure is all we have to work with, any two events to which I assign probability 0.5 would seem to be probabilistically indistinguishable—both just have probability 0.5, end of story. As a result, the basic Bayesian model is not fine-grained enough to represent the full richness of my credence states. Halpern (2003, p. 24) summarizes the objection succinctly: “Probability is not good at representing ignorance”.

3 Credal imprecision: a sets-of-measures model

The proposed alternative is to represent an agent a’s information not by a single probability measure $P_a$, but by a set of probability measures ${\mathbb {P}}_a$ (e.g., Levi 1974; Jeffrey 1983; Bradley 2014). This is often called an “imprecise probability model”. (We have to be careful here not to confuse this controversial formal model with the uncontroversially real phenomenon of “credal imprecision”, as exemplified by scenario (2).) The set of measures itself is sometimes called a’s “representor” (van Fraassen 1990). The sets-of-measures model has no expressive difficulty in the sporting examples. In the first scenario, where I am confident that the teams are evenly matched, my representor contains only measures P such that $P({\text {A}}\;{\text {wins}}) = 0.5$. In the second scenario, where I have no relevant information, my representor contains, for every $r \in [0,1]$, a measure P such that $P({\text {A}}\;{\text {wins}}) = r$. In the first case I have an “extremely definite belief” (Joyce 2010) that $P({\text {A}}\;{\text {wins}}) = 0.5$, and I am right to. In the second I have no definite belief about the value of $P({\text {A}}\;{\text {wins}})$, and I am right not to.

Despite this apparent success, some important objections have been made to the use of sets of measures as a formalization of credal imprecision. One is that it is difficult to frame a plausible decision theory using sets of probability measures. Elga (2010), in particular, canvasses a number of options and shows that each makes pathological predictions in certain cases; see also White (2010). A second kind of objection involves examples where imprecise models seem to predict, rather oddly, that learning a proposition B can lead to a loss of information about a different proposition A, even in some cases when B is intuitively irrelevant to A.⁵ These particular objections are two of many, and they are still a matter of active controversy in the epistemological literature. I don’t want to take a stand on whether they are decisive, but I do think they give plenty of reason to look for an alternative model of credal imprecision that fits naturally with well-understood, well-behaved Bayesian models of learning and decision. First I will discuss a third puzzle that also introduces some of the motivation for the hierarchical alternative.

The most troubling objection to sets-of-measures models of credence, to my mind, is the observation that they “preclude[] inductive learning in situations of extreme ignorance” (Joyce 2010, p. 290; see also White 2010; Rinard 2013). For example, consider a biased coin example analogous to scenario 2 above. Suppose I am maximally uncertain about the bias $\pi$ of a certain coin, which could in principle be anywhere in [0, 1]. On any given toss, the probability of getting heads—$P({{\text {heads}}})$—is equal to $\pi$, which is a fixed fact about the world determined by the coin’s objective properties. My uncertainty about $P({{\text {heads}}})$ reduces to uncertainty about the value of $\pi$.

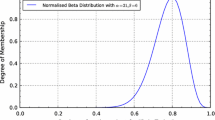
If we represent my credences with a single probability measure, we would model the scenario by placing a prior distribution on $\pi$—say, a Beta distribution. If I wanted to be maximally noncommittal, I might use a ${\text {Beta}}(1,1)$ distribution, which puts equal prior probability on every bias $\pi \in [0,1]$ (see Fig. 1, left). Given this model, conditioning on n heads and m tails yields a ${\text {Beta}}(1 + n, 1 + m)$ posterior.⁶ So, for example, if I had a maximally noncommittal ${\text {Beta}}(1,1)$ prior, after observing 150 heads in 300 tosses my beliefs about the bias $\pi$ would be updated to a ${\text {Beta}}(151, 151)$ distribution. This prior-to-posterior mapping is pictured in Fig. 1. The quite reasonable prediction is that, after observing 150/300 heads, I can be quite confident that the coin’s bias $\pi$ is close to 0.5—even if I was maximally noncommittal about $\pi$ to begin with.

Fig. 1

Prior-to-posterior mapping for an agent with precise credences and a Beta(1,1) prior, after observing 150 heads/successes out of 300 trials. The dashed red line indicates the expected value of the parameter $\pi$, which does not change with this evidence even though our uncertainty about the estimate (i.e., the variance of $\pi$) decreases dramatically. (Color figure online)

Not so in the sets-of-measures model with the standard update rule of pointwise conditioning (e.g., Levi 1974; van Fraassen 1990; Grove and Halpern 1998). This rule maps any set of measures ${\mathbb {P}}$ and evidence E to the set $\{P(\cdot \mid E) \mid P \in {\mathbb {P}} \wedge P(E) > 0\}$, filtering out measures that cannot be conditioned on E because they assign it probability 0, and conditioning the rest on E. Since I have no idea about the probability of heads to begin with, my initial representor ${\mathbb {P}}_0$ should contain, for every $r \in [0,1]$, a credence function P such that $P({{\text {heads}}}) = r$. For example, ${\mathbb {P}}_0$ might contain, for every possible Beta prior, a measure that encodes a binomial model with that prior.

$$\begin{aligned} {\mathbb {P}}_0 = \{P \mid P(\pi ) \sim {\text {Beta}}(a,b),\ \ \forall a, b \in [0, \infty )\} \end{aligned}$$

(Using only Beta priors is a significant restriction relative to Joyce’s (2005, 2010) philosophical desiderata, but using the full range of possible distributions on $\pi$ would only make the problem worse.) Now, suppose I observe 150/300 heads and update ${\mathbb {P}}_0$ to ${\mathbb {P}}_1$ by pointwise conditionalization, discarding measures that assign probability 0 to the observations and so cannot generate the sequence. In this case, the latter condition requires us to discard any Beta prior with a 0 in either position, which could only generate “all heads” or “all tails” sequences. All other measures in ${\mathbb {P}}_0$ assign positive probability to the observed sequence of 150 heads and 150 tails, and survive in conditionalized form as ${\text {Beta}}(a + 150, b + 150)$ measures:

$$\begin{aligned} {\mathbb {P}}_1&= \{P \mid P(\pi ) \sim {\text {Beta}}(a + 150, b + 150), \ \ \forall a, b \in (0, \infty )\} \\&= \{P \mid P(\pi ) \sim {\text {Beta}}(a', b'), \forall a', b' \in (150, \infty )\} \end{aligned}$$

When we look at a few of these distributions, it is clear that something has gone wrong. Alongside reasonable-ish posteriors like ${\text {Beta}}(160,200)$ [so $P({\text {heads}}) \approx .44$] and ${\text {Beta}}(200,160)$ [so $P({\text {heads}}) \approx .56$], the posterior belief state contains a ${\text {Beta}}(150.1, 10^{14})$ posterior [where $P({\text {heads}}) < 10^{-10}$] and a ${\text {Beta}}(10^{14}, 150.1)$ posterior, where $P({\text {heads}})$ is indistinguishable from 1. This is truly remarkable, since the probability that we would have seen 150 or more heads in 300 if $P({\text {heads}}) = 10^{-10}$ is around $10^{-87}$—but this failure of prediction is not taken into account in update by pointwise conditioning. In fact, for every r in the open interval (0, 1), there is a measure in ${\mathbb {P}}_1$ such that $P({\text {heads}}) = r$. As far as the spread of probabilities for heads is concerned, all that we have gained from our observations is to contract the interval [0, 1] to (0, 1), ensuring that both heads and tails are possible outcomes. We have learned nothing else about the probability of heads.

In reality, a sequence of 150 heads and 150 tails can and should teach us a lot, even if we know nothing at all about the coin to begin. The coin is almost certainly either fair or very close to fair. Inductive learning is possible from a starting point of ignorance, and our theory of belief must make room for this fact.

Several responses are possible here. Most obviously, we could search for an alternative to pointwise conditioning as an update rule. It is of course not possible to rule out a priori the possibility that this search will be successful. However, the candidates that I am aware of do not seem to offer promising solutions. For example, Grove and Halpern (1998) canvas a number of alternative update rules for sets of probabilities, all of which are weaker than pointwise conditioning. What we need, though, is a stronger rule—one that allows us to privilege measures on which the likelihood of the data is high over those on which it is very low. Another update rule is proposed by Walley (1996), who describes a general method of updating sets of probability measures using a model with a single free parameter. However, many of the philosophical objections to the single-measure model apply equally to Walley’s, and indeed many of the numerous commentaries on his article (collected in the same issue of Journal of the Royal Statistical Society) note that his solution to the problem of updating sets of measures is neither assumption-free nor uniquely justified. If Walley’s approach is any guide, it seems that the search for a stronger update rule for sets of measures might well locate something that works well enough in practice. However, a solution along these lines would likely succeed precisely by smuggling in additional assumptions that are not compatible with the philosophical motivations for sets-of-measures models that Joyce and others have elaborated.

A second kind of response to the learning problem would be to rule out a priori representors where $P({\text {heads}})$ may fall anywhere in [0, 1] or (0, 1). This would avoid the narrow problem addressed here: if the representor contains only measures with $a< P({\text {heads}}) < b$ for some $a > 0$ and/or $b < 1$, pointwise conditioning will contract the interval over which $P({\text {heads}})$ is distributed. However, this solution is sorely lacking in conceptual and philosophical motivation. If the sets-of-measures model of credal imprecision was motivated in the first place by considering justified belief under ignorance, how can we justify dealing with theoretical problems by pretending to know something that we don’t? Surely the fact that it is the only way to generate plausible learning behavior is not sufficient motivation—unless we already know for sure that the sets-of-measures model is the only game in town.

A third option, discussed with some sympathy by Joyce (2010), is to conclude that it is in fact not possible to learn in a rational way from a starting point of total ignorance. However, real people employ non-rational heuristics to help them get by psychologically, such as restricting attention to measures that give high enough probability to the observed evidence. The solution is, unfortunately, much worse than the problem it is meant to solve. For each of my beliefs, there was presumably some point at which I had no evidence relevant to this belief. Indeed we all began life in a situation of extreme ignorance about most or all topics that are currently of interest to our adult selves. On Joyce’s analysis, the only rational response to such a lack of evidence is to adopt a representor that is maximally noncommittal regarding every belief. But then it follows that none of our beliefs are rationally held, since learning is impossible from a starting point of ignorance.

Another way to make the point is that Joyce’s argument for the sets-of-measures model of credal imprecision, if taken seriously, implies that the only rational starting point of learning for a new lifeform is the set of all probability measures. But my current credence state could not possibly have resulted by starting with the set of all probability measures, and pointwise conditioning this set on my total evidence. This set contains too many bizarre measures (for example, for each possible world w it includes a measure that assigns probability 1 to $\{w\}$, so that no non-trivial conditionalization is possible). This observation is closely related to something that psychologists, statisticians, and machine learning researchers have been reminding us for many years: assumption-free learning is simply not possible (e.g., Wolpert 1996). In the probabilistic case, this means that we have no choice but to start the learning process with a non-trivial prior distribution. The need for inductive biases to get learning off the ground holds equally for other formats for knowledge representation and learning, though. A recent machine learning text states the problem pithily: “one cannot learn rules that generalize to unseen examples without making assumptions about the mechanism generating the data” (Simeone 2017, p. 12). This is, of course, just Hume’s problem of induction in another guise. The key question is whether it is better to adopt a purist model that implies that rational belief is practically impossible, or a pragmatic model that allows us to make some assumptions—perhaps not uniquely justified—to allow learning to proceed. I will return to this issue briefly in Sect. 6 below, when discussing the objection to single-measure models from the lack of uniquely justified priors.⁷

My preferred response is to reject sets of probability measures as a model of individual credence. To plump for this option, let me point out the key technical difference between our single-measure and sets-of-measures models of the coin with unknown bias: whether we placed a probability distribution on top of the set of credence functions in ${\mathbb {P}}_0$. Sets-of-measures models decline to assign probabilities to the elements of ${\mathbb {P}}_0$, leaving it as an unstructured set, or a “flat” representation of the set of candidate data-generating models. If we did put a distribution on ${\mathbb {P}}_0$, we would end up with a single-measure model with a hierarchical structure, as I will describe in the next section. In this case, many kinds of (hyper-)priors on ${\mathbb {P}}_0$ would yield plausible results with ordinary conditioning. We can see why this small change makes a difference if we break down conditioning using Bayes’ rule. With a distribution on the measures in ${\mathbb {P}}_0$, the posterior probability of each $P \in {\mathbb {P}}_0$ would be proportional to the product of the prior and the likelihood, where the latter is the probability that we would have observed the data if P were the true distribution. Conditioning re-ranks credence functions to take into account such facts—e.g., that 150/300 heads is moderately likely under a ${\text {Beta}}(160,200)$ distribution, and astronomically unlikely under a ${\text {Beta}}(150.1, 10^{14})$ distribution. In contrast, sets-of-measures models do not represent information about the relative plausibility of the measures in the representor (a prior), and update by pointwise conditioning does not take into account how well the measures in ${\mathbb {P}}_0$ fare in the goal of predicting the data (a likelihood term). This is why sets-of-measures models fare so poorly when confronted with simple examples of inductive learning.

In order to extract a plausible treatment of learning from information given by a set of probability measures, we need to put a distribution on the measures themselves so that we can (a) apply ordinary conditioning, and so (b) take into account each measure’s ability to account for the data when reassessing its plausibility in light of evidence. In other words, we need a prior on our priors, which is the basic idea of hierarchical models.

4 Credal imprecision: a hierarchical model

This is, to be sure, a roundabout way of getting to a simple objection. We just don’t need sets of measures to represent the difference between credal precision and imprecision—between clear, definite probability assignments and assignments made on the basis of weak and partial information. Arguments against single-measure models based on a supposed failure to represent this distinction are misdirected, because the distinction has an illuminating treatment with a well-developed and strongly motivated class of single-measure models—those with an explicit hierarchical structure.

Recall Joyce’s (2010, p. 285) objection to precise models quoted above: in a situation of ignorance, it is not justifiable for you to have “extremely definite beliefs ...and very specific inductive policies”, because “the evidence comes nowhere close to warranting such beliefs and policies”. Already in the coin-bias example, though, this objection is partly misplaced.⁸ If your prior on the bias parameter $\pi$ is a ${\text {Beta}}(1,1)$ distribution—see again Fig. 1, left panel—your belief is anything but definite. It is true that $\pi$ has a precise expected value 0.5, and also that your marginal belief about $P({\mathbf{heads}})$ is therefore 0.5. However, you are extremely uncertain about both of these beliefs: depending on what evidence you receive, you could come to a very definite conclusion that $\pi$ and $P({\mathbf{heads}})$ are both 0, both 1, or anywhere in between. For example, after observing 0/300 heads, your posterior distribution on $\pi$ would be ${\text {Beta}}(1,301)$, with $P({\mathbf{heads}})$ indistinguishable from 0. This would be an “extremely definite” opinion, with very low variance on the estimate of $\pi$—and a definite opinion that is justified by the evidence. Similarly, after seeing 150/300 heads, you have a fairly definite opinion that $\pi$ and $P({\mathbf{heads}})$ are close to 0.5 (Fig. 1, right). Even though the summary estimate $P({\mathbf{heads}}) = 0.5$ (Fig. 1, dashed line) does not change from prior to posterior when you observe 150/300 heads, the transition from the information state described by the left of Fig. 1 to the one on the right clearly represents a significant change in your beliefs about $P({\mathbf{heads}})$.

More generally, I suggest—building on observations made in a somewhat different context by de Finetti (1977) and Pearl (1988, p. 357ff.)—that many of the intuitive arguments for sets-of-measures models discussed above can be accounted for in a better-motivated way once we take into account the hierarchical structure of belief. Our beliefs are interconnected, and probability estimates involving one variable usually depend on uncertain beliefs about others. Uncertainty about one variable—e.g., the bias $\pi$ of a coin—may influence our uncertainty about a probability estimate of interest—e.g., the probability that the coin will come up heads on a given flip. Given the richness of our belief systems, there will usually be many layers of uncertainty. Even though such a model will always yield a precise numerical probability for any event of interest, this numerical value does not have any special place in the model: it is just what you get when you marginalize over your uncertainty about other relevant variables. In a hierarchical model, probability estimates can vary enormously in how “definite” they are, and we have standard tools for measuring the definiteness of an estimate—for example, its spread, variance, and the width of its high confidence intervals.

Hierarchical models are used in many modern applications in psychology, philosophy, artificial intelligence, and statistics. In these models, probabilities are derived from graphs representing statistical or causal relations among variables, together with the conditional distribution on each variable given its parents. Uncertainty about one variable may influence the kind and degree of uncertainty in the value of another. For simplicity I will focus on Bayesian networks (“Bayes nets”), a simple propositional language for describing hierarchical models.⁹ I will impose a causal interpretation on the Bayes nets described in this paper. While this is not obligatory, it helps to gain intuitions about their meaning, and it is crucial to their psychological motivation (e.g., Glymour 2001; Sloman 2005).

The sporting example that we began with allows us to illustrate Bayes nets and their ability to represent credal precision and imprecision alike. Formally, a Bayes net B consists of an event space (set of possible worlds) W together with:

• 1. A set of variables $V \in {\mathbb {V}}$, where each V is a partition of W. A cell is a “value” of V.

• 2. A set of arrows, i.e., an acyclic binary relation on ${\mathbb {V}}$. The inclusion of an arrow from $V_i$ to $V_j$ indicates that $V_i$ is immediately causally relevant to $V_j$.

• 3. A set of conditional probability tables which assign a distribution $P_B(V \mid {\textit{Parents}}(V))$ to each $V \in {\mathbb {V}}$, where ${\textit{Parents}}(V) = \{V' \mid \langle V', V \rangle \in {\mathbb {V}}\}$.

A probability measure P is compatible with Bayes net B if and only if P and $P_B$ agree on all conditional probability assignments, and P satisfies the Markov condition: each $V \in {\mathbb {V}}$ is independent in P of its nondescendents in B, given its parents in B.

To situate the hierarchical modeling concept within our sporting examples, consider: In case (2), when asked to reason about the competition between unknown soccer teams A and B, did you really know nothing at all about these teams? I doubt it. Most likely, you brought to bear on the problem a rich network of relevant background knowledge. You knew that the outcomes of soccer matches are determined largely by the performance of the teams; that teams are composed of players who have different roles; that they have latent characteristics like skill and consistency; that not all teams are equally skilled or consistent; and so forth. In addition, your experience may have provided you with relevant population statistics which can help you to make an informed guess about the distribution of these characteristics among soccer teams, even without any specific knowledge of the team. All of this background knowledge enabled you to make a reasonable guess about how a randomly chosen team would perform, and what factors you should attend to if you want to use observations to improve your forecast of a team’s performance.

As a start in modeling the richer background knowledge that we implicitly bring to bear on such problems, consider the simplified representation in Fig. 2.¹⁰ This model represents two key features of teams that are relevant to their performance: their skill and their consistency. Performance of team i is modeled as a Gaussian (normal) distribution with parameters $\mu _i$ (skill) and $\sigma _i$ (consistency). As a result, the team’s performance in any given competition is a noisy reflection of the team’s true skill. Skill and consistency are, in turn, objects of uncertainty that we are trying to estimate when observing the outcomes of competitions. This means that we must place a prior on them as well. In a realistic model, these variables might be connected to many further factors—e.g., the team’s composition, quality of coaching, motivation, etc. To simplify the example, I will summarize all of these sources of uncertainty with simple priors on the parameters: $\mu _{\mathbf{A}}$ and $\mu _{\mathbf{B}}$ are both distributed as ${\mathcal {N}}(0,1)$, and $\sigma _{\mathbf{A}} = \sigma _{\mathbf{B}} = .1$.

Fig. 2

Hierarchical model of a match between teams A and B

In this model $P({\mathbf{A}}\; {\mathbf{wins}})$ is equal to $P({\textit{perf}}_{\mathbf{A}} > {\textit{perf}}_{\mathbf{B}})$—the probability that $\mathbf{A}$’s noisy performance exceeds B’s. Note that this model does not generate a single, determinate prediction about A’s performance in any given match. Instead it generates for each team a distribution over an infinite set of performance values $(-\infty , \infty )$. A few of these distributions are shown in the top left of Fig. 3. As a result, the model encodes a distribution over an infinite set of values for $P({\mathbf{A}}\; {\mathbf{wins}})$, which could be turn out to be anywhere in (0, 1) depending on subsequent observations.

Fig. 3

Some distributions implicit in the Fig. 2 model. Top left: some of the $\infty$ performance distributions that could turn out to be the true distribution for either team. Top right: marginal on ${\mathbf{perf}}_{A/B}$ with no specific evidence. Bottom row: distribution of ${\mathbf{perf}}_A - {\mathbf{perf}}_B$ with no observations (left) and after observing that each team won 15 of 30 matches (right)

While the model does yield a precise best guess about the performance difference—and so about $P({\mathbf{A}}\; {\mathbf{wins}})$—this guess has no special status in the model: it is merely the result of marginalizing over our uncertainty about the parent variables (skill and consistency). Indeed, two models that generate the same probability estimate for this event—say, $P({\mathbf{A}}\; {\mathbf{wins}}) = .5$—may vary considerably in how confident (“precise”, “definite”, “determinate”) the probability estimate is (Fig. 3, bottom row). A key factor is, of course, how much evidence the estimate is based on.

Consider our two leading examples again. In case (2), we “know nothing”—i.e., only general domain knowledge is available. As a result, the variance of the estimated performance difference is high, and confidence in the estimate $P({\mathbf{A}}\; {\mathbf{wins}}) = .5$ is low (Fig. 3, bottom left). In case (1), there is ample evidence to indicate equal skill—many previous matches, with each team winning an equal number. In this case, the variance of the estimated performance difference is low, and confidence in the estimate $P({\mathbf{A}}\; {\mathbf{wins}}) = .5$ is high. The bottom right panel of Fig. 3 shows the model’s predictions about $P({\textit{perf}}_{\mathbf{A}} > {\textit{perf}}_{\mathbf{B}})$ once we have observed each team winning 15 of 30 matches. Here we can infer that the teams have roughly equal skill, and that we should forecast roughly equal performance in the next game: $P({\mathbf{A}}\; {\mathbf{wins}}) = .5$.

To summarize the point of this example, I can’t do better than to quote Judea Pearl (1988, pp. 361–362):

[B]y specifying a causal model for predicting the outcome ...we automatically specified the variance of that prediction. In other words, when humans encode probabilistic knowledge as a causal model of interacting variables, they automatically specify not only the marginal and joint distributions of the variables in the system, but also a particular procedure by which each marginal is to be computed, which in turn determines how these marginals may vary in the future. It is this implicit dynamic that makes probabilistic statements random events, admitting distributions, intervals, and other confidence measures.

In a hierarchical model, statements about probabilities—say, “$P({\text {A}}\;{\text {wins}}) = .5$”’—are just marginals. They are themselves objects of uncertainty and inference, and are sensitive to changes in our beliefs about other causally related variables. These models directly falsify Joyce’s (2010, p. 283) claim that “[p]roponents of precise models ...all agree that a rational believer must take a definite stand by having a sharp degree of belief” in any proposition whatsoever. While Joyce is right that taking a “definite stand” in case of ignorance is unreasonable, hierarchical models allow us to encode an imprecise ($\approx$ high-variance) probability estimate when this is appropriate, and a precise ($\approx$ low-variance) estimate when appropriate. Precise probability estimates can be extracted from hierarchical models as desired, but these models do not generally imply a “definite stand” on these estimates.

Bayes nets offer a precise credence model that represents the distinction between credal precision and imprecision in a straightforward way. The need to represent this distinction does not, therefore, give us a reason to abandon single-measure models of belief in favor of a more complex representation that also introduces difficult new problems involving learning and decision. The apparent problem with precise models—that radically different credal states could generate the same probability estimate $P({\mathbf{A}}\; {\mathbf{wins}}) = .5$—was not due to any expressive limitation. Instead, the problem was generated by our habit as theorists of forgetting that these numerical estimates give only a narrow window into the rich structure of a probability distribution.

5 Objections from behavioral limitations and psychological plausibility

Many authors have argued that the basic Bayesian model of belief is psychologically implausible. One argument along these lines is the claim, discussed in some detail in the last section, that the model implies that agents maintain a “definite” real-valued credence for every proposition represented in their belief states (Joyce 2005, 2010). However, I showed in the last section that this objection does not create problems for hierarchically structured Bayesian models. Beyond this, there are quite a few distinct arguments that can be extracted from the literature, some of which may still apply.

• (Self-report) When asked, agents often find it difficult or impossible to report a real value representing their credence in a proposition.

• (Betting) Agents are not always able to assign fair betting odds, or to assess the relative desirability of a range of bets. In addition, their betting behavior is sometimes inconsistent with the basic Bayesian model together with a standard decision theory.

• (Completeness) Single-measure representations imply “a certain superhuman completeness” of belief (Jeffrey 1983, p. 137), in that the question whether A is more likely than B for some agent a should always have a determinate answer. In reality, though, we frequently find ourselves unable to compare the likelihood of two options (e.g., Keynes 1921).

5.1 Self-report

The argument from self-report is fairly common in the literature. For instance, van Fraassen (2006, p. 403) writes:

Our subjective probabilities are not usually very precise. Rain does seem more likely to me than not, but does it seem more than $\pi$ times as likely as not? That may not be an answerable question.

Hájek and Smithson (2012) expand on the “answerable” part of this reasoning:

What is your degree of belief that the Democrats will win the next presidential election in the USA? If you report a sharp number, we will question you further. For example, if you report a credence of 0.6, we will ask whether you really mean 0.6000, sharp to infinitely many decimal places. If you are anything like us, your credence is sharp only up to one or two decimal places. And in that case, you are not an ideal Bayesian agent. For such an agent assigns perfectly sharp credences to all propositions.

The issue of whether a question is answerable should not, of course, be confused with the question of whether a question has a determinate answer. In the case at hand, it is easy to think of reasons why an agent would be unable to answer such questions even if they had perfectly precise credences. For example, there is much evidence that introspective access to our cognitive states is quite limited in many domains (e.g., Nisbett and Wilson 1977; Wilson 2004). Given this, the series of questions that Hájek and Smithson (2012) suggest posing to their subjects is unlikely to be illuminating about the cognitive state that they are probing. The mere fact that people are often unable to answer questions about some hypothetical feature of their mental states does not imply that the feature in question does not exist. Indeed, this point is made very aptly by Levi (1985)—no friend of the basic Bayesian model—in the course of making the crucial distinction between imperfectly introspected and genuinely indeterminate credences.

As an analogy, suppose that someone were to claim that the highly precise quantitative models employed in psychophysics can be shown on philosophical grounds to be psychologically implausible. The evidence that our theorist offers in support of this surprising claim is the observation that people are unable to give precise quantitative answers—or, more likely, any answer at all—to verbal queries about their absolute and relative perceptual discrimination thresholds. This argument would be impossible to take seriously: neither an ordinary participant nor a highly trained psychophysicist could answer such questions on the basis of introspection. Instead, the answers emerge after experimental testing and interpretation of the results against a substantial background of psychological theory and statistical analysis. Similarly, I would expect that van Fraassen’s question “Is rain more then $\pi$ times as likely as not, according to your credence state?” could be answered only against a background of extensive (self-)experimentation, combined with sophisticated psychological theorizing about the way that responses to the questions employed reflect the various mental states and processes involved in their generation.

Similarly, it is a truism in linguistics that ordinary people have no conscious access to features of the grammar of their language. We implicitly command complex grammatical structures, but cannot answer even simple questions—“How many relative clauses in your last utterance?”—without substantial linguistic training. Few theorists would take this obvious point to count against the psychological reality of relative clauses. Yet analogous reasoning about our ability to self-report credences has been given significant weight in the literature.

I see no reason to think that our introspective access to features of our credence states should be of a different character from our introspective access to features of our perceptual or grammatical mechanisms. Given this, our ability or lack of ability to report features of these mechanisms or to make overt judgments about them cannot be used as evidence. The argument from self-report would go through only if we were to adopt a thesis about the transparency of our mental lives that is known to be empirically false.

5.2 Betting

A related argument against single-measure models, focusing on betting behavior, is given by Joyce (2010, pp. 282–283):

As many commentators have observed ..., numerically sharp degrees of belief are psychologically unrealistic. It is rare, outside casinos, to find opinions that are anywhere near definite or univocal enough to admit of quantification. An agent with a precise credence for, say, the proposition that it will rain in Detroit next July 4th should be able to assign an exact “fair price” to a wager that pays $100 if the proposition is true and costs $50 if it is false. The best most people can do, however, is to specify some vague range.

The mistake in this argument is very close to the mistake in arguments from self-report. Why should an agent with a precise credence in A be able to assign a precise fair value to some wager on A? This would follow only if we assume that the agent has perfect introspective access to her own subjective probability in A, and the ability to use this information to assign fair prices to the wager in question without noise or error. Neither of these assumptions is especially psychologically plausible. There is a straightforward explanation of why someone with a precise probability in A might not be able to do better than (say) “somewhere between $80 and $100” here: she may not have explicit knowledge of her credence in A, and may also not know how to translate her imperfect self-knowledge into a fair bet. None of this impugns the theory that she has a perfectly precise probability for A, and a well-functioning set of decision-making mechanisms. All that it entails is that she has limited conscious access to features of her credences and decision-making mechanisms, of the kind that would be required to formulate verbal responses to such questions. While explicit verbal responses are not necessarily unilluminating, they are handled with considerable care in psychological work on decision-making, and expected-value assignments that are implicit in action choice are generally thought to provide stronger evidence for or against a theory of decision (see, for example, Körding and Wolpert 2004; Trommershäuser et al. 2008).

Ellsberg cases (Ellsberg 1961) provide a more convincing betting argument against single-measure models (cf. Levi 1985). While hierarchical models do not have any difficulty in representing the distinction between known and unknown probabilities, as I emphasized above, they do not offer any straightforward explanation of the Ellsberg cases if we utilize a standard decision theory. On the other hand, some theorists have suggested that sets-of-measures models can be supplemented with a decision theory that can make sense of the patterns of preference in Ellsberg cases (see Bradley 2014 for discussion). However, the details of a plausible decision theory with sets of measures are far from clear, with many extant options being subject to clear counter-examples (Elga 2010). In addition, some theorists continue to question whether the Ellsberg cases are actually problematic for single-measure models with a standard decision theory (Al-Najjar and Weinstein 2009). The upshot of the Ellsberg cases for the debate at hand is correspondingly unclear. However, framing a decision theory that is able to cope with them is a significant outstanding challenge for the hierarchical approach and the sets-of-measures approach alike.

5.3 Completeness

A third kind of common objection is exemplified by Jeffrey’s (1983, p. 137) claim that the basic Bayesian model requires “a certain superhuman completeness”. This objection goes back at least to Keynes (1921), and it can be interpreted in either of two ways, one less troubling and one more so. The less troubling reading is closely related to the objections just canvassed: people are not always able to render a confident judgment about whether they find some event A more likely than event B. This is true, but not necessarily very revealing. Here again, without making strong assumptions about our introspective access to features of our cognitive states, we cannot draw strong conclusions about the structure of the underlying states from such a failure of self-report.

However, there is a related but more complex argument that has more bite. The issue is not just that we don’t always know whether we find A more likely than B. Rather, the issue is that the situations in which we are hesitant about making such a judgment seem to be precisely the situations in which we are in a state of credal imprecision, in the sense that there are many assignments of probability that seem plausible. While both the hierarchical model and the sets-of-measures model have the resources to model credal imprecision, at first blush it seems that only the sets-of-measures model gives us an obvious explanation for the correlation between credal imprecision and incompleteness. As I will argue, though, the hierarchical approach actually does better here as well.

Consider, for example, the soccer examples that we began with. Under credal precision, with much evidence of evenly matched teams, we might answer the question “Is A more likely to win than B is?” with a confident “No: they are equally likely to win”. Under credal imprecision, with no specific evidence about either team, we would, I take it, rather be inclined to answer “I don’t know”. The sets-of-measures model can explain this difference by adding a simple supervaluationist response rule: answer “yes” or “no” only if all measures in your representor agree on that response. Otherwise, answer “I don’t know”. This accounts for the correlation immediately. In a state of credal precision, all of the measures in our representor have P(A wins) = P(B wins) = .5, and so they all agree on a “No” answer to the question of whether A is more likely to win than B is. Under credal imprecision, some of the measures in our representor answer “Yes”, and some answer “No”. Since they disagree, the appropriate answer is “I don’t know”. By enriching the sets-of-measures theory with this modest linking hypothesis tying the theory to behavioral data, we have a neat explanation of why credal imprecision should lead to uncertainty about the comparative probability of events.

While this looks like a success for the sets-of-measures model, a similar—but more general and independently motivated—account is available within the hierarchical model. The key is Pearl’s (1988) insight, quoted above, that hierarchical models allow us to treat estimates of probabilities as being themselves random variables, with variance properties, etc. In the model described above, the distribution on likely performance values for unknown teams A and B was given by two identical Gaussian distributions, which themselves reflected uncertainty about the upstream variables skill and consistency. As a result, $P({\mathbf{A}}\; {\mathbf{wins}})$ and $P({\mathbf{B}}\; {\mathbf{wins}})$ are themselves associated with identical distributions.

Compare this situation to an experimental scenario where we are asked to make a comparative judgment that does not involve probabilities directly—say, which of two stimuli is louder or brighter, which of two bowls of water is hotter, which of two cities is larger, which of two items is more expensive, etc. This is an unusual experiment, though, where we don’t get to perceive the items compared directly, and indeed we don’t have any information about the items except that they both come from the same class. (Note that the experiment is meant to be precisely analogous to soccer example (2), where we have no information about the teams.) For example, we have just been asked to guess which of two cities is larger, and all we know about them is that they are in Germany, and that one has been labeled “City A” and the other “City B”. The appropriate answer to the question “Is City A larger than City B?” would presumably be “I don’t know”. In contrast, if we were in a situation where we had estimates of A’s and B’s sizes that were sufficiently differentiated—without yet being certain—a “yes” or “no” answer would be appropriate. In other words, this scenario displays the same kind of correlation between likely response patterns and confidence in our estimate of a random variable that we are trying to account for in the probability-comparison case.

Fig. 4

Three detection problems involving comparing the sizes of two cities on the basis of probabilistic estimates of the true values. Discrimination is impossible in problem 1, difficult in problem 2, and easy in problem 3

But note that the supervaluationist linking theory that served the sets-of-measures model so well in the probability-comparison example does not help us to understand why the same kind of correlation exists here. Both kinds of uncertainty models being compared here would treat our uncertainty about the sizes of Cities A and B as a distribution over degrees of size, and not as a flat set of options to which a supervaluation rule could be applied. Given this, we are dealing with a classic signal detection problem (Macmillan and Creelman 2005), where the signal in question is a mental variable—our probabilistic estimates of the sizes of two cities. Accounting for the hypothetical response pattern described above would require us to frame a linking hypothesis to behavioral data that fits the following (non-exhaustive) set of rough rules:

• If the distributions $P(\mathbf{size}\;\mathbf{of}\;\mathbf{A})$ and $P(\mathbf{size}\;\mathbf{of}\;\mathbf{B})$ are identical as in Problem 1 in Fig. 4, or very close to identical, then answer “I don’t know”.

• If the distribution $P(\mathbf{size}\;\mathbf{of}\;\mathbf{B})$ is clearly separated from and probabilistically greater than the distribution $P(\mathbf{size}\;\mathbf{of}\;\mathbf{A})$, as in Problem 3 in Fig. 4, then answer “B is larger”.

• ...

For intermediate cases like Problem 2 in Fig. 4 we need a more complex linking theory. People might, for example, make their best guess in a probabilistic way, or hedge, or say “I don’t know” depending on their level of risk-aversion and other factors. While the resulting theory will be quite complex, this is presumably what is needed in a general theory of how people make such judgments under uncertainty.

Framing a precise quantitative theory of discrimination is no trivial task, but it is obviously necessary independent of the concerns of this paper. With such a theory in hand, though, the hierarchical theory is able to explain the correlation between credal imprecision and refusal to render a probability judgment. Situations of extreme credal imprecision are precisely analogous to Problem 1 in Fig. 4, where the discrimination task that the participant is being asked to perform is impossible because they have no information that would allow them to distinguish the two distributions. The right response is thus “I don’t know”, exactly as in the case of judging the relative sizes of two unknown German cities.

While the problem of accounting for incomplete comparative probability judgments seemed at first to be a strong argument in favor of the sets-of-measures model, I suggest that it actually provides a further argument in favor of the hierarchical approach. In order to account for response behavior, the sets-of-measures theorist is forced to posit an ad hoc response rule that applies only to comparative probability judgments. In contrast, hierarchical models can account for failures of comparative judgment without any special-purpose machinery, appealing only to the general theory that is needed to explain how people make comparative judgments in general in (for example) signal detection tasks. This is a desirable theoretical unification that is made possible by the fact that probability estimates can be treated as random variables in hierarchical models.

6 Objections from the need for arbitrary priors

This section turns to a final objection to single-measure models, argued eloquently by Joyce (2005, 2010). Earlier I quoted Joyce’s primary objections to single-measure models: in a state of credal imprecision, one should not have any particular precise credence because one has no justification for such “extremely definite beliefs ...and very specific inductive policies”. Simply put, “the evidence comes nowhere close to warranting such beliefs and policies” (Joyce 2010, p. 285).

In Sect. 4 I argued that Joyce’s first objection is misplaced: the most successful way of spelling out single-measure Bayesian models, using hierarchical structures, does not generally give rise to the kinds of “extremely definite” beliefs that Joyce finds objectionable. However, I did not address the equally important objection from “specific inductive policies”. In brief, this objection involves the fact that our evidence typically underdetermines what a rational prior would be for a single-measure model. If there were a uniquely rational prior, then it would encode a specific policy for updating our evidence via conditionalization given any incoming stream of evidence—thus, “inductive policies”. If this objection is compelling, it does problematize hierarchical Bayesian models. However, I will argue that the use of “arbitrary” priors, even if rationally objectionable, is far better than the alternative.

While Joyce focuses his discussion of this point on his rejection of the Principle of Indifference (e.g., Jaynes 2003), he rightly points out that it applies to any single-measure model. For the sake of argument, I will simply grant that the Principle of Indifference is unworkable. I will also grant, more generally, that there is no general principle that determines, given a body of evidence, a unique rational credence distribution. (I am making these concessions simply because, if they are not true, then the issues discussed in this section do not arise.)

Let’s return briefly to the discussion of learning in Sect. 3 above. Recall that a sets-of-measures model—at least, one spelled out according to Joyce’s desiderata—is unable to treat simple examples of inductive learning. As we discussed, the reason relates to the familiar point that learning is impossible without inductive biases. From this perspective, Joyce’s objection can be reframed along the following lines: in any non-trivial probability model, there will always be an infinite number of distinct probability distributions P. Each P is a candidate prior for a Lewisian superbaby—a distribution that a Bayesian agent could have in advance of observing any evidence. But, having no evidence to work with, a superbaby could not even in principle choose among this infinite set of distributions on the basis of evidence. Unfortunately, this is what Joyce’s strictures demand: inductive policies are rationally required to be chosen on the basis of evidence. So, a Bayesian agent is condemned either to be rational, but unable to learn—or irrational, but able to learn from experience and navigate the world.

If an agent chooses the pragmatic option of functional irrationality, she overcomes the learning paradox by adopting inductive biases. While these are not warranted by evidence per se, this does not mean that they are necessarily arbitrary. Humans have a long evolutionary history that has presumably led to sharp constraints on the kinds of candidate priors that are available in the development of a normal infant. Evolutionary pressure presumably leaves many options still on the table, though. Is it necessary to have a rational justification for choosing among them? Why would it be? Evolution tends to create bodies and brains that are designed to get the job done. They may not be the best possible bodies and brains for some purpose, and they are sharply constrained by evolutionary history, environmental factors, physical laws, and the workings of chance. However, they are good enough to allow organisms to survive and reproduce, at least often enough. Our minds presumably work this way as well.

To the extent that a broadly Bayesian perspective on belief and learning is psychologically plausible at all, we have every reason to expect that our evolutionary history would have enabled us to make arbitrary but useful choices among priors. Imagine yourself as a Bayesian superbaby surveying a range of candidate priors that are all equally (un)attractive. If you choose one arbitrarily, you can proceed to learn and pursue your goals. If, like Buridan’s ass, you refuse—citing the lack of a rational justification for any particular choice—you will be unable to learn and navigate the world, and your genes will quickly disappear from the gene pool. When the alternative to choosing arbitrarily is guaranteed failure, making an arbitrary choice is the only rational choice.

7 Conclusion

Representations of credal imprecision in terms of sets of probability measures have considerable intuitive and philosophical appeal. However, they encounter severe problems as a representation of individual-level uncertainty, particularly in the limits that they place on learning from a starting point of ignorance. I argued that a hierarchical picture of belief states gives us a better model of learning while also accounting for many of the puzzles that have motivated the rejection of the basic Bayesian (single-measure) model of credence states. In particular, hierarchical models already account for the distinction between credal precision and imprecision that been used to motivate sets-of-measures models, and they excel at tasks where sets-of-measures models fail: explaining our ability to learn rapidly from limited data and form abstract generalizations. Hierarchical models have access to an independently motivated account of incomplete probability judgments based on models of discrimination from psychophysics. I discussed this along with several other objections that I argued are not real problems, or that (in the case of the Ellsberg cases) problematize both theories equally.

Nothing in this conclusion should be taken as an argument against the use of representations involving sets of probability measures for representing group belief, conversational common ground, in robust Bayesian analysis in statistics, as interesting objects of mathematical study in their own right, and so forth. The conclusions of this paper are directed only at the use of sets of measures to model individuals’ psychological states.