Introduction

Physiologically-based pharmacokinetics (PBPK) is a modeling approach that enables analysis and predictions of drug concentrations over time in plasma/blood and peripheral tissues. Among the key factors utilized in PBPK models, tissue-to-plasma partition coefficients (Kp) determine the extent of drug distribution to each tissue. The volume of distribution at steady-state (VSS) is a function of Kp values for various organs (1,2,3). A typical PBPK equation for a perfusion-limited and non-eliminating tissue based on the well-stirred organ model is (4, 5):

$${V}_T\frac{d{C}_T}{dt}={Q}_T\cdot {R}_b\cdot \left({C}_p-\frac{C_T}{K_p}\right)$$
(1)

where CT and Cp are the drug concentrations in tissue and arterial plasma (venous plasma for lung), VT is the anatomical tissue volume, QT is the blood perfusion rate, and Rb is the blood-to-plasma partition coefficient. In Eq. 1, CT/Kp denotes the outflow plasma concentration from the tissue (Cout) after drug partitioning, since the ratio CT/Cout is expressed as:

$${K}_p=\frac{C_T}{C_{out}}=\frac{\frac{C_{uT}}{f_{uT}}}{\frac{C_{up}}{f_{up}}}=\frac{PS_{in}\cdot {f}_{up}}{P{S}_{out} \cdot {f}_{uT}}$$
(2)

where CuT and Cup are unbound drug concentrations in tissue and plasma, fuT and fup are corresponding free fractions of drug, and PSin and PSout are permeability-surface area clearances of unbound compounds into and out of tissues. Based on the free drug hypothesis (6, 7), in vitro binding studies in plasma and tissue homogenates seeking fup and fuT with considerations of reliable dilution factors (8, 9) can be utilized for predictions of Kp and thus VSS (10). Many in silico methods have been developed for predicting Kp values in different tissues using physicochemical properties of compounds such as log P and fup (11,12,13) along with their ionization status (pKa) (14,15,16) to estimate tissue binding properties (fuT), though such methods show only approximate agreement with direct experimental measurements. The main basis for these methods is that drug molecules are reversibly distributed into tissue-specific constituent(s) (e.g., lipids and/or proteins) by passive diffusion (i.e., symmetrical movement of unbound drugs across the tissue membrane; PSin = PSout), such that the term Kp in Eq. 2 is expressed as the ratio fup/fuT. When active transport mechanisms (17, 18) are significant, the concentration ratio of tissue (CT) to plasma (Cout) would theoretically deviate from fup/fuT.

In practice, constant-rate drug infusion is necessary to reach steady-state for experimental determination of Kp values that are applicable for PBPK equations (Kp,ss; typically using arterial plasma), since the role of equilibration rate (e.g., QT ∙ Rb for perfusion-limited distribution) is factored out at steady-state in Eq. 1. While the experimental Kp,ss for non-eliminating organs represents Kp adopted in Eqs. 1 and 2, the Kp,ss value determined for eliminating organs needs to be corrected by the extraction ratio (ER) to account for loss (19). For linear and stationary pharmacokinetics based on n-compartment models, n slopes (viz., n eigenvalues of the system matrix) are shared across all the plasma and tissues (20), which means that tissue concentration profiles in the terminal phase would decline in parallel with plasma profiles in semi-log plots. Therefore, tissue-to-plasma concentration ratios measured in this post-distributive phase after intravenous (IV) bolus injection (viz., CT/Cp) are also useful for estimating Kp. This is especially so for a compound that has a long half-life that inconveniently requires a very long duration of infusion to reach steady-state or for a drug candidate with insufficient drug amount available in the early phase of drug development. To enhance the usefulness of measured CT/Cp for estimating the ‘PBPK-applicable’ Kp, the Chen and Gross (C&G) method (21), has been used for theoretical conversion of a terminal slope CT/Cp to Kp,ss based on the assumption of perfusion-limited distribution. However, when considering both blood flow (QT) and apparent tissue permeability (fupPSin) in the rate of tissue distribution (22, 23), the practical utility of the C&G method may be compromised for compounds with low permeability.

Therefore, the primary objective of this report is to propose extensions of the C&G method for determination of more reliable Kp estimates from IV bolus studies that are applicable for PBPK models, considering both QT and fupPSin in the rate of tissue distribution. Previously, a fractional distributional parameter fd was introduced to define the permeability limitations in tissue distribution processes in minimal PBPK (24) and whole-body PBPK models (22), where the product of QT and fd denotes apparent distributional clearance (CLapp) to each tissue. An fd can be reasonably calculated using fup, Rb, and a permeability coefficient P obtained from a parallel artificial membrane permeability assay (PAMPA) (i.e., compound-specific) along with QT and the effective surface area across the interface between the systemic circulation and tissues (Seff) of rats (i.e., system-specific). Utilizing fd in an extended C&G method, we herein demonstrate the theoretical conversion of the terminal CT/Cp to Kp,ss measured for 8 compounds with a wide range of apparent PAMPA P coefficients. Since many different types of Kp are present in the literature and used in PBPK models, extended mathematical relationships were developed between Kp and Kp,ss that are generally applicable for eliminating organs with a tissue permeability limitation, necessitating the use of ER and fd. These experimental Kp,ss values are also compared with values obtained using four in silico prediction methods (11,12,13,14,15,16).

Theoretical Considerations

Non-eliminating Organ

Kinetic assumptions applied for Eqs. 1 and 2 include (i) instant drug binding to biological constituents in plasma and tissues, (ii) rapid equilibrium between plasma and red blood cells, and (iii) well-stirred tissue compartments with no permeability limitation. Adding tissue permeability PS into Eq. 1 based on the previous literature (22, 24), a differential equation for non-eliminating organs utilizing fd is:

$${V}_T\frac{d{C}_T}{dt}={Q}_T\cdot {f}_d\cdot {R}_b\cdot \left({C}_p-\frac{C_T}{K_p}\right)$$
(3)

where all symbols are consistent with Eq. 1 and fd incorporates PS as will be shown later. At steady-state, both sides of Eq. 3 become 0, providing:

$${K}_p={K}_{p, ss}=\frac{C_{T, ss}}{C_{p, ss}}$$
(4)

where CT,ss and Cp,ss denote tissue and plasma concentrations at steady-state. Since no elimination term is included in Eq. 3, the Kp,ss for non-eliminating organs represents Kp, the operative parameter in PBPK models. Based on linear pharmacokinetics that leads to a parallel decline in the terminal phase for tissue and plasma concentrations in semi-log plots (20), the terminal phase concentrations after an IV bolus administration are:

$${C}_p=A\cdot {e}^{-\beta t}$$
(5a)
$${C}_T=B\cdot {e}^{-\beta t}$$
(5b)

where A and B are the y-intercepts extrapolated from the terminal-phase concentration profiles in plasma and tissue, and β is the terminal phase slope. Utilizing Eqs. 5a and 5b, Eq. 3 can be expressed as:

$${V}_T\cdot \left(-B\cdot \beta \cdot {e}^{-\beta t}\right)={Q}_T\cdot {f}_d\cdot {R}_b\cdot \left(A\cdot {e}^{-\beta t}-\frac{B\cdot {e}^{-\beta t}}{K_p}\right)$$
(6)

Since CT/Cp = B/A, the rearrangement of Eq. 6 results in:

$${K}_p={K}_{p, ss}=\frac{1}{\frac{C_p}{C_T}+\frac{V_T\beta }{Q_T{f}_d{R}_b}}$$
(7)

Equation 7 indicates that Kp,ss (or Kp for a non-eliminating organ) can be converted from CT/Cp, with the anatomical/physiological information (VT and QT), in vivo (β determined from a series of blood samples after IV injection) and in vitro observations (fd and Rb). Assuming that Rb and fd are 1 in Eq. 7 leads to the same relationship derived by Chen and Gross (21).

Eliminating Organ

Similar to Eq. 3, a differential equation for an eliminating organ utilizing fd is:

$${V}_T\frac{d{C}_T}{dt}={Q}_T\cdot{f}_d\cdot{R}_b\cdot\left({C}_p-\frac{C_T}{K_p}\right)-{CL}_{u,int}\cdot{f}_{uT}\cdot{C}_T$$
(8)

where CLu,int is the intrinsic clearance for unbound drug in the eliminating organ (i.e., CuT = fuT ∙ CT). At steady-state, both sides of Eq. 8 become 0, and the rearranged equation is:

$${K}_p\neq {K}_{p, ss}=\frac{C_{T, ss}}{C_{p, ss}}=\frac{1}{\frac{1}{K_p}+\frac{C{L}_{u,int}{f}_{uT}}{Q_T{f}_d{R}_b}}$$
(9)

It should be noted that Kp,ss is different from Kp due to the presence of the term CLu,intfuT/(QTfdRb) in the denominator of Eq. 9 which rearranges to:

$$\frac{C{L}_{u,int}{f}_{uT}}{Q_T{f}_d{R}_b}=\frac{1}{K_{p, ss}}-\frac{1}{K_p}$$
(10)

Utilizing the same relationships of Eqs. 5a and 5b in Eq. 8 for eliminating organs, a differential equation for tissue distribution in the terminal phase slope is:

$$\begin{array}{c}V_T\cdot\left(-B\cdot\beta\cdot e^{-\beta t}\right)=Q_T\cdot f_d\cdot R_b\cdot\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\\left(A\cdot e^{-\beta t}-\frac{B\cdot e^{-\beta t}}{K_p}\right)-{CL}_{u,int}\cdot f_{uT}\cdot B\cdot e^{-\beta t}\end{array}$$
(11)

and

$$\frac{C_T}{C_p}=\frac{B}{A}=\frac{1}{\frac{1}{K_p}+\frac{C{L}_{u,int}{f}_{uT}-{V}_T\beta }{Q_T{f}_d{R}_b}}$$
(12)

Melding Eq. 10 into Eq. 12 yields:

$${K}_p\neq {K}_{p, ss}=\frac{1}{\frac{C_p}{C_T}+\frac{V_T\beta }{Q_T{f}_d{R}_b}}$$
(13)

In comparison of Eqs. 7 and 13, Kp,ss could be converted from CT/Cp by the same mathematical relationship, regardless of the presence of tissue elimination. As shown in Eq. 10, determinations of CLu,int, fuT, QT, fd, and Rb along with the estimated Kp,ss from Eq. 13 can lead to estimation of Kp from Kp,ss for eliminating organs. Analogously, assuming Rb and fd in Eq. 13 are equal to unity leads to the same relationship derived by Chen and Gross (21) for an eliminating organ.

Lung Tissue Case

The rates of drug distribution in the lung and arterial blood are expressed (e.g., lung as a non-eliminating organ) as:

$${V}_{LU}\frac{dC_{LU}}{dt}={Q}_{LU}\cdot {f}_{d, LU}\cdot {R}_b\cdot \left({C}_{ven,p}-\frac{C_{LU}}{K_{p, LU}}\right)$$
(14a)
$${V}_{art}\cdot {R}_b\cdot \frac{d{C}_p}{dt}={Q}_{LU}\cdot {R}_b\cdot \left({C}_{out, LU}-{C}_p\right)$$
(14b)

where LU, art, and p in the subscripts denote lung, arterial blood, and arterial plasma. The blood perfusion rate to lung is regarded as cardiac output (QLU = QCO). The Cven,p is the outflow plasma concentration from the venous blood pool that takes a role of input concentration into lung tissue. Stringently, therefore, PBPK-applicable Kp,LU denotes the lung-to-‘venous’ plasma partition coefficient. Based on Fick’s law of perfusion in Eq. 14a, Cout,LU, the outflow plasma concentration from lung, is written as:

$${C}_{out, LU}={C}_{ven,p}\cdot \left(1-{f}_{d, LU}\right)+\frac{C_{LU}}{K_{p, LU}}{f}_{d, LU}$$
(15)

At steady-state, both sides of Eqs. 14a and 14b become 0 (i.e., Cp,ss = Cout,LU,ss = Cven,p,ss), and rearrangement leads to:

$${K}_{p, LU}={K}_{p, LU, ss}=\frac{C_{LU, ss}}{C_{p, ss}}=\frac{C_{LU, ss}}{C_{ven,p, ss}}$$
(16)

In the terminal phase after an IV bolus injection with the slope β, the division of both sides of Eq. 14a by CLU results in:

$$\frac{V_{LU}\cdot \left(-\beta \right)}{Q_{LU}{f}_{d, LU}{R}_b}=\frac{C_{ven,p}}{C_{LU}}-\frac{1}{K_{p, LU}}$$
(17)

Based on Fick’s law of perfusion, Eq. 14a after a bolus injection can be also re-written using Eq. 15 as:

$$\frac{V_{LU}\cdot \left(-\beta \right)}{Q_{LU}\cdot {R}_b}=\frac{C_{ven,p}-{C}_{out, LU}}{C_{LU}}$$
(18)

In addition, Eq. 14b can be expressed by rearrangements as:

$$\frac{V_{art}\cdot \left(-\beta \right)}{Q_{LU}}=\frac{C_{out, LU}-{C}_p}{C_p}$$
(19a)
$${C}_{out, LU}={C}_p\cdot \left(1+\frac{V_{art}\cdot \left(-\beta \right)}{Q_{LU}}\right)$$
(19b)

From the mathematical relationships in Eqs. 17 to 19, Kp,LU is:

$${K}_{p, LU}=\frac{1}{\frac{C_p}{C_{LU}}\cdot \left(1-\frac{V_{art}\beta }{Q_{LU}}\right)+\frac{V_{LU}\beta }{Q_{LU}{R}_b}\cdot \left(\frac{1}{f_{d, LU}}-1\right)}$$
(20)

The application of the perfusion-limited model in Eq. 20 (fd,LU = 1) leads to a mathematical relationship consistent with the C&G method (21).

Liver Compartment Connected to Spleen and Gut

In the physiology of the body, the outflow blood from the splanchnic tissues including gut and spleen enters the liver via the hepatic portal vein while the remaining (circa 40% for rat and 20% for man) liver blood flow (25) comes from the hepatic artery. The equations for the rate of drug distribution to the liver, gut, and spleen are defined in whole-body PBPK as (22):

$${V}_{LI}\frac{d{C}_{LI}}{dt}={Q}_{LI}\cdot {f}_{d, LI}\cdot {R}_b\cdot \left({C}_{in, LI}-\frac{C_{LI}}{K_{p, LI}}\right)-{CL}_{u,int}\cdot {f}_{u, LI}\cdot {C}_{LI}$$
(21a)
$${V}_{GU}\frac{dC_{GU}}{dt}={Q}_{GU}\cdot {f}_{d, GU}\cdot {R}_b\cdot \left({C}_p-\frac{C_{GU}}{K_{p, GU}}\right)$$
(21b)
$${V}_{SP}\frac{dC_{SP}}{dt}={Q}_{SP}\cdot {f}_{d, SP}\cdot {R}_b\cdot \left({C}_p-\frac{C_{SP}}{K_{p, SP}}\right)$$
(21c)

where LI, GU, and SP in the subscripts denote liver, gut, and spleen. The Cin,LI is the plasma concentration entering the liver, expressed as:

$${C}_{in, LI}=\frac{\left({Q}_{LI}-{Q}_{SP}-{Q}_{GU}\right)\cdot {C}_p+{Q}_{SP}\cdot {C}_{out, SP}+{Q}_{GU}\cdot {C}_{out, GU}}{Q_{LI}}$$
(22)

where Cout,SP and Cout,GU are the outflow plasma concentrations from spleen and gut. Since Cin,SP = Cin,GU = Cp as shown in Eqs. 21b and 21c, Cout,SP and Cout,GU can be written, based on Fick’s law of perfusion in Eqs. 21b and 21c, as:

$${C}_{out, SP}={C}_p\cdot \left(1-{f}_{d, SP}\right)+\frac{C_{SP}}{K_{p, SP}}{f}_{d, SP}$$
(23a)
$${C}_{out, GU}={C}_p\cdot \left(1-{f}_{d, GU}\right)+\frac{C_{GU}}{K_{p, GU}}{f}_{d, GU}$$
(23b)

At steady-state, both sides of Eqs. 21a to 21c are 0, which leads to the relationship of Cout,SP,ss = Cout,GU,ss = Cp,ss from Eqs. 23a and 23b, and thereby Cin,LI,ss = Cp,ss in Eq. 22. Therefore, the differential equation for the liver compartment at steady-state can be rearranged as:

$${K}_{p, LI}\neq {K}_{p, LI, ss}=\frac{C_{LI, ss}}{C_{p, ss}}=\frac{1}{\frac{1}{K_{p, LI}}+\frac{C{L}_{u,int}{f}_{u, LI}}{Q_{LI}{f}_{d, LI}{R}_b}}$$
(24)

Utilizing drug concentrations in arterial plasma (Cp), liver (CLI), spleen (CSP), and gut (CGU) in the terminal phase (with the same slope of β) after an IV bolus injection, the rearrangement of Eq. 21a with Eq. 24 yields:

$${V}_{LI}\cdot \left(-\beta \right)=\left\{\left({Q}_{LI}-{Q}_{SP}-{Q}_{GU}\right)+{Q}_{SP}\cdot \left(\left(1-{f}_{d, SP}\right)+\frac{C_{SP}}{C_p}\frac{1}{K_{p, SP}}{f}_{d, SP}\right)+{Q}_{GU}\cdot \left(\left(1-{f}_{d, GU}\right)+\frac{C_{GU}}{C_p}\frac{1}{K_{p, GU}}{f}_{d, GU}\right)\right\}\cdot \frac{C_p}{C_{LI}}{R}_b\cdot {f}_{d, LI}-{Q}_{LI}{f}_{d, LI}{R}_b\frac{1}{K_{p, LI, ss}}$$
(25)

From Eqs. 21b and 21c, the equations for the spleen and gut in the terminal phase after IV bolus injection are:

$${V}_{SP}\cdot \left(-\beta \right)={Q}_{SP}\cdot {f}_{d, SP}\cdot {R}_b\cdot \left(\frac{C_p}{C_{SP}}-\frac{1}{K_{p, SP}}\right)$$
(26a)
$${V}_{GU}\cdot \left(-\beta \right)={Q}_{GU}\cdot {f}_{d, GU}\cdot {R}_b\cdot \left(\frac{C_p}{C_{GU}}-\frac{1}{K_{p, GU}}\right)$$
(26b)

Application of Eqs. 26a and 26b in Eq. 25 leads to:

$${K}_{p, LI, ss}=\frac{1}{\frac{C_p}{C_{LI}}\cdot \left(1+\frac{V_{SP}\beta \left({C}_{SP}/{C}_p\right)+{V}_{GU}\beta \left({C}_{GU}/{C}_p\right)}{Q_{LI}{R}_b}\right)+\frac{V_{LI}\beta }{Q_{LI}{f}_{d, LI}{R}_b}}$$
(27)

Plugging the value of 1 into Rb and fd in Eq. 27 for the case of Kp,LI = fup/fu,LI (viz., symmetrical transport) in Eq. 24 leads to the C&G equation (21).

Theoretical Conversion of Kp,ss to Kp Using fd and Extraction Ratio (ER)

An estimated Kp,ss as discussed above needs to be corrected to the ‘true’ or operative Kp that is applicable in PBPK equations for eliminating organs. Based on Fick’s law of perfusion, Eq. 8 can be re-written by utilizing Cin and Cout terms (with regard to plasma concentration) as:

$${V}_T\frac{d{C}_T}{dt}={Q}_T\cdot {R}_b\cdot \left({C}_{in}-{C}_{out}\right)-{CL}_{u,int}\cdot {f}_{uT}\cdot {C}_T$$
(28)

In the typical well-stirred model (26), elimination rate is kinetically driven by Cout where the elimination term in Eq. 28 is replaced with CLu,int ∙ fup ∙ Cout under the assumption that fup ∙ Cout = CuT. However, the unbound concentrations between plasma and tissue are not the same when PSin ≠ PSout. Eqs. 8 and 28 are thus based on considering CuT as the driving concentration for elimination in tissues. When Eq. 10 is rearranged:

$${K}_p=\frac{1}{\frac{C_{p, ss}}{C_{T, ss}}-\frac{C{L}_{u,int}{f}_{uT}}{Q_T{f}_d{R}_b}}=\frac{Q_T{f}_d{R}_b\cdot {C}_{T, ss}}{Q_T{f}_d{R}_b\cdot {C}_{p, ss}-C{L}_{u,int}{f}_{uT}\cdot {C}_{T, ss}}$$
(29)

At steady-state, both sides of Eq. 28 are zero, resulting in:

$${K}_p=\frac{Q_T{f}_d{R}_b\cdot {C}_{T, ss}}{Q_T{f}_d{R}_b\cdot {C}_{p, ss}-{Q}_T\cdot {R}_b\cdot \left({C}_{in, ss}-{C}_{out, ss}\right)}=\frac{C_{T, ss}}{C_{p, ss}}\cdot \frac{f_d}{f_d-\frac{C_{in, ss}-{C}_{out, ss}}{C_{p, ss}}}={K}_{p, ss}\cdot \frac{1}{1- ER/{f}_d}$$
(30)

where Cin,ss = Cp,ss and ER is the traditionally defined extraction ratio (4). Based on Eq. 30, for example in liver, the relationship Kp,ss = Kp ∙ (1 − ER) = Kp ∙ QLI/(QLI + fupCLu,int/Rb) (19) is only applicable for the well-stirred perfusion-limited liver model (26) with fd,LI = 1.

Methods

Application of the Extended Chen and Gross Method for Eight Compounds in Rats

Rats are widely used for experimental determination of tissue partitioning properties, e.g., Kp,ss from infusion studies and CT/Cp from an IV bolus injection. Measured data for both Kp,ss and CT/Cp in available tissues of rats were collected for 8 compounds (cefazolin, cyclosporine, dexamethasone, etoposide, furosemide, methotrexate, propranolol, and quinidine) as summarized in Tables I (for Kp,ss) and II (for CT/Cp). If numerical tissue distribution data were not directly available from the literature, plasma/blood and tissue concentration profiles were digitized from published graphs using GetData Graph Digitizer version 2.26 (http://getdata-graph-digitizer.com/). The CT/Cp data for dexamethasone at 24 h after a subcutaneous bolus administration were available from our recent study (27). For etoposide, methotrexate, and propranolol, terminal phase slopes were assumed to be the same between plasma and all tissues. Concentration-time profiles of dexamethasone in plasma and various tissues (27) experimentally showed parallel declines when plotted in semi-log graphs, providing adequate justification of using the same slope for different tissues. When terminal phase tissue slopes appear to be different from plasma/blood (for furosemide, cefazolin, cyclosporine, and quinidine), the assumption of linear pharmacokinetics leads to adoption of the terminal phase slope of tissue profiles (βT), where Eqs. 7 and 13 for typical tissues, Eq. 20 for lung, and Eq. 27 for liver can be expressed as:

$${K}_{p, ss}=\frac{1}{\frac{C_p}{C_T}+\frac{V_T{\beta}_T}{Q_T{f}_d{R}_b}}$$
(31a)
$${K}_{p,LU}=\frac{1}{\frac{C_p}{C_{LU}}\cdot \left(1-\frac{V_{art}\beta }{Q_{LU}}\right)+\frac{V_{LU}{\beta}_{LU}}{Q_{LU}{R}_b}\cdot \left(\frac{1}{f_{d, LU}}-1\right)}$$
(31b)
$${K}_{p, LI, ss}=\frac{1}{\frac{C_p}{C_{LI}}\cdot \left(1+\frac{V_{SP}{\beta}_{SP}\left({C}_{SP}/{C}_p\right)+{V}_{GU}{\beta}_{GU}\left({C}_{GU}/{C}_p\right)}{Q_{LI}{R}_b}\right)+\frac{V_{LI}{\beta}_{LI}}{Q_{LI}{f}_{d, LI}{R}_b}}$$
(31c)

where β, βLU, βSP, βGU, and βLI reflect the terminal phase slopes in arterial plasma, lung, spleen, gut, and liver. Eqs. 31a to 31c are derived in the same manner as done for Eqs. 7, 13, 20, and 27, except that the tissue concentration at the observed point (Eq. 5b) is replaced with the relationship \({C}_T=B\cdot {e}^{-{\beta}_Tt}\). It was assumed that elimination kinetics did not take place in lung tissue for the 8 compounds assessed (Kp,LU = Kp,LU,ss).

Table I Literature Data for Kp,ss After Constant Infusion of 8 Compounds to Rats
Full size table

Tissue partitioning properties were reported as tissue-to-blood concentration ratio for dexamethasone (CT/CB) and cyclosporine (CT/CB and CT,ss/CB,ss) (27, 32, 34). Based on the assumption of rapid equilibrium between plasma and red blood cells, the CT/CB at 24 h after a subcutaneous bolus injection of dexamethasone was converted to CT/Cp by multiplication of Rb (0.725) and CT/CB values. Since two Rb values were available for cyclosporine depending on the infusion rate (e.g., 1.28 for lower dose and 1.18 for higher dose) (32), the reported CT/CB and CT,ss/CB,ss are used without further correction with Rb as noted in Tables I and II. In this case, tissue-to-blood partition coefficients at steady-state (Kp,TB,ss) for typical tissues, lung, and liver are expressed as:

$${K}_{p, TB, ss}=\frac{1}{\frac{C_B}{C_T}+\frac{V_T{\beta}_T}{Q_T{f}_d}}$$
(32a)
$${K}_{p, TB, LU}=\frac{1}{\frac{C_B}{C_{LU}}\cdot \left(1-\frac{V_{art}\beta }{Q_{LU}}\right)+\frac{V_{LU}{\beta}_{LU}}{Q_{LU}}\cdot \left(\frac{1}{f_{d, LU}}-1\right)}$$
(32b)
$${K}_{p, TB, LI, ss}=\frac{1}{\frac{C_B}{C_{LI}}\cdot \left(1+\frac{V_{SP}{\beta}_{SP}\left({C}_{SP}/{C}_B\right)+{V}_{GU}{\beta}_{GU}\left({C}_{GU}/{C}_B\right)}{Q_{LI}}\right)+\frac{V_{LI}{\beta}_{LI}}{Q_{LI}{f}_{d, LI}}}$$
(32c)
Table II Literature Data Values of CT/Cp After Bolus Injections of 8 Compounds to Rats. Terminal Phase Slopes for Plasma/Blood (β) and/or Tissues (βT) are Included. The Same Sources Listed in Table I were Used Unless Otherwise Noted
Full size table

For cyclosporine, tissue-specific terminal phase slopes were available in the literature (34) (Table II). If all terminal phase slopes in blood and tissues could be assumed to be the same, then βLU, βSP, βGU, and βLI could be replaced with β in Eqs. 32a to 32c.

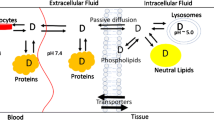
When necessary to calculate fd for various tissues, two distribution models proposed in whole-body PBPK for rats (Fig. 1) were used (22) with fd equations expressed as:

$${f}_{d, Model1}=1-{e}^{-\frac{f_{up}\cdot P\cdot {S}_{eff}}{Q_T\cdot {R}_b}}$$
(33a)
$${f}_{d, Model2}=\frac{f_{up}\cdot P\cdot {S}_{eff}}{Q_T\cdot {R}_b+{f}_{up}\cdot P\cdot {S}_{eff}}$$
(33b)

where distribution Model 1 is based on the capillary permeability model (e.g., TUBE model) (38, 39) and the vascular compartment of Model 2 (e.g., JAR model) is a well-stirred compartment (23). The kinetics in the vascular compartment of the JAR model (viz., Vvas/QT) is assumed to be negligible to obtain Eq. 33b (22). From the derivation, it should be noted that the product P ∙ Seff in Eqs. 33a and 33b denotes the uptake clearance of unbound concentrations in plasma (PSin) (22). Input parameters specific for the 8 compounds (9 cases with two dose levels for cyclosporine) are listed in Table III. System-specific input parameters (Vart, VT, QT, and Seff) for major tissues of rats with a typical body weight of 250 g are summarized in Table IV. Experimental Kp,ss values were compared with CT/Cp and those converted from the C&G method (i.e., perfusion-limited distribution) and Models 1 and 2. Since Kp,ss is theoretically equivalent with AUCT/AUCp from a single dose study based on the assumption of linear pharmacokinetics, tissue concentration data as listed in Table II were also used for calculating AUCT/AUCp, where the initial concentration was set to be 0. Despite the limited tissue concentrations in the literature (40), the data after an IV administration of propranolol at 1.5 mg/kg (with the terminal phase slope of 0.66 h−1) were used for calculating AUCT/AUCp.

Fig. 1
figure 1

Structures of two distribution models used for calculation of fd (22). Symbols for Models 1 and 2 are described in the text

Full size image
Table III Compound-Specific Input Parameters Used in the Calculations of fd for Various Tissues of Rats. Sources are Listed in Tables I and II
Full size table
Table IV System-Specific Input Parameters for 250 g Rat Used for the Conversion of CT/Cp to Kp,ssa
Full size table

In addition, in silico Kp values were estimated by utilizing the physicochemical properties of the 8 compounds (Table III) with 4 different methods [i.e., Poulin and Theil (P&T) (11, 12), Berezhkovskiy (13), Rodgers and Rowland (R&R) (14, 15), and Lukacova (16), available from GastroPlus version 9.8.0002; Simulations Plus Inc., Lancaster, CA]. The in silico Kp for gut tissue was calculated by Simcyp Simulator (Version 20 Release 1; Certara Ltd., Sheffield, UK), using Method 1 for P&T and Berezhkovskiy and Method 2 for R&R and Lukacova. For fair comparisons of Kp,ss values in eliminating organs (e.g., liver and kidney), the in silico-predicted Kp values were corrected to Kp,ss considering the experimental ER (calculated from organ clearances in Table IV) and the model-dependent fd (from Eqs. 33a and 33b), based on the Eq. 30.

Results

Refinement of Collected Data from the Literature

Tsuji et al. (1983) (29) reported Kp values for cefazolin in liver (0.788) and kidney (2.79) of rats that differ from Kp,ss where Kp,ss was already corrected using an ER in those tissues. Since the steady-state arterial plasma concentration of cefazolin (i.e., free and bound) was 77.5 μg/mL, the fup at steady-state was expected to be 0.163 with a Cup of 12.6 μg/mL based on its binding kinetics (i.e., binding site concentration, [nP] = 3.15 × 10−4 M, and association constant, KA = 2.98 × 104 M−1) (29). Hepatic elimination of cefazolin was assumed to be mainly mediated by biliary excretion with an unbound Michaelis-Menten constant Km, u of 163.3 μg/mL (in terms of unbound concentration in liver) and the maximum rate Vmax of 238.8 μg/min, which may reasonably lead to linear excretion kinetics of cefazolin into bile. Therefore, CLu,int (viz., Vmax/Km,u) for biliary excretion was estimated as 1.46 mL/min, and the ER for the well-stirred perfusion-limited liver model (26) calculated with hepatic plasma flow of 3.7 mL/min adopted in Tsuji et al. (1983) (29) was 0.0605 and thus the original Kp,ss,LI was estimated to be 0.740 (Table I). Renal clearance (CLR) calculated as the slope of the plot of urinary excretion rate versus unbound arterial plasma concentration of cefazolin divided by fup was 5.03 mL/min. Similarly, the ER for the well-stirred kidney compartment [viz., CLR/RPF, where renal plasma flow RPF = 7.3 mL/min in Tsuji et al. (1983) (29)] led to back estimation of Kp,ss for rat kidney to be 0.867 (Table I).

For propranolol, Kp values were reported in Shibasaki et al. (36) after the correction of CT/Cp values obtained from an IV injection using the traditional C&G method. Using the reported values of Rb (1.16), fup ∙ CLu,int (97.3 mL/min) and QLI (24.7 mL/min) for liver of a 290-g rat, hepatic ER is estimated as 0.773 (26). Considering the terminal phase slope (0.696 h−1) along with QT and VT values for a 290-g rat, the original CT/Cp data at 2 h after IV injection were estimated (Table II). In addition, Yata et al. (33) reported propranolol partitioning in liver as CLI,ss/Cout,LI,ss = 11.6 (viz., Cout,LI,ss, the outflow plasma concentrations from liver, measured from hepatic vein). However, Kp,ss is defined as the tissue-to-‘input’ plasma concentration ratio at steady-state (CLI,ss/Cin,LI,ss in Eq. 24 for liver). We calculated Kp,ss by multiplying CLI,ss/Cout,ss with 0.227 (i.e., 1 − ER) (Table I). For calculating AUCT/AUCp, the tissue concentration profiles of propranolol at 1.5 mg/kg (40) was used since the terminal phase slope (0.66 h−1) was comparable with the literature value (0.696 h−1) at 10 mg/kg (36).

In addition, the steady-state liver-to-plasma concentration ratio was reported for quinidine using the plasma from hepatic portal vein (33). Since it could be assumed that quinidine elimination in rats is mainly mediated by the liver with hepatic blood clearance (CLH/Rb) of 16.1 mL/min (adjusted by body weight) (37, 48), the ER of quinidine was calculated to be 0.830 (CLH/QLI). Therefore, Kp,ss was calculated by multiplication of CLI,ss/Cout,LI,ss (16.5) and 1 − ER (0.172) as noted in Table I.

Correction of the Chen and Gross Method Considering fd

Figures 2a and b  exemplify our extension of the C&G method for the theoretical conversion of CT/Cp to Kp,ss using the concentration profiles of furosemide in rat plasma and gut. Using the indicated tri-exponential profile fitted to the observed plasma concentration-time data as a forcing function (i.e., nonlinear regression by the maximum likelihood method in ADAPT 5) (49), tissue distribution parameters (Coefficient of Variation, CV%) for gut were estimated by Eq. 3 with system parameters in Table IV in terms of rate [fd = 0.00771 (16.2%)] and extent [Kp = 2.61 (22.0%)]. The observed CT/Cp was calculated as 10.1 (Table II), which is much higher than the fitted Kp (i.e., model-simulated AUCT/AUCp) due to the presence of delayed equilibrium in the early time mediated by both QT and fupPSin. The calculated fd values from Models 1 and 2 were 0.0130 and 0.0143, both of which were comparable with the fitted fd within a factor of 2. When fd was assumed to be 1 (i.e., the C&G method) and 0.130 (e.g., 10-fold of fd,Model1), tissue concentration profiles projected from one-time tissue measurement at 8 h (Fig. 2b) become markedly divergent from the experimental observations. This leads to deviations in Kp estimation (e.g., 9.20 for the C&G method and 7.46 for the case of 10 × fd,Model1, compared to the fitted Kp of 2.61).

Fig. 2
figure 2

Concentration profiles of furosemide in rat plasma (closed circles) and gut (open circles). (a) Solid lines show fittings to the concentration-time data in the plasma (Cp = 455.3∙e−40.2 ∙ t+287∙e−2.42 ∙ t+113∙e−0.282 ∙ t) and gut (fd and Kp optimized by Eq. 3 with Cp used as a forcing function; see text). (b) For the case of one-time measurement of tissue concentration at 8 h, dashed lines show tissue concentration profiles assumed in determination of Kp,ss (or AUCT/AUCp) depending on fd values (e.g., 0.0130 from Model 1 and 1 from the C&G method)

Full size image

Based on the assumption of (i) the same terminal slope (β), (ii) gut tissue to be a non-eliminating organ, and (iii) model-dependent fd values, therefore, Kp,ss was estimated from CT/Cp by Eq. 7, resulting in comparable values (2.53 and 2.72 for Models 1 and 2) with the fitted Kp (i.e., Kp = Kp,ss for a non-eliminating organ). However, the experimentally measured Kp,ss was 0.517, which is less than the fitted Kp (28). Since this Kp,ss was determined after bolus injection of a 25-mg/kg dose followed by a 3-h infusion (11.5 mg/kg/h) and this infusion duration may not be sufficient for the complete equilibrium between plasma and gut (Fig. 2a), one explanation for discrepant Kp,ss values between infusion (CT,ss/Cp,ss) and injection studies (model-simulated AUCT/AUCp) could be that a steady-state with regard to gut concentrations might not have been achieved for furosemide by 3 h. Although a steady-state condition is typically confirmed based on serial plasma concentrations, the limited capability in analytical methodologies could have restricted the resolution of all components of drug distribution kinetics specific for those slowly equilibrating tissue(s).

As shown in Fig. 3, tissue partition coefficients (CT/Cp and Kp,ss from different approaches) collected for 8 compounds in various tissues of rats ranged about 4 orders of magnitude. When CT/Cp is directly compared with Kp,ss for the 8 compounds, 69 out of 74 points showed CT/Cp values larger than Kp,ss, supporting the contribution of an equilibrium time between plasma and tissues emerging in the terminal phase after bolus dosing (Fig. 3a). For furosemide having the lowest permeability coefficient amongst our assessed compounds, Kp,ss for gut was obviously different than CT/Cp (19.5-fold). For quinidine, the highest permeability drug, Kp,ss for liver was different from CT/Cp (14.7-fold). As shown in Fig. 3b, however, the Kp,ss estimated with the C&G method employing the same terminal slope (β) and Rb = 1 appears to have comparable values with the uncorrected CT/Cp. Since the C&G method does not consider a tissue permeability term fupPSin, the Kp,ss estimation based on the traditional method is expected to be problematic for drugs having lower permeability coefficients.

Fig. 3
figure 3

Estimation of Kp,ss (a) from direct comparison with CT/Cp (Table II), converted from (b) traditional Chen and Gross (C&G) method (i.e., Rb = 1 and the same terminal slope), and revised methods with (c) Model 1 and (d) Model 2. Solid line has a slope of 1.0, and dashed lines show 3-fold differences

Full size image

In our extensions of the C&G approach, a compound-specific Rb was utilized (Table III), and tissue-specific slopes were considered where the tissue kinetic profiles were found for furosemide, cefazolin, cyclosporine, and quinidine as listed in Table II. Otherwise, all the profiles in tissues and plasma/blood were assumed to decline in parallel, using Eqs. 7, 13, 20 and 27. However, Fig. S1 shows that consideration of different slopes (βT) for the 4 drugs in the calculation of Kp,ss from CT/Cp was not significantly different than using the same slope (β). When fd values for Models 1 and 2 (Figs. 3c and d) were calculated for the 8 compounds in the major tissues of rats, our estimations of Kp,ss were improved particularly for the lower permeability compound, viz., furosemide. The coefficients of determination (R2) for Fig. 3a to d for the 4 different methods are very close: 0.9104 (CT/Cp), 0.9102 (C&G), 0.9184 (Model 1), and 0.9173 (Model 2).

As shown in Fig. 4, the predicted Kp,ss (i.e., 4 in silico approaches plus 4 different experimentally-based approaches) and in vivo Kp,ss values are plotted in terms of fold-differences (Kp,ss,pred/Kp,ss). In agreement with the regressions shown in Fig. 3, the four versions of the C&G calculations produce Kp ratios near unity (Fig. S2) and the acceptable predictability was shown with Models 1 and 2 (i.e., the fold-differences closer to 1). While the improvements of Kp,ss predictions in many different types of tissues for furosemide (gut), cefazolin (kidney and skin), etoposide (gut, muscle, and spleen), and propranolol (brain and lung) supports the usefulness of the extended C&G method, some overpredictions in Kp,ss,pred/Kp,ss remained unimproved despite the current fd considerations. There appeared to be no consistency when comparing specific tissues. Very striking in Fig. 4 are the disparate Kp ratios observed with the four in silico estimation methods. Of note, the experimental ER values calculated as the ratios of CLH/(QLIRb) and CLR/(QKIRb) are less than the model-dependent fd values, or comparable with fd (within a factor of 2). When ER > fd, the in silico Kp was not further converted to Kp,ss for furosemide and methotrexate (liver and kidney), cefazolin (kidney), and propranolol (liver). In general, these in silico methods for the 8 compounds assessed function poorly for predicting Kp,ss (Fig. 4), compared to the experimental AUCT/AUCp or CT/Cp values (i.e., Kp,ss,pred/Kp,ss closer to 1). The greatest mis-predictions occurred with the liver, especially for high ER drugs, viz., propranolol and quinidine.

Fig. 4
figure 4

Comparisons of Kp,ss with (i) AUCT/AUCp, (ii) CT/Cp, and Kp,ss calculated from (iii) the Chen and Gross method (C&G), (iv) Model 1, and (v) Model 2, for 8 compounds assessed. The in silico calculations employed the Poulin and Theil (P&T) (11, 12), Berezhkovskiy (13), Rodgers and Rowland (R&R) (14, 15), and Lukacova (16) methods. The Y-axis denotes the predictability of each method (Kp,ss,pred/Kp,ss) and dots are connected to visualize the specific tissues

Full size image

Discussion

The classic drug-specific components of PBPK models are the clearance (e.g., CLu,int) and the operative tissue-partition (Kp) parameters that, along with system components such as QT and VT, serve in the simplest of PBPK models. The gold-standard approach to assessing both clearances and Kp values is a steady-state infusion study. The second-most common method is to enact single-dose studies to assess (systemic) clearance from Dose/AUC and Kp from AUCT/AUCp. The limitation of this method, even by performing computational fitting, is that an IV bolus study often assumes an initial condition Cp(0) of Dose/VB or Dose/Vp, which may not be supported by sufficient early blood samples. All experimental methods have concerns when metabolism, permeability, or transporters affect the measured tissue drug concentration. The terminal phase in a pharmacokinetic profile, if not limited by assay sensitivity, often has the richest data and can be visualized with both plasma (blood) and tissue measurements, which prompted the derivation of the C&G method for calculating Kp. This method has been widely used with 166 citations based on a Google Scholar search (last accessed 28 Jan 2022).

In line with Eq. 1, a typical PBPK equation for a perfusion-limited tissue compartment (eliminating organ) is written as:

$${V}_T\frac{d{C}_T}{dt}={Q}_T\cdot {R}_b\cdot \left({C}_p-\frac{C_T}{K_p}\right)-{CL}_{u,int}\cdot {f}_{up}\cdot \frac{C_T}{K_p}$$
(34)

where CT/Kp denotes Cout under the assumption of symmetrical transport. Therefore, when the perfusion-limited model is assumed for non-eliminating (Eq. 1) and eliminating organs (Eq. 34) with PSin = PSout, a ‘PBPK-applicable’ Kp (viz., fup/fuT in this case) could be obtained from the direct measurement of CT/Cout, as attempted for propranolol and quinidine in rat liver (33). However, since measurement of Cout from general tissues is experimentally difficult, investigators mostly take advantage of using Cin (e.g., arterial concentration), which is widely used to determine Kp,ss in experimental animal species. However, if significant elimination occurs in particular tissues, Cout will be smaller than Cin, and ER determined by the organ clearance divided by blood flow (e.g., CLH/QLI) can be used for the conversion of Kp,ss to Kp. Based on perfusion-limited distribution kinetics, ER could be calculated in another way by using CLu,int and QLI, depending on the clearance models. Recently, we reviewed the usefulness of classical hepatic clearance models such as well-stirred model (WSM), parallel tube model (PTM), and dispersion model (DM) (50), which have different kinetic characteristics in terms of elimination clearance leading to the model-dependent estimates of CLu,int to achieve the same systemic exposure. These clearance models are based on the same unbound concentration between plasma and liver (e.g., Cu,LI = Cup = fupCout for WSM), which is the driving concentration of hepatic elimination. Therefore, it is worth noting that, since the total liver concentration is instantaneously equilibrated with plasma (e.g., CLI = Kp,LICout for WSM), all these models assume well-mixed kinetics with regard to drug distribution to liver (i.e., no diffusion barrier). Accordingly, the relationship of Kp = CT/Cout in traditional clearance models is useful for eliminating organs (Eq. 34) as applied for non-eliminating organs (Eq. 1), but only for compounds following perfusion-limited distribution kinetics. As noted in the previous literature (19) regarding elimination in peripheral tissues without a permeability limitation, the conversion of Kp,ss to Kp by the C&G method is based on the well-stirred and perfusion-limited distribution model (21).

However, the following conditions violate Eq. 34: First, asymmetric transport (i.e., PSin ≠ PSout). Active transport mediated by membrane transporters (17) and/or electrogenic transport driven by membrane potential (51) could lead to different unbound concentrations between plasma and tissue cells. In this case, Cup would not be adequate for describing the driving force concentration in tissue, since CuT, which would be effectively acting upon the metabolism / excretion by enzymes / transporters inside the cells, is now different from Cup. For asymmetric transport, therefore, Eq. 28 should be considered. If the use of Eq. 34 is still applicable even when asymmetric transport between plasma and tissue cells is involved with the eliminating organ, employing Cup as the driving force concentration in such conditions should be discussed and rationalized.

Secondly, a limitation in tissue permeability (i.e., fupPSin/Rb ≪ QT) necessitates the use of Eq. 8. For a non-eliminating organ, the steady-state condition leads to the relationship of Kp = Kp,ss regardless of whether fd is considered in Eq. 1 or not. For an eliminating organ, however, Eq. 8 shows that the term fd needs to be present in the mathematical relationship between Kp and Kp,ss at steady-state. Eq. 30 was derived showing that traditional conversion of Kp,ss to Kp (19) would not be valid for the case of fd ≠ 1. For imipramine, propranolol, and quinidine, the concentration ratio between liver and plasma in the hepatic vein (CLI,ss/Cout,ss) observed in the literature (33) was reported as Kp, probably based on perfusion-limited distribution kinetics. For propranolol, the model-dependent fd for liver was calculated to be 0.728 and 0.578 for Models 1 and 2, which are comparable with the ER (0.773), suggesting that PSout ≪ CLu,int (see Eq. A4 in the APPENDIX). For quinidine, fd values for liver in Models 1 and 2 were estimated as 0.981 and 0.807, also suggesting sufficient tissue permeability. However, if a significant limitation in tissue permeability is evident (i.e., fupPSin/Rb ≪ QT or fd ≪ 1), CLI,ss/Cout,ss would not represent Kp.

In addition, Eq. A4 derived for ER is consistent with the extended clearance model that factors membrane transport into the elimination kinetics (18, 52). Thus, kinetic interpretation of ER determined by (Cin − Cout)/Cin would be reasonable with Eq. A4 when membrane transport takes part in the elimination process. In terms of distribution kinetics, however, Eq. 30 shows that the traditional relationship [i.e., Kp,ss = Kp ∙ (1 − ER)] (19) is not always the case. When Eq. A2 is derived based on distribution Model 2, this traditional relationship would operate properly only when PSout ≫ CLu,int. For the case of PSout ≪ CLu,int, ER determined by using Cin and Cout from an isolated liver perfusion study would appear to be representative of, or limited by, fd (Eq. A4). Since furosemide is a substrate of organic anion transporting polypeptide 2B1 (OATP2B1) (53) and organ anion transporters (OATs) (54,55,56) and cefazolin is a substrate of OAT3 (57), the inclusions of these active uptake kinetics in PSin of Eqs. 33a and 33b for liver and/or kidney would lead to improved predictions of fd and thus the relationship ER < fd. Of note, the previous review of the extended clearance concept (18) reported the general Kp equation as fupPSin/(fuT(PSout + CLu,int)), which seems to satisfy the traditional relationship (19). However, the ‘true’ Kp that is applicable for PBPK equations should be expressed in accordance with Eq. 2, which is independent of the elimination kinetic variable, CLu,int.

Collectively, therefore, the traditional C&G method that facilitates conversion of CT/Cp from a bolus injection to the PBPK-applicable Kp appears problematic when fd ≪ 1 in terms of two aspects: fd involvements (i) from CT/Cp to Kp,ss (Eqs. 7 and 13), and (ii) from Kp,ss to Kp for eliminating organs (Eq. 30). Compared to the traditional C&G method, our extension considering fd shows considerable improvement when Kp,ss was estimated from CT/Cp particularly for furosemide (Figs. 3c and d), the compound with the lowest apparent PAMPA P coefficient (Table III). We also included the blood partitioning property (Rb) in the original C&G relationship, as expanded in Shibasaki et al. (36). Tissue concentration-time profiles were available for furosemide (28), cefazolin (29), cyclosporine (34), and quinidine (37), showing that the terminal phase slope could be different depending on tissues. When linear pharmacokinetics applies, terminal phase slopes for all biological tissue matrices should become the same (20), which is the major kinetic basis considered in the C&G method. However, if terminal phases are evidently different and a limitation in analytical methodology hinders the determination of lower concentrations sufficient to experimentally prove the parallel decline, Eqs. 31a to 31c could be useful for Kp,ss estimation.

The parameter Kp,LU denotes the lung-to-‘venous’ plasma partition coefficient, and Eq. 20 enables the theoretical estimation of Kp,LU from bolus dose studies when arterial Cp is determined instead of Cven,p, which should be the theoretically complete mixture of outflow concentrations from various tissues and would be experimentally difficult to measure. Levitt (58) provided site-dependent plasma concentration-time profiles for ethanol, thiopental, Tc-99 m-diethylene triamine pentaacetate, and ketamine, dosed in humans (e.g., blood collected from antecubital vein and artery). For these drugs, arterial concentrations were higher than venous concentrations especially in the early phase after drug administration, both of which became comparable later in time. In a poly-exponential disposition curve, the apparent slope could be expressed as βapp(t). Since βapp(t) in lung and arterial plasma (i.e., for short term infusion, an upcurve resulting from negative coefficient) would be mainly governed by steeper slopes (or larger positive eigenvalues) in the early phase after drug dosing, the application of βapp(t) in the term β of left-hand sides of Eqs. 18 and 19a would result in the early-phase discrepancy between Cven,p and Cout,LU (normalized by CLU) and between Cout,LU and Cp (normalized by Cp) where Cp ≫ Cven,p. With the passage of time, however, a more shallow slope emerging with transit times such as VLU/QLU (e.g., 0.0155 min for rat, and 1170/5600 = 0.209 min for man) and Vart/QLU (0.0639 min for rat and 1730/5600 = 0.310 min for man) (25) leads to insignificant differences between Cven,p and Cp, as observed with the 4 drugs above.

The physical meaning of Eqs. 7 and 13 for typical tissues is that an instantaneous equilibrium between CT and Cp may not be physically possible due to the presence of a distribution rate process such as QT and fupPSin, and thus CT/Cp could be significantly larger than Kp,ss (Fig. 3a). The relative error of CT/Cp for estimation of Kp,ss can be calculated by rearrangement of Eqs. 7 and 13 as:

$$\frac{C_T/{C}_p-{K}_{p, ss}}{K_{p, ss}}=\frac{V_T\beta }{Q_T{f}_d{R}_b}\cdot \frac{C_T}{C_p}$$
(35)

Therefore, the direct consideration of CT/Cp, which is frequently reported as the apparent tissue-to-plasma partition coefficient, as Kp, ss may be less problematic for the cases (i) with a sufficiently long half-life, (ii) high tissue permeability coefficient (higher fd), (iii) highly perfused organs (low VT/QT), and (iv) low CT/Cp value itself. Theoretically, steady-state Kp,ss can be determined by measurements of CT,ss and Cp,ss after infusion as well as AUCT and AUCp after a bolus injection. Thus, when early-time tissue data are not sufficient to adequately determine Kp,ss = AUCT/AUCp, our theoretical relationships would be also useful for Kp,ss estimation from even a one-time observation of CT/Cp.

Linear pharmacokinetic theories feature the same eigenvalues (or slopes) for disposition functions regardless of route of administration (e.g., oral, subcutaneous, intramuscular, etc.). However, slow absorption rates lead to addition of a late exponential phase with the slope representing the absorption rate constant ka (i.e., first-order absorption under linear kinetics). For the case of ka faster than β, Eqs. 7, 13, 20, and 27 would be still applicable. For flip-flop kinetics (ka ≪ β), post-distributive concentration profiles would decline in parallel with the slope of ka that takes the role of terminal phase slope β in the above four equations.

While the derived extensions of the C&G method proved advantageous for only 1 of 8 compounds where Kp was measured by several methods in rats, our methodology provides new insights into the role of tissue permeability in PBPK models and has the potential to be relevant to numerous additional drugs. For example, most of the compounds (22 out of 24) administered to rats assessed in Jeong et al. (22) are expected to have permeability-limited distribution kinetics whose contribution appears in the plasma concentration profiles (i.e., fupPSin < 1.0 × 10−6 cm/s). When Benet (59) examined 698 drugs on the market and 28,912 new molecular entities (NMEs), 27% of the marketed drugs and 28% of NMEs fall into the BDDCS low-permeability categories 3 and 4. Since the contribution of active transport mechanisms to the overall permeability across the biological membranes of tissues could become dominant for such low permeability compounds (60), caution is needed in assuming perfusion-limited distribution and trusting in silico methods of estimating Kp values for such cases when performing top-down PBPK modeling.

The current approach and applications extending the C&G method have some limitations. Firstly, only 8 compounds were assessed owing to the few drugs studied where tissue distribution data were available from both steady-state infusions and single-dose bolus studies in rats. Non-linear pharmacokinetics could result in potential discrepancies. From the literature (37), nonlinear binding of quinidine in rat blood was observed, and fup and Rb (Table III) reflect a saturable plasma concentration at 6 μg/mL with an fupP/Rb value of 1.01 × 10−6 cm/s. However, a lower plasma concentration (0.455 μg/mL) of quinidine with different values of fup (0.25) and Rb (1.1) had a fupP/Rb value of 0.955 × 10−6 cm/s. More dramatic differences in fup depending on the concentration were observed for furosemide from 0.00716 to 0.0224 (10 to 250 μg/mL) (28), which could be variable up to 0.13 (at 10 μg/mL) (41). If a concentration decay leads to fupP/Rb changing from above to below the threshold condition of fupP/Rb = 1 × 10−6 cm/s proposed for perfusion-limited distribution kinetics (22), the whole-body PBPK model structure should be able to operate with the perfusion-limited kinetics in the initial phase with higher concentrations, followed by permeability-limited kinetics in the later phase with lower concentrations. Nevertheless, the consideration of a potentially saturable fup for furosemide was useful for reasonable correction of CT/Cp to Kp,ss (Figs. 3c and d). Kitani et al. (28) showed furosemide concentrations in gut (CGU) that were consistently around 100 μg/mL when plotted against free concentrations in plasma (Cup) from 0.1 to 10 μg/mL, suggesting a possibility of saturated binding properties in the Cup range ([nP] ≪Cup). However, this interpretation would need further refinement since instantaneous equilibrium between Cup and CuT may not be achieved for furosemide due to its low permeability. For methotrexate, non-linear distribution to liver, kidney, and bone marrow of rats was evident with increased CT/Cp over time (61). Quinidine was suggested to be distributed into rat liver in a concentration-dependent manner, resulting in a liver-specific βLI (37). When non-linear kinetics is evident, however, the application of βLI in Eq. 31c may be problematic. For quinidine, Eq. 31c was not sufficient for more reliable estimation of Kp,ss compared to the C&G method since the perfusion-limited liver model would be applicable based on fd values close to 1 (e.g., 0.981 and 0.807 for Models 1 and 2).

In line with this, the majority of the data points with CT/Cp values larger than Kp,ss found in Fig. 3a supports the contribution of an equilibrium process between plasma and tissues after bolus dosing, while many of the points remain under the unity line in Figs. 3c and d even with our consideration of fd in the C&G method. When the plasma (blood for dexamethasone and cyclosporine) concentrations (μg/mL) measured for the calculations of CT/Cp and Kp,ss are collected for furosemide (11.7 and 111), cefazolin (84.5 and 77.5), methotrexate (3.11 and 11.1), etoposide (1.3 and 15.9), dexamethasone (0.00145 and 0.355), cyclosporine (0.2 and 0.49/2.7), propranolol (0.501 and 0.830), and quinidine (0.763 and 0.843), the values from bolus studies are smaller than, or comparable, with steady-state values. If non-linear kinetics are involved with tissue binding and/or uptake processes (e.g., driven by plasma concentration), then lower plasma concentrations after bolus injections may lead to CT/Cp-derived estimates that are generally higher than Kp,ss. In addition, the tlast for determining CT/Cp would need to be long enough to ensure the parallel decline between plasma and tissues. In rats, the terminal phase half-life of etoposide at tlast = 1 h was 20 min (31) whereas the half-life at tlast = 8 h was 110 min (62). Thus, determination of CT/Cp for etoposide at a later phase would reflect more complete achievement of equilibrium between plasma and tissues. For compounds having time-dependent (rather than rapid) distribution into red blood cells as shown for tacrolimus (63) and metformin (64), it would be necessary to use the equilibrated Rb value in Eqs. 7, 13, 20, and 27 derived in this study.

Conclusions

Over time, many complexities have been encountered in pharmacokinetics and application of PBPK models. These include the involvement of plasma and tissue drug binding, red blood cell distribution, permeability-limited tissue uptake, transporters, alternative organ models, and others (50). Since determinations of tissue concentrations at different times are labor-intensive and time-consuming when assessing many different tissues, the C&G method was derived to enhance the practical utility of a one-time measurement of CT/Cp in the terminal phase. However, it is evident that the perfusion-limited distribution is not always the case in PBPK models (22) and thus this report primarily addresses our extension of the C&G method for the extent of tissue distribution (e.g., CT/Cp and Kp,ss) that are theoretically associated with the distribution rates (e.g., QT and fupPSin). We herein included the fractional distribution parameter fd, which readily enables considerations of membrane permeability limitations in the rate of tissue distribution, into the traditional C&G concept. The theoretical relationship between CT/Cp and Kp,ss was derived for typical non-eliminating (Eq. 3), eliminating tissues (Eq. 4), lung (Eq. 20), and liver (Eq. 27). When different terminal slopes are obtained, a tissue-specific βT can be applied based on a linear kinetic assumption. We demonstrated the theoretical conversion of CT/Cp to Kp,ss measured for 8 compounds with a wide range of apparent PAMPA P coefficients. For conversion of Kp,ss to the PBPK-applicable Kp for eliminating organs, we showed that the traditional correction method utilizing ER would not be valid when fd ≪ 1. When more realistic fd values are considered along with the inclusions of a passive component of tissue permeability, the current extension of the C&G method should increase the utility of interpreting tissue-plasma concentration ratios in PBPK. Lastly, while the use of 8 compounds represents a limited database, it is noteworthy that none of the four in silico methods performed well with a considerable spread of Kp ratios among the up to 11 tissue types. It should be kept in mind that published graphs showing concordance of calculated versus measured Kp values feature data from diverse drugs and tissues in log-log plots where discrepancies are obscured by such a wide scaling of data. Predictability should be considered as only approximate with limited confirmation possible by calculation of in vivo VSS values.