1 Introduction

Localized optical structures in nonlinear media such as surface and guided waves, and solitons are studied extensively (Malomed and Mihalache 2019; Mihalache 2021). The interest in such research is due to their wide technical applications, including nonlinear fiber optics (Agrawal 2008, 2019; Kaminow et al. 2013) and photonics (Knight et al. 1999; Poli et al. 2007; Novoa and Joly 2021; Khusyainov et al. 2020).

The properties of nonlinear waves are determined by the optical response of nonlinear medium, which can be significantly nonlocal (Dong and Wang 2006). In particular, soliton self-bending during its propagation in a medium with nonlocal nonlinearity is described (Kartashov et al. 2004).

Nonlocal nonlinear systems are studied theoretically based on the nonlinear Schrödinger equation in recent years (Gürses and Pekcan 2018; Darti et al. 2012). Oscillatory responses are used to describe the unique features of nonlocal nonlinear systems (Liang et al. 2020; Liang 2022). Nonlinear media with nonlocal nonlinearity can demonstrate optical instability (Tabi et al. 2022). Exact solutions corresponding to optical solitons in dispersive medium with nonlocal nonlinearity are found (Arnous et al. 2022). Problems of finding exact solutions to the wave equations with nonlocal nonlinearities remain relevant (Kudryashov 1991, 2021, 2022).

Note that metal-coated optical fibers and waveguides are widely used in various technical applications (Albert et al. 2018), including chemical and biochemical sensing technologies (Spackova et al. 2016; Savkare 2023; Shen et al. 2023). Also, in modern industry, many types of single-mode and multimode fibers with a heat-resistant coating made of aluminum or copper alloy are produced. A thin layer of metal provides mechanical strength and eliminates out-gassing, while simultaneously increasing the temperature range and thermal conductivity of the fiber. Fibers coated with a heat-resistant metal material can withstand temperatures up to 600 °C or higher, depending on heating conditions and atmospheric composition (Cherpak et al. 2020). For example, single-mode fibers with copper and aluminum coating for the near-infrared range have an operating wavelength ranges depending on the type of fiber: 450–600 nm, 800–600 nm, 800–1000 nm, 1300–1600 nm; attenuation at 800/1300 nm depending on the type of fiber is: 14 dB/km, 12 dB/km, 10.5 dB/km, 9.5 dB/km, 4.0 dB/km 1.5 dB/km; the coating thickness is about 10–15 μm with a single-mode fiber radius of about 100 μm. Therefore, the study of the waveguide properties of metal-coated waveguides with the nonlocal nonlinearity is important for developing technical applications of photonics, optoelectronics, physicochemical and bio-technologies.

In this paper, we derive the dispersion equation of the wave propagating in a metal-film covered waveguide using an exact solution to stationary self-consistent wave equation with a weak nonlocal nonlinear response. We generalize the procedure of finding the dispersion equation and eigenmodes, which was presented for one dimension slab waveguide in Smirnov et al. (2022), in the case of 3D model. In particular, we find the propagation constant and eigenmodes via explicit equations in the case of circular fiber covered by a metal film.

The obtained results expand theoretical studies of optical nonlinear fibers (Horak and Poletti 2012; Zhang and Lu 2021; Krupa et al. 2019), including graded-index multimode fibers (Mafi 2012; Renninger and Wise 2013; Ahsan and Agrawal 2018). Despite of the dispersion and propagation properties of circular cylindrical optical fibers are described well (Morishita 1983; Yeh 1987; Shu and Bass 2007), we describe the new features of the light distribution in a fiber cross section induced by a weak nonlocal nonlinear response. In particular, the explicit dependence of the fiber radius on the nonlinearity coefficient, for which the mode of the certain order can be excited, is obtained analytically.

2 Governing equations

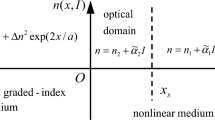
Let the nonlinear medium occupies region D limited by the surface Г in the transverse direction (xy cross-sectional plan) and unlimited in the longitudinal direction (z direction) (see the schematic sketch of the waveguide with an arbitrary cross-section in Fig. 1). We describe the light propagation in a nonmagnetic lossless medium with weak nonlocal nonlinear response in the region D. We neglect the anisotropic properties of the medium basing on the paraxial approximation. The light propagation is described along the z axis in the waveguide region with inhomogeneous dielectric function in a transversal direction and a nonlocal contribution to nonlinear response.

Fig. 1
figure 1

Schematic sketch of the waveguide with an arbitrary cross-section at xy plane where the nonlinear medium occupies the region D bounded by surface Γ along the longitudinal direction z

Full size image

We present the transverse component of the electric field as:\(E({\mathbf{r}}_{ \bot } ,z) = \psi ({\mathbf{r}}_{ \bot } )\exp (i\beta z)\) where \(\psi ({\mathbf{r}}_{ \bot } )\) is the spatial transverse distribution of the wave propagating along z direction as, r⊥ is the transverse coordinate vector (in particular, r⊥ = (x, y) in Cartesian coordinates and r⊥ = (r, φ) in polar coordinates), z is the longitudinal propagation coordinate. The spatial transverse distribution obeys the nonlinear wave equation

$$\Delta_{ \bot } \psi + (\varepsilon (\left| \psi \right|^{2} )k_{0}^{2} - \beta^{2} )\psi = 0$$
(1)

where \(\Delta_{ \bot }\) is the Laplace operator in transverse coordinates r⊥ (note that the Laplace operator can be presented as \(\Delta = \Delta_{ \bot } + \frac{{\partial^{2} }}{{\partial z^{2} }}\), in particular, \(\Delta_{ \bot } = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}\) in Cartesian coordinates), \(\varepsilon (\left| \psi \right|^{2} )\) is the dielectric permittivity of the nonlinear medium, β is the propagation constant, k0 = ω/c is the wave number, ω is the wave frequency, c is the speed of light (Adams 1981; Chen 2005).

We assume that the dielectric permittivity of the nonlinear medium can be written as ε = ε0 + δε, where ε0 is the unperturbed dielectric constant, \(\delta \varepsilon = \delta \varepsilon (\left| \psi \right|^{2} )\) is the small nonlinear addition. In the case of nonlocal nonlinearity, the nonlinear addition can be written as (Darti et al. 2012)

$$\delta \varepsilon (\left| \psi \right|^{2} ) = \int\limits_{D} {R({\mathbf{r}}_{ \bot } - {\mathbf{r}}_{ \bot }^{\prime } )\left| {\psi ({\mathbf{r}}_{ \bot }^{\prime } )} \right|^{2} d{\mathbf{r}}_{ \bot }^{\prime } }$$
(2)

where R is the function described the nonlocal nonlinear response in D region of the transverse space of coordinates r⊥.

In the case of a local Kerr nonlinear response, we can replace \(R({\mathbf{r}}_{ \bot } - {\mathbf{r}}_{ \bot }^{\prime } )\) with the Dirac delta function \(\alpha \delta ({\mathbf{r}}_{ \bot } - {\mathbf{r}}_{ \bot }^{\prime } )\) where α is the nonlinearity coefficient. Then \(\delta \varepsilon (\left| \psi \right|^{2} ) = \alpha \left| {\psi ({\mathbf{r}}_{ \bot }^{\prime } )} \right|^{2}\) and Eq. (1) transforms into the well known stationary nonlinear Schrodinger equation.

In the case of a weak local approximation, the Kerr-like nonlinear response can be presented as \(R({\mathbf{r}}_{ \bot } - {\mathbf{r}}_{ \bot }^{\prime } ) = \alpha /S_{0}\), where S0 is an area of D region (sse Fig. 1). Therefore, the nonlinear addition (2) transforms into

$$\delta \varepsilon (\left| \psi \right|^{2} ) = \frac{\alpha }{{S_{0} }}\int\limits_{D} {\left| {\psi ({\mathbf{r}}_{ \bot }^{\prime } )} \right|^{2} d{\mathbf{r}}_{ \bot }^{\prime } }$$
(3)

The average of the field intensity is given by

$$\overline{I} = \overline{{\left| \psi \right|^{2} }} = \frac{1}{{S_{0} }}\int\limits_{D} {\left| {\psi ({\mathbf{r}}_{ \bot }^{\prime } )} \right|^{2} d{\mathbf{r}}_{ \bot }^{\prime } }$$
(4)

Therefore, the nonlinear dielectric permittivity can be written as

$$\varepsilon (\left| \psi \right|^{2} ) = \varepsilon_{0} + \alpha \overline{{\left| \psi \right|^{2} }}$$
(5)

The dielectric permittivity given by Eq. (5) corresponds to the modified Kerr weak nonlocal nonlinearity. The positive value of α corresponds to a self-focusing nonlinearity, and the negative value of α corresponds to a defocusing one. In the case of a plane shielded waveguide the problem of a TE-wave propagation with a similar one-dimension analog of Eq. (5) is investigated in Albert et al. (2018).

Wave Eq. (1) with substitution of Eq. (5) transforms into

$$\Delta_{ \bot } \psi + (\varepsilon_{0} k_{0}^{2} - \beta^{2} )\psi + \tilde{\alpha }\overline{{\left| \psi \right|^{2} }} \psi = 0$$
(6)

where \(\tilde{\alpha } = \alpha k_{0}^{2}\).

Equation (6) can be also considered as the stationary Schrodinger equation with self-consistent potential, which is interpreted as the charge localized in the quantum well occupying region D in the case of a one-particle state (Presilla et al. 1991).

3 Metal-film coated waveguide

We consider a waveguide coated with a thin metal with a nonlinear optical core, the radius of which is much greater than the thickness of the coating (see an arbitrary cross-section of the waveguide in Fig. 2). The use of metallic fiber coating is related to its properties. When light passes through the fiber core, it induces very weak currents at the surface of the metal, which drain power from the waveguide. In special fibers with a larger cladding, the metal is further away from the core and the attenuation is much lower.

Fig. 2
figure 2

The arbitrary cross-section of the metal coated waveguide where n is the normal vector to the waveguide boundary Γ

Full size image

The metal coating is typically quite thin compared to the radius of the fiber. For example, the authors of Song et al. (2011) studied waveguide modes in a fiber with a silica core of radius of 0.55 μm, coated with a silver film of 0.05 μm thickness. Therefore, we will assume that the coating thickness is negligibly small compared to the characteristic transverse size of the waveguide.

We write the transverse field distribution as \(\psi ({\mathbf{r}}_{ \bot } ) = U_{0} F(g(q,{\mathbf{r}}_{ \bot } ))\), where U0 is the unknown constant, the function F solves the equation

$$F^{\prime\prime}\nabla_{ \bot } g + F^{\prime}\Delta_{ \bot } g + q^{2} F = 0$$
(7)

where, \(q^{2} = \varepsilon_{0} k_{0}^{2} - \beta^{2} + \tilde{\alpha }U_{0}^{2} \overline{{\left| F \right|^{2} }}\) and the function \(g = g(q,{\mathbf{r}}_{ \bot } )\) relates the coefficients of the Eq. (6) and the transverse coordinates r⊥. It is assumed that the function F is limited anywhere in the waveguide region D, in particular, at the origin O.

We assume that the waveguide region D is covered by a thin metal film. In this case, the field at the boundary between region D and metal film cladding turns to zero and we get the boundary condition

$$\left. \psi \right|_{\Gamma } = 0$$
(8)

where Γ is the boundary of the waveguide region D. We write the second boundary condition using the normal derivative as (see Fig. 2)

$$\left. {\frac{\partial \psi }{{\partial n}}} \right|_{\Gamma } = V$$
(9)

where V is known constant.

Therefore, the function F satisfies the boundary conditions

$$\left. {F(g(q,{\mathbf{r}}_{ \bot } ))} \right|_{\Gamma } = 0$$
(10)
$$U_{0} F^{\prime}\left. {\frac{\partial g}{{\partial n}}} \right|_{\Gamma } = V$$
(11)

From Eq. (10) we obtain

$$\left. {g(q,{\mathbf{r}}_{ \bot } )} \right|_{\Gamma } = \xi$$
(12)

where ξ is the zero of the function F (here we suppose that there is at least one root of the equation F(ξ) = 0).

From Eq. (11) we can find the amplitude

$$U_{0} = V\left( {F^{\prime}\left. {\frac{\partial g}{{\partial n}}} \right|_{\Gamma } } \right)^{ - 1}$$
(13)

Using Eq. (13) we obtain

$$q^{2} = \varepsilon_{0} k_{0}^{2} - \beta^{2} + \tilde{\alpha }V_{{}}^{2} \overline{{\left| F \right|^{2} }} \left( {F^{\prime}\left. {\frac{\partial g}{{\partial n}}} \right|_{\Gamma } } \right)^{ - 2}$$

Thus, we derive Eq. (12) relating the propagation constant, waveguide system parameters, and zero of the function F, which can be considered as a dispersion equation of the metal-film covered waveguide with the modified Kerr weak nonlocal nonlinearity. By solving Eq. (12) with known functions F and g in the case of the specified boundary of the waveguide region, one can obtain the propagation constant as a function of the waveguide system parameters.

4 Metal-film coated circular fiber

Let us consider, for example, the circular fiber of R radius covered by thin metal-film with s small thickness h (see cross-section of the circular fiber in Fig. 3). We assume that h <  < R. The r⊥ = (r, φ), where r and φ are the polar coordinates, in the case considered. The Laplace operator in the polar coordinates is \(\Delta_{ \bot } = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial }{\partial r}} \right) + \frac{1}{{r^{2} }}\frac{{\partial^{2} }}{{\partial \phi^{2} }}\). Therefore Eq. (6) after substitution of the transverse distribution \(\psi (r,\phi ,z) = u(r)\exp (im\phi )\), m = 0, ± 1,… transforms into:

$$\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{{\partial r}} + \left( {\varepsilon_{0} k_{0}^{2} - \beta^{2} + \tilde{\alpha }\overline{{\left| u \right|^{2} }} - \frac{{m^{2} }}{{r^{2} }}} \right)u = 0$$
(14)
Fig. 3
figure 3

The cross-section of the circular metal coated fiber of radius R and the metal-film thickness of h (h <  < R)

Full size image

The boundary conditions (8) and (9) transforms into.

$$u(R) = 0$$
(15)
$$u^{\prime } (R) = V$$
(16)

Exact solution to Eq. (14) limited at 0 < r < R is given by

$$u(r) = U_{0} J_{m} (qr{)}$$
(17)

where Jm(x) is the Bessel function of the first kind, and

$$q^{2} = \varepsilon_{0} k_{0}^{2} - \beta^{2} + \tilde{\alpha }U_{0}^{2} \overline{I}$$
(18)

From the boundary condition (15) it follows the equation: \(J_{m} (qR{)} = {0}\), therefore,

$$qR = \xi_{mj}$$
(19)

where ξmj are the zeros with number j of the Bessel function of m order: Jm(ξmj) = 0.

We find the amplitude from the boundary condition (16) using Eq. (19) as

$$U_{0} = V/J^{\prime}_{m} (\xi_{mj} {)}$$
(20)

We calculate the average of the field intensity (4) using Eq. (19) in case considered as

$$\overline{I} = \frac{1}{{\pi R^{2} }}2\pi \int\limits_{0}^{R} {J_{m}^{2} (qr)rdr} = \frac{2}{{\xi_{mj}^{2} }}\int\limits_{0}^{{\xi_{mj} }} {J_{m}^{2} (z)zdz} = (J^{\prime}_{m} (\xi_{mj}^{{}} ))^{2}$$
(21)

Therefore, we obtain the discrete spectrum of the propagation constant combining Eqs. (18)–(20):

$$\beta_{mj}^{2} = k_{0}^{2} (\varepsilon_{0} + \alpha V^{2} ) - \left( {\frac{{\xi_{mj}^{{}} }}{R}} \right)^{2}$$
(22)

where m is the mode order, j is number of zero of the Bessel function of m order.

We plot the dependencies of the propagation constant defined by Eq. (22) on the nonlinearity parameter αV2 in Fig. 4. Figures 4a, b, and c demonstrate the functions βmj = βmj(αV2) for modes of orders m = 0, m = 1, and m = 2 respectively for five numbers of zero of the Bessel function j = 1, 2, 3, 4, 5. The propagation constant for each mode increases monotonically with an increase in absolute value of the nonlinearity coefficient.

Fig. 4
figure 4

Dependencies of the propagation constant defined by Eq. (22) on the nonlinearity parameter αV.2 for modes of orders m = 0 (a), m = 1 (b), and m = 2 (c) respectively for different numbers of zero of the Bessel function j, and for number j = 3 (d) of zero of the Bessel function and different mode orders m with k = 1, ε0 = 1, R = 10 (in dimensionless conventional units)

Full size image

We find that a mode of the corresponding order m can be excited for values of j starting from a certain number at values of the nonlinearity parameter αV2 exceeding the minimum value.

Figure 4d demonstrates for example the functions βmj = βmj(αV2) for the number of zero of the Bessel function j = 3 and three modes of orders m = 0, m = 1, and m = 2. We obtain that the value of the propagation constant increases with an increase in the mode order m at the fixed number of zero of the Bessel function j and the nonlinearity coefficient.

Thus, we find that the spectrum of modes of the metal-film coated circular fiber with the modified Kerr weak nonlocal nonlinearity is linearly shifted by a value proportional to the coefficient of nonlinearity. A similar result was obtained in the case of a planar waveguide (Kudryashov 2022).

The modes of the metal-film coated circular fiber can be obtained combining Eqs. (17), (19) and (20) as

$$u_{mj} (r) = V\frac{{J_{m} (\xi_{mj} r/R{)}}}{{J_{m}^{\prime } (\xi_{mj} )}}$$
(23)

We plot the radial distributions of the intensity \(I_{mj} = (u_{mj} (r)/V)^{2}\) of modes of different orders and numbers of zero of the Bessel function inside the fiber in Figs. 5 and 6. Figures 5a, b, and c demonstrate the radial distributions of the intensity for modes of orders m = 0, m = 1, and m = 2 respectively for numbers of zero of the Bessel function j = 1, 2, 3, 4. The intensity of the main peak increases with the increasing zero number of the Bessel function j.

Fig. 5
figure 5

Radial distributions of the intensity for modes of orders m = 0 (a), m = 1 (b), and m = 2 (c) for different numbers of zero of the Bessel function j with the values of parameters as in Fig. 4

Full size image
Fig. 6
figure 6

Radial distributions of the intensity for number of zero of the Bessel function j = 1 (a), j = 2 (b), and j = 3 (c) and different mode orders m with the values of parameters as in Fig. 4

Full size image

Figures 6a, b, and c demonstrate the radial distributions of the intensity for number of zero of the Bessel function j = 1, 2, 3 and three modes of orders m = 0, m = 1, and m = 2 respectively. The intensity of the main peak decreases with an increase in the mode order m at the fixed value of zero number of the Bessel function j.

Each mode of order m corresponds to a set of j values of the propagation constant, which are generated by the zeros of the Bessel functions ξmj. The number of such modes is limited by the requirement that one should choose only those zeros of the Bessel function for a fixed fiber radius, for which \(\xi_{mj}^{2} < R^{2} k_{0}^{2} (\varepsilon_{0} + \alpha V^{2} )\).

On the other hand, the mode of the fixed order m and number of j can be excited in the fiber with radius, for which \(R^{2} > \xi_{mj}^{2} /k_{0}^{2} (\varepsilon_{0} + \alpha V^{2} )\). Therefore, there is a minimum fiber radius \(R_{\min } = \xi_{mj}^{{}} /k_{0}^{{}} (\varepsilon_{0} + \alpha V^{2} )^{1/2}\), in which a mode of the fixed order m and number of j can be excited. We derive that the presence of a self-focusing nonlinear response makes it possible to reduce the minimum allowable fiber radius Rmin. A defocusing nonlinear response adduces to an increase in the minimum allowable fiber radius Rmin. However, the admissible defocusing nonlinear response must be such that: \(\left| \alpha \right| < \varepsilon_{0} /V^{2}\).

Thus, one can control a localization diameter of a light beam by using nonlinearity coefficient. From a technical point of view, this means that the fiber diameter can be adjusted to optimize the waveguide characteristics.

5 Conclusions

We described the features of light propagation in a nonmagnetic lossless medium with weak nonlocal nonlinear response. We proposed the function of nonlinear response in a weak nonlocal approximation included in the dielectric permittivity. We formulated the stationary self-consistent wave equation in the term of the average of the field intensity. We derived that the wave equation describing the light propagation in such a medium is actually a stationary nonlinear Schrodinger equation with a self-consistent potential, which plays the role of the charge localized in the quantum well in the case of a one-particle state.

We indicated a procedure that allows us to find the spectrum of stationary states of such an equation in relation to the metal-film covered waveguide. We obtained the dispersion equation determining the propagation constant as a function of the waveguide system parameters in general form of the waveguide region.

We applied the proposed theory to calculate the eigenmode spectrum of metal-film covered circular fiber. We found the exact solution to the self-consistent wave equation describing the radial symmetric distribution of the electric field in a fiber cross section. We obtained the explicit equation determining the discrete spectrum of the propagation constant. We showed that each mode of order m corresponds to a set of j values of the propagation constant, which are generated by the zeros of the Bessel functions. The fiber diameter can be adjusted to optimize the waveguide characteristics by using nonlinearity coefficient.

Obtained results may be useful for improvement of light propagation properties of the nonlinear optical fibers and supplement the nonlinear and waveguide optics and applications.