1 Introduction

Solitons can be used for long-distance optical communication links in communication applications. Many nonlinear physical systems exist in the physical world and can be described by different nonlinear systems (Tang 2022; Muniyappan et al. 2021a; Palacios and Fernández-Diaz 2001; Tantawy and Abdel-Gawad 2020). Soliton solutions are typically the endpoint of the analytical analysis of the nonlinear Schrödinger equation (NLSE), which is one such equation model with a high degree of universality in nonlinear science (Muniyappan et al. 2022c; Cao and Dai 2021). Soliton in optical fibers is formed by the balance of self-phase modulation and dispersion caused by group velocity. Optical solitons have not only been predicted theoretically (Rao et al. 2020; Butcher and Cotter 1990; Kivshar and Agrawal 2003; Muniyappan et al. 2022a), but they have also been observed experimentally (Hasegawa and Kodama 1995; Cundiff et al. 2002). Solitons have been proposed for use in a variety of applications, including optical pulse compression, all optical switching, logic devices, and so on. The non-linear Schrödinger equation describes low-loss soliton transmission in optical fibers. In general, brigh and dark solitons are present in the optical fibers, but kink and antikink soliton is another type of soliton that can exist mathematically. Kink/antikink solitons can be found in many areas of physics, but their prevalence in nonlinear optics is gradually increasing nowadays (Seadawy et al. 2022; Yu et al. 2022; Qin Zhou and Zhong 2022; Rizvi et al. 2023a; Al-Kalbani et al. 2023; Yue et al. 2020; Seadawy et al. 2023). The probable existence of kink/antikink solitons in optical fibers has come to the attention of the researchers at this time. SRS, or stimulated Raman scattering, is a process that gives rise to kink/antikink solitons. A generalized nonlinear Schrödinger equation governs wave transmission in optical fibers with the addition of SRS. It would be quite interesting to observe such kink/antikink solitons experimentally. The kink soliton mode is a sharply turning, many-decaying oscillation tails, semi-local nonlinear mode (Huang et al. 2011). Kink solitons produce self-steepness or nonlinear effects in nonlinear fibers, so the wavefront shape influences the high-intensity short-pulse properties. Kink solitons can be employed as optical logic components or as polarization switches between two domains in real-world applications (Huang et al. 2012; Yu et al. 2022). Solitons are subjected to stimulated Raman scattering as well as Kerr nonlinearity when propagating in an optical fiber. The optical spectrum gets so broad for very short solitons (like 100 fs) that Raman amplification can occur in the longer-wavelength tail at the expense of power in the shorter-wavelength tail. This causes a soliton self-frequency shift, or an overall spectral shift of the soliton towards longer wavelengths (Soloman Raju et al. 2005; Voronin and Zheltikov 2008; Saini et al. 2015).

In this study, we investigate the complex dynamics of the GNLSE model using a methodical approach based on the extended rational sinh–cosh method to construct the shape-changing property of solitons from kink to antikink, dark to bright solitons, or vice versa, and from linear stability analysis, we analyze the stability and instability nature of the optical soliton. Our research is based on four physical coefficients: intermodal dispersion (IMD), third-order dispersion (TOD), self-frequency shift (SFS), and the self-steepening (SS) effect. Each of these coefficients, when combined with stability analysis, reveals the nature of the optical pulses’ characteristics in an optical fiber. It is significant to note that the IMD, TOD, SFS, and SS coefficients play an indispensable part in the change of amplitude and altering of forms of \(|u(x,t)|^2\). Our research gives a thorough understanding of the dynamics and profiles of dark, bright, kink, and antikink solitons within this complex optical system. These discoveries have a great deal of promise for experimentalists studying the nonlinear pulse propagation phenomenon in optical fiber. Due to several unique characteristics of ultrashort pulses during their propagation in the medium, several additional phenomena, including dispersion effects and nonlinear effects of higher orders, have been discovered in comparison to the propagation process of short pulses (in fs). This manuscript is organized as follows: Sec. II will present the method’s foundation and derive a general equation for the pulse propagation process in a nonlinear dispersion medium with all orders of dispersion and nonlinearity from these considerations. In Sect. 3, we will thoroughly interpret the effects of intermodal dispersion, third-order dispersion, self-frequency shift, and self-steepening on ultrashort pulses. We present the linear stability analysis in Sect. 4. The conclusion is reported in Sect. 5.

2 Mathematical model and its background

The nonlinear Schrödinger (GNLS) equation, which explains the intensification or soaking up of pulses traveling in a monomode optical fiber with distribution nonlinearity and dispersion, is crucial to communication through an optical fiber (Nasreen et al. 2023a; Seadawy et al. 2020; Houwe et al. 2022). The concept holds significant value in real-world scenarios, particularly for the reliable transmission of soliton control as well as the enhancement and contraction of optical solitons in non-uniform systems. The nonlinear Schrödinger (NLS) equation constitutes one of the approaches in nonlinear science since it represents a perfectly integrable system and has wide applications in almost all branches of the physical sciences, which include optical fibers (Choudhuri and Porsezian 2012), magnetic systems (Gerasimchuk et al. 2016), Bose-Einstein condensates (Biasi et al. 2023), Josephson junctions (Goodman et al. 2015), and so on. In order to study the effects of higher-order dispersion, intermodal dispersion, and self-steepening effects on the propagation dynamics, we employ a generalized scalar nonlinear Schrödinger equation (GNLSE) to model the pulse propagation inside the fiber (Cao Long 2010).

$$\begin{aligned} iu_x +i\alpha _1 u_t - \left[ \frac{\alpha _2}{2}\right] u_{tt} - i\left[ \frac{\alpha _3}{6}\right] u_{ttt} +|u|^2u + i\left[ \frac{\beta }{\omega _0}\right] (|u|^2u)_t + T_R (|u|^2)_t u = 0, \end{aligned}$$
(1)

where \(\alpha _1\) is an intermodal dispersion, \(\alpha _2\) is a group velocity dispersion, \(\alpha _3\) is a third-order dispersion, \(\omega _0\) is a wave frequency, \(\beta\) is a self- steepening and \(T_R\) is a self-frequency shift. Compared to the nonlinear Schrödinger equation that describes the propagation of short pulses (Boyd 2003; Van et al. 2003), the dynamical equation for ultrashort pulses (1) has more complex terms that are higher order dispersive and nonlinear. We choose the following traveling wave solution in the following form:

$$\begin{aligned} u(x,t)=u(\xi )\,exp{\left[ i(kx-\omega t)\right] },\,\,\,\,\xi =t-\chi x, \,\,\,\chi =1/v, \end{aligned}$$
(2)

where v, \(\omega\) & k, indicate the velocity, angular frequency, and wavevector of the traveling wave solutions, respectively. Equation (2) is substituted into Eq. (1) to produce the following ordinary differential equation (ODE), which includes real and imaginary parts:

$$\begin{aligned} u''(\xi ) + D_1 u(\xi ) - D_2 u^3(\xi ) -D_3 u^2(\xi ) u'(\xi ) + i \left[ u'''(\xi ) - E_1 u'(\xi ) + E_2u^2(\xi ) u'(\xi ) \right] = 0, \end{aligned}$$
(3)

where \(D_1=\left[ k-\alpha _1\omega -\frac{\alpha _2\omega ^2}{2}-\frac{\alpha _3\omega ^3}{6}\right] ,\,\,D_2=\left[ \frac{\beta \omega }{\omega _0\left( \frac{\alpha _2}{2}+\frac{\alpha _3\omega }{3}\right) }\right] ,\,\,D_3=\left[ \frac{2T_R}{\frac{\alpha _2}{2}+\frac{\alpha _3\omega }{3}}\right]\)

\(E_1=\left[ \frac{6\left( \alpha _1+\alpha _2\omega +\frac{\alpha _3\omega ^2}{2}-\frac{1}{v}\right) }{\alpha _3}\right]\), and \(E_2=\left[ \frac{18\beta }{\alpha _3 \omega _0}\right]\). The dynamics of the soliton in the optical fiber communication system are governed by Eq. (3). Our goal is to ascertain the shape property of the solitonic pulses that are traveling through the optical fiber while being influenced by the extended rational sinh–cosh approach, which is covered in the subsection that follows.

2.1 Exact solution for generalized NLS equation

Nonlinear physical phenomena research frequently investigates soliton solutions for nonlinear equations. Magnetic systems, optical systems, biological systems, condensed matter physics, plasma, and other technical and scientific disciplines all exhibit nonlinear wave phenomena. Numerous problems have been solved using a variety of mathematical techniques, including Hirota’s method (Wazwaz 2021; Sheppard and Kivshar 1997), modified extended tangent hyperbolic function method (Muniyappan et al. 2021b, 2022b), extended simple equation method (Dianchen et al. 2017), Backlund transformation (Zhao and He 2020), sine-cosine function method (Muniyappan et al. 2021c), complex envelope ansatz solution (Rizvi et al. 2023b), Jacobi elliptical function method (Song and Wang 2010; Soloman Raju and Panigrahi 2011), extended and modified rational expansion method (Nasreen et al. 2023b), new extended direct algebraic method (Nasreen et al. 2023c, d), Hirota bilinear method (Ismael et al. 2023), Riccati equation mapping method (Nasreen et al. 2024), new generalized extended direct algebraic method (Abbagari et al. 2021a), and new modified Sardar sub-equation technique (Abbagari et al. 2021b). In general, analytical solutions to nonlinear partial differential equations are presented below.

$$\begin{aligned} F\left( u, \frac{\partial u}{\partial t}, \frac{\partial u}{\partial x}, \frac{\partial ^2 u}{\partial x}, \frac{\partial ^2 u}{\partial x^2}\right) = 0, \end{aligned}$$

new extended rational strategies are provided. The function \(q = q(x, t)\) is unknown in this case, and the variable F is a polynomial in q and all of its partial derivatives. The formal approach is proposed in the extended rational sinh–cosh approach (Muniyappan et al. 2021d).

$$\begin{aligned} u(\xi )=\frac{a_0 sinh(\mu \xi )}{a_2+a_1cosh(\mu \xi )}, \,cosh(\mu \xi ) \ne -\frac{a_2}{a_1}, \end{aligned}$$
(4a)

where the values that need to be determined in relation to the other factors are \(a_0,\,a_1\), and \(a_2\). Utilizing the nonzero constant \(\mu\) as the wave number, substituting Eq. (4a) into Eq. (3), we may get the real and imaginary parts as follows:

$$\begin{aligned}{} & {} -\mu ^2a_2^3+\mu ^2a_2a_1^2cosh(\mu \xi )^2+2\mu ^2a_2a_1^2+2\mu ^2a_1^3cosh(\mu \xi )-D_1a_2^3-3D_1a_2^2a_1cosh(\mu \xi ) \nonumber \\{} & {} \quad -3D_1a_2a_1^2cosh(\mu \xi )^2-D_1a_1^3cosh(\mu \xi )^3+D_2a_0^2a_2cosh(\mu \xi )^2-D_2a_0^2a_2+D_2a_0^2a_1cosh(\mu \xi )^3 \nonumber \\{} & {} \quad -D_2a_0^2a_1cosh(\mu \xi )+D_3\mu a_0^2sinh(\mu \xi )cosh(\mu \xi )a_2+D_3a_0^2\mu a_1sinh(\mu \xi ) = 0, \end{aligned}$$
(4b)

&

$$\begin{aligned}{} & {} 4a_1\mu ^2a_2^2-4cosh(\mu \xi )^2\mu ^2a_2^2a_1+cosh(\mu \xi )^3\mu ^2a_2a_1^2-2E_1cosh(\mu \xi )^2a_2^2a_1 \nonumber \\{} & {} \quad -E_1cosh(\mu \xi )^3a_2a_1^2 +cosh(\mu \xi )\mu ^2a_2^3-E_1cosh(\mu \xi )a_2^3-E_2a_0^2cosh(\mu \xi )a_2-E_2a_0^2a_1 \nonumber \\{} & {} \quad -4\mu ^2a_2a_1^2cosh(\mu \xi )-E_1a_2^2a_1 -2E_1a_2a_1^2cosh(\mu \xi )+E_2a_0^2a_1cosh(\mu \xi )^2+4\mu ^2a_1^3cosh(\mu \xi )^2 \nonumber \\{} & {} \quad -E_1a_1^3cosh(\mu \xi )^2+E_2a_0^2cosh(\mu \xi )^3a_2-6a^2a_1^3 = 0. \end{aligned}$$
(4c)

After simplification of Eqs. (4b and 4c), we obtain the following values for \(a_1\) and \(a_2\) using Maple

$$\begin{aligned}{} & {} a_1 = \frac{\sqrt{-(\mu ^2-E_1)E_2}\,a_0}{\mu ^2-E_1},\nonumber \\{} & {} a_2 =\frac{\left[ D_3 a_0^2 \mu \,exp^2(\mu \xi )-\mu a_0^2D_3\right] }{12D_1 a_1\,exp(\mu \xi )} \nonumber \\{} & {} \qquad + \frac{\left[ D_3^2a_0^4\mu ^2\,exp^4(\mu \xi ) +\left[ (96a_1^2\,\mu ^2 -48D_2a_0^2)D_1a_1^2 -2D_3^2a_0^4\mu ^2\right] \,exp^2(\mu \xi ) +\mu ^2a_0^4D_3R^2\right] ^{\frac{1}{2}}}{12D_1 a_1\,exp(\mu \xi )}. \end{aligned}$$
(5)

In Eq. (2), by inserting the aforementioned equation, we get

$$\begin{aligned} u(x,t)=\left( \frac{a_0 sinh(\mu \xi )}{a_2 + \left( \frac{\sqrt{-(\mu ^2-E_1)E_2}a_0}{\mu ^2-E_1}\right) cosh(\mu \xi )}\right) \,\,exp{\left[ i(kx-\omega t)\right] }. \end{aligned}$$
(6)

By plotting the aforementioned equation and the descriptions of the plots, which are provided below, we were able to generate several types of solitonic profiles under the impact of IMD, TOD, SS, and SFS factors.

3 Physical interpretation of optical soliton profile

The variance in group velocity for all modes at an individual frequency leads to IMD. Due to the massive multimode dispersion that results in the maximum pulse broadening, multimode step index fibers exhibit a high value of dispersion. For these obvious reasons, pulse broadening can be a very important issue in multimode fiber optical systems. In this system, it is frequently necessary to keep the pulses long enough to guarantee an appropriate temporal coincidence of components from different modes in order to avoid considerable pulse distortion. Under the effect of TOD, both the pulse form and the spectrum undergo complex changes. The spectrum is spread out to both ends and divided into multiple high amplitudes when the transmission range is greater because the envelope function oscillates more strongly at longer distances (Agrawal 2003). The pulse’s self-steepening causes a steep front to form in the pulse’s following edge, simulating the typical shock wave creation. The optical shock is the name of this phenomenon. The pulse’s transmission grows increasingly unbalanced when its tail eventually separates out (Cao Long et al. 2003). Basically, the Stokes process performs better than the anti-Stokes process in stimulated Raman scattering. This information explains why the pulse’s reported self-shift frequency exists. The spectrum moves to the low-frequency area as a result. Or, to put it another way, the medium of transmission "amplifies" the pulse’s long-wavelength components. When a pulse crosses a medium strongly, it loses strength and goes through a complicated transformation (Agrawal 2003). An abrupt curve is seen in the waveform between a fixed bottom height and numerous decaying oscillation tails in the kink soliton, one of the different types of soliton modes (Rizvi et al. 2023a). This mode is semi-local and nonlinear. High-intensity short-pulse properties are influenced by the wavefront shape because kink solitons cause self-steepness or nonlinear effects in nonlinear fibers. Kink solitons have real-world uses as optical logic units or as polarization switches between two distinct domains (Al-Kalbani et al. 2023; Yue et al. 2020). When the group velocity dispersion regime is anomalous, the bright soliton format can be accepted, and it exhibits an intensity maximum in the time domain. Despite the particle-like nature of dark solitons in practical applications, nonlinearity, variable dispersion, and fiber degradation or enhancement remain significant issues. During soliton propagation, it is not only impossible to maintain a constant GVD coefficient and nonlinearity balance, but the balance will also unavoidably be impacted by optical fiber loss. Additionally, the interaction between solitons limits the quality of signal transmission in long-distance, high-speed transmission. We observed the shape-changing property of a soliton using the tunable coefficients of intermodal dispersion, third-order dispersion, the self-stepening effect, and a self-frequency shift. Selecting the appropriate physical parameters allows one to regulate the soliton’s shape by modifying the significant physical parameter of the resultant kink/antikink, bright/dark soliton. In addition to providing guidance for the detection and advancement of shape-changing solitons in nonlinear systems like liquid crystals and nonlinear optical fibers, the theoretical results extracted from this work can enhance research on the properties of shape-changing solitons.

Cao Long (2016) explored these novel results and the current state of the optical solitons in the GNLS equation. The GNLS equation in optical fiber was solved by him using the variational method, the F-expansion method, Split-Step, Runge–Kutta, and imaginary-time algorithms, and Jacobi elliptic function expansion. He showed that the parameters controlling self-steepening, third-order dispersion, and self-frequency shift caused the pulse shape to change. We are inspired to carry out comparable investigations using other analytical and numerical techniques by the intriguing results of the shape-changing property of the solitonic structure in the GNLS equation in optical fiber. Via the effective extended rational sinh–cosh approach, we revealed the shape-changing property in the present study under the influence of self steepening, third-order dispersion, self-frequency shift, and also intermodal dispersion parameters. Subsequently, we shall address the graphical depiction of the optical soliton in relation to the parameters of self steepening, third-order dispersion, intermodal dispersion, and self-frequency shift.

3.1 Effect of intermodal dispersion (IMD)

The intermodal dispersion has very little impact on the soliton’s form. With the parametric values \(a_0=1, \alpha _2=0.5, \alpha _3=0.1, \beta =0.05, \omega =1.5, \omega _0=0.5, k=0.9, T_R=1.5, v=10^6\,m/s\), and \(\alpha _1=0.00001\), we obtain the M-shaped dark soliton under the effect of intermodal dispersion, as shown in Fig. 1a. When we increase the value of the IMD term, the middle region of the M-shaped dark soliton decreases, which is illustrated in Fig. 1b of the contour plot. Finally, we obtain the dark soliton structure with \(\alpha _1=1.0\), which is shown in Fig. 1c. In this scenario, intermodal dispersion transfers energy between the two mode components of a soliton while preserving the fundamental characteristics of the solitons. We conclude that the difference in propagation durations between the different modes inside multi-mode fibers is what causes the intermodal dispersion, which causes pulse broadening as the coefficient of \(\alpha _1\) is decreased.

Fig. 1
figure 1

Profile of dark soliton from M-shaped dark soliton

Full size image

3.2 Effect of third order dispersion

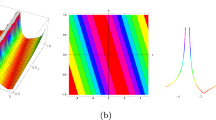
It has been clarified that the third-order dispersion (TOD) is essential for reducing the soliton diversion and supplying the shape-changing property. We stated that TOD can lessen the high-order optical soliton pulse compression, which is distinguished by soliton fission and the type of profile modification. The TOD benefits optical communication and digital pulse processing. As shown in Fig. 2a, the dark soliton is calculated by applying the third-order dispersion term to the parametric values \(a_0=100, \alpha _1=1.0, \alpha _2=1.5, \beta =0.05, \omega =1.0, \omega _0=0.5, k=1.0, T_R=1.0, v=10^6\) m/s, and \(\alpha _3=0.01\). The antikink soliton is represented in Fig. 2b by increasing the value of the third-order dispersion term (\(\alpha _3=1.0\)). When \(\alpha _3=15.0\), the TOD term influences the shape-changing property of the soliton from dark soliton to kink soliton via antikink soliton, as shown in Fig. 2c. The soliton pulses have a tendency to overlap due to third-order dispersion and the spreading effect, which prevents the receiver from reading them and reduces the maximum bandwidth that may be used. In order to prevent it, the maximum transmission rate needs to be smaller than the broadened pulse duration reciprocal (Keiser 2000). We infer that, as the magnitude of \(\alpha _3\) increases, the appearance of the pattern significantly brodends due to the impact of third-order dispersion.

Fig. 2
figure 2

Shape changing profile from dark soliton to kink soliton

Full size image

3.3 Effect of self steepening

The self-steepening effect may cause envelope pulses to kink as well as dark soliton with a decrease in amplitude, but this type of shape-changing property will not affect the propagation of ultrashort pulses (soliton) through the optical fiber. With the parametric values \(a_0=100, \alpha _1=1.0, \alpha _2=1.5, \alpha _3=0.1, \omega =0.1, \omega _0=0.5, k=1.0, T_R=1.0, v=10^6\) m/s, and \(\beta =0.00001\), we obtain the kink soliton, which is shown in Fig. 3a. When we increase \(\beta =0.1\) from 0.00001, we get the dark solitonic structure represented in Fig. 3b. Essentially, the self-steepening always makes the trailing region steeper, but this equation illustrates how the structure of the solitons can change depending on the magnitude of the SS term and provides information on energy distribution. Moreover, the self-steepening might lead to a temporal switching of the soliton from one configuration to another. The distribution properties of the leading and trailing pulses are different.

Fig. 3
figure 3

Shape changing profile from kink soliton to dark soliton

Full size image

3.4 Effect of self frequency shift

With extremely short pulse solitons, the optical range becomes so vast that the longer wavelength tail can be amplified at the expense of the power of the shorter wavelength tail. The sole component that can cause the form shift from one solitonic pulse to another is frequency-dependent loss or gain in the optical systems. The antikink soliton to kink soliton is obtained by applying the self-frequency shift term \(T_R\) to the parametric values \(a_0=100, \alpha _1=1.0, \alpha _2=1.5, \alpha _3=1.0, \omega =1.0, \omega _0=0.5, k=1.0, \beta =0.5, v=10^6\) m/s. For \(T_R=30\) from \(T_R=15\), the profile changes from antikink soliton to an antikink–kink profile, which is shown in Fig. 4b. Finally, for \(T_R=10^3\), the profile shifts to kink soliton, as shown in Fig. 4c. A self-frequency shift coefficient causes significant solitonic profile reshaping with amplitude decrement from anti-kink to kink evolution.

Fig. 4
figure 4

Shape changing profile from antikink soliton to kink soliton

Full size image

4 Linear stability analysis

This section investigates the effectiveness of stationary solutions to Eq. (1) and retrieves nonlinear eigenvalue spectrum diagrams. The stability of the system under the tiny perturbation is determined, and the following expansion is introduced as a result.

$$\begin{aligned} u(x,t) = e^{i\mu t} \left[ p(x) + {{{\widetilde{p}}}}(x) e^{\lambda t} + {{{\widetilde{q}}}}^*(x) e^{\lambda ^* t}\right] , \end{aligned}$$
(7)

here \(|{{{\widetilde{p}}}}|,\,|{{{\widetilde{q}}}}^*|<<|q(x)|\), substitute Eq. (7) into Eq. (1), and linearizing,

$$\begin{aligned} i{{\mathcal {L}}} \begin{pmatrix} {{{\widetilde{p}}}} \\ {{{\widetilde{q}}}} \end{pmatrix} =\lambda \begin{pmatrix} {{{\widetilde{p}}}} \\ {{{\widetilde{q}}}} \end{pmatrix}, \end{aligned}$$
(8)

where

$$\begin{aligned} {{\mathcal {L}}}= \begin{pmatrix} L_{11}\,\,\,L_{12}\\ L_{21}\,\,\,L_{22} \end{pmatrix} = \lambda \begin{pmatrix} {{{\widetilde{p}}}} \\ {{{\widetilde{q}}}} \end{pmatrix}, \end{aligned}$$
(9)

and

$$\begin{aligned}{} & {} L_{11}= \alpha _1 \mu \lambda + \left( \frac{\alpha _2}{2}\right) \mu ^2\lambda ^2 + \left( \frac{\alpha _3}{6}\right) \mu ^3\lambda ^3 + 2 |u|^2 - T_R \left[ \lambda - 2i\mu \right] \,|u|^2 \nonumber \\{} & {} \quad \qquad + \left( \frac{2i\beta }{\omega _0}\right) \left[ \lambda |u|^2+ i\mu u^2 -\mu |u|^2\right], \nonumber \\{} & {} L_{12} = \beta u^2 + \left( \frac{2i\beta }{\omega _0}\right) |u|^2, \nonumber \\{} & {} L_{21} = \beta u^2 - \left( \frac{\beta }{\omega _0}\right) \left[ 2 - \lambda ^*\right] \mu u^2, \nonumber \\{} & {} L_{22} = \alpha _1 \mu \lambda ^* + \left( \frac{\alpha _2}{2}\right) \mu ^2\lambda ^{*2} + \left( \frac{\alpha _3}{6}\right) \mu ^3\lambda ^{*3} + 2 |u|^2 - T_R \left[ \lambda ^* - 2i\mu \right] \,|u|^2 \nonumber \\{} & {} \quad \qquad - \left( \frac{i\mu \beta }{\omega _0}\right) \left[ 2 u^*- u^2) \right]. \end{aligned}$$
(10)

We evaluated the above eigenvalue problem (Muniyappan et al. 2023; Kavitha et al. 2017) with the help of the Fourier collocation method and acquired the spectrum of eigenvalues as illustrated in Figs. 5, 6, 7 and 8. The soliton is described as linearly stable by the positive real parts of the eigenvalue parts, whereas the soliton is described as unstable by the imaginary parts of the spots. The above eigenvalue spectrum of the matrix determines the stability of the soliton, and the physical parameters of the system also determine the stability of the soliton. Therefore, in this section, we have analyzed the system parameters and their role in the stability of a soliton. We chose four cases to investigate the stability of soliton, and in the first case, we varied \(\alpha _1\) while keeping \(\alpha _2=0.1, \alpha _3=0.1, \beta =2.5, \omega _0=0.1\) and \(T_R=0.11\) constant. Similarly, for the remaining cases, we have adjusted the values of \(\alpha _3, \beta\), and \(T_R\). In the first case, the eigenvalue spots lie in the positive face for the value of \(\alpha _1\)=0.1, and hence, it shows that soliton is linearly stable as shown in Fig. 5a. As the value of \(\alpha _1\) is increased from 1.0 to 2.5, the positive sides of some spots weaken and some spots appear in the imaginary part, indicating that soliton is unstable at high \(\alpha _1\) values, as shown in Fig. 5b, c. In the second case, we changed the value of \(\alpha _3\) from 0.1 to 2.5, and the spots are on both sides of real and imaginary, resulting in an unstable soliton, as shown in Fig. 6a–c, whereas in the third case, the soliton is stable at first and becomes unstable as we increase the value of \(\beta\) from 1.0 to 2.5, as shown in Fig. 7a–c. In the last case, the \(T_R\) ranged from 0.1 to 2.5, and it was discovered that spots are located in the real part at the initial value, with minor changes on the spots at the final value of \(T_R\). As shown in Fig. 8a–c, the exit spot confirms that the soliton is unstable. According to the results of the analysis, soliton is unstable when the values of \(\alpha _1\), \(\alpha _3\), and \(\beta\) are high, whereas soliton is stable for any value of \(T_R\).

Fig. 5
figure 5

Eigenvalue spectrum of the soliton under the influences of IMD (\(\alpha _1\))

Full size image
Fig. 6
figure 6

Eigenvalue spectrum of the soliton under the TOD (\(\alpha _3\))

Full size image
Fig. 7
figure 7

Eigenvalue spectrum of the soliton under the influences of SS (\(\beta\))

Full size image
Fig. 8
figure 8

Eigenvalue spectrum of the soliton under the influences of SFS (\(T_R\))

Full size image

4.1 Fourier collocation method for the whole spectrum

Analyzing the stability of the spectrum, which is made up of the eigenvalue of the linear stability of the solitonic wave operator, is a crucial part of the problem once the soliton solution has been obtained. The solitonic wave is linearly unstable if the spectrum has eigenvalues with positive real components. In this instance, the maximum growth rate of perturbations is provided by the biggest real part of the eigenvalues. If there are only imaginary discrete eigenvalues in the spectrum, these eigenvalues are the internal modes that give rise to the solitonic wave’s long-lasting form oscillations. Therefore, using the Fourier collocation approach, we expand the eigen function \(\psi =[p,q]^{T}\) as well as functions \(L_{11}\) to \(L_{22}\) into Fourier series in order to obtain the entire spectrum of the linear stability operator \(\underline{L}\):

$$\begin{aligned}{} & {} P(x)=\sum _{n} a_n e^{ink_0 x}, \,\, q(x)=\sum _{n} b_n e^{ink_0 x}, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} L_{rj}=\sum _{n} c_n^{rj} e^{ink_0 x}, \,\,\,r,j=1,2, 3..... \end{aligned}$$
(12)

Here, \(k_0=\frac{2\pi }{L}\). The eigenvalue system for the coefficients \({a_{rj}, b_{rj}}\) can be obtained by applying the aforementioned expansions to the eigenvalue problem of Eq. (8) and equating the coefficients of the same Fourier modes.

$$\begin{aligned}{} & {} \sum _{n} c_{n}^{(0)} a_{rj-n}-(k_{0}rj)^2b_{rj}+\sum _{n}c_{n}^{(1)}b_{rj-n}=i\lambda a_{rj}, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} -(k_{0}rj)^2a_{rj}+\sum _{n} c_{n}^{(2)} a_{rj-n}-\sum _{n}c_{n}^{(0)}b_{rj-n}=i\lambda b_{rj}, \end{aligned}$$
(14)

where \(-\infty< rj < \infty\). After truncating the number of Fourier modes to \(-N \le rj \le N\), the finite-dimensional eigenvalue problem is obtained from the infinite-dimensional one.

$$\begin{aligned} \begin{pmatrix} C_{11}\,\,\,\,\,\,\,\,\,D+C_{12}\\ D+C_{21}\,\,\,\,\,\,\,\,-C_{11} \end{pmatrix} \begin{pmatrix} A\\ B \end{pmatrix} =\lambda \begin{pmatrix} A\\ B \end{pmatrix}, \end{aligned}$$
(15)

where

$$\begin{aligned} A=(a_{-N}, a_{N+1},\ldots a_N)^T,\,\,\,B=(b_{-N}, b_{N+1},\ldots b_N)^T \end{aligned}$$

We can use the QR algorithm (Golub and Van Loan 1996) to solve the matrix eigenvalue problem Eq. (15).

5 Conclusions

We successfully investigated the generalized nonlinear Schrödinger equation subject to parameter constraint relations. The obtained ordinary differential equation could be processed using an approach based on the parametric function’s extended rational sinh–cosh method. The obtained results show that the intermodal dispersion, self-steepening, third-order dispersion, and self-frequency shift parameters determine the interval between kink-dark soliton and antikink soliton. We conclude that the proposed method is effective in finding soliton solutions based on the generalized nonlinear Schrödinger equation. Higher-order terms play an important role in compensating for nonlinear absorption during propagation in highly nonlinear materials, as well as in soliton shrinkage to produce a highly stable short optical pulse.

Solitons are used extensively in engineering and applied physics. By assigning special values to the parameters involved in these methods, wave solutions derived from existing techniques and novel solitons can be obtained. The analysis of stability is used to investigate the stability of this model, which confirms that it is stable or unstable. The movements of some results are graphically depicted, assisting researchers in comprehending the complex phenomena of this mode. As a result, our results are novel and have never been articulated before. The movements of some results are graphically depicted, assisting researchers in comprehending the complex phenomena of this mode. As a result, our results are novel and have never been articulated before. This area of study is highly active, with many new models and methods being developed for the analysis and use of soliton solutions. Numerous branches of science, such as the transmission of signals through optical fibers and pulses in nonlinear media, make use of the distinctive shape-changing property of soliton and its solutions. Future studies and applications in optical wave propagation, data transmission, and other fields depend on the observed shape-changing nature of solitary wave structures that fit the found solutions.

The considered equation governs the ultrashort pulse propagation model, which describes soliton pulse dynamics. When the parameters are constrained, physical terms such as SS, TOD, and SFS produce various types of dark, dark-kink, and kink–antikink optical solitons. In the context of our study, it is shown that the IMD produces dark soliton with wing form but not anti-kink or kink solitons. These solitonic pulses are useful for increasing the capacity to carry information in order to achieve ultra-fast communication. We anticipate that these findings will be useful in physical and experimental nonlinear optics applications.