1 Introduction

Non-linear partial differential equations with fractional components play an important role in describing non-linear processes in science and engineering. It is necessary to obtain an exact solution of the differential equations in order to recognise the non-linearities. This encourages researchers to explore acceptable methods for determining the exact solutions of linear and non-linear differential equations. Indeed, there has been a growing interest in fractional calculus and partial fractional differential equations (PFDEs) in recent years. Fractional calculus extends the traditional concept of differentiation and integration to non-integer orders, allowing for the analysis of systems and phenomena with memory and long-range dependencies. Fractional models and fractional differential equations have found applications in various fields, including physics, engineering, finance, biology, modeling complex systems, control systems, electrochemical processes, viscoelasticity, mechanics and vibrations and many others (Wazwaz 2010; Kopçasız et al. 2022; Yong et al. 2011; Suret et al. 2020; Shakeel et al. 2023a, b; Losseva et al. 2012; Raza et al. 2021; Arshed et al. 2022).

Fractional calculus is indeed a generalization of classical calculus that deals with non-integer orders of differentiation and integration. This generalization provides a powerful framework for analyzing and modelling systems and phenomena that exhibit memory, long-range dependencies, and non-local behaviors. In fractional calculus, the concept of a fractional derivative (or integral) is extended to include non-integer orders, such as fractional or even complex orders. This allows for the development of new mathematical formulas that are specifically designed to handle fractional differential equations. These equations involve fractional derivatives, and they can describe various processes that don’t adhere to classical integer-order behaviors. A number of researches have been done in the recent past in which the behaviour of PFDEs and their solutions have been found such as, soliton solutions to the space-time-fractional telegraph equation (Arefin et al. 2022), time fractional Klein–Gordon equation (Sadiya et al. 2022), fractional-order Phi-4 equation and Allen–Cahn equation (Zaman et al. 2022), fractional simplified Camassa–Holm equation (Khatun et al. 2022), fractional-coupled Burgers equation (Khatun et al. 2022), fractional order nonlinear coupled type Boussinesq equation (Zaman et al. 2023), space-time fractional Camassa–Holm equation (Arefin et al. 2023) and fractional space-time advection-dispersion equation (Aljahdaly et al. 2022) etc.

The use of fractional derivatives to describe memory and hereditary properties has found numerous applications in various materials and processes, including polymers. Polymers are complex materials with intricate molecular structures, and their behaviors often exhibit non-local effects, memory, and time-dependent responses that can be effectively described using fractional calculus. In the past few years, the researchers have used some derivatives that have fractional order such as Atangana beta and conformable derivatives (Qureshi et al. 2021), Caputo fractional derivative (Almeida 2017; Singh et al. 2023; Abdulazeez and Modanli 2023), \(\psi\)-Hilfer fractional derivative (Sousa and De Oliveira 2018), fractional Grünwald–Letnikov derivative (Ortigueira and Machado 2015), Riemann–Liouville definition of fractional derivative (Atangana and Gómez-Aguilar 2018), k-Riemann–Liouville derivative (Romero et al. 2013), Modified Riemann–Liouville derivative (Jumarie 2006), Atangana–Baleanu derivative (Atangana and Koca 2016) and Caputo–Liouville generalized fractional derivative (Sene 2020).

Finding exact solutions for FPDEs is a significant and challenging area of research while finding exact solutions to fractional PDEs is often challenging due to their inherent complexity. Various techniques have been proposed to address the challenges of solving FPDEs such as modified double sub-equation method (Yépez-Martínez and Rezazadeh 2022), generalized new Auxiliary equation approach (Zhang 2007), Modified E-Function technique (Attaullah et al. 2022), new generalized exponential rational function method (Ghanbari and Inc 2018), modified exponential function method (Muhamad et al. 2023), \((\frac{G^{{\prime }}}{G})\)-expansion technique (Zafar et al. 2023; Bibi et al. 2023), the \((\frac{G^{\prime }}{G^2},\frac{1}{G})\)-expansion method (Mamun Miah et al. 2017), Kurchatov’s method (Ezquerro et al. 2013), sine-cosine method (Taşcan and Bekir 2009), the new exponential-expansion scheme (Jaradat and Alquran 2022), right-left-moving wave solutions of two non-linear PDEs (Jaradat et al. 2018), the extended tanh-coth expansion method and the polynomial-function technique (Alquran et al. 2021), the modified exponential-expansion algorithm (Jaradat and Alquran 2022), Kudryashov expansion method and simplified bilinear method (Jaradat and Alquran 2020), modified rational sine-cosine functions (Alquran and Jaradat 2023) and the extended transformed rational function technique (Jannat et al. 2022) and many more (Khatun et al. 2023, Shakeel et al. (2023c)). These methods involve breaking down the original equation into simpler sub-equations or modified versions of them, which can then be solved more easily.

Moreover, in the present study, we will use the \((\frac{G^{\prime }}{G^2})\)-expansion technique (Arshed et al. 2018) for the exact optical soliton solution. Additionally, \(\left( \frac{w}{g}\right)\)-expansion technique detailed to discuss in the research paper (Wen-An et al. 2009), where w, g are the functions that completely fulfil the requirements of the following equation,

$$\begin{aligned} g w^{\prime }-w g^{\prime }={\Lambda \text {g}}^2+\varUpsilon w^2, \end{aligned}$$
(1.1)

where \(\Lambda\) and \(\varUpsilon\) are the arbitrary constants. The latter technique introduces the generic solutions to Eq. (1.1) and finds the explicit formulas for evaluating the solutions of precise non-linear evolution problems (NEPs). The extended \(\left( \frac{w}{g}\right)\)-expansion approach (Gepreel 2016) is taken to be considered in this investigation, where w, g are the functions that completely fulfil the requirements of the following equation

$$\begin{aligned} g w^{\prime }-w g^{\prime }=\Lambda w^2+{\varUpsilon \text {g}}^2+\upsilon wg, \end{aligned}$$
(1.2)

if \(\upsilon \ne 0\) and we take \(w=(\frac{G^{\prime }}{G})\) and \(g=G\), then we have

$$\begin{aligned} G^{\prime \prime }(\Phi )= \frac{\Lambda G^{\prime }(\Phi )^2}{G(\Phi )^2}+\frac{2 G^{\prime }(\Phi )^2}{G(\Phi )}+\varUpsilon G^{\prime }(\Phi )+\upsilon G(\Phi )^2, \end{aligned}$$
(1.3)

this change produces numerous new and exact travelling wave solutions to particular NEPs with the free parameters \(\upsilon , \varUpsilon\) and \(\Lambda\). To see the research papers (Aljahdaly 2019; Al-Harbi et al. 2023) for the detailed discussion about modified \((\frac{G^{\prime }}{G^2})\)-expansion technique. This method offers exact solutions for a broad array of fractional differential equations. In our current study, we apply the modified \((\frac{G^{\prime }}{G^2})\)-expansion technique, aided by the \(\beta\)-D (Yusuf et al. 2019; Atangana and Doungmo Goufo 2014), M-TD (Hussain et al. 2020) and C-D (Alharbi et al. 2019) to explore the novel soliton solutions for the NLCRW equation (Ansar et al. 2023) and NLWKB equation (Silambarasan and Nisar 2023). In this research work, we explored the three fractional order derivatives for the purpose of analysing the effective solutions of the non-linear coupled Riemann wave equation and Wazwaz Kaur Boussinesq equation. \(\beta\)-D extends the concept of fractional derivatives by introducing parameters \(\alpha\) and \(\beta\) from the beta function. This derivative allows for greater flexibility compared to conventional fractional derivatives like Riemann–Liouville or Caputo derivatives. It’s worth noting that the fractional \(\beta\)-D is less commonly used than other definitions. The choice of derivative hinges on the specific problem, the modelled behavior, and desired solution properties.

Among these techniques, modified \((\frac{G^{\prime }}{G^2})\)-expansion technique (Al-Harbi et al. 2023) has gained attention for its ability to construct exact solutions for time-fractional and space-time fractional differential equations. This method aims to provide analytical solutions for a wide range of fractional differential equations. In this research work, we explore the new fractional solutions for the NLCRW equation by utilizing the modified \((\frac{G^{\prime }}{G^2})\)-expansion technique, with the help of \(\beta\)-D. The fractional beta derivative generalizes the concept of fractional derivatives by introducing the beta function parameters \(\alpha\) and \(\beta\). It allows for differentiation with fractional orders that can be more flexible and versatile than traditional fractional derivatives. However, it’s important to note that the fractional beta derivative is not as commonly studied or utilized as some other fractional derivative definitions.

In this work, the researchers find the optical soliton solutions for two nonlinear models, namely Wazwaz Kaur Boussinesq equation (Ansar et al. 2023) and coupled Riemann wave equation (Silambarasan and Nisar 2023) by utilizing the modified \((\frac{G^{\prime }}{G^2})\)-expansion technique (Al-Harbi et al. 2023) with the help of Conformable, M-truncated and beta derivatives. These nonlinear equations have applications in modern communication network technology, optical fiber, ion-acoustic, and magneto-sound waves in plasma, homogeneous, and stationary media, particularly in the propagation of tidal and tsunami waves. The proposed scheme gives five different types of solutions such as M-shaped soliton, W-shaped soliton, bright soliton and dark soliton solutions etc.

We divided the present study into six different sections. Section 2 provides definitions for beta, conformable, and M-truncated derivatives. Section 3 covers the general steps of the proposed scheme, while Sect. 4 covers its applications, graphical discussion and graph-finding using Mathematica are presented in Sect. 5. The conclusion is presented in the last Sect. 6.

2 Preliminaries

This section provides a compilation of derivative definitions and their fundamental attributes.

2.1 Beta derivative

Definition

Let \(x\in {\mathbb {R}}, t\ge 0\) and \(u:[x,\infty )\rightarrow {\mathbb {R}}\) be a continuous function. Then \(\beta\)-derivative of order \(\beta\) is defined as (Ansar et al. 2023)

$$\begin{aligned} D^\beta u(t)=\lim _{\epsilon \rightarrow 0}{\frac{u(t+\epsilon (t+\frac{1}{\Gamma (\beta )})^{1-\beta })-u(t)}{\epsilon }},\quad \textrm{where}\;\beta \in (0,1] \end{aligned}$$

where \(\Gamma\) is gamma function defined as: \(\Gamma (\nu )=\int _{0}^{\infty }t^{\nu -1}e^{-t}dt\)

Properties of Beta derivative: let \(\kappa (t)\) and \(\chi (t)\) be differentiable functions of order \(\beta\) such that \(0<\beta \le 1\) and \(t\ge 0\), then

  1. 1.

    \(D^\beta (a\kappa (t)+b\chi (t))=aD^\beta (\kappa (t))+b D^\beta (\chi (t)), \forall a,b \in {\mathbb {R}}\).

  2. 2.

    \(D^\beta (\kappa (t)\chi (t))= \kappa (t)D^\beta (\chi (t))+\chi (t)D^\beta (\kappa (t))\).

  3. 3.

    \(D^\beta (\frac{\kappa (t)}{\chi (t)})=\frac{\kappa (t)D^\beta (\chi (t))-\chi (t)D^\beta (\kappa (t))}{\chi (t)^2}\).

  4. 4.

    \(D^\beta (c)=0\), for any constant c.

  5. 5.

    Considering \(\epsilon =(t+\frac{1}{\Gamma (\beta )})^{1-\beta }\delta , \delta \rightarrow 0\) when \(\epsilon \rightarrow 0\), therefore we get

    $$\begin{aligned} D^\beta (\chi (t))=\left( t+\frac{1}{\Gamma (\beta )}\right) ^{1-\beta } \frac{d\chi (t)}{dt}, \end{aligned}$$

    with \(\psi =\frac{c}{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }\), where c is arbitrary constant. The research (Khalil et al. 2014) provided the proofs of the above-mentioned properties of \(\beta\)-derivative.

2.2 M-Truncated derivative

The M-TD for \(u:[x,\infty )\rightarrow {\mathbb {R}}\) of order \(\beta \in (0,1]\) is defined as (Hussain et al. 2020)

$$\begin{aligned} D_{M,t}^\beta u(t)=\lim _{\epsilon \rightarrow 0}{\frac{u(t+_kE_\chi (\epsilon t^{-\beta }))-u(t)}{\epsilon }}, \end{aligned}$$

for \(t>0\) and \(_kE_\chi (\cdot ), \chi >0\), where \(_kE_\chi (\cdot )\) is truncated Mittag–Leffler function (Sousa and de Oliveira 2017) with one parameter is defined as follows:

$$\begin{aligned} {}_k E_\chi (t)=\sum _{i=0}^k\frac{t^i}{\Gamma (\chi i+1)}. \end{aligned}$$

Theorem 1

Let \(\beta \in (0,1], \chi >0, a,b\in {\mathbb {R}}\) and G, H are differentiable functions of order \(\beta\).

  1. 1.

    \(D_{M,\psi }^\beta (aG(\psi )+bH(\psi ))=aD_{M,\psi }^\beta (G(\psi ))+b D_{M,\psi }^\beta (H(\psi )), \forall a,b \in {\mathbb {R}}\).

  2. 2.

    \(D_{M,\psi }^\beta (G(\psi )H(\psi ))= G(\psi )D_{M,\psi }^\beta (H(\psi ))+H(\psi )D_{M,\psi }^\beta (G(\psi ))\).

  3. 3.

    \(D_{M,\psi }^\beta (\frac{G(\psi )}{H(\psi )})=\frac{G(\psi )D_{M,\psi }^\beta (H(\psi ))-H(\psi )D_{M,\psi }^\beta (G(\psi ))}{H(\psi )^2}\).

  4. 4.

    \(D_{M,\psi }^\beta (c)=0\), for any constant c.

  5. 5.

    \(D_{M,\psi }^\beta G(\psi )=\frac{\psi ^{1-\beta }}{\Gamma (\chi +1)}\frac{dG}{d\psi }\).

2.3 Conformable derivative

Suppose \(u:[x,\infty )\rightarrow {\mathbb {R}}\) be a function then the Conformable derivative (C-D) for the function u[t] of order \(\beta\), defined as \(D_{C,t}^\beta u(t)=\lim _{\epsilon \rightarrow 0}{\frac{u(t+\epsilon (t)^{1-\beta })-u(t)}{\epsilon }}\), for \(t>0\) and \(\beta \in (0,1]\). Additionally, the properties and theorems associated with C-D are thoroughly addressed in the work of reference (Shahen et al. 2020).

Theorem 2

Let \(\beta \in (0,1], \mu ,\eta \in {\mathbb {R}}\) and u, v are differentiable functions of order \(\beta\) at \(t>0\).

  1. 1.

    \(D_{C,\psi }^\beta (\mu u(\psi )+\eta v(\psi ))=\mu D_{C,\psi }^\beta (u(\psi ))+\eta D_{C,\psi }^\beta (v(\psi )), \forall \mu ,b \in {\mathbb {R}}\).

  2. 2.

    \(D_{C,\psi }^\beta (u(\psi )v(\psi ))= u(\psi )D_{C,\psi }^\beta (v(\psi ))+v(\psi )D_{C,\psi }^\beta (u(\psi ))\).

  3. 3.

    \(D_{C,\psi }^\beta (\frac{u(\psi )}{v(\psi )})=\frac{u(\psi )D_{C,\psi }^\beta (v(\psi ))-v(\psi )D_{C,\psi }^\beta (u(\psi ))}{v(\psi )^2}\).

  4. 4.

    \(D_{C,\psi }^\beta (c)=0\), for any constant c.

  5. 5.

    \(D_{C,\psi }^\beta u(\psi )=\psi ^{1-\beta }\frac{du}{d\psi }\).

3 The strategy of scheme

In this section, we describe the general steps of the modified \(\left( \frac{G'}{G^2}\right)\)-expansion scheme:

Let’s assume the following travelling wave equation in the form of PDE as

$$\begin{aligned} F ( Q, Q_t, Q_{x}, Q_{y}, Q_{t t}, Q_{x x}, Q_{y y}, Q_{x t}\ldots )=0, \end{aligned}$$
(3.1)

where \(Q=Q(x,y,t)\). Let us assume the below given propagational waves transformation

$$\begin{aligned} Q = Q (\Phi ), \Phi = \Phi (x,y,t), \end{aligned}$$
(3.2)

putting the Eq. (3.2) into Eq. (3.1), then we get the non-linear ODE such as

$$\begin{aligned} F(Q, Q^{\prime }, Q^{\prime \prime }, Q^{\prime \prime \prime },...)=0. \end{aligned}$$
(3.3)

Where the superscript \(^{\prime }\) is derivative w.r.t \(\Phi\) and we assume the solution of Eq. (3.3) can be demonstrate in generalized form as follows:

$$\begin{aligned} Q(\Phi )=a_0+\sum _{n=1}^N \left[ a_n \left( \frac{G^{\prime }}{G^2}\right) ^n+b_n \left( \frac{G^{\prime }}{G^2}\right) ^{-n}\right] , \end{aligned}$$
(3.4)

where \(G=G(\Phi )\) and satisfy the equation

$$\begin{aligned} G^{\prime \prime }(\Phi )= \frac{\Lambda G^{\prime }(\Phi )^2}{G(\Phi )^2}+\frac{2 G^{\prime }(\Phi )^2}{G(\Phi )}+\varUpsilon G^{\prime }(\Phi )+\upsilon G(\Phi )^2, \end{aligned}$$
(3.5)

where \(\Lambda , \varUpsilon\) and \(\upsilon\) are the arbitrary constants. Now we find the positive value of N (where N is the balance number), the value of the highest order linear term and the highest order non-linear term present in the Eq. (3.3). By equating the highest order of both linear term and non-linear term involved in the equation. If n is the order of \(Q(\Phi )\) and \(DQ(\Phi )\), then the degree of the other expression is given below.

$$\begin{aligned} D\left[ \frac{d^gQ(\Phi )}{d{\Phi }^g}\right] =g+n, D\left[ Q^g \left( \frac{d^hQ(\Phi )}{d{\Phi }^h}\right) ^k\right] =k(h+n)+ng, \end{aligned}$$
(3.6)

we find all the values of derivatives of the Eq. (3.4) by using Eq. (3.5) according to the given ODE as in Eq. (3.3). Then collect all terms involving \(\left( \frac{G^{\prime }}{G^2}\right) ^j\), where \((\textrm{j} = 0, 1, 2,\ldots , \textrm{n})\) and setting all the coefficients of \(\left( \frac{G^{\prime }}{G^2}\right) ^j\) equal to zero. As a result, we get a system of algebraic equations. By using these equations, we find the values of unknown constants by using the Mathematica tool.

The general solution of the Eq. (3.5) has three cases such as:


Case:1 If \(\Lambda \upsilon >0\) and \(\varUpsilon =0\), then we have

$$\begin{aligned} \frac{G^{\prime }(\Phi )}{G(\Phi )^2}=\frac{\sqrt{\Lambda \upsilon } \left( \phi _1 \cos \left( \Phi \sqrt{\Lambda \upsilon }\right) +\phi _2 \sin \left( \Phi \sqrt{\Lambda \upsilon }\right) \right) }{\upsilon \left( \phi _2 \cos \left( \Phi \sqrt{\Lambda \upsilon }\right) -\phi _1 \sin \left( \Phi \sqrt{\Lambda \upsilon }\right) \right) }, \end{aligned}$$
(3.7)

where \(\phi _1, \phi _2\) be arbitrary constants.


Case:2 If \(\Lambda \upsilon <0\) and \(\varUpsilon =0\), then we have

$$\begin{aligned} \frac{G^{\prime }(\Phi )}{G(\Phi )^2}=-\frac{\sqrt{| \Lambda \upsilon | } \left( \phi _1 \sinh \left( 2 \Phi \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \Phi \sqrt{| \Lambda \upsilon | }\right) +\phi _2\right) }{\upsilon \left( \phi _1 \sinh \left( 2 \Phi \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \Phi \sqrt{| \Lambda \upsilon | }\right) -\phi _2\right) }, \end{aligned}$$
(3.8)

Case:3 If \(\Lambda \ne 0,\upsilon =\varUpsilon =0\), then we have

$$\begin{aligned} \frac{G^{\prime }(\Phi )}{G(\Phi )^2}=-\frac{\phi _1}{\Lambda (\phi _1 \Phi +\phi _2)}, \end{aligned}$$
(3.9)

Case:4 If \(\varUpsilon \ne 0,\Delta \ge 0\), then we have

$$\begin{aligned} \frac{G^{\prime }(\Phi )}{G(\Phi )^2}=-\frac{\varUpsilon }{2 \Lambda }-\frac{\sqrt{\Delta } \left( \phi _1 \cosh \left( \frac{\sqrt{\Delta }}{2 \Phi }\right) +\phi _2 \sinh \left( \frac{\sqrt{\Delta }}{2 \Phi }\right) \right) }{2 \Lambda \left( \phi _1 \sinh \left( \frac{\sqrt{\Delta }}{2 \Phi }\right) +\phi _2 \cosh \left( \frac{\sqrt{\Delta }}{2 \Phi }\right) \right) }, \end{aligned}$$
(3.10)

where \(\Delta =\varUpsilon ^2-4 \Lambda \upsilon\).


Case:5 If \(\varUpsilon \ne 0,\Delta <0\), then we have

$$\begin{aligned} \frac{G^{\prime }(\Phi )}{G(\Phi )^2}=-\frac{\varUpsilon }{2 \Lambda }-\frac{\sqrt{-\Delta } \left( \phi _1 \cos \left( \frac{\sqrt{-\Delta }}{2 \Phi }\right) -\phi _2 \sin \left( \frac{\sqrt{-\Delta }}{2 \Phi }\right) \right) }{2 \Lambda \left( \phi _2 \cos \left( \frac{\sqrt{-\Delta }}{2 \Phi }\right) +\phi _1 \sin \left( \frac{\sqrt{-\Delta }}{2 \Phi }\right) \right) }, \end{aligned}$$
(3.11)

4 Applications of modified \(\left( \frac{G^{\prime }}{G^2}\right)\)-expansion scheme

4.1 Coupled Riemann wave equation

Consider the (\(2+1\))-dimensional non-linear CRW equation (Ansar et al. 2023) of the form

$$\begin{aligned} {\mathcal {U}}_t+p{\mathcal {U}}_{xxy}+q{\mathcal {U}}E_x+rE{\mathcal {U}}_x=0, E_x={\mathcal {U}}_y, \end{aligned}$$
(4.1)

where p, q and r are the nonzero parameters. This model can be expressed in the sense of \(\beta\)-derivative such as

$$\begin{aligned} D_{\beta ,t}^{\kappa } {\mathcal {U}}_t+p {\mathcal {U}}_{xxy}+q {\mathcal {U}}E_x+rE{\mathcal {U}}_x=0, E_x={\mathcal {U}}_y, \end{aligned}$$
(4.2)

Here p, q and r are also the nonzero parameters that discuss the interaction between a long wave propagation and a Riemann wave. Where \(D_{\beta ,t}^{\kappa }\) is \(\beta\)-D of \({\mathcal {U}}(x,y,t)\) and the term \(\kappa\) shows the fractional parameter and \(0<\kappa \le 1\).

In M-TD, the suggested model has the following structure.

$$\begin{aligned} D_{M,t}^{\kappa } {\mathcal {U}}_t+p {\mathcal {U}}_{xxy}+q{\mathcal {U}}E_x+rE{\mathcal {U}}_x=0, E_x={\mathcal {U}}_y, \end{aligned}$$
(4.3)

where \(D_{M,t}^{\kappa }\) is M-TD with \(\kappa\) is fractional order.

In C-D, the suggested model has the following structure.

$$\begin{aligned} D_{C,t}^{\kappa } {\mathcal {U}}_t+p {\mathcal {U}}_{xxy}+q {\mathcal {U}} E_x+rE {\mathcal {U}}_x=0, E_x={\mathcal {U}}_y, \end{aligned}$$
(4.4)

where \(D_{C,t}^{\kappa }\) is C-D with \(\kappa\) is conformable operator.

Consider the wave transformation and there are three different definitions for the travelling wave parameter \(\zeta\).

In \(\beta\)-D, \(\zeta\) takes on the following form

$$\begin{aligned} {\mathcal {U}}(x,y,t)={\mathcal {U}}(\zeta ), \zeta =\mu x+\sigma y-\frac{\nu \left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }}{\beta }, \end{aligned}$$
(4.5)

where \(\mu ,\sigma\) and \(\nu \ne 0\).

In M-TD, \(\zeta\) takes on the following form

$$\begin{aligned} {\mathcal {U}}(x,y,t)={\mathcal {U}}(\zeta ), \zeta =\mu x+\sigma y-\nu \frac{\Gamma (\chi +1 )}{\beta } t^{\beta }, \end{aligned}$$
(4.6)

in C-D, \(\zeta\) takes on the following form

$$\begin{aligned} {\mathcal {U}}(x,y,t)={\mathcal {U}}(\zeta ), \zeta =\mu x+\sigma y-\frac{\nu }{\beta } t^{\beta }, \end{aligned}$$
(4.7)

convert the Eqs. (4.2), (4.3) and (4.4) into ODE by using the wave transformation (4.5), (4.6) and (4.7) and we have

$$\begin{aligned} p \mu ^2 \sigma {\mathcal {U}}^{\prime \prime \prime }+q\mu {\mathcal {U}} E^{\prime }+r\mu E {\mathcal {U}}^{\prime }-\nu {\mathcal {U}}^{\prime }=0, \sigma {\mathcal {U}}^{\prime }=\mu E^{\prime }, \end{aligned}$$
(4.8)

using the zero integration by the second equation of (4.8), we obtain

$$\begin{aligned} E=\frac{\sigma {\mathcal {U}}}{\mu }, \end{aligned}$$
(4.9)

after integration, we substitute the Eq. (4.9) into the 1st Eq. of (4.8) and we have

$$\begin{aligned} 2 \mu ^2 p \sigma {\mathcal {U}}^{\prime \prime }+\sigma (q+r) {\mathcal {U}}^2-2 \nu {\mathcal {U}}=0, \end{aligned}$$
(4.10)

where \({\mathcal {U}}^{\prime \prime }=\frac{d^2 {\mathcal {U}}}{d\zeta ^2}\). Applying the balancing method, balancing the highest linear and non-linear terms of Eq. (4.10) and we get the balance number is \(N=2\). By using the balance number, we can express the Eq. (3.4) as

$$\begin{aligned} {\mathcal {U}}(\zeta )=a_0+a_1\left( \frac{G^{\prime }}{G^2} \right) +a_2\left( \frac{G^{\prime }}{G^2} \right) ^2+b_1\left( \frac{G^{\prime }}{G^2} \right) ^{-1}+b_2\left( \frac{G^{\prime }}{G^2} \right) ^{-2}, \end{aligned}$$
(4.11)

where \(G=G(\zeta )\), and \(a_0,a_1,a_2,b_1,b_2\) are the unknown constants whose values we want to find. We substitute the Eq. (4.11) with the aid of Eq. (3.5) into the Eq. (3.10) and after substitution, we have collected all such coefficients like power as \(\left( \frac{G^{\prime }}{G^2}\right) ^j,\;(j=0,\pm 1,\pm 2,\pm 3,\ldots )\). Due to this, we attain with the help of Mathematica an algebraic system of equations such as

$$\begin{aligned}&2 a_1 b_1 q \sigma +2 a_1 b_1 r \sigma -2 a_0 \nu +4 a_2 \mu ^2 p \sigma \upsilon ^2+2 a_1 \mu ^2 p \sigma \upsilon \varUpsilon +a_0^2 q \sigma +a_0^2 r \sigma +2 b_1 \Lambda \mu ^2 p \sigma \varUpsilon \\&2 a_2 b_2 q \sigma +2 a_2 b_2 r \sigma ++4 b_2 \Lambda ^2 \mu ^2 p \sigma =0,\\&4 b_1 \mu ^2 p \sigma \upsilon ^2+20 b_2 \mu ^2 p \sigma \upsilon \varUpsilon +2 b_1 b_2 q \sigma +2 b_1 b_2 r \sigma =0, \\&2 a_0 b_2 q \sigma +2 a_0 b_2 r \sigma -2 b_2 \nu +16 b_2 \Lambda \mu ^2 p \sigma \upsilon +6 b_1 \mu ^2 p \sigma \upsilon \varUpsilon \\&\quad +8 b_2 \mu ^2 p \sigma \varUpsilon ^2+b_1^2 q \sigma +b_1^2 r \sigma =0, \\&2 a_0 b_1 q \sigma +2 a_1 b_2 q \sigma +2 a_0 b_1 r \sigma +2 a_1 b_2 r \sigma -2 b_1 \nu +4 b_1 \Lambda \mu ^2 p \sigma \upsilon \\&\quad +12 b_2 \Lambda \mu ^2 p \sigma \varUpsilon +2 b_1 \mu ^2 p \sigma \varUpsilon ^2=0, \\&2 a_2 b_1 q \sigma +2 a_2 b_1 r \sigma -2 a_1 \nu +4 a_1 \Lambda \mu ^2 p \sigma \upsilon +12 a_2 \mu ^2 p \sigma \upsilon \varUpsilon \\&\quad +2 a_1 \mu ^2 p \sigma \varUpsilon ^2+2 a_0 a_1 q \sigma +2 a_0 a_1 r \sigma =0, \\&-2 a_2 \nu +16 a_2 \Lambda \mu ^2 p \sigma \upsilon +6 a_1 \Lambda \mu ^2 p \sigma \varUpsilon +8 a_2 \mu ^2 p \sigma \varUpsilon ^2+a_1^2 q \sigma \\&\quad +2 a_0 a_2 q \sigma +a_1^2 r \sigma +2 a_0 a_2 r \sigma =0,\\&4 a_1 \Lambda ^2 \mu ^2 p \sigma +20 a_2 \Lambda \mu ^2 p \sigma \varUpsilon +2 a_1 a_2 q \sigma +2 a_1 a_2 r \sigma =0, \\&12 b_2 \mu ^2 p \sigma \upsilon ^2+b_2^2 q \sigma +b_2^2 r \sigma =0, \\&12 a_2 \Lambda ^2 \mu ^2 p \sigma +a_2^2 q \sigma +a_2^2 r \sigma =0, \end{aligned}$$
(4.12)

we solve the equations of an algebraic system (4.12) and we get the following outcomes

Set:1

$$\begin{aligned} a_0&=-\frac{12 \Lambda \mu ^2 p \upsilon }{q+r},a_1=-\frac{12 \Lambda \mu ^2 p \varUpsilon }{q+r},a_2=-\frac{12 \Lambda ^2 \mu ^2 p}{q+r},b_1=b_2= 0,\\ \nu&=\mu ^2 p \sigma \varUpsilon ^2-4 \Lambda \mu ^2 p \sigma \upsilon , \end{aligned}$$

we putting the above values of unknown constants in the Eq. (4.11) and have different types of solutions mentioned in (3.7), (3.8), (3.9), (3.10) and (3.11).

Case:1 if \(\Lambda \upsilon >0\) and \(\varUpsilon =0\), then we have trigonometric solution as

$$\begin{aligned} {\mathcal {U}}_{1a}(\zeta )&=-\frac{12 \Lambda \mu ^2 p \upsilon }{q+r}-\frac{12 \Lambda \mu ^2 p \varUpsilon }{q+r}\left( \frac{\sqrt{\Lambda \upsilon } \left( \phi _2 \sin \left( \zeta \sqrt{\Lambda \upsilon }\right) +\phi _1 \cos \left( \zeta \sqrt{\Lambda \upsilon }\right) \right) }{\upsilon \left( \phi _2 \cos \left( \zeta \sqrt{\Lambda \upsilon }\right) -\phi _1 \sin \left( \zeta \sqrt{\Lambda \upsilon }\right) \right) }\right) \\&\quad -\frac{12 \Lambda ^2 \mu ^2 p}{q+r}\left( \frac{\sqrt{\Lambda \upsilon } \left( \phi _2 \sin \left( \zeta \sqrt{\Lambda \upsilon }\right) +\phi _1 \cos \left( \zeta \sqrt{\Lambda \upsilon }\right) \right) }{\upsilon \left( \phi _2 \cos \left( \zeta \sqrt{\Lambda \upsilon }\right) -\phi _1 \sin \left( \zeta \sqrt{\Lambda \upsilon }\right) \right) }\right) ^2, \end{aligned}$$
(4.13)

where \(\zeta =\mu x+\sigma y-\frac{\nu \left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }}{\beta }\), \(\zeta =\mu x+\sigma y-\nu \frac{\Gamma (\chi +1 )}{\beta } t^{\beta }\) and \(\zeta =\mu x+\sigma y-\frac{\nu }{\beta } t^{\beta }\).

Case:2 if \(\Lambda \upsilon <0\) and \(\varUpsilon =0\), then we get hyperbolic function as

$$\begin{aligned} {\mathcal {U}}_{1b}(\zeta )&= -\frac{12 \Lambda \mu ^2 p \upsilon }{q+r}-\frac{12 \Lambda \mu ^2 p \varUpsilon }{q+r}\\&\quad \times \left( \frac{-\sqrt{| \Lambda \upsilon | } \left( \phi _1 \sinh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _2\right) }{\upsilon \left( \phi _1 \sinh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) -\phi _2\right) }\right) \\&\quad -\frac{12 \Lambda ^2 \mu ^2 p}{q+r}\left( -\frac{\sqrt{| \Lambda \upsilon | } \left( \phi _1 \sinh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _2\right) }{\upsilon \left( \phi _1 \sinh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) -\phi _2\right) }\right) ^2, \end{aligned}$$
(4.14)

Case:3 if \(\Lambda \ne 0,\upsilon =\varUpsilon =0\), then we attain rational function as

$$\begin{aligned} {\mathcal {U}}_{1 c}(\zeta )=-\frac{12 \Lambda \mu ^2 p \upsilon }{q+r}-\frac{\left( -\phi _1\right) \left( 12 \Lambda \mu ^2 p \varUpsilon \right) }{(q+r) \left( \Lambda \left( \zeta \phi _1+\phi _2\right) \right) }-\frac{\left( -\frac{\phi _1}{\Lambda \left( \zeta \phi _1+\phi _2\right) }\right) {}^2 \left( 12 \Lambda ^2 \mu ^2 p\right) }{q+r}, \end{aligned}$$
(4.15)

Case:4 if \(\varUpsilon \ne 0,\Delta \ge 0\), where \(\Delta =\varUpsilon ^2-4 \Lambda \upsilon\) then we attain

$$\begin{aligned} {\mathcal {U}}_{1 d}(\zeta )&= -\frac{12 \Lambda \mu ^2 p \upsilon }{q+r}-\frac{\left( 12 \Lambda \mu ^2 p \varUpsilon \right) \left( -\frac{\sqrt{\Delta } \left( \phi _2 \sinh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) +\phi _1 \cosh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) \right) }{2 \Lambda \left( \phi _1 \sinh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) +\phi _2 \cosh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) }{q+r}\\&\quad -\frac{\left( 12 \Lambda ^2 \mu ^2 p\right) \left( -\frac{\sqrt{\Delta } \left( \phi _2 \sinh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) +\phi _1 \cosh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) \right) }{2 \Lambda \left( \phi _1 \sinh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) +\phi _2 \cosh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^2}{q+r}, \end{aligned}$$
(4.16)

Case:5 if \(\varUpsilon \ne 0,\Delta < 0\), then we have

$$\begin{aligned} {\mathcal {U}}_{1 e}(\zeta )&=-\frac{12 \Lambda \mu ^2 p \upsilon }{q+r}-\frac{\left( 12 \Lambda \mu ^2 p \varUpsilon \right) \left( -\frac{\sqrt{-\Delta } \left( \phi _1 \cos \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) -\phi _2 \sin \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) \right) }{2 \Lambda \left( \phi _1 \sin \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) +\phi _2 \cos \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) }{q+r} \\&\quad -\frac{\left( 12 \Lambda ^2 \mu ^2 p\right) \left( -\frac{\sqrt{-\Delta } \left( \phi _1 \cos \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) -\phi _2 \sin \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) \right) }{2 \Lambda \left( \phi _1 \sin \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) +\phi _2 \cos \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^2}{q+r}, \end{aligned}$$
(4.17)

Set:2

$$\begin{aligned} a_0&=-\frac{2 \mu ^2 p \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{q+r},a_1=a_2=0,b_1=-\frac{12 \mu ^2 p \upsilon \varUpsilon }{q+r},b_2=-\frac{12 \mu ^2 p \upsilon ^2}{q+r},\\ \nu&=\mu ^2 p \sigma \left( 4 \Lambda \upsilon -\varUpsilon ^2\right) , \end{aligned}$$

we put the above solutions of unknown constants in the Eq. (4.11).

Case:1 if \(\Lambda \upsilon >0\) and \(\varUpsilon =0\), then we have

$$\begin{aligned} {\mathcal {U}}_{2 a}(\zeta )&=-\frac{2 \mu ^2 p \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{q+r}-\frac{\left( 12 \mu ^2 p \upsilon \varUpsilon \right) \left( \frac{\sqrt{\Lambda \upsilon } \left( \phi _2 \sin \left( \zeta \sqrt{\Lambda \upsilon }\right) +\phi _1 \cos \left( \zeta \sqrt{\Lambda \upsilon }\right) \right) }{\upsilon \left( \phi _2 \cos \left( \zeta \sqrt{\Lambda \upsilon }\right) -\phi _1 \sin \left( \zeta \sqrt{\Lambda \upsilon }\right) \right) }\right) ^{-1}}{q+r} \\&\quad -\frac{\left( 12 \mu ^2 p \upsilon ^2\right) \left( \frac{\sqrt{\Lambda \upsilon } \left( \phi _2 \sin \left( \zeta \sqrt{\Lambda \upsilon }\right) +\phi _1 \cos \left( \zeta \sqrt{\Lambda \upsilon }\right) \right) }{\upsilon \left( \phi _2 \cos \left( \zeta \sqrt{\Lambda \upsilon }\right) -\phi _1 \sin \left( \zeta \sqrt{\Lambda \upsilon }\right) \right) }\right) ^{-2}}{q+r}, \end{aligned}$$
(4.18)

Case:2 if \(\Lambda \upsilon <0\) and \(\varUpsilon =0\), then we get

$$\begin{aligned} {\mathcal {U}}_{2 b}(\zeta )&=-\frac{2 \mu ^2 p \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{q+r}\\&\quad -\frac{\left( 12 \mu ^2 p \upsilon \varUpsilon \right) \left( -\frac{\sqrt{| \Lambda \upsilon | } \left( \phi _1 \sinh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _2\right) }{\upsilon \left( \phi _1 \sinh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) -\phi _2\right) }\right) ^{-1}}{q+r} \\&\quad -\frac{\left( 12 \mu ^2 p \upsilon ^2\right) \left( -\frac{\sqrt{| \Lambda \upsilon | } \left( \phi _1 \sinh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _2\right) }{\upsilon \left( \phi _1 \sinh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \zeta \sqrt{| \Lambda \upsilon | }\right) -\phi _2\right) }\right) ^{-2}}{q+r}, \end{aligned}$$
(4.19)

Case:3 if \(\Lambda \ne 0,\upsilon =\varUpsilon =0\), then we attain rational function as

$$\begin{aligned} {\mathcal {U}}_{2 c}(\zeta )&=-\frac{2 \mu ^2 p \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{q+r}-\frac{\left( -\frac{\phi _1}{\Lambda \left( \zeta \phi _1+\phi _2\right) }\right) ^{-1} \left( 12 \mu ^2 p \upsilon \varUpsilon \right) }{q+r}\nonumber \\&\quad -\frac{\left( -\frac{\phi _1}{\Lambda \left( \zeta \phi _1+\phi _2\right) }\right) ^{-2} \left( 12 \mu ^2 p \upsilon ^2\right) }{q+r}, \end{aligned}$$
(4.20)

Case:4 if \(\varUpsilon \ne 0,\Delta \ge 0\), where \(\Delta =\varUpsilon ^2-4 \Lambda \upsilon\) then we ascertain

$$\begin{aligned} {\mathcal {U}}_{2 d}(\zeta )&= -\frac{2 \mu ^2 p \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{q+r}\\&\quad -\frac{\left( 12 \mu ^2 p \upsilon \varUpsilon \right) \left( -\frac{\sqrt{\Delta } \left( \phi _2 \sinh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) +\phi _1 \cosh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) \right) }{2 \Lambda \left( \phi _1 \sinh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) +\phi _2 \cosh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^{-1}}{q+r}\\&\quad -\frac{\left( 12 \mu ^2 p \upsilon ^2\right) \left( -\frac{\sqrt{\Delta } \left( \phi _2 \sinh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) +\phi _1 \cosh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) \right) }{2 \Lambda \left( \phi _1 \sinh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) +\phi _2 \cosh \left( \frac{\sqrt{\Delta }}{2 \zeta }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^{-2}}{q+r}, \end{aligned}$$
(4.21)

Case:5 if \(\varUpsilon \ne 0,\Delta < 0\), then we have

$$\begin{aligned} {\mathcal {U}}_{2 e}(\zeta )&= -\frac{2 \mu ^2 p \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{q+r}\\&\quad -\frac{\left( 12 \mu ^2 p \upsilon \varUpsilon \right) \left( -\frac{\sqrt{-\Delta } \left( \phi _1 \cos \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) -\phi _2 \sin \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) \right) }{2 \Lambda \left( \phi _1 \sin \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) +\phi _2 \cos \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^{-1}}{q+r}\\&\quad -\frac{\left( 12 \mu ^2 p \upsilon ^2\right) \left( -\frac{\sqrt{-\Delta } \left( \phi _1 \cos \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) -\phi _2 \sin \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) \right) }{2 \Lambda \left( \phi _1 \sin \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) +\phi _2 \cos \left( \frac{\sqrt{-\Delta }}{2 \zeta }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^{-2}}{q+r}, \end{aligned}$$
(4.22)

4.2 Wazwaz Kaur Boussinesq equation

Consider the (\(2+1\))-dimensional non-linear WKB equation (Silambarasan and Nisar 2023) of the form

$$\begin{aligned} \vartheta _{tt}+\varkappa _3 \vartheta _{ty}-\varkappa _1 \vartheta _{xx}^2-\vartheta _{xx}-\varkappa _2 \vartheta _{xxxx}+\frac{1}{4} \varkappa _3^2 \vartheta _{yy}=0, \end{aligned}$$
(4.23)

here, \(\vartheta =\vartheta (x,y,t)\) and \(\varkappa _i, i=1,2,3\) are the nonzero constants. This non-linear model can be expressed as in the sense of \(\beta\)-derivative such as

$$\begin{aligned} D_{\beta ,t}^{\kappa } \vartheta _{tt}+\varkappa _3 D_{\beta ,t}^{\kappa } \vartheta _{ty}-\varkappa _1 \vartheta _{xx}^2-\vartheta _{xx}-\varkappa _2 \vartheta _{xxxx}+\frac{1}{4} \varkappa _3^2 \vartheta _{yy}=0, \end{aligned}$$
(4.24)

where \(D_{\beta ,t}^{\kappa }\) is \(\beta\)-D of \(\vartheta (y,z,t)\) and the term \(\kappa\) shows the fractional parameter and \(0<\kappa \le 1\).

In M-TD, the suggested model has the following structure.

$$\begin{aligned} D_{M,t}^{\kappa } \vartheta _{tt}+\varkappa _3 D_{M,t}^{\kappa } \vartheta _{ty}-\varkappa _1 \vartheta _{xx}^2-\vartheta _{xx}-\varkappa _2 \vartheta _{xxxx}+\frac{1}{4} \varkappa _3^2 \vartheta _{yy}=0, \end{aligned}$$
(4.25)

where \(D_{M,t}^{\kappa }\) is M-TD with \(\kappa\) is fractional order.

In C-D, the suggested model has the following structure.

$$\begin{aligned} D_{C,t}^{\kappa } \vartheta _{tt}+\varkappa _3 D_{C,t}^{\kappa } \vartheta _{ty}-\varkappa _1 \vartheta _{xx}^2-\vartheta _{xx}-\varkappa _2 \vartheta _{xxxx}+\frac{1}{4} \varkappa _3^2 \vartheta _{yy}=0, \end{aligned}$$
(4.26)

where \(D_{C,t}^{\kappa }\) is C-D with \(\kappa\) is conformable operator.

Consider the wave transformation \(\vartheta (x,y,t)=\vartheta (\psi )\) and \(\psi =u(x+y+\lambda t)\), where u is represent the wave number and \(\lambda\) represent the frequency. There are three different types of definitions for the travelling wave parameter \(\psi\).

In \(\beta\)-D, \(\psi\) takes on the following form

$$\begin{aligned} \vartheta (x,y,t)=\vartheta (\psi ), \psi =u\left( x+y+\frac{\lambda \left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }}{\beta }\right) . \end{aligned}$$
(4.27)

In M-TD, \(\psi\) takes on the following form

$$\begin{aligned} \vartheta (x,y,t)=\vartheta (\psi ), \psi =u\left( x+y+\lambda \frac{\Gamma (\chi +1 )}{\beta } t^{\beta }\right) . \end{aligned}$$
(4.28)

In C-D, \(\psi\) takes on the following form

$$\begin{aligned} \vartheta (x,y,t)=\vartheta (\psi ), \psi =u\left( x+y+ \frac{\lambda }{\beta } t^{\beta }\right) . \end{aligned}$$
(4.29)

Convert the PDE’s represents in Eq. (4.24), (4.25) and (4.26) into ODE by using the wave transformations showed in (4.27), (4.28) and (4.29) and we get

$$\begin{aligned} -4 u^2 \varkappa _2 \vartheta ^{(4)}+ \left( 4 \lambda ^2-4 \lambda \varkappa _3+\varkappa _3^2-4\right) \vartheta ^{(2)} -8 \varkappa _1 \left( \vartheta \vartheta ^{(2)}+\left( \vartheta ^{(1)}\right) ^2\right) =0, \end{aligned}$$
(4.30)

here, Eq. (4.30) is integrable and also integrates twice with respect to \(\psi\) and taking integration constant equal to zero and we attain the ODE such as

$$\begin{aligned} -4 u^2 \varkappa _2\vartheta ^{(2)} -4 \varkappa _1 \vartheta ^2+\left( 4 \lambda ^2-4 \lambda \varkappa _3+\varkappa _3^2-4\right) \vartheta =0, \end{aligned}$$
(4.31)

in Eq. (4.31), compare the highest linear term and non-linear term according to the balancing principle and we get balance number \(N=2\). Initially, we assume the solution of the Eq. (4.31) by using Eq. (3.4) as

$$\begin{aligned} \vartheta (\psi )=a_0+a_1\left( \frac{ G^{\prime }(\psi )}{G(\psi )^2}\right) +a_2 \left( \frac{G^{\prime }(\psi )}{G(\psi )^2}\right) ^2+b_1 \left( \frac{G^{\prime }(\psi )}{G(\psi )^2}\right) ^{-1}+b_2 \left( \frac{G^{\prime }(\psi )}{G(\psi )^2}\right) ^{-2}, \end{aligned}$$
(4.32)

where \(G=G(\psi )\), and \(a_0,a_1,a_2,b_1,b_2\) are the unknown constants whose values we want to find. According to the Eq. (4.31), we substitute the Eq. (4.32) with the help of Eq. (3.5) into the Eq. (4.31). After substitution, we have collected all such coefficients like power as \(\left( \frac{G^{\prime }}{G^2}\right) ^i,\,(i=0,\pm 1,\pm 2,\pm 3,\ldots )\). Due to this process, we attain an algebraic system of equations and by solving this system of equations by using Mathematica software, we get the following outcomes

Set:1

$$\begin{aligned} a_0&=-\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1},a_1=a_2=0,b_1=-\frac{6 u^2 \upsilon \varkappa _2 \varUpsilon }{\varkappa _1},\\ \lambda&=\frac{1}{2} \left( \varkappa _3-2 \sqrt{4 \Lambda \upsilon u^2 \varkappa _2+u^2 \varkappa _2 \left( -\varUpsilon ^2\right) +1}\right) ,\\ b_2&=-\frac{6 u^2 \upsilon ^2 \varkappa _2}{\varkappa _1}, \end{aligned}$$

we putting the values of unknown constants in the Eq. (4.32), that are included in (Set:1) and the term \(\left( \frac{G^{\prime }}{G^2}\right)\) involved in Eq. (4.32) have different types of solutions represents in Eqs. (3.7), (3.8), (3.9), (3.10) and (3.11), then we have

Case:1 if \(\Lambda \upsilon >0\) and \(\varUpsilon =0\), then we have trigonometric solution as

$$\begin{aligned} \vartheta _{1 a}(\psi )&=-\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1}-\frac{\left( 6 u^2 \upsilon \varkappa _2 \varUpsilon \right) \left( \frac{\sqrt{\Lambda \upsilon } \left( \phi _2 \sin \left( \psi \sqrt{\Lambda \upsilon }\right) +\phi _1 \cos \left( \psi \sqrt{\Lambda \upsilon }\right) \right) }{\upsilon \left( \phi _2 \cos \left( \psi \sqrt{\Lambda \upsilon }\right) -\phi _1 \sin \left( \psi \sqrt{\Lambda \upsilon }\right) \right) }\right) ^{-1}}{\varkappa _1} \\&\quad -\frac{\left( 6 u^2 \upsilon ^2 \varkappa _2\right) \left( \frac{\sqrt{\Lambda \upsilon } \left( \phi _2 \sin \left( \psi \sqrt{\Lambda \upsilon }\right) +\phi _1 \cos \left( \psi \sqrt{\Lambda \upsilon }\right) \right) }{\upsilon \left( \phi _2 \cos \left( \psi \sqrt{\Lambda \upsilon }\right) -\phi _1 \sin \left( \psi \sqrt{\Lambda \upsilon }\right) \right) }\right) ^{-2}}{\varkappa _1}, \end{aligned}$$
(4.33)

where \(\psi =u\left( x+y+\frac{\lambda \left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }}{\beta }\right) , \psi =u\left( x+y+\lambda \frac{\Gamma (\chi +1 )}{\beta } t^{\beta }\right)\) and \(\psi =u\left( x+y+ \frac{\lambda }{\beta } t^{\beta }\right)\).

Case:2 if \(\Lambda \upsilon <0\) and \(\varUpsilon =0\), then we get hyperbolic function as

$$\begin{aligned} \vartheta _{1 b}(\psi )&=-\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1}\\&\quad -\frac{\left( 6 u^2 \upsilon \varkappa _2 \varUpsilon \right) \left( -\frac{\sqrt{| \Lambda \upsilon | } \left( \phi _1 \sinh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _2\right) }{\upsilon \left( \phi _1 \sinh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) -\phi _2\right) }\right) ^{-1}}{\varkappa _1} \\&\quad -\frac{\left( 6 u^2 \upsilon ^2 \varkappa _2\right) \left( -\frac{\sqrt{| \Lambda \upsilon | } \left( \phi _1 \sinh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _2\right) }{\upsilon \left( \phi _1 \sinh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) -\phi _2\right) }\right) ^{-2}}{\varkappa _1}, \end{aligned}$$
(4.34)

Case:3 if \(\Lambda \ne 0,\upsilon =\varUpsilon =0\), then we ascertain rational function as

$$\begin{aligned} \vartheta _{1 c}(\psi )&=-\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1}-\frac{\left( -\frac{\phi _1}{\Lambda \left( \psi \phi _1+\phi _2\right) }\right) ^{-1} \left( 6 u^2 \upsilon \varkappa _2 \varUpsilon \right) }{\varkappa _1}\nonumber \\&\quad -\frac{\left( -\frac{\phi _1}{\Lambda \left( \psi \phi _1+\phi _2\right) }\right) ^{-2} \left( 6 u^2 \upsilon ^2 \varkappa _2\right) }{\varkappa _1}, \end{aligned}$$
(4.35)

Case:4 if \(\varUpsilon \ne 0,\Delta \ge 0\), where \(\Delta =\varUpsilon ^2-4 \Lambda \upsilon\) then we get

$$\begin{aligned} \vartheta _{1 d}(\psi )&= -\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1}\\&\quad -\frac{\left( 6 u^2 \upsilon \varkappa _2 \varUpsilon \right) \left( -\frac{\sqrt{\Delta } \left( \phi _2 \sinh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) +\phi _1 \cosh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) \right) }{2 \Lambda \left( \phi _1 \sinh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) +\phi _2 \cosh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^{-1}}{\varkappa _1}\\&\quad -\frac{\left( 6 u^2 \upsilon ^2 \varkappa _2\right) \left( -\frac{\sqrt{\Delta } \left( \phi _2 \sinh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) +\phi _1 \cosh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) \right) }{2 \Lambda \left( \phi _1 \sinh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) +\phi _2 \cosh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^{-2}}{\varkappa _1}, \end{aligned}$$
(4.36)

Case:5 if \(\varUpsilon \ne 0,\Delta < 0\), then we have

$$\begin{aligned} \vartheta _{1 e}(\psi )&=-\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1}\\&\quad -\frac{\left( 6 u^2 \upsilon \varkappa _2 \varUpsilon \right) \left( -\frac{\sqrt{-\Delta } \left( \phi _1 \cos \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) -\phi _2 \sin \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) \right) }{2 \Lambda \left( \phi _1 \sin \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) +\phi _2 \cos \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^{-1}}{\varkappa _1} \\&\quad -\frac{\left( 6 u^2 \upsilon ^2 \varkappa _2\right) \left( -\frac{\sqrt{-\Delta } \left( \phi _1 \cos \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) -\phi _2 \sin \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) \right) }{2 \Lambda \left( \phi _1 \sin \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) +\phi _2 \cos \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^{-2}}{\varkappa _1}, \end{aligned}$$
(4.37)

Set:2

$$\begin{aligned} a_0&=-\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1},a_1=-\frac{6 \Lambda u^2 \varkappa _2 \varUpsilon }{\varkappa _1},a_2=-\frac{6 \Lambda ^2 u^2 \varkappa _2}{\varkappa _1},\\ \lambda&=\frac{1}{2} \left( 2 \sqrt{4 \Lambda \upsilon u^2 \varkappa _2+u^2 \varkappa _2 \left( -\varUpsilon ^2\right) +1}+\varkappa _3\right) ,\\ b_1&=b_2=0, \end{aligned}$$

we putting the values of unknown constants in the Eq. (4.32), that are included in (Set:2) and we get

Case:1 if \(\Lambda \upsilon >0\) and \(\varUpsilon =0\), then we have

$$\begin{aligned} \vartheta _{2 a}(\psi )&= -\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1}\\&\quad -\frac{\left( 6 \Lambda u^2 \varkappa _2 \varUpsilon \right) \left( \sqrt{\Lambda \upsilon } \left( \phi _2 \sin \left( \psi \sqrt{\Lambda \upsilon }\right) +\phi _1 \cos \left( \psi \sqrt{\Lambda \upsilon }\right) \right) \right) }{\varkappa _1 \left( \upsilon \left( \phi _2 \cos \left( \psi \sqrt{\Lambda \upsilon }\right) -\phi _1 \sin \left( \psi \sqrt{\Lambda \upsilon }\right) \right) \right) } \\&\quad -\frac{\left( 6 \Lambda ^2 u^2 \varkappa _2\right) \left( \frac{\sqrt{\Lambda \upsilon } \left( \phi _2 \sin \left( \psi \sqrt{\Lambda \upsilon }\right) +\phi _1 \cos \left( \psi \sqrt{\Lambda \upsilon }\right) \right) }{\upsilon \left( \phi _2 \cos \left( \psi \sqrt{\Lambda \upsilon }\right) -\phi _1 \sin \left( \psi \sqrt{\Lambda \upsilon }\right) \right) }\right) ^2}{\varkappa _1}, \end{aligned}$$
(4.38)

Case:2 if \(\Lambda \upsilon <0\) and \(\varUpsilon =0\), then we get hyperbolic function as

$$\begin{aligned} \vartheta _{2 b}(\psi )&= -\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1}\\&\quad -\frac{\left( 6 \Lambda u^2 \varkappa _2 \varUpsilon \right) \left( -\sqrt{| \Lambda \upsilon | } \left( \phi _1 \sinh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _2\right) \right) }{\varkappa _1 \left( \upsilon \left( \phi _1 \sinh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) -\phi _2\right) \right) }\\&\quad -\frac{\left( 6 \Lambda ^2 u^2 \varkappa _2\right) \left( -\frac{\sqrt{| \Lambda \upsilon | } \left( \phi _1 \sinh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _2\right) }{\upsilon \left( \phi _1 \sinh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) +\phi _1 \cosh \left( 2 \psi \sqrt{| \Lambda \upsilon | }\right) -\phi _2\right) }\right) ^2}{\varkappa _1}, \end{aligned}$$
(4.39)

Case:3 if \(\Lambda \ne 0,\upsilon =\varUpsilon =0\), then we ascertain rational function as

$$\begin{aligned} \vartheta _{2 c}(\psi )= -\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1}-\frac{\phi _1 \left( 6 \Lambda u^2 \varkappa _2 \varUpsilon \right) }{\varkappa _1 \left( \Lambda \left( \psi \phi _1+\phi _2\right) \right) }-\frac{\left( -\frac{\phi _1}{\Lambda \left( \psi \phi _1+\phi _2\right) }\right) ^2 \left( 6 \Lambda ^2 u^2 \varkappa _2\right) }{\varkappa _1}, \end{aligned}$$
(4.40)

Case:4 if \(\varUpsilon \ne 0,\Delta \ge 0\), then we get

$$\begin{aligned} \vartheta _{2 d}(\psi )&= -\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1}\\&\quad -\frac{6 \Lambda u^2 \varkappa _2 \varUpsilon }{\varkappa _1} \left( -\frac{\sqrt{\Delta } \left( \phi _2 \sinh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) +\phi _1 \cosh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) \right) }{2 \Lambda \left( \phi _1 \sinh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) +\phi _2 \cosh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) \\&\quad -\frac{\left( 6 \Lambda ^2 u^2 \varkappa _2\right) \left( -\frac{\sqrt{\Delta } \left( \phi _2 \sinh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) +\phi _1 \cosh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) \right) }{2 \Lambda \left( \phi _1 \sinh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) +\phi _2 \cosh \left( \frac{\sqrt{\Delta }}{2 \psi }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^2}{\varkappa _1}, \end{aligned}$$
(4.41)

Case:5 if \(\varUpsilon \ne 0,\Delta < 0\), then we have

$$\begin{aligned} \vartheta _{2 e}(\psi )&= -\frac{u^2 \varkappa _2 \left( 2 \Lambda \upsilon +\varUpsilon ^2\right) }{\varkappa _1}-\frac{\left( 6 \Lambda u^2 \varkappa _2 \varUpsilon \right) \left( -\frac{\sqrt{-\Delta } \left( \phi _1 \cos \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) -\phi _2 \sin \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) \right) }{2 \Lambda \left( \phi _1 \sin \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) +\phi _2 \cos \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) }{\varkappa _1}\\&\quad -\frac{\left( 6 \Lambda ^2 u^2 \varkappa _2\right) \left( -\frac{\sqrt{-\Delta } \left( \phi _1 \cos \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) -\phi _2 \sin \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) \right) }{2 \Lambda \left( \phi _1 \sin \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) +\phi _2 \cos \left( \frac{\sqrt{-\Delta }}{2 \psi }\right) \right) }-\frac{\varUpsilon }{2 \Lambda }\right) ^2}{\varkappa _1}. \end{aligned}$$
(4.42)

5 Graphical results and discussion

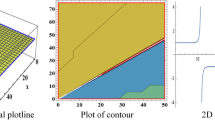
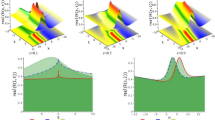
In this research, some fractional derivative operators were used to solve the non-linear coupled Riemann wave equation and Wazwaz Kaur Boussinesq equation. The solutions were attained by employing the reliable integration technique known as modified \((\frac{G^{\prime }}{G^2})\)-expansion with the aid of conformable, Beta and M-truncated derivative operators. The results of this method’s multiple solutions generation are contrasted in 2D and 3D graphs for three different derivative operators. This method provides the different types of optical solitary wave solutions including dark soliton, bright soliton, dark-bright soliton, and W-shaped soliton solutions. C-D and the fractional derivatives, such as \(\beta\)-D and M-TD, can be compared perfectly using 2-dimensional graphs, which is quite useful. We observe that the solitary waves tiny shifts when the change fractional derivative operator is without changing the shape of the curve. This demonstrates that their travelling wave solutions are symmetric. A single solution can lead to the production of multiple types of solutions if the parameters take on various specific values. The modified \((\frac{G^{\prime }}{G^2})\)-expansion technique was used to obtain the soliton solutions. They provide a visual representation of the spatial and temporal behaviour of solitary waves. The analytical solution’s graphs make it abundantly evident that the modified \((\frac{G^{\prime }}{G^2})\)-expansion method is more reliable and effective (Figs. 1, 2 and 3).

Fig. 1
figure 1

The 2-D and 3-D W-type wave representation of \({\mathcal {U}}_{2 b}\) for the specific values of \(p=0.6,\sigma =0.2,\mu =0.4,\Lambda =-1.2,\upsilon =1,\phi _1=1,\varUpsilon =0,\phi _2=3,q=0.3,r=0.2\). a \(\beta\)-D with fractional order is 0.6, b M-TD with fractional order is 0.6 and \(\chi =1.3\), c C-D with fractional order is 0.6

Full size image
Fig. 2
figure 2

The 2-D and 3-D dark type wave form representation of \(\vartheta _{1 b}\) for the specific values of \(u=0.9,\varkappa _1=0.2,\varkappa _2=0.5,\varkappa _3=0.1,\Lambda =0.1,\upsilon =-1.5,\varUpsilon =0,\phi _1=2,\phi _2=1\). a \(\beta\)-D with fractional order is 0.7, b M-TD with fractional order is 0.7 and \(\chi =1.5\), c C-D with fractional order is 0.7

Full size image
Fig. 3
figure 3

The 2-D and 3-D dark-bright type wave form of \(\vartheta _{2 d}\) for the specific values of \(u=0.2,\varkappa _1=0.2,\varkappa _2=0.5,\varkappa _3=0.5,\Lambda =0.2,\upsilon =0.1,\varUpsilon =2,\phi _1=1,\phi _2=2\). a \(\beta\)-D with fractional order is 0.6, b M-TD with fractional order is 0.6 and \(\chi =0.8\), c C-D with fractional order is 0.6

Full size image

6 Conclusion

Modified \((\frac{G^{\prime }}{G^2})\)-expansion technique has been successfully applied to construct new traveling optical wave solutions for the non-linear CRW equation and NLWKB equation. The ability to find new solutions using this technique can provide valuable insights into the behavior of non-linear problems described by fractional differential equations. We construct new solitary wave solutions such as dark, dark-bright and W-type soliton solutions with the help of C-D, \(\beta\)-D and M-TD. In this work, the fractional derivatives are successfully compared and analysed. This demonstrates the effectiveness and reliability of C-D and the fractional derivatives such as \(\beta\)-D and M-TD, but the \(\beta\) derivative works better than the other two derivatives. The solitary wave solutions that have been found will be useful in the study of issues involving engineering, mechanical theory, tsunamis, and tidal waves. Graphically it has been observed that the solitary waves tiny shifts when the change fractional derivative operator is without changing the shape of the curve. This demonstrates that their travelling wave solutions are symmetric. Modified \((\frac{G^{\prime }}{G^2})\)-expansion technique, involves assuming an expansion for the solution and using algebraic manipulation to determine the functions in the expansion. The success of this method in constructing solutions for the non-linear CRW and WKB equations indicates its versatility in dealing with various types of fractional differential equations and capturing the dynamics of such models accurately.