1 Introduction

The study of wave scattering, diffraction, and gratings caused by periodic patterns is critical in electromagnetic and optical theory. A variety of numerical and analytical techniques have been evolved, and diffraction mechanisms for a wide range of periodic structures have been investigated (Nosich 1993). An analytical regularization technique has been developed for wave scattering and eigenvalue problems and this bases on the conversion of a first kind or strongly singular second kind integral equation to a second kind integral equation of smoother kernel (Nosich 1999). For electromagnetic field with inhomogeneous media, a combination of improved Fourier series expansion method and extrapolation method has been used to obtain the correct value of eigenvalue and eigenvectors for the case of TM wave (Yamasaki et al. 2005). The exact relativistic outcome has been obtained for scattering of electromagnetic wave by a perfectly conducting wedge in uniform translational motion and the simulation results of Doppler frequency spectra have been presented (De Cupis et al. 2002). A comprehensive study on electromagnetic wave propagation in free space and complex geometries has been performed which has explored the comparison of simulation results with analytical solutions, experimental data, and other numerical methods to ensure the accuracy and reliability of the analysis (Kunnz and Luebbers 1993). The Wiener–Hopf method is still useful for modern scientists, and its range of applications is expanding (Lawrie and Abrahams 2007). The majority of foregoing published work subject to this technique demonstrates the Wiener–Hopf technique’s applicability to several disciplines of natural sciences and engineering (Noble 1958). It provides a powerful way of coping with a diverse range of problems related to scattering that may be tackled through Mellin, Laplace, and Fourier transforms. A mathematical model was developed for line and point source diffraction of electromagnetic wave theory by conductible half plane (Jones 1964) which was further applied to acoustic model for line/point source diffraction by considering rigid half plane (Jones 1972). This innovative idea was used to calculate the scattering by junction of transmissive and soft-hard plane (Ayub et al. 2008). The line source diffraction for slit was modelled to figure out the effects of absorption and Mach number on the amplitude of the velocity potential (Ayub et al. 2009) which was further extended to a three dimensional study in terms of the point source to calculate the diffraction of spherical waves (Nawaz et al. 2014). The scattering theory of electromagnetic waves for more complex structures such as semi-infinite parallel-plate wave-guide with sinusoidal wall corrugation (Zheng and Kobayashi 2009) as well as finite sinusoidal grating (Eizawa and Kobayashi 2014) were investigated through combined analysis of Wiener–Hopf method and perturbation technique. A series solution of electromagnetic plane wave scattering was obtained in terms of the eigenfunctions appearing as the generalized Gamma function (Nawaz and Ayub 2015). Also, a few years ago, the boundary diffraction wave theory in three-dimensions was used to investigate the plane-wave scattering by a non-continuous edge curves (Umul 2019). The Wiener–Hopf technique has benefited in modelling the diffraction of waves by the obstacles in moving fluid (Ayub et al. 2009). This technique also works well to calculate the scattering of waves by vibrating objects (Alkinidri et al. 2023).

The transmission of electromagnetic waves in a hot plasma has piqued the researchers curiosity for many years. The aforementioned issue is incredibly important since it can provide natural communications networks. The reflection and transmission of radio waves from and through the ionosphere, in particular, have got a great deal of attention. It is a worth mentioning that non-thermal plasma is defined as plasma with little or no pressure change but a fixed temperature. The wave propagation qualities of spacecrafts sitting in the non-thermal plasma ionosphere and antenna are critical for signal connection between ground stations and space vehicles. Researchers have spent the last several decades studying traditional diffraction difficulties in the context of non-thermal plasma in a variety of configurations. At atmospheric pressure, plasma considered as a reflector as well as absorber of electromagnetic radiation (Vidmar 1990). The bidirectional wave transformation of equations formulated for non-thermal plasma were investigated (Tippet and Ziolkowski 1991). The propagation of ultra-wide band electromagnetic pulses in a homogenous cold plasma was studied (Dvorak et al. 1997). Many researchers expressed a strong desire to explore the impact of non-thermal plasma on plane-wave diffraction challenges for various geometries. The effects of non-thermal plasma were investigated on plane-wave diffraction by a half-plane with Leontovich conditions (Yener and Serbest 2002). In the recent years, a rapid advancement in the diffraction theory of electromagnetic waves in the vicinity of non-thermal plasma as an anisotropic medium has been observed. To mention a few, a parallel plate wave-guide for the diffraction of polarized plane-wave was modelled along with impedance conditions on the surface to investigate the effects of impedance characteristics in the presence of non-thermal plasma (Khan et al. 2014). A similar study was also performed to look in to two distinct types of antennas in Ayub et al. (2016). Later, a mathematical model for diffraction of EM-waves by a finite length flat plate with Dirichlet conditions was devised by assuming a medium of non-thermal plasma (Hussain et al. 2018) which was further extended to symmetric plate (Javaid et al. 2020) with same assumptions to investigate the impact of symmetry on amplitude of the field. The diffraction model for EM-wave incident on a non-symmetric finite plate with Neumann conditions in the medium of non-thermal was proposed and investigated (Hussain and Ayub 2020) which was further extended for symmetric plate (Javaid et al. 2022). These studies were performed to analyse to build a comparative analysis with those of Dirichlet case. An EM-wave diffraction model was also devised for a slit of finite width with Dirichlet surface surrounded by non-thermal plasma (Javaid et al. 2021). The an-isotropic plasma for magnetic line source diffraction was considered for a conductive half-plane (Basdemir 2020). The most recent mathematical models have been devised on diffraction of EM-waves by a finite-width non-symmetric strip to observe the effects of impedance and non-thermal plasma (Hussain et al. 2021) which has been modified to symmetric strip (Hussain and Almalki 2023). The Leontovich conditions for slit have been taken into an account to consider the impedance effects on diffraction of incident EM-wave in the existence of non-thermal plasma (Hussain 2023).

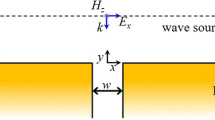
In this analysis, we consider an electromagnetic plane wave interacting with a finite-width slit. The slit is assumed to be perfectly conducting and located within an anisotropic medium. This study is a new version of the research presented in Javaid et al. (2021), but with different boundary conditions. Prior to the incident electromagnetic plane wave, there is no field present. The aim of this investigation is to examine and develop the comparative analysis of the anisotropic plasma medium on the diffraction of electromagnetic waves by a finite slit that is uniformly aligned along the horizontal axis and symmetric about the vertical axis. This model can be thought of as radio signals being transmitted between two antenna plates positioned apart from each other, which behave as a finite-width slit surrounded by an anisotropic medium.

2 Problem statement

Fig. 1
figure 1

Geometrical interpretation of the model

Full size image

We investigate the diffraction pattern of plane electromagnetic waves due to a finite-width slit in non-thermal plasma, as illustrated in Fig. 1. Furthermore, Neumann conditions are assumed on the slit and angle of incidence is \(\theta _{0}\). The total field can be represented in terms of incident, reflected and diffracted fields as follows:

$$\begin{aligned} H_{z}^{tot}(x,y)=H_{z}^{inc}(x,y)-H_{z}^{ref}(x,y)+H_{z}^{diff}(x,y), \end{aligned}$$
(1)

where the incident and refracted fields are defined as

$$\begin{aligned}{} & {} H_{z}^{inc}(x,y)=e^{-i{k_{eff}}(x\cos {\theta _{0}}+y\sin {\theta _{0}})}, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} H_{z}^{ref}(x,y)=e^{-i{k_{eff}}(x\cos {\theta _{0}-}y\sin {\theta _{0}})}. \end{aligned}$$
(3)

Suppose that medium is slightly lossy, and constant \(K_{eff}\) appearing in above equations is complex in such a way \((0<\mathfrak {Im}\{k_{eff}\} \ll \mathfrak {Re}\{k_{eff}\})\). At the end, for real \(K_{eff}\) solution could be determined by taking its imaginary part to zero. The Helmholtz equation for \(H_{z}^{tot}(x,y)\) with existence of non-thermal plasma (Hussain 2023) is expressed as

$$\begin{aligned}{}[\partial _{xx}+\partial _{yy}+k_{eff}^{2}]H_{z}^{tot}(x,y)=0. \end{aligned}$$
(4)

Substituting the value of \(H_{z}^{tot}(x,y)\) from (1), we get the equation for diffracted field as follows:

$$\begin{aligned}{}[\partial _{xx}+\partial _{yy}+k_{eff}^{2}]H_{z}^{diff}(x,y)=0. \end{aligned}$$
(5)

In order to establish the Wiener–Hopf equation, conditions at \(x-\pm l\) in conjunction with continuity relations are used. Neumann boundary conditions on a finite-width slit are specified as

$$\begin{aligned} \partial _{y}H_{z}^{tot}\left( x,y\right) =0, \text{ for } \quad \left| x\right| \ge l, \text{ and }\quad y=0^{\pm }, \end{aligned}$$
(6)

along with

$$\begin{aligned} H_{z}^{tot}(x,0^{+})=H_{z}^{tot}(x,0^{-})=0,\quad \text {at} \quad \left| x\right| <l, \end{aligned}$$
(7)

To ensure the validity of the mixed boundary value problem presented in this study on non-thermal plasma, it is vital to consider the radiation conditions mentioned in Noble (1958). These conditions, denoted as (8), (9) and (10), are as follows:

$$\begin{aligned}{} & {} \sqrt{r}\left[ \partial _{r} H_{z}^{diff}\left( x,y\right) -ik_{eff}H_{z}^{diff}\left( x,y\right) \right] \rightarrow 0\text { for } r\rightarrow \infty , \end{aligned}$$
(8)
$$\begin{aligned}{} & {} H_{z}^{tot}\left( x,0\right) =\left\{ \begin{array}{c} -1+O\left( x+l\right) ^{1/4} \text { for } x\longrightarrow -l^{-}, \\ -1+O\left( x-l\right) ^{1/4} \text { for } x\longrightarrow l^{+}, \end{array} \right. \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \partial _{y}H_{z}^{tot}\left( x,0\right) =\left\{ \begin{array}{c} O\left( x+l\right) ^{-3/4} \text { for } x\longrightarrow -l^{-}, \\ O\left( x-l\right) ^{-3/4} \text { for } x\longrightarrow l^{+}. \end{array} \right. \end{aligned}$$
(10)

3 Problem transformation

Following results are obtained with the use of Fourier Transforms:

$$\begin{aligned} {\mathcal {F}}(\beta ,y)&=\frac{1}{\sqrt{2\pi }} {\displaystyle \int \limits _{-\infty }^{\infty }} e^{i\beta x}H_{z}(x,y)dx\nonumber \\&=e^{i\beta l}{\mathcal {F}}_{+}(\beta ,y)+e^{-i\beta l}{\mathcal {F}}_{-}(\beta ,y)+{\mathcal {F}}_{l}(\beta ,y), \end{aligned}$$
(11)

where \(\beta =\sigma +i{\tau }\).

Fig. 2
figure 2

Illustration of analytic continuation for the model

Full size image

For larger x, the diffracted field is interpreted as follows:

$$\begin{aligned} H_{z}\left( x,y\right) =\left\{ \begin{array}{c} O\left( e^{- \mathfrak {Im}\left\{ k_{eff}\right\} x}\right) \text { for } x\longrightarrow \infty , \\ O\left( e^{\mathfrak {Im}\left\{ k_{eff}\right\} x\cos \theta _{0}}\right) \text { for } x\longrightarrow -\infty . \end{array} \right. \end{aligned}$$
(12)

The regions of regularity in the complex plane for \({\mathcal {F}}_{+}(\beta ,y)\) and \({\mathcal {F}}_{-}(\beta ,y)\) are \(\mathfrak {Im}\{ \beta \}>-\mathfrak {Im}\{k_{eff}\}\) and \(\mathfrak {Im}\{ \beta \}<\mathfrak {Im}\{k_{eff}\cos \theta _{0}\}\). From Fig. 2, we can see the common region \(-\mathfrak {Im}\{k_{eff}\}<\mathfrak {Im} \{ \beta \}<\mathfrak {Im}\{k_{eff}\cos \theta _{0}\}\) of analyticity, where \({\mathcal {F}}_{l}(\beta ,y)\) is also analytic and hence, we can define

$$\begin{aligned}{} & {} {\mathcal {F}}_{\pm }(\beta ,y)={\pm }\frac{1}{\sqrt{2\pi }}\int \limits _{{\pm } l}^{{\pm }\infty }e^{i\beta (x\mp l)}H_{z}(x,y)dx, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} {\mathcal {F}}_{l}(\beta ,y)=\frac{1}{\sqrt{2\pi }}\int \limits _{-l}^{l} e^{i\beta x}H_{z}(x,y)dx, \end{aligned}$$
(14)
$$\begin{aligned}{} & {} {\mathcal {F}}^{inc}(\beta ,y)=\frac{\exp (-i{y}k_{eff}\sin \theta _{0})}{\sqrt{2\pi }}\left( \frac{\exp [i l(\beta -k_{eff}\cos \theta _{0} )]-\exp [-i l(\beta -k_{eff}\cos \theta _{0})]}{i(\beta -k_{eff} \cos \theta _{0})}\right), \end{aligned}$$
(15)
$$\begin{aligned}{} & {} {\mathcal {F}}^{ref}(\beta ,y)=\frac{\exp (i{y}k_{eff}\sin \theta _{0})}{\sqrt{2\pi }}\left( \frac{\exp [i l(\beta -k_{eff}\cos \theta _{0} )]-\exp [-i l(\beta -k_{eff}\cos \theta _{0})]}{(\beta -k_{eff} \cos \theta _{0})}\right) . \end{aligned}$$
(16)

The following transformed boundary value problem is obtained by applying the Fourier transformation to Eqs. (5–7):

$$\begin{aligned} \left( D_{y}^{2}+\gamma ^{2}\right) {\mathcal {F}}=0 \end{aligned}$$
(17)

where \(D_{y}^{2}=\frac{d^{2}}{dy^{2}}\) and \(\gamma (\beta )=\sqrt{k_{eff}^{2}-\beta ^{2}}\).

$$\begin{aligned} \left. \begin{array}{c} \partial _{y}{\mathcal {F}}(\beta ,0^{+})=\partial _{y}{\mathcal {F}} ^{ref}(\beta ,0)-\partial _{y}{\mathcal {F}}^{inc}(\beta ,0),\\ \partial _{y}{\mathcal {F}}(\beta ,0^{-})=0, \end{array} \right. \end{aligned}$$
(18)

and

$$\begin{aligned} {\mathcal {F}}_{\pm }(\beta ,0^{+})={\mathcal {F}}_{\pm }(\beta ,0^{-}). \end{aligned}$$
(19)

4 Solution of the Wiener–Hopf equation

The solution to the transformed boundary value problem (17), fulfilling the radiation conditions, is as follows :

$$\begin{aligned} {\mathcal {F}}(\beta ,y)= {\left\{ \begin{array}{ll} A_{1}(\beta )\exp (-i{\gamma }y)\quad y\ge {0},\\ A_{2}(\beta )\exp (i{\gamma }y)\qquad y<0. \end{array}\right. } \end{aligned}$$
(20)

Now using Eqs. (18–20), following Wiener–Hopf equation is obtained:

$$\exp (i{\beta }l){\mathcal {F}}_{+}^{\prime}(\beta ,0)+\exp (-i{\beta }l){\mathcal {F}}_{-}^{\prime }(\beta ,0)+{\mathcal {K}}(\beta )\tilde {{\mathcal{F}}}_{l}(\beta ,0)=-i {\mathcal {G}}(\beta ).$$
(21)

The factorisation of \({\mathcal {K}}\left( \beta \right)\) (which can be seen in Appendix A) is required to solve the above equation. From Eq. (21), we equate the terms which are regular in their corresponding regions by creating a common region of analyticity. Hence, by analytic continuation, we get an entire function \({\mathcal {P}}(\beta )\) and by Liouville’s theorem, \({\mathcal {P}}\left( \beta \right)\) must be equal to zero (Noble 1958), yielding the following results:

$$\begin{aligned} {\mathcal {F}}_{\pm }(\beta ,0)=\frac{{\mathcal {A}}}{\sqrt{2\pi }}[{\mathcal {K}}_{\pm }(\beta ){\mathcal {G}}_{1,2}({\pm }\beta )+{\mathcal {K}}_{\pm } (\beta ){\mathcal {T}}({\pm }\beta ){\mathcal {C}}_{1,2}], \end{aligned}$$
(22)

where \({\mathcal {G}}_{1,2}({\pm }\beta ),\) \({\mathcal {T}}({\pm }\beta ),\) \({\mathcal {C}}_{1,2}\) are given in appendix A.

Solving Eqs. (20) and (21), diffracted field is given by

$$\begin{aligned} {\mathcal {F}}^{\pm }(\beta ,y)=-\frac{1}{{\mathcal {K}}(\beta )}\big [\exp (i\beta {l}){\mathcal {F}}_{+}(\beta ,0)+\exp (-i\beta {l}){\mathcal {F}}_{-}(\beta ,0)+{\mathcal {F}}_{l}(\beta ,0)\big ]e^{-i \gamma {|y|}}, \end{aligned}$$
(23)

where

$$\begin{aligned} {\mathcal {F}}_{l}(\beta ,0)=i{\mathcal {G}}(\beta ).\quad \end{aligned}$$
(24)

Inverse Fourier transformation of Eq. (23), yields the diffracted field as:

$$\begin{aligned} H_{z}(x,y)=\frac{1}{\sqrt{2\pi }}\int \limits _{-\infty }^{\infty }{\mathcal {F}} (\beta ,y)\exp (-i \beta {x}-i \gamma {|y|})d\beta . \end{aligned}$$
(25)

Inserting (23) in (25), we have

$$\begin{aligned} H_{z}(x,y) = -\frac{1}{\sqrt{2\pi }}\int \limits _{-\infty }^{\infty }\frac{1}{{\mathcal {K}}(\beta )}\left\{ \begin{array}{c} \exp (i \beta {l}){\mathcal {F}}_{+}(\beta ,0)+\tilde{{\mathcal {F}}}_{l}(\beta ,0) \\ \quad +\exp (-i \beta {l}){\mathcal {F}}_{-}(\beta ,0) \end{array} \right\} \exp (-i \beta {x}-i \gamma {|y|})d\beta . \end{aligned}$$
(26)

Diffracted field \(H_{z}(x,y)\) further bifurcates in the separated and interaction fields \(H_{z}^{sep}(x,y)\) and \(H_{z}^{int}(x,y)\), respectively as,

$$\begin{aligned} H_{z}(x,y)=H_{z}^{sep}(x,y)+H_{z}^{int}(x,y), \end{aligned}$$
(27)

where

$$\begin{aligned}{} & {} H_{z}^{sep}(x,y) =\frac{1}{2\pi }\int \limits _{\infty }^{\infty } \frac{{\mathcal {A}}}{{\mathcal {K}}(\beta )}\left\{ \begin{array}{c} \frac{{\mathcal {K}}_{+}(\beta )\exp [i(\beta -k_{eff}\cos \theta _{0})l]}{{\mathcal {K}}_{+}(k_{eff} \cos \theta _{0})(\beta -k_{eff}\cos \theta _{0})} \\ -\frac{{\mathcal {K}}_{+}(-\beta )\exp [-i(\beta -k_{eff}\cos \theta _{0})l]}{{\mathcal {K}}_{+}(-k_{eff}\cos \theta _{0})(\beta -k_{eff}\cos \theta _{0})} \end{array} \right\} \exp (-i \beta {x}-i \gamma {|y|})d\beta , \end{aligned}$$
(28)
$$\begin{aligned}{} & {} H_{z}^{int}(x,y) =\frac{1}{2\pi }\int \limits _{-\infty }^{\infty } \frac{{\mathcal {A}}}{{\mathcal {K}}(\beta )}\left\{ \begin{array}{c} \exp (i\beta {l}){\mathcal {K}}_{+}(\beta ){\mathcal {T}}(\beta ){\mathcal {C}}_{1} \\ -\exp [i(\beta +k_{eff}\cos \theta _{0})l]\\ \times {\mathcal {K}}_{+}(\beta ){\mathcal {R}}_{1}(\beta )\\ +\exp (-i \beta {l}){\mathcal {K}}_{-}(\beta ){\mathcal {T}}(-\beta ){\mathcal {C}}_{2}\\ -\exp [-i(\beta +k_{eff}\cos \theta _{0})l]\\ \times {\mathcal {K}}_{-}(\beta ){\mathcal {R}}_{2}(-\beta ) \end{array} \right\} \exp (-i \beta {x}-i \gamma {|y|})d\beta . \end{aligned}$$
(29)

The separated field given by (28) depicts diffraction separately at the edges \(x=\pm l\) whereas the interaction field represented by Eq. (29) explains the interaction of one end with the other.

5 Diffracted field

The diffracted field due to slit of finite width for the far field can be obtained asymptotically by coping with the integral appearing in (25). Polar coordinates are introduced for the evaluation of Eq. (25) with the following transformation:

$$\begin{aligned} \beta =-k_{eff}\cos (\phi +i \eta ),\quad 0<\phi<\pi ,\quad -\infty<\eta <\infty . \end{aligned}$$
(30)

Now we employ the method of stationary phase (Copson 1967) for Eq. (25), and the following result is obtained:

$$\begin{aligned} H_{z}(r,\phi )\sim \frac{i{k_{eff}}}{\sqrt{k_{eff}r}}{\mathcal {F}}(-k_{eff} \cos \phi ,{\pm }r\sin \phi )\sin \phi \exp \left( {i}k_{eff}r+i \frac{\pi }{4}\right) . \end{aligned}$$
(31)

Incorporating the same polar coordinates, the transformation and subsequently the method of stationary phase are used to assess and yield the \(H_{z}^{sep}\) and \(H_{z}^{int}\) as follows:

$$\begin{aligned} \{H_{z}^{sep},H_{z}^{int}\}(r,\phi )\sim \frac{1}{\sqrt{2\pi }}\frac{i {k}_{eff}}{\sqrt{k_{eff}r}}\{f_{sep},-f_{int}\}(-k_{eff}\cos \phi )\sin \phi \exp \left( i k_{eff}r+i \frac{\pi }{4}\right) , \end{aligned}$$
(32)

where \(f^{sep}\left( -k_{eff}\cos \phi \right)\) and \(f^{int}\left( -k_{eff}\cos \phi \right)\) are given in Appendix B.

From Eq. (31), we can clearly see that the asymptotic expressions for far field can be obtained by letting \(k_{eff}r\rightarrow \infty\) and the resulting expressions will hold true for any observational angle. The \(H_{z}^{sep}\) is investigated in order to characterize both the field diffracted by the corners of a slit and the influence of the geometrical wave field. The \(H_{z}^{sep}\) gives the physical evidence for the diffraction in non-thermal plasma. \(H_{z}^{int}\), on the other hand, provides no distinct physical information due to contact at one extremity with the other, which has been counted by \(H_{z}^{sep}\). As a result, we have only talked about the \(H_{z}^{sep}\) because it conveyed a full physical comprehension of diffracted wave at the established boundaries. Additionally, we have revealed that the \(H_{z}^{int}\) is created by diffraction from the corners of slit at \(x = \pm l\). As a consequence, we merely examine the \(H_{z}^{sep}\), as illustrated visually in the next section.

6 Results

In this section, we elaborate the EM-waves by finite-width slit graphically by the variation of physical parameters in an an-isotropic media with Neumann case versus the \(\theta\). For the ionosphere, we take the value of \(\omega _{p}\) as 56.4 MHz and \(\omega _{c}\) as 8.78 MHz. Also, the values of \(\omega\) are taken between 80 MHz and 600 MHz as given in Table 1. The values of \(\varepsilon _{1}\) and \(\varepsilon _{2}\) for different frequencies \(\omega\) in the ionosphere of non-thermal plasma have been computed numerically and are presented in Table 1. In the ionosphere, the plasma frequency \(\omega _{p}\) represents the natural oscillation frequency of the plasma electrons, and the cyclotron frequency \(\omega _{c}\) represents the frequency at which the electrons rotate in the Earth’s magnetic field. As the frequency \(\omega\) increases, the value of \(\varepsilon _{2}\) becomes comparably very small compared to \(\varepsilon _{1}\). This can be attributed to the fact that at higher frequencies, the effect of the plasma electrons’ natural oscillation becomes dominant over their rotation in the magnetic field. In an isotropic medium without spatial dispersion, we can assign equal values to \(\varepsilon _{1}\) and \(\varepsilon _{3}\), and set \(\varepsilon _{2}\) to zero. This implies that the medium behaves the same way in all directions and does not exhibit any anisotropy. In the presence of a non-gyrotropic anisotropic medium, we set \(\varepsilon _{1}\) to 1, \(\varepsilon _{3}\) to a non-zero value, and \(\varepsilon _{2}\) to zero. This indicates that the medium exhibits anisotropy in certain directions, but does not exhibit any rotation or gyration. In the case of a gyrotropic anisotropic medium, the values of \(\varepsilon _{1}\) and \(\varepsilon _{2}\) can be obtained from Table 1. This indicates that the medium exhibits both anisotropy and rotation or gyration, which can occur in the presence of a magnetic field. Therefore, the values of \(\varepsilon _{1}\) and \(\varepsilon _{2}\) for different frequencies provide information about the anisotropic and gyrotropic properties of the ionosphere of non-thermal plasma.

Table 1 Values of \(\varepsilon _{1}\) and \(\varepsilon _{2}\) for corresponding \(\omega\)
Full size table

The graphical analysis is elaborated to explore the influence of physical parameters on diffracted field due to a finite-width slit lying in the ionosphere of non-thermal plasma. These physical parameters are \(\theta _{0}\), k, l and \(\varepsilon _{1}.\) Fig. 3 (rectangular plot) and Fig. 4 (polar plot) depict the pattern of the \(H_{z}^{sep}\) for variation of \(\theta _{0}\), and it gets maxima for \(\theta _{0}=\pi /6\), \(\pi /4\), \(\pi /3\), occurring at \(\phi =5\pi /6\), \(3\pi /4\), \(2\pi /3\), respectively. These maxima actually predict the shadow of reflecting boundaries. As the angle of incidence changes, the diffracted wavefronts and their interference patterns alter accordingly. In this case, the larger amplitude for \(\theta _{0}=\pi /3\) suggests that the diffraction pattern will be more pronounced at this angle. This means that the wave will spread out more and exhibit stronger interference effects, resulting in a larger amplitude in the observed pattern. The difference in amplitude at different incidence angles can be attributed to the interference of waves diffracted from different parts of the slit. At \(\theta _{0}=\pi /3\), the diffracted waves from different parts of the slit constructively interfere, leading to a larger amplitude. At \(\theta _{0}=\pi /6\) and \(\theta _{0}=\pi /4\) degrees, the interference is less constructive, resulting in smaller amplitudes. Figure 5 (rectangular plot) and Fig. 6 (polar plot) reveal the sketch of \(H_{z}^{sep}\) for k which is directly related to the spatial frequency of the electromagnetic wave. A higher wave-number corresponds to a shorter wavelength and a higher frequency. Therefore, \(k=9\) represents a higher frequency wave that gives a larger amplitude of diffracted field (brighter region in the diffraction pattern) compared to \(k=7\) and 5. The width of the slit relative to the wavelength of the incident wave plays a crucial role. A narrower slit causes more pronounced diffraction effects, resulting in a broader and more spread-out diffraction pattern. Conversely, a wider slit leads to less diffraction and a narrower diffraction pattern. As extension of the slit-width is actually the widening of the aperture which is responsible for the diffraction of electromagnetic radiations, and so, the far field \(H_{z}^{sep}\) gets amplified as well as more oscillated as pictured in Fig. 7. This amplified amplitude could be controlled by introducing the non-thermal plasma as can be observed through Fig. 7b. By comparing Figs. 3b, 4, 5, 6 and 7b of the separated field in an-isotropic medium with their respective Figs. 3a, 4, 5, 6 and 7a for the isotropic medium, it is explored that an-isotropy of the medium because of non-thermal plasma has influenced the separation field in both amplitude reduction and wavelength expansion. The reduction in the amplitude and number of oscillations of the diffracted field when non-thermal plasma is present can be attributed to the energy transfer and interaction between the incident waves and the plasma. The absorption and scattering of the waves by the non-thermal plasma cause energy to be dissipated, leading to a decrease in the amplitude. The modification of the refractive index affects the phase of the waves, resulting in a change in the number of oscillations observed. Fig. 8 explores the trend of the field for \(\varepsilon _{1}\), while its mathematical interpretation predicts its physical nature. It is expressed by Eq. \(\left( 2\right)\) in Hussain (2023) and can be described as \(\omega _{c}\) has no big difference in the values in various parts of earth whereas \(\omega _{p}\) has direct relation with the square root of \(N_{e}\) (ion concentration) (see Eq. \(\left( 4\right)\) in Hussain (2023)). This fluctuates massively with the variation of seasons and days to night. Therefore, with no change in \(\omega\), \(\varepsilon _{1}\) still can have the variation. Since \(\varepsilon _{1}\) has inverse relation with \(\omega\), so increase in \(N_{e}\) with fixed \(\omega\), \(\varepsilon _{1}\) declines and wavelength increases. It means that the separated field with longer wavelength will occur for increasing number of free charges in the medium. One common observation across all the plots in the rectangular graphs is the presence of null behavior in the far field around the observational angles of 0 and \(\pi\). This behavior is not seen in the study referenced as Javaid et al. (2021), where the null behavior appears only around the observational angle of 0 in the investigation of diffraction by a slit with Leontovich conditions (Hussain 2023). The difference in these results can be attributed to the use of Leontovich conditions in the study, which establish a relationship between the tangential components of the electric and magnetic fields at the boundary. These conditions take into account the impedance and ensure the continuity of the fields. Furthermore, it is interesting to note that the results of the current analysis are identical to the diffraction of electromagnetic waves by a finite symmetric strip with Dirichlet conditions, as described in Javaid et al. (2020). This similarity arises because the Wiener–Hopf equation used in the current analysis has the same kernel function as the Wiener–Hopf equation for the finite symmetric strip with Dirichlet conditions. Similarly, the diffraction pattern of electromagnetic waves by a slit with Dirichlet conditions, as mentioned in Javaid et al. (2021), is identical to the diffraction pattern observed when considering a symmetric strip of finite width with Neumann conditions, as discussed in Javaid et al. (2022).

From above analysis, it is observed that the influence of non-thermal plasma on the electromagnetic wave scattering by a finite-width slit with Neumann boundary conditions open up avenues for controlling, manipulating, and characterizing electromagnetic waves in plasma environments. These effects find applications in fields such as plasma optics, diagnostics, material processing, and sensing.

Fig. 3
figure 3

Rectangular plot: The separated field for \(\theta _{0}\) in the (a) isotropic and (b) anisotropic medium

Full size image
Fig. 4
figure 4

Polar plot: The separated field for \(\theta _{0}\) in the (a) isotropic and (b) anisotropic medium

Full size image
Fig. 5
figure 5

Rectangular plot: The separated field for k in the (a) isotropic and (b) an-isotropic medium

Full size image
Fig. 6
figure 6

Polar plot: The separated field for k in the (a) isotropic and (b) an-isotropic medium

Full size image
Fig. 7
figure 7

The separated field for l in the (a) isotropic and (b) an-isotropic medium

Full size image
Fig. 8
figure 8

The separated field for \(\varepsilon _{1}\)

Full size image

7 Conclusion

The current topic looks at the diffraction of an EM-waves by a finite-width slit in the context of non-thermal plasma under Neumann conditions which is a new version of the model (Javaid et al. 2021). This article’s important conclusions are summarized below:

  • At the corresponding incremental trend of wave number and slit width, the number of oscillations increases, resulting in the peaks for the relevant angles of incidence.

  • Because the existence of the an-isotropic medium regulates the magnitude of the separated field, the likelihood of EM-wave dispersion is reduced.

  • The greater wavelength of the separated field is characterized by expanding \(N_{e}\) (electron charge density).

  • The separated field shows nullity around observation angles 0 and \(\pi\).

In terms of future development, the current challenge might be extended to instances including line/point sources. It would also be worthwhile to explore the differences in the diffracted field induced by geometrical modifications with almost identical arrangement.