1 Introduction

Various forms of differential equations of fractional and integer orders are appear in modeling applied problems in optics, science, physics, ocean, etc. (Murad et al. 2023a, b, c; Malo et al. 2021; Ismael et al. 2022a, b; Murad 2022). One of the most important and well known type of applied differential equations is the Schrodinger-type equation which has a significant ability to explain various nonlinear phenomena in different areas of science particularly in optic and plasma physics (Ghanbari 2021; Awan et al. 2021; Akinyemi 2023; Houwe et al. 2023). The mechanism of the propagation of nonlinear modified envelope localized waves (bright solitons, dark solitons, and rogue waves), as well as periodic structures was demonstrated using a family of nonlinear Schrodinger’s equation (NLSE). The analytical techniques aim is to utilized suitable transformations to transfer the nonlinear partial differential equations (NLPDEs) into ordinary differential equations (ODEs) (Huang et al. 2020; Manafian et al. 2020; Akinyemi et al. 2021; Akinyemi 2021). In this study, we purpose to analyze the following time-fractional nonlinear Schrodinger equation:

$$\begin{aligned} i\left( \frac{\partial u(x,t)}{\partial x}+{{\mu }_{1}}\frac{{{\partial }^{\alpha }}u(x,t)}{\partial {{t}^{\alpha }}} \right) +{{\mu }_{2}}\frac{{{\partial }^{2\alpha }}u(x,t)}{\partial {{t}^{2\alpha }}}+{{\mu }_{3}}\frac{{{\partial }^{2}}u(x,t)}{\partial {{x}^{2}}}+{{\left| u(x,t) \right| }^{2}}u(x,t)=0,\,\,0<\alpha \le 1, \end{aligned}$$
(1)

where u(x, t) is the macroscopic complex valued wave profile, \({{\mu }_{1}}\) represents the proportional to the ratio of group speed, \({{\mu }_{2}}\) and \({{\mu }_{3}}\) are the group velocity dispersion and the spatial dispersion, respectively. Further, the time-fractional order derivative \(\alpha\) represents the conformable fractional derivative.

Various techniques have been employed to explore novel optical soliton solutions to the present model. To construct several novel mixed bright, dark, and complex soliton solutions, the extended direct algebraic technique is implemented to equation (1) in Baskonus et al. (2021). The proposed type of Schrodinger equation with group velocity distribution and second-order spatio-temporal dispersal parameters is considered with local M-derivative in Ghanbari and Gomez-Aguilar (2019). The modified sinh-Gordon equation expansion method and generalized exponential rational function method are considered to explore novel categories of optical soliton solutions to this model (Rezaei et al. 2022). Through a new extension of the Backlund approach, certain innovative analytical traveling wave solutions to the proposed model with conformable derivative are effectively produced in Rezazadeh et al. (2021). The present model is proposed to describe the pulse phenomena beyond the conventional slowly-varying envelope approximation, also the space-time structure of the problem and its transformation properties discussed in Christian et al. (2012). The auxiliary equation approach is used to construct a number of traveling solutions to the present equation see Tariq and Seadawy (2018). Various cases of optical soliton solutions such as dark, bright, and dark-bright solitary wave solutions are found using the amplitude ansatz method (Seadawy 2017).The impact of the fractional order derivative on the bright soliton and W-soliton solution of this model is discussed in Yousif et al. (2018). The modulation instability of the present model is discussed and the F-expansion method is applied to construct the solitary wave and soliton solutions of the present problem (Nasreen et al. 2018). Several new traveling wave solutions are explored by employing the sine-Gordon expansion method to this model (Rezazadeh et al. 2021). Very recently, The modified extended direct algebraic approach is utilized to derive a class of optical solutions and other solitary wave solutions for the variety of nonlinear Schrodinger equation in Ghayad et al. (2023). The extended improved tanh expansion method is used to construct the optical bright, dark, periodic, breathers type and hybrid type soliton solutions in Ahmad et al. (2023). However, the impact of the conformable fractional order derivative on the existing solutions have not been reported in the literature. Further, Zhao and Luo discussed the geometrical interpretations and physical significance of the conformable fractional derivative which thus indicate the potential implements in engineering and physics (Zhao and Luo 2017).

In this paper, the extended simplest equation method is used to find several new optical solutions to the proposed time-fractional nonlinear Schrodinger equation. These results can help to interpret various nonlinear scientific theories, such as the modulated envelope localized structures in fluid dynamics and plasma physics. Further, the influence of different values of the temporal parameter and fractional order derivative on the new optical solutions is illustrated via several illustrative graphs. Recently, the extended simplest equation method (ESEM) has been suggested as an efficient approach to solve a class of differential equations (Ahmed et al. 2021). The advantage of the extended simplest equation method is that various forms of exact traveling wave solutions can be constructed by using this method which can not be acquired via other methods such as the Exp-function method, F-expansion method, and tanh-function method. The ESEM is used to solve various fifth-order KdV equation forms in Bilige and Chaolu (2010). The solution of a coupled Schrodinger-Boussinesq equation is analyzed using extended simplest equation method in Bilige et al. (2013). This method is also applied to solve the higher-order nonlinear Schrodinger model and modified Zakharov?Kuznetsov in Zayed et al. (2018, 2019). Various optical solutions for Biswas?Arshed equation are obtained using ESEM in Zayed and Shohib (2019).

2 Conformable derivatives

Many phenomena in the real world are described by differential equations with fractional orders. Thus, various fractional operators have been utilized recently to analyze the magnitude of applied differential equations such as the Beta derivative, the Riemann Liouville, and the Caputo Fabrizio. In applied sciences and engineering, these types of operators have an essential role in solving applied differential equations. The conformable derivative is considered one of these operators which improves our understanding of the model’s nature.

Definition 1

(Khalil et al. 2014) Let \(g:(0,\infty )\rightarrow R\). The conformable derivative with order \(\alpha\) is defined as follows:

$$\begin{aligned} {{L}_{\alpha }}\left( g \right) (s)=\underset{\delta \rightarrow 0}{\mathop {\lim }}\,\frac{g(s+\delta {{s}^{1-\alpha }})-g(s)}{\delta }, \end{aligned}$$

for all \(s>0\) and \(\tau \in (0,1]\).

Consider the functions g and h are differentiable conformable with order \(\alpha\),\(\forall \,s>0\), and \({{a}_{1}},{{a}_{2}}\in R\). The following rules of the conformable derivative are hold:

i. \({{L}_{\alpha }}({{a}_{1}}g+{{a}_{2}}h)={{a}_{1}}{{L}_{\alpha }}(g)+{{a}_{2}}{{L}_{\alpha }}(h).\)

ii. \({{L}_{\alpha }}({{s}^{r}})=r{{s}^{r-\alpha }}\)for all \(r\in R\).

iii. \({{L}_{\alpha }}(gh)=h{{L}_{\alpha }}(g)+g{{L}_{\alpha }}(h)\).

iv. \({{L}_{\alpha }}(\frac{g}{h})=\frac{h{{L}_{\alpha }}(g)-g{{L}_{\alpha }}(h)}{{{h}^{2}}}\).

3 Application of the method

In this section, the extended simplest equation method is applied to the proposed nonlinear time-fractional Schrodinger equation, and various novel optical soliton solutions to the model are constructed. First, we have utilized the following wave transformations:

$$\begin{aligned} u(x,t)=u(\varsigma ){{e}^{i\vartheta (x,t)}},\,\varsigma =x-\frac{\upsilon {{t}^{\alpha }}}{\alpha },\vartheta (x,t)=-\kappa x+\frac{w{{t}^{\alpha }}}{\alpha }, \end{aligned}$$
(2)

where w, k are constants, and \(\upsilon\) represents the speed of the traveling wave. To transfer the partial differential equations into ordinary differential equations, the above transformers are used which probably considered the most widely employed transformers in literature. Here, substituting transformations (2) into equation (1) with some simplifications, the following real and imaginary parts are obtained:

$$\begin{aligned}{} & {} \upsilon =\frac{1-2{{\mu }_{3}}k}{{{\mu }_{1}}+2w{{\mu }_{2}}}, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \left( {{\mu }_{2}}{{\upsilon }^{2}}+{{\mu }_{3}} \right) {u}''\left( \varsigma \right) +\left( k-{{\mu }_{1}}w-{{\mu }_{2}}{{w}^{2}}-{{\mu }_{3}}{{k}^{2}} \right) u\left( \varsigma \right) +{{u}^{3}}\left( \varsigma \right) =0. \end{aligned}$$
(4)

Inserting Eq. (3) into Eq. (4), we obtain the following equation:

$$\begin{aligned} \left( {{\mu }_{3}}{{A}_{1}}+{{\mu }_{2}}{{A}_{2}} \right) {u}''\left( \varsigma \right) +{{A}_{1}}{{A}_{3}}u\left( \varsigma \right) +{{A}_{1}}{{u}^{3}}\left( \varsigma \right) =0, \end{aligned}$$
(5)

where

$$\begin{aligned} {{A}_{1}}={{\left( {{\mu }_{1}}+2{{\mu }_{2}}w \right) }^{2}}, \,{{A}_{2}}={{\left( 1-2k{{\mu }_{3}} \right) }^{2}}, {{A}_{3}}=k-w{{\mu }_{1}}-{{w}^{2}}{{\mu }_{2}}-{{k}^{2}}{{\mu }_{3}}. \\ \end{aligned}$$

Balancing \({u}''\) with \({{u}^{3}}\) yields \(N=1\). Here, Eq. (5) has the following formula solution (Bilige et al. 2013; Zayed et al. 2018):

$$\begin{aligned} u(\varsigma )={{b}_{0}}+{{b}_{1}}\left[ \frac{G'(\varsigma )}{G(\varsigma )} \right] +{{b}_{2}}\left[ \frac{1}{G(\varsigma )} \right] , \end{aligned}$$
(6)

where \({{b}_{0}},{{b}_{1}},{{b}_{2}}\) are considered to be arbitrary constants and \(G(\varsigma )\) represents the solution of the following equation

$$\begin{aligned} G''(\varsigma )+\sigma \,G(\varsigma )=\nu , \end{aligned}$$
(7)

where \(\nu , \sigma\) are real number. Hence, The above equation has the following solutions:

  1. 1.

    The following hyperbolic solution for Eq. (7) is obtained, if \(\sigma <0\):

    $$\begin{aligned} G(\varsigma )={{C}_{1}}\cosh \left( \varsigma \sqrt{-\sigma } \right) +{{C}_{2}}\sinh \left( \varsigma \sqrt{-\sigma } \right) +\frac{\nu }{\sigma }. \end{aligned}$$
    (8)

    Hence, we have

    $$\begin{aligned} {{\left( \frac{G'}{G} \right) }^{2}}=\left( \sigma C_{1}^{2}-\sigma C_{2}^{2}-\frac{{{v}^{2}}}{\sigma } \right) {{\left( \frac{1}{G} \right) }^{2}}+\frac{2v}{G}-\sigma . \end{aligned}$$
    (9)
  2. 2.

    The following trigonometric solution for Eq. (7) is obtained, if \(\sigma >0\):

    $$\begin{aligned} G(\varsigma )={{C}_{1}}\cos \left( \varsigma \sqrt{\sigma } \right) +{{C}_{2}}\sin \left( \varsigma \sqrt{\sigma } \right) +\frac{\nu }{\sigma }. \end{aligned}$$
    (10)

    Hence, we have

    $$\begin{aligned} {{\left( \frac{G'}{G} \right) }^{2}}=\left( \sigma C_{1}^{2}+\sigma C_{2}^{2}-\frac{{{v}^{2}}}{\sigma } \right) {{\left( \frac{1}{G} \right) }^{2}}+\frac{2\nu }{G}-\sigma . \end{aligned}$$
    (11)
  3. 3.

    The following solution is obtained if \(\sigma =0\):

    $$\begin{aligned} G(\varsigma )=\frac{\nu }{2}{{\varsigma }^{2}}+{{C}_{1}}\varsigma +{{C}_{2}}. \end{aligned}$$
    (12)

    Hence, we have

    $$\begin{aligned} {{\left( \frac{G'}{G} \right) }^{2}}=\left( \sigma C_{1}^{2}-2\nu {{C}_{2}} \right) {{\left( \frac{1}{G} \right) }^{2}}+\frac{2\nu }{G}, \end{aligned}$$
    (13)

    where \({{C}_{1}}\) and \({{C}_{2}}\) are real values. Now, the following three solutions are dissected:

i. If \(\sigma <0\).

Inserting Eq. (6) along with Eq. (8) and using Eq. (9) into Eq. (5), then the same orders of \(\frac{1}{{{G}^{i}}}\) and \(\frac{1}{{{G}^{j}}}\left( \frac{G'}{G} \right)\), \((i=0,1,2,3,j=0,1,2)\) are taken in consideration. Here, we equalize their coefficients to zero, we obtain the following:

Fig. 1
figure 1

The 3D plot, 2D plot and contour plot of \({{\left| {{u}_{1}}(x,t) \right| }^{2}}\)for \({\mu }_{1} =0.5,{\mu }_{2} =w=0.1,{\mu }_{3} =\sigma =-0.1,{{C}_{1}}=5,{{C}_{2}}=1,\) and \(\nu =-2\)

Full size image
Fig. 2
figure 2

The 3D plot, 2D plot and contour plot of \({{\left| {{u}_{7}}(x,t) \right| }^{2}}\) for \({\mu }_{1} =-0.8,{\mu }_{2} =0.8, k=0.1,{\mu }_{3} =-0.1,\sigma =-0.12,{{C}_{1}}=1,{{C}_{2}}=-1,\) and \(\nu =-2\)

Full size image
Fig. 3
figure 3

The 3D plot, 2D plot and contour plot of \({\text {Re}}({{u}_{7}}(x,t))\) and \({\text {Im}}({{u}_{7}}(x,t))\) for \({\mu }_{1} =-0.8,{\mu }_{2} =0.8, k=0.1,{\mu }_{3} =-0.1,\sigma =-0.12,{{C}_{1}}=1,{{C}_{2}}=-1,\) and \(\nu =-2\)

Full size image
Fig. 4
figure 4

The 3D plot, 2D plot and contour plot of \({{\left| {{u}_{10}}(x,t) \right| }^{2}}\) for \({\mu }_{1} =-0.5,{\mu }_{2} =0.1, w=0.2,{\mu }_{3} =-0.1,\sigma =0.1,{{C}_{1}}=-1,{{C}_{2}}=-3,\) and \(\nu =-2\)

Full size image
Fig. 5
figure 5

The 3D plot, 2D plot and contour plot of \({\text {Re}}({{u}_{10}}(x,t))\) and \({\text {Im}}({{u}_{10}}(x,t))\) for \({\mu }_{1} =-0.5,{\mu }_{2} =0.1, w=0.2,{\mu }_{3} =-0.1,\sigma =0.1,{{C}_{1}}=-1,{{C}_{2}}=-3,\) and \(\nu =-2\)

Full size image
$$\begin{aligned}&{{\left( \frac{1}{G} \right) }^{0}}:k{{b}_{0}}\mu _{1}^{2}+b_{0}^{3}\mu _{1}^{2}-3\sigma {{b}_{0}}b_{1}^{2}\mu _{1}^{2}-w{{b}_{0}}\mu _{1}^{3}+4kw{{b}_{0}}{{\mu }_{1}}{{\mu }_{2}}+4wb_{0}^{3}{{\mu }_{1}}{{\mu }_{2}}-12w\sigma {{b}_{0}}b_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}-5{{w}^{2}}{{b}_{0}}\mu _{1}^{2}{{\mu }_{2}}+ \\&4k{{w}^{2}}{{b}_{0}}\mu _{2}^{2}+4{{w}^{2}}b_{0}^{3}\mu _{2}^{2}-12{{w}^{2}}\sigma {{b}_{0}}b_{1}^{2}\mu _{2}^{2}-8{{w}^{3}}{{b}_{0}}{{\mu }_{1}}\mu _{2}^{2}-4{{w}^{4}}{{b}_{0}}\mu _{2}^{3}-{{k}^{2}}{{b}_{0}}\mu _{1}^{2}{{\mu }_{3}}-4{{k}^{2}}w{{b}_{0}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}} \\&-4{{k}^{2}}{{w}^{2}}{{b}_{0}}\mu _{2}^{2}{{\mu }_{3}}=0, \\&\left( \frac{1}{G} \right) \,\,:\,6\nu {{b}_{0}}b_{1}^{2}\mu _{1}^{2}+k{{b}_{2}}\mu _{1}^{2}+3b_{0}^{2}{{b}_{2}}\mu _{1}^{2}-3\sigma b_{1}^{2}{{b}_{2}}\mu _{1}^{2}-w{{b}_{2}}\mu _{1}^{3}-\sigma {{b}_{2}}{{\mu }_{2}}+24w\nu {{b}_{0}}b_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}+4kw{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}} \\&+12wb_{0}^{2}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}} -12w\sigma b_{1}^{2}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}-5{{w}^{2}}{{b}_{2}}\mu _{1}^{2}{{\mu }_{2}}+24{{w}^{2}}\nu {{b}_{0}}b_{1}^{2}\mu _{2}^{2}+4k{{w}^{2}}{{b}_{2}}\mu _{2}^{2}+12{{w}^{2}}b_{0}^{2}{{b}_{2}}\mu _{2}^{2} \\&-12{{w}^{2}}\sigma b_{1}^{2}{{b}_{2}}\mu _{2}^{2}-8{{w}^{3}}{{b}_{2}}{{\mu }_{1}}\mu _{2}^{2} -4{{w}^{4}}{{b}_{2}}\mu _{2}^{3}-{{k}^{2}}{{b}_{2}}\mu _{1}^{2}{{\mu }_{3}}-\sigma {{b}_{2}}\mu _{1}^{2}{{\mu }_{3}}+4k\sigma {{b}_{2}}{{\mu }_{2}}{{\mu }_{3}}-4{{k}^{2}}w{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}} \\&-4w\sigma {{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-4{{k}^{2}}{{w}^{2}}{{b}_{2}}\mu _{2}^{2}{{\mu }_{3}}-4{{w}^{2}}\sigma {{b}_{2}}\mu _{2}^{2}{{\mu }_{3}} -4{{k}^{2}}\sigma {{b}_{2}}{{\mu }_{2}}\mu _{3}^{2}=0 \\&\left( \frac{G'}{G} \right) :\,k{{b}_{1}}\mu _{1}^{2}+3b_{0}^{2}{{b}_{1}}\mu _{1}^{2}-\sigma b_{1}^{3}\mu _{1}^{2}-w{{b}_{1}}\mu _{1}^{3}+4kw{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}+12wb_{0}^{2}{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}-4w\sigma b_{1}^{3}{{\mu }_{1}}{{\mu }_{2}}-5{{w}^{2}}{{b}_{1}}\mu _{1}^{2}{{\mu }_{2}} \\&+4k{{w}^{2}}{{b}_{1}}\mu _{2}^{2}+12{{w}^{2}}b_{0}^{2}{{b}_{1}}\mu _{2}^{2}-4{{w}^{2}}\sigma b_{1}^{3}\mu _{2}^{2}-8{{w}^{3}}{{b}_{1}}{{\mu }_{1}}\mu _{2}^{2}-4{{w}^{4}}{{b}_{1}}\mu _{2}^{3}-{{k}^{2}}{{b}_{1}}\mu _{1}^{2}{{\mu }_{3}}-4{{k}^{2}}w{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}} \\&-4{{k}^{2}}{{w}^{2}}{{b}_{1}}\mu _{2}^{2}{{\mu }_{3}}=0, \\&{{\left( \frac{1}{G} \right) }^{2}}:\,-\frac{3{{\nu }^{2}}{{b}_{0}}b_{1}^{2}\mu _{1}^{2}}{\sigma }+6\nu b_{1}^{2}{{b}_{2}}\mu _{1}^{2}+3{{b}_{0}}b_{2}^{2}\mu _{1}^{2}+3\sigma {{b}_{0}}b_{1}^{2}C_{1}^{2}\mu _{1}^{2}-3\sigma {{b}_{0}}b_{1}^{2}C_{2}^{2}\mu _{1}^{2}+3\nu {{b}_{2}}{{\mu }_{2}}-\frac{12w{{\nu }^{2}}{{b}_{0}}b_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}}{\sigma } \\&+24w\nu b_{1}^{2}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}+12w{{b}_{0}}b_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}+12w\sigma {{b}_{0}}b_{1}^{2}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}-12w\sigma {{b}_{0}}b_{1}^{2}C_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}-\frac{12{{w}^{2}}{{\nu }^{2}}{{b}_{0}}b_{1}^{2}\mu _{2}^{2}}{\sigma } \\&+24{{w}^{2}}\nu b_{1}^{2}{{b}_{2}}\mu _{2}^{2}+12{{w}^{2}}{{b}_{0}}b_{2}^{2}\mu _{2}^{2}+12{{w}^{2}}\sigma {{b}_{0}}b_{1}^{2}C_{1}^{2}\mu _{2}^{2}-12{{w}^{2}}\sigma {{b}_{0}}b_{1}^{2}C_{2}^{2}\mu _{2}^{2}+3\nu {{b}_{2}}\mu _{1}^{2}{{\mu }_{3}}-12k\nu {{b}_{2}}{{\mu }_{2}}{{\mu }_{3}} \\&+12w\nu {{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}+12{{w}^{2}}\nu {{b}_{2}}\mu _{2}^{2}{{\mu }_{3}}+12{{k}^{2}}\nu {{b}_{2}}{{\mu }_{2}}\mu _{3}^{2}=0 \\&\frac{1}{G}\left( \frac{G'}{G} \right) :\,2\nu b_{1}^{3}\mu _{1}^{2}+6{{b}_{0}}{{b}_{1}}{{b}_{2}}\mu _{1}^{2}+\nu {{b}_{1}}{{\mu }_{2}}+8w\nu b_{1}^{3}{{\mu }_{1}}{{\mu }_{2}}+24w{{b}_{0}}{{b}_{1}}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}+8{{w}^{2}}\nu b_{1}^{3}\mu _{2}^{2}+24{{w}^{2}}{{b}_{0}}{{b}_{1}}{{b}_{2}}\mu _{2}^{2} \\&+\nu {{b}_{1}}\mu _{1}^{2}{{\mu }_{3}}-4k\nu {{b}_{1}}{{\mu }_{2}}{{\mu }_{3}}+4w\nu {{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}+4{{w}^{2}}\nu {{b}_{1}}\mu _{2}^{2}{{\mu }_{3}}+4{{k}^{2}}\nu {{b}_{1}}{{\mu }_{2}}\mu _{3}^{2}=0, \\&\,{{\left( \frac{1}{G} \right) }^{3}}:\,-\frac{3{{\nu }^{2}}b_{1}^{2}{{b}_{2}}\mu _{1}^{2}}{\sigma }+b_{2}^{3}\mu _{1}^{2}+3\sigma b_{1}^{2}{{b}_{2}}C_{1}^{2}\mu _{1}^{2}-3\sigma b_{1}^{2}{{b}_{2}}C_{2}^{2}\mu _{1}^{2}-\frac{2{{\nu }^{2}}{{b}_{2}}{{\mu }_{2}}}{\sigma }+2\sigma {{b}_{2}}C_{1}^{2}{{\mu }_{2}}-2\sigma {{b}_{2}}C_{2}^{2}{{\mu }_{2}} \\&-\frac{12w{{\nu }^{2}}b_{1}^{2}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}}{\sigma }+4wb_{2}^{3}{{\mu }_{1}}{{\mu }_{2}}+12w\sigma b_{1}^{2}{{b}_{2}}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}-12w\sigma b_{1}^{2}{{b}_{2}}C_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}-\frac{12{{w}^{2}}{{\nu }^{2}}b_{1}^{2}{{b}_{2}}\mu _{2}^{2}}{\sigma }+4{{w}^{2}}b_{2}^{3}\mu _{2}^{2} \\&+12{{w}^{2}}\sigma b_{1}^{2}{{b}_{2}}C_{1}^{2}\mu _{2}^{2}-12{{w}^{2}}\sigma b_{1}^{2}{{b}_{2}}C_{2}^{2}\mu _{2}^{2}-\frac{2{{\nu }^{2}}{{b}_{2}}\mu _{1}^{2}{{\mu }_{3}}}{\sigma }+2\sigma {{b}_{2}}C_{1}^{2}\mu _{1}^{2}{{\mu }_{3}}-2\sigma {{b}_{2}}C_{2}^{2}\mu _{1}^{2}{{\mu }_{3}}+\frac{8k{{\nu }^{2}}{{b}_{2}}{{\mu }_{2}}{{\mu }_{3}}}{\sigma } \\&-8k\sigma {{b}_{2}}C_{1}^{2}{{\mu }_{2}}{{\mu }_{3}}+8k\sigma {{b}_{2}}C_{2}^{2}{{\mu }_{2}}{{\mu }_{3}}-\frac{8w{{\nu }^{2}}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}}{\sigma }+8w\sigma {{b}_{2}}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-8w\sigma {{b}_{2}}C_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-\frac{8{{w}^{2}}{{\nu }^{2}}{{b}_{2}}\mu _{2}^{2}{{\mu }_{3}}}{\sigma } \\&+8{{w}^{2}}\sigma {{b}_{2}}C_{1}^{2}\mu _{2}^{2}{{\mu }_{3}}-8{{w}^{2}}\sigma {{b}_{2}}C_{2}^{2}\mu _{2}^{2}{{\mu }_{3}}-\frac{8{{k}^{2}}{{\nu }^{2}}{{b}_{2}}{{\mu }_{2}}\mu _{3}^{2}}{\sigma }+8{{k}^{2}}\sigma {{b}_{2}}C_{1}^{2}{{\mu }_{2}}\mu _{3}^{2}-8{{k}^{2}}\sigma {{b}_{2}}C_{2}^{2}{{\mu }_{2}}\mu _{3}^{2}=0, \\&\frac{1}{{{G}^{2}}}\left( \frac{G'}{G} \right) :\,-\frac{{{\nu }^{2}}b_{1}^{3}\mu _{1}^{2}}{\sigma }+3{{b}_{1}}b_{2}^{2}\mu _{1}^{2}+\sigma b_{1}^{3}C_{1}^{2}\mu _{1}^{2}-\sigma b_{1}^{3}C_{2}^{2}\mu _{1}^{2}-\frac{2{{\nu }^{2}}{{b}_{1}}{{\mu }_{2}}}{\sigma }+2\sigma {{b}_{1}}C_{1}^{2}{{\mu }_{2}}-2\sigma {{b}_{1}}C_{2}^{2}{{\mu }_{2}} \\&-\frac{4w{{\nu }^{2}}b_{1}^{3}{{\mu }_{1}}{{\mu }_{2}}}{\sigma }+12w{{b}_{1}}b_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}+4w\sigma b_{1}^{3}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}-4w\sigma b_{1}^{3}C_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}-\frac{4{{w}^{2}}{{\nu }^{2}}b_{1}^{3}\mu _{2}^{2}}{\sigma }+12{{w}^{2}}{{b}_{1}}b_{2}^{2}\mu _{2}^{2}+4{{w}^{2}}\sigma b_{1}^{3}C_{1}^{2}\mu _{2}^{2} \\&-4{{w}^{2}}\sigma b_{1}^{3}C_{2}^{2}\mu _{2}^{2}-\frac{2{{\nu }^{2}}{{b}_{1}}\mu _{1}^{2}{{\mu }_{3}}}{\sigma }+2\sigma {{b}_{1}}C_{1}^{2}\mu _{1}^{2}{{\mu }_{3}}-2\sigma {{b}_{1}}C_{2}^{2}\mu _{1}^{2}{{\mu }_{3}}+\frac{8k{{\nu }^{2}}{{b}_{1}}{{\mu }_{2}}{{\mu }_{3}}}{\sigma }-8k\sigma {{b}_{1}}C_{1}^{2}{{\mu }_{2}}{{\mu }_{3}}+8k\sigma {{b}_{1}}C_{2}^{2}{{\mu }_{2}}{{\mu }_{3}} \\&-\frac{8w{{\nu }^{2}}{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}}{\sigma }+8w\sigma {{b}_{1}}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-8w\sigma {{b}_{1}}C_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-\frac{8{{w}^{2}}{{\nu }^{2}}{{b}_{1}}\mu _{2}^{2}{{\mu }_{3}}}{\sigma }+8{{w}^{2}}\sigma {{b}_{1}}C_{1}^{2}\mu _{2}^{2}{{\mu }_{3}}-8{{w}^{2}}\sigma {{b}_{1}}C_{2}^{2}\mu _{2}^{2}{{\mu }_{3}} \\&-\frac{8{{k}^{2}}{{\nu }^{2}}{{b}_{1}}{{\mu }_{2}}\mu _{3}^{2}}{\sigma }+8{{k}^{2}}\sigma {{b}_{1}}C_{1}^{2}{{\mu }_{2}}\mu _{3}^{2}-8{{k}^{2}}\sigma {{b}_{1}}C_{2}^{2}{{\mu }_{2}}\mu _{3}^{2}=0. \end{aligned}$$

After solving the above system via Mathematica program, we acquired the following results:

First

$$\begin{aligned}{} & {} {{b}_{1}}=\pm \frac{\sqrt{-{{\mu }_{2}}-\mu _{1}^{2}{{\mu }_{3}}}}{\sqrt{2{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}-4\sigma {{\mu }_{2}}{{\mu }_{3}}}},{{b}_{2}}=\pm \sqrt{\frac{\left( {{\nu }^{2}}+{{\sigma }^{2}}\left( -C_{1}^{2}+C_{2}^{2} \right) \right) {{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( {{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}} \right) }{\sigma 2{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{4}}-4{{\sigma }^{2}}{{\mu }_{2}}{{\mu }_{3}}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}}}, \nonumber \\{} & {} k=\pm \frac{1}{2{{\mu }_{3}}}\left( 1+\sqrt{-\frac{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( -1+4w\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) {{\mu }_{3}}-2\sigma \mu _{3}^{2} \right) }{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}-2\sigma {{\mu }_{2}}{{\mu }_{3}}}} \right) , {{b}_{0}}=0,w=w.~~~~~~~~~~~~~ \end{aligned}$$
(14)

The following hyperbolic solutions are acquired from (2), (6), (8), and (14):

$$\begin{aligned} {{u}_{1}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }\pm kx \right) }}\left( \begin{aligned}&\pm \frac{\left( \sinh \left( \sqrt{-\sigma }\left( x+\frac{{{B}_{2}}{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{1}}+\cosh \left( \sqrt{-\sigma }\left( x+\frac{{{B}_{2}}{{t}^{\alpha }}}{\alpha } \right) \right) \right) {{B}_{3}}}{\left( \frac{\nu }{\sigma }+\cosh \left( \sqrt{-\sigma }\left( x+\frac{{{B}_{2}}{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{1}}+\sinh \left( \sqrt{-\sigma }\left( x+\frac{{{B}_{2}}{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{2}} \right) } \\&\pm \frac{\sqrt{2}{{B}_{1}}}{2\left( \frac{\nu }{\sigma }+\cosh \left( \sqrt{-\sigma }\left( x+\frac{{{B}_{2}}{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{1}}+\sinh \left( \sqrt{-\sigma }\left( x+\frac{{{B}_{2}}{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{2}} \right) } \\ \end{aligned} \right) , \end{aligned}$$
(15)

where \({{B}_{1}}=\frac{\sqrt{\frac{\left( {{\nu }^{2}}+{{\sigma }^{2}}\left( -C_{1}^{2}+C_{2}^{2} \right) \right) {{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( {{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}} \right) }{-{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}+2\sigma {{\mu }_{2}}{{\mu }_{3}}}}}{\sqrt{-\sigma {{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}}}\), \({{B}_{3}}=\frac{\sqrt{\sigma {{\mu }_{2}}+\sigma \mu _{1}^{2}{{\mu }_{3}}}}{\sqrt{2{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}-4\sigma {{\mu }_{2}}{{\mu }_{3}}}}\), and

\({{B}_{2}}=\pm \frac{1}{{{\mu }_{1}}+2w{{\mu }_{2}}}\sqrt{-\frac{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( -1+4w\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) {{\mu }_{3}}-2\sigma \mu _{3}^{2} \right) }{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}-2\sigma {{\mu }_{2}}{{\mu }_{3}}}}\).

Inserting \({{C}_{1}}\ne 0,{{C}_{2}}= 0\), and \(\nu =0\) in (15), we obtain the following optical solutions:

$$\begin{aligned} {{u}_{2}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }\pm kx \right) }}\left( \pm {\text {sech}}\left( \sqrt{-\sigma }\left( x\pm \frac{{{B}_{2}}{{t}^{\alpha }}}{\alpha } \right) \right) \frac{{{B}_{1}}}{\sqrt{2}{{C}_{1}}}\pm \tanh \left( \sqrt{-\sigma }\left( x+\frac{{{B}_{2}}{{t}^{\alpha }}}{\alpha } \right) \right) {{B}_{3}} \right) . \end{aligned}$$
(16)

Inserting \({{C}_{1}}= 0,{{C}_{2}}\ne 0\), and \(\nu =0\) in (15), we obtain the following singular solutions:

$$\begin{aligned} {{u}_{3}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }\pm kx \right) }}\left( \pm \coth \left( \sqrt{-\sigma }\left( x\pm \frac{{{B}_{2}}{{t}^{\alpha }}}{\alpha } \right) \right) {{B}_{3}}\pm {\text {csch}}\left( \sqrt{-\sigma }\left( x+\frac{{{B}_{2}}{{t}^{\alpha }}}{\alpha } \right) \right) \frac{{{D}_{1}}}{\sqrt{2}{{C}_{2}}} \right) , \end{aligned}$$
(17)

where \({{D}_{1}}=\sqrt{\frac{{{\sigma }^{2}}C_{2}^{2}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( {{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}} \right) }{\sigma {{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{4}}-2{{\sigma }^{2}}{{\mu }_{2}}{{\mu }_{3}}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}}}\).

Fig. 6
figure 6

The 3D plot, 2D plot and contour plot of \({{\left| {{u}_{13}}(x,t) \right| }^{2}}\) for \({\mu }_{1} =-0.4,{\mu }_{2} =-0.1, w=0.1,{b}_{1} =-0.6,\sigma =0.1,{{C}_{1}}=-1,{{C}_{2}}=-3,\) and \(\nu =-2\)

Full size image
Fig. 7
figure 7

The 3D plot, 2D plot and contour plot of \({{\left| {{u}_{12}}(x,t) \right| }^{2}}\) and \({\text {Re}}({{u}_{12}}(x,t))\) for \({\mu }_{1} =\sigma =0.1,{\mu }_{2} =-0.1, w=0.1,{\mu }_{3} =-0.1,w=0.2,{{C}_{1}}=\nu =0,\) and \({{C}_{2}}=1\)

Full size image
Fig. 8
figure 8

The 3D plot, 2D plot and contour plot of \({{\left| {{u}_{19}}(x,t) \right| }^{2}}\) for \({\mu }_{1} =0.8,{\mu }_{2}={\mu }_{3} =0.2, w=0.1,{{C}_{1}}=0.2,{{C}_{2}}=0.4,\) and \(\nu =2\)

Full size image
Fig. 9
figure 9

The 3D plot, 2D plot and contour plot of \({\text {Re}}({{u}_{19}}(x,t))\) and \({\text {Im}}({{u}_{19}}(x,t))\) for \({\mu }_{1} =0.8,{\mu }_{2}={\mu }_{3} =0.2, w=0.1,{{C}_{1}}=0.2,{{C}_{2}}=0.4,\) and \(\nu =2\)

Full size image
Fig. 10
figure 10

The 3D plot, 2D plot and contour plot of \({\text {Im}}({{u}_{20}}(x,t))\) for \({\mu }_{1} =0.8,{\mu }_{2}=0.2,{\mu }_{3} =0.5, w=0.3,{{C}_{1}}=0.2,{{C}_{2}}=0.4,k=0.9,\) and \(\nu =2\)

Full size image

Second

$$\begin{aligned} {{b}_{0}}=0,{{b}_{1}}=\pm \sqrt{\frac{-{{\mu }_{3}}}{2}},{{b}_{2}}=\pm \sqrt{\frac{{{\mu }_{3}}}{2}}\sqrt{\frac{{{\nu }^{2}}}{\sigma }+\sigma \left( -C_{1}^{2}+C_{2}^{2} \right) },k=\frac{1}{2{{\mu }_{3}}},{{\mu }_{1}}=-w{{\mu }_{2}}+\frac{1}{4w{{\mu }_{3}}}+\frac{{{\mu }_{3}}\sigma }{2w}. \end{aligned}$$
(18)

We obtain the following hyperbolic solutions from (2), (6), (8), and (18):

$$\begin{aligned} {{u}_{4}}(x,y,t)={{\text {e}}^{\text {i}\left( tw-\frac{x}{2{{\mu }_{3}}} \right) }}\left( \begin{aligned}&\pm \frac{\left( \sinh \left( x\sqrt{-\sigma } \right) {{C}_{1}}+\cosh \left( x\sqrt{-\sigma } \right) {{C}_{2}} \right) \sqrt{\sigma {{\mu }_{3}}}}{\sqrt{2}\left( \frac{\nu }{\sigma }+\cosh \left( x\sqrt{-\sigma } \right) {{C}_{1}}+\sinh \left( x\sqrt{-\sigma } \right) {{C}_{2}} \right) } \\&\pm \frac{\sqrt{{{\nu }^{2}}+{{\sigma }^{2}}\left( -C_{1}^{2}+C_{2}^{2} \right) }\sqrt{{{\mu }_{3}}}}{\sqrt{2\sigma }\left( \frac{\nu }{\sigma }+\cosh \left( x\sqrt{-\sigma } \right) {{C}_{1}}+\sinh \left( x\sqrt{-\sigma } \right) {{C}_{2}} \right) } \\ \end{aligned} \right) . \end{aligned}$$
(19)

Inserting \({{C}_{1}}\ne 0,{{C}_{2}}=0\), and \(\nu =0\) in (19), the following soliton solutions are obtained:

$$\begin{aligned} {{u}_{5}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }-\frac{x}{2{{\mu }_{3}}} \right) }}\left( \pm \frac{\sqrt{-{{\sigma }^{2}}{{\mu }_{3}}C_{1}^{2}}}{\sqrt{2}\sqrt{\sigma }{{C}_{1}}}{\text {sech}}\left( x\sqrt{-\sigma } \right) \pm i\sqrt{\frac{\sigma {{\mu }_{3}}}{2}}\tanh \left( x\sqrt{-\sigma } \right) \right) . \end{aligned}$$
(20)

Inserting \({{C}_{1}}=0, {{C}_{2}}\ne 0\), and \(\nu =0\) in (19), we obtain the following singular solutions:

$$\begin{aligned} {{u}_{6}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }-\frac{x}{2{{\mu }_{3}}} \right) }}\left( \pm \sqrt{\frac{\sigma {{\mu }_{3}}}{2}}\coth \left( x\sqrt{-\sigma } \right) \pm \frac{\sqrt{{{\sigma }^{2}}{{\mu }_{3}}C_{2}^{2}}}{\sqrt{2}\sqrt{\sigma }{{C}_{2}}}{\text {csch}}\left( x\sqrt{-\sigma } \right) \right) . \end{aligned}$$
(21)

Third

$$\begin{aligned}{} & {} {{b}_{1}}=\pm \sqrt{\frac{\mu _{1}^{2}+2{{\mu }_{2}}\left( 2k-\left( 2{{k}^{2}}+\sigma \right) {{\mu }_{3}} \right) \mp {{E}_{1}}}{64{{\sigma }^{2}}{{\mu }_{2}}}},w=\frac{{{\mu }_{1}}}{2{{\mu }_{2}}}-\frac{\sqrt{2}}{4{{\mu }_{2}}}\sqrt{\mu _{1}^{2}+2{{\mu }_{2}}\left( 2k+\left( -2{{k}^{2}}+\sigma \right) {{\mu }_{3}} \right) \pm {{E}_{1}}}, \nonumber \\{} & {} {{b}_{2}}=\pm \sqrt{\frac{\left( {{\nu }^{2}}+{{\sigma }^{2}}\left( -C_{1}^{2}+C_{2}^{2} \right) \right) \left( -\mu _{1}^{2}+2{{\mu }_{2}}\left( -2k+\left( 2{{k}^{2}}+\sigma \right) {{\mu }_{3}} \right) \pm {{E}_{1}} \right) }{8{{\sigma }^{2}}{{\mu }_{2}}}},{{b}_{0}}=0, \end{aligned}$$
(22)

where \({{E}_{1}}=\sqrt{\mu _{1}^{4}+4\mu _{1}^{2}{{\mu }_{2}}\left( 2k+\left( -2{{k}^{2}}+\sigma \right) {{\mu }_{3}} \right) +4\left( 2{{k}^{2}}+\sigma \right) \mu _{2}^{2}\left( 2-4k{{\mu }_{3}}+\left( 2{{k}^{2}}+\sigma \right) \mu _{3}^{2} \right) }\).

We obtain the following hyperbolic solutions from (2), (6), (8) and (22):

$$\begin{aligned} {{u}_{7}}(x,t)={{\text {e}}^{\text {i}\left( -kx+\frac{{{t}^{\alpha }}\left( -2{{\mu }_{1}}+\sqrt{2}{{E}_{3}} \right) }{4{{\mu }_{2}}\alpha } \right) }}\left( \begin{aligned}&\mp \frac{i\left( \sinh \left( \sqrt{-\sigma }\left( x\mp \frac{{{t}^{\alpha }}{{E}_{2}}}{\alpha } \right) \right) {{C}_{1}}+\cosh \left( \sqrt{-\sigma }\left( x\mp \frac{{{t}^{\alpha }}{{E}_{2}}}{\alpha } \right) \right) {{C}_{2}} \right) {{E}_{3}}}{\left( \frac{\nu }{\sigma }+\cosh \left( \sqrt{-\sigma }\left( x\mp \frac{{{t}^{\alpha }}{{E}_{2}}}{\alpha } \right) \right) {{C}_{1}}+\sinh \left( \sqrt{-\sigma }\left( x\mp \frac{{{t}^{\alpha }}{{E}_{2}}}{\alpha } \right) \right) {{C}_{2}} \right) } \\&\pm \frac{\sqrt{\frac{\left( {{\nu }^{2}}+{{\sigma }^{2}}\left( -C_{1}^{2}+C_{2}^{2} \right) \right) \left( {{E}_{1}}-\mu _{1}^{2}+2{{\mu }_{2}}\left( -2k+\left( 2{{k}^{2}}+\sigma \right) {{\mu }_{3}} \right) \right) }{8{{\sigma }^{2}}{{\mu }_{2}}}}}{\left( \frac{\nu }{\sigma }+\cosh \left( \sqrt{-\sigma }\left( x\mp \frac{{{t}^{\alpha }}{{E}_{2}}}{\alpha } \right) \right) {{C}_{1}}+\sinh \left( \sqrt{-\sigma }\left( x\mp \frac{{{t}^{\alpha }}{{E}_{2}}}{\alpha } \right) \right) {{C}_{2}} \right) } \\ \end{aligned} \right) , \end{aligned}$$
(23)

where \({{E}_{2}}=\frac{\left( 1-2k{{\mu }_{3}} \right) }{{{\mu }_{1}}+\frac{1}{2}\left( -2{{\mu }_{1}}+\sqrt{2}\sqrt{\mu _{1}^{2}+2{{\mu }_{2}}\left( 2k+\left( -2{{k}^{2}}+\sigma \right) {{\mu }_{3}} \right) +{{E}_{1}}} \right) }\) and \({{E}_{3}}=\sqrt{\frac{-{{E}_{1}}+\mu _{1}^{2}+2{{\mu }_{2}}\left( 2k-\left( 2{{k}^{2}}+\sigma \right) {{\mu }_{3}} \right) }{8{{\mu }_{2}}}}\).

Inserting \({{C}_{1}}\ne 0,{{C}_{2}}=0\), and \(\nu =0\) in (23), we obtain the following solutions:

$$\begin{aligned} {{u}_{8}}(x,t)={{\text {e}}^{\text {i}\left( -kx+\frac{{{t}^{\alpha }}\left( -2{{\mu }_{1}}+\sqrt{2}{{E}_{3}} \right) }{4{{\mu }_{2}}\alpha } \right) }}\left( \begin{aligned}&\pm \frac{\left| \sigma {{C}_{1}} \right| }{\sigma {{C}_{1}}}\sqrt{\frac{\mu _{1}^{2}-2{{\mu }_{2}}\left( -2k+\left( 2{{k}^{2}}+\sigma \right) {{\mu }_{3}} \right) -{{E}_{1}}}{8{{\mu }_{2}}}}{\text {sech}}\left( \sqrt{-\sigma }\left( x-\frac{{{t}^{\alpha }}{{E}_{2}}}{\alpha } \right) \right) \\&\mp i\frac{{{E}_{3}}}{\sqrt{8}}\tanh \left( \sqrt{-\sigma }\left( x-\frac{{{t}^{\alpha }}{{E}_{2}}}{\alpha } \right) \right) \\ \end{aligned} \right) . \end{aligned}$$
(24)

Inserting \({{C}_{1}}=0,{{C}_{2}}\ne 0\), and \(\nu =0\) in (23), we obtain the following singular solutions:

$$\begin{aligned} {{u}_{9}}(x,t)={{\text {e}}^{\text {i}\left( -kx+\frac{{{t}^{\alpha }}\left( -2{{\mu }_{1}}+\sqrt{2}{{E}_{3}} \right) }{4{{\mu }_{2}}\alpha } \right) }}\left( \begin{aligned}&\mp i\coth \left( \sqrt{-\sigma }\left( x-\frac{{{t}^{\alpha }}{{E}_{2}}}{\alpha } \right) \right) \frac{{{E}_{3}}}{\sqrt{8}} \\&\pm \frac{|\sigma {{C}_{2}}|}{\sigma {{C}_{2}}}\sqrt{\frac{-\mu _{1}^{2}+2{{\mu }_{2}}\left( -2k+\left( 2{{k}^{2}}+\sigma \right) {{\mu }_{3}} \right) +{{E}_{1}}}{8{{\mu }_{2}}}}{\text {csch}}\left( \sqrt{-\sigma }\left( x-\frac{{{t}^{\alpha }}{{E}_{2}}}{\alpha } \right) \right) \\ \end{aligned} \right) . \end{aligned}$$
(25)

ii. If \(\sigma >0\).

Putting Eq. (6) along with Eq. (10) and using Eq. (11) into Eq. (5), then the same orders of \(\frac{1}{{{G}^{i}}}\) and \(\frac{1}{{{G}^{j}}}\left( \frac{G'}{G} \right)\), \((i=0,1,2,3,j=0,1,2)\) are taken in consideration. Here, we equalize their coefficient to zero, we obtain the following system:

$$\begin{aligned}&{{\left( \frac{1}{G} \right) }^{0}}:k{{b}_{0}}\mu _{1}^{2}+b_{0}^{3}\mu _{1}^{2}-3\sigma {{b}_{0}}b_{1}^{2}\mu _{1}^{2}-w{{b}_{0}}\mu _{1}^{3}+4kw{{b}_{0}}{{\mu }_{1}}{{\mu }_{2}}+4wb_{0}^{3}{{\mu }_{1}}{{\mu }_{2}}-12w\sigma {{b}_{0}}b_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}-5{{w}^{2}}{{b}_{0}}\mu _{1}^{2}{{\mu }_{2}} \\&4k{{w}^{2}}{{b}_{0}}\mu _{2}^{2}+4{{w}^{2}}b_{0}^{3}\mu _{2}^{2}-12{{w}^{2}}\sigma {{b}_{0}}b_{1}^{2}\mu _{2}^{2}-8{{w}^{3}}{{b}_{0}}{{\mu }_{1}}\mu _{2}^{2}-4{{w}^{4}}{{b}_{0}}\mu _{2}^{3}-{{k}^{2}}{{b}_{0}}\mu _{1}^{2}{{\mu }_{3}}-4{{k}^{2}}w{{b}_{0}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}} \\&-4{{k}^{2}}{{w}^{2}}{{b}_{0}}\mu _{2}^{2}{{\mu }_{3}}=0, \\&\left( \frac{1}{G} \right) \,\,:6\nu {{b}_{0}}b_{1}^{2}\mu _{1}^{2}+k{{b}_{2}}\mu _{1}^{2}+3b_{0}^{2}{{b}_{2}}\mu _{1}^{2}-3\sigma b_{1}^{2}{{b}_{2}}\mu _{1}^{2}-w{{b}_{2}}\mu _{1}^{3}-\sigma {{b}_{2}}{{\mu }_{2}}+24w\nu {{b}_{0}}b_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}+4kw{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}} \\&+12wb_{0}^{2}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}-12w\sigma b_{1}^{2}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}-5{{w}^{2}}{{b}_{2}}\mu _{1}^{2}{{\mu }_{2}}+24{{w}^{2}}\nu {{b}_{0}}b_{1}^{2}\mu _{2}^{2}+4k{{w}^{2}}{{b}_{2}}\mu _{2}^{2}+12{{w}^{2}}b_{0}^{2}{{b}_{2}}\mu _{2}^{2} \\&-12{{w}^{2}}\sigma b_{1}^{2}{{b}_{2}}\mu _{2}^{2}-8{{w}^{3}}{{b}_{2}}{{\mu }_{1}}\mu _{2}^{2}-4{{w}^{4}}{{b}_{2}}\mu _{2}^{3}-{{k}^{2}}{{b}_{2}}\mu _{1}^{2}{{\mu }_{3}}-\sigma {{b}_{2}}\mu _{1}^{2}{{\mu }_{3}}+4k\sigma {{b}_{2}}{{\mu }_{2}}{{\mu }_{3}}-4{{k}^{2}}w{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}} \\&-4w\sigma {{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-4{{k}^{2}}{{w}^{2}}{{b}_{2}}\mu _{2}^{2}{{\mu }_{3}}-4{{w}^{2}}\sigma {{b}_{2}}\mu _{2}^{2}{{\mu }_{3}}-4{{k}^{2}}\sigma {{b}_{2}}{{\mu }_{2}}\mu _{3}^{2}=0, \\ \\&\left( \frac{G'}{G} \right) :\,k{{b}_{1}}\mu _{1}^{2}+3b_{0}^{2}{{b}_{1}}\mu _{1}^{2}-\sigma b_{1}^{3}\mu _{1}^{2}-w{{b}_{1}}\mu _{1}^{3}+4kw{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}+12wb_{0}^{2}{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}-4w\sigma b_{1}^{3}{{\mu }_{1}}{{\mu }_{2}}-5{{w}^{2}}{{b}_{1}}\mu _{1}^{2}{{\mu }_{2}} \\&+4k{{w}^{2}}{{b}_{1}}\mu _{2}^{2}+12{{w}^{2}}b_{0}^{2}{{b}_{1}}\mu _{2}^{2}-4{{w}^{2}}\sigma b_{1}^{3}\mu _{2}^{2}-8{{w}^{3}}{{b}_{1}}{{\mu }_{1}}\mu _{2}^{2}-4{{w}^{4}}{{b}_{1}}\mu _{2}^{3}-{{k}^{2}}{{b}_{1}}\mu _{1}^{2}{{\mu }_{3}}-4{{k}^{2}}w{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}} \\&-4{{k}^{2}}{{w}^{2}}{{b}_{1}}\mu _{2}^{2}{{\mu }_{3}}=0, \\&{{\left( \frac{1}{G} \right) }^{2}}:\,-\frac{3{{\nu }^{2}}{{b}_{0}}b_{1}^{2}\mu _{1}^{2}}{\sigma }+6\nu b_{1}^{2}{{b}_{2}}\mu _{1}^{2}+3{{b}_{0}}b_{2}^{2}\mu _{1}^{2}+3\sigma {{b}_{0}}b_{1}^{2}C_{1}^{2}\mu _{1}^{2}+3\sigma {{b}_{0}}b_{1}^{2}C_{2}^{2}\mu _{1}^{2}+3\nu {{b}_{2}}{{\mu }_{2}}-\frac{12w{{\nu }^{2}}{{b}_{0}}b_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}}{\sigma } \\&+24w\nu b_{1}^{2}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}+12w{{b}_{0}}b_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}+12w\sigma {{b}_{0}}b_{1}^{2}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}+12w\sigma {{b}_{0}}b_{1}^{2}C_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}-\frac{12{{w}^{2}}{{\nu }^{2}}{{b}_{0}}b_{1}^{2}\mu _{2}^{2}}{\sigma } \\&+24{{w}^{2}}\nu b_{1}^{2}{{b}_{2}}\mu _{2}^{2}+12{{w}^{2}}{{b}_{0}}b_{2}^{2}\mu _{2}^{2}+12{{w}^{2}}\sigma {{b}_{0}}b_{1}^{2}C_{1}^{2}\mu _{2}^{2}+12{{w}^{2}}\sigma {{b}_{0}}b_{1}^{2}C_{2}^{2}\mu _{2}^{2}+3\nu {{b}_{2}}\mu _{1}^{2}{{\mu }_{3}}-12k\nu {{b}_{2}}{{\mu }_{2}}{{\mu }_{3}} \\&+12w\nu {{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}+12{{w}^{2}}\nu {{b}_{2}}\mu _{2}^{2}{{\mu }_{3}}+12{{k}^{2}}\nu {{b}_{2}}{{\mu }_{2}}\mu _{3}^{2}=0, \\&\frac{1}{G}\left( \frac{G'}{G} \right) :\,2\nu b_{1}^{3}\mu _{1}^{2}+6{{b}_{0}}{{b}_{1}}{{b}_{2}}\mu _{1}^{2}+\nu {{b}_{1}}{{\mu }_{2}}+8w\nu b_{1}^{3}{{\mu }_{1}}{{\mu }_{2}}+24w{{b}_{0}}{{b}_{1}}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}+8{{w}^{2}}\nu b_{1}^{3}\mu _{2}^{2} \\&+24{{w}^{2}}{{b}_{0}}{{b}_{1}}{{b}_{2}}\mu _{2}^{2}+\nu {{b}_{1}}\mu _{1}^{2}{{\mu }_{3}}-4k\nu {{b}_{1}}{{\mu }_{2}}{{\mu }_{3}}+4w\nu {{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}+4{{w}^{2}}\nu {{b}_{1}}\mu _{2}^{2}{{\mu }_{3}}+4{{k}^{2}}\nu {{b}_{1}}{{\mu }_{2}}\mu _{3}^{2}=0, \\&{{\left( \frac{1}{G} \right) }^{3}}:-\frac{3{{\nu }^{2}}b_{1}^{2}{{b}_{2}}\mu _{1}^{2}}{\sigma }+b_{2}^{3}\mu _{1}^{2}+3\sigma b_{1}^{2}{{b}_{2}}C_{1}^{2}\mu _{1}^{2}+3\sigma b_{1}^{2}{{b}_{2}}C_{2}^{2}\mu _{1}^{2}-\frac{2{{\nu }^{2}}{{b}_{2}}{{\mu }_{2}}}{\sigma }+2\sigma {{b}_{2}}C_{1}^{2}{{\mu }_{2}}+2\sigma {{b}_{2}}C_{2}^{2}{{\mu }_{2}} \\&-\frac{12w{{\nu }^{2}}b_{1}^{2}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}}{\sigma }+4wb_{2}^{3}{{\mu }_{1}}{{\mu }_{2}}+12w\sigma b_{1}^{2}{{b}_{2}}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}\,+12w\sigma b_{1}^{2}{{b}_{2}}C_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}-\frac{12{{w}^{2}}{{\nu }^{2}}b_{1}^{2}{{b}_{2}}\mu _{2}^{2}}{\sigma }+4{{w}^{2}}b_{2}^{3}\mu _{2}^{2} \\&+12{{w}^{2}}\sigma b_{1}^{2}{{b}_{2}}C_{1}^{2}\mu _{2}^{2}+12{{w}^{2}}\sigma b_{1}^{2}{{b}_{2}}C_{2}^{2}\mu _{2}^{2}-\frac{2{{\nu }^{2}}{{b}_{2}}\mu _{1}^{2}{{\mu }_{3}}}{\sigma }+2\sigma {{b}_{2}}C_{1}^{2}\mu _{1}^{2}{{\mu }_{3}}+2\sigma {{b}_{2}}C_{2}^{2}\mu _{1}^{2}{{\mu }_{3}}+\frac{8k{{\nu }^{2}}{{b}_{2}}{{\mu }_{2}}{{\mu }_{3}}}{\sigma } \\&-8k\sigma {{b}_{2}}C_{1}^{2}{{\mu }_{2}}{{\mu }_{3}}-8k\sigma {{b}_{2}}C_{2}^{2}{{\mu }_{2}}{{\mu }_{3}}-\frac{8w{{\nu }^{2}}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}}{\sigma }+8w\sigma {{b}_{2}}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}+8w\sigma {{b}_{2}}C_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-\frac{8{{w}^{2}}{{\nu }^{2}}{{b}_{2}}\mu _{2}^{2}{{\mu }_{3}}}{\sigma } \\&+8{{w}^{2}}\sigma {{b}_{2}}C_{1}^{2}\mu _{2}^{2}{{\mu }_{3}}+8{{w}^{2}}\sigma {{b}_{2}}C_{2}^{2}\mu _{2}^{2}{{\mu }_{3}}-\frac{8{{k}^{2}}{{\nu }^{2}}{{b}_{2}}{{\mu }_{2}}\mu _{3}^{2}}{\sigma }+8{{k}^{2}}\sigma {{b}_{2}}C_{1}^{2}{{\mu }_{2}}\mu _{3}^{2}+8{{k}^{2}}\sigma {{b}_{2}}C_{2}^{2}{{\mu }_{2}}\mu _{3}^{2}=0, \\&\frac{1}{{{G}^{2}}}\left( \frac{G'}{G} \right) :\,-\frac{{{\nu }^{2}}b_{1}^{3}\mu _{1}^{2}}{\sigma }+3{{b}_{1}}b_{2}^{2}\mu _{1}^{2}+\sigma b_{1}^{3}C_{1}^{2}\mu _{1}^{2}+\sigma b_{1}^{3}C_{2}^{2}\mu _{1}^{2}-\frac{2{{\nu }^{2}}{{b}_{1}}{{\mu }_{2}}}{\sigma }+2\sigma {{b}_{1}}C_{1}^{2}{{\mu }_{2}}+2\sigma {{b}_{1}}C_{2}^{2}{{\mu }_{2}} \\&-\frac{4w{{\nu }^{2}}b_{1}^{3}{{\mu }_{1}}{{\mu }_{2}}}{\sigma }+12w{{b}_{1}}b_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}+4w\sigma b_{1}^{3}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}+4w\sigma b_{1}^{3}C_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}-\frac{4{{w}^{2}}{{\nu }^{2}}b_{1}^{3}\mu _{2}^{2}}{\sigma }+12{{w}^{2}}{{b}_{1}}b_{2}^{2}\mu _{2}^{2} \\&+4{{w}^{2}}\sigma b_{1}^{3}C_{1}^{2}\mu _{2}^{2}+4{{w}^{2}}\sigma b_{1}^{3}C_{2}^{2}\mu _{2}^{2}-\frac{2{{\nu }^{2}}{{b}_{1}}\mu _{1}^{2}{{\mu }_{3}}}{\sigma }+2\sigma {{b}_{1}}C_{1}^{2}\mu _{1}^{2}{{\mu }_{3}}+2\sigma {{b}_{1}}C_{2}^{2}\mu _{1}^{2}{{\mu }_{3}}+\frac{8k{{\nu }^{2}}{{b}_{1}}{{\mu }_{2}}{{\mu }_{3}}}{\sigma } \\&-8k\sigma {{b}_{1}}C_{1}^{2}{{\mu }_{2}}{{\mu }_{3}}-8k\sigma {{b}_{1}}C_{2}^{2}{{\mu }_{2}}{{\mu }_{3}}-\frac{8w{{\nu }^{2}}{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}}{\sigma }+8w\sigma {{b}_{1}}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}+8w\sigma {{b}_{1}}C_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}} \\&-\frac{8{{w}^{2}}{{\nu }^{2}}{{b}_{1}}\mu _{2}^{2}{{\mu }_{3}}}{\sigma }+8{{w}^{2}}\sigma {{b}_{1}}C_{1}^{2}\mu _{2}^{2}{{\mu }_{3}}+8{{w}^{2}}\sigma {{b}_{1}}C_{2}^{2}\mu _{2}^{2}{{\mu }_{3}}-\frac{8{{k}^{2}}{{\nu }^{2}}{{b}_{1}}{{\mu }_{2}}\mu _{3}^{2}}{\sigma }+8{{k}^{2}}\sigma {{b}_{1}}C_{1}^{2}{{\mu }_{2}}\mu _{3}^{2}\\&+8{{k}^{2}}\sigma {{b}_{1}}C_{2}^{2}{{\mu }_{2}}\mu _{3}^{2}=0. \end{aligned}$$

After solving the above system via Mathematica program, we acquired the following results:

First

$$\begin{aligned}{} & {} {{b}_{1}}=\pm \frac{\sqrt{-{{\mu }_{2}}-\mu _{1}^{2}{{\mu }_{3}}}}{\sqrt{2{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}-4\sigma {{\mu }_{2}}{{\mu }_{3}}}},{{b}_{2}}=\pm \sqrt{-\frac{\left( {{\nu }^{2}}-{{\sigma }^{2}}\left( C_{1}^{2}+C_{2}^{2} \right) \right) {{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( {{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}} \right) }{-2\sigma {{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{4}}+2\sigma {{\mu }_{2}}{{\mu }_{3}}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}}}, \nonumber \\{} & {} k=\frac{\pm 1}{2{{\mu }_{3}}}+\sqrt{-\frac{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( -1+4w\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) -2\sigma {{\mu }_{3}} \right) }{4{{\mu }_{3}}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}-8\sigma {{\mu }_{2}}\mu _{3}^{2}}},\,{{b}_{0}}=0,w=w.~~~~~~~~~~~~~~~~~ \end{aligned}$$
(26)

The following periodic solutions are obtained from (2), (6), (10) and (26):

$$\begin{aligned} {{u}_{10}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }+x\left( \frac{\pm 1}{2{{\mu }_{3}}}+\frac{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) {{B}_{4}}}{2{{\mu }_{3}}} \right) \right) }}\left( \begin{aligned}&\pm \frac{{{B}_{5}}\sqrt{\sigma }\left( -\sin \left( \sqrt{\sigma }\left( x-{{B}_{4}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{1}}+\cos \left( \sqrt{\sigma }\left( x-{{B}_{4}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{2}} \right) }{\left( \frac{\nu }{\sigma }+\cos \left( \sqrt{\sigma }\left( x-{{B}_{4}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{1}}+\sin \left( \sqrt{\sigma }\left( x-{{B}_{4}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{2}} \right) } \\&\pm \frac{\frac{{{B}_{6}}}{\sqrt{\sigma 2}}}{\left( \frac{\nu }{\sigma }+\cos \left( \sqrt{\sigma }\left( x-{{B}_{4}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{1}}+\sin \left( \sqrt{\sigma }\left( x-{{B}_{4}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{2}} \right) } \\ \end{aligned} \right) , \end{aligned}$$
(27)

where \({{B}_{4}}=\sqrt{-\frac{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( -1+4w\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) {{\mu }_{3}}-2\sigma \mu _{3}^{2} \right) }{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{4}}-2\sigma {{\mu }_{2}}{{\mu }_{3}}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}}}\), \({{B}_{5}}=\frac{\sqrt{-{{\mu }_{2}}-\mu _{1}^{2}{{\mu }_{3}}}}{\sqrt{2{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}-4\sigma {{\mu }_{2}}{{\mu }_{3}}}}\), and

\({{B}_{6}}=\sqrt{-\frac{\left( {{\nu }^{2}}-{{\sigma }^{2}}\left( C_{1}^{2}+C_{2}^{2} \right) \right) {{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( {{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}} \right) }{-\sigma {{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{4}}+2{{\sigma }^{2}}{{\mu }_{2}}{{\mu }_{3}}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}}}\).

Inserting \({{C}_{1}}\ne 0,{{C}_{2}}=0\), and \(\nu =0\) in (27), we obtain the following solutions:

$$\begin{aligned} {{u}_{11}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }+x\left( \frac{\pm 1}{2{{\mu }_{3}}}+\frac{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) {{B}_{4}}}{2{{\mu }_{3}}} \right) \right) }}\left( \begin{aligned}&\pm \frac{1}{{{C}_{1}}}\sqrt{\frac{\sigma C_{1}^{2}\left( {{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}} \right) }{-2{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}+4\sigma {{\mu }_{2}}{{\mu }_{3}}}}\sec \left( \sqrt{\sigma }\left( x-{{B}_{4}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) \\&\mp \frac{\sqrt{\sigma }\sqrt{-{{\mu }_{2}}-\mu _{1}^{2}{{\mu }_{3}}}\tan \left( \sqrt{\sigma }\left( x-{{B}_{4}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) }{\sqrt{2{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}-4\sigma {{\mu }_{2}}{{\mu }_{3}}}} \\ \end{aligned} \right) . \end{aligned}$$
(28)

Inserting \({{C}_{1}}=0,{{C}_{2}}\ne 0\), and \(\nu =0\) in (27), we obtain the following solutions:

$$\begin{aligned} {{u}_{12}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }+x\left( \frac{\pm 1}{2{{\mu }_{3}}}+\frac{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) {{B}_{4}}}{2{{\mu }_{3}}} \right) \right) }}\left( \begin{aligned}&\frac{\pm \sqrt{-\sigma {{\mu }_{2}}-\sigma \mu _{1}^{2}{{\mu }_{3}}}\cot \left( \sqrt{\sigma }\left( x-{{B}_{4}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) }{\sqrt{2{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}-4\sigma {{\mu }_{2}}{{\mu }_{3}}}}\pm \\&\frac{1}{{{C}_{2}}}\sqrt{\frac{{{\sigma }^{2}}C_{2}^{2}\left( {{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}} \right) }{-2\sigma {{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}+4{{\sigma }^{2}}{{\mu }_{2}}{{\mu }_{3}}}}\csc \left( \sqrt{\sigma }\left( x-{{B}_{4}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) \\ \end{aligned} \right) . \end{aligned}$$
(29)

Second

$$\begin{aligned}{} & {} {{b}_{0}}=0,{{b}_{2}}=\pm {{b}_{1}}\sqrt{-\frac{{{\nu }^{2}}}{\sigma }+\sigma \left( C_{1}^{2}+C_{2}^{2} \right) },{{\mu }_{3}}=\frac{{{\mu }_{2}}+2b_{1}^{2}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}}{-\mu _{1}^{2}+4\sigma b_{1}^{2}{{\mu }_{2}}},w=w, \nonumber \\{} & {} k=\pm \frac{\left( \mu _{1}^{2}-4\sigma b_{1}^{2}{{\mu }_{2}} \right) \left( 1+\sqrt{\frac{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( 1+8\sigma b_{1}^{4}+8wb_{1}^{2}\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) \right) }{\mu _{1}^{2}-4\sigma b_{1}^{2}{{\mu }_{2}}}} \right) }{2\left( {{\mu }_{2}}+2b_{1}^{2}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}} \right) }. \end{aligned}$$
(30)

The following periodic solutions are achieved from (2), (6), (8) and (30):

$$\begin{aligned} {{u}_{13}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }+x\left( {{B}_{7}}-\frac{1}{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) } \right) \right) }}\left( \begin{aligned}&\frac{{{b}_{1}}\sqrt{\sigma }\left( -\sin \left( \sqrt{\sigma }\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{7}} \right) \right) {{C}_{1}}+\cos \left( \sqrt{\sigma }\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{7}} \right) \right) {{C}_{2}} \right) }{\frac{\nu }{\sigma }+\cos \left( \sqrt{\sigma }\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{7}} \right) \right) {{C}_{1}}+\sin \left( \sqrt{\sigma }\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{7}} \right) \right) {{C}_{2}}} \\&\pm \frac{{{b}_{1}}\sqrt{-\frac{{{\nu }^{2}}}{\sigma }+\sigma \left( C_{1}^{2}+C_{2}^{2} \right) }}{\left( \frac{\nu }{\sigma }+\cos \left( \sqrt{\sigma }\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{7}} \right) \right) {{C}_{1}}+\sin \left( \sqrt{\sigma }\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{7}} \right) \right) {{C}_{2}} \right) } \\ \end{aligned} \right) , \end{aligned}$$
(31)

where \({{B}_{7}}=\frac{1}{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }\left( 1\mp \left( 1+\sqrt{\frac{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}\left( 1+8\sigma b_{1}^{4}+8wb_{1}^{2}\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) \right) }{\mu _{1}^{2}-4\sigma b_{1}^{2}{{\mu }_{2}}}} \right) \right)\).

Inserting \({{C}_{1}}\ne 0,{{C}_{2}}= 0\), and \(\nu =0\) in (31), we obtain the following singular solutions:

$$\begin{aligned} {{u}_{14}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }+x\left( {{B}_{7}}-\frac{1}{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) } \right) \right) }}\left( \begin{aligned}&\mp \frac{{{b}_{1}}\sqrt{{{\sigma }^{2}}C_{1}^{2}}}{\sqrt{\sigma }{{C}_{1}}}\sec \left( \sqrt{\sigma }\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{7}} \right) \right) \\&-{{b}_{1}}\sqrt{\sigma }\tan \left( \sqrt{\sigma }\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{7}} \right) \right) \\ \end{aligned} \right) .~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(32)

Inserting \({{C}_{1}}=0,{{C}_{2}}\ne 0\), and \(\nu =0\) in (31), we obtain the following singular solutions:

$$\begin{aligned} {{u}_{15}}(x,t)={{\text {e}}^{\text {i}\left( w\frac{{{t}^{\alpha }}}{\alpha }+x\left( {{B}_{7}}-\frac{1}{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) } \right) \right) }}\left( \begin{aligned}&\frac{{{b}_{1}}}{\sqrt{\sigma }}\cot \left( \sqrt{\sigma }\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{7}} \right) \right) \\&\mp \frac{{{b}_{1}}\sqrt{{{\sigma }^{2}}C_{2}^{2}}}{\sqrt{\sigma }{{C}_{2}}}\csc \left( \sqrt{\sigma }\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{7}} \right) \right) \\ \end{aligned} \right) .~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(33)

Third

$$\begin{aligned} {{b}_{0}}=0,{{b}_{1}}=\frac{\pm {{\mu }_{1}}}{2\sqrt{\sigma }\sqrt{{{\mu }_{2}}}},{{b}_{2}}=\frac{\sqrt{-{{\nu }^{2}}+{{\sigma }^{2}}\left( C_{1}^{2}+C_{2}^{2} \right) }{{\mu }_{1}}}{\pm 2\sigma \sqrt{{{\mu }_{2}}}},k=\frac{\mu _{1}^{2}\pm \sqrt{\mu _{1}^{4}+2\sigma \mu _{1}^{2}{{\mu }_{2}}{{\mu }_{3}}}}{2\mu _{1}^{2}{{\mu }_{3}}},w=\frac{\pm \sqrt{-\sigma }}{\sqrt{2}{{\mu }_{1}}}-\frac{{{\mu }_{1}}}{2{{\mu }_{2}}}, \end{aligned}$$
(34)

where \({{B}_{8}}=\frac{\left( 1-\frac{\mu _{1}^{2}-\sqrt{\mu _{1}^{4}+2\sigma \mu _{1}^{2}{{\mu }_{2}}{{\mu }_{3}}}}{\mu _{1}^{2}} \right) }{{{\mu }_{1}}+2\left( \frac{\text {i}\sqrt{\sigma }}{\sqrt{2}{{\mu }_{1}}}-\frac{{{\mu }_{1}}}{2{{\mu }_{2}}} \right) {{\mu }_{2}}}\).

The following periodic solutions from (2), (6), (8) and (34):

$$\begin{aligned} {{u}_{16}}(x,t)={{\text {e}}^{\text {i}\left( \left( \pm \frac{\sqrt{-\sigma }}{\sqrt{2}{{\mu }_{1}}}-\frac{{{\mu }_{1}}}{2{{\mu }_{2}}} \right) \frac{{{t}^{\alpha }}}{\alpha }-x{{B}_{9}} \right) }}\left( \begin{aligned}&\frac{\frac{\pm {{\mu }_{1}}}{2\sqrt{{{\mu }_{2}}}}\left( -\sin \left( \sqrt{\sigma }\left( x-{{B}_{8}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{1}}+\cos \left( \sqrt{\sigma }\left( x-{{B}_{8}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{2}} \right) }{\left( \frac{\nu }{\sigma }+\cos \left( \sqrt{\sigma }\left( x-{{B}_{8}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{1}}+\sin \left( \sqrt{\sigma }\left( x-{{B}_{8}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{2}} \right) } \\&\pm \frac{\frac{{{\mu }_{1}}}{2\sigma \sqrt{{{\mu }_{2}}}}\sqrt{-{{\nu }^{2}}+{{\sigma }^{2}}\left( C_{1}^{2}+C_{2}^{2} \right) }}{\left( \frac{\nu }{\sigma }+\cos \left( \sqrt{\sigma }\left( x-{{B}_{8}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{1}}+\sin \left( \sqrt{\sigma }\left( x-{{B}_{8}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) {{C}_{2}} \right) } \\ \end{aligned} \right) , \end{aligned}$$
(35)

where \({{B}_{8}}=\frac{\left( \frac{1}{\mu _{1}^{2}}\pm \frac{1}{{{\mu }_{1}}}\sqrt{\mu _{1}^{2}+2\sigma {{\mu }_{2}}{{\mu }_{3}}}-1 \right) }{{{\mu }_{1}}\pm \left( -\frac{\text {i}{{\mu }_{2}}\sqrt{2\sigma }}{{{\mu }_{1}}}-{{\mu }_{1}} \right) }\) and \({{B}_{9}}=\frac{1}{2{{\mu }_{3}}}\pm \frac{1}{2{{\mu }_{1}}{{\mu }_{3}}}\sqrt{\mu _{1}^{2}+2\sigma {{\mu }_{2}}{{\mu }_{3}}}\).

Inserting \({{C}_{1}}\ne 0,{{C}_{2}}=0\), and \(,\nu =0\) in (35), we obtain the following solutions:

$$\begin{aligned} {{u}_{17}}(x,t)={{\text {e}}^{\text {i}\left( \left( \pm \frac{\sqrt{-\sigma }}{\sqrt{2}{{\mu }_{1}}}-\frac{{{\mu }_{1}}}{2{{\mu }_{2}}} \right) \frac{{{t}^{\alpha }}}{\alpha }-x{{B}_{9}} \right) }}\left( \begin{aligned}&\pm \frac{\sqrt{{{\sigma }^{2}}C_{1}^{2}}{{\mu }_{1}}}{2\sigma {{C}_{1}}\sqrt{{{\mu }_{2}}}}\sec \left( \sqrt{\sigma }\left( x-{{B}_{8}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) \\&\mp \frac{{{\mu }_{1}}}{2\sqrt{{{\mu }_{2}}}}\tan \left( \sqrt{\sigma }\left( x-{{B}_{8}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) \\ \end{aligned} \right) . \end{aligned}$$
(36)
Fig. 11
figure 11

The 2D plot of \({{\left| {{u}_{7}}(x,t) \right| }^{2}}\) and \({\text {Re}}({{u}_{7}}(x,t))\) for \({\mu }_{1} =-0.8,{\mu }_{2}=0.8,{\mu }_{3} =-0.1, w=0.3,{{C}_{1}}=1,{{C}_{2}}=-1,k=0.1,\) and \(\nu =-2\)

Full size image
Fig. 12
figure 12

The 2D plot of \({{\left| {{u}_{19}}(x,t) \right| }^{2}}\) and \({\text {Im}}({{u}_{19}}(x,t))\) for \({\mu }_{1} =0.8,{\mu }_{2}=0.2,{\mu }_{3} =0.2, w=0.1,{{C}_{1}}=0.2,{{C}_{2}}=0.4,\) and \(\nu =2\)

Full size image

In case, we set \({{C}_{1}}= 0,{{C}_{2}}\ne 0\), and \(\nu =0\), in (35), we obtain the following singular solutions:

$$\begin{aligned} {{u}_{18}}(x,t)={{\text {e}}^{\text {i}\left( \left( \pm \frac{\sqrt{-\sigma }}{\sqrt{2}{{\mu }_{1}}}-\frac{{{\mu }_{1}}}{2{{\mu }_{2}}} \right) \frac{{{t}^{\alpha }}}{\alpha }-x{{B}_{9}} \right) }}\left( \begin{aligned}&\pm \frac{{{\mu }_{1}}}{2\sqrt{{{\mu }_{2}}}}\cot \left( \sqrt{\sigma }\left( x-{{B}_{8}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) \\&\pm \frac{\sqrt{{{\sigma }^{2}}C_{2}^{2}}{{\mu }_{1}}}{2\sigma {{C}_{2}}\sqrt{{{\mu }_{2}}}}\csc \left( \sqrt{\sigma }\left( x-{{B}_{8}}\frac{{{t}^{\alpha }}}{\alpha } \right) \right) \\ \end{aligned} \right) . \end{aligned}$$
(37)

iii. If \(\sigma =0\).

Putting Eq. (6) along with Eq. (12) and using Eq. (13) into equation (5), then the same orders of \(\frac{1}{{{G}^{i}}}\) and \(\frac{1}{{{G}^{j}}}\left( \frac{G'}{G} \right)\), \((i=0,1,2,3,j=0,1,2)\) are taken in consideration. Here, we equalize their coefficient to zero, the following algebraic equations are acquired:

$$\begin{aligned} ~~&{{\left( \frac{1}{G} \right) }^{0}}:k{{b}_{0}}\mu _{1}^{2}+b_{0}^{3}\mu _{1}^{2}-w{{b}_{0}}\mu _{1}^{3}+4kw{{b}_{0}}{{\mu }_{1}}{{\mu }_{2}}+4wb_{0}^{3}{{\mu }_{1}}{{\mu }_{2}}-5{{w}^{2}}{{b}_{0}}\mu _{1}^{2}{{\mu }_{2}}+4k{{w}^{2}}{{b}_{0}}\mu _{2}^{2}+4{{w}^{2}}b_{0}^{3}\mu _{2}^{2} \\&-8{{w}^{3}}{{b}_{0}}{{\mu }_{1}}\mu _{2}^{2}-4{{w}^{4}}{{b}_{0}}\mu _{2}^{3}-{{k}^{2}}{{b}_{0}}\mu _{1}^{2}{{\mu }_{3}}-4{{k}^{2}}w{{b}_{0}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-4{{k}^{2}}{{w}^{2}}{{b}_{0}}\mu _{2}^{2}{{\mu }_{3}}=0, \\&\left( \frac{1}{G} \right) \,\,:6\nu {{b}_{0}}b_{1}^{2}\mu _{1}^{2}+k{{b}_{2}}\mu _{1}^{2}+3b_{0}^{2}{{b}_{2}}\mu _{1}^{2}-w{{b}_{2}}\mu _{1}^{3}+24w\nu {{b}_{0}}b_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}+4kw{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}+12wb_{0}^{2}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}} \\&-5{{w}^{2}}{{b}_{2}}\mu _{1}^{2}{{\mu }_{2}}+24{{w}^{2}}\nu {{b}_{0}}b_{1}^{2}\mu _{2}^{2}+4k{{w}^{2}}{{b}_{2}}\mu _{2}^{2}+12{{w}^{2}}b_{0}^{2}{{b}_{2}}\mu _{2}^{2}-8{{w}^{3}}{{b}_{2}}{{\mu }_{1}}\mu _{2}^{2}-4{{w}^{4}}{{b}_{2}}\mu _{2}^{3}-{{k}^{2}}{{b}_{2}}\mu _{1}^{2}{{\mu }_{3}} \\&-4{{k}^{2}}w{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-4{{k}^{2}}{{w}^{2}}{{b}_{2}}\mu _{2}^{2}{{\mu }_{3}}=0, \\&\left( \frac{G'}{G} \right) :\,k{{b}_{1}}\mu _{1}^{2}+3b_{0}^{2}{{b}_{1}}\mu _{1}^{2}-w{{b}_{1}}\mu _{1}^{3}+4kw{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}+12wb_{0}^{2}{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}-5{{w}^{2}}{{b}_{1}}\mu _{1}^{2}{{\mu }_{2}}+4k{{w}^{2}}{{b}_{1}}\mu _{2}^{2} \\&+12{{w}^{2}}b_{0}^{2}{{b}_{1}}\mu _{2}^{2}-8{{w}^{3}}{{b}_{1}}{{\mu }_{1}}\mu _{2}^{2}-4{{w}^{4}}{{b}_{1}}\mu _{2}^{3}-{{k}^{2}}{{b}_{1}}\mu _{1}^{2}{{\mu }_{3}}-4{{k}^{2}}w{{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-4{{k}^{2}}{{w}^{2}}{{b}_{1}}\mu _{2}^{2}{{\mu }_{3}}=0,~~~~~~ \\&{{\left( \frac{1}{G} \right) }^{2}}:\,6\nu b_{1}^{2}{{b}_{2}}\mu _{1}^{2}+3{{b}_{0}}b_{2}^{2}\mu _{1}^{2}+3{{b}_{0}}b_{1}^{2}C_{1}^{2}\mu _{1}^{2}-6\nu {{b}_{0}}b_{1}^{2}{{C}_{2}}\mu _{1}^{2}+3\nu {{b}_{2}}{{\mu }_{2}}+24w\nu b_{1}^{2}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}} \\&+12w{{b}_{0}}b_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}+12w{{b}_{0}}b_{1}^{2}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}-24w\nu {{b}_{0}}b_{1}^{2}{{C}_{2}}{{\mu }_{1}}{{\mu }_{2}}+24{{w}^{2}}\nu b_{1}^{2}{{b}_{2}}\mu _{2}^{2}+12{{w}^{2}}{{b}_{0}}b_{2}^{2}\mu _{2}^{2} \\&+12{{w}^{2}}{{b}_{0}}b_{1}^{2}C_{1}^{2}\mu _{2}^{2}-24{{w}^{2}}\nu {{b}_{0}}b_{1}^{2}{{C}_{2}}\mu _{2}^{2}+3\nu {{b}_{2}}\mu _{1}^{2}{{\mu }_{3}}-12k\nu {{b}_{2}}{{\mu }_{2}}{{\mu }_{3}}+12w\nu {{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}\\&+12{{w}^{2}}\nu {{b}_{2}}\mu _{2}^{2}{{\mu }_{3}}+12{{k}^{2}}\nu {{b}_{2}}{{\mu }_{2}}\mu _{3}^{2}=0, \\&\frac{1}{G}\left( \frac{G'}{G} \right) :\,2\nu b_{1}^{3}\mu _{1}^{2}+6{{b}_{0}}{{b}_{1}}{{b}_{2}}\mu _{1}^{2}+\nu {{b}_{1}}{{\mu }_{2}}+8w\nu b_{1}^{3}{{\mu }_{1}}{{\mu }_{2}}+24w{{b}_{0}}{{b}_{1}}{{b}_{2}}{{\mu }_{1}}{{\mu }_{2}}+8{{w}^{2}}\nu b_{1}^{3}\mu _{2}^{2} \\&+24{{w}^{2}}{{b}_{0}}{{b}_{1}}{{b}_{2}}\mu _{2}^{2}+\nu {{b}_{1}}\mu _{1}^{2}{{\mu }_{3}}\,-4k\nu {{b}_{1}}{{\mu }_{2}}{{\mu }_{3}}+4w\nu {{b}_{1}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}+4{{w}^{2}}\nu {{b}_{1}}\mu _{2}^{2}{{\mu }_{3}}+4{{k}^{2}}\nu {{b}_{1}}{{\mu }_{2}}\mu _{3}^{2}=0, \\ \\&\,{{\left( \frac{1}{G} \right) }^{3}}:\,b_{2}^{3}\mu _{1}^{2}+3b_{1}^{2}{{b}_{2}}C_{1}^{2}\mu _{1}^{2}-6\nu b_{1}^{2}{{b}_{2}}{{C}_{2}}\mu _{1}^{2}+2{{b}_{2}}C_{1}^{2}{{\mu }_{2}}-4\nu {{b}_{2}}{{C}_{2}}{{\mu }_{2}}+4wb_{2}^{3}{{\mu }_{1}}{{\mu }_{2}}+12wb_{1}^{2}{{b}_{2}}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}} \\&-24w\nu b_{1}^{2}{{b}_{2}}{{C}_{2}}{{\mu }_{1}}{{\mu }_{2}}+4{{w}^{2}}b_{2}^{3}\mu _{2}^{2}+12{{w}^{2}}b_{1}^{2}{{b}_{2}}C_{1}^{2}\mu _{2}^{2}-24{{w}^{2}}\nu b_{1}^{2}{{b}_{2}}{{C}_{2}}\mu _{2}^{2}+2{{b}_{2}}C_{1}^{2}\mu _{1}^{2}{{\mu }_{3}}-4\nu {{b}_{2}}{{C}_{2}}\mu _{1}^{2}{{\mu }_{3}} \\&-8k{{b}_{2}}C_{1}^{2}{{\mu }_{2}}{{\mu }_{3}}+16k\nu {{b}_{2}}{{C}_{2}}{{\mu }_{2}}{{\mu }_{3}}+8w{{b}_{2}}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-16w\nu {{b}_{2}}{{C}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}+8{{w}^{2}}{{b}_{2}}C_{1}^{2}\mu _{2}^{2}{{\mu }_{3}} \\&-16{{w}^{2}}\nu {{b}_{2}}{{C}_{2}}\mu _{2}^{2}{{\mu }_{3}}+8{{k}^{2}}{{b}_{2}}C_{1}^{2}{{\mu }_{2}}\mu _{3}^{2}-16{{k}^{2}}\nu {{b}_{2}}{{C}_{2}}{{\mu }_{2}}\mu _{3}^{2}=0, \\&\frac{1}{{{G}^{2}}}\left( \frac{G'}{G} \right) :3{{b}_{1}}b_{2}^{2}\mu _{1}^{2}+b_{1}^{3}C_{1}^{2}\mu _{1}^{2}-2\nu b_{1}^{3}{{C}_{2}}\mu _{1}^{2}+2{{b}_{1}}C_{1}^{2}{{\mu }_{2}}-4\nu {{b}_{1}}{{C}_{2}}{{\mu }_{2}}+12w{{b}_{1}}b_{2}^{2}{{\mu }_{1}}{{\mu }_{2}}+4wb_{1}^{3}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}} \\&-8w\nu b_{1}^{3}{{C}_{2}}{{\mu }_{1}}{{\mu }_{2}}+12{{w}^{2}}{{b}_{1}}b_{2}^{2}\mu _{2}^{2}+4{{w}^{2}}b_{1}^{3}C_{1}^{2}\mu _{2}^{2}-8{{w}^{2}}\nu b_{1}^{3}{{C}_{2}}\mu _{2}^{2}+2{{b}_{1}}C_{1}^{2}\mu _{1}^{2}{{\mu }_{3}}-4\nu {{b}_{1}}{{C}_{2}}\mu _{1}^{2}{{\mu }_{3}} \\&-8k{{b}_{1}}C_{1}^{2}{{\mu }_{2}}{{\mu }_{3}}+16k\nu {{b}_{1}}{{C}_{2}}{{\mu }_{2}}{{\mu }_{3}}\,+8w{{b}_{1}}C_{1}^{2}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}-16w\nu {{b}_{1}}{{C}_{2}}{{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}+8{{w}^{2}}{{b}_{1}}C_{1}^{2}\mu _{2}^{2}{{\mu }_{3}} \\&-16{{w}^{2}}\nu {{b}_{1}}{{C}_{2}}\mu _{2}^{2}{{\mu }_{3}}+8{{k}^{2}}{{b}_{1}}C_{1}^{2}{{\mu }_{2}}\mu _{3}^{2} -16{{k}^{2}}\nu {{b}_{1}}{{C}_{2}}{{\mu }_{2}}\mu _{3}^{2}=0. \end{aligned}$$

After solving the above system via Mathematica program, we acquired the following results:

First.

$$\begin{aligned}{} & {} {{b}_{0}}=0,{{b}_{1}}=\pm \frac{\sqrt{-{{\mu }_{2}}-\mu _{1}^{2}{{\mu }_{3}}}}{\sqrt{2}\sqrt{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}}},{{b}_{2}}=\pm \frac{\sqrt{C_{1}^{2}-2\nu {{C}_{2}}}\sqrt{-{{\mu }_{2}}-\mu _{1}^{2}{{\mu }_{3}}}}{\sqrt{2}\sqrt{{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}}}, \nonumber \\{} & {} k=\pm \frac{-1+\sqrt{1-4w\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) {{\mu }_{3}}}}{2{{\mu }_{3}}}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(38)

The following soliton solutions can be achieved from (2), (12), (13) and (38):

$$\begin{aligned} {{u}_{19}}(x,t)={{\text {e}}^{i\left( w\frac{{{t}^{\alpha }}}{\alpha }\mp \frac{x\left( 1+\sqrt{1-4w\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) {{\mu }_{3}}} \right) }{2{{\mu }_{3}}} \right) }}\left( \begin{aligned}&\pm \frac{\sqrt{2\nu {{C}_{2}}-C_{1}^{2}}{{B}_{11}}}{\left( {{C}_{2}}+{{C}_{1}}\left( x\pm \frac{{{t}^{\alpha }}}{\alpha }{{B}_{10}} \right) +\frac{1}{2}\nu {{\left( x\pm \frac{{{t}^{\alpha }}}{\alpha }{{B}_{10}} \right) }^{2}} \right) } \\&\pm \frac{\left( {{C}_{1}}+\nu \left( x+\frac{{{t}^{\alpha }}}{\alpha }{{B}_{10}} \right) \right) {{B}_{11}}}{\left( {{C}_{2}}+{{C}_{1}}\left( x\pm \frac{{{t}^{\alpha }}}{\alpha }{{B}_{10}} \right) +\frac{1}{2}\nu {{\left( x\pm \frac{{{t}^{\alpha }}}{\alpha }{{B}_{10}} \right) }^{2}} \right) } \\ \end{aligned} \right) , \end{aligned}$$
(39)

where \({{B}_{10}}=\frac{\sqrt{1-4w\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) {{\mu }_{3}}}}{({{\mu }_{1}}+2w{{\mu }_{2}})}\) and \({{B}_{11}}=\frac{\sqrt{{{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}}}}{\sqrt{2}\left| {{\mu }_{1}}+2w{{\mu }_{2}} \right| }\).

Second

$$\begin{aligned}{} & {} {{b}_{0}}=0,{{b}_{1}}=\pm \frac{\sqrt{{{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}}}}{\sqrt{-2\mu _{1}^{2}+8k{{\mu }_{2}}\left( -1+k{{\mu }_{3}} \right) }},{{b}_{2}}=\pm \frac{\sqrt{2\nu {{C}_{2}}-C_{1}^{2}}\sqrt{{{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}}}}{\sqrt{2\mu _{1}^{2}+8k{{\mu }_{2}}-8{{k}^{2}}{{\mu }_{2}}{{\mu }_{3}}}}, \nonumber \\{} & {} w=\frac{-{{\mu }_{1}}\pm \sqrt{\mu _{1}^{2}-4k{{\mu }_{2}}\left( -1+k{{\mu }_{3}} \right) }}{2{{\mu }_{2}}}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(40)

The following rational solutions are obtained from (2), (12), (13) and (40):

$$\begin{aligned} {{u}_{20}}(x,t)={{\text {e}}^{i\left( -kx+\frac{{{t}^{\alpha }}\left( -{{\mu }_{1}}\pm \sqrt{\mu _{1}^{2}-4k{{\mu }_{2}}\left( -1+k{{\mu }_{3}} \right) } \right) }{2\alpha {{\mu }_{2}}} \right) }}\left( \begin{aligned}&\pm \frac{\sqrt{2\nu {{C}_{2}}-C_{1}^{2}}{{B}_{13}}}{\left( {{C}_{2}}+{{C}_{1}}\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{12}} \right) +\frac{1}{2}\nu {{\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{12}} \right) }^{2}} \right) } \\&\mp \frac{i\left( {{C}_{1}}+\nu \left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{12}} \right) \right) {{B}_{13}}}{\left( {{C}_{2}}+{{C}_{1}}\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{12}} \right) +\frac{1}{2}\nu {{\left( x-\frac{{{t}^{\alpha }}}{\alpha }{{B}_{12}} \right) }^{2}} \right) } \\ \end{aligned} \right) , \end{aligned}$$
(41)

where \({{B}_{12}}=\frac{\left( 1-2k{{\mu }_{3}} \right) }{\sqrt{\mu _{1}^{2}-4k{{\mu }_{2}}\left( -1+k{{\mu }_{3}} \right) }}\) and \({{B}_{13}}=\frac{\sqrt{{{\mu }_{2}}+\mu _{1}^{2}{{\mu }_{3}}}}{\sqrt{2\mu _{1}^{2}+8k{{\mu }_{2}}-8{{k}^{2}}{{\mu }_{2}}{{\mu }_{3}}}}\).

Third

$$\begin{aligned}{} & {} {{b}_{0}}=0,{{b}_{2}}=\sqrt{b_{1}^{2}\left( C_{1}^{2}-2\nu {{C}_{2}} \right) },{{\mu }_{3}}=-\frac{{{\mu }_{2}}+2b_{1}^{2}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}}}{\mu _{1}^{2}},~~~~~~~~~~~~~~~~~~~~ \nonumber \\{} & {} k=-\frac{{{\mu }_{1}}\left( 2w{{\mu }_{2}}\sqrt{1+8wb_{1}^{2}\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) }+{{\mu }_{1}}\left( 1+\sqrt{1+8wb_{1}^{2}\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) } \right) \right) }{2\left( {{\mu }_{2}}+2b_{1}^{2}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}} \right) }. \end{aligned}$$
(42)

The following rational solutions are obtained from (2), (7), (13) and (42):

$$\begin{aligned} {{u}_{21}}(x,t)={{\text {e}}^{i\left( w\frac{{{t}^{\alpha }}}{\alpha }\pm x{{B}_{15}} \right) }}\left( \begin{aligned}&\pm \frac{\sqrt{b_{1}^{2}\left( C_{1}^{2}-2\nu {{C}_{2}} \right) }}{{{C}_{2}}+{{C}_{1}}\left( x-\frac{{{t}^{\alpha }}\left( 1\mp {{B}_{14}} \right) }{\alpha ({{\mu }_{1}}+2w{{\mu }_{2}})} \right) +\frac{1}{2}\nu {{\left( x-\frac{{{t}^{\alpha }}\left( 1\mp {{B}_{14}} \right) }{\alpha ({{\mu }_{1}}+2w{{\mu }_{2}})} \right) }^{2}}} \\&\pm \frac{{{b}_{1}}\left( {{C}_{1}}+\nu \left( x-\frac{{{t}^{\alpha }}\left( 1-{{B}_{14}} \right) }{\alpha ({{\mu }_{1}}+2w{{\mu }_{2}})} \right) \right) }{{{C}_{2}}+{{C}_{1}}\left( x-\frac{{{t}^{\alpha }}\left( 1\mp {{B}_{14}} \right) }{\alpha ({{\mu }_{1}}+2w{{\mu }_{2}})} \right) +\frac{1}{2}\nu {{\left( x-\frac{{{t}^{\alpha }}\left( 1\mp {{B}_{14}} \right) }{\alpha ({{\mu }_{1}}+2w{{\mu }_{2}})} \right) }^{2}}} \\ \end{aligned} \right) , \end{aligned}$$
(43)

where \({{B}_{14}}=\sqrt{1+8wb_{1}^{2}\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) }\left( \frac{2w{{\mu }_{2}}}{{{\mu }_{1}}}+1 \right) +1\) and \({{B}_{15}}=\frac{\sqrt{1+8wb_{1}^{2}\left( {{\mu }_{1}}+w{{\mu }_{2}} \right) }\left( 2w{{\mu }_{1}}{{\mu }_{2}}+\mu _{1}^{2} \right) +\mu _{1}^{2}}{2\left( {{\mu }_{2}}+2b_{1}^{2}{{\left( {{\mu }_{1}}+2w{{\mu }_{2}} \right) }^{2}} \right) }\).

4 Results and discussion

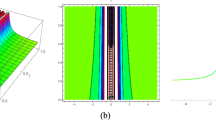
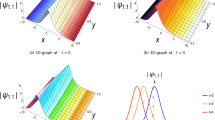
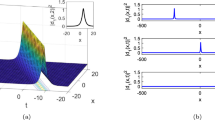
The graphical representations and the behavior of the present optical solutions are depicted in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12, as follows: In Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 graphs (a) and (b) the contour plots, the three-dimensional graphs, and the two-dimensional graphs of the square of modulus, real, and imaginary soliton solutions are illustrated, respectively. In Figs. 11 and 12 graphs (a) and (b) the two-dimensions plots of the square of modulus, real, and imaginary optical solutions are depicted. We have chosen the suitable values for the fractional order derivative \(\alpha\) and the physical parameters to show the effect of \(\alpha\) and the parameter of time on the behavior of the optical soliton solutions. It is noticed that the square modulus solutions of \({{u}_{1}}(x,t)\) and \({{u}_{7}}(x,t)\) are dark optical soliton solutions from Figs. 1a, b, and 2a. Here, the wave with a constant amplitude is modulational stable, and localized pulses can only be seen as holes against a background of a continuous wave. The imaginary and real parts of \({{u}_{7}}(x,t)\) are mixed bright optical solutions from Fig. 3a, b, the square modulus, real, and imaginary wave optical solutions of \({{u}_{10}}(x,t)\) and the square modulus solutions of \({{u}_{13}}(x,t)\) are periodic wave solutions from Figs. 4a, b, 5a, b, and 6a, respectively. the singular optical soliton solutions depicted in Fig. 7a and b represent the square modulus solutions of \({{u}_{12}}(x,t)\), the square modulus solution of \({{u}_{19}}(x,t)\) and the real soliton solution of \({{u}_{19}}(x,t)\) are bright optical solution from Figs. 8a, b, and 9a. Here, the group-velocity dispersion is anomalous, and due to the modulational instability, a constant amplitude continuous wave is unstable. The imaginary parts of \({{u}_{19}}(x,t)\) and \({{u}_{20}}(x,t)\) are dark-bright soliton solutions from Figure a9 and a10. Here, the two paired beams are mutually incoherent and have the same polarization and wavelength. Furthermore, the two-dimensional plot of the square modulus solutions of \({{u}_{7}}(x,t)\) and \({{u}_{19}}(x,t)\), real \({{u}_{7}}(x,t)\), and imaginary \({{u}_{19}}(x,t)\) for different values of order \(\alpha\) are depicted in Figs. 11a, b, 12a, b to show the effect of \(\alpha\) on the obtained optical solutions. The impact of the parameter of time is illustrated in Figs. 2b, 6b, and 10b. Compare with the results obtained in Baskonus et al. (2021), Ghanbari and Gomez-Aguilar (2019), Rezaei et al. (2022), Rezazadeh et al. (2021), Christian et al. (2012), Tariq and Seadawy (2018), Seadawy (2017), Yousif et al. (2018), Nasreen et al. (2018), Rezazadeh et al. (2021), Ghayad et al. (2023), Ahmad et al. (2023), Zhao and Luo (2017), we have successfully constructed various novel optical soliton solutions to the present time-fractional Schrodinger equation.

5 Conclusion

In this work, the extended simplest equation method is used to construct the exact optical solutions to a variety of time-fractional Schrodinger equation in optical fibers and plasma physics. The singular, wave, dark, bright, dark-bright, and mixed dark-bright optical soliton solutions for the proposed model are successfully construed. The proposed time-fractional Schrodinger equation is converted into a non-linear ordinary differential equation via widely used wave transformations. Different types of graphs are depicted to show the physical significance of the acquired optical solutions such as contour plots, three-dimensional plots, and two-dimensional plots using suitable physical parameters. Here, we have found a new category of optical soliton solutions that can be helpful for mathematicians and physicists who are interested in applied mathematics and plasma physics. Furthermore, the effect of the fractional order derivative and parameter of time is also given via illustrative graphs. In the future, one can use the extended simplest equation technique as an effective technique for generating different solitary wave solutions to fractional differential equations.