1 Introduction

Hollow core fiber based on anti-resonance finds its applicability in many research areas such as in communication systems for their properties of low loss (Komanec et al. 2020; Belardi and Knight 2014; Sakr et al. 2020; Shaha et al. 2020; Meng et al. 2021; Jasion et al. 2020), single mode guidance (Ge et al. 2019; Provino 2018; Md et al. 2019), and in high power laser delivery systems (Gu et al. 2022), in tera-Hertz sensing applications (Mahmud Ankan et al. 2020). Hollow core fibers are mainly classified into two types based on their light guidance mechanism - one is photonic band gap and second is anti-resonance properties. Anti-resonant fiber (ARF) gets our interest for low loss over broad band due to its air core guidance of light which removes the material loss of solid silica core. Hollow core anti resonant fibers (HC-ARF) are available in multiple structures and designs with different number of cladding tubes surrounding the central hollow core, with and without noded and nested configurations (Mousavi et al. 2016; Yan et al. 2020; Petry et al. 2022; Poletti 2014; Chen et al. 2019). The thicknesses of silica tubes decide the anti-resonant band which inhibits the coupling between core and cladding modes. Along with the low confinement loss of such fiber, bending is another important parameter while handling these fibers. Macro-bending introduces the loss depending on the bending curvature diameter. Although the macro-bending losses are calculated for these kinds of fibers, the resonance peaks are observed at certain bending curvature unlike the conventional bending loss (Belardi and Knight 2014; Wei et al. 2017; Bhardwaj et al. 2011; Beaudou et al. 2014). The resonance peaks are seen due to the chosen ratio of cladding to core diameter, hence fiber design needs to be optimized to reduce these peaks. Fabrication of these fibers are also reported with their characterization results of confinement loss, bending loss and cross-sectional images (Sakr et al. 2020; Jasion et al. 2020; Poletti 2014; Yelistratova et al. 2022).

Bending loss profiles of these fibers are discussed in detail (Belardi and Knight 2014; Liu et al. 2022; Belardi and Knight 2013; Yelistratova et al. 2019). Ref (Belardi and Knight 2014) has improved the design to reduce the bending loss in HC-ARF in IR and mid-IR range. The peak in the bending loss spectrum is observed at certain bending radii due to the local material attenuation in IR wavelength range (Belardi and Knight 2014). The peaks are observed also for Kagome type fibers (Bhardwaj et al. 2011; Beaudou et al. 2014), where it is reported in simulation as well as in experiments due to the coupling of core and cladding modes at certain bend radius. Most of them have shown the bending loss within the bend radius of 20 cm over the IR wavelength range (Shaha et al. 2020; Md et al. 2019; Liu et al. 2022). It is found from these studies that the bending loss spectrum changes over the wavelength for a fixed bending radius. Ref (Debord et al. 2017) has shown the lowest bending of 0.03 dB/turn in the visible wavelength at 750 nm. The bending loss can be reduced by modifying/tuning the fiber design parameters (Poletti 2014) but it is done only by tuning fiber core diameter. All the design parameters such as fiber core and clad diameters, tube thickness, gap between tubes along with the bending radius play a major role in bending loss profile so it is important to study the multiparametric design optimization. Our study gives more generalized results by considering the simultaneous tuning of the fiber design parameters (gap and thickness) and the bending radius within the optimized range of low confinement loss.

Simulation of fibers under bending condition is done by using conformal mapping techniques where the refractive index profile is modified by the radius of curvature of bend fiber. Fiber modes are solved using this modified bend fiber profile by Eigen mode solver. Lumerical gives the bending loss calculation in its inbuilt software by solving the angular propagation constant which has effective index and arc length calculated by angle and radius of bending while in COMSOL, the modified refractive index profile using conformal mapping technique should be embedded in the simulation method in the geometry definition and the loss is calculated by imaginary effective index. Ref (Azadeh et al. 2021) has discussed for multi-core fibers and ref (Chatterjee et al. 2022) has reported bending loss using Lumerical for ARF. Ref (Velamuri et al. 2019) has discussed the COMSOL based bending loss studies in few mode fiber. Most of the bending loss simulation for ARF or Kagome fibers have used finite-element based Eigen mode solver of COMSOL using conformal mapping method (Belardi and Knight 2014; Shaha et al. 2020; Md et al. 2019; Poletti 2014; Beaudou et al. 2014; Sultana et al. 2022; Velamuri 2018).

In our earlier reported work (Suchita et al. 2022; Kaushalram 2023), we have optimized the fiber design parameter to achieve low confinement loss in visible wavelength range. In this work, we propose the optimization of bending loss while maintaining the straight fiber design with low confinement loss. The best optimized fiber parameters with low confinement loss can show the huge bending loss but it can be reduced by tuning the design parameters. The simulation is done for the simplest fiber design - nodeless, without nested HC-ARF to study the macro-bending loss. The macro-bending is added in the refractive index profile of this fiber where the bending is considered around X- and Y-axis of the fiber. Since the fiber is having non-uniform refractive index profile around X- and Y- axis, the bending loss profile will be different for the bending around these two axes. We discuss the theory and simulation method in Sect. 2. We have shown the simulation results of bending loss for the ARF using its optimized parameters as done in Suchita et al. (2022) in Sect. 3. The results are analyzed by tuning the bending parameters in Sect. 3.1 and the operating wavelengths in Sect. 3.2. Section 3.3 shows the fine tuning of design parameters - gap and thickness to reduce the bending loss in operating regime.

2 Theory and smulation

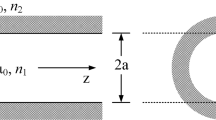
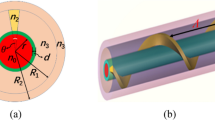
We will study the commonly used ARF design which is a 6-tube ARF-HCF. The chosen fiber design supports two polarization degenerate fundamental mode (FM) of x-polarized (x-pol) and y-polarized (y-pol). The schematic of chosen fiber structure is shown in Fig. 1a where all the structural parameters are indicated. \(D_{core}\) and \(d_{clad}\) are the diameters of core and cladding, T and t are the thickness of outer capillary tube and inner cladding tubes and g is the gap between the cladding tubes. The inner silica tubes give the anti-resonance guidance inside the core as its tube thickness (t) decides the resonance peak wavelengths \((\lambda )\) expressed by Eq. (1) (Poletti 2014).

$$\begin{aligned} \lambda = \frac{2t \sqrt{(n^2-1)}}{m}. \end{aligned}$$
(1)

where n is the refractive index of silica which is obtained using Sellmeier’s equation over the visible wavelength range, m is an integer representing the resonant order. Our operating wavelength range of 550–750 nm lies in between \(2^{nd}\) and \(3^{rd}\) resonance wavelength which is third anti-resonant band corresponding to the tube thickness of 0.8 µm.

Fig. 1
figure 1

a Schematic of fiber structure of six tube ARF-HCF and b 2D plot of confinement loss of FM by tuning the gap and the core diameter

Full size image

The simulation of these fibers is done by solving optical modes using an Eigen mode solver based on finite-element method in COMSOL Multiphysics. In the simulation, the maximum mesh element of silica region is optimized at \(\lambda\)/8 (0.07 µm) when the loss is found to be constant within the range \(\lambda\)/6 to \(\lambda\)/10. Convergence test is performed on the PML thickness and is set to 5 µm where the loss is found to be constant over a large tuning range as the PML thickness is sufficiently larger than the silica tube thicknesses. The chosen simulation region and design parameters are consistent with the reported work (Poletti 2014; Zhang et al. 2014). To ensure the accuracy of our method, we have verified some of the reported results (Shaha et al. 2020; Habib et al. 2016) using this set of optimized parameters obtained from convergence test. The confinement loss (CL) has been previously reported for the six-tube ARF-HCF using this method by our group where the fiber design parameters are optimized in the wavelength range of 550–750 nm for low confinement loss (Suchita et al. 2022). Fiber design parameters are defined as follows;

$$\begin{aligned} d_{clad} = d-g-2t. \end{aligned}$$
(2)

where fiber clad diameter \((d_{clad})\)is given in terms of gap (g) and silica tube thickness (t) by Eq. (2). d is the diameter of closely packed cladding tubes without considering any gap as shown by dashed circle in Fig. 1a and is defined by the number of silica clad tubes (N) and core diameter \((D_{core})\) using Eq. (3).

$$\begin{aligned} d = D_{core}\left( \frac{sin\frac{\pi }{N}}{1-sin\frac{\pi }{N}}\right) \end{aligned}$$
(3)

The design parameters are varied to optimize the CL of fundamental mode. Figure 1b shows the CL by simultaneous tuning of the gap between the silica tubes in the range of 1–5 µm and the core diameter in the range of 20–35 µm at chosen silica tube thickness of 0.8 µm. The CL does not change much with the gap, but it is significantly varying with the core diameter. It is found to be minimum for the core diameter within the range of 30–35 µm and \(D_{core}\) of 30 µm is optimized for single mode operation. From Fig. 1b, the optimized parameters for straight fiber are g=2 µm, \(D_{core}\)=30 µm, t=0.8 µm and \(d_{clad}\)=26.4 µm and these are further used for the simulation of bend fiber.

The bending loss (BL) of the fiber modes at a given wavelength (\(\lambda\)) is directly calculated from their imaginary part of the mode effective index (\(n_{eff}\)) and bending radius (\(R_{b}\)) as given by the Eq. (4) (Beaudou et al. 2014; Velamuri et al. 2019),

$$\begin{aligned} BL=\frac{40\pi Im(n_{eff})}{ln(10)\lambda }\pi R_b \,\,\,\,\,\,[dB/turn] \end{aligned}$$
(4)

The fiber refractive index (n(r)) profile will be modified by the radius of curvature of bend fiber which is expressed by Eq. (5) (Bhardwaj et al. 2011).

$$\begin{aligned} n_b=n(r)\left( 1+\frac{(1-\chi )r}{R_b}\right) \end{aligned}$$
(5)

This ‘r’ will take the value of ‘x’ or ‘y’ depending on the bending along the corresponding axis. ‘\(\chi\)’ compensates the elastic coefficient of the material and it is − 0.22 for silica and zero for air (Bhardwaj et al. 2011). This is a well-known technique called ‘conformal mapping’ to calculate the modes for the modified refractive index profile of the fiber under bending conditions. The modified fiber profile is shown in Fig. 2 along with the straight fiber. Figure 2a shows the 2D refractive index profile for the chosen fiber geometry where six silica hollow tubes are arranged in a bigger silica capillary tube. Refractive index of the hollow region/air is shown by blue and the tube thickness is shown by yellow having the refractive index of silica as 1.45. The arrows in Fig. 2a indicate the bending directions around X- (blue) and Y- (red) axis individually. The 1D refractive index profiles of bend fiber are shown around X- axis and Y-axis in Fig. 2b and c respectively along with the straight fiber profile. The fiber bending by radius of 1 mm is shown here just to visualize the bent fiber profile and this bending radius may not support any physical mode inside the core. The modified refractive index profile has a tilt with respect to straight fiber profile which interrupts the confined modes inside the core.

Fig. 2
figure 2

a 2D refractive index profile of fiber geometry, 1D bend fiber profile (b) around-X axis and c around Y-axis along with the straight fiber profile

Full size image

It is clearly seen from the profile that the bending around X-axis lies on two silica cladding tubes while it does not fall on any silica tubes around Y-axis. Hence, the bending effect will be very different for X- and Y- cases. Therefore, the bending loss profile for these specialty fibers needs to be checked in both the cases whether bending is around X- or Y- axis.

Figure 3a shows the simulated mode profile of a fundamental mode at 650 nm where the mode is confined into the core region for a straight fiber. Figure 3b and c show the mode profiles for the bend fiber when the bending radius is 10 cm around X- axis and Y-axis respectively. The corresponding bent axes are shown by black solid lines in 3b and 3c. The simulation takes care of modified refractive index under bending condition as expressed by Eq. (5). The mode profile for the bending around X- axis in Fig. 3b shows that the mode is perturbed on right side of X-axis. When bending is around Y-axis as in Fig. 3c, the mode is perturbed in upward direction on Y-axis. These perturbed modes lose their confinement inside the core and hence lead to the loss under bending. The bending loss depends on the amount of bending and also, on the direction of bending specially when the fiber design is non-uniform along X- and Y-axis. The non-uniformity in the fiber profile along X- and Y- axis can be justified by the mode profiles where the fundamental mode is moving towards the gap between two silica rings in case of bending around Y-axis in Fig. 3c while it is suppressed in case of bending around X- axis because it does not fall in the gap. In case of bending around X-axis, the transmission of core modes to cladding modes will be easier and hence the resonance peaks are more in case of bend X-axis as seen in the later subsections.

Fig. 3
figure 3

Simulated mode profile shown for fundamental mode at 650 nm for a straight fiber, for bend fiber, b around X-axis, c around Y-axis by 10 cm and the real and imaginary part of the effective index over bend radius in case of bending around X- and Y- axis for modes d x-pol and e y-pol

Full size image

The mode confinement is decided by its effective index and the imaginary part of the effective index gives the losses in the fiber as depicted by Eq. (4). Both the real and imaginary parts of the effective index of the degenerate fundamental modes under the bending condition are shown for x-pol in Fig. 3d and y-pol in Fig. 3e where the bending radius is tuned over the range of 2-50 cm around X- and Y- axis. In both the Fig. 3d and e, the real part (shown by values on left y-axis) increases exponentially as the fiber is bent more with smaller radius <10 cm. The variation of real part over bending radius follows the trend of bending loss profile of conventional fiber. The imaginary effective index is plotted along right y-axis. Unlike the real part, it shows the peaks at selective bending radius values of 26 cm around X-axis and 8 cm, 48 cm around Y-axis for x-pol of FM in Fig. 3d and the peaks for y-pol of FM are found at 8 cm, 26 cm around X-axis and 8 cm, 48 cm around Y-axis as can be seen in Fig. 3e. Among all these, the peak is common at 8 cm for imaginary effective index except the X-axis of x-pol mode. These peak values at certain bending radius appeared due to the fact that the phases of core modes at certain bending axis match with the transmission condition of nearby silica tube thickness. One can note that the bending radii corresponding to the peak values are different for X- and Y- axis but similar for x-pol and y-pol modes. The pattern of imaginary part directly leads to the bending loss profile. In the next section, the bending loss is studied by tuning bending radius, wavelength, and fiber design parameter for both the modes and both the bend axes.

3 Results and dscussions

The simulation results of bending loss are discussed in three subsequent subsections for three different parameters; 1.by tuning the bending radius over a certain range of 2-120 cm for a fixed wavelength of 650 nm, 2.by tuning the wavelength range for a chosen bending radius and 3.by tuning the fiber design parameters to get the optimized design for low bending loss.

3.1 Bending loss by tuning bending radius

In this section, Fig. 4a and b show the simulated bending loss for both the x-pol and y-pol of fundamental modes over the tuning range of bending radius around X- and Y-axis respectively. From the previous section, we found that the bending conditions around X and Y and their corresponding mode profiles are very different and hence, we will deal with two axes separately. Over the tuning range of bending radius, it is observed that there are three resonance peaks for each FM at bending radius of 8 cm (for y-pol) and 10 cm (for x-pol), 26 cm (for both the x-pol and y-pol), 55 cm (for both the x-pol and y-pol) around X-axis in Fig. 4a and two resonance peaks at 8 cm (for both the x-pol and y-pol), 48 cm (for both the x-pol and y-pol) around Y-axis in Fig. 4b. These resonance peaks are due to the core mode coupling to the cladding modes as can be seen in the insets of Fig. 4a and b where corresponding mode profiles are shown at each peak value for both the modes of x-pol and y-pol. The nomenclature used for these inset mode profiles are in the form of bend radius values with modes x-pol and y-pol as superscripts. In Fig. 4a, the bending loss curves have peaks of more than 1 dB/turn at the bending radius of 26 cm and in the order of 10 dB/turn at the bending radius of 55 cm around X-axis, the corresponding mode profiles show the leakage/coupling of core modes into the nearby cladding tubes towards right side as shown by \(26^{x-pol}\) and \(26^{y-pol}\) and, to the horizontal tube as shown by \(55^{x-pol}\) and \(55^{y-pol}\). The bending around Y-axis has the loss with the peak value of the order of 10 dB/turn at bending radii of 8 cm and 48 cm and their corresponding mode profiles are leaking to the upward cladding tubes shown by \(8^{x-pol}\), \(8^{y-pol}\),\(48^{x-pol}\) and \(48^{y-pol}\) in Fig. 4b. The mode profiles corresponding to bend radius of 100 cm for x-pol and y-pol modes indicated by \(100^{x-pol}\) and \(100^{y-pol}\) in the insets of Fig. 4 are confined inside the core with confinement loss lower than \(10^{-1}\) dB/turn around both the axes. It should be noted that these loss values are calculated in dB/turn by tuning the bending radii at 650 nm. The maximum loss values at resonance peaks are 11 dB/m at 55 cm (19.1 dB/turn) around X-axis and 8 dB/m at 48 cm (12.5 dB/turn) around Y-axis while the straight fiber has the loss of 1.46 \(\times 10^{-3}\) dB/m at 650 nm. For tight bending radius, the higher order modes are well confined inside the core, so the smaller bending radius \(\le\)1 cm is ignored in the bending spectra shown in Fig. 4a and b.

Fig. 4
figure 4

Simulated bending loss profile for fundamental modes by tuning the bending radius around a X- axis and b Y- axis. Mode profiles in the inset are labeled with the corresponding bending radius and polarization

Full size image

These peaks in the bending loss profiles in the range of 2–10 cm are similar to those reported in Belardi and Knight (2014), Wei et al. (2017). These results are totally in agreement with the fact that the fiber modes under bending conditions modify the anti-resonance band and include their own resonance to the silica tubes, so that core modes can easily couple into the cladding at certain bending radius values around the fiber bend axis in a similar form for x-pol and y-pol modes. These resonance peaks can be further reduced or shifted towards lower bending radii by optimizing the ratio of cladding and core diameters. This will be explored in the later subsections.

3.2 Bending loss by tuning wavelength

From the previous subsection, it must be noted that the phase matching condition of core mode to cladding mode is modified under the bending of the fiber at a fixed wavelength of 650 nm. In this section, the wavelength values are tuned for a fixed bending radius of the fiber where the phase matching will be manipulated by tuning the operating wavelength range of 550–750 nm. The loss resonance peaks observed for a certain bending radius in Fig. 4 are individually tuned over the wavelength to check their behavior around detuning from 650 nm and the results are shown in Fig. 5 for both the bend FM modes of x-pol and y-pol along with the straight fiber. Figure 5a shows the bending loss over the wavelength tuning from 550–750 nm for the bending radius of 55 cm having highest loss around X-axis (as shown in Fig. 4a). Figure 5b shows the bending loss over wavelength at the bending radius of 48 cm corresponding to the highest loss obtained around Y-axis (as shown in Fig. 4b). These two results of Fig. 5a and b show the highest bending loss resonances near 550–560 nm due to the original anti-resonance band set by the silica tube thickness and at 650 nm due to the bending radius. The peak value of the order of 10 dB/m at 650 nm is for the bent fiber and it is not seen for the straight fiber as shown in Fig. 5a and b. The bending loss reduces by the order of \(10^1\) around 600 nm and by \(10^2\) at higher wavelength region of 680–750 nm. For a fixed bending radius of 8 cm as shown in Fig. 5c, both the X- axis and Y-axis show the different loss resonance peaks and oscillatory behavior over the wavelength range of 550–750 nm. The strong dependence of bending loss on the wavelength gives us the flexibility to slightly tune the operating wavelength to reduce the bending loss even at a fixed bend condition. For a straight fiber, the loss is < 0.1 dB/m within the wavelength range considered except their resonance wavelength peaks at 560 nm which comes from the phase matching of core and cladding modes.

Fig. 5
figure 5

Bending loss (in dB/m) over wavelength range for bend radius of a 55 cm around X- axis and b 48 cm around Y-axis and c 8 cm around both the axis along with the straight fiber

Full size image

These fibers seem to be highly bend sensitive depending on the combination of wavelength range and the bending conditions - bend radius and bend axis. Hence, the optimization of other fiber parameters needs to be carried out in order to get the low bending loss range. The design parameters need to be tuned in the vicinity of optimized fiber design for low CL of fundamental mode with single mode regime which is mentioned earlier in Section 2.

3.3 Design optimization for bending loss

For specialty fibers, the bending loss is very sensitive to the fiber design parameters, so this subsection is dedicated to the tuning of fiber parameters.

3.3.1 Tuning of gap and thickness

Fig. 6
figure 6

Bending loss (in dB/turn) by tuning gap between the tubes and thickness of the silica inner rings for bending around X-axis with bend radius of a 8 cm, b 26 cm, c 55 cm and for bending around Y-axis with bend radius of d 8 cm and e 48 cm. All the 2D plots are shown for fundamental mode of x-pol

Full size image

In this section, the bending loss is calculated by tuning gap and thickness of the fiber design at fixed bend radius (corresponding to the loss resonance peak). Since the CL shows the low value and a small variation over the gap of 1–5 µm for a fixed core diameter of 30 µm, the bending loss profile is simulated in this range. By tuning g, the ratio of cladding to core diameter (\(d_{clad}/D_{core}\)) is tuned which is responsible for the resonance peaks in bending loss profile. The gap is tuned over 1–5 µm with the simultaneous tuning of thickness of silica tubes in the range of 0.7\(-\)0.8 µm to operate in the wavelength range of 550–750 nm. Figure 6a–c show the 2D bending loss profile for bending radius of 8 cm, 26 cm and 55 cm around X-axis showing the resonance peaks in the range of \(10^1\) dB/turn (chosen from Fig. 4a) respectively. The highest bending loss is in the order of \(10^1\) dB/turn around a gap of 2 µm for the cases shown in Fig. 6a–c and it is uniform over the full range of thickness. For the larger gap of 4–5 µm, the bending loss is reduced significantly by three orders in the range of \(10^{-2}\) dB/turn for all the thickness. Hence, the large gap of fiber should be used to reduce the bending loss but this is specific for the bending radii of 8 cm, 26 cm and 55 cm around X-axis. One needs to check whether this range of fiber design parameter supports the bending around Y-axis. Figure 6d and e show the bending loss for bending radii of 8 cm and 48 cm around Y-axis respectively. In this case, the loss is not uniform over the thickness and low loss of the order of \(10^{-2}\) dB/turn is found in the range of gap > 3 µm and thickness > 0.75 µm.

It can be summarized from Fig. 6 that the fiber design parameters in case of ARF-HCF play an important role in deciding the bending loss even at a fixed bend radius and bend axis. The variation of bending loss in Fig. 6 is found mainly due to gap between the silica tubes while the loss of straight fiber is uniform over the gap of 1–5 µm (Fig. 1b). Surprisingly, the bending loss over the thickness of silica tubes deciding the anti-resonance band does not change much for the fixed gap in most of the cases except bending radius of 48 cm around Y-axis in Fig. 6e. This could be specific to bending radius also. Next, we need to check the dependence of the bending radii on gap variation as the gap is found to be a crucial parameter.

3.3.2 Tuning of gap and bending radius

In this section, the range of bending radius is optimized by tuning the gap. A gap that minimizes the loss and gives the smaller bending radius corresponding to resonance peak is desirable. Figure 7 shows the 2D profiles of calculated bending loss in dB/turn by simultaneously tuning bend radii of 5–200 cm and the gap of 1–5 µm for a fixed silica tube thickness of 0.8 µm. Figure 7a and b show the bending loss for x-pol and y-pol modes around X-axis respectively. It is clearly seen that there are three resonance peaks of loss values of the order of \(10^1\) dB/turn ranging from the bending radius of 5 cm to 100 cm selectively over the gap of 2 µm and above the gap of 2 µm, two resonance peaks are shown with reduced bending radius ranging from 5 cm to 50-60 cm. Other than the resonance peak values (shown by yellow region), the bending losses are lower of the order of \(10^{-2}\) dB/turn shown by blue region. At the gap of 4–5 µm, the bending radius reduces less than 50 cm, and it again starts increasing at bending radius higher than of 100 cm. The low bending loss of \(10^{-2}\) dB/turn is found for the gap of 4 µm with the bending radius \(\ge\) 50 cm. A similar behavior is followed when the bending is around Y-axis. Figure 7c and d show the bending loss profiles for the x-pol mode and y-pol mode around Y-axis respectively. It shows the lowest loss of \(10^{-2}\) dB/turn near the bending radius of 10 cm for the gap of 1–5 µm shown by dark blue region. Then, a single resonance peak (shown by red-yellow region) with loss of \(10^1\) dB/turn appears near 60 cm at gap of 1 µm and it reduces to smaller bend radius of 30 cm over the gap of 5 µm unlike the case of X-axis in Fig. 7a and b where two- and three- resonance peaks appeared. In all the cases shown in Fig. 7, the resonance peak is reducing towards smaller bending radius and to lower loss values as the gap increases from 1–5 µm. Figure 7 gives more generalized parameters of fiber design and bending radius where the lowest bending loss of \(10^{-2}\) dB/turn (blue region) is found at the bending radius > 50 cm in the gap range of 3–4 µm around both the bend axes of X and Y for the both the modes of x-pol and y-pol.

Fig. 7
figure 7

Bending loss (in dB/turn) by tuning the gap and bending radius around X-axis for modes, a x-pol, b y-pol and around Y-axis for modes, c x-pol and d y-pol

Full size image
Fig. 8
figure 8

Bending loss for the optimized gap of 4 µm by tuning the bending radii for x-pol mode (solid curve) and y-pol mode (dotted curve) around fiber bend axis of X (blue curve) and Y (red curve). Vertical lines indicate the resonance peaks of unoptimized loss profile and arrows show the corresponding shifts in bending radius

Full size image

From the optimized result shown in Figs. 6 and 7, the best parameters are chosen for the reduced bending loss with reduced bending radius of resonance peak and it is plotted in Fig. 8. In this loss profile, the optimized gap is found to be 4 µm which gives the ratio of cladding to core diameter (\(d_{clad}/D_{core}\)) of 0.81. This optimization of bend fiber takes care of the optimized confinement loss of straight fiber as well and is found slightly different from the reported ratio (\(d_{clad}/D_{core}\)) of 0.88 (Suchita et al. 2022). The optimized bending loss profile is shown in Fig. 8 for both the modes (shown by solid and dotted curves) and around both the fiber bend axes (shown by blue and red curves). The resonance peaks are indicated by the corresponding bending radius values with the subscripts of x-pol and y-pol modes. In Fig. 8, the resonance peaks are shifted to lower bending radii of 15 cm and 35 cm which was earlier appeared at 26 cm and 55 cm around X-axis (Fig. 4a) and the peak is shifted to 30 cm which was 48 cm around Y- axis (Fig. 4b). The resonance peaks of unoptimized bending loss values from Fig. 4 are indicated in Fig. 8 for FM x-pol and y-pol at 55 cm around X-axis by blue vertical line and at 48 cm around Y-axis by red vertical line. The shifts of resonance peaks to smaller bending radius are shown by horizontal ‘arrows’ in Fig. 8 where the reduction in bend radii of 20 cm and 18 cm are obtained in case of X- and Y-axis respectively. Their corresponding loss values are also reduced to 2.4 dB/m at 35 cm (2.2 dB/turn) and 3.6 dB/m at 30 cm (3.4 dB/turn) around X- and Y-axis respectively. For other peaks appearing at smaller bending radii, the loss values are lower than of 1 dB/turn.

The results presented here show that a fine tuning of a single parameter can lead to a large reduction in the loss values and in the bending radius of resonance peaks. The parameters in our case are thickness of silica cladding tubes of 0.8 µm and gap between two silica tubes of 4 µm which take care of fabrication feasibility of such fibers. The ARF chosen in our case for bending loss studies has the simplest fiber structure while the confinement loss is further reduced by addition of the resonance layers as done in single- and double- nested silica tubes (Belardi and Knight 2014; Suchita et al. 2022). Bending loss optimization can be done in a similar way for other fiber structures having nodes and nested elements.

4 Conclusion

In this work, the bending loss is simulated for ARF-HCF where the anti-resonant properties dominate. It is found that the inhibited coupling between core and cladding modes can be broken in such fibers under the bending conditions by tuning bend radius and bend axis, which changes the bending loss profiles and introduces some resonance peaks. The coupling between core and cladding modes can be manipulated by tuning the ratio of cladding to core diameters and by introducing bends in fiber. The tuning of operating wavelength also affects the bending loss profile. It is found that that the bending loss of FM modes is reduced by an order of \(10^1\) at 600 nm and by \(10^2\) in the range of 700 nm when detuned from the central wavelength of 650 nm. There is an interplay between the bending radii and the fiber design parameters. The fiber design parameters - gap between the tubes and tube thickness along with the bending radius are tuned to achieve a low bending loss and small bending radius corresponding to the resonance peak. It is concluded that the bending loss follows an unconventional, specific trend which strongly depends on the fiber design parameters. This optimization is done for both the degenerate fundamental modes around both the bending axes as these fibers are having non-uniform profile around X- and Y- direction. Here, we report the optimized fiber design parameters: gap of 4 µm and thickness of 0.8 µm for core diameter of 30 µm which give the shifted resonance peak towards the smaller bending radius of 35 cm around X-axis and 30 cm around Y-axis. Along with the reduction in bending radius of resonance peak, the corresponding bending losses are also reduced from 11 dB/m to 2.4 dB/m around bend X-axis and from 8 dB/m to 3.6 dB/m around bend Y-axis. The ratio of cladding to core diameters is found to be 0.81 to lower the coupling between core and cladding modes under bend conditions and is maintained within the range of low confinement loss of a straight fiber. The optimized bending loss ranges in the order of \(10^{-1}\) dB/turn below a bending radius of 50 cm and in the order of \(10^{-2}\) above 50 cm. This study will be useful in realizing the optimized bending loss profiles for other fiber structure with- and without- noded and nested.