1 Introduction

NLPDEs play a crucial and practical role in many branches of technology, science, and theoretical physics Yépez-Martínez et al. (2022), Akinyemi et al. (2022), Arqub et al. (2020), Mohamed and El-Sherif (2010), Jeragh et al. (2007), Osman (2019), Osman et al. (2020), Aljahdali et al. (2013), Akinyemi et al. (2022), Houwe et al. (2022), Osman and Ghanbari (2018), Osman et al. (2019). Numerous scientists have developed cutting-edge methods for obtaining precise solutions to the myriad fascinating nonlinear models that appear in contemporary science Nisar et al. (2022), Abbagari et al. (2022), Arqub et al. (2022), Osman and Wazwaz (2019). An essential subject in the research of nonlinear phenomena is the development of analytical solutions for NLPDEs Rezazadeh et al. (2021), Tarla et al. (2022), Chu et al. (2021), Jin et al. (2022).

Many effective methods for handling these models have been employed in the present era of practical science and engineering, such as the Hirota’s bilinear transform approach Kumar and Mohan (2021), Özkan et al. (2022), exp-function method Nisar et al. (2021), Gepreel and Zayed (2021), the unified method and its generalized form Osman (2017), Wazwaz and Osman (2018), Osman (2016), the technique of Kudryashov Tarla et al. (2022), Malik et al. (2021), Sain et al. (2021), Dan et al. (2020), the soliton ansatz method Fan and Hona (2002), Savescu et al. (2014), the improved trial equation method Zhou et al. (2016), Günerhan et al. (2020), invariant subspace method Hashemi (2018, 2021), and Lie symmetry method Malik et al. (2021), Hu and Li (2022), Kumar et al. (2021, 2022). Over the past few decades, one of the most fascinating areas of current research has been the study of the solitonic and optical behaviour of nonlinear models Zayed and Arnous (2013); our perspective is still applicable even though the provided model suggests additional odd order partial derivative terms El-Shiekh and Al-Nowehy (2013).

In the past few years, many efficient studies were done to typify the soliton solutions for different complicated nonlinear differential equations, including the extended sinh- and sine-Gordon equation expansion approach Baskonus et al. (2018), Ali et al. (2020), the extended Jocobi’s elliptic approach Hong and Lu (2009), Tarla et al. (2022a, 2022b), the modified auxiliary equation mapping method Cheemaa et al. (2020), the modify extended direct algebraic technique Yaro et al. (2020), the inverse scattering transformation method Zhang and Chen (2019), the extended rational sine-cosine method Mahak and Akram (2019), semi-inverse variational principle Kohl et al. (2020) and many more Hosseini et al. (2020), Kudryashov (2020), Qureshi et al. (2022), Arqub et al. (2022), Rashid et al. (2022), Adel et al. (2022), Ismael et al. (2022), Yao et al. (2022). The main object of this study is to use the new Kudryashov approach Tarla et al. (2022), Malik et al. (2021), Sain et al. (2021), Dan et al. (2020) to analyze three different important models namely: the (1+1)-dimensional Klein-Gordan equation (1D-KGE) Opanasenko and Popovych (2020), Chargui et al. (2010), the (2+1)-dimensional Kadomtsev-Petviashvili equation (2D-KPE) Gai et al. (2016), Alharbi et al. (2020), and the (3+1)-dimensional Boussinesq equation (3D-BE) Wazwaz and Kaur (2019), Hu and Li (2022) by finding their analytical solutions and discuss their behaviors graphically through some 3D and 2D charts.

This article is devised as follows: in Sect. 2, the new Kudryashov method is introduced. Section 3, deals with the solution of 1D-KGE by using the new Kudryashov technique. In Sect. 4, this method is utilized for extracting exact solutions of the 2D-KPE. Solitons of the 3D-BE is considered in Sect. 5. The last section, contains some conclusions and final remarks.

2 The new Kudryashov method

Assume the next NLPDE:

$$\begin{aligned} \Omega (u,u_{t},u_{x},u_{tt},\dots )=0, \end{aligned}$$
(1)

where \(\Omega\) simply represents a polynomial. Using another transformation of the form

$$\begin{aligned} \begin{aligned} u(x,t) = U(\vartheta ), \quad \vartheta = x - \sigma t, \end{aligned} \end{aligned}$$
(2)

where \(\sigma\) represents the speed of wave. Rewriting Eq. (2) as the following nonlinear ODE

$$\begin{aligned} G(U,U_{\vartheta },U_{\vartheta \vartheta },U_{\vartheta \vartheta \vartheta },\dots )=0. \end{aligned}$$
(3)

Consider (3) has a solution as:

$$\begin{aligned} U(\vartheta ) = \sum _{i=0}^{N} c_{i} Q^{i}(\vartheta ), \end{aligned}$$
(4)

where \(c_{i}, (i=0,1,\dots ,N)\) are the coefficients of \(Q^{i}(\vartheta )\) with \(c_{N} \ne 0\) and \(Q(\vartheta ) = \dfrac{1}{a A^{\Theta \vartheta } + b A^{-\Theta \vartheta }}\) is the solution of

$$\begin{aligned} (Q^{\prime }(\vartheta ))^{2} = (\Theta (\ln A)Q(\vartheta ))^2(1-4abQ^{2}(\vartheta )), \end{aligned}$$
(5)

where the constants \(a,\,b,\,\Theta\) and A are non-zero, with \(A>0\) and \(A \ne 1\).

Here we will find N by the classical balance procedure and then putting Eq. (4) into Eq. (3). Since \(Q(\vartheta ) \ne 0\), and we equated all the coefficients of \(Q^{i}(\vartheta )\) to zero. Then, this system is solved for a, b and \(c_{i}\)’s. Whenever a, b and \(c_{i}\)’s are determined, then solutions are obtained with the help of parameters by using the explicit strategy. Then by substitution of \(\vartheta = x - \sigma t\) into the solutions satisfying (5), the procedure is going to end.

3 The (1+1)-dimensional Klein–Gordan equation Opanasenko and Popovych (2020), Chargui et al. (2010)

$$\begin{aligned} u_{tt} - u_{xx} + q u + s u^{3} = 0, \end{aligned}$$
(6)

where \(u=u(x,t)\) is the unknown function with a real value that results from the real independent variables x and t, and \(q,\,s\) are real constants. The 1D-KGE is a relativistic wave equation, related to the Schrödinger equation. Opanasenko and Popovych Opanasenko and Popovych (2020) have described generalized symmetries and local conservation laws for the 1D-KGE. Furthermore, Chargui et al. (2010) solved Eq. (6) in one spatial dimension for the case of mixed scalar and vector linear potentials in the context of deformed quantum mechanics characterized by a finite minimal uncertainty in position.

Assuming that Eq. (6) has a traveling wave

$$\begin{aligned} \begin{aligned} u(x,t) = U(\vartheta ), \quad \vartheta = x - \sigma t, \end{aligned} \end{aligned}$$
(7)

where \(\sigma\) is wave velocity. Inserting (7) in (6), we get the following nonlinear ODE:

$$\begin{aligned} (\sigma ^{2}-1)U_{\vartheta \vartheta } + q U + s U^{3} = 0. \end{aligned}$$
(8)

Balancing the terms \(U_{\vartheta \vartheta }\) and \(U^{3}\) to get \(N = 1\). By substituting \(N = 1\) in to (4) to get

$$\begin{aligned} U({\vartheta }) = c_{0} + c_{1} Q(\vartheta ). \end{aligned}$$
(9)

Substituting (9) in (8) and equate the coefficient of \(Q(\vartheta )\) yields

$$\begin{aligned} \begin{aligned}&Q^{0}: \qquad qc_{{0}}+s{c_{{0}}}^{3} = 0,\\&Q^{1}: \qquad qc_{{1}}+3\,s{c_{{0}}}^{2}c_{{1}}+c_{{1}}{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}{\sigma }^{2} -c_{{1}}{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2} = 0,\\&Q^{2}: \qquad 3\,sc_{{0}}{c_{{1}}}^{2} = 0,\\&Q^{3}: \qquad s{c_{{1}}}^{3}-8\,c_{{1}}{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}{\sigma }^{2}ab+8\,c_{{1}}{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}ab = 0. \end{aligned} \end{aligned}$$
(10)

Solving the above system, we get

$$\begin{aligned} c_{0} = 0, \qquad c_{1} = \pm 2\,\sqrt{-{\dfrac{2abq}{s}}}, \qquad \sigma = {\frac{\sqrt{-q+{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}}}{\Theta \,\ln \left( A \right) }}. \end{aligned}$$
(11)

By substituting (11) in to (9), we recover this exact solution

$$\begin{aligned} u(x,t) = \pm \sqrt{-{\dfrac{2abq}{s}}} \dfrac{2}{a A^{\Theta \vartheta } + b A^{-\Theta \vartheta }}, \end{aligned}$$
(12)

where \(\vartheta = x - {\dfrac{\sqrt{-q+{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}}}{\Theta \,\ln \left( A \right) }}t\).

Fig. 1
figure 1

New exact solution u(x, t) (12) of the Klein–Gordon equation (6), for \(a= 2, b=1.5, q=-2, s=0.15, \Theta = 1.5\), when \(A = 2.7\)

Full size image

4 The (2+1)-dimensional Kadomtsev–Petviashvili equation Gai et al. (2016), Alharbi et al. (2020)

$$\begin{aligned} (u_{t} +6 u u_{x} + u_{xxx})_{x} + u_{yy} = 0, \end{aligned}$$
(13)

where \(u=u(x,y,t)\) is the unknown function with a real value that results from the real independent variables x, y, and t and It is used to describe the plasma’s electrostatic wave potential or the fluid’s shallow-water wave amplitude. Gai et al. (2016) used three different analytical techniques namely: the Lie symmetry, the extended tanh and the homotopy perturbation methods to investigate some exact and approximate solutions for the 2D-KPE. The \(\exp (\phi (\eta ))\)-expansion method is used by Alharbi et al. (2020) to find a variety of exact solutions with different wave structures for Eq. (13) and they discussed the stability of the obtained solutions via the commonly used form of the Hamiltonian system.

Assume that Eq. (13) has a traveling wave solution

$$\begin{aligned} \begin{aligned} u(x,y,t) = U(\vartheta ), \quad \vartheta = x + \omega y- \sigma t, \end{aligned} \end{aligned}$$
(14)

where \(\sigma\) is wave velocity. Using (14) in (13), we get the following nonlinear ODE:

$$\begin{aligned} U_{\vartheta \vartheta \vartheta \vartheta } + 6 U U_{\vartheta \vartheta } + (\omega ^{2}- \sigma ) U_{\vartheta \vartheta } + 6 U_{\vartheta }^{2} = 0. \end{aligned}$$
(15)

Then, with respect to \(\vartheta\), integrate equation (15) twice and simplify to get

$$\begin{aligned} U_{\vartheta \vartheta } + 3 U^{2} + (\omega ^{2}- \sigma ) U = 0, \end{aligned}$$
(16)

with integral constants treating as zero. Balancing the terms \(U_{\vartheta \vartheta }\) and \(U^{2}\) to get \(N = 2\). By substituting \(N = 2\) in to (4) to get

$$\begin{aligned} U({\vartheta }) = c_{0} + c_{1} Q(\vartheta ) + c_{2} Q(\vartheta )^{2}. \end{aligned}$$
(17)

Substituting (17) in (16) and equate the coefficient of \(Q(\vartheta )\) to zero yields

$$\begin{aligned} \begin{aligned}&Q^{0}: {\omega }^{2}c_{{0}}-\sigma \,c_{{0}}+3\,{c_{{0}}}^{2} = 0,\\&Q^{1}: {\omega }^{2}c_{{1}} - \sigma \,c_{{1}} + 6\,c_{{0}}c_{{1}} + {\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}c_{{1}} = 0,\\&Q^{2}: {\omega }^{2}c_{{2}} - \sigma \,c_{{2}} + 6\,c_{{0}}c_{{2}} + 3\,{c_{{1}}}^{2} + 4\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}c_{{2}} = 0,\\&Q^{3}: 6\,c_{{1}}c_{{2}}-8\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}c_{{1}}ab = 0,\\&Q^{4}: 3\,{c_{{2}}}^{2}-24\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}c_{{2}}ab = 0. \end{aligned} \end{aligned}$$
(18)

Following the aforementioned system’s solution, we obtain the sets:


Set 1:

$$\begin{aligned} c_{0} = 0, \qquad c_{1} = 0, \qquad c_{2} = 8\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}ab, \qquad \sigma = {\omega }^{2}+4\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}. \end{aligned}$$
(19)

By substituting (19) in to (14), we recover this exact solution

$$\begin{aligned} u(x,y,t) = \dfrac{8\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}ab}{\left( a A^{\Theta \vartheta } + b A^{-\Theta \vartheta }\right) ^{2}}, \end{aligned}$$
(20)

where \(\vartheta = x + \omega y - \left( {\omega }^{2}+4\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}\right) t\).


Set 2:

$$\begin{aligned} c_{0} = -\dfrac{4}{3}\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}, \qquad c_{1} = 0, \qquad c_{2} = 8\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}ab, \qquad \sigma = {\omega }^{2}-4\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}. \end{aligned}$$
(21)

By substituting (21) in to (14), we recover this exact solution

$$\begin{aligned} u(x,y,t) = -\dfrac{4}{3}\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2} + \dfrac{8\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}ab}{\left( a A^{\Theta \vartheta } + b A^{-\Theta \vartheta }\right) ^{2}}, \end{aligned}$$
(22)

where \(\vartheta = x + \omega y - \left( {\omega }^{2}-4\,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}\right) t\).

Fig. 2
figure 2

New exact solution u(x, y, t) (20) of the KP equation (13), for \(a = 1.5, b = 0.5, \Theta = 1.4, \omega = 0.3, y = 1\), when \(A = 1.6\)

Full size image

5 The (3+1)-dimensional Boussinesq equation Wazwaz and Kaur (2019), Hu and Li (2022)

$$\begin{aligned} u_{tt} - u_{xx} - \beta (u^{2})_{xx} - \gamma u_{xxxx} + \dfrac{\alpha ^{2}}{4} u_{yy} + \alpha u_{yt} + \delta u_{xz} = 0. \end{aligned}$$
(23)

where \(u=u(x,y,z,t)\) is the unknown function with a real value that results from the real independent variables x, y, z, and t, and \(\beta ,\,\gamma ,\,\alpha\) and \(\delta\) are real constants. It is commonly recognized that the 3D-BE is a crucial mathematical physics model with large application background, including in wave motion, weather forecast, and ocean ecology, all of which have undergone intensive research. In Hu and Li (2022), the nonlocal symmetry of the 3D-BE is obtained with the truncated Painleve’ method. Wazwaz and Kaur (2019) tested the integrability of Eq. (23) by Painleve’ test and obtained complex and real soliton solutions for this equation by using the simplified Hirota’s method.

Suppose that Eq. (23) has a traveling wave solution

$$\begin{aligned} \begin{aligned} u(x,y,z,t) = U(\vartheta ), \quad \vartheta = x + \omega y + s z- \sigma t, \end{aligned} \end{aligned}$$
(24)

where \(\sigma\) is wave velocity. Substituting (24) into (23), we get the following nonlinear ODE:

$$\begin{aligned} - \gamma U_{\vartheta \vartheta \vartheta \vartheta } - 2 \beta U U_{\vartheta \vartheta } + \left( \sigma ^{2}- 1 - \alpha \omega \sigma + \delta s + \frac{1}{4} \alpha ^{2} \omega ^{2}\right) U_{\vartheta \vartheta } - 2 \beta U_{\vartheta }^{2} = 0. \end{aligned}$$
(25)

Then, with respect to \(\vartheta\), integrate equation (25) twice and simplify to get

$$\begin{aligned} - \gamma U_{\vartheta \vartheta } - \beta U^{2} + \left( \sigma ^{2}- 1 - \alpha \omega \sigma + \delta s + \frac{1}{4} \alpha ^{2} \omega ^{2}\right) U = 0. \end{aligned}$$
(26)

with integral constants treating as zero. Balancing the terms \(U_{\vartheta \vartheta }\) and \(U^{2}\) to get \(N = 2\). By substituting \(N = 2\) in to (4) to get

$$\begin{aligned} U({\vartheta }) = c_{0} + c_{1} Q(\vartheta ) + c_{2} Q(\vartheta )^{2}. \end{aligned}$$
(27)

Substituting (27) in (26) and equate the coefficient of \(Q(\vartheta )\) to zero yields

$$\begin{aligned} \begin{aligned}&Q^{0}: -c_{{0}} + {\sigma }^{2}c_{{0}} - \beta \,{c_{{0}}}^{2} + (1/4)\,{\alpha }^{2}{\omega }^{2}c_{{0}} + \delta \,sc_{{0}} - \alpha \,\omega \,\sigma \,c_{{0}} = 0,\\&Q^{1}: (1/4)\,{\alpha }^{2}{\omega }^{2}c_{{1}} + \delta \,sc_{{1}} - 2\,\beta \,c_{{0}}c_{{1}} - \alpha \,\omega \,\sigma \,c_{{1}} - \gamma \,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}c_{{1}} - c_{{1}}+{\sigma }^{2}c_{{1}} = 0,\\&Q^{2}:(1/4)\,{\alpha }^{2}{\omega }^{2}c_{{2}}+\delta \,sc_{{2}}-2\,\beta \,c_{{0}}c_{{2}}+{\sigma }^{2}c_{{2}}-\beta \,{c_{{1}}}^{2}-\alpha \,\omega \,\sigma \,c_{{2}}-4\,\gamma \,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}c_{{2}}-c_{{2}} = 0,\\&Q^{3}: 8\,\gamma \,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}c_{{1}}ab-2\,\beta \,c_{{1}}c_{{2}} = 0,\\&Q^{4}: -\beta \,{c_{{2}}}^{2}+24\,\gamma \,{\Theta }^{2} \left( \ln \left( A\right) \right) ^{2}c_{{2}}ab = 0. \end{aligned} \end{aligned}$$
(28)

Following the aforementioned system’s solution, we obtain the sets:


Set 1:

$$\begin{aligned}&c_{0} = 0, \qquad c_{1} = 0, \qquad c_{2} = 24\,{\frac{\gamma \,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}ab}{\beta }} \qquad \nonumber \\&s = {\frac{-{\alpha }^{2}{\omega }^{2}-4\,{\sigma }^{2}+4\,\alpha \,\omega \,\sigma +16\,\gamma \,{\Theta }^{2} \left( \ln \left( A\right) \right) ^{2}+4}{4\delta }}. \end{aligned}$$
(29)

By substituting (29) in to (24), we recover this exact solution

$$\begin{aligned} u(x,y,z,t) = 24\,{\frac{\gamma \,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}ab}{\beta \, \left( a{A}^{\Theta \,\vartheta } + b{A}^{-\Theta \, \vartheta }\right) ^{2}}}, \end{aligned}$$
(30)

where \(\vartheta = x + \omega y + \left( {\dfrac{-{\alpha }^{2}{\omega }^{2}-4\,{\sigma }^{2}+4\,\alpha \,\omega \,\sigma +16\,\gamma \,{\Theta }^{2} \left( \ln \left( A\right) \right) ^{2}+4}{4\delta }}\right) z- \sigma t\).


Set 2:

$$\begin{aligned}&c_{0} = -4\,{\frac{\gamma \,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}}{\beta }}, \qquad c_{1} = 0, \qquad c_{2} = 24\,{\frac{\gamma \,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}ab}{\beta }}, \qquad \nonumber \\&s = -{\frac{{\alpha }^{2}{\omega }^{2}+16\,\gamma \,{\Theta }^{2}\left( \ln \left( A \right) \right) ^{2} + 4\,{\sigma }^{2} - 4 - 4\,\alpha \,\omega \,\sigma }{4\delta }}. \end{aligned}$$
(31)

By substituting (31) in to (24), we recover this exact solution

$$\begin{aligned} u(x,y,z,t) = -4\,{\frac{\gamma \,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}}{\beta }}+24\,{\frac{\gamma \,{\Theta }^{2} \left( \ln \left( A \right) \right) ^{2}ab}{\beta \, \left( a{A}^{\Theta \,\vartheta } + b {A}^{-\Theta \,\vartheta } \right) ^{2}}}, \end{aligned}$$
(32)

where \(\vartheta = x + \omega y - \left( {\frac{{\alpha }^{2}{\omega }^{2}+16\,\gamma \,{\Theta }^{2}\left( \ln \left( A \right) \right) ^{2} + 4\,{\sigma }^{2} - 4 - 4\,\alpha \,\omega \,\sigma }{\delta }}\right) z- \sigma t\).

Fig. 3
figure 3

New exact solution u(x, y, z, t) (30) of the Boussinesq equation (23), for \(a = 2.5, b = 1.5, \alpha = 1, \sigma = 1.5, \gamma = 0.2, \delta = -0.5, \beta = 2 \Theta = 2, \omega = 0.3, y = 0.5, z = 0.5\), when \(A = 2\)

Full size image

6 Conclusion

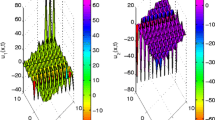
The new type of the Kudryashov technique is utilized to get some new exact solutions of the nonlinear problems. Some of the well-known nonlinear differential equations, e.g. Klein–Gordon equation, Kadomtsev–Petviashvili equation, and Boussinesq equation in higher dimensions are considered. Solitons of discussed equations are reported and some figures are shown to demonstrate the behavior of models in two and three dimensions. Figs. 1, 2, and 3 represent the solutions given by Eqs. (12), (20), and (30) for the models the Klein–Gordon equation, the KP equation, and the Boussinesq equation, respectively. Using the assumed values for the relevant parameter, we found that all obtained solutions depict bright soliton solutions created in 3D through x and t as \(-4.5\le x \le 4.5\) and \(-4.5\le t \le 4.5\). Whereas the 2D spreading is depicted for various t. It is evident that the wave solutions sweep from left to right along x-axis with the same amplitude. We mention that the solutions existed in Yomba (2007), Pandir and Ulusoy (2013) are special cases of the obtained solutions given by (12), (20), and (30) when \(a=b\). The Kudryashov method is a useful and strong mathematical instrument that may be used to provide the analytical solutions to a variety of other different NLPDEs.