1 Introduction

There has been significant and thorough research into the generation of soliton waves and their applications in recent decades. Optical solitons, which are made up of soliton transmission technology and soliton molecules, are one sort of this research. They can transport information across intercontinental distances all over the world. Optical solitons are confined electromagnetic waves with constant intensity due to dispersion and nonlinearity effects. For example, parabolic law nonlinearity (Triki and Biswas 2011), dual-power law nonlinearity (Triki and Biswas 2011; Zhang and Si 2010), power law nonlinearity (Biswas 2001), cubic-quintic-septic nonlinearities (Mirzazadeh et al. 2021), non-Kerr law nonlinearity (Biswas 2003), various polynomial nonlinearities (Kudryashov 2020), Kudryashov’s sextic power-law of refractive index (Zayed et al. 2021) and so on.

Nonlinear complex physical processes are vital in physics, chemistry, biology, plasma, fibers, nonlinear optics, geochemistry, illumination, energy transmission, and communications, among other fields of science. There has been a review of nonlinear Schrödinger equations (NLSEs) with group velocity dispersion (GVD) (Baskonus et al. 2021), Kerr nonlinearities (Houwe et al. 2020), spatio-temporal dispersion (Yildirim et al. 2017), self-steepening (Seadawy et al. 2022), and other solutions. Optical solitons are seen in nonlinear models such as nano-fibers (Biswas et al. 2016), optical fibers (Hasegawa and Matsumoto 2003), quantum electronics, optoelectronics, and photonics (Zhou et al. 2014; Karasawa 2012; Husko et al. 2016).

Breather solutions for NPDEs in addition to solitons are among the important models for exploring nonlinear wave solutions, since breather synchronization associated with their self-oscillating properties is complicated and has great challenges in many cases.

Recently, due to this perspective, phase-sensitive breather interactions have been one of the most studied areas. Some interesting studies that can easily be found on internet search, such as heart-cusp and bell-shaped-cusp optical solitons of an extended two-mode version of the complex Hirota model (Alquran et al. 2021), dynamics of optical solitons and nonautonomous complex wave solutions for the nonlinear Schrödinger equation with variable coefficients (Sulaiman et al. 2021), the nonautonomous complex wave solutions of the (2 + 1)-dimensional variable-coefficients nonlinear chiral Schrödinger equation (Sulaiman et al. 2020), exact solution of time-dependent Ginzburg–Landau equations, specifying the superconducting-normal interface propagation speed in superconductors (Panna and Islam 2013), the phase-dependent appearance of optical rogue waves (Anti Kainen et al. 2012), ultrafast digital soliton logic gates (Islam et al. 1992), new approach to chaotic encryption (Akhmediev et al. 2009), nonlinear stage of modulation instability (Zakharov and Gelash 2013), monitoring of rogue wave triplets in water waves (Chabchoub and Akhmediev 2590), breather wave molecules (Xu et al. 2019) and so on can be given as examples. There are many various types of solutions that have been proposed in the literature, but there are still many more that have yet to be investigated. In epitome, the key point is to investigate the pRKL equation with Kerr law nonlinearity (Singh 2016; Biswas et al. 2018; Ozdemir et al. 2021) by eMETEM.

The perturbed generalized Radhakrishnan-Kundu-Lakshmanan model with Kerr law is given:

$$i\frac{\partial u}{{\partial t}} + \alpha \frac{{\partial^{2} u}}{{\partial x^{2} }} + \beta \left| u \right|^{2} u = i\sigma \frac{\partial u}{{\partial x}} + i\lambda \frac{\partial }{\partial x}\left( {\left| u \right|^{2} u} \right) + i\mu \frac{\partial }{\partial x}\left( {\left| u \right|^{2} } \right)u - i\delta \frac{{\partial^{3} u}}{{\partial x^{3} }}\,.$$
(1)

In Eq. (1), i denotes imaginary unit (\(\,i^{2} = - 1\)), \(u(x,t)\) is the dependent variable which represents the complex valued wave profile, spatial x and temporal t are the independent variables. The first term \(iu_{t}\) stands for temporal evolution of the nonlinear wave, \(\alpha\) is the GVD, \(\beta\) is the coefficient of nonlinearity, \(\sigma\) is the inter-modal dispersion, \(\lambda\) is the coefficient of self-steepening for short pulses, \(\mu\) is the coefficient of the higher-order dispersion and \(\delta\) is the coefficient of the third order dispersion (TOD) term (Singh 2016; Biswas et al. 2018; Ozdemir et al. 2021).

Generally, in the optical system, the waveguides are of the Kerr type, and to describe the dynamics of light pulse propagation, the nonlinear Schrödinger equations (NLSEs) with cubic nonlinear terms are used. When the power of incident light increases to produce shorter (femtosecond-fs) pulses, the effects of non-Kerr nonlinearity become an important key that also very complicated to describe and investigate. The one of the best ways which to identify the dynamics of pulse, use the NLSEs with higher order nonlinear terms. So, Eq. (1) is one of the important models to describe for short pulse propagation in optical fiber. In order to investigate the pRKL in Eq. (1), pulse widths should be less than 100 fs (Radhakrishnan et al. 1999; Biswas 2009) and the interaction between the GVD and TOD is also crucial importance. If the group velocity dispersion closes to zero, in order to keep and enhance the performance of the pulse interaction along trans-oceanic distances it should be needed to consider the third order dispersions. Similarly, if the group velocity dispersion changes, it needs to be considered the higher order dispersion terms (Biswas 2009).

In this study, the proposed eMETEM has been applied to pRKL equation.

We have organized the rest of the sections: The mathematical analysis of the investigated pRKL equation has been given in Sect. 2. The proposed and applied eMETEM have been presented and implemented to the investigated pRKL equation in Sect. 3. We have explained the results and given graphical presentations of the obtained solutions in Sect. 4. We have presented the conclusion in the final section.

2 Mathematical analysis of the problem

We start by considering the following wave transform equations,

$$M(x,t) = e^{i\theta } M(\eta )\,\,,\,\,\,\eta = x - vt\,\,\,,\,\,\,\,\,\theta = - kx + \omega t + \varphi$$
(2)

where \(k,\,\omega ,\,\varphi\) and v are non-zero real values,\(\theta\) symbolizes the phase-component, \(\varphi\) is the phase-constant, k denotes the frequency, \(\omega\) is the parameter of wave number, v is the velocity, \(M(\eta )\) is the amplitude and \(M(x,t)\) for pulse shape.

Inserting the Eqs. (2) into (1) and decomposing the resultant equation as real and imaginary components, we reach the following nonlinear ordinary differential equations (NLODEs):

$$\left( { - k\lambda + \beta } \right)\left( {M\left( \eta \right)} \right)^{3} + \left( { - \delta {\mkern 1mu} k^{3} - \alpha {\mkern 1mu} k^{2} - k\sigma - \omega } \right)M\left( \eta \right) + \left( {3{\mkern 1mu} \delta {\mkern 1mu} k + \alpha } \right)\frac{{{\text{d}}^{2} M\left( \eta \right)}}{{{\text{d}}\eta^{2} }} = 0,$$
(3)
$$\delta {\mkern 1mu} \frac{{{\text{d}}^{3} M\left( \eta \right)}}{{{\text{d}}\xi^{3} }} + \left( {\left( { - 3{\mkern 1mu} \lambda - 2{\mkern 1mu} \mu } \right)\left( {M\left( \eta \right)} \right)^{2} - 3{\mkern 1mu} \delta {\mkern 1mu} k^{2} - 2{\mkern 1mu} \alpha {\mkern 1mu} k - v - \sigma } \right)\frac{{{\text{d}}M\left( \eta \right)}}{{{\text{d}}\eta }} = 0.$$
(4)

Integrate the Eq. (4), then assume the integration constant to zero, one can derive the Eq. (5).

$$\left( { - 3{\mkern 1mu} \lambda - 2{\mkern 1mu} \mu } \right)\left( {M\left( \eta \right)} \right)^{3} + \left( { - 9{\mkern 1mu} \delta {\mkern 1mu} k^{2} - 6{\mkern 1mu} \alpha {\mkern 1mu} k - 3{\mkern 1mu} \sigma - 3{\mkern 1mu} v} \right)M\left( \eta \right) + 3{\mkern 1mu} \delta {\mkern 1mu} \frac{{{\text{d}}^{2} M\left( \eta \right)}}{{{\text{d}}\eta^{2} }} = 0.$$
(5)

Since the function \(M(\eta )\) must satisfy the eqs. (3) and (4), according the homogeneous balance principle one can write following constraint equations:

$$\beta = - \frac{{6{\mkern 1mu} \delta k\lambda + 6{\mkern 1mu} \delta {\mkern 1mu} k\mu + 3{\mkern 1mu} \alpha {\mkern 1mu} \lambda + 2{\mkern 1mu} \alpha {\mkern 1mu} \mu }}{{3{\mkern 1mu} \delta }},$$
(6)
$$v = - \frac{{8{\mkern 1mu} \delta^{2} k^{3} + 8{\mkern 1mu} \alpha {\mkern 1mu} \delta {\mkern 1mu} k^{2} + 2{\mkern 1mu} \alpha^{2} k + 2{\mkern 1mu} \delta {\mkern 1mu} k\sigma + \alpha {\mkern 1mu} \sigma - \delta {\mkern 1mu} \omega }}{{3{\mkern 1mu} \delta k + \alpha }}.$$
(7)

Under the constraint equations eqs. (6) and (7), we can take into account nonlinear ordinary differential equation (NLODE) form of Eq. (1) as Eq. (3) or Eq. (5). Let we take Eq. (3) as NLODE form of Eq. (1).

$$\left( {\beta - k\lambda } \right)M^{3} - \left( {\delta {\mkern 1mu} k^{3} + {\mkern 1mu} k^{2} + k\sigma + \omega } \right)M + \left( {\alpha + 3{\mkern 1mu} k\delta } \right)M^{\prime\prime} = 0,$$
(8)

where \(M = M(\eta )\) and the superscript ′ denotes for ordinary derivative with respect to \(\eta\).

3 eMETEM and implementatiton to pRKL equation

Let us take in to account that the solution of NLODE in the Eq. (8) is proposed in the form:

$$M\left( \eta \right) = A_{0} + \sum\limits_{i = 1}^{m} {\left( {A_{i} \kappa^{i} (\eta ) + B_{i} \kappa^{ - i} (\eta )} \right)} \ldots \ldots \ldots ,A_{m} ,B_{m} \ne 0$$
(9)

where \(A_{0} ,...,A_{m} ,B_{1} ,...,B_{m}\) are real constants to be computed later (\(A_{m} ,B_{m}\) should not be zero simultaneously). m is the balancing constant which is obtained by using the balancing rule. We derive m = 1, by considering the terms \(M^{\prime\prime}(\eta )\) and \(M(\eta )^{3}\) in Eq. (8). Thus, Eq. (9) will be in in the following form:

$$M(\eta ) = A_{0} + A_{1} \kappa (\eta ) + B_{1} \frac{1}{\kappa (\eta )} \ldots \ldots ,\,A_{1} ,B_{1} \ne 0$$
(10)

where \(\kappa (\eta )\) realizes the Eq. (11).

$$\frac{d\kappa (\eta )}{{d\eta }} = w + \left[ {\kappa (\eta )} \right]^{2}$$
(11)

where w is an arbitrary real constant.

As it is well known from the literature, the Eq. (11) is the auxiliary equation of the generalized tanh method (Fan and Hon 2002) or METFM (Darwish et al. 2021; Elwakil et al. 2003; Raslan et al. 2017), which is widely used by researchers, and has the general solutions \(\kappa_{1} (\eta ),\,\,\kappa_{2} (\eta ),\,\,\kappa_{8} (\eta ),\,\,\kappa_{9} (\eta ),\,\,\kappa_{15} (\eta )\) in Table 1.

Table 1 The generalized (Fan and Hon 2002) and enhanced (Tang et al. 2010; Ozisik 2022) solutions of Eq. (11)
Full size table

Substitute the Eq. (10) and its derivatives according to Eq. (11) into Eq. (8), then get the polynomial in powers of \(\kappa (\eta ).\) Collect the all terms considering the same power of \(\kappa^{i} (\eta )\) and assume the each coefficients to zero, result is the following system:

$$\begin{gathered} \kappa^{ - 3} (\eta ):\frac{{B_{1} \left( {3{\mkern 1mu} \delta {\mkern 1mu} k + \alpha } \right)\left( {6{\mkern 1mu} \delta {\mkern 1mu} w^{2} - 3{\mkern 1mu} \lambda {\mkern 1mu} B_{1}^{2} - 2{\mkern 1mu} \mu {\mkern 1mu} B_{1}^{2} } \right)}}{{3{\mkern 1mu} \delta }} = 0, \hfill \\ \kappa^{ - 2} (\eta ): - \frac{{B_{1}^{2} \left( {3{\mkern 1mu} \delta {\mkern 1mu} k + \alpha } \right)\left( {2{\mkern 1mu} \mu + 3{\mkern 1mu} \lambda } \right)A_{0} }}{\delta } = 0, \hfill \\ \kappa^{ - 1} (\eta ): - \frac{{B_{1} }}{\delta }\left( \begin{gathered} k\left( {k^{2} - 6{\mkern 1mu} w} \right)\delta^{2} + \left( {k^{2} \alpha + \left( {6{\mkern 1mu} A_{1} \left( {\mu + 3/2{\mkern 1mu} \lambda } \right)B_{1} + 6{\mkern 1mu} \mu {\mkern 1mu} A_{0}^{2} + 9{\mkern 1mu} \lambda {\mkern 1mu} A_{0}^{2} + \sigma } \right)k - 2{\mkern 1mu} w\alpha + \omega } \right)\delta \hfill \\ + 2{\mkern 1mu} \left( {\mu + 3/2{\mkern 1mu} \lambda } \right)\left( {A_{0}^{2} + A_{1} B_{1} } \right)\alpha \hfill \\ \end{gathered} \right) = 0, \hfill \\ \kappa^{0} (\eta ): - \frac{{A_{0} }}{\delta }\left( \begin{gathered} \delta^{2} k^{3} + \left( {k^{2} \alpha + \left( {\left( {2{\kern 1pt} \mu + 3{\kern 1pt} \lambda } \right)A_{0}^{2} + 12{\kern 1pt} A_{1} \left( {\mu + 3/2{\kern 1pt} \lambda } \right)B_{1} + \sigma } \right)k + \omega } \right)\delta + 4{\kern 1pt} \alpha {\kern 1pt} \left( {\mu + 3/2{\kern 1pt} \lambda } \right) \hfill \\ \left( {A_{1} B_{1} + 1/6{\kern 1pt} A_{0}^{2} } \right) \hfill \\ \end{gathered} \right) = 0, \hfill \\ \end{gathered}$$
$$\begin{gathered} \kappa^{1} (\eta ): - \frac{{A_{1} }}{\delta }\left( \begin{gathered} k\left( {k^{2} - 6{\kern 1pt} w} \right)\delta^{2} + \left( {k^{2} \alpha + \left( {6{\kern 1pt} A_{1} \left( {\mu + 3/2{\kern 1pt} \lambda } \right)B_{1} + 6{\kern 1pt} \mu {\kern 1pt} A_{0}^{2} + 9{\kern 1pt} \lambda {\kern 1pt} A_{0}^{2} + \sigma } \right)k - 2{\kern 1pt} w\alpha + \omega } \right)\delta \hfill \\ + 2{\kern 1pt} \left( {\mu + 3/2{\kern 1pt} \lambda } \right)\left( {A_{0}^{2} + A_{1} B_{1} } \right)\alpha \hfill \\ \end{gathered} \right) = 0, \hfill \\ \kappa^{2} (\eta ): - \frac{{A_{1}^{2} \left( {3{\kern 1pt} \delta {\kern 1pt} k + \alpha } \right)\left( {2{\kern 1pt} \mu + 3{\kern 1pt} \lambda } \right)A_{0} }}{\delta } = 0, \hfill \\ \kappa^{3} (\eta ): - 2{\kern 1pt} \frac{{\left( {\delta {\kern 1pt} k + \alpha /3} \right)A_{1} \left( {\left( {\mu + 3/2{\kern 1pt} \lambda } \right)A_{1}^{2} - 3{\kern 1pt} \delta } \right)}}{\delta } = 0. \hfill \\ \end{gathered}$$
(12)

Solutions of the Eq. (12), gives the possible solution sets as given:

$$\begin{gathered} Rset^{1,2} = \left\{ {\omega = - \delta {\kern 1pt} k^{3} - \alpha {\kern 1pt} k^{2} + \left( { - 12{\kern 1pt} \delta {\kern 1pt} w - \sigma } \right)k - 4{\kern 1pt} w\alpha ,A_{0} = 0,A_{1} = \mp \frac{{\sqrt {6\left( {2{\kern 1pt} \mu + 3{\kern 1pt} \lambda } \right)\delta } }}{{2{\kern 1pt} \mu + 3{\kern 1pt} \lambda }},B_{1} = \mp \frac{{w\sqrt {6\left( {2{\kern 1pt} \mu + 3{\kern 1pt} \lambda } \right)\delta } }}{{2{\kern 1pt} \mu + 3{\kern 1pt} \lambda }}} \right\} \hfill \\ Rset^{3,4} = \left\{ {\omega = - \delta {\kern 1pt} k^{3} - \alpha {\kern 1pt} k^{2} + \left( {24{\kern 1pt} \delta {\kern 1pt} w - \sigma } \right)k + 8{\kern 1pt} w\alpha ,A_{0} = 0,A_{1} = \mp \frac{{\sqrt {6\left( {2{\kern 1pt} \mu + 3{\kern 1pt} \lambda } \right)\delta } }}{{2{\kern 1pt} \mu + 3{\kern 1pt} \lambda }},B_{1} = \pm \frac{{w\sqrt {6\left( {2{\kern 1pt} \mu + 3{\kern 1pt} \lambda } \right)\delta } }}{{2{\kern 1pt} \mu + 3{\kern 1pt} \lambda }}} \right\} \hfill \\ \end{gathered}$$
(13)

Let we substitute the functions \(\kappa_{i} (\eta )\) (i = 1, 2, …, 15) in Table 1 into Eq. (10) by considering.

Equations (2). We can easily derive the solutions of Eq. (1) by inserting the \(Rset^{1 - 4}\) above into \(M_{i} \left( {x,t} \right)\), (i = 1, 2,…, 15). It would be more appropriate to give the solution functions of Eq. (1) in general form as follows, instead of taking up much space in the article and giving a solution functions for each set separately.

$$M_{1} {\text{(x,t) = e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( {A_{0} - A_{1} \sqrt { - w} \tanh \left( {\sqrt { - w} \left( {x - vt} \right)} \right) - \frac{{B_{1} }}{{\sqrt { - w} \tanh \left( {\sqrt { - w} \left( {x - vt} \right)} \right)}}} \right)$$
(14)
$$M_{2} {\text{(x,t)}} = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( {A_{0} - A_{1} \sqrt { - w} {\text{coth}}\left( {\sqrt { - w} \left( {x - vt} \right)} \right) - \frac{{B_{1} }}{{\sqrt { - w} {\text{coth}}\left( {\sqrt { - w} \left( {x - vt} \right)} \right)}}} \right)$$
(15)
$$M_{3} {\text{(x,t)}} = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( \begin{gathered} A_{0} - A_{1} \sqrt { - w} \left( {\tanh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right) + i{\text{sech}}\left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right)} \right) \hfill \\ - \frac{{B_{1} }}{{\sqrt { - w} \left( {\tanh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right) + i{\text{sech}}\left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right)} \right)}} \hfill \\ \end{gathered} \right)$$
(16)
$$M_{4} {\text{(x,t)}} = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( {A_{0} + A_{1} \frac{{w - \sqrt { - w} \tanh \left( {\sqrt { - w} \left( {x - vt} \right)} \right)}}{{1 + \sqrt { - w} \tanh \left( {\sqrt { - w} \left( {x - vt} \right)} \right)}} + B_{1} \frac{{1 + \sqrt { - w} \tanh \left( {\sqrt { - w} \left( {x - vt} \right)} \right)}}{{w - \sqrt { - w} \tanh \left( {\sqrt { - w} \left( {x - vt} \right)} \right)}}} \right)$$
(17)
$$M_{5} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( {A_{0} + A_{1} \frac{{\sqrt { - w} \left( {5 - 4{\kern 1pt} \cosh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right)} \right)}}{{3 + 4{\kern 1pt} \sinh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right)}} + B_{1} \frac{{3 + 4{\kern 1pt} \sinh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right)}}{{\sqrt { - w} \left( {5 - 4{\kern 1pt} \cosh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right)} \right)}}} \right)$$
(18)
$$M_{6} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( \begin{gathered} A_{0} + A_{1} \frac{{\sqrt { - \left( {a^{2} + b^{2} } \right)w} - a\sqrt { - w} \cosh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right)}}{{\left( {a\sinh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right) + b} \right)}} \hfill \\ +\,B_{1} \frac{{a\sinh \left( {2{\kern 1pt} \sqrt { - w} \left( { - vt + x} \right)} \right) + b}}{{\sqrt { - \left( {a^{2} + b^{2} } \right)w} - a\sqrt { - w} \cosh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right)}} \hfill \\ \end{gathered} \right)$$
(19)
$$M_{7} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( \begin{gathered} A_{0} + A_{1} \left( {\sqrt { - w} - 2{\kern 1pt} \frac{{a\sqrt { - w} }}{{a + \cosh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right) - \sinh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right)}}} \right) \hfill \\ +\, \frac{{B_{1} }}{{\sqrt { - w} - 2{\kern 1pt} \frac{{a\sqrt { - w} }}{{a + \cosh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right) - \sinh \left( {2{\kern 1pt} \sqrt { - w} \left( {x - vt} \right)} \right)}}}} \hfill \\ \end{gathered} \right)$$
(20)
$$M_{8} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( {A_{0} + A_{1} \sqrt w \tan \left( {\sqrt w \left( {x - vt} \right)} \right) + \frac{{B_{1} }}{{\sqrt w \tan \left( {\sqrt w \left( {x - vt} \right)} \right)}}} \right)$$
(21)
$$M_{9} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( {A_{0} - A_{1} \sqrt w \cot \left( {\sqrt w \left( {x - vt} \right)} \right) - \frac{{B_{1} }}{{\sqrt w \cot \left( {\sqrt w \left( {x - vt} \right)} \right)}}} \right)$$
(22)
$$M_{10} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( \begin{gathered} A_{0} + A_{1} \sqrt w \left( {\tan \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right) + \sec \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right)} \right) \hfill \\ + \frac{{B_{1} }}{{\sqrt w \left( {\tan \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right) + \sec \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right)} \right)}} \hfill \\ \end{gathered} \right)$$
(23)
$$M_{11} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( {A_{0} - A_{1} \sqrt w \frac{{1 - \tan \left( {\sqrt w \left( {x - vt} \right)} \right)}}{{1 + \tan \left( {\sqrt w \left( {x - vt} \right)} \right)}} - B_{1} \frac{{1 + \tan \left( {\sqrt w \left( {x - vt} \right)} \right)}}{{\sqrt w \left( {1 - \tan \left( {\sqrt w \left( {x - vt} \right)} \right)} \right)}}} \right)$$
(24)
$$M_{12} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( {A_{0} + A_{1} \sqrt w \frac{{4 - 5{\kern 1pt} \cos \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right)}}{{3 + 5{\kern 1pt} \sin \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right)}} + B_{1} \frac{{3 + 5{\kern 1pt} \sin \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right)}}{{\sqrt w \left( {4 - 5{\kern 1pt} \cos \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right)} \right)}}} \right)$$
(25)
$$M_{13} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( {A_{0} + A_{1} \frac{{\sqrt {\left( {a^{2} - b^{2} } \right)w} - a\sqrt w \cos \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right)}}{{a\sin \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right) + b}} + B_{1} \frac{{a\sin \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right) + b}}{{\sqrt {\left( {a^{2} - b^{2} } \right)w} - a\sqrt w \cos \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right)}}} \right)$$
(26)
$$M_{14} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( \begin{gathered} A_{0} + A_{1} \left( {i\sqrt w - \frac{{2{\kern 1pt} ia\sqrt w }}{{a + \cos \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right) - i\sin \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right)}}} \right) \hfill \\ +\, \frac{{B_{1} }}{{\left( {i\sqrt w - \frac{{2{\kern 1pt} ia\sqrt w }}{{a + \cos \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right) - i\sin \left( {2{\kern 1pt} \sqrt w \left( {x - vt} \right)} \right)}}} \right)}} \hfill \\ \end{gathered} \right)$$
(27)
$$M_{15} (x,t) = {\text{e}}^{{i\left( { - kx + \omega {\mkern 1mu} t + \phi } \right)}} \left( {A_{0} - \frac{{A_{1} }}{x - vt} - B_{1} \left( {x - vt} \right)} \right)$$
(28)

Here, we have drawn the graphs of the solution functions which have been derived in eqs. (14–28) by using the solution sets given by Eq. (13) and some special parameter values.

Substituting the \(Rset^{1}\) and \(Rset^{3}\) into Eq. (16) and selecting the \(w = - 0.4,\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = - 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 1}}\,\) and \(\varphi { = 1,}\) the various graphs of the resultant functions of \(M_{3} (x,t)\) are given by Figs. 1 and 2, respectively. Inserting the \(Rset^{1}\) and \(Rset^{4}\) into Eq. (18) and selecting the \(w = - 0.4,\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = - 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 1}}\,\) and \(\varphi { = 1,}\) the various graphs of the resultant functions of \(M_{5} (x,t)\) are given by Figs. 3 and 4, respectively. Plugging the \(Rset^{1}\) into Eq. (23) and selecting the \(w = {0}{\text{.41}},\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 0}}{.1}\) and \(\varphi { = 1,}\) the various graphs of the resultant function of \(M_{10} (x,t)\) are given by Fig. 5. Substituting the \(Rset^{2}\) into Eq. (25) and selecting the \(w = {4},\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 1}}\,\) and \(\varphi { = 1,}\) the various graphs of the resultant function of \(M_{12} (x,t)\) are given by Fig. 6. Lastly, inserting the \(Rset^{3}\) into Eq. (28) and selecting the \(w = {0},\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 20}}\,\) and \(\varphi { = 1,}\) the various graphs of the resultant function of \(M_{15} (x,t)\) are given by Fig. 7.

Fig. 1
figure 1

The various portraits of \(M_{3} (x,\,t)\) in Eq. (16) by selecting set \(Rset^{1}\) in Eq. (13) and \(w = - 0.4,\,\,\alpha { = 0}{\text{.5, }}\sigma { = - 0}{\text{.5,}}\,\lambda { = 0}{\text{.5,}}\,\mu { = 0}{\text{.5,}}\,\delta { = 0}{\text{.5,}}\,{\text{k = 1,}}\,\varphi { = 1}{\text{.}}\)a \(\left| {M_{3} (x,\,t)} \right|^{2}\). b The contour portrait of \(\left| {M_{3} (x,\,t)} \right|^{2}\). c \({\text{Re}} \left( {M_{3} (x,\,t)} \right)\), d \({\text{Im}} \left( {M_{3} (x,\,t)} \right)\), e \(\left| {M_{3} (x,\,t)} \right|^{2}\) where \(t_{f} = 0,\,\,1\,\,and\,\,2.\), f \(\left| {M_{3} (x,\,1)} \right|^{2} ,\,{\text{Im}} \left( {M_{3} (x,\,1)} \right),\,{\text{Re}} \left( {M_{3} (x,1)} \right)\)

Full size image
Fig. 2
figure 2

The various portraits of \(M_{3} (x,\,t)\) in Eq. (16) by selecting set \(Rset^{3}\) in Eq. (13) and \(w = - 0.4,\,\,\alpha { = 0}{\text{.5, }}\sigma { = - 0}{\text{.5,}}\,\lambda { = 0}{\text{.5,}}\,\mu { = 0}{\text{.5,}}\,\delta { = 0}{\text{.5,}}\,{\text{k = 1,}}\,\varphi { = 1}{\text{.}}\) a \(\left| {M_{3} (x,\,t)} \right|^{2}\), b The contour portrait of \(\left| {M_{3} (x,\,t)} \right|^{2}\), c \({\text{Re}} \left( {M_{3} (x,\,t)} \right)\), d \({\text{Im}} \left( {M_{3} (x,\,t)} \right)\), e \(\left| {M_{3} (x,\,t)} \right|^{2}\) where \(t_{f} = 0,\,\,1\,\,and\,\,2.\), f \(\left| {M_{3} (x,1)} \right|^{2} ,\,{\text{Im}} \left( {M_{3} (x,1)} \right),\,{\text{Re}} \left( {M_{3} (x,1)} \right)\)

Full size image
Fig. 3
figure 3

The various portraits of \(M_{5} (x,\,t)\) in Eq. (18) by selecting set \(Rset^{1}\) in Eq. (13) and \(w = - 0.4,\,\,\alpha { = 0}{\text{.5, }}\sigma { = - 0}{\text{.5,}}\,\lambda { = 0}{\text{.5,}}\,\mu { = 0}{\text{.5,}}\,\delta { = 0}{\text{.5,}}\,{\text{k = 1,}}\,\varphi { = 1}{\text{.}}\) a \(\left| {M_{5} (x,\,t)} \right|^{2}\), b The contour portrait of \(\left| {M_{5} (x,\,t)} \right|^{2}\), c \({\text{Re}} \left( {M_{5} (x,\,t)} \right)\), d \({\text{Im}} \left( {M_{5} (x,\,t)} \right)\), e \(\left| {M_{5} (x,\,t)} \right|^{2}\) where \(t_{f} = 0,\,\,1\,\,and\,\,2.\), f \(\left| {M_{5} (x,1)} \right|^{2} ,\,{\text{Im}} \left( {M_{5} (x,1)} \right),\,{\text{Re}} \left( {M_{5} (x,1)} \right)\)

Full size image
Fig. 4
figure 4

The various portraits of \(M_{5} (x,\,t)\) in Eq. (18) by selecting set \(Rset^{4}\) in Eq. (13) and \(w = - 0.4,\,\alpha { = 0}{\text{.5, }}\sigma { = - 0}{\text{.5,}}\,\lambda { = 0}{\text{.5,}}\,\mu { = 0}{\text{.5,}}\,\delta { = 0}{\text{.5,}}\,{\text{k = 1,}}\,\varphi { = 1}{\text{.}}\) a \(\left| {M_{5} (x,\,t)} \right|^{2}\), b The contour portrait of \(\left| {M_{5} (x,\,t)} \right|^{2}\), c \({\text{Re}} \left( {M_{5} (x,\,t)} \right)\), d \({\text{Im}} \left( {M_{5} (x,\,t)} \right)\), e \(\left| {M_{5} (x,\,t)} \right|^{2}\) where \(t_{f} = 0,\,\,1\,\,and\,\,2.\), f \(\left| {M_{5} (x,1)} \right|^{2} ,\,{\text{Im}} \left( {M_{5} (x,1)} \right),\,{\text{Re}} \left( {M_{5} (x,1)} \right)\)

Full size image
Fig. 5
figure 5

The various portraits of \(M_{10} (x,\,t)\) in Eq. (23) by selecting set \(Rset^{1}\) in Eq. (13) and \(w = {0}{\text{.41}},\,\,\alpha { = 0}{\text{.5, }}\sigma { = 0}{\text{.5,}}\,\,\lambda { = 0}{\text{.5,}}\,\mu { = 0}{\text{.5,}}\,\delta { = 0}{\text{.5,}}\,{\text{k = 0}}{.1,}\,\varphi { = 1}{\text{.}}\) a \(\left| {M_{10} (x,\,t)} \right|^{2}\), b The contour portrait of \(\left| {M_{10} (x,\,t)} \right|^{2}\), c \({\text{Re}} \left( {M_{10} (x,\,t)} \right)\), d \({\text{Im}} \left( {M_{10} (x,\,t)} \right)\), e \(\left| {M_{10} (x,\,t)} \right|^{2}\) where \(t_{f} = 0,\,\,1\,\,and\,\,2.\), f \(\left| {M_{10} (x,1)} \right|^{2} ,\,{\text{Im}} \left( {M_{10} (x,1)} \right),\,{\text{Re}} \left( {M_{10} (x,1)} \right)\)

Full size image
Fig. 6
figure 6

The various portraits of \(M_{12} (x,\,t)\) in Eq. (25) by selecting set \(Rset^{2}\) in Eq. (13) and \(w = 4,\,\,\alpha { = 0}{\text{.5, }}\sigma { = 0}{\text{.5,}}\,\lambda { = 0}{\text{.5,}}\,\mu { = 0}{\text{.5,}}\,\delta { = 0}{\text{.5,}}\,{\text{k = 1,}}\,\,\varphi { = 1}{\text{.}}\) a \(\left| {M_{12} (x,\,t)} \right|^{2}\), b The contour portrait of \(\left| {M_{12} (x,\,t)} \right|^{2}\), c \({\text{Re}} \left( {M_{12} (x,\,t)} \right)\), d \({\text{Im}} \left( {M_{12} (x,\,t)} \right)\), e \(\left| {M_{12} (x,\,t)} \right|^{2}\) where \(t_{f} = 0,\,\,1\,\,and\,\,2.\), f \(\left| {M_{12} (x,1)} \right|^{2} ,\,{\text{Im}} \left( {M_{12} (x,1)} \right),\,{\text{Re}} \left( {M_{12} (x,1)} \right)\)

Full size image
Fig. 7
figure 7

The various portraits of \(M_{15} (x,t)\) in Eq. (28) by selecting set \(Rset^{3}\) in Eq. (13) and \(w = 0,\,\,\alpha { = 0}{\text{.5, }}\sigma { = 0}{\text{.5,}}\,\lambda { = 0}{\text{.5,}}\,\mu { = 0}{\text{.5,}}\,\delta { = 0}{\text{.5,}}\,{\text{k = 20,}}\,\,\varphi { = 1}{\text{.}}\) a \(\left| {M_{15} (x,\,t)} \right|^{2}\), b The contour portrait of \(\left| {M_{15} (x,\,t)} \right|^{2}\), c \({\text{Re}} \left( {M_{15} (x,\,t)} \right)\), d \({\text{Im}} \left( {M_{15} (x,\,t)} \right)\), e \(\left| {M_{15} (x,\,t)} \right|^{2}\) where \(t_{f} = 0,\,\,1\,\,and\,\,2.\), f \(\left| {M_{15} (x,1)} \right|^{2} ,\,{\text{Im}} \left( {M_{15} (x,1)} \right),\,{\text{Re}} \left( {M_{15} (x,1)} \right)\)

Full size image

4 Result and discussion

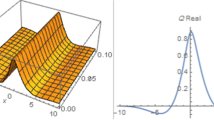
In this paper, we have proposed and applied an enhanced version of existing method namely, eMETEM. We have successfully obtained plethora of soliton solutions for pRKL equation and we have presented the graphs of the derived solutions in the figures. Selecting appropriate values of the parameters, we have drawn seven figures to analyze the behavior of the solutions. In the presented figures, each figure includes six sub-figures. They are modulus square in 3D (a), a contour plot of modulus square (b), 3D plots of \({\text{Re}} \left( {M_{i} (x,\,\,t)} \right),\,\,{\text{Im}} \left( {M_{i} (x,\,\,t)} \right)\) components of considered solutions (c,d), the plots of the modulus square, real and imaginary parts of the related solutions at t = 1 (e) and the plots of modulus squares at t = 0, 1 and t = 2 (f), respectively.

In Fig. 1, we have visualized the some portraits of \(M_{3} (x,t)\) in Eq. (16) by using \(Rset^{1}\) and the selected values, \(w = - \,0.4,\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = - 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 1}}\,\) and \(\varphi { = 1}{\text{.}}\) The Fig. 1a, b and c, represent the bright soliton. Figure 1c, d depict the breather-like soliton and Fig. 1e, shows the traveling wave property of \(M_{3} (x,t)\), so the soliton moves to the right along the x-axis.

In Fig. 2, we have depicted the plots of \(M_{3} (x,t)\) in Eq. (16) by using \(Rset^{3}\) and the selected values, \(w = - 0.4,\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = - 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 1}}\,\) and \(\varphi { = 1}{\text{.}}\) The Figs. 2a, 2b and c, denote the dark soliton. Figures 2c, d represent the periodic and mixed (multi-combined) bright-dark soliton. Figure 2e, also shows the traveling wave property of \(M_{3} (x,t)\), so the soliton again moves to the right along the x-axis.

In Fig. 3, we have obtained the some portraits of \(M_{5} (x,t)\) in Eq. (18) by using \(Rset^{1}\) and the selected values, \(w = - 0.4,\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = - 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 1}}\,\) and \(\varphi { = 1}{\text{.}}\) The Fig. 3, represent the singular multiple solution. Figure 3e, shows the traveling wave property of \(M_{5} (x,t)\) and the soliton moves to the right along the x-axis.

In Fig. 4, we have plotted the some portraits of \(M_{5} (x,t)\) in Eq. (18) by using \(Rset^{4}\) and the selected values, \(w = - 0.4,\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = - 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 1}}\,\) and \(\varphi { = 1}{\text{.}}\) The Fig. 4a, b represent the singular solution, Fig. 4c, d represent singular kink solution. \(M_{5} (x,t)\) the soliton moves to the right along the x-axis.

In Fig. 5, we have illustrated the some plots of \(M_{10} (x,t)\) in Eq. (23) by using \(Rset^{1}\) and the selected values, \(w = {0}{\text{.41}},\,\,\)\(\alpha { = 0}{\text{.5,}}\)\(\, \sigma { = 0}{\text{.5,}}\,\)\(\lambda { = 0}{\text{.5,}}\)\(\mu { = 0}{\text{.5,}}\,\)\(\delta { = 0}{\text{.5,}}\,\)\({\text{k = 0}}{.1}\) and \(\varphi { = 1}{\text{.}}\) The Fig. 5a, represents periodic singular solution, Fig. 5c, d represents periodic multi singular solution.

In Fig. 6, we have depicted the graphs of \(M_{12} (x,t)\) in Eq. (25) by using \(Rset^{2}\) and the selected values, \(w = {4},\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 1}}\,\) and \(\varphi { = 1}{\text{.}}\) The Fig. 6a, b represent the periodic singular solution. Figures 6c, d, show the quite different (strange) multi singular solution. \(M_{12} (x,t)\) moves to the right along the x-axis.

In the last figure, namely Fig. 7, we have presented the graphs of \(M_{15} (x,t)\) in Eq. (28) by using \(Rset^{3}\) and the selected values, \(w = {0},\,\,\) \(\alpha { = 0}{\text{.5,}}\) \(\, \sigma { = 0}{\text{.5,}}\,\) \(\lambda { = 0}{\text{.5,}}\) \(\mu { = 0}{\text{.5,}}\,\) \(\delta { = 0}{\text{.5,}}\,\) \({\text{k = 20}}\,\) and \(\varphi { = 1}{\text{.}}\) The Fig. 7a, b represent the flat kink-like solution. Figure 7c, d, show the multiple different (strange) periodic solution. \(M_{15} (x,t)\) does not move along the x-axis.

5 Conclusion

In this paper, we have utilized an efficient eMETEM to establish robust analytical optical soliton solutions for the pRKL equation with Kerr law. This effective scheme has been shown as very effective for the governing model. Bright, dark, combined bright–dark, singular, multiple singular, periodic, flat kink-like, breather like, different (strange) periodc optical solitons have been successfully exposed using the Maple and Matlab symbolic computation packages. On the 3-dimensional, 2-dimensional and contour graphs, the derived and physical features have been depicted. We strongly believe that both the results obtained and the enhanced version of the method applied to this problem for the first time in this article, will be very useful guide for the scientists who study in this field.