Modulational instability and soliton trains in a model for two-mode fiber ring lasers

Abstract

A model of orthogonally polarized two-field fiber ring laser with a linear gain is considered, with emphasis on the continuous-wave stability and the existence of soliton trains. The continuous-wave stability analysis is carried out within the framework of the modulational-instability approach, the variations of the gain spectrum with the modulation frequency and characteristic parameters of the model give rise to a rich variety of stability features including single-band and multiband stability regions. Seeking for pulse structures of the model, the two coupled cubic complex Ginzburg–Landau equations describing individual mode propagations are transformed into a set of coupled, first-order nonlinear ordinary-differential equations for the amplitudes and phases of the two modes. Numerical simulations of the last set of coupled equations indicate that in the anomalous dispersion regime, envelopes of the two fields are periodic trains of pulses the amplitudes of which are affected by the linear gain.

1 Introduction

Mode-locked fiber lasers have attracted a great deal of attention in the recent past (Haus 1975; Haus and Silberberg 1986; Ippen et al. 1989; Martinez et al. 1984; Weill et al. 2007; Akhmediev et al. 1998; Chen et al. 1995; Pschotta and Keller 2001; Kalashnikov et al. 2003; Tang et al. 2008; Fandio Jubgang et al. 2015; Fandio Jubgang and Dikandé 2017), because of their outstanding potential in optical transmissions of high-intensity pulses of short durations. Passively mode-locked lasers (Chen et al. 1995; Pschotta and Keller 2001; Kalashnikov et al. 2003) in particular are much attractive for they require only a saturable absorber in the gain medium, whose absorption coefficient decreases with increase in light intensity, inducing a nonlinear coupling between longitudinal modes that causes the relative amplitudes and phases to lock thereby generating short pulses.

Although high-intensity ultrashort pulses are hallmarks of mode-locked fiber lasers with saturable absorbers, in real applications mode-locked lasers do not usually set up instantly in the pulse regime. The typical input will be a continuous-wave (cw) field which is designed to undergo spatio-temporal modulations upon propagation, growing in amplitude due to four-wave mixing related to nonlinearity either from self-phase modulation or cross-phase modulation processes inherent to the propagation medium. Such growth can occur through several distinct phases in the laser dynamics including quasi-cw, chaotic, single-pulse, multipulse or pulse-train structures. In this context the laser self-starting will refer to the physical situation where conditions are no more favourable to cws, such that the laser field stabilizes in a regime dominated by pulses (Chen et al. 1995).

Concerning laser self-starting, it is instructive stressing that there are several approaches to this problem (Chen et al. 1995; Hermann 1993; Haus and Ippen 1991; Krausz et al. 1991) depending on the type of laser, and on the type of mode-locking process. One approach involves the picture of a transition from cw to steady-state mode-locked operations (Krausz et al. 1991). This transition is governed by a modulational instability (MI) of the cw field, a process whereby a small noise signal coupled to the cw field will grow exponentially as a result of the interplay between nonlinearity and dispersion (Hickmann et al. 1993; Martijn de Sterke 1998; Agrawal 1987; Tanemura and Kikuchi 2003; Dai et al. 2009). As for passively mode-locked lasers, their theoretical investigations rest on two different approaches namely ab initio simulations, in which one simulates the entire evolution of light in the fiber starting from noise, and a second approch which assumes that the light evolution during one roundtrip is small. In this second approach the propagation equation is the Complex Ginzburg–Landau equation (CGLE) for which the equilibria can be determined, and their stability studied following a linear-stability theory (Haus 1975; Chen et al. 1995; Dikandé et al. 2017).

Earlier studies on laser self-starting within the framework of the MI theory have considered mostly a single CGLE (Chen et al. 1995; Dikandé et al. 2017), or two linearly coupled CGLEs with linear gain (Trillo et al. 1989; Tasgal and Malomed 1999; Li et al. 2011). In this work we shall be interested in a theoretical model describing a fiber ring laser supporting two orthogonally-polarized fields with nonlinear interactions between them. The model is represented by two coupled CGLEs for which a MI analysis will be carried out in both normal and anomalous dispersion regimes. Next, numerical simulations will enable us explore shape profiles of pulse structures stabilized by characteristic parameters of the model.

2 The model and cw stability

Consider a fiber laser with two orthogonally polarized modes propagating in an optical medium with Kerr nonlinearity. The dynamics of this laser field is assumed to be described by the following set of two nonlinearly coupled CGLEs:

$$\begin{aligned} \frac{\partial u}{\partial z} & = {} i\frac{{\varDelta }\beta }{2}u-\delta \frac{\partial u}{\partial T} -i\frac{\beta ''}{2}\frac{\partial ^{2} u}{\partial T^{2}} \nonumber \\&+\,i\gamma \left( |u|^{2}+\frac{2}{3}|v|^{2}\right) u+ \frac{i\gamma }{3}v^{2}u^{*} \nonumber \\&+\, \frac{g}{2}u +\frac{g}{2{\varOmega }_{g}^{2}}\frac{\partial ^{2}u }{\partial T^{2}}, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial v}{\partial z}& = {} -i\frac{{\varDelta }\beta }{2}v+\delta \frac{\partial v}{\partial T} -i\frac{\beta ''}{2}\frac{\partial ^{2} v}{\partial T^{2}}\nonumber \\&+\,i\gamma \left( |v|^{2}+\frac{2}{3}|u|^{2}\right) v+\frac{i\gamma }{3}u^{2}v^{*}\nonumber \\&+\, \frac{g}{2}v +\frac{g}{2{\varOmega }_{g}^{2}}\frac{\partial ^{2}v }{\partial T^{2}}. \end{aligned}$$

(2)

The variables u(z, T) and v(z, T) in the above set are normalized envelopes of the two orthogonally polarized fields, ${\varDelta }\beta$ is their wavenumber difference, $\delta$ is their linear group velocity difference, $\beta ''$ is the second-order dispersion coefficient while $\gamma$, g and ${\varOmega }_{g}$ represent the nonlinearity parameter, the saturable gain coefficient and the bandwidth of the laser gain respectively. Note that the model Eqs. (1)–(2) is close to the one studied recently by Yue et al. (2013), where account was taken of the effects of a third-order dispersion on the generation and stability of dark-dark soliton pairs. In the present context we are interested in the stability of cws and on shapes of the two envelopes, laying emphasis on the influence of the linear gain g on the envelope amplitudes.

Let the steady-state solutions to Eqs. (1)–(2) be of the following forms:

$$\begin{aligned}{}[u(z,0), v(z,0)]=[u_0, v_0]\,e^{-i\alpha z}, \end{aligned}$$

(3)

for which ${\varDelta }\beta =0$ and the wavenumber $\alpha$ is obtained as:

$$\begin{aligned} \alpha =-\gamma \left( u_{0}^{2}+v_{0}^{2}\right) +i\frac{g}{2}. \end{aligned}$$

(4)

The complex part of $\alpha$ suggests an exponential damping (amplification) of the cw amplitudes during the laser roundtrips, for negative (positive) values of the linear gain g. To investigate the stability of the steady-state solutions Eq. (3) with the wavenumber given by Eq. (4), we consider small amplitude perturbations ${\tilde{u}}(z, T)$ and ${\tilde{v}}(z,T)$ such that solutions to Eqs. (1)–(2) now read:

$$\begin{aligned} u=(u_{0}+{\tilde{u}})\,e^{-i\alpha z}, \quad v=(v_{0}+{\tilde{v}})\,e^{-i\alpha z}. \end{aligned}$$

(5)

Replacing these in Eqs. (1)–(2) and linearizing we obtain:

$$\begin{aligned} {{\tilde{u}}}_{z}& = {} -i\gamma \left( u_{0}^{2}+v_{0}^{2}\right) \tilde{u}-\delta {{\tilde{u}}}_{T} -i\frac{\beta ''}{2}{{\tilde{u}}}_{TT}\nonumber \\&+\,i\gamma u_0^2\left( {{\tilde{u}}}+{{\tilde{u}}}^{*}+{{\tilde{u}}}\right) +i\frac{2}{3}v_0\gamma \left( v_0{{\tilde{u}}}+u_0{{\tilde{v}}}^{*}+u_0{{\tilde{v}}} \right) \nonumber \\&+\,i\frac{\gamma }{3}v0\left( v_0{{\tilde{u}}}^{*}+2u_0{{\tilde{v}}}\right) +\frac{g}{2{\varOmega }_{g}^{2}}{{\tilde{u}}}_{TT}, \end{aligned}$$

(6)

$$\begin{aligned} {{\tilde{v}}}_{z}& = {} -i\gamma \left( u_{0}^{2}+v_{0}^{2}\right) \tilde{v}+\delta {{\tilde{v}}}_{T} -i\frac{\beta ''}{2}{{\tilde{v}}}_{TT}\nonumber \\&+\,i\gamma _0^2\left[ \left( {{\tilde{v}}}+{{\tilde{v}}}^{*}+{{\tilde{v}}}\right) +\frac{2}{3}\left( u_{0}^{2}{{\tilde{v}}}+u_{0}v_{0}{{\tilde{u}}}^{*}+u_{0} v_{0}{{\tilde{u}}}\right) \right] \nonumber \\&+\,i\frac{\gamma }{3}u_0\left( u_0{{\tilde{v}}}^{*}+2v_0{{\tilde{u}}}\right) + \frac{g}{2{\varOmega }_{g}^{2}}{{\tilde{v}}}_{TT}. \end{aligned}$$

(7)

We pick the following solutions for the linear Eqs. (6)–(7):

$$\begin{aligned} \left[ {\tilde{u}}, {\tilde{u}}^{*}\right]& = {} \left[ A_1, A_2\right] \,e^{(\lambda z+i\omega T)}, \end{aligned}$$

(8)

$$\begin{aligned} \left[ {\tilde{v}}, {\tilde{v}}^{*}\right]& = {} \left[ B_1, B_2\right] \,e^{(\lambda z+i\omega T)}, \end{aligned}$$

(9)

where $\lambda$ is the rate of spatial growth of perturbations and $\omega$ the modulation frequency. With Eqs. (8) and (9), the coupled set Eqs. (6)–(7) can be represented in matrix form i.e.:

$$\begin{aligned} \lambda \begin{pmatrix} A_{1}\\ A_{2}\\ B_{1}\\ B_{2} \end{pmatrix} = \begin{pmatrix} a &{}\quad b &{}\quad c &{}\quad d\\ -b &{}\quad e &{}\quad -d &{}\quad -c\\ c &{}\quad d &{}\quad f &{}\quad k\\ -d &{}\quad -c &{}\quad -k &{}\quad h \end{pmatrix} \begin{pmatrix} A_{1}\\ A_{2}\\ B_{1}\\ B_{2} \end{pmatrix}, \end{aligned}$$

(10)

where

$$\begin{aligned} a & = {} i\gamma \left( u_{0}^{2}-\frac{v_{0}^{2}}{3}\right) -i \delta \omega +i\frac{\omega ^{2}}{2}\beta '' -\frac{g\omega ^{2}}{2{\varOmega }_{g}^{2}}, \nonumber \\ b & = {} i\gamma \left( u_{0}^{2}+\frac{v_{0}^{2}}{3}\right) , \quad c=\frac{4}{3}i\gamma u_{0}v_{0}, \quad d=\frac{2}{3}i\gamma u_{0}v_{0}, \nonumber \\ e & = {} i\gamma \left( -u_{0}^{2}+\frac{v_{0}^{2}}{3}\right) - i\delta \omega -i\frac{\omega ^{2}}{2}\beta '' -\frac{g\omega ^{2}}{2{\varOmega }_{g}^{2}},\nonumber \\ f & = {} i\gamma \left( -\frac{u_{0}^{2}}{3}+v_{0}^{2}\right) + i\delta \omega +i\frac{\omega ^{2}}{2}\beta '' -\frac{g\omega ^{2}}{2{\varOmega }_{g}^{2}},\nonumber \\ k & = {} i\gamma \left( \frac{u_{0}^{2}}{3}+v_{0}^{2}\right) , \nonumber \\ h & = {} i\gamma \left( \frac{u_{0}^{2}}{3}-v_{0}^{2}\right) +i\delta \omega -i\frac{\omega ^{2}}{2}\beta '' -\frac{g\omega ^{2}}{2{\varOmega }_{g}^{2}}. \nonumber \\ \end{aligned}$$

(11)

The $4\times 4$ matrix equation (10) is a cumbersome eigenvalue problem for which analytical solutions are not easy to find, we therefore resort to considerations enabling anlytical solutions. In this last respect we have seen above that the gain causes an exponential growth or damping of the field amplitudes, depending on the sign of the linear gain parameter g. Hence we can ignore the contribution of the linear gain in the linear-wave stability analysis for its effect is already known, focusing mainly on the possible amplification or decay of the small perturbations. With this consideration, we obtain a secular equation for the eigenvalues in terms of the following fourth-order polynomial in $\lambda$:

$$\begin{aligned} Q+t\lambda ^{2}+\lambda ^{4}=0, \end{aligned}$$

(12)

where we defined:

$$\begin{aligned} Q & = {} -\frac{2}{3}\gamma ^{2}\omega ^{4}u_{0}^{2}v_{0}^{2} \beta ''^{2}-\frac{1}{3}\gamma ^{2}\omega ^{4}\beta ''^{2} \left( u_{0}^{4}+v_{0}^{4}\right) \nonumber \\&+\,\frac{1}{6}\gamma \omega ^{6}\beta ''^{2}\left( u_{0}^{2}+ v_{0}^{2}\right) +\frac{1}{16}\omega ^{8}\beta ''^{4}, \end{aligned}$$

(13)

$$\begin{aligned} t & = {} \frac{2}{3}\gamma \omega ^{2}\beta ''\left( u_{0}^{2}+v_{0}^{2} \right) +\frac{1}{2}\omega ^{4}\beta ''^{2}. \end{aligned}$$

(14)

The four possible roots of the polynomial (12) are:

$$\begin{aligned} \lambda ^2 & = {} -\frac{1}{3}\gamma \omega ^{2}\beta ''\left( u_{0}^{2} +v_{0}^{2}\right) -\frac{1}{4}\omega ^{4}\beta ''^{2} \pm \frac{\sqrt{2}}{6}\sqrt{{\varDelta }}, \nonumber \\ {\varDelta } & = {} \gamma \omega ^{4}\beta ''^{2}\left( u_{0}^{2}+v_{0}^{2}\right) \left[ 3\omega ^{2} \left( \beta ''-1\right) +8\gamma \left( u_{0}^{2}+v_{0}^{2}\right) \right] , \end{aligned}$$

(15)

and are functions of the modulation frequency $\omega$, besides their dependence on characteristic parameters of the model. To discuss the cw stability from these eigenvalues, it is useful to stress that according to Eqs. (8) and (9) the linear cw solutions will be stable if eigenvalues are either purely imaginary or their real parts are negative. In view of the dependence of $\lambda$ on the modulation frequency, it is evident that these stability conditions will depend on the range of values of $\omega$. A very simple picture of cw stability emerges in the case of zero modulation frequency, where the four eigenvalues are all zero. In this case the amplitudes $(A_1, A_2)$, $(B_1, B_2)$ of the perturbations do not undergo spatio-temporal modulations and hence remain finite, thus favouring the stability of cw modes.

In the general case of nonzero modulation frequency, if we let $P=u_{0}^{2}+v_{0}^{2}$ (where P is the total input power), we can rewrite the eigenvalue $\lambda$ obtained in (15) as:

$$\begin{aligned} \lambda ^{2} & = {} -\frac{1}{3}\gamma \omega ^{2}\beta ''P-\frac{1}{4}\omega ^{4}\beta ''^{2} \nonumber \\&\pm \, \frac{\sqrt{2}}{6}\left[ \gamma \omega ^{4}\beta ''^{2}P\left( 3\omega ^{2} \left( \beta ''-1\right) +8\gamma P\right) \right] ^{1/2}. \end{aligned}$$

(16)

This enables us consider another simple picture of cw stability i.e. when ${\varDelta }=0$, which for $\beta ''\ne 1$ corresponds to a modulation frequency:

$$\begin{aligned} \omega ^{2}=\frac{8}{3}\frac{\gamma P}{(1-\beta '')}, \end{aligned}$$

(17)

such that the eigenvalues (16) can be expressed in terms of the total power P as:

$$\begin{aligned} \lambda ^2=-\frac{8}{9}\frac{\gamma ^{2}P^{2}\beta ''(1+\beta '')}{(1-\beta '')^{2}}. \end{aligned}$$

(18)

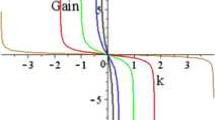
Since the modulation frequency $\omega$ is always real, Eq. (17) suggests that $\beta ''$ should be smaller than one for positive $\gamma$. However Eq. (18) shows that the term $\beta ''(1+\beta '')$ can be negative for values of $\beta ''<1$, hence for the eigenvalues $\lambda$ in Eq. (18) to be real we need $\beta ''\in \left]-1, 0\right[$ and self-starting is favoured. In Fig. 1, we plot the amplification gain $Re(\lambda )$ versus the second-order dispersion coefficient $\beta ''$ in the relevant range of values of this later parameter, for $\gamma =0.5$ and different values of the total power i.e. $P=160$ kW, $P=180$ kW and $P=200$ kW. Note that for negative values of $\gamma$ the modulation frequency will be real if $\beta ''$ is greater than one. Since for these values of the second-order dispersion coefficient the product $\beta ''(1+\beta '')$ is always positive, $\lambda$ should be purely imaginary and the laser cannot self-start.

Fig. 1

Plot of gain i.e. Re($\lambda$)/(/m) as a function of $\beta ''$, for $\gamma =0.5$ /(kWm)

In the most general case when the modulation frequency is arbitrary, the self-starting dynamics of the cw laser is complex but we can still gain a clear picture of the cw stability. To this end let us first take the upper branch of Eq. (15), i.e.:

$$\begin{aligned} \lambda ^{2}=\frac{\sqrt{2}}{6}\sqrt{{\varDelta }}-\left( \frac{1}{3} \gamma \omega ^{2}\beta ''P +\frac{1}{4}\omega ^{4}\beta ''^{2}\right) . \end{aligned}$$

(19)

We have the following situations:

• If ${\varDelta }>0$ with $\left| (1/3)\gamma \omega ^{2}\beta ''P+(1/4) \omega ^{4}\beta ''^{2}\right| <(\sqrt{2}/6)\sqrt{{\varDelta }}$ for nonzero values of $\omega$, then $\lambda ^2$ should be real and positive and cws are unstable.

• If ${\varDelta }>0$ and $\left| (1/3)\gamma \omega ^{2}\beta ''P+(1/4) \omega ^{4}\beta ''^{2}\right| >(\sqrt{2}/6)\sqrt{{\varDelta }}$, then $\lambda ^2$ is complex which favours the stability of cws.

• If ${\varDelta }<0$ then we can write ${\varDelta }=i^{2}S$, where S is a real quantity. Therefore $\lambda ^{2}$ is a complex number the imaginary part of which contributes a constant amplitude. The real part will engender a predominant instability that results in an exponential growth or decay of the noise amplitudes, depending on the sign of its exponent.

The lower branch of Eq. (15) is given by:

$$\begin{aligned} \lambda ^2=-\left( \frac{1}{3}\gamma \omega ^2\beta ''P+\frac{1}{4} \omega ^4\beta ''^{2} +\frac{\sqrt{2}}{6}\sqrt{{\varDelta }}\right) , \end{aligned}$$

(20)

and implies the following situations:

• If ${\varDelta }>0$ and $(1/3)\gamma \omega ^{2}\beta ''P+(1/4)\omega ^{4}\beta ''^{2} +(\sqrt{2}/6)\sqrt{{\varDelta }}>0$, then $\lambda$ is purely imaginary thus favouring the stability of cws.

• If ${\varDelta }>0$ and $(1/3)\gamma \omega ^{2}\beta ''P+(1/4)\omega ^{4}\beta ''^{2} +(\sqrt{2}/6)\sqrt{{\varDelta }}<0$, then $\lambda$ will be real and positive and self-starting is favoured.

• If ${\varDelta }<0$ then $\lambda$ is a complex number: the dominant behaviour will be an exponential growth or decay of noise amplitudes depending on the sign of its real part.

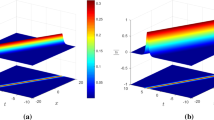
These behaviours are summarized in Figs. 2 and 3, where we represented the variation of the amplification gain $Re(\lambda )$ as a function of the modulation frequency $\omega$ and the input power P in three and two dimensions, in the case of normal dispersion (Fig. 2) and anomalous dispersion (Fig. 3). Parameter values are indicated on the graphs and figure captions.

Fig. 2

(Color online) 3D (left graph) and 2D (right graph) plots showing the MI gain spectrum as a function of the modulation frequency $\omega$ and total power P, calculated for the normal dispersion regime with $\gamma =0.1 /(\hbox {kWm})$ and $\beta ''=1.6 \, \hbox {ps}^2/\hbox {m}$

Fig. 3

(Color online) 3D (left graph) and 2D (right graph) plots showing the MI gain spectrum of a function of the modulation frequency $\omega$ total power, P calculated for the anomalous dispersion regime with $\gamma =0.1 /(\hbox {kWm})$ and $\beta ''=-1.6 \, \hbox {ps}^2/\hbox {m}$

In the case with normal dispersion there is a single MI band, with the maximum gain increasing with increase in the total input power P (Fig. 2). On the contrary, when $\beta ''$ is negative Fig. 3 suggests two MI bands as the modulation frequency increases. This two-band structure can actually be seen in Eq. (19) as being related to the existence of at least one nonzero characteristic modulation frequency, for positive values of the nonlinear coefficient $\gamma$ (here also playing the role of coupling parameter between the two fields) and negative values of the second-order dispersion coefficient $\beta$”. This characteristic modulation frequency corresponds to the value of $\omega$ at which the modulation gain vanishes in Fig. 3, and according to the figure it is a function of the input power P. Note that the multiband structure of the MI gain observed in Fig. 3 is not specific to the present context, indeed a similar behaviour is observed for linearly coupled CGLEs (Li et al. 2011) and is generally favored by the combination of the coupling and an anomalous group-velocity dispersion.

3 Pulse trains

The MI analysis of cws has a long history in the study of linear-wave stability in systems described by nonlinear Schrödinger equations (Zakharov and Ostrovsky 2009). Usually, when linear waves become unstable, direct simulations of these equations assuming an input field with a cw profile leads to modulated-wave structures with envelopes having the shape of a pulse or a dark soliton. In the case of CGLE, which can readily be regarded as a nonlinear Schrödinger equation with complex coefficients, the MI analysis enables us determine parameter values for which cw fields are stable. However the CGLE has a far richer dynamics compared with the nonlinear Schrödinger equation, thus in addition to modulated-wave structures which can be generated by direct simulations of the equation using an input cw field, a wealth of interesting distinct soliton-type solutions have so far been proposed (see for instance Aranson and Kramer 2002; Akhmediev et al. 1997, 2001; Issokolo and Dikandé 2018).

We are interested in a particular form of nonlinear solutions to the coupled CGLEs (1)–(2), which describe real-amplitude envelopes undergoing spatio-temporal modulations in their course of propagation. Such solutions are represented as Soto-Crespo et al. (2002):

$$\begin{aligned} u(z, \tau ) & = {} a_1(\tau ){\text {exp}}[i\phi _{1}(\tau )-i\xi z], \end{aligned}$$

(21)

$$\begin{aligned} v(z, \tau ) & = {} a_2(\tau ){\text {exp}}[i\phi _{2}(\tau )-i\xi z], \end{aligned}$$

(22)

where $a_1$, $a_{2}$, $\phi _1$ and $\phi _{2}$, which are real functions of $\tau =T-v_{1}z$, represent the amplitudes and phases of the two fields. The quantity $v_{1}$ is the inverse velocity of pulses and $\xi$ is the pulse propagation constant. Replacing these solutions in Eqs. (1)–(2) and isolating real from imaginary terms, we obtain:

$$\begin{aligned} a_{1}'' & = {} \frac{4{\varOmega }_{g}^{4}}{g^{2}+\beta ''^{2}{\varOmega }_{g}^{4}} \Bigg \{\Big [\frac{\beta ''\xi }{2} +\frac{\beta ''{\varDelta }\beta }{4}- \frac{\beta ''}{2}\delta \phi _{1}' +\frac{\beta ''^{2}}{4}\phi _{1}'^{2}\nonumber \\&+\,\frac{\beta ''\gamma }{2}\left( a_{1}^{2}+ \frac{2}{3}a_{2}^{2} \right) +\frac{\beta ''}{6}\gamma a_{2}^{2}\cos 2(\phi _{2}-\phi _{1})\nonumber \\&-\,\frac{g^{2}}{4{\varOmega }_{g}^{2}}+\frac{g^{2}}{4 {\varOmega }_{g}^{4}} \phi _{1}'^{2}+\frac{\gamma g}{6{\varOmega }_{g}^{2}} a_{2}^{2}\sin 2(\phi _{2}-\phi _{1})\Big ]a_{1}\nonumber \\&+\,\left[ \frac{\beta ''g}{2{\varOmega }_{g}^{2}}\phi _{1}'- \frac{g}{2{\varOmega }_{g}^{2}}(v_{1}-\delta +\beta ''\phi _{1}') \right] a_{1}'+\frac{\beta ''}{2}v_{1}\phi _{1}'\Bigg \}, \end{aligned}$$

(23)

$$\begin{aligned} \phi _{1}'' & = {} \frac{4{\varOmega }_{g}^{4}}{(g^{2}+\beta ''^{2} {\varOmega }_{g}^{4})a_{1}}\Bigg \{\Big [\frac{g\delta \phi _{1}'}{2{\varOmega }_{g}^{2}}-\frac{g{\varDelta }\beta }{4 {\varOmega }_{g}^{2}}-\frac{g\xi }{2{\varOmega }_{g}^{2}} \nonumber \\&-\,\frac{g\gamma }{2{\varOmega }_{g}^{2}}\left( a_{1}^{2}+ \frac{2}{3}a_{2}^{2}\right) -\frac{\beta ''}{4}g -\frac{g\gamma }{6{\varOmega }_{g}^{2}}a_{2}\cos 2(\phi _{2}- \phi _{1})\nonumber \\&+\frac{\beta ''a_{2}^{2}}{6}\sin 2(\phi _{2}-\phi _{1}) \Big ]a_{1}\nonumber \\&-\left[ \frac{\beta ''}{2}(v_{1}-\delta +\beta ''\phi _{1}') +\frac{g^{2}}{2{\varOmega }_{g}^{4}}\phi _{1}'\right] a_{1}' -\frac{gv_{1}}{2{\varOmega }_{g}^{2}}\phi _{1}'\Bigg \}, \end{aligned}$$

(24)

$$\begin{aligned} a_{2}'' & = {} \frac{4{\varOmega }_{g}^{4}}{g^{2}+\beta ''^{2} {\varOmega }_{g}^{4}}\Bigg \{\Bigg [\frac{\beta ''\xi }{2} -\frac{\beta ''{\varDelta }\beta }{4}+\frac{\beta ''}{2}\delta \phi _{2}'\nonumber \\&+\,\frac{\beta ''^{2}}{4}\phi _{2}'^{2}+\frac{\beta ''}{2}\gamma \left( a_{2}^{2}+\frac{2}{3}a_{1}^{2}\right) +\frac{\beta ''}{6}\gamma a_{1}^{2}\cos 2(\phi _{1}-\phi _{2})\nonumber \\&+\,\frac{g}{6{\varOmega }_{g}^{2}}\gamma a_{1}^{2}\sin 2 (\phi _{1}-\phi _{2})-\frac{g^{2}}{4{\varOmega }_{g}^{2}} +\frac{g^{2}}{4{\varOmega }_{g}^{4}}\phi _{2}'^{2}\Bigg ]a_{2}\nonumber \\&+\left[ \frac{\beta ''}{2{\varOmega }_{g}^{2}}g\phi _{2}'- \frac{g}{2{\varOmega }_{g}^{2}}(v_{1}+\delta +\beta '' \phi _{2}')\right] a_{2}'+\frac{\beta ''}{2}\phi _{2}'v_{1}\Bigg \}, \end{aligned}$$

(25)

$$\begin{aligned} \phi _{2}'' & = {} \frac{4{\varOmega }_{g}^{4}}{(g^{2}+\beta ''^{2} {\varOmega }_{g}^{4})a_{2}}\Bigg \{\Bigg [\frac{g}{4{\varOmega }_{g}^{2}}{\varDelta }\beta -\frac{g}{2{\varOmega }_{g}^{2}} \xi -\frac{g}{2{\varOmega }_{g}^{2}}\delta \phi _{2}'\nonumber \\&-\,\frac{g}{2{\varOmega }_{g}^{2}}\gamma \left( a_{2}^{2}+ \frac{2}{3}a_{1}^{2}\right) -\frac{g}{6{\varOmega }_{g}^{2}} \gamma a_{1}^{2}\cos 2(\phi _{1}-\phi _{2})\nonumber \\&+\,\frac{\beta ''}{6}\gamma a_{1}^{2}\sin 2(\phi _{1}- \phi _{2})-\frac{\beta ''}{4}g\Bigg ]a_{2}\nonumber \\&-\,\left[ \frac{\beta ''}{2}\left( v_{1}+\delta +\beta '' \phi _{2}'\right) +\frac{g^{2}}{2{\varOmega }_{g}^{4}} \phi _{2}'\right] a_{2}'-\frac{g}{2{\varOmega }_{g}^{2}}\phi _{2}'v_{1}\Bigg \}, \end{aligned}$$

(26)

where the prime and double-prime symbols on field variables refer to first and second-order derivatives respectively, with respect to $\tau$. The above system of four coupled second-order nonlinear ordinary differential equations, can be transformed to a set of coupled first-order nonlinear ordinary differential equations by defining: $\phi _1'=M_1, \phi _1''=M_1', \phi _2'=M_2, \phi _2''=M_2', a_1'=y_1, a_1''=y_1', a_2'=y_2, a_2''=y_2'$. These lead to (details of the steps of derivation of the equations are given in the appendix):

$$\begin{aligned} y_{1}' & = {} \frac{4{\varOmega }_{g}^{4}}{g^{2}+\beta ''^{2} {\varOmega }_{g}^{4}}\Bigg \{\Bigg [\frac{\beta ''\xi }{2} +\frac{\beta ''{\varDelta }\beta }{4}-\frac{\beta ''}{2} \delta M_{1}+\frac{\beta ''^{2}}{4}M_{1}^{2}\nonumber \\&+\,\frac{\beta ''\gamma }{2}\left( a_{1}^{2}+ \frac{2}{3}a_{2}^{2}\right) +\frac{\beta ''}{6}\gamma a_{2}^{2}\cos 2(\phi _{2}-\phi _{1})\nonumber \\&-\,\frac{g^{2}}{4{\varOmega }_{g}^{2}}+\frac{g^{2}}{4 {\varOmega }_{g}^{4}}M_{1}^{2}+\frac{\gamma g}{6{\varOmega }_{g}^{2}} a_{2}^{2}\sin 2(\phi _{2}-\phi _{1})\Bigg ]a_{1}\nonumber \\&+\,\left[ \frac{\beta ''g}{2{\varOmega }_{g}^{2}}M_{1}-\frac{g}{2{\varOmega }_{g}^{2}}(v_{1}-\delta +\beta ''M_{1}) \right] y_{1}+\frac{\beta ''}{2}v_{1}M_{1}\Bigg \}, \end{aligned}$$

(27)

$$\begin{aligned} M_{1}' & = {} \frac{4{\varOmega }_{g}^{4}}{(g^{2}+\beta ''^{2} {\varOmega }_{g}^{4})a_{1}}\Bigg \{\Big [\frac{g\delta M_{1}}{2{\varOmega }_{g}^{2}}-\frac{g{\varDelta }\beta }{4{\varOmega }_{g}^{2}} -\frac{g\xi }{2{\varOmega }_{g}^{2}} \nonumber \\&-\,\frac{g\gamma }{2{\varOmega }_{g}^{2}}\left( a_{1}^{2}+ \frac{2}{3}a_{2}^{2}\right) -\frac{\beta ''}{4}g -\frac{g\gamma }{6{\varOmega }_{g}^{2}}a_{2}\cos 2(\phi _{2}-\phi _{1})\nonumber \\&+\,\frac{\beta ''a_{2}^{2}}{6}\sin 2(\phi _{2}-\phi _{1})\Big ]a_{1}\nonumber \\&-\,\left[ \frac{\beta ''}{2}(v_{1}-\delta +\beta ''M_{1})+ \frac{g^{2}}{2{\varOmega }_{g}^{4}}M_{1}\right] y_{1} -\frac{gv_{1}}{2{\varOmega }_{g}^{2}}M_{1}\Bigg \}, \end{aligned}$$

(28)

$$\begin{aligned} y_{2}' & = {} \frac{4{\varOmega }_{g}^{4}}{g^{2}+\beta ''^{2} {\varOmega }_{g}^{4}}\Bigg \{\Bigg [\frac{\beta ''\xi }{2} -\frac{\beta ''{\varDelta }\beta }{4}+\frac{\beta ''}{2}\delta M_{2}\nonumber \\&+\,\frac{\beta ''^{2}}{4}M_{2}^{2}+\frac{\beta ''}{2}\gamma \left( a_{2}^{2}+\frac{2}{3}a_{1}^{2}\right) +\frac{\beta ''}{6}\gamma a_{1}^{2}\cos 2(\phi _{1} -\phi _{2})\nonumber \\&+\,\frac{g}{6{\varOmega }_{g}^{2}}\gamma a_{1}^{2}\sin 2(\phi _{1}- \phi _{2})-\frac{g^{2}}{4{\varOmega }_{g}^{2}} +\frac{g^{2}}{4{\varOmega }_{g}^{4}}M_{2}^{2}\Bigg ]a_{2}\nonumber \\&+\,\left[ \frac{\beta ''}{2{\varOmega }_{g}^{2}}gM_{2}- \frac{g}{2{\varOmega }_{g}^{2}}(v_{1}+\delta +\beta '' M_{2})\right] y_{2}+\frac{\beta ''}{2}M_{2}v_{1}\Bigg \}, \end{aligned}$$

(29)

$$\begin{aligned} M_{2}' & = {} \frac{4{\varOmega }_{g}^{4}}{(g^{2}+\beta ''^{2}{\varOmega }_{g}^{4}) a_{2}}\Bigg \{\Bigg [\frac{g}{4{\varOmega }_{g}^{2}} {\varDelta }\beta -\frac{g}{2{\varOmega }_{g}^{2}}\xi - \frac{g}{2{\varOmega }_{g}^{2}}\delta M_{2}\nonumber \\&-\,\frac{g}{2{\varOmega }_{g}^{2}}\gamma \left( a_{2}^{2}+\frac{2}{3} a_{1}^{2}\right) -\frac{g}{6{\varOmega }_{g}^{2}} \gamma a_{1}^{2}\cos 2(\phi _{1}-\phi _{2})\nonumber \\&+\,\frac{\beta ''}{6}\gamma a_{1}^{2}\sin 2(\phi _{1}-\phi _{2})- \frac{\beta ''}{4}g\Bigg ]a_{2}\nonumber \\&-\,\left[ \frac{\beta ''}{2}\left( v_{1}+\delta +\beta ''M_{2}\right) +\frac{g^{2}}{2{\varOmega }_{g}^{4}} M_{2}\right] y_{2}-\frac{g}{2{\varOmega }_{g}^{2}}M_{2}v_{1}\Bigg \}. \end{aligned}$$

(30)

The coupled first-order nonlinear ordinary differential Eqs. (27)–(30) have been solved numerically using a sixth-order Runge-Kutta algorithm with fixed step (${\varDelta }\tau =10^{-5}$) (Luther 1968; Dikandé Bitha and Dikandé 2018). Below we present numerical results of the time series for the amplitudes $a_1$ and $a_2$, for some positive values of the linear gain g.

Figure 4 represents profiles of the field amplitudes $a_1$ (left graph) and $a_2$ (right graph) as a function of time $\tau$, when the linear gain is zero(i.e. $g=0$). In all our simulations we have fixed ${\varOmega }_g=5.0$, and values of other characteristic parameters in the equations are given in the figure captions. Figure 4 shows that envelopes of the two fields are periodic trains of pulses of constant amplitudes. As we increase the linear gain g in the positive branch, we notice an amplification of pulse amplitudes which is more and more pronounced as g is increased. Figure 5 corresponds to $g=0.025$, and Fig. 6 to $g=0.05$.

Fig. 4

(Color online) Time series of the laser-field amplitudes $a_1$ (left graph) and $a_2$ (right graph), for $\beta ''=-0.6$, $\gamma =0.9$, $\delta =0.01$, ${\varDelta }\beta =0.9$, $\omega =0.8$: $g=0$

Fig. 5

(Color online) Time series of the laser-field amplitudes $a_1$ (left graph) and $a_2$ (right graph), for $\beta ''=-0.6$, $\gamma =0.9$, $\delta =0.01$, ${\varDelta }\beta =0.9$, $\omega =0.8$: $g=0.025$

Fig. 6

(Color online) Time series of the laser-field amplitudes $a_1$ (left graph) and $a_2$ (right graph), for $\beta ''=-0.6$, $\gamma =0.9$, $\delta =0.01$, ${\varDelta }\beta =0.9$, $\omega =0.8$: $g=0.05$

Instructively, as in the case of nonlinear Schrödinger equation the cubic CGLE does not admit pulse-soliton solutions in the normal dispersion regime. Kivshar and Turitsyn (1993) have shown that in the normal dispersion regime, two coupled nonlinear Schrödinger equations admit dark-dark soliton pairs which they referred to as vector dark solitons. Yue et al. (2013) carried out numerical simulations on the model Eqs. (1)–(2) including a third-order dispersion term. They established that when the effective (i.e. total) dispersion was positive, nonlinear solutions to the coupled CGLEs would be dominantly dark-dark soliton pairs irrespective of the contribution of the third-order dispersion.

4 Conclusion

We considered the dynamics of a two-mode laser model assumed to describe the propagation of two orthogonally polarized optical fields. This model is closely related to a recent one studied in ref. Yue et al. (2013), where the authors includes a third-order dispersion term and investigated its effects on the generation and propagation of a train of dark soliton pairs. Starting with the modulational-instability analysis of linear waves, we found that in the cw regime the laser stability was governed by a complex combination of characteristic parameters of the model. However, at zero modulation frequency a simple picture of modulational instability of cws was obtained in terms of a process determined by the sign and magnitude of the second-order dispersion coefficient. Thus, for positive values of this coefficient corresponding to a normal dispersion regime, the MI gain was characterized by a single band the maximum of which was increased with increase of the input power. In the anomalous dispersion region, a positive value of the nonlinear coupling coefficient $\gamma$ resulted into a nonzero characteristic modulation frequency for which the MI gain was zero. Numerical simulations of the two coupled CGLEs were carried out to gain a firm picture about profiles of the envelopes of the two fields. In the anomalous dispersion regime, we found that envelopes of the two fields were periodic trains of pulses the amplitudes of which were amplified by an increase of the linear gain in the positive branch.

As indicated in the introduction, the concept of laser self-starting can be linked with the MI in that this picture assumes a transition from cw to pulse operation when the cw regime is unstable. However this is not always the case, indeed when the cw amplitude starts growing there are transient regimes driven by period-doubling biburcations of the field amplitudes before a permanent regime dominated by stable pulses. A detailed analysis of these transient regimes is expected to provide more insight onto the stability of both cws and pulses, but also on other possible forms of optical soliton patterns supported by the model. This analysis is under consideration.

Appendix

To derive Eqs. (23)–(26) or Eqs. (27)–(30) from the model Eqs. (1)–(2), we consider nonlinear solutions in the forms of Eqs. (21) and (22). Substituting in Eqs. (1)–(2) we obtain:

$$\begin{aligned} -v_{1}a_{1}'-iv_{1}\phi _{1}'-i\xi a_{1} & = {} i\frac{{\varDelta }\beta }{2}a_{1}- \delta \left( a_{1}'+ia_{1}\phi _{1}'\right) \nonumber \\&-\,i\frac{\beta ''}{2}\left( a_{1}''+2ia_{1}'\phi _{1}' +ia_{1}\phi _{1}''-a_{1}\phi _{1}'^{2}\right) \nonumber \\&+\,i\gamma \left( a_{1}^{2}+\frac{2}{3}a_{2}^{2}\right) a_{1}+ i\frac{\gamma }{3}a_{1}a_{2}^{2}\cos 2(\phi _{2}-\phi _{1})\nonumber \\&-\,\frac{\gamma }{3}a_{1}a_{2}^{2}\sin 2(\phi _{2}-\phi _{1})+\frac{g}{2}a_{1} \nonumber \\&+\,\frac{g}{2{\varOmega }_{g}^{2}}\left( a_{1}''+2ia_{1}' \phi _{1}'+ia_{1}\phi _{1}''-a_{1}\phi _{1}'^{2}\right) , \end{aligned}$$

(31)

$$\begin{aligned} -v_{1}a_{2}'-iv_{1}\phi _{2}'-i\xi a_{2} & = {} -i\frac{{\varDelta }\beta }{2} a_{2}+\delta (a_{2}'+ia_{2}\phi _{2}') \nonumber \\&-\,\frac{\beta ''}{2}\left( ia_{2}''-2a_{2}'\phi _{2}'- a_{2}\phi _{2}''-ia_{2}\phi _{2}'^{2}\right) +i\gamma \left( a_{2}^{2}+\frac{2}{3}a_{1}^{2}\right) a_{2}\nonumber \\&+\,\frac{\gamma }{3}a_{1}^{2}a_{2}\left[ i\cos 2(\phi _{1}-\phi _{2})- \sin 2(\phi _{1}-\phi _{2})\right] \nonumber \\&+\,\frac{g}{2}a_{2}+\frac{g}{2{\varOmega }_{g}^{2}}\left( a_{2}''+ 2ia_{2}'\phi _{2}'+ia_{2}\phi _{2}'' -a_{2}\phi _{2}'^{2}\right) . \end{aligned}$$

(32)

By separating the real part from the imaginary part in Eqs. (31) and (32) we obtain a system of four coupled second-order nonlinear differential equations given by,

$$\begin{aligned}&\left[ \frac{\beta ''}{2}\phi _{1}''+\frac{g}{2}- \frac{g}{2{\varOmega }_{g}^{2}}\phi _{1}'^{2}-\frac{\gamma }{3}a_{2}^{2} \sin 2(\phi _{2}-\phi _{1})\right] a_{1} \nonumber \\&\quad +\,(v_{1}-\delta +\beta ''\phi _{1}')a_{1}'+ \frac{g}{2{\varOmega }_{g}^{2}}a_{1}''=0, \end{aligned}$$

(33)

$$\begin{aligned}&\left[ \xi +\frac{{\varDelta }\beta }{2}-\delta \phi _{1}'+\frac{\beta ''}{2} \phi _{1}'^{2}+\gamma \left( a_{1}^{2}+ \frac{2}{3}a_{2}^{2}\right) +\frac{\gamma }{3}a_{2}^{2}\cos 2(\phi _{2} -\phi _{1})+\frac{g}{2{\varOmega }_{g}^{2}}\phi _{1}'' \right] a_{1} \nonumber \\&\quad +\,\frac{g}{{\varOmega }_{g}^{2}}\phi _{1}'a_{1}'+v_{1}\phi _{1}'- \frac{\beta ''}{2}a_{1}''=0, \end{aligned}$$

(34)

$$\begin{aligned}&\left[ \frac{\beta ''}{2}\phi _{2}''-\frac{\gamma }{3}a_{1}^{2} \sin 2(\phi _{1}-\phi _{2})+\frac{g}{2} -\frac{g}{2{\varOmega }_{g}^{2}}\phi _{2}'^{2}\right] a_{2}\nonumber \\&\quad +\,(v_{1}+\delta +\beta ''\phi _{2}')a_{2}'+ \frac{g}{2{\varOmega }_{g}^{2}}a_{2}''=0, \end{aligned}$$

(35)

$$\begin{aligned}&\Bigg [\xi -\frac{{\varDelta }\beta }{2}+\delta \phi _{2}'+ \frac{\beta ''}{2}\phi _{2}'^{2}+\gamma \left( a_{2}^{2}+\frac{2}{3}a_{1}^{2}\right) \nonumber \\&\quad +\,\frac{\gamma }{3}a_{1}^{2}\cos 2(\phi _{1}-\phi _{2})+ \frac{g}{2{\varOmega }_{g}^{2}}\phi _{2}''\Bigg ]a_{2} \nonumber \\&\quad +\,\frac{g}{{\varOmega }_{g}^{2}}\phi _{2}'a_{2}'+v_{1}\phi _{2}' -\frac{\beta ''}{2}a_{2}''=0. \end{aligned}$$

(36)

By defining $\phi _{1}'=M_{1}, \phi _{1}''=M_{1}'; \phi _{2}'=M_{2}, \phi _{2}''=M_{2}'; a_{1}'=y_{1}, a_{1}''=y_{1}'; a_{2}'=y_{2}, a_{2}''=y_{2}'$ in Eqs. (33), (34), (35)and (36) we obtain a set of coupled first-order nonlinear ordinary differential equations given in matrix form as,

$$\begin{aligned} \begin{pmatrix} \frac{\beta ''}{2}a_{1} &{}\quad \frac{g}{2{\varOmega }_{g}^{2}} &{}\quad 0 &{}\quad 0\\ \frac{g}{2{\varOmega }_{g}^{2}}a_{1} &{}\quad -\frac{\beta ''}{2} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \frac{\beta ''}{2}a_{2} &{}\quad \frac{g}{2{\varOmega }_{g}^{2}}\\ 0 &{}\quad 0 &{}\quad \frac{g}{{\varOmega }_{g}^{2}}a_{2} &{}\quad -\frac{\beta ''}{2} \end{pmatrix} \begin{pmatrix} M_{1}'\\ y_{1}'\\ M_{2}'\\ y_{2}' \end{pmatrix} = \begin{pmatrix} A\\ B\\ C\\ D \end{pmatrix}, \end{aligned}$$

(37)

where A, B, C and D are given by,

$$\begin{aligned} A & = {} \Big [-\frac{g}{2}+\frac{g}{2{\varOmega }_{2}^{2}}M_{1}^{2} +\frac{\gamma }{3}a_{2}^{2}\sin 2(\phi _{2}-\phi _{1})\Big ] a_{1}-(v_{1}-\delta +\beta ''M_{1})y_{1},\nonumber \\ B & = {} \Big [-\xi -\frac{{\varDelta }\beta }{2}+\delta M_{1}-\frac{\beta ''}{2} M_{1}^{2}-\gamma (a_{1}^{2}+\frac{2}{3} a_{2}^{2})\nonumber \\&-\,\frac{\gamma }{3}a_{2}^{2}\cos 2(\phi _{2}-\phi _{1})\Big ]a_{1} +\left(\frac{g}{{\varOmega }_{g}^{2}}y_{2} +v_{1}\right)M_{1},\nonumber \\ C & = {} \Big [-\frac{\gamma }{3}a_{1}^{2}\sin 2(\phi _{1}-\phi _{2})- \frac{g}{2}+\frac{g}{2{\varOmega }_{g}^{2}}M_{2}^{2}\Big ] a_{2} +(v_{1}+\delta +\beta ''M_{2})y_{2},\nonumber \\ D & = {} \Big [-\xi +\frac{{\varDelta }\beta }{2}-\frac{\beta ''}{2}M_{2}^{2}- \gamma (a_{2}^{2}+\frac{2}{3}a_{1}^{2}) \nonumber \\&-\,\frac{\gamma }{3}a_{1}^{2}\cos 2(\phi _{1}-\phi _{2})\Big ]a_{2} +\left(\frac{g}{{\varOmega }_{g}^{2}}y_{2}+v_{1}\right). \end{aligned}$$

(38)

By carrying out the following operation on the matrix equation (37): $R_{2}\times g/(2{\varOmega }_{g}^{2})+ R_{1}\times (\beta ''/2)$, $R_{3}\times (\beta ''/2)+R_{4}\times g/(2{\varOmega }_{g}^{2})$ where $R_{j}(j=1, 2, 3, 4)$ is the $j^{th}$ row of the matrix, we obtain,

$$\begin{aligned}&\begin{bmatrix} (a_{1}/4)(\beta ''^{2}+g^{2}/{\varOmega }_{g}^{4})&\quad 0&\quad 0&\quad 0\\ ga_{1}/(2{\varOmega }_{g}^{2})&\quad -\beta ''/2&\quad 0&\quad 0 \\ 0&\quad 0&\quad (a_{2}/4)(\beta ''^{2}+g^{2}/{\varOmega }_{g}^{4})&\quad 0\\ 0&\quad 0&\quad ga_{2}/(2{\varOmega }_{g}^{2})&\quad -\beta ''/2 \end{bmatrix} \begin{bmatrix} M_{1}'\\ y_{1}'\\ M_{2}'\\ y_{2}' \end{bmatrix} \nonumber \\&\quad =\begin{bmatrix} (g/(2{\varOmega }_{g}^{2}))B+(\beta ''/2)A\\ B\\ (\beta /2)C+(g/(2{\varOmega }_{g}^{2}))D\\ D \end{bmatrix}. \end{aligned}$$

(39)

From the matrix equation (39) we write the following four simple equations:

$$\begin{aligned} M_{1}' & = {} \left[ \frac{4{\varOmega }_{g}^{4}}{a_{1}(g^{2}+ \beta ''^{2}{\varOmega }_{g}^{4})}\right] \left[ \frac{g}{2{\varOmega }_{g}^{2}}B+\frac{\beta ''}{2}A\right] , \end{aligned}$$

(40)

$$\begin{aligned} B & = {} \frac{ga_{1}}{2{\varOmega }_{g}^{2}}M_{1}'-\frac{\beta ''}{2}y_{1}', \end{aligned}$$

(41)

$$\begin{aligned} M_{2}' & = {} \left[ \frac{4{\varOmega }_{g}^{4}}{a_{2}(g^{2}+ \beta ^{2}{\varOmega }_{g}^{4})}\right] \left[ \frac{\beta ''}{2}C+ \frac{g}{2{\varOmega }_{g}^{2}}D\right] , \end{aligned}$$

(42)

$$\begin{aligned} D & = {} \frac{ga_{2}}{2{\varOmega }_{g}^{2}}M_{2}'-\frac{\beta ''}{2}y_{2}'. \end{aligned}$$

(43)

Therefore, simplifying Eqs. (40)–(43) we obtain the equations for $y_{1}', M_{1}', y_{2}'$ and $M_{2}'$.