1 Introduction

The dynamics of optical solitons provide cutting edge technology to fiber-optic communication system. There are several models that govern this dynamics for polarization-preserving fibers as well as birefringent fibers. One of the most visible equations is the nonlinear Schrödinger’s equation (NLSE). While this model is very commonly studied in nonlinear optics, there are three models that are a byproduct of this equation. They are referred to as derivative NLSE (DNLSE) and are commonly designated as DNLSE-I, DNLSE-II and DNLSE-III. This paper will be studying DNLSE-II model that is alternatively referred to as Chen–Lee–Liu (CLL) equation. There have been considerable studies with regards to this equation in the past (Triki et al. 2017, 2018a; Biswas et al. 2018a, b; Banaja et al. 2017; Bakodah et al. 2017; Asma et al. 2018). However, the results that have been reported thus far are all outcomes of analytical findings. This paper will address CLL equation using a purely numerical scheme. It is the Laplace Adomian decomposition (LADM) method. This algorithm will retrieve numerical simulations to the model to reveal W-shaped optical soliton solutions to the model. After a quick re-visitation of the model, the numerical scheme will be introduced and finally the results will be exhibited. Recently, very interesting results have been published related to the theory of solitons, see for example Wazwaz (2018), Baonan and Wazwaz (2018).

2 Governing model

We consider the propagation of an optical pulse inside in a monomode fiber modeled by a family of the following Chen–Lee–Liu equation (Chen et al. 1979)

$$iu_{t}+au_{xx}+ib\vert u\vert ^{2}u_{x}=0,$$
(1)

where \(u = u(x, t)\) is the complex wave function, while a and b are constants. In the optical fiber setting, the term involving the parameter b is usually associated with the self-steepening phenomena (Rogers and Chow 2012), while the term related to a is group velocity dispersion. In such contexts, the coordinates t and x denote propagation distance and retarded time, but represent slow time and spatial coordinate traveling with the group velocity in hydrodynamics, respectively (Rogers and Chow 2012). Equation (1) collapses to the case of regular Chen–Lee–Liu equation when \(a=b=1\) (Triki et al. 2018a; Inc et al. 2018).

In optical fiber contexts, the generation of the combined solitary waves in the normal dispersion regime for Chen–Lee–Liu equation was first reported by Li et al. (2000). In Zhang et al. (2015), the rogue wave solutions of the Chen–Lee–Liu equation with higher order terms were reported. The traveling wave approach was utilized to retrieve the chirped singular optical soliton solutions in Triki et al. (2018a). Further more, Triki et al. (2018b) retrieved the dark and gray type soliton solutions by using an ansatz technique. Finally in Triki et al. (2018c), the chirped W-shaped solitary waves of the model were reported.

In this paper we will use ADM combined with the Laplace transform in order to find analytical solutions to the Chen–Lee–Liu equation. In particular, analytical chirped soliton solution that takes the shape of W is obtained for the first time in presence of all physical effects through the ADM combined with the Laplace transform. The combination of ADM with Laplace transform is one of the very latest achievements in the field of Numerical Photonics and this advanced and modern integration architecture surpasses a variety of the known schemes that are visible thus far. This LADM technique first appeared in the year 2001 (Khuri 2001). Since its first appearance, it has gained considerable popularity and has been successfully implemented in a number of nonlinear evolution equations, including applications to mathematical photonics.

2.1 W-shaped soliton solution

The W-shaped soliton solution to (1) is given by Triki et al. (2018c):

$$u(x,t)=\left(\beta \pm \rho {\text {sech}}[\mu (x-\nu t)] \right)^{1/2}e^{i[-\kappa x+\omega t+\theta s]},$$
(2)

where the soliton parameter definitions and the corresponding constraints are defined as

$$\beta =\frac{C_{2}}{4C_{3}}, \quad \rho =\pm \sqrt{\frac{3C_{2}^{2}+8C_{1}C_{3}}{8C_{3}^2}},\quad \mu =\sqrt{\frac{3C_{2}^{2}+8C_{1}C_{3}}{8C_{3}}}.$$
(3)

Here, the constants \(C_1, C_2\) and \(C_3\) are such that

$$C_{1}=\frac{4a\omega +bA-\nu ^{2}-4a\nu \kappa }{a^2}, \quad C_{2}=\frac{b\nu }{a^2},\quad C_{3}=\frac{b^2}{4a^2}.$$
(4)

The constraint conditions that guarantees the existence of W-shaped solitons are Triki et al. (2018c):

$$3C_{2}^{2}+8C_{3}C_{1}>0\;\;\text{ and }\; \; C_{3}>0.$$
(5)

Physically, Eq. (2) describes the evolution of two different type soliton pulses on a cw background for the Chen–Lee–Liu equation (1). In these propagating envelope solutions, parameter \(\beta\) decides the strength of the background, in which these solutions propagate. Here we only consider soliton solution given in Eq. (2) with the sign −. The soliton solution (2) with the sign \(+\) corresponds to a bright pulse solution on a cw background for the Chen–Lee–Liu equation. The study of the case with sign \(+\) through LADM would be analogous to which the minus sign is taken.

It needs to be noted here that although Chen–Lee–Liu equations supports W-shaped solitons, two other forms of solitons are also products of this model. They are bright soliton and dark solitons. The application of LADM scheme to study such solitons are reserved for future endeavors.

3 The Laplace–Adomian decomposition method

The ADM is a semi-analytical method to solve ordinary and partial, linear and nonlinear differential equations. Using this method one can express analytic solutions in terms of a convergent series (Adomian 1994). The LADM was initially proposed by Khuri (2001) for solving differential equations.

A problem in nonlinear science is modeled by the functional equation

$$Fu(x,t)=g(x,t)$$
(6)

with initial condition

$$u(x,0)=f(x)$$
(7)

where F is a differential operator that could, in general, be nonlinear and the function g is a source term.

In general, Eq. (6) can be explicitly rewritten as

$$L_{t}u(x,t)+Ru(x,t)+Nu(x,t)=g(x,t)$$
(8)

where \(L_{t}u=u_{t}\), R is a linear operator that includes partial derivatives with respect to x and N is a nonlinear operator.

Solving for \(L_{t}u(x,t)\) and applying Laplace transform on both sides of the Eq. (8), we get

$${\mathscr {L}}\{L_{t}u(x,t)\}= {\mathscr {L}}\{g(x,t)-Ru(x,t)-Nu(x,t).\}$$
(9)

Using the laplace property for derivative, that is, \({\mathscr {L}}\{u_{t}(x,t)\}=s{\mathscr {L}}\{u(x,t)\}-u(x,0)\), an equivalent expression to (9) is

$$su(x,s)-u(x,0)= {\mathscr {L}}\{g(x,t)-Ru(x,t)-Nu(x,t)\}$$
(10)

In the homogeneous case, because \({\mathscr {L}}\) is a linear operator we have

$$u(x,s)=\frac{f(x)}{s}-\frac{1}{s}{\mathscr {L}}\{Ru(x,t)+Nu(x,t)\}$$
(11)

now, considering the initial condition given in Eq. (7), u(x, t) are obtained easily by applying the inverse Laplace transform \({\mathscr {L}}^{-1}\) on both sides of the Eq. (11)

$$u(x,t)=f(x)-{\mathscr {L}}^{-1}\left[\frac{1}{s}{\mathscr {L}}\{Ru(x,t)+Nu(x,t)\}\right].$$
(12)

The ADM consists of decomposing the unknown function u(x, t) into in a series of functions, given by,

$$u(x,t)= \sum _{n=0}^{\infty }u_{n}(x,t)$$
(13)

The nonlinear operator N is decomposed as

$$Nu(x,t)= \sum _{n=0}^{\infty }A_{n}(u_{0},u_{1},\ldots , u_{n})$$
(14)

where \(\{A_{n}\}_{n=0}^{\infty }\) is the so-called Adomian polynomials sequence established in Wazwaz (2000) that are given by

$$A_{n}(u_{0},\ldots ,u_{n})=\frac{1}{n!}\frac{d^{n}}{d\lambda ^{n}}\left[N\left(\sum _{i=1}^{\infty }\lambda ^{i}u_{i}\right) \right]_{\lambda =0},\quad n=0,1,2,\ldots$$
(15)

Substituting (13) and (14) into Eq. (12) gives rise to

$$\sum _{n=0}^{\infty }u_{n}(x,t)= f(x)-{\mathscr {L}}^{-1}\left[\frac{1}{s}{\mathscr {L}}\{R\sum _{n=0}^{\infty }u_{n}(x,t)+\sum _{n=0}^{\infty }A_{n}(u_{0},u_{1},\ldots , u_{n})\}\right],$$
(16)

From the Eq. (16) the components of the series (13) are determined by using the recurrence relation

$$\left\{ \begin{array}{ll} u_{0}(x,t)=f(x),\\ u_{n+1}(x,t)=-{\mathscr {L}}^{-1}\left[\frac{1}{s}{\mathscr {L}}\{Ru_{n}(x,t)+A_{n} (u_{0},u_{1},\ldots , u_{n})\}\right],\;\; n=0,1,2,\ldots \end{array} \right.$$
(17)

The convergence of this series has been studied for example in Cherruault and Adomian (1993). Finally, using (17) an N-term approximate solution is given by

$$u_{N}(x,t)= \sum _{n=0}^{N-1}u_{n}(x,t),\;\; N\ge 1,$$
(18)

and the exact solution is

$$u(x,t)= \lim \limits _{N\rightarrow \infty }u_{N}(x,t).$$
(19)

Now we will implement the algorithm provided by LADM for the solution of the Chen–Lee–Liu equation.

3.1 Solution of the Chen–Lee–Liu equation for W-shaped solitons through LADM

We now describe how the LADM can be used to construct the solution to the initial-value problem for the Chen–Lee–Liu equation (1),

$$u_{t}(x,t)=iau_{xx}(x,t)-b\vert u(x,t)\vert ^{2}u_{x}(x,t).$$
(20)

Comparing (20) with Eq. (8) we have that \(L_t\) and R can be written as:

$$L_{t}u(x,t)=u_{t}(x,t),\;\; Ru=i a\partial ^{2}_{x}u(x,t).\;\;$$
(21)

Moreover, the nonlinear term is given by

$$Nu=bu(x,t)\bar{u}(x,t)u_{x}(x,t)=\sum _{n=0}^{\infty }A_{n}(u_{0},u_{1},\ldots , u_{n}),$$
(22)

where, the Adomian’s polynomials \(A_{n}\) are calculated by using the formula (15) and which for the present case, turn out to be:

$$\begin{aligned} A_{0}&=u_{0}\bar{u}_{0}u_{0x}, \\ A_{1}&=u_{1}\bar{u}_{0}u_{0x}+u_{0}\bar{u}_{1}u_{0x}+u_{0}\bar{u}_{0}u_{1x}, \\ A_{2}&=u_{2}\bar{u}_{0}u_{0x}+u_{1}\bar{u}_{1}u_{0x}+u_{0}\bar{u}_{2}u_{0x}+u_{1}\bar{u}_{0}u_{1x}+u_{0}\bar{u}_{1}u_{1x}+u_{0}\bar{u}_{0}u_{2x}, \\ A_{3}&=u_{3}\bar{u}_{0}u_{0x}+u_{2}\bar{u}_{1}u_{0x}+u_{1}\bar{u}_{2}u_{0x}+u_{0}\bar{u}_{3}u_{0x}+u_{2}\bar{u}_{0}u_{1x}+u_{1}\bar{u}_{1}u_{1x}+u_{0}\bar{u}_{2}u_{1x}+u_{1}\bar{u}_{0}u_{2x}\\&\quad +u_{0}\bar{u}_{1}u_{2x}+u_{0}\bar{u}_{0}u_{3x},\\ A_{4}&=u_{4}\bar{u}_{0}u_{0x}+u_{3}\bar{u}_{1}u_{0x}+u_{2}\bar{u}_{2}u_{0x}+u_{1}\bar{u}_{3}u_{0x}+u_{0}\bar{u}_{4}u_{0x}+u_{3}\bar{u}_{0}u_{1x} +u_{2}\bar{u}_{1}u_{1x}+u_{1}\bar{u}_{2}u_{1x}\\&\quad +u_{0}\bar{u}_{3}u_{1x}+u_{2}\bar{u}_{0}u_{2x}+u_{1}\bar{u}_{1}u_{2x}+u_{0}\bar{u}_{2}u_{2x}+u_{1}\bar{u}_{0}u_{3x}+u_{0}\bar{u}_{1}u_{3x}+u_{0}\bar{u}_{0}u_{4x},\\&\qquad \qquad \qquad \vdots\end{aligned}$$

Using Eq. (17) through the LADM method, we obtain the next recursive algorithm:

$$\begin{aligned} u_{0}(x,t)&=f(x), \\ u_{1}(x,t)&={\mathscr {L}}^{-1}\left[\frac{ai}{s}{\mathscr {L}}\{u_{0,xx}(x,t)-bA_{0}(u_{0})\}\right],\\ u_{2}(x,t)&={\mathscr {L}}^{-1}\left[\frac{ai}{s}{\mathscr {L}}\{u_{1,xx}(x,t)-bA_{1}(u_{0},u_{1})\}\right], \\ \vdots \\ u_{n}(x,t)&={\mathscr {L}}^{-1}\left[\frac{ai}{s}{\mathscr {L}}\{u_{n-1,xx}(x,t)-bA_{n-1}(u_{0},u_{1},\ldots , u_{n-1})\}\right].\end{aligned}$$

In the next section, we illustrate the LADM for solving the cubic NLSE. All our computations are performed by MATHEMATICA software package.

4 Numerical simulations

In this section, four numerical examples are presented to illustrate the effectiveness of the theoretical result obtained in the above section. We perform numerical simulations for W-shaped solitons for Chen–Lee–Liu equation.

4.1 Application to W-shaped solitons

Table 1 W-shaped solitons
Full size table
Fig. 1
figure 1

W-shaped soliton: Case 1: numerically computed profile (left) and absolute error (right)

Full size image
Fig. 2
figure 2

W-shaped soliton: Case 2: numerically computed profile (left) and absolute error (right)

Full size image
Fig. 3
figure 3

W-shaped soliton: Case 3: numerically computed profile (left) and absolute error (right)

Full size image
Fig. 4
figure 4

W-shaped soliton: Case 4: numerically computed profile (left) and absolute error (right)

Full size image

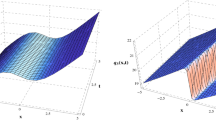
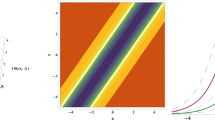
The numerical solutions are compared with the exact solution (2) for the W-shaped solitons of the Chen–Lee–Liu equation in Figs. 1, 2, 3 and 4. It is to be note that ten terms only were used in evaluating the approximate solutions and the maximum error between the exact solution and the simulation results for the for the parameters shown in Table 1 are \(1.2\times 10^{-11}, 1.2\times 10^{-9}, 1.0\times 10^{-10}\) and \(1.5\times 10^{-9}\), respectively. The obtained results show the validity and accuracy of using LADM for solving the Chen–Lee–Liu equation.

5 Conclusions

This paper retrieved W-shape optical solitons to CLL equation by the aid of LADM. The results are displayed along with the error analysis plots. The accuracy of the algorithm is overwhelming. The results of the paper are thus extremely encouraging to investigate further along into the future. Later on, DNLSE-I and DNLSE-III will be addressed using this integration scheme. The search will be for bright and dark solitons. Future studies will also be extended to the cases of vector-coupled CLL equations that are applicable to optical couplers and birefringent fibers. The results of those research findings will be sequentially displayed in several additional publications. All the numerical work was accomplished with the Mathematica software package.