1 Introduction

Nonlinear localized structures or solitons are ubiquitous in nature (Kivshar and Agrawal 2003). Rotating propagation systems provide more interesting dynamics than their straight counterparts, because the centripetal force modifies the effect of potentials present and the interaction with the medium or other beams. Rotating structures in optical photonic lattices are of special interest (Petrović 2006). Rotating soliton states in radial invariable potentials was first presented in Kartashov et al. (2004a, b); controlled soliton rotation in the optically-induced periodic Bessel-like ring lattices was demonstrated experimentally in Wang et al. (2006), Huang et al. (2010). Rotating multipole modes in dynamical Bessel lattices were predicted in Kartashov et al. (2005). Solitons in rotating periodic lattices were considered in Cuevas et al. (2007), Longhi (2007), Jia and Fleischer (2009), Sakaguchi and Malomed (2009). The starting point in understanding these curious optical phenomena is the analogy between paraxial beam propagation in an optical waveguide with a bent axis and the single-electron dynamics in an atomic system (Longhi et al. 2003). This analogy originates from the formal equivalence of the scalar beam propagation equation for the waveguide in the paraxial approximation and the one-electron temporal Schrödinger equation, represented in the Kramers–Henneberger (KH) reference frame (Henneberger 1968).

2 The model

We start from the well-known paraxial wave equation for the beam propagation in a nonlinear photorefractive crystal. The model equation in the steady-state and in the dimensionless three-dimensional (3D) computational region (one x or y coordinate unit corresponds to 8.5 \(\mu\)m and the z unit corresponds to 4 mm) is given by Petrović et al. (2005), Belić et al. (2002):

$$i \frac{\partial \varPsi }{\partial z} + \triangle \varPsi + \varGamma \frac{I+I_w}{1+I+I_w} \varPsi = 0,$$
(1)

where \(\varPsi\) is the beam envelope, \(\triangle\) is the transverse Laplacian, \(\varGamma\) is the coupling constant, \(I=|\varPsi |^2\) is the laser light intensity measured in units of the background intensity, and \(I_w\) is the intensity of the optically-induced spiraling waveguide. We assume that the refractive index change of the waveguide channel has a Gaussian shape.

We transform the coordinates into a reference frame where the waveguide is straight:

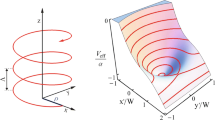
$$x'=x-R\cos (\varOmega z), \quad y'=y-R\sin (\varOmega z), \quad z'=z,$$
(2)

where R is the helix radius, \(\varOmega\) is the spatial frequency and \(\varLambda =2\pi /\varOmega\) is the period of rotation. A single spiral waveguide is sketched in Fig. 1. In the transformed reference frame \((x',y')\), the light evolution is described by:

$${i \frac{\partial \varPsi }{\partial z} = \left( i \overrightarrow{\nabla }' + \frac{1}{2} \overrightarrow{A}(z') \right) ^2 \varPsi - \frac{1}{4} R^2 \varOmega ^2 \varPsi + V \varPsi } ,$$
(3)

where \(\varPsi =\varPsi (x',y',z')\) is the transformed envelope, \(\overrightarrow{\nabla }' = \frac{\partial }{\partial x'} \overrightarrow{e_{x'}} + \frac{\partial }{\partial y'} \overrightarrow{e_{y'}}\) the transformed gradient, \(\overrightarrow{A}(z') = R \varOmega [- \sin (\varOmega z') \overrightarrow{e_{x'}} + \cos (\varOmega z') \overrightarrow{e_{y'}} ]\) the vector potential, and \(V = -\varGamma (I+I_w)/({1+I+I_w})\) the scalar potential.

Fig. 1
figure 1

Sketch of the single spiral waveguide

Full size image

3 The eigenvalue procedure

There are no known exact analytical solitonic solutions for our system. Owing to the symmetry and dynamics of the problem, we are searching for the self-localized wave packet continuously rotating and recreating its shape periodically (in every cycle of the rotation), following the waveguide. The numerical solutions can be found from Eq. (3), using the modified Petviashvili’s iteration method Petviashvili (1976), Yang et al. (2004), Aleksić et al. (2012). Our system allows the existence of a fundamental soliton solution in the form:

$${\varPsi (x',y',z')=a(x',y',z') e^{i\mu z'}}$$
(4)

where \(\mu\) is the propagation constant and \(a(x',y',z')\) is a z-periodic complex function of period \(\varLambda\). Physical requirements for obtaining a rotationally-invariant solution lead to the following mathematical condition:

$${\frac{\partial a}{\partial z'} = \varOmega y' \frac{\partial a}{\partial x'} - \varOmega x' \frac{\partial a}{\partial y'} }.$$
(5)

After substituting Eqs. (4) and (5) into Eq. (3), one obtains the soliton equation in a reference frame where the waveguide is straight:

$$i \varOmega \left[ \left( R\sin (\varOmega z')+y'\right) \frac{\partial }{\partial x'}+\left( -R\cos (\varOmega z')-x'\right) \frac{\partial }{\partial y'} \right] a - \mu a + \triangle ' a - \varGamma V a = 0$$
(6)

We separate linear and nonlinear terms on different sides of the equation for the complex-valued amplitude function \(a(x',y')\) (Petrović et al. 2017). We first perform Fourier transformation of that equation, and then apply the modified Petviashvili’s iteration method. In this manner, starting from a calculated initial soliton profile at \(z'=0\), we find stable self-consistent fundamental soliton solutions. The details of the eigenvalue procedure and the iteration method are given in Petrović et al. (2017). In the regime of high spatial frequencies of the waveguide rotation—of interest here—the Petviashvili’s iteration method gives only solutions of low accuracy (relative error is between 0.01 and 0.001), that is, the solutions that do not follow the waveguide closely.

Fig. 2
figure 2

Fundamental soliton intensity profile for \(\mu = 25 L_D^{-1}\). Parameters: \(\varOmega =-2\) rad\(/L_D\), \(P_{w}=10.05\) (\(I_{w0}=5\), \(W_w=0.8\)), \(R=0.5\), \(\varGamma =30\)

Full size image

The fundamental soliton solution for \(\mu = 25 L_D^{-1}\) at \(z=0\) is presented in Fig. 2. One can see that the optical field intensity \(|a(x,y)|^2\) is almost perfectly radially-symmetric. The main quantity characterizing the spatial soliton is its power \(P = \int \int I dx dy = \int \int |a(x,y)|^2 dx dy\). The imprinted spiral waveguide can also be characterized by its power. Since it carries its own intensity, which we take to be Gaussian, \(I_w(x',y') = I_{w0} \exp [-(x'^2+y'^2)/W_w^2]\), one obtains \(P_w = \int \int I_w(x',y') dx' dy' = \pi I_{w0} W_w^2\). In Fig. 3 we present a family of fundamental solitonic solutions with different propagation constants and beam powers. The solutions are located close to the waveguide center (the helix radius is \(R=0.5\)) and exactly at the potential barrier minimum, as expected. Because of the saturation nature of the photorefractive nonlinearity, for large intensities the potential V tends to \(-\varGamma\) (\(\varGamma =30\) here).

Fig. 3
figure 3

Fundamental soliton intensity profiles (left) and the corresponding potential profiles (right) at \(\hbox {y} = 0\). The parameters are as in Fig. 2. (Colour figure online)

Full size image

The soliton power, width, and peak intensity as functions of the propagation constant are shown in Fig. 4. We marked the unstable solutions in Fig. 4 in red: below the lower power threshold they start to radiate, and above the upper power threshold they escape from the potential well. One can notice from Fig. 4 that the obtained solitonic solution is stable, according to the Vakhitov–Kolokolov stability criterion (Vakhitov and Kolokolov 1973), which posits that the solitary wave should be stable as long as \(dP/d\mu >0\).

Fig. 4
figure 4

Fundamental soliton power, width, and peak intensity as functions of the propagation constant. The black dots represent the stable rotary solitonic solutions, the red dots the unstable solutions. The parameters are as in Fig. 3. (Colour figure online)

Full size image

4 Results

Numerical procedure applied to the propagation equation is the split-step beam propagation method based on the fast Fourier transform. We apply the fourth-order symplectic algorithm. We launch a soliton (from the point \(y=0\)) with an initial angular momentum in the form of an input phase tilt in the y direction, which introduces beam velocity tangential to the spiral waveguide; the helix radius is constant here, in difference to Longhi (2005). The beam can be set into a steady spiraling motion with a period dictated by the period of the helical waveguide. To check the iterative procedure for finding such solitons with low accuracy, we propagate this input solution in the stationary frame of reference.

The peak intensity as a function of the propagation distance for several different values of the propagation constant is shown in Fig. 5. At the lower power threshold, the solitons radiate energy in the beginning. In the central part of the existence domain, the fundamental solutions perform persistent quasi-stable rotary motion (three such cases, \(\mu = 15 L_D^{-1}\), \(\mu = 20 L_D^{-1}\), and \(\mu = 26 L_D^{-1}\), are shown in Fig. 5). Above the upper power threshold, the solitons escape from the waveguide. We present one case of a higher value of the propagation constant, \(\mu = 35 L_D^{-1}\), where one can observe an unstable soliton propagation supported by the spiraling waveguide.

Fig. 5
figure 5

Peak intensity as a function of the propagation distance (\(z = 8 \varLambda\) left, \(z = 96 \varLambda\) right) for four different values of the propagation constant. Parameters are as in Fig. 3

Full size image

Characteristic oscillatory trajectories of the quasi-stable rotating soliton supported by the spiral waveguide are presented in Fig. 6, for three different propagation constants. One can notice that for \(\mu = 15 L_D^{-1}\), the quasi-soliton oscillates around the waveguide during propagation fairly regularly. However, for the propagation constants significantly higher than \(\mu = 15 L_D^{-1}\), solitons escape from the waveguide fast, with significant decay through radiation. We present one case with such high value of the propagation constant, \(\mu = 35 L_D^{-1}\), where the unstable trajectory escapes the waveguide rapidly. Overall, one can observe interesting quasi-stable and unstable cases of soliton propagation supported by the spiral waveguide. We thus demonstrate a novel interesting type of soliton dynamics.

Fig. 6
figure 6

Typical trajectory of a rotating soliton (red line) supported by the spiral waveguide (black line): 3D view (the first row), 2D view (the second row). Propagation distances are given in the pictures, \(\varLambda = 3.14 L_D\). The first, second and third columns are for \(\mu = 15 L_D^{-1}\), \(\mu = 25 L_D^{-1}\) and \(\mu = 35 L_D^{-1}\) , respectively. Parameters are as in Fig. 3. (Colour figure online)

Full size image

In Fig. 7, we present the power output of quasi-solitons as a function of the propagation distance, for several values of the propagation constant and three values of the spatial frequency. One can notice that for each frequency there exists the value of the propagation constant where the decay of power is minimal. The radiation or decay, over many rotation periods and diffraction lengths, increases with the increase in frequency.

Fig. 7
figure 7

Power output as a function of the propagation distance for the three values of the spatial frequency and several different values of the propagation constant. a \(\varOmega =-\,1\) rad\(/L_D\), b \(\varOmega =-\,2\) rad\(/L_D\), c \(\varOmega =-\,3\) rad\(/L_D\). Parameters are as in Fig. 3. (Colour figure online)

Full size image

Potential experimental verification of this effect for the photorefractive type of nonlinearity is open question at the moment. In spite of the great advance in our knowledge of the femtosecond-laser micromachining for direct three-dimensional fabrication of transparent optical materials in recent years (Chen and de Aldana 2014), unsatisfactory progress has been made in the field of research which deals with the photorefractive direct laser writing of arbitrary optical waveguiding structures (Kroesen et al. 2014; Vittadello et al. 2016). But, in the regime where quasi-stable rotating solitons supported by a single spiraling waveguide exist, parameter \(I_{w0}\) which characterize intensity of the imprinted spiral waveguide is large (\(I_{w0}\)=5 for the cases presented here), then scalar potential \(V \rightarrow -\varGamma\), and Eq. (1) transforms to:

$$i \frac{\partial \varPsi }{\partial z} + \triangle \varPsi + \varGamma \varPsi \approx 0.$$
(7)

This equation is analogous to the linear Schrödinger-type equation for paraxial propagation of light in fused silica and other glasses (Rechtsman et al. 2013), where fabrication of various waveguiding structures is easily feasible by using the laser writing technique. All this means that experimental realization of these spiraling solitons is possible in some glasses, if parameters in Eq. (7) are appropriately chosen for the specific glass; the rescaling of parameters from the (photorefractive) propagation Eq. (1) is straightforward. The region in the parameter space, where such solitonic solutions may exist, is large.

5 Conclusions

In this paper, we have studied numerically nonlinear light propagation in a helically twisted optical waveguide formed in a photorefractive medium, for the high spatial frequency. The general procedure for finding exact fundamental solitonic solutions in the spiraling guiding structures is based on the modified Petviashvili’s iteration method. We showed that there exist only the solitons of low accuracy—that is, the solutions that do not follow the waveguide too closely. A region in the parameter space is determined, in which quasi-stable rotating solitons exist. Below the lower power threshold, the rotating solitons supported by the spiral waveguide start to radiate, and above the upper threshold, they escape from the waveguide. Their stability was tested by a direct numerical simulation of propagation. Spiraling spatial solitons supported by the 3D helical waveguide structure perform quasi-stable rotational-oscillatory motion, over many rotation periods and diffraction lengths. We demonstrated that there exists the beam power with the minimal wave radiation. Also, we presented the influence of the spatial frequency of waveguide rotation on the stability of solitons. As the frequency which corresponds to the quasi-stable rotary motion increases, the radiation and decay od the soliton accelerates.