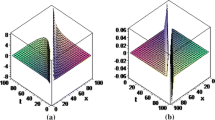
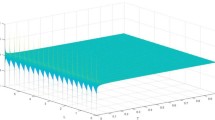
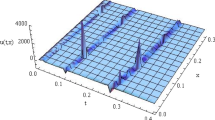
Abstract
In this paper, the first integral method and the functional variable method are used to establish exact traveling wave solutions of the space–time fractional Schrödinger–Hirota equation and the space–time fractional modified KDV–Zakharov–Kuznetsov equation in the sense of conformable fractional derivative. The results obtained confirm that proposed methods are efficient techniques for analytic treatment of a wide variety of the space–time fractional partial differential equations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During recent years, fractional differential equations have gained much attention attracted due to their numerous applications in areas of control theory, biology, engineering and other areas. There are several definitions of fractional integrals and derivatives in the literature, but the most popular definitions are the Riemann–Liouville and Caputo senses (Podlubny 1999; Ross 1975). Recently, Khalil et al. (2014) introduced a new simple well-behaved definition of the fractional derivative called conformable fractional derivative. This new fractional derivative definition has governed much attention in recent months. For instance Abdeljawad (2015) provide fractional versions of the chain rule, exponential functions, Gronwall’s inequality, integration by parts, Chung (2015) used the conformable fractional derivative and integral to discuss fractional Newtonian mechanics and Rezazadeh et al. (2016) investigated stability of linear conformable fractional systems from the point of view of control.
Eslami and Rezazadeh (2016) firstly studied exact solution of conformable fractional partial differential equations. They applied the conformable fractional derivative with properties and first integral method to obtain exact solutions of the conformable fractional Wu–Zhang system. Other researchers used this idea, and many powerful and efficient methods have been proposed to obtain exact solutions of conformable fractional differential equations so far. For example, these methods include the Riccati sub equation method (Eslami 2016; Aminikhah et al. 2016; Rezazadeh and Ziabarya 2016), the Modified Kudryashov method (Rezazadeh et al. 2017; Hosseini et al. 2016, 2017), the \({{G^{\prime}} \mathord{\left/ {\vphantom {{G^{\prime}} G}} \right. \kern-0pt} G}\)-expansion method (Eslami et al. 2012; Neamaty et al. 2016), and so on (Kurt et al. 2015; Çenesiz et al. 2017; Hosseini et al. 2017).
The aim of this paper is to find exact solutions of the space–time fractional Schrödinger–Hirota equation and the space–time fractional modified KDV–Zakharov–Kuznetsov (KDV–ZK) equation by using the first integral method and the functional variable method.
2 Conformable fractional derivative
Conformable fractional derivative of order \(\alpha\) is defined by the following definition.
Definition 1
Suppose \(f:(0,\infty ) \to {\mathbb{R}}\), be a function. Then, the conformable fractional derivative of \(f\) of order \(\alpha\) is defined as
for all \(t > 0,\alpha \in (0,1)\). The geometric and physical interpretation of the fractional derivatives was given in Zhao (2017).
Definition 2
(Fractional Integral) Let \(a \ge 0\) and \(t \ge a\). Also, let \(f\) be a function defined on \((a,t]\) and \(\alpha \in {\mathbb{R}}\). Then, the \(\alpha\)-fractional integral of \(f\) is defined by,
if the Riemann improper integral exists.
The new definition satisfies the properties which given in the following theorem.
Theorem 3
Let \(\alpha \in (0,1]\) , and \(f\) and \(g\) be \(\alpha\) -differentiable at a point \(t\) , then (Khalil et al. 2014)
-
(i)
\({\kern 1pt} T_{\alpha } (af + bg) = a{\kern 1pt} {\kern 1pt} T_{\alpha } (f) + b{\kern 1pt} {\kern 1pt} T_{\alpha } (g)\), \(\forall \;a,b \in {\mathbb{R}}\).
-
(ii)
\(T_{\alpha } (t^{\mu } ) = \mu t^{\mu - \alpha }\), \(\forall \;\mu \in {\mathbb{R}}\).
-
(iii)
\({}_{t}{\kern 1pt} T_{\alpha } (fg) = fT_{\alpha } (g) + g{\kern 1pt} T_{\alpha } (f)\).
-
(iv)
\(T_{\alpha } \left( {\frac{f}{g}} \right) = \frac{{g\,{\kern 1pt} T_{\alpha } (f) - f\,{\kern 1pt} T_{\alpha } (g)}}{{g^{2} }}\).
Furthermore, if \(f\) is differentiable, then \({\kern 1pt} T_{\alpha } (f)(t) = t^{1 - \alpha } \frac{df}{dt}\).
Abdeljawad (2015) established the chain rule for conformable fractional derivatives as following theorem.
Theorem 4
Suppose \(f:(0,\infty ) \to {\mathbb{R}}\) be a function such that \(f\) is differentiable and also \(\alpha\) -differentiable. Let \(g\) be a function defined in the range of \(f\) and also differentiable; then, one has the following rule
Now, we list here the fractional derivatives of certain functions (Khalil et al. 2014)
-
(i)
\({\kern 1pt} T_{\alpha } \left( {e^{{\frac{1}{\alpha }t^{\alpha } }} } \right) = e^{{\frac{1}{\alpha }t^{\alpha } }}\).
-
(ii)
\({\kern 1pt} T_{\alpha } \left( {\sin \frac{1}{\alpha }t^{\alpha } } \right) = \cos \frac{1}{\alpha }t^{\alpha }\).
-
(iii)
\({\kern 1pt} T_{\alpha } \left( {\cos \frac{1}{\alpha }t^{\alpha } } \right) = - \sin \frac{1}{\alpha }t^{\alpha }\).
-
(iv)
\({\kern 1pt} T_{\alpha } \left( {\frac{1}{\alpha }t^{\alpha } } \right) = 1\).
On letting \(\alpha = 1\) in these derivatives, we get the corresponding ordinary derivatives.
Remark 5
We write \(\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}(f)\) for \(T_{\alpha } (f)\), to denote the conformable fractional derivatives of \(f\) with respect to the variable \(t\) of order \(\alpha\).
3 Methods
In this section we describe the first step of the first integral method and the functional variable method for finding exact solutions of conformable fractional partial differential equations.
Suppose that a space–time conformable fractional partial differential equations, say, in three independent variables \(x,\,\,y\), and \(t\) is given by
where \(u(x,y,t)\) is an unknown function, \(F\) is a polynomial in \(u\) and its various partial derivatives, in which the highest order derivatives and nonlinear terms are involved.
Using a wave transformation
where \(l\) is constant to be determined later. This enables us to use the following changes:
Using Eq. (5) to transfer the nonlinear conformable fractional partial differential equation Eq. (4) to nonlinear ordinary differential equation
where the prime denotes the derivation with respect to \(\xi\).
In two next subsection, we express the main step for finding the exact solutions of Eq. (6) by using the first integral method and the functional variable method.
Remark 6
Where generalized hyperbolic and triangular functions are defined as (Ren and Zhang 2006; Liu and Jiang 2002)
The generalized hyperbolic sine function is
generalized hyperbolic cosine function is
generalized hyperbolic tangent function is
generalized hyperbolic cotangent function is
generalized hyperbolic secant function is
generalized hyperbolic cosecant function is
where \(\xi\) is an independent variable, \(p\) and \(q\) are arbitrary constants greater than zero and called deformation parameters. The above six kinds of functions are said generalized hyperbolic functions.
The generalized triangular sine function is
generalized triangular cosine function is
generalized triangular tangent function is
generalized triangular cotangent function is
generalized triangular secant function is
generalized triangular cosecant function is
where \(\xi\) is an independent variable, \(p\) and \(q\) are arbitrary constants greater than zero and called deformation parameters. The above six kinds of functions are said generalized triangular functions.
3.1 The first integral method
The first integral method was first proposed by Feng (2002) in solving Burgers–KdV equation which is based on the ring theory of commutative algebra. Recently, this useful method is widely used by many such as in (Aminikhah et al. 2015; Eslami et al. 2014; Hosseini et al. 2012; Hosseini and Gholamin 2015) and by the reference therein.
Now, we introduced a new independent variables
Equation (6) can be reduced to a two-dimensional autonomous system of the form
By the qualitative theory of ordinary differential equations (Ding and Li 1996), if we can find the integrals to Eq. (8) under the same conditions, then the general solutions to Eq. (8) can be solved directly. However, in general, it is really difficult for us to realize this even for one first integral, because for a given plane autonomous system, there is no systematic theory that can tell us how to find its first integrals, nor is there a logical way for telling us what these first integrals are. We will apply the Division Theorem to obtain one first integral to Eq. (8) which reduces Eq. (6) to a first order integrable ordinary differential equation. An exact solution to Eq. (4) is then obtained by solving this equation. Now, let us recall the Division Theorem:
Theorem 7
(Division theorem) Suppose that \(P(x,y)\) and \(Q(x,y)\) be polynomials of two variables \(x\) and \(y\) in \({\mathbb{C}}[x,y]\) , and let \(P(x,y)\) be irreducible in \(C[x,y]\) . If \(Q(x,y)\) vanishes at all zero points of \(P(x,y)\) , then there exists a polynomial \(G(x,y)\) in \(C[x,y]\) such that \(Q(x,y) = P(x,y)G(x,y)\).
Remark 8
The first integral method definitely can be applied to equations which can be converted to a first order ordinary differential equation through the Division Theorem.
Remark 9
Following Riccati equation
admits following exact solutions:
Type I When \(\Delta = a_{1}^{2} - 4a_{0} a_{2} > 0\), the solutions of Eq. (9) are
Type II When \(\Delta = a_{1}^{2} - 4a_{0} a_{2} < 0\), the solutions of Eq. (9) are
Type III When \(\Delta = a_{1}^{2} - 4a_{0} a_{2} = 0\), the solution of Eq. (9) is
3.2 The functional variable method
Zerarka and Ouamane (2010) introduced the so-called functional variable method to find the exact solutions for a wide class of linear and nonlinear wave equations. This method was further developed by many authors (Aminikhah et al. 2014, 2015; Nazarzadeh et al. 2013; Ayati et al. 2017). The advantage of this method is that one treats nonlinear problems by essentially linear methods, based on which it is easy to construct in full the exact solutions such as soliton-like waves, compacton solutions and non-compacton solutions, trigonometric function solutions, pattern soliton solutions, black solitons or kink solutions, and so on.
If all terms contain derivatives, then Eq. (6) is integrated where integration constants are considered zeros. Then we make a transformation in which the unknown function \(U\) is considered as a functional variable in the form
and some successive derivatives of \(U\) are
where “′” stands for \(\frac{d}{dU}\).
The ordinary differential Eq. (6) can be reduced in terms of \(U,\;F\) and its derivative upon using the expressions of Eq. (16) into Eq. (6) gives
The key idea of this particular form Eq. (17) is of special interest because it admits analytical solutions for a large class of nonlinear wave type equations. After integration, Eq. (17) provides the expression of \(F\) and this, together with Eq. (15), give appropriate solutions to the original problem.
Remark 10
The functional variable method definitely can be applied to nonlinear partial differential equations which can be converted to a second-order ordinary differential equation through the travelling wave transformation.
Remark 11
Consider the following second-order ordinary differential equation
where \(k_{1}\) and \(k_{2}\) are constants and \(U\) is a functional variable in the form (15). Then using (16) transformation, the exact solutions of the Eq. (18) are obtained as
Type I When \(k_{1} > 0\), the solutions of Eq. (18) are
Type II When \(k_{1} < 0\), the solutions of Eq. (18) are
4 Applications
4.1 Exact solutions to the conformable fractional Schrödinger–Hirota equation
Let us consider the nonlinear conformable fractional Schrödinger–Hirota equation which governs the propagation of optical solitons in a dispersive optical fiber (for \(\alpha = 1\), see (Biswas 2003))
Since \(u = u(x,t)\) in Eq. (23) is a complex function we suppose that
where \(\beta\) and \(\omega\) are constants.
On substituting these into Eq. (23) yields
Substituting Eqs. (25)–(27) into Eq. (23), we obtain that \(\omega = - \frac{1}{3\lambda }\) and \(U(\xi )\) satisfy the ordinary differential equation:
where the prime denotes the derivation with respect to \(\xi\). Rewrite the Eq. (28) into following form
or
where \(k_{1} = \frac{2}{3},\,\,k_{2} = \frac{2}{3}\left( {\frac{5}{{54\lambda^{2} }} + \beta } \right)\).
4.1.1 The first integral method
Now, using (7), (8) and Eq. (30) is equivalent to the two-dimensional autonomous system
According to the first integral method, we suppose that \(X(\xi ) = X\) and \(Y(\xi ) = Y\) are nontrivial solutions of (31) and \(q(X,Y) = \sum\nolimits_{i = 0}^{m} {a_{i} (X)Y^{i} }\) is an irreducible polynomial in the complex domain \(C[X,Y]\) such that
where \(a_{i} (X)\), \((i = 0,1, \ldots ,m)\) are polynomials of \(X\) and \(a_{m} (X) \ne 0\). Equation (32) is called the first integral to (31), due to the Division Theorem, there exists a polynomial \(g(X) + h(X)Y\) in the complex domain \(C[X,Y]\) such that
For this equation, we assume that \(m = 1\) in (32).
Supposing \(m = 1\), by comparing the coefficients of \(Y^{i} (i = 0,1,2)\) on both sides of Eq. (33), we have
Since \(a_{i} (X)(i = 0,1)\) are polynomials, then from (34) we deduce that \(a_{1} (X)\) is constant and \(h(X) = 0\). For simplicity, take \(a_{1} (X) = 1\). Balancing the degrees of \(g(X)\) and \(a_{0} (X)\), we conclude that \(\deg (g(X)) = 1\) only. Suppose that \(g(X) = A_{1} X + B_{0}\) and \(A_{1} \ne 0\), then we find \(a_{0} (X)\)
where \(A_{0}\) is arbitrary integration constant.
Substituting \(a_{0} (X)\), \(a_{1} (X)\) and \(g(X)\), \(h(X)\) in Eq. (36) and setting all the coefficients of powers \(X\) to be zero, then we obtain a system of nonlinear algebraic equations and by solving it, we obtain
and
Using the conditions (37) and (38) in Eq. (32), we obtain
Combining (39) with (31) and Remark 8, we obtain the exact solution to Eq. (30) and then the exact solution to conformable fractional Schrödinger–Hirota equation can be written as:
Type 1 When \(k_{2} > 0\), the solutions of Eq. (23) are
and
where \(\xi_{0}\) is an arbitrary constant.
Type 2 When \(k_{2} < 0\), the solutions of Eq. (23) are
and
where \(\xi_{0}\) is an arbitrary constant.
Notice that the solutions found under \(m = 2\) are the same solutions to \(m = 1\).
4.1.2 The functional variable method
Using (15), (30) and Remark 10 we have the following traveling wave solutions of the conformable fractional Schrödinger–Hirota equation which contain traveling wave solutions as follows.
So we can obtain following solution for \(k_{2} > 0\) as
and for \(k_{2} < 0,\)
where \(\xi_{0}\) is an arbitrary constant.
Remark 12
Comparing our results with earlier results (Akbari 2014; Jawad et al. 2014), when we put \(\alpha = 1\) in (40)–(47), it can be seen that the current results are new.
4.2 Exact solutions to the conformable fractional modified KDV–ZK equation
We consider the nonlinear conformable fractional modified KDV–ZK equation (for \(\alpha = 1\), see (Khan and Akbar 2013))
where \(d\) is a nonzero constant. Let
where \(l\) is constants and \(U(\xi )\) is real function.
Substituting (49) into (48), we obtain ordinary differential equation
where the prime denotes the derivation with respect to \(\xi\).
Integrating Eq. (50) once respect to \(\xi\), then we have
or
4.2.1 The first integral method
And using (7) and (8), Eq. (52) is equivalent to the two-dimensional autonomous system
According to the first integral method, we suppose that \(X(\xi ) = X\) and \(Y(\xi ) = Y\) are nontrivial solutions of (53) and \(q(X,Y) = \sum\nolimits_{i = 0}^{m} {a_{i} (X)Y^{i} }\) is an irreducible polynomial in the complex domain \(C[X,Y]\) such that
where \(a_{i} (X)\), \((i = 0,1, \ldots ,m)\) are polynomials of \(X\) and \(a_{m} (X) \ne 0\). Equation (54) is called the first integral to (53), due to the Division Theorem, there exists a polynomial \(g(X) + h(X)Y\) in the complex domain \(C[X,Y]\) such that
For this equation, For this equation, we assume that \(m = 1\) in (54).
Supposing \(m = 1,\) by comparing the coefficients of \(Y^{i} (i = 0,1,2)\) on both sides of Eq. (55), we have
Since \(a_{i} (X)(i = 0,1)\) are polynomials, then from (56) we deduce that \(a_{1} (X)\) is constant and \(h(X) = 0.\) For simplicity, take \(a{\kern 1pt}_{1} (X) = 1\). Balancing the degrees of \(g(X)\) and \(a_{0} (X)\), we conclude that \(\deg (g(X)) = 1\) only. Suppose that \(g(X) = A{\kern 1pt}_{1} X + B_{0}\) and \(A{\kern 1pt}_{1} \ne 0\), then we find \(a_{0} (X)\)
where \(A_{0}\) is arbitrary integration constant.
Substituting \(a_{0} (X)\), \(a{\kern 1pt}_{1} (X)\) and \(g(X)\), \(h(X)\), in Eq. (58) and setting all the coefficients of powers \(X\) to be zero, then we obtain a system of nonlinear algebraic equations and by solving it, we obtain
and
Using the conditions (59) and (60) in Eq. (54), we obtain
Combining (61) with (53) and Remark 8, we obtain the exact solution to Eq. (52) and then the exact solution to conformable fractional modified KDV–ZK equation can be written as:
Type 1 When \(l > 0\), the solutions of Eq. (48) are
and
where \(\xi_{0}\) is an arbitrary constant.
Type 2 When \(l < 0\), the solutions of Eq. (48) are
and
where \(\xi_{0}\) is an arbitrary constant.
Notice that the solutions found under \(m = 2\) are the same solutions to \(m = 1\).
4.2.2 The functional variable method
Using (15), (52) and Remark 10 we have the following traveling wave solutions of the conformable fractional modified KDV–ZK equation which contain traveling wave solutions as follows.
So we can obtain following hyperbolic solution for \(l > 0\) as
and for \(l < 0,\)
where \(\xi_{0}\) is an arbitrary constant.
Remark 13
Comparing our results with earlier results (Khan and Akbar 2013; Islam et al. 2014), when we put \(\alpha = 1\) in (62)–(69), it can be seen that the current results are new.
5 Conclusion
This paper studied the space–time fractional Schrödinger–Hirota equation and the space–time fractional modified KDV–ZK equation with conformable fractional derivative. Two integration techniques applied for finding the exact solutions to the equations, namely, the first integral method and the functional variable method. The performance of these methods is reliable and effective and gives more solutions. These methods have more advantages: they are direct and concise. Thus, we deduce that the proposed methods can be extended to solve many nonlinear conformable fractional partial differential equations which are arising in the theory of solitons and other areas. All exact solutions were put back into the corresponding systems, by means of Maple software, and their satisfactions confirm the validity of the solutions obtained in this paper.
References
Abdeljawad, T.: On conformable fractional calculus. J. Comput. Appl. Math. 279, 57–66 (2015)
Akbari, M.: The modified simplest equation method for finding the exact solutions of nonlinear PDEs in mathematical physics. Quantum Phys. Lett. 3(3), 33–36 (2014)
Aminikhah, H., Refahi Sheikhani, A., Rezazadeh, H.: Exact solutions of some nonlinear systems of partial differential equations by using the functional variable method. Mathematica 56, 103–116 (2014)
Aminikhah, H., Sheikhani, A.R., Rezazadeh, H.: Exact solutions for the fractional differential equations by using the first integral method. Nonlinear Eng. 4, 15–22 (2015a)
Aminikhah, H., Porreza, B., Rezazadeh, H.: The functional variable method for solving some equationswith power law nonlinearity. Nonlinear Eng. Model. Appl. 4, 181–188 (2015b)
Aminikhah, H., Refahi Sheikhani, A., Rezazadeh, H.: Sub-equation method for the fractional regularized long-wave equations with conformable fractional derivatives. Sci. Iran. B 23, 1048–1054 (2016)
Ayati, Z., Hosseini, K., Mirzazadeh, M.: Application of Kudryashov and functional variable methods to the strain wave equation in microstructured solids. Nonlinear Eng. 6, 25–29 (2017)
Biswas, A.: Optical solitons: Quasi-stationarity versus Lie transform. Opt. Quantum Electron. 35, 979–998 (2003)
Çenesiz, Y., Baleanu, D., Kurt, A., Tasbozan, O.: New exact solutions of Burgers’ type equations with conformable derivative. Waves Random Complex Media 27, 103–116 (2017)
Chung, W.S.: Fractional Newton mechanics with conformable fractional derivative. J. Comput. Appl. Math. 290, 150–158 (2015)
Ding, T.R., Li, C.Z.: Ordinary Differential Equations. Peking University Press, Peking (1996)
Eslami, M.: Exact traveling wave solutions to the fractional coupled nonlinear Schrodinger equations. Appl. Math. Comput. 285, 141–148 (2016)
Eslami, M., Rezazadeh, H.: The first integral method for Wu–Zhang system with conformable time-fractional derivative. Calcolo 53, 475–485 (2016)
Eslami, M ., Neyrame, A., Ebrahimi, M.: Explicit solutions of nonlinear (2+ 1)-dimensional dispersive long wave equation. J. King Saud Univ.-Sci. 24(1), 69–71 (2012)
Eslami, M., Vajargah, B.F., Mirzazadeh, M., Biswas, A.: Application of first integral method to fractional partial differential equations. Indian J. Phys. 88, 177–184 (2014)
Feng, Z.: On explicit exact solutions to the compound Burgers–KdV equation. Phys. Lett. A 293, 57–66 (2002)
Hosseini, K., Gholamin, P.: Feng’s first integral method for analytic treatment of two higher dimensional nonlinear partial differential equations. Diff. Equ. Dyn. Syst. 23(3), 317–325 (2015)
Hosseini, K., Ansari, R., Gholamin, P.: Exact solutions of some nonlinear systems of partial differential equations by using the first integral method. J. Math. Anal. Appl. 387, 807–814 (2012)
Hosseini, K., Mayeli, P., Ansari, R.: Modified Kudryashov method for solving the conformable time-fractional Klein–Gordon equations with quadratic and cubic nonlinearities. Opt. Int. J. Light Electron Opt. 130, 737–742 (2016)
Hosseini, K., Bekir, A., Ansari, R.: New exact solutions of the conformable time-fractional Cahn–Allen and Cahn–Hilliard equations using the modified Kudryashov method. Opt. Int. J. Light Electron Opt. 132, 203–209 (2017a)
Hosseini, K., Bekir, A., Ansari, R.: Exact solutions of nonlinear conformable time-fractional Boussinesq equations using the exp (−φ(ɛ))-expansion method. Opt. Quantum Electron. 49, 131 (2017b). doi:10.1007/s11082-017-1105-5
Islam, M.H., Khan, K., Akbar, M.A., Salam, M.A.: Exact traveling wave solutions of modified KdV–Zakharov–Kuznetsov equation and viscous Burgers equation. SpringerPlus 3, 105 (2014)
Jawad, A.M., Kumar, S., Biswas, A.: Solition solutions of a few nonlinear wave equations in engineering sciences. Sci. Iran. Trans. D Comput. Sci. Eng. Electr. 21, 861–869 (2014)
Khalil, R., Al Horani, M., Yousef, A., Sababheh, M.: A new definition of fractional derivative. J. Comput. Appl. Math. 264, 65–70 (2014)
Khan, K., Akbar, M.A.: Exact and solitary wave solutions for the Tzitzeica–Dodd–Bullough and the modified KdV–Zakharov–Kuznetsov equations using the modified simple equation method. Ain Shams Eng. J. 4, 903–909 (2013)
Kurt, A., Çenesiz, Y., Tasbozan, O.: On the solution of Burgers’ equation with the new fractional derivative. Open. Phys. 13, 355–360 (2015)
Liu, X.Q., Jiang, S.: The sec q-tanh q-method and its applications. Phys. Lett. A 298(4), 253–258 (2002)
Nazarzadeh, A., Eslami, M., Mirzazadeh, M.: Exact solutions of some nonlinear partial differential, equations using functional variable method. Pramana 81, 225–236 (2013)
Neamaty, A., Agheli, B., Darzi, R.: Exact travelling wave Solutions for some nonlinear time fractional fifth-order Caudrey–Dodd–Gibbon equation by G′/G-expansion method. SeMA J. 73, 121–129 (2016)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Ren, Y., Zhang, H.: New generalized hyperbolic functions and auto-Bäcklund transformation to find new exact solutions of the (2 + 1)-dimensional NNV equation. Phys. Lett. A 357, 438–448 (2006)
Rezazadeh, H., Ziabarya, B.P.: Sub-equation method for the conformable fractional generalized Kuramoto–Sivashinsky equation. Comput. Res. Prog. Appl. Sci. Eng. 2, 106–109 (2016)
Rezazadeh, H., Aminikhah, H., Refahi Sheikhani, A.: Stability analysis of conformable fractional systems. Iran. J. Numer. Anal. Optim. 7, 13–32 (2016)
Rezazadeh, H., Samsami Khodadad, F., Manafian, J.: New structure for exact solutions of nonlinear time fractional Sharma–Tasso–Olver equation via conformable fractional derivative. Appl. Appl. Math. Int. J. 12, 405–414 (2017)
Ross, B.: Fractional Calculus and Its Applications. Springer, New York (1975)
Zerarka, A., Ouamane, S.: Application of the functional variable method to a class of nonlinear wave equations. World J. Model. Simul. 6, 150–160 (2010)
Zhao, D., Luo, M.: General conformable fractional derivative and its physical interpretation. Calcolo 1–15 (2017). doi:10.1007/s10092-017-0213-8
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Eslami, M., Rezazadeh, H., Rezazadeh, M. et al. Exact solutions to the space–time fractional Schrödinger–Hirota equation and the space–time modified KDV–Zakharov–Kuznetsov equation. Opt Quant Electron 49, 279 (2017). https://doi.org/10.1007/s11082-017-1112-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-017-1112-6