Optimal control approaches for open pit planning

Abstract

This work tackles the open pit planning problem in an optimal control framework. We study the optimality conditions for the so-called continuous formulation using Pontryagin’s Maximum Principle, and introduce a new, semi-continuous formulation that can handle the optimization of a two-dimensional mine profile. Numerical simulations are provided for several test cases, including global optimization for the one-dimensional final open pit, and first results for the two-dimensional sequential open pit. Theses indicate a good consistency between the different approaches, and with the theoretical optimality conditions.

1 Introduction

In long-term planning of mine operation, a common task consists in determining the profile of the total mass of material to be extracted from the site to optimally design an opencast mine. This so-called final open pit problem was introduced in the early works (Lerchs and Grossman 1965; Johnson 1968), with a more recent overview in Newman et al. (2010).

The typical approach used to solve this problem is based on a discrete block model of the site, each block having an associated extraction cost and profit value, based on topographical and geological data. Using a graph of block precedence (i.e. order of extraction) allows to take into account slope constraints for the mine stability, and gives rise to large Integer Programming problems, see for instance (Caccetta 2007). The dynamic programming approach was also investigated in this framework, see e.g. Wright (1987). Yet another approach presented in Griewank and Strogies (2013) describes the optimal digging sequence using time labeling functions in a partial differential equation context.

The present paper follows the continuous reformulation of the Open Pit introduced in Alvarez et al. (2011) in a calculus of variation framework, and then in (Amaya et al. 2019) in an optimal control framework. The main contributions of the present work include the analysis of the final open pit (FOP in the following) with capacity, slope and initial profile constraints, using Pontryagin’s Maximum Principle to extend the optimality conditions previously obtained in Amaya et al. (2019) and characterize the optimal profile in relation to the optimal control structure. Then we introduce a new semi-continuous formulation that can handle the sequential open pit problem (SOP in the following), i.e. optimization of the mine profile over a sequence of several time-frames, for a 2D space domain. Finally, numerical simulations are provided for both the continuous and semi-continuous approaches, including global optimization for the 1D FOP case, and to our knowledge the first results for the 2D profile optimization as an optimal control problem. The outline of the paper is as follows. After the introduction presenting context, Sect. 2 covers the SOP problem statement with the continuous approach, and introduces the semi-continuous formulation. Section 3 presents the FOP analysis using Pontryagin’s Maximum Principle and in particular discusses the control structure in terms of bang, constrained and singular arcs. Section 4 present the numerical simulations for three test cases: 1D FOP, 1D SOP and 2D SOP, and is followed by the conclusions.

2 Problem statement

For a given spatial domain $\Omega$, we consider a continuous function $p:\Omega \rightarrow \textbf{R}$ called profile that delimits the shape of the mine pit. The aim is to determine the profile that maximizes the gain from the excavated soil, while respecting some limits for the excavated capacity and maximal slope of the mine. We recall now the continuous approach for open pit planning, and introduce a new semi-continuous approach that can handle the 2D profile case. Both of these approaches lead to optimal control formulations of the problem.

2.1 Continuous formulation

The key idea in the so-called continuous formulation, originally introduced in (Alvarez et al. 2011), is to use the distance (position along the x-axis) as independent variable, which allows to define the mine profile as a function of this new ’time’. Introducing a suitable dynamics for this function, with the associated control function, allows to formulate the open pit planning as an optimal control problem (OCP).

2.1.1 Final open pit planning

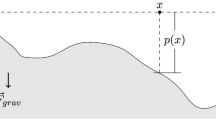
Pit domain For the 1-dimensional case, the domain $\Omega =[a,b]$ will correspond to the independent variable or ’time’ of the optimal control problem.

Pit profile The depth of the pit is defined by the state variable $P: [a,b]\rightarrow \mathbb {R^+}$, with the boundary conditions $P(a)=P_0(a),P(b)=P_0(b)$ enforcing that no further digging occurs at the domain boundaries.

State equation and slope constraint The original slope constraint as stated in (Alvarez et al. 2011) for a differentiable profile was $|\dot{P}| \le \kappa (t,P(t))$, $\forall t\in [a,b]$, where $\kappa (t,z) > 0$ is the maximal allowed slope at position t and depth z. We restrict here ourselves to the case of a constant maximal slope, and use a normalized control $u:[a,b]\rightarrow [-1,1]$ with the corresponding profile dynamics $\dot{P}(t)= u(t)\kappa ,\ \forall t\in [a,b]$.

Initial profile Denoting $P_0 \ge 0$ the initial profile corresponding to the natural shape of the ground, we have the constraint $P(t) \ge P_0(t),\ \forall t\in [a,b]$, i.e. no backfilling is allowed. This is a so-called pure state constraint since it does not involve the control variable.

Capacity limit Since the overall excavation effort is typically limited, we define a second state variable $C: [a,b]\rightarrow \mathbb {R^+}$ with dynamics $\dot{C}(t) = P(t) - P_0(t),\ \forall t\in [a,b]$¹ and intial condition $C(a)=0$. The overall capacity limit is then written as the final condition $C(b) \le C_{max}$.

Objective The aim is to maximize the gain from the excavated soil $\int _a^b\int _{P_0(t)}^{P(t)}G(t,z)dzdt$, with $G:[a,b]\times \mathbb {R}\rightarrow \mathbb {R}$ the gain density at a given position and depth. Note that G is typically defined by interpolation over tabular data, and has to be integrated numerically along the depth z.

The optimal control formulation of $(FOP^{1D})$ is then as follows, with Fig. 1 illustrating the problem:

$$\begin{aligned} (FOP^{1D}) \left\{ \begin{array}{ll} \min \displaystyle - \int _a^b\int _{P_0(t)}^{P(t)}G(t,z)dzdt\\ \\ \dot{P}(t)= u(t)\kappa &{}\forall t\in [a,b]\\ \dot{C}(t)= P(t) - P_0(t) &{}\forall t\in [a,b]\\ \\ u(t)\in U=[-1,1] &{}\forall t\in [a,b]\\ P_0(t)-P(t)\le 0 &{}\forall t\in [a,b]\\ \\ P(a)=P_0(a),\,\,P(b)=P_0(b)\\ C(a)=0,\, C(b)\le C_{max} \end{array} \right. \end{aligned}$$

Fig. 1

Schematic illustration of the final open pit problem $(FOP^{1D})$

2.1.2 Sequential open pit planning

We introduce now an extended version of $(FOP^{1D})$, in which we want to schedule an extraction program over N consecutive time-frames. This case is quite relevant in mine planning since mining companies divide the digging process into periods for operational purposes. We extend the notations of $(FOP^{1D})$ to the multi-frame framework, and note $P_i$ the mine profile at time-frame i, with the associated control $u_i$, while $C_i$ is the excavated capacity during time-frame i. Each mine profile has to be deeper than the previous one, i.e. the constraint $P \ge P_0$ from $(FOP^{1D})$ is generalized as $P_{i} \ge P_{i-1},i=1\ldots N$. The capacity limit $C_{max}^i$ is now enforced at each individual time-frame. Finally, the objective function now takes into account a depreciation rate $\alpha >0$ over time, with the gains for the more distant time-frames being valued less than for the more immediate time-frames. This new optimal control problem reads as follows

$$\begin{aligned} (SOP^{1D}) \left\{ \begin{array}{lr} \max \displaystyle \sum _{i=1}^N\int _a^b\int _{P_{i-1}(t)}^{P_i(t)} \frac{G(t,z)}{(1+\alpha )^{t-1}}dzdt &{}\\ \\ \dot{P}_i(t)= u_i\kappa (t,P_i(t)) &{} \forall t\in [a,b],\quad i=1,\ldots ,N\\ \dot{C}_i=\displaystyle \int _{P_{i-1}(t)}^{P_i(t)}E(t,z)dz &{} \forall t\in [a,b],\quad i=1,\ldots ,N\\ \\ u_i(t)\in [-1,1], &{} \forall t\in [a,b],\quad i=1,\ldots ,N\\ P_{i-1}(t)- P_i(t)\le 0 &{} \forall t\in [a,b],\quad i=1,\ldots ,N\\ \\ P_i(a)=P_0(a),\, P_i(b)=P_0(b) &{}\quad i=1,\ldots ,N\\ C_i(a)=0,\,C_i(b)\le C_{max}^i &{}\quad i=1,\ldots ,N\\ \end{array} \right. \end{aligned}$$

Remark 1

Note that $(SOP^{1D})$ with $N=1$ corresponds to $(FOP^{1D})$. Numerically, the multi-stage $(SOP^{1D})$ can be reformulated by duplicating the state and control variables (as well as the constraints) for each time-frame. Adding the proper linking constraints between the final and initial conditions of the successive time-frames, we obtain a single stage version of $(SOP^{1D})$ that can be solved by standard methods. The overall problem dimension, however, is higher, therefore computationally expensive methods such as global optimization may be able to handle $(FOP^{1D})$ but not $(SOP^{1D})$, see Sect. 4.

Remark 2

For the discrete (block) formulation, it is known [see for instance (Caccetta and Hill 2003; Molina and Amaya 2017)] that each profile (or ’pit’) which is solution of $(SOP^{1D})$ is not deeper than the optimal pit of $(FOP^{1D})$ with the same parameters and infinite capacity, i.e., $C_{max}=\infty$. A similar result has been obtained for the continuous framework in Alvarez et al. (2011).

Fig. 2

1D/2D space discretization of the mine profile

2.2 Semi-continuous formulation for SOP

The main limitation of the continuous approach is that using the independent variable to represent the position in space makes it difficult to handle the 2D profile case, both in terms of dynamics/controls and profile slopes. This is why we introduce a new approach called the semi-continuous formulation, based on an explicit discretization of the space domain $\Omega$. The mine profile is therefore represented by a finite set of variables at the discretization nodes, as illustrated in Fig. 2. Control variables are defined as the excavation effort at each discretization node. Slope constraints are modeled as state constraint linking each node with their neighbors. The independent variable is here standard time, expressed in time-frames such that the final time T is the total number of time-frames. Since SOP is a multi-phase problem, one standard way to formulate it is to normalize the time interval to [0, 1] and duplicate the variables for each time-frame. This approach yields another optimal control formulation of the sequential open pit problem, for which extension from 1D to 2D space domain is rather straightforward, at the cost of an increase in overall problem dimension.

Notations In the context of the semi-continuous approach, for functions of both space and time such as profile, controls and slopes, we will typically use subscripts for the space discretization node in $\Omega$, and exponents for the time-frame of the multi-phase sequential open pit. For instance, $P_i^k$ will represent the profile depth at node i and time-frame k, and $P^k:= (P_i^k), i=0,\ldots ,N$ refers to the mine profile at time-frame k. Similarly, $U_i^k$ will denote the digging at node i and time-frame k, with $U^k:= (P_i^k), i=0,\ldots ,N$ corresponding to the overall excavation effort over the domain $\Omega$ at time-frame k. We will also denote by $\int _{P^k}^{P^{k+1}}$ the integral of a function between the two mine profiles at time-frames k and $k+1$; for 1D profiles this is a 2D integral along x and the depth z, and a 3D integral along x, y, z for 2D profiles.

2.2.1 One dimensional profile space domain

Discrete profile We discretize the space domain $\Omega = [a,b]$ into N equal intervals of length $\Delta x=\frac{b-a}{N}$, with $N+1$ discretization nodes $(x_i)$, and note $I=\{0,\ldots ,N\}$ the set of indices for the nodes. We define the state variables for the profile nodes $(P_i)_{i\in I}$ as functions of time. We also introduce the control variables at each node $(U_i)_{i\in I} \ge 0$, corresponding to the excavation effort, so that the profile variables follow the simple dynamics

$$\begin{aligned} \dot{P}_i(t) = U_i(t) \ ,\ \forall i \in I \ ,\ \forall t \in [0,T]. \end{aligned}$$

(1)

Gain The gain realized during time-frame k is the integral of G between the current profile $P^k$ and the previous $P^{k-1}$. Taking into account the depreciation rate $\alpha$ introduced in 2.1.2, the overall gain to be maximized is

$$\begin{aligned} \sum _{k=1}^T \int _{P^{k-1}}^{P^k} \frac{G(x,z)}{(1+\alpha )^{t_k-1}} dxdz. \end{aligned}$$

(2)

The computation of this objective is detailed in A.

Slope We denote $S_i^k$ the slope at node i and time-frame k, which is a function of time. The maximal slope condition writes as

$$\begin{aligned} -1 \le \frac{S_i^k(t)}{\kappa \left( x_i,P_i^k(t)\right) } \le 1 \ , \ \forall i\in I \ , \ \forall k=0\ldots T\ ,\ \forall t \in [0,1] \end{aligned}$$

(3)

In the 1D case we will use the simple slope formula

$$\begin{aligned} S_i^k = (P_i^k-P_{i-1}^k)/\Delta x \end{aligned}$$

(4)

and the slope limits are state constraints.

Capacity The excavation effort at each time-frame k corresponds to the integral of the effort E between the two consecutive profiles $P^{k-1}$ and $P^k$, and the capacity limit writes as

$$\begin{aligned} \int _{P^{k-1}}^{P^k} E(x,z) dxdz \le C_{k},\quad \forall k=1,\ldots ,T. \end{aligned}$$

(5)

The computation of this integral is detailed in A.

Initial profile This is now a standard initial condition of the form

$$\begin{aligned} P^0_i(0)=p_0(x_i)\ ,\ \forall i \in I. \end{aligned}$$

(6)

We obtain the following multi-phase problem $(SOP)_{SC}^{1D}$ with Fig. 3 illustrating the profile discretization in the 1D case, with $N=7$ and $T=2$. Implementation details regarding the approximation of the various integrals are presented in A

$$\begin{aligned}(SOP)_{SC}^{1D} \left\{ \begin{array}{lrrr} \max \displaystyle \sum _{k=1}^T \int _{P^{k-1}}^{P^k} \frac{G}{(1+\alpha )^{k-1}} &{}&{}&{}\\ \\ \dot{P}_i^k(t) = U_i^k(t), ~~~~~~~~~~~~~~~~~~~~~ i\in I, k=1,\ldots ,T, &{} t\in [0,1]\\ \\ -1 \le \frac{S_i^k(t)}{\kappa (x_i,P_i^k(t)} \le 1, ~~~~~~~~~~~~~ i\in I, k=1,\ldots ,T, &{} t\in [0,1]\\ \\ \displaystyle \int _{P^{k-1}}^{P^k} E(x,z) dxdz \le C_{k},~~~~~ k=1,\ldots ,T &{}\\ \\ P_i^0(0)=p_0(x_i), ~~~~~~~~~~~~~~~~~~~~~ i\in I &{}&{} \end{array} \right. \end{aligned}$$

Fig. 3

Illustration of the 1D profile model discretized w.r.t. space and time as a set of $P_i^k$ state variables with $i=0,\ldots ,N$ profile nodes and $k=0,\ldots ,T$ time-frames. Controls $U_i^k$ are the depths excavated from the previous time-frame at each node. Slopes $S_i^k$ between neighbor nodes must be smaller than the local maximal slopes i.e. $\kappa (X_i,P_i^k)$

Remark 3

Setting $T=1$ corresponds to the final open pit problem with a single time-frame.

Remark 4

The boundary condition $P_{|\partial \Omega }=0$ is in practice built in directly in the problem formulation by eliminating the profile and control variables at the nodes corresponding to the boundary of the space domain.

Remark 5

Moreover, the constraint that each profile must be deeper than the previous one, which was a state constraint in the continuous formulation, is now simply enforced by the conditions $U_i \ge 0$.

Remark 6

The step size $\Delta x$ for the discretization of $\Omega$ in the semi-continuous approach can be seen as the analogue of the time step $\Delta t$ for the continuous approach, which uses distance as independent variable.

2.2.2 Two dimensional profile space domain

For the two dimensional case, the extraction domain considered is $\Omega =[a,b]\times [c,d]$. Generalizing the 1D case, we discretize [a, b] and [c, d] into N and M intervals of length $\Delta x=\frac{b-a}{N}$ and $\Delta y=\frac{d-c}{M}$ respectively, and obtain a grid with $(N+1)\times (M+1)$ nodes. Noting $J=\{0,\ldots ,M\}$, we introduce the state variables (functions of time) $(P_{i,j})_{i,j \in I\times J}$ representing the mine depth at each node $(x_i,y_j):=(a+i\Delta x,c+j\Delta y)$. The mine profile at time-frame k is now a surface represented by the set of points $P^k:= (P_{i,j}^k(0))$. We introduce the $(N+1)\times (M+1)$ non-negative controls $U_{i,j}^k \ge 0 \,\ i,j \in I\times J$, with the same dynamics $\dot{P}_{i,j}^k = U_{i,j}^k$.

Initial profile conditions are written as:

$$\begin{aligned} P_{i,j}^0(0)=p_0(x_i,y_j) \ ,\ i,j \in I\times J. \end{aligned}$$

(7)

The objective and capacity limit are similar to the 1D case, except that the integrals of G and E between two consecutive profiles are now in 3D instead of 2D. The relevant implementation details are provided in A.

The main adjustment concerns the slope constraint: for each point $P_{i,j}$ of the profile we now choose to consider two slopes $S_{i,j}$ and $T_{i,j}$, in the x-axis and y-axis directions respectively. Using the same basic forward finite differences as in 1D, we obtain the two sets of slope constraints at time-frame k:

$$\begin{aligned}{} & {} -1 \le \frac{P_{i+1,j}^k(t) - P_{i,j}^k(t)}{\kappa \left( x_i,y_j,P_{i,j}^k(t)\right) \Delta x} \le 1,\quad \forall i=0,\ldots ,N-1,\nonumber \\{} & {} \quad j=0,\ldots ,M-1,\quad \forall t \in [0,1]. \end{aligned}$$

(8)

$$\begin{aligned}{} & {} -1 \le \frac{P_{i,j+1}^k(t) - P_{i,j}^k(t)}{\kappa \left( x_i,y_j,P_{i,j}^k(t)\right) \Delta y} \le 1,\quad \forall i=0,\ldots ,N-1, \nonumber \\{} & {} \quad j=0,\ldots ,M-1,\quad \forall t \in [0,1]. \end{aligned}$$

(9)

Note that more sophisticated choices could be used for the slopes, such as centered differences formulas or increasing the number of slopes considered at each point. The formulation of $(SOP)_{SC}^{2D}$ is summarized below, with Fig. 4 illustrating the profile discretization in the 2D case with $N=5$ and $M=3$.

$$\begin{aligned}(SOP)_{SC}^{2D} \left\{ \begin{array}{ll} \max \displaystyle \sum _{k=1}^T \int _{P^{k-1}}^{P^k} \frac{G}{(1+\alpha )^{k-1}} &{}\\ \\ \dot{P}_{i,j}^k(t) = U_{i,j}^k(t), &{}\quad \forall (i,j)\in I\times J,\, k=1,\ldots ,T,\, t\in [0,1]\\ \\ -1 \le \frac{S_{i,j}^k(t)}{\kappa \left( x_i,y_j,P_{i,j}^k(t)\right) } \le 1, &{}\quad \forall (i,j)\in I\times J,\, k=1,\ldots ,T,\, t\in [0,1]\\ -1 \le \frac{T_{i,j}^k(t)}{\kappa \left( x_i,y_j,P_{i,j}^k(t)\right) } \le 1, &{}\quad \forall (i,j)\in I\times J,\, k=1,\ldots ,T,\, t\in [0,1]\\ \\ \displaystyle \int _{P^{k-1}}^{P^k} E(x,y,z) dxdydz \le C_{k}, &{}\quad k=1,\ldots ,T \\ \\ P_{i,j}^0(0)=p_0(x_i,y_j), &{}\quad \forall (i,j)\in I\times J \end{array} \right. \end{aligned}$$

Fig. 4

Illustration of the 2D profile model with $N=5$ and $M=3$. View is from ’above’, with the state variable $P_{i,j}^k$ giving the profile depth at node $(x_i,y_j)$ at time-frame k. Slopes $S_{i,j}^k, T_{i,j}^k$ with neighbors along the x-axis and y-axis must be smaller than the maximal allowed slopes given by the function $\kappa$. The control $U_{i,j}^k$ (along the z-axis) corresponds to the excavated depth from the same profile node at the previous time-frame $P_{i,j}^{k-1}$

3 Characterization of solution for $(FOP^{1D})$

We study the final open pit problem in continuous formulation $(FOP^{1D})$ by analyzing the necessary optimality conditions from Pontryagin’s Maximum Principle, and in particular have a look of the possible control structure of optimal profiles and the corresponding interpretation. Looking at $(FOP^{1D})$, the dynamics is linear w.r.t the control, which typically implies a solution where the optimal control is a sequence of so-called bang arcs where it saturates its bounds, and singular arcs where it does not. In addition to this, the initial profile constraint $P \le P_0$ is a so-called pure state constraint since it does not involve the control directly. The handling of pure state constraints in the PMP and indirect shooting methods is a significant and still open subject, and we limit ourselves to a basic expression of the necessary optimality conditions for $(FOP^{1D})$ that we can check for the numerical solutions obtained in 4, without delving into the mathematical details. These results expand the analysis of singular arcs obtained in Amaya et al. (2019) with calculus of variations techniques. We refer readers to for instance (Bonnans and Hermant 2008) for an illustration of the so-called alternative adjoint formulation applied to shooting methods, as well as (Bonnard et al. 2003; Cots 2017) for the geometric control approach.

Optimality conditions for $(SOP^{1D})$ are not detailed here, and are more involved in particular due to the state constraint $P \le P_0$ being generalized over the sequence of time-frames, i.e. $P_i \le P_{i-1}, i=1,\ldots ,N$.

Optimality conditions for the semi-continuous formulation in both 1D and 2D cases remain to be investigated thoroughly. On one hand the constraints $P_i \le P_{i-1}, i=1,\ldots ,N$ are now trivially enforced by the lower bound $U_i \ge 0$. On the other hand the maximal slope limits are now state constraints that involve at least two adjacent nodes of the discretized profile, and the coupling between several controls means the expression of the boundary control is not straightforward.

3.1 Applying Pontryagin’s minimum principle

We introduce here the generic notations $x:=(P,C)$ for the state variables and denote the final conditions as $x(b) \in C_f$, as well as the functions for the dynamics $f: (t,x,u) \mapsto (u(t)\kappa ; P(t)-P_0(t))$, the running cost $l: (t,x,u) \mapsto - \int _{P_0(t)}^{P(t)}G(t,z)dz$, and the state constraint $c: (t,x) \mapsto P_0(t) - P(t)$. Assume the trajectory $\textbf{x}$ associated to the control $\textbf{u}$ is optimal, there must exist $p_0 \le 0$, an adjoint vector $\textbf{p}$ and a multiplier $\mu$ for the state constraint, with $(\textbf{p}, p_0, \mu )\ne 0$, such that the following necessary optimality conditions are satisfied. Define the pre-Hamiltonian

$$\begin{aligned} H(t, x, p, p_0, u) = <p, f(t, x, u)> + p_0 l(t, x, u). \end{aligned}$$

Then

• (i) Adjoint equation:

  $$\begin{aligned} -d\textbf{p}(t) = \frac{\partial H}{\partial x}(t,\textbf{x}(t), \textbf{p}(t), p_0 , \textbf{u}(t))dt + \frac{\partial c}{\partial x}(t,\textbf{x}(t)) d\mu (t) \quad a.e. \end{aligned}$$

  (10)

• (ii) Hamiltonian minimization:

  $$\begin{aligned} H(t, \textbf{x}(t), \textbf{p}(t), p_0 , \textbf{u}(t)) = min_{v \in U}\ H (t, \textbf{x}(t), \textbf{p}(t), p_0 , v) \quad a.e. \end{aligned}$$

  (11)

• (iii) Transversality conditions: the initial state being fixed, we only have the condition on the adjoint at the final time, namely $\textbf{p}(b)$ is normal to $C_f$ at $\textbf{x}(b)$.

• (iv) State constraint complementarity condition:

  $$\begin{aligned} d\mu \ge 0 \quad ,\quad \int _a^b c(t,\textbf{x}(t)) d\mu (t) = 0. \end{aligned}$$

  (12)

We assume here the so-called normal case i.e. $p_0 \ne 0$, and use the normalization $p_0 = 1$. Let us now rewrite the necessary conditions using the original variable notations from $(FOP^{1D})$.

3.1.1 Hamiltonian

Introducing $(p_P,p_C)=p$ the individual adjoints corresponding to the state variables P, C for the profile and capacity, the pre-Hamiltonian rewrites as

$$\begin{aligned}{} & {} H(t,P(t),C(t),p_P(t),p_C(t),u(t)) = p_P(t)u(t)\kappa + p_C(t)(P(t)-P_0(t)) \\{} & {} \qquad \qquad \qquad \qquad - \int _{P_0(t)}^{P(t)} G(t,z)dz. \end{aligned}$$

3.1.2 Adjoint equation

• (i) $\dot{p}_P(t) = -\frac{\partial H}{\partial P}(.) - \frac{\partial c}{\partial P}(.) \frac{d\mu }{dt}(t) = - p_C(t) + G(t,P(t)) + \frac{d\mu }{dt}(t)$.

• (ii) $\dot{p}_C = 0$ i.e. the adjoint associated to the capacity C is constant.

3.1.3 Transversality conditions

• (i) $p_P(b)$ is free since $P(b) = 0$.

• (ii) If the capacity limit is not reached i.e. $C(b) < C_{max}$, then $p_C = p_C(b) = 0$, and $p_C = p_C(b) \ge 0$ otherwise.

We now study more specifically the optimal control structure.

3.2 Inactive constraint case: bang/singular arcs

We start by studying the case when the state constraint is not active. Since per (11) the optimal control minimizes the pre-Hamiltonian which is linear in the control, solutions typically consist in a sequence of bang (saturated control) and/or singular control arcs. We introduce the switching function whose sign will determine the optimal control

$$\begin{aligned} \psi (t) := \frac{\partial H}{\partial u}(t) = p_P(t)\kappa \end{aligned}$$

(13)

Since $\kappa >0$ we obtain the control law:

$$\begin{aligned} \bar{u}(t)={\left\{ \begin{array}{ll} 1 &{} \text {if}\quad p_P(t)<0\\ -1 &{} \text {if}\quad p_P(t)>0\\ u_s(t) &{} \text {if}\quad p_P(t)=0\text { over an interval} \end{array}\right. } \end{aligned}$$

(14)

The value of the singular control $u_s$ is traditionally determined from the fact that $\psi$ and all its time derivatives vanish over a singular arc. Keeping in mind that $d\mu =0$ when the state constraint is inactive as per (12), the first time derivative is

$$\begin{aligned} \dot{\psi }(t) = \kappa \dot{p}_P(t) = \kappa (G(t,P(t)) - p_C(t)). \end{aligned}$$

(15)

As well known, the control does not appear in this expression. However, the second derivative is enough, with

$$\begin{aligned} \ddot{\psi }(t) = \kappa \dot{G}(t,P(t)) = \kappa ( G_t(t,P(t)) + u\kappa G_P(t,P(t)) ) \end{aligned}$$

(16)

where $G_t,G_P$ denote the derivatives of G w.r.t t and P. Solving $\ddot{\psi }(t) = 0$ for the singular control leads to

$$\begin{aligned} u_s(t) = - \frac{G_t(t,P(t))}{\kappa G_P(t,P(t))}. \end{aligned}$$

(17)

We observe that a singular arc is not admissible when $|\frac{G_t(t,P)}{\kappa G_P(t,P)}| > 1$, and in particular when $G_P(t,P)=0$. Furthermore, we have the following result.

Lemma 1

Let $\bar{P}$ be an optimal profile solution of $(FOP^{1D})$, then, over a singular arc the curve $(t, \bar{P}(t))$ follows a level sets of G, and more specifically the level set of null gain $G=0$ if the maximal capacity limit is not reached.

Proof

From (15), over a singular arc the equation $\dot{\psi }= 0$ indicates that the derivative $\dot{G}:= G_t(t,\bar{P}(t)) + \dot{P} G_P(t,\bar{P}(t))$ vanishes, therefore the mine profile will follow a level sets of G. Additionally, if the final constraint for the maximal capacity is not active, then $p_C=0$ and $\dot{\psi }= 0$ then gives $G=0$. $\square$

3.3 Active constraint case: boundary arcs

Over a boundary arc, the associated feedback control $u_c$ is such that the constraint remains active, i.e. $P = P_0$, thus

$$\begin{aligned} u_c(t) = \frac{\dot{P}_0(t)}{\kappa }. \end{aligned}$$

(18)

Note that a constrained arc can only occur if the $u_c$ is admissible, i.e. $| \dot{P}_0 | \le \kappa$, which simply means that the initial profile must satisfy the maximal slope constraint. In the general case the adjoint state may present discontinuities at the junctions between boundary and interior arcs. However, for a first order scalar constraint with a scalar control, it is known that the adjoint is continuous if the control is discontinuous at the junction [see for example Bonnard et al. (2003)], which is the situation we will encounter in the numerical simulations.

3.4 Control structure summary for the final open pit

To summarize, the optimal profile, in terms of control structure, is a sequence of bang, singular and/or constrained arcs. Constrained arcs are where the profile is the initial one, meaning there was no further excavation at these parts of the domain. Bang arcs correspond to the parts of the profile where the slope reaches its maximal allowed value, i.e. the digging is as steep as possible. Singular arcs, finally, are parts where the optimal profile follows the level sets of the gain function, meaning the gain is constant along these parts of the profile. Moreover, if the capacity limit is not reached, then this level set is more specifically the one of null gain, i.e. the digging stops at the depth where excavation is not profitable anymore.

4 Numerical simulations

We present now the numerical simulations that illustrate the continuous and semi-continuous formulations of the Open Pit problem. After a brief description of the algorithms used for the global and local optimizations, we detail three test cases. First is the 1D FOP with limited capacity, that we solve with the continuous (both global and local optimization) and semi-continuous formulation (local optimization). The second example is the 1D SOP with limited capacity, for which we compare the results of both continuous and semi-continuous formulations (both with local optimization). Finally, we present a test case for the 2D SOP problem with the semi-continuous formulation. All simulations were carried out on a standard laptop, with numerical settings for all methods recalled in Table 1 p.15.

4.1 Numerical methods

4.1.1 Global optimization: FOP with continuous formulation

The final open pit problem is low-dimensional, with only two state variables (not counting the running cost) and one control variable. Therefore it makes sense to try a global optimization method such as dynamic programming, or the so-called Hamilton–Jacobi–Bellman (HJB) approach. We use here the software BocopHJB (Bonnans et al. 2019a), and refer to for instance (Falcone and Ferretti 2013) for a detailed description of the HJB method. In this approach the value function of a fully discretized (time, state and control variables) version of the problem is computed, with the global optimum then being reconstructed from this information. In addition to finding the global optimum, this method also does not require an initial guess.

4.1.2 Local optimization: FOP and SOP with continuous and semi-continuous formulations

Since the numerical cost of the global method is too high for the sequential open pit problem, we also use a local optimization method, namely the direct transcription approach. This method approximates the original (OCP) problem by a discretized reformulation as a nonlinear optimization problem (NLP), using a discretization of the time interval. We refer interested readers to for instance (Betts 2001) for a review of direct methods. We use here the software Bocop (Bonnans et al. 2019b), based on the solver Ipopt (Waechter and Biegler 2006) with sparse derivative computed by the automatic differentiation tool Cppad (Bell 2012). This local optimization method is also used for the semi-continuous formulation with explicit discretization of the space domain.

4.1.3 Numerical settings

In Table 1 are the settings for the different numerical methods used in the simulations.

Table 1 Numerical settings for the continuous and semi continuous formulations

4.2 Final open pit (1D): global and local optimization

We start with the 1D FOP as first example, since it is the only one for which all formulations, including global optimization, are available. We set a maximal capacity $C_{max}= 20.000$. The gain function G is interpolated from values found in the Marvin block model of Minelib, a publicly available library of test problem instances for open pit mining problems (see (Espinoza et al. 2013)).

Remark 7

Solutions for the unlimited capacity case, with a different control structure (i.e. singular arcs), are shown in B, with both constant and variable maximal slope.

4.2.1 1D FOP with global optimization for continuous approach

The solution obtained by the global optimization is displayed in Fig. 5. At first glance, the control structure seems to be of the form Constrained-Bang-Bang-Constrained. On both sides the constraint $P=P_0$ is active, meaning there is no additional digging from the initial profile. In the middle, digging occurs with maximal slope, leading to the two bang arcs.

Remark 8

The non zero control around $x=200$ simply follows the existing initial profile $P_0$, and is part of the first constrained arc. See 4.2.2 for more details.

Remark 9

It is worth noting that an estimate of the PMP costate can be derived from the gradient of the value function computed by the global method, see for instance Refs. (Clarke and Vinter 1987; Cristiani and Martinon 2010). In the present case however, the gradient turns out to be quite noisy and of little practical use. This could be improved by increasing the discretizations, although the increase in computational times would not be competitive with respect to using a direct method.

Fig. 5

1D profile with limited capacity—global optimization (HJB method)

4.2.2 1D FOP with local optimization for continuous approach

The solution from the local optimization is displayed in Fig. 6 with the optimal profile and control as well as the PMP costate check. This solution is actually extremely close to the one in Sect. 4.2.1, which indicates that the direct method actually found the global optimum as well, with the benefit of a more accurate solution. In particular, we can here clearly see that the first two arcs with nonzero control around $x=200$ are not bang arcs since $|u|<1$: they are actually part of the first constrained arc and correspond to the region where $P_0$ varies, thus the control $u_c(t) = \frac{\dot{P}_0(t)}{\kappa (t,P(t))}$ from (18) is not just zero.

Moreover, we can now check that the Constrained-Bang-Bang- Constrained control structure is consistent with the switching function and the path constraint. We observe a perfect match between the adjoint estimate from the discretized problem and the recomputed PMP costate. Figure 6 shows the value of the state constraint $g = P_0 - P$ and its associated multiplier $d\mu$. We retrieve $d\mu$ from the multiplier of the state constraint in the discretized problem (the correspondence can be inferred from comparing the expression of the PMP Hamiltonian and the Lagrangian of the NLP problem). In accordance with (12), the multiplier $d\mu$ is positive, and null when the constraint is not active. We also observe that the costate $p_P$ is continuous at the junctions between bang and singular arcs, while the control is discontinuous.

Remark 10

In this particular case, the solution has no singular arcs, which is due to the capacity limit that prevents reaching the null gain region. The example with unlimited capacity in B illustrate a solution with singular arcs where the optimal profile follows the level set $G=0$.

Fig. 6

1D profile with limited capacity—local optimization (direct method) and optimality conditions

4.2.3 1D FOP with semi-continuous approach

We finally present the solution obtained for the same problem using the semi-continuous formulation with a single phase (i.e $T=1$). As can be seen in Fig. 7 and Table 2, the solution is similar to the global and local optimizations using the continuous approach, with close values for the objective. CPU times are of the same order of magnitude for the two local optimizations with continuous and semi-continuous formulation, while global optimization is significantly slower (two orders).

Fig. 7

1D profile, limited capacity—local optimization using semi-continuous formulation

Table 2 Solutions for the 1D FOP with limited capacity

4.3 Sequential open pit (1D and 2D): local optimization

In this section we present solutions for the sequential open pit. First we solve a 1D example using both the continuous and semi-continuous formulations. Then we show a solution for a more realistic 2D problem using the semi-continuous formulation. To our knowledge, this is the first attempt to tackle the 2D case in an optimal control framework.

4.3.1 1D SOP with continuous and semi-continuous approach

Continuous approach We solve the 1D SOP problem for 12 time-frames, with a constant function $\kappa =1$, a rate $\alpha =0.1$ and a maximal capacity $C_{max} = 1e4$ for each time-frame. The solution indicates that most of the excavation effort is concentrated in the high gain regions of the domain, which is not surprising.

Semi continuous approach We now solve the same SOP problem with the semi-continuous formulation. Both approaches give similar solutions, as can be seen in Fig. 8. The objective values showed in Table 3 are quite close with a difference of $1.3\%$, while CPU times are in the same order of magnitude.

Table 3 Solutions for the 1D SOP problem

Fig. 8

1D SOP: continuous and semi-continuous formulations

4.3.2 2D SOP with semi continuous approach

For the 2D case we consider a domain $\Omega =[0,1200]\times [0,400]$ and an analytical gain density function stated by

$$\begin{aligned} G(x,y,z)=1000-\sqrt{(x- 600)^2+(y- 200)^2+(z- 350)^2} \end{aligned}$$

(19)

that reaches its maximal value in (600, 200, 350) and which decreases radially from this point. The initial profile used in this instance is showed in Fig. 9.

Fig. 9

Initial profile for the 2D SOP case

We set a discount factor $\alpha =0.1$ and solve the 2D SOP for different capacity limits and number of time-frames, using a $30\times 10$ discretization of $\Omega$. Figures 10 and 11 illustrate the optimal sequence of 2D profile corresponding to $C_{max}=10^6$ and $5\times 10^6$ respectively, with $T=2,3,6$ time-frames. Table 4 shows the objective values and CPU times. Results are consistent overall, with solutions trying to reach the region of highest gain as fast as allowed by the slope and capacity constraints. Increasing the capacity limit and / or the duration of the time interval both yield better objective values, as expected. CPU times are still reasonable, with the longest run at 139 s.

Fig. 10

2D profile optimization with limited capacity $C=1e6$, for $T=2,3$ and 6 time-frames

Fig. 11

2D profile optimization with limited capacity $C_{max}=5e6$, for $T=2,3$ and 6 time-frames

Table 4 2D SOP: solutions from the semi-continuous formulation, for different time intervals and capacity limit per time-frame

Remark 11

It is worth noting that, in real instances, the information about gain is discretized into blocks since the block model is widespread used in mine planning. An open challenge is to build a gain density G using this type of information. A first approach might be to use a three-dimensional linear interpolation, but it could require a big computational effort so more sophisticated techniques should be investigated.

5 Conclusions

In the present work we focused on the Open Pit problem in an optimal control framework. We extended some previous results on the optimality conditions for the final open pit, and introduced a new semi-continuous formulation that handles the 2D profile sequential optimization. Numerical simulations are provided for the continuous and semi-continuous approaches on several test cases. The 1D FOP case showed a good consistency between global and local optimization for the continuous approach, as well as local optimization for semi-continuous, and matched the optimality conditions from Pontryagin’s Principle. Then the 1D SOP case again indicated a good match for the continuous and semi-continuous formulations. Finally we solved a 2D SOP test case, to our knowledge for the first time in an optimal control framework. Perspectives in the continuation of the present work include solving a more complete 2D SOP example using 3D interpolated data for the gain and maximal slope, as well as studying the optimality conditions for the semi-continuous approach. The latter could prepare for the use of indirect shooting methods such as Hampath (Caillau et al. 2012), especially since the local optimization method used here can provide the knowledge of the optimal control structure and a costate approximation.

Appendices

Appendix A: Implementation details for the semi-continuous approach

Time discretization The sequential open pit for the semi-continuous approach described in 2.2 is a multi phase problem. Instead of duplicating the variables for each time-frame, we use here in practice a more compact implementation, by using a time step $\Delta t$ of 1 time-frame, i.e. the time discretization $t_k = 0 \ldots T$ is the sequence of time-frames. This choice makes sense from the operational point of view, since the sequential open pit planning precisely consists in determining the optimal mine profile at each time-frame. It also simplifies a lot the computation of the integrals of the gain and effort functions between two successive mine profiles. We choose an implicit Euler scheme for the time discretization, which gives the trivial discrete dynamics

$$\begin{aligned} P_i^{k+1} = P_i^k + U_i^{k+1} \end{aligned}$$

(20)

that easily gives the next / previous mine profile when needed in the computations.

Gain An additional state variable g is added to represent the gain realized along the time-frames, whose dynamics can be written as

$$\begin{aligned} \dot{g}(t_k) = \frac{1}{(1+\alpha )^{k-1}} \int _{P^{k-1}}^{P^k} G(x,z) dxdz, \quad \forall k=1,\ldots ,T \end{aligned}$$

(21)

The objective is then to maximize g(T). For the 1D case, we approximate the 2-dimensional integral of G by trapezoidal rule over x then along z. In the 2D profile case, the 3D integral of G for the computation of the gain is approximated using a 2D trapezoidal rule along (x, y) then a standard trapezoidal rule along z.

Capacity At each time-frame, the integral of the excavation effort over the domain $\Omega$ can be approximated by

$$\begin{aligned} \int _{P^{k-1}}^{P^k} E(x,z) dxdz \approx \sum _{i=0}^{N} \Delta x \left( \int _{P_i^{k-1}}^{P_i^k} E(x_i,z) dz \right) \end{aligned}$$

(22)

Since $E=1$ and from the discrete dynamics $P_i^{k} = P_i^{k-1} + U_i^{k}$, we can use the following formula

$$\begin{aligned} \int _{P^{k-1}}^{P^k} E(x,z) dxdz \approx \Delta x \sum _{i=0}^{N-1} U_i^k. \end{aligned}$$

(23)

Similarly, for the 2D profile case, the excavation effort at time-frame k is approximated as

$$\begin{aligned} \int _{P^{k-1}}^{P^k} E(x,y,z) dxdydz \approx \Delta x \Delta y \sum _{i=0}^{N-1} \sum _{j=0}^{M-1} U_{i,j}^k. \end{aligned}$$

(24)

B: Additional examples for the final open pit: continuous formulation

1.1 B.1: FOP with infinite capacity and constant slope

Fig. 12

1D profile with infinite capacity—global optimization (HJB method)

We show here the basic example with unconstrained capacity, namely $C_{max} = \infty$. Figure 12 shows the solution obtained by the global method, and Fig. 13 shows the solution from the local method, and we observe that both solutions match. With infinite capacity, the solution, as expected, digs as much as possible with respect to the maximal slope, until it reaches negative gain. This corresponds to the observed Bang-Singular-Bang control structure (neglecting the two very small constrained arcs $P=P_0=0$ at the extremities). As stated in Lemma 2, the singular arc in the middle follows the geodesic $G=0$. The corresponding control also matches the theoretical expression of the singular control (14), despite some oscillations at the junctions with the bang arcs.

Fig. 13

1D profile with infinite capacity—local optimization (direct method) and consistency with PMP optimality condition