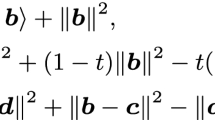A refined inertial DC algorithm for DC programming

Abstract

In this paper we consider the difference-of-convex (DC) programming problems, whose objective function is the difference of two convex functions. The classical DC Algorithm (DCA) is well-known for solving this kind of problems, which generally returns a critical point. Recently, an inertial DC algorithm (InDCA) equipped with heavy-ball inertial-force procedure was proposed in de Oliveira et al. (Set-Valued Variat Anal 27(4):895–919, 2019), which potentially helps to improve both the convergence speed and the solution quality. Based on InDCA, we propose a refined inertial DC algorithm (RInDCA) equipped with enlarged inertial step-size compared with InDCA. Empirically, larger step-size accelerates the convergence. We demonstrate the subsequential convergence of our refined version to a critical point. the Kurdyka-Łojasiewicz (KL) property of the objective function, we establish the sequential convergence of RInDCA. Numerical simulations on checking copositivity of matrices and image denoising problem show the benefit of larger step-size.

1 Introduction

Difference-of-convex (DC) programming, referring to the problems of minimizing a function which is the difference of two convex functions, forms an important class of nonconvex programming and has been studied extensively for decades, see e.g., (Hartman 1959; Hiriart-Urruty 1985; Pham and Souad 1986; Pham and Le Thi 1997; Pham and Le Thi 1998; Horst and Thoai 1999; Le Thi and Pham 2005; Aleksandrov 2012; Le Thi et al. 2012; Pham and Le Thi 2014; Souza et al. 2016; Joki et al. 2017; Pang et al. 2017; Le Thi and Pham 2018; de Oliveira 2020).

In the paper, we consider the standard DC program in form of

$$\begin{aligned} \text {min}&\big \{f(\mathbf{x }) := f_1(\mathbf{x }) - f_2(\mathbf{x }):\mathbf{x }\in \mathbb {R}^n\big \}, \quad (P) \end{aligned}$$

where $f_1$ and $f_2$ are proper closed and convex functions. Such a function f is called a DC function, while $f_1-f_2$ is a DC decomposition of f with $f_1$ and $f_2$ being DC components. Formulation (P) also includes convex constrained problems $\min \{{\widetilde{f}}_1(\mathbf{x })-f_2(\mathbf{x }):\mathbf{x }\in X\}$, where ${\widetilde{f}}_1:\mathbb {R}^n\rightarrow \mathbb {R}$ is convex and $X\subseteq \mathbb {R}^n$ is nonempty, closed and convex. By introducing the indicator function of X, i.e., $\delta _X(\mathbf{x }) = 0$ if $\mathbf{x }\in X$ and $\delta _X(\mathbf{x }) = \infty$ otherwise, this model recovers (P) as $\min \{({\widetilde{f}}_1+\delta _{X})(\mathbf{x })-f_2(\mathbf{x }):\mathbf{x }\in \mathbb {R}^n\}$. Throughout the manuscript, we make the next assumptions for problem (P).

Assumption 1

• (a) $\text {dom}(f_1) \subseteq Y \subseteq \text {int}(\text {dom}(f_2))$, where $Y\subseteq \mathbb {R}^n$ is closed.

• (b) The function f is bounded below, i.e., there exists a scalar $f^*$ such that $f(\mathbf{x }) \ge f^*$ for all $\mathbf{x }\in \mathbb {R}^n$.

The term (a) of Assumption 1 guarantees the nonemptiness of the subdifferential of $f_2$ at any point of $\text {dom}(f_1)$. It will be also used in Theorem 4.1.

The DC Algorithm (DCA) (Pham and Le Thi 1997; Pham and Le Thi 1998; Le Thi and Pham 2005, 2018) is renowned for solving (P), which has been introduced by Pham Dinh Tao in 1985 and extensively developed by Le Thi Hoai An and Pham Dinh Tao since 1994. Specifically, at iteration k, DCA obtains the next iterate $\mathbf{x }^{k+1}$ by solving the convex subproblem

$$\begin{aligned} \mathbf{x }^{k+1}\in {{\,\mathrm{argmin}\,}}\big \{f_1(\mathbf{x })-\langle \mathbf{y }^k, \mathbf{x }\rangle :\mathbf{x }\in \mathbb {R}^n\big \}, \end{aligned}$$

where $\mathbf{y }^k \in \partial f_2(\mathbf{x }^k)$. It has been proved in Pham and Le Thi (1997) that any limit point $\bar{\mathbf{x }}$ of the generated sequence $\{\mathbf{x }^k\}$ is a (DC) critical point of problem (P), i.e., the necessary local optimality condition $\partial f_1(\bar{\mathbf{x }})\cap \partial f_2(\bar{\mathbf{x }}) \ne \emptyset$ is verified.

Recently, several accelerated algorithms for DC programming have been studied. Actacho et al. proposed in Artacho et al. (2018); Artacho and Vuong (2020) the boosted DC algorithms for unconstrained smooth/nonsmooth DC program, where the direction $\mathbf{x }^{k+1}-\mathbf{x }^k$, determined by the consecutive iterates of DCA, is verified as a descent direction of f at $\mathbf{x }^{k+1}$ when $f_2$ is strongly convex, thus a line-search procedure can be conducted along it to obtain a better candidate with lower objective value. Next, Niu et al. Niu andWang (2019) developed a boosted DCA by incorporating the line-search procedure for DC program (both smooth and nonsmooth) with convex constraints. Later, Actacho et al. Artacho et al. (2019) investigated the line-search idea in DC program with linear constraint, where a sufficient and necessary condition for determining the feasibility of the direction $\mathbf{x }^{k+1}-\mathbf{x }^k$ is proposed. Different from the boosted approaches above, another type of acceleration is the momentum methods. There are two renowned momentum methods: the Polyak’s heavy-ball method (Polyak 1987; Zavriev and Kostyuk 1993) and the Nesterov’s acceleration technique (Nesterov 1983, 2013). Indeed, Nesterov’s acceleration belongs to the heavy-ball family. These two momentum methods have been successfully applied for various nonconvex optimizations problems (see, e.g., Adly et al. 2021; Ochs et al. 2014; Pock and Sabach 2016; Mukkamala et al. 2020). In de Oliveira and Tcheou (2019), de Oliveira et al. proposed an inertial DC algorithm (InDCA) for problem (P) in the premise that $f_2$ is strongly convex, where the heavy-ball inertial-force procedure is introduced. Phan et al. developed in Phan et al. (2018) an accelerated variant of DCA for (P) by incorporating the Nesterov’s acceleration technique. At the same time, Wen et al. (2018) used the same technique for a special class of DC program, where $f_1$ is the sum of a smooth convex function and a (possibly non-smooth) convex function. Adly et al. Adly et al. (2021) proposed a gradient-based method, using both heavy-ball and Nesterov’s inertial-forces, for optimizing a smooth function. They apply the algorithm for (P) by minimizing the DC Moreau envelope ${}^{\mu } f_1-{}^{\mu } f_2$¹, which can return a critical point of $f_1-f_2$. However, their methods require computing the proximal operators of $f_1$ and $f_2$. The above inertial-type methods often help to improve the performances (compared with their counterparts without inertial-forces) in both the convergence speed and the solution quality. Concerning the optimality condition of the DC program (P), the aforementioned methods only guarantee the critical point, which is weaker than the d-stationary point (see, e.g., Pang et al. 2017; de Oliveira 2020). Next, we introduce some works about obtaining the d-stationary solution of (P). By exploring the structure of $f_2$, i.e., $f_2$ is the supremum of finitely many convex smooth functions, Pang et al. (2017) proposed a novel enhanced DC algorithm (EDCA) to obtain a d-stationary solution. Later, Lu et al. (2019) developed an inexact variant of EDCA in order to make EDCA cheaper at each iteration. Furthermore, considering additionally the same structure of $f_1$ as that in Wen et al. (2018), a proximal version of EDCA was developed, whose cost in each iteration is lower than the inexact version, besides, this algorithm incorporated the Nesterov’s extrapolation for possible acceleration.

In this paper, based on the inertial DC algorithm (InDCA) (de Oliveira and Tcheou 2019), we propose a refined version (RInDCA) equipped with larger inertial step-size. Indeed, both InDCA and RInDCA can handle exactness and inexactness in the solution of the convex subproblems. The basic idea of the exact versions of InDCA and RInDCA (denoted by InDCA$_\text {e}$ and RInDCA$_\text {e}$) are described as follows. RInDCA$_\text {e}$ obtains at the k-th iteration the next iterate $\mathbf{x }^{k+1}$ by solving the convex subproblem

$$\begin{aligned} \mathbf{x }^{k+1} \in {{\,\mathrm{argmin}\,}}\{f_1(\mathbf{x }) - \langle \mathbf{y }^k + \gamma (\mathbf{x }^k-\mathbf{x }^{k-1}),\mathbf{x }\rangle :\mathbf{x }\in \mathbb {R}^n\}, \end{aligned}$$

where $\mathbf{y }^k \in \partial f_2(\mathbf{x }^k)$. Our analysis shows that the inertial step-size $\gamma \in [0, (\sigma _1+\sigma _2)/2)$ is adequate for the convergence of RInDCA$_\text {e}$ compared with $[0,\sigma _2/2)$ in InDCA$_\text {e}$, where $\sigma _1$ and $\sigma _2$ are the strong convex parameters of $f_1$ and $f_2$. Thus, the inertial range of RInDCA$_\text {e}$ is larger than that of InDCA$_\text {e}$ when $\sigma _1, \sigma _2 >0$. Empirically, larger step-size accelerates the convergence. In some applications, we will encounter the case where $f_1$ is strongly convex and $f_2$ is not, then RInDCA$_\text {e}$ is applicable but not InDCA$_\text {e}$. Later, the details about the exact and inexact versions can be found in Sect. 3. The benefit of larger inertial step-size is discussed in Sect. 6.

Our contributions are: (1) propose a refined inertial DC algorithm, which is equipped with larger inertial step-size compared with InDCA (de Oliveira and Tcheou 2019). Besides, the relation between the inertial-type DCA and the classical DCA is pointed out. (2) establish the subsequential convergence of our refined version and the sequential convergence by further assuming the Kurdyka-Łojasiewicz (KL) property of the objective function.

The rest of the paper is organized as follows: Sect. 2 reviews some notations and preliminaries in convex and variational analysis. In Sect. 3, we first introduce our refined inertial DC algorithm (RInDCA), followed by some DC programming applications. Next, the relation between the inertial-type DCA and the successive DCA is discussed. Section 4 focuses on establishing the subsequential convergence of RInDCA. By assuming additionally the KL property of the objective function, we prove in Sect. 5 the sequential convergence of RInDCA. Section 6 summarizes the numerical results on checking copositivity of matrices and image denoising problem, in which the benefit of enlarged inertial step-size is demonstrated. Some concluding remarks are given in the final section.

2 Notations and preliminaries

Let $\mathbb {R}^n$ denote the finite dimensional vector space endowed with the canonical inner product $\langle \cdot , \cdot \rangle$, and the Euclidean norm $\Vert \cdot \Vert$, i.e., $\Vert \cdot \Vert = \sqrt{\langle \cdot ,\cdot \rangle }$. The entry of a vector x is denoted as $\mathbf{x }_i$, and the entry of a matrix $\mathbf{A }$ is denoted as $\mathbf{A }_{i,j}$.

For an extended real-valued function $h:\mathbb {R}^n\rightarrow (-\infty ,\infty ]$, the set

$$\begin{aligned} \text {dom}(h) := \{\mathbf{x }\in \mathbb {R}^n:h(\mathbf{x }) < \infty \} \end{aligned}$$

denotes its effective domain. If $\text {dom}(h) \ne \emptyset$, and h does not attain the value $-\infty$, then h is called a proper function. The set

$$\begin{aligned} \text {epi}(h):=\{(\mathbf{x },t):h(\mathbf{x })\le t,\mathbf{x }\in \mathbb {R}^n,t\in \mathbb {R}\} \end{aligned}$$

denotes the epigraph of h, and h is closed (resp. convex) if $\text {epi}(h)$ is closed (resp. convex). The conjugate function of h is defined as

$$\begin{aligned} h^*(\mathbf{y }) = \sup \limits \{\langle \mathbf{y },\mathbf{x }\rangle - h(\mathbf{x }):\mathbf{x }\in \mathbb {R}^n\}, \quad \mathbf{y }\in \mathbb {R}^n. \end{aligned}$$

Given a proper closed function $h: \mathbb {R}^n\rightarrow (-\infty ,\infty ]$, the Fréchet subdifferential of h at $\mathbf{x }\in \text {dom}(h)$ is given by

$$\begin{aligned} \partial ^F h(\mathbf{x }):= \left\{ \mathbf{y }\in \mathbb {R}^n:\liminf \limits _{\mathbf{z }\rightarrow \mathbf{x }} \frac{h(\mathbf{z })-h(\mathbf{x })-\langle \mathbf{y },\mathbf{z }-\mathbf{x }\rangle }{\Vert \mathbf{z }-\mathbf{x }\Vert } \ge 0\right\} , \end{aligned}$$

while for $\mathbf{x }\notin \text {dom}h$, $\partial ^F h(\mathbf{x }):= \emptyset$. The (limiting) subdifferential of f at $\mathbf{x }\in \text {dom}(h)$ is defined as

$$\begin{aligned} \partial h(\mathbf{x }) :=\{\mathbf{y }\in \mathbb {R}^n:&\exists (\mathbf{x }^k\rightarrow \mathbf{x }, h(\mathbf{x }^k)\rightarrow h(\mathbf{x }), \mathbf{y }^k \in \partial ^F h(\mathbf{x }^k)) \text { such that } \mathbf{y }^k\rightarrow \mathbf{y }\}, \end{aligned}$$

and $\partial h(\mathbf{x }):=\emptyset$ if $\mathbf{x }\notin \text {dom}(h)$. Note that if h is also convex, then the Fréchet subdifferential and the limiting subdifferential will coincide with the convex subdifferential, that is,

$$\begin{aligned} \partial ^{F} h(\mathbf{x }) = \partial h(\mathbf{x }) = \{\mathbf{y }\in \mathbb {R}^n:h(\mathbf{z }) \ge h(\mathbf{x })+\langle \mathbf{y },\mathbf{z }-\mathbf{x } \rangle \;\text {for all}\;\mathbf{z }\in \mathbb {R}^n\}. \end{aligned}$$

Given a nonempty set ${\mathcal {C}} \subseteq \mathbb {R}^n$, the distance from a point $\mathbf{x }\in \mathbb {R}^n$ to ${\mathcal {C}}$ is denoted as $\text {dist}(\mathbf{x },{\mathcal {C}}):=\inf \{\Vert \mathbf{x }-\mathbf{z }\Vert :\mathbf{z }\in {\mathcal {C}}\}$. We now recall the Kurdyka-Łojasiewicz (KL) property (Bolte et al. 2007; Attouch and Bolte 2009; Attouch et al. 2013). For $\eta \in (0,\infty ]$, we denote by $\Xi _{\eta }$ the set of all concave continuous functions $\varphi :[0,\eta )\rightarrow [0,\infty )$ that are continuously differentiable over $(0,\eta )$ with positive derivatives and satisfy $\varphi (0)=0$.

Definition 2.1

(KL property) A proper closed function h is said to satisfy the KL property at $\bar{\mathbf{x }} \in \text {dom}(\partial h) := \{\mathbf{x }\in \mathbb {R}^n:\partial h(\mathbf{x })\ne \emptyset \}$ if there exist $\eta \in (0,\infty ]$, a neighborhood U of $\bar{\mathbf{x }}$, and a function $\varphi \in \Xi _{\eta }$ such that for all $\mathbf{x }$ in the intersection

$$\begin{aligned} U\cap \{\mathbf{x }\in \mathbb {R}^n:h(\bar{\mathbf{x }})<h(\mathbf{x })<h(\bar{\mathbf{x }})+\eta \}, \end{aligned}$$

it holds that

$$\begin{aligned} \varphi '(h(\mathbf{x })-h(\bar{\mathbf{x }}))\text {dist}(\mathbf{0 },\partial h(\mathbf{x })) \ge 1. \end{aligned}$$

If h satisfies the KL property at any point of $\text {dom}(\partial h)$, then h is called a KL function.

The following uniformized KL property plays an important role in our sequential convergence analysis.

Lemma 2.1

(Uniformized KL property, see Bolte et al. (2014)) Let $\Omega \subseteq \mathbb {R}^n$ be a compact set and let $h:\mathbb {R}^n \rightarrow (-\infty ,\infty ]$ be a proper closed function. If h is constant on $\Omega$ and satisfies the KL property at each point of $\Omega$, then there exist $\varepsilon , \eta >0$ and $\varphi \in \Xi _{\eta }$ such that

$$\begin{aligned} { \varphi '(h(\mathbf{x })-h(\bar{\mathbf{x }}))\text {dist}(\mathbf{0 },\partial h(\mathbf{x })) \ge 1} \end{aligned}$$

for any $\bar{\mathbf{x }}\in \Omega$ and any $\mathbf{x }$ satisfying $\text {dist}(\mathbf{x },\Omega ) < \varepsilon$ and $h(\bar{\mathbf{x }})< h(\mathbf{x }) < h(\bar{\mathbf{x }}) + \eta$.

Now, let $h:\mathbb {R}^n\rightarrow (-\infty ,\infty ]$ be a proper closed and convex function, and let $\varepsilon > 0$, the set

$$\begin{aligned} \partial _{\varepsilon } h(\mathbf{x }) := \{\mathbf{y }\in \mathbb {R}^n:h(\mathbf{z }) \ge h(\mathbf{x })+\langle \mathbf{y },\mathbf{z }-\mathbf{x } \rangle -\varepsilon \;\text {for all}\;\mathbf{z }\in \mathbb {R}^n\} \end{aligned}$$

denotes the $\varepsilon$-subdifferential of h at $\mathbf{x }$, and any point in $\partial _{\varepsilon } h(\mathbf{x })$ is called a $\varepsilon$-subgradient of h at $\mathbf{x }$. Clearly, $\partial _{\varepsilon } h(\mathbf{x }) \ne \emptyset$ implies that $\mathbf{x } \in \text {dom}(h)$. A proper closed function h is called $\sigma$-strongly convex (cf. $\sigma$-convex) with $\sigma \ge 0$ if for any $\mathbf{x }, \mathbf{z } \in \text {dom}(h)$ and $\lambda \in [0,1]$, it holds that

$$\begin{aligned} h(\lambda \mathbf{x } +(1-\lambda )\mathbf{z }) \le \lambda h(\mathbf{x }) + (1-\lambda )h(\mathbf{z })-\frac{\sigma }{2}\lambda (1-\lambda )\Vert \mathbf{x }-\mathbf{z }\Vert ^2. \end{aligned}$$

Moreover, let h be a $\sigma$-convex function. Then it was known (Beck 2017) that for any $\mathbf{x }\in \text {dom}(\partial h)$, $\mathbf{y } \in \partial h(\mathbf{x })$ and $\mathbf{z }\in \text {dom}(h)$, we have

$$\begin{aligned} h(\mathbf{z })\ge h(\mathbf{x })+\langle \mathbf{y },\mathbf{z }-\mathbf{x }\rangle +\frac{\sigma }{2}\Vert \mathbf{z }-\mathbf{x }\Vert ^2. \end{aligned}$$

Finally, we give a result related to strong convexity and $\varepsilon$-subdifferential, which will be used in analyzing our refined inexact DC algorithm.

Lemma 2.2

( Pham et al. (2021)) Let $h:\mathbb {R}^n \rightarrow (-\infty ,\infty ]$ be a $\sigma$-convex function, and let $\varepsilon \ge 0$, $t \in (0,1]$. Then for any $\mathbf{x }\in \text {dom}(h)$, $\mathbf{z }\in \text {dom}(h)$, and $\mathbf{y }\in \partial _{\varepsilon } h(\mathbf{x })$,

$$\begin{aligned} h(\mathbf{z })\ge h(\mathbf{x }) +\langle \mathbf{y },\mathbf{z }-\mathbf{x }\rangle + \frac{\sigma (1-t)}{2}\Vert \mathbf{z }-\mathbf{x }\Vert ^2 - \frac{\varepsilon }{t}. \end{aligned}$$

(1)

3 A refined inertial DC algorithm

In this section, we first describe a general inertial-type DC algorithm for problem (P), which is taken from de Oliveira and Tcheou (2019) except that the values of $\lambda$ and $\gamma$ are not specified. By setting different $\lambda$ and $\gamma$ we derive the classical DCA, the inertial DC algorithm (InDCA) proposed in de Oliveira and Tcheou (2019), and our refined version (RInDCA). Next, some practical applications of DC programming problems are introduced, followed by a discussion of the relation between the inertial-type DCA and the successive DCA.

From now on, suppose that the objective function f has a DC decomposition $f = f_1-f_2$, where $f_1$ is $\sigma _1$-convex and $f_2$ is $\sigma _2$-convex. We describe below in Algorithm 1 a general inertial-type DC algorithm for (P).

Note that Algorithm 1 includes exact and inexact cases. The exact case occurs when $\lambda = 0$, then $\varepsilon _{k+1} = 0$ and $\partial _{\varepsilon _{k+1}} f_1(\mathbf{x }^{k+1}) = \partial f_1(\mathbf{x }^{k+1})$, thus the iteration point $\mathbf{x }^{k+1}$ in (2) is obtained by exactly solving the next convex subproblem:

$$\begin{aligned} \mathbf{x }^{k+1} \in {{\,\mathrm{argmin}\,}}\{f_1(\mathbf{x }) - \langle \mathbf{y }^k + \gamma (\mathbf{x }^k-\mathbf{x }^{k-1}),\mathbf{x }\rangle :\mathbf{x }\in \mathbb {R}^n\}, \end{aligned}$$

(3)

where $\mathbf{y }^k\in \partial f_2(\mathbf{x }^k)$. On the other hand, the inexact case occurs when $\lambda > 0$ and $\sigma _2 > 0$, then the iterate $\mathbf{x }^{k+1}$ in (2), which is an approximate minimizer of (3), could be computed by some bundle methods (see de Oliveira and Tcheou 2019). The classical DCA is derived when setting $\lambda = 0$ and $\gamma = 0$ in Algorithm 1. Next, we denote the exact (resp. inexact) versions of InDCA and RInDCA as InDCA$_\text {e}$ and RInDCA$_\text {e}$ (resp. InDCA$_\text {n}$ and RInDCA$_\text {n}$). The following table summarizes the four algorithms which are recovered by specifying some parameters in Algorithm 1 together with the assumptions about $\sigma _1$ and $\sigma _2$.

Algorithm	$\lambda$	$\gamma$	t	Assumption
InDCA$_\text {e}$	0	$[0,\sigma _2/2)$	–	$\sigma _2>0$
InDCA$_\text {n}$	(0,1)	$[0,(1-\lambda )\sigma _2/2)$	–	$\sigma _2>0$
RInDCA$_\text {e}$	0	$[0,(\sigma _1+\sigma _2)/2)$	–	$\sigma _1+\sigma _2>0$
RInDCA$_\text {n}$	(0,1)	$[0, (\sigma _1(1-t)+\sigma _2-\lambda \sigma _2/t)/2)$	(0,1]	$\sigma _2>0$

Comparing InDCA$_\text {e}$ with RInDCA$_\text {e}$, the inertial range of the latter is larger than the former if $\sigma _1>0$. Moreover, RInDCA$_\text {e}$ is applicable when $\sigma _2=0$ and $\sigma _1>0$, while this is not the case for InDCA$_\text {e}$. Next, for comparing InDCA$_\text {n}$ and RInDCA$_\text {n}$, we need to optimize t in RInDCA$_\text {n}$ such that the supremum of the inertial step-size $\gamma$ is maximized. To this end, fixing $\lambda \in (0,1)$ and let $\sigma (\lambda ,t):=\sigma _1(1-t)+\sigma _2-\lambda \sigma _2/t$, we can maximize $\sigma (\lambda ,t)$ with respect to $t\in [0,1)$. It is easy to verify that

$$\begin{aligned} {{\,\mathrm{argmax}\,}}\{\sigma (\lambda ,t):t\in (0,1]\} = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if } \sigma _1 = 0,\\ 1 &{}\quad \text {if }\sigma _1 \ne 0, \sqrt{\lambda \sigma _2/\sigma _1} \ge 1,\\ \sqrt{\lambda \sigma _2/\sigma _1} &{}\quad \text {if }\sigma _1 \ne 0, \sqrt{\lambda \sigma _2/\sigma _1} < 1. \end{array}\right. } \end{aligned}$$

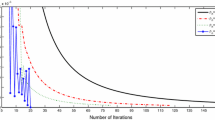
For the first two cases, $\sigma (\lambda ,1) = (1-\lambda )\sigma _2$, this implies the same inertial range between InDCA$_\text {n}$ and RInDCA$_\text {n}$. Next, for the last case, we have $\sigma (\lambda ,1)<\sigma (\lambda ,\sqrt{\lambda \sigma _2/\sigma _1})$, thus the inertial range of RInDCA$_\text {n}$ is larger than that in InDCA$_\text {n}$. Now, let $H_1(\lambda ) := \sigma (\lambda ,\sqrt{\lambda \sigma _2/\sigma _1})/2$ and $H_2(\lambda ) :=(1-\lambda )\sigma _2/2$, we visualize in Fig. 1 the values of $H_1$ for $(\sigma _1,\sigma _2) \in \{ (1,1), (2,1), (3,1), (4,1)\}$ as well as the values of $H_2$ for $\sigma _1 = 1$ with respect to $\lambda \in (0,1)$ respectively.

Fig. 1

The values of $H_1$ with $(\sigma _1,\sigma _2) \in \{ (1,1), (2,1), (3,1), (4,1)\}$ and $H_2$ with respect to $\lambda \in (0,1)$

It can be observed that when fixing $\lambda \in (0,1)$ and $\sigma _2=1$, the value of $H_1(\lambda )$ is getting larger as $\sigma _1$ increases, moreover, all of these values are larger than $H_2(\lambda )$. This observation implies that a larger strong convexity parameter of $f_1$ will result in a larger inertial range.

Now, we introduce some DC programming problems, in which the first DC components are strongly convex.

Example 3.1

(Convex constraint quadratic problem) Consider the quadratic problem with convex constraint

$$\begin{aligned} \min \bigg \{f(\mathbf{x }) = \frac{1}{2}\mathbf{x }^{\top } \mathbf{A }\mathbf{x }+\delta _Y(\mathbf{x }):\mathbf{x }\in \mathbb {R}^n\bigg \}, \end{aligned}$$

where $\mathbf{A }\in \mathbb {R}^{n\times n}$ is symmetric and Y is a closed convex set. This model has a DC decomposition $f= f_1-f_2$ with $f_1(\mathbf{x })=\frac{L}{2}\Vert \mathbf{x }\Vert ^2 + \delta _{Y}(\mathbf{x })$ and $f_2(\mathbf{x }) = \frac{L}{2}\Vert \mathbf{x }\Vert ^2 - \frac{1}{2}\mathbf{x }^{\top }\mathbf{A }\mathbf{x }$, where $L \ge \Vert \mathbf{A }\Vert$². When Y is the nonnegative orthant $\mathbb {R}_+^n$, DCA applied for the above DC decomposition has been used for checking copositivity of matrices (Dür and Hiriart-Urruty 2013). Note that for this DC decomposition, the first DC component is L-convex.

Example 3.2

(1D signals denoising) Consider the nonconvex sparse signal recovery problem for 1D signals:

$$\begin{aligned} \min \bigg \{\frac{\mu }{2}\Vert \mathbf{x }-\mathbf{b }\Vert ^2 + \sum _{i=1}^{n-1}\phi (|\mathbf{x }_{i+1}-\mathbf{x }_i|):\mathbf{x }\in \mathbb {R}^n\bigg \}, \end{aligned}$$

where $\mu >0$ is a trade-off constant, $\mathbf{b }$ is the noise signal in $\mathbb {R}^n$, and $\phi$ is a concave function for inducing sparsity, e.g., $\phi (r) := \log (1+2r)/r$. In this model, taking $\phi (r) = \log (1+2r)/r$, we obtain a DC decomposition as $f_1 - f_2$ with $f_1(\mathbf{x }) = \frac{\mu }{2}\Vert \mathbf{x }-\mathbf{b }\Vert ^2 + \sum _{i=1}^{n-1}|\mathbf{x }_{i+1}-\mathbf{x }_i|$ and $f_2 = \sum _{i=1}^{n-1}|\mathbf{x }_{i+1}-\mathbf{x }_i| - \sum _{i=1}^{n-1}\phi (|\mathbf{x }_{i+1}-\mathbf{x }_i|)$. Note that $f_1$ is strongly convex, while $f_2$ is not. Thus InDCA can not be directly applied. In order to apply InDCA, a strong convexity term $\psi :\mathbf{x }\mapsto \rho \Vert \mathbf{x } \Vert ^2/2$ is added into both $f_1$ and $f_2$ in de Oliveira and Tcheou (2019), yielding the new DC decomposition $(f_1+\psi ) - (f_2+\psi )$, where the DC components are both strongly convex.

Remark 3.1

As shown in Examples 3.1 and 3.2, the first DC components are strongly convex. However, InDCA only takes into account the strong convexity of the second DC component. This often causes the inertial range smaller than that of our refined version RInDCA, which involves the strong convexity of both DC components.

Before ending this section, we mention out that the inertial-type DCA (both InDCA$_\text {e}$ and RInDCA$_\text {e}$) is related to the successive DCA, namely SDCA (see Le Thi and Pham 2018). Let us take at the k-th iteration of DCA the successive DC decomposition $f= (f_1+\varphi ^k) - (f_2+\varphi ^k)$ with $\varphi ^k(\mathbf{x }) = \frac{\gamma }{2}\Vert \mathbf{x }- \mathbf{x }^{k-1}\Vert ^2$, then DCA applied to this special DC decomposition yields

$$\begin{aligned} \mathbf{x }^{k+1}\in {{\,\mathrm{argmin}\,}}\big \{ f_1(\mathbf{x }) + \varphi ^k(\mathbf{x }) - \langle \nabla \varphi ^k(\mathbf{x }^k) + \mathbf{y }^k , \mathbf{x }\rangle :\mathbf{x }\in \mathbb {R}^n\big \}, \end{aligned}$$

(4)

where $\mathbf{y }^k\in \partial f_2(\mathbf{x }^k)$. Then (4) reads as

$$\begin{aligned} \mathbf{x }^{k+1}\in {{\,\mathrm{argmin}\,}}\big \{ f_1(\mathbf{x }) + \varphi ^k(\mathbf{x }) - \langle \mathbf{y }^k +\gamma (\mathbf{x }^k-\mathbf{x }^{k-1}) , \mathbf{x }\rangle :\mathbf{x }\in \mathbb {R}^n\big \}. \end{aligned}$$

(5)

Comparing SDCA described in (5) with RInDCA$_\text {e}$ (or InDCA$_\text {e}$) in (2), we observe that the only difference is the presence of the proximal term $\varphi ^k(\mathbf{x })$ in (5). This term plays a role of regularizer which can be interpreted as finding a point $\mathbf{x }^{k+1}$ close to $\mathbf{x }^{k-1}$ and a minimizer of the function $\mathbf{x }\mapsto f_1(\mathbf{x }) - \langle \mathbf{y }^k + \gamma (\mathbf{x }^k-\mathbf{x }^{k-1}),\mathbf{x }\rangle$. This is the basic idea of proximal point methods, thus this SDCA is often called proximal DCA as well. The absence of $\varphi ^k$ in RInDCA$_\text {e}$ means that the iteration point $\mathbf{x }^{k+1}$ is not supposed to be close to $\mathbf{x }^{k-1}$, which will lead to potential acceleration. In conclusion, the term $\varphi ^k$ plays a key role to make RInDCA$_\text {e}$ differ from SDCA, and possibly yields acceleration in RInDCA$_\text {e}$.

Remark 3.2

Indeed, the convex problem of (5) is irrelevant to $\mathbf{x }^{k-1}$ since

$$\begin{aligned} {(5)} = {{\,\mathrm{argmin}\,}}\big \{ f_1(\mathbf{x }) + \frac{\gamma }{2}\Vert \mathbf{x }\Vert ^2 - \langle \mathbf{y }^k +\gamma \mathbf{x }^k , \mathbf{x }\rangle :\mathbf{x }\in \mathbb {R}^n\big \}, \end{aligned}$$

which is exactly the subproblem of DCA for the fixed DC decomposition

$$\begin{aligned} f = \big (f_1 + \frac{\gamma }{2}\Vert \cdot \Vert ^2\big ) - \big (f_2 + \frac{\gamma }{2}\Vert \cdot \Vert ^2\big ). \end{aligned}$$

4 Subsequential convergence analysis

This section focuses on showing the subsequential convergence of RInDCA (both RInDCA$_\text {e}$ and RInDCA$_\text {n}$), some results for further developing the sequential convergence of RInDCA in the next section are also proved.

4.1 Subsequential convergence of RInDCA$_\text {e}$

The following assumption is made in this subsection.

Assumption 2

Suppose that the DC components $f_1$ and $f_2$ are respectively $\sigma _1$-convex and $\sigma _2$-convex with $\sigma _1+\sigma _2>0$.

Now, we start to establish the subsequential convergence of RInDCA$_\text {e}$.

Lemma 4.1

Let $\{\mathbf{x }^k\}$ be the sequence generated by RInDCA$_\text {e}$ and $\gamma \in [0,(\sigma _1+\sigma _2)/2)$, then the sequence $\{f(\mathbf{x }^k)+ \frac{\sigma _1+\sigma _2-\gamma }{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 \}$ is nonincreasing and for all $k \ge 0$,

$$\begin{aligned} f(\mathbf{x }^{k+1}) + \frac{\sigma _1+\sigma _2-\gamma }{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2 \le \, &f(\mathbf{x }^{k}) + \frac{\sigma _1+\sigma _2-\gamma }{2}\Vert \mathbf{x }^{k}-\mathbf{x }^{k-1}\Vert ^2 \nonumber \\&-\frac{\sigma _1+\sigma _2-2\gamma }{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2. \end{aligned}$$

(6)

Proof

Because $\mathbf{x }^{k+1}$ satisfies (3), thus $\mathbf{y }^k+\gamma (\mathbf{x }^k-\mathbf{x }^{k-1}) \in \partial f_1(\mathbf{x }^{k+1})$, then by $\sigma _1$-convexity of $f_1$, we have

$$\begin{aligned} f_1(\mathbf{x }^k) \ge f_1(\mathbf{x }^{k+1}) + \langle \mathbf{y }^k + \gamma (\mathbf{x }^k-\mathbf{x }^{k-1}),\mathbf{x }^k-\mathbf{x }^{k+1}\rangle +\frac{\sigma _1}{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2. \end{aligned}$$

(7)

On the other hand, it follows from $\mathbf{y }^k \in \partial f_2(\mathbf{x }^k)$ and $\sigma _2$-convexity of $f_2$ that

$$\begin{aligned} f_2(\mathbf{x }^{k+1}) \ge f_2(\mathbf{x }^k) + \langle \mathbf{y }^k,\mathbf{x }^{k+1}-\mathbf{x }^k \rangle +\frac{\sigma _2}{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2. \end{aligned}$$

(8)

Summing (7) to (8) and reshuffling the terms, we derive that

$$\begin{aligned} f(\mathbf{x }^k) \ge f(\mathbf{x }^{k+1}) + \gamma \langle \mathbf{x }^k-\mathbf{x }^{k-1},\mathbf{x }^k-\mathbf{x }^{k+1}\rangle + \frac{\sigma _1+\sigma _2}{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2. \end{aligned}$$

(9)

By applying $\langle \mathbf{x }^k-\mathbf{x }^{k-1},\mathbf{x }^k-\mathbf{x }^{k+1}\rangle \ge -(\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 + \Vert \mathbf{x }^k-\mathbf{x }^{k+1}\Vert ^2)/{2}$ to (9), we obtain

$$\begin{aligned} f(\mathbf{x }^{k+1}) + \frac{\sigma _1+\sigma _2-\gamma }{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2 \le \, &f(\mathbf{x }^{k}) + \frac{\sigma _1+\sigma _2-\gamma }{2}\Vert \mathbf{x }^{k}-\mathbf{x }^{k-1}\Vert ^2 \nonumber \\&-\frac{\sigma _1+\sigma _2-2\gamma }{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2. \end{aligned}$$

Moreover, we get from $\gamma < (\sigma _1+\sigma _2)/2$ that $(\sigma _1 + \sigma _2 -2\gamma )/2 > 0$, thus the sequence $\{f(\mathbf{x }^k)+ \frac{\sigma _1+\sigma _2-\gamma }{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 \}$ is nonincreasing. $\square$

Theorem 4.1

Let $\{\mathbf{x }^k\}$ be the sequence generated by RInDCA$_\text {e}$ and $\gamma \in [0,(\sigma _1+\sigma _2)/2)$. Then the following statements hold:

• (i) $\lim \limits _{k\rightarrow \infty }{\Vert \mathbf{x }^{k}-\mathbf{x }^{k-1}\Vert = 0}$;

• (ii) If $\{\mathbf{x }^k\}$ is bounded, then any limit point of $\{\mathbf{x }^k\}$ is a critical point of (P).

Proof

(i) Let us denote $\eta _1 := (\sigma _1+\sigma _2-\gamma )/2$ and $\eta _2 := (\sigma _1+\sigma _2-2\gamma )/{2}$. Clearly, $\eta _1>0$, $\eta _2 >0$, and the inequality (6) reads as

$$\begin{aligned} f(\mathbf{x }^{k+1}) + \eta _1\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2 \le f(\mathbf{x }^{k}) + \eta _1\Vert \mathbf{x }^{k}-\mathbf{x }^{k-1}\Vert ^2 -\eta _2 \Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2. \end{aligned}$$

(10)

By summing (10) from $k=0$ to n, we obtain that

$$\begin{aligned} \eta _2\sum _{k=0}^{n}\Vert \mathbf{x }^{k}-\mathbf{x }^{k-1}\Vert ^2 \le f(\mathbf{x }^0) - \left( f(\mathbf{x }^{n+1})+\eta _1\Vert \mathbf{x }^{n+1}-\mathbf{x }^n\Vert ^2\right) . \end{aligned}$$

(11)

Recalling that f is bounded below by a scalar $f^*$ (term (b) of Assumption 1), then we have

$$\begin{aligned} f(\mathbf{x }^{n+1})+\eta _1\Vert \mathbf{x }^{n+1}-\mathbf{x }^n\Vert ^2\ge f^*, \end{aligned}$$

thus we obtain

$$\begin{aligned} \sum _{k=0}^{n}\Vert \mathbf{x }^{k}-\mathbf{x }^{k-1}\Vert ^2 \le \frac{f(\mathbf{x }^0)-f^*}{\eta _2},\quad \forall n\in \mathbb {N}. \end{aligned}$$

Thus, $\sum _{k=0}^{\infty } \Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 < \infty$ which implies $\lim \limits _{k\rightarrow \infty } \Vert \mathbf{x }^k -\mathbf{x }^{k-1}\Vert = 0.$ (ii) The boundedness of $\{\mathbf{x }^k\}$ together with term (a) of Assumption 1 implies the boundedness of $\{\mathbf{y }^k\}$ (see Theorem 3.16 in Beck (2017)). Let $\bar{\mathbf{x }}$ be any limit point of $\{\mathbf{x }^k\}$, then there exists a convergent subsequence such that $\lim \limits _{i\rightarrow \infty }\mathbf{x }^{k_i} = \bar{\mathbf{x }}$. Moreover, since $\{\mathbf{y }^{k_i}\}$ is bounded in $\mathbb {R}^n$, there exists a convergent subsequence of $\{\mathbf{y }^{k_i}\}$. Without loss of generality, we can assume that the sequence $\{\mathbf{y }^{k_i}\}$ is convergent and $\lim \limits _{i\rightarrow \infty }\mathbf{y }^{k_i} = \bar{\mathbf{y }}$. Then taking into account that $\mathbf{y }^{k_i}\in \partial f_2(\mathbf{x }^{k_i})$ for all i, $\mathbf{y }^{k_i} \rightarrow \bar{\mathbf{y }}$, $\mathbf{x }^{k_i} \rightarrow \bar{\mathbf{x }}$, and the closedness of the graph $\partial f_2$ (see Theorem 24.4 in Rockafellar (1970)), we obtain

$$\begin{aligned} \bar{\mathbf{y }}\in \partial f_2(\bar{\mathbf{x }}). \end{aligned}$$

(12)

On the other hand, the next relation holds for all i

$$\begin{aligned} \mathbf{y }^{k_i}+\gamma (\mathbf{x }^{k_i}-\mathbf{x }^{k_i-1})\in \partial f_1(\mathbf{x }^{k_i+1}). \end{aligned}$$

By the fact that $\lim \limits _{i\rightarrow \infty }\mathbf{x }^{k_i+1} = \bar{\mathbf{x }}$ since $\lim \limits _{i\rightarrow \infty }{\Vert \mathbf{x }^{k_i+1}-\mathbf{x }^{k_i}\Vert = 0}$, then combining $\mathbf{y }^{k_i} \rightarrow \bar{\mathbf{y }}$, $\gamma (\mathbf{x }^{k_i}-\mathbf{x }^{k_i-1}) \rightarrow 0$, $\mathbf{x }^{k_i+1} \rightarrow \bar{\mathbf{x }}$, and the closedness of the graph $\partial f_1$, we have

$$\begin{aligned} \bar{\mathbf{y }}\in \partial f_1(\bar{\mathbf{x }}). \end{aligned}$$

(13)

We conclude from (12) and (13) that $\bar{\mathbf{y }} \in \partial f_1(\bar{\mathbf{x }})\cap \partial f_2(\bar{\mathbf{x }}) \ne \emptyset$, thus $\bar{\mathbf{x }}$ is a critical point of problem (P). $\square$

4.2 Subsequential convergence of RInDCA$_\text {n}$

The following assumption is made in this part.

Assumption 3

Suppose that the second DC component $f_2$ is $\sigma _2$-convex with $\sigma _2>0$.

Now, we start to establish the subsequential convergence of RInDCA$_\text {n}$.

Lemma 4.2

Let $\{\mathbf{x }^k\}$ be the sequence generated by RInDCA$_\text {n}$ and $\gamma \in [0,{\bar{\sigma }}/2)$, where ${\bar{\sigma }} = \sigma _1(1-t) + \sigma _2 -\lambda \sigma _2/t$ with $\lambda \in (0,1)$, $t\in (0,1]$. Then the sequence $\{f(\mathbf{x }^k) + \frac{{\bar{\sigma }}-\gamma }{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2\}$ is nonincreasing and for all $k\ge 0$, we have

$$\begin{aligned} f({ \mathbf{x }^{k+1} }) + \frac{{\bar{\sigma }} -\gamma }{2}\Vert { \mathbf{x }^{k+1}-\mathbf{x }^k}\Vert ^2 \le \, &f({ \mathbf{x }^k }) + \frac{{\bar{\sigma }} -\gamma }{2}\Vert { \mathbf{x }^k-\mathbf{x }^{k-1} }\Vert ^2 \nonumber \\&-\frac{{\bar{\sigma }}-2\gamma }{2}\Vert { \mathbf{x }^k-\mathbf{x }^{k-1} } \Vert ^2. \end{aligned}$$

(14)

Proof

Because $\mathbf{x }^{k+1}$ satisfies (2), let $\mathbf{y }^k \in \partial f_2(\mathbf{x }^k)$ such that $\mathbf{y }^k+\gamma (\mathbf{x }^k-\mathbf{x }^{k-1}) \in \partial _{\varepsilon ^{k+1}} f_1(\mathbf{x }^{k+1})$, we have

$$\begin{aligned} f_1(\mathbf{x }^k) \overset{{(1)}}{\ge} \, &f_1(\mathbf{x }^{k+1}) + \langle \mathbf{y }^k + \gamma (\mathbf{x }^k-\mathbf{x }^{k-1}),\mathbf{x }^k-\mathbf{x }^{k+1}\rangle \nonumber \\&+\frac{\sigma _1(1-t)}{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2 -\frac{\varepsilon ^{k+1}}{t} \nonumber \\ \ge \, &f_1(\mathbf{x }^{k+1}) + \langle \mathbf{y }^k + \gamma (\mathbf{x }^k-\mathbf{x }^{k-1}),\mathbf{x }^k-\mathbf{x }^{k+1}\rangle \\&+\frac{\sigma _1(1-t)-\lambda \sigma _2/t}{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2, \nonumber \end{aligned}$$

(15)

where the second inequality is implied by the fact $\varepsilon ^{k+1}\le \lambda \frac{\sigma _2}{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2$. On the other hand, $\mathbf{y }^k \in \partial f_2(\mathbf{x }^k)$ and $\sigma _2$-convexity of $f_2$ imply that

$$\begin{aligned} f_2(\mathbf{x }^{k+1}) \ge f_2(\mathbf{x }^k) + \langle \mathbf{y }^k,\mathbf{x }^{k+1}-\mathbf{x }^k \rangle +\frac{\sigma _2}{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2. \end{aligned}$$

(16)

Summing (15) to (16) and reshuffling the terms, we obtain that

$$\begin{aligned} f(\mathbf{x }^k) \ge f(\mathbf{x }^{k+1}) + \gamma \langle \mathbf{x }^k-\mathbf{x }^{k-1},\mathbf{x }^k-\mathbf{x }^{k+1}\rangle + \frac{{\bar{\sigma }}}{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2. \end{aligned}$$

(17)

By applying $\langle \mathbf{x }^k-\mathbf{x }^{k-1},\mathbf{x }^k-\mathbf{x }^{k+1}\rangle \ge -(\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 + \Vert \mathbf{x }^k-\mathbf{x }^{k+1}\Vert ^2)/{2}$ to (17), we obtain (14). Moreover, $\gamma \in [0,{\bar{\sigma }}/2)$ implies $({\bar{\sigma }} -2\gamma )/2> 0$, thus the sequence $\{f(\mathbf{x }^k) + \frac{{\bar{\sigma }} -\gamma }{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2\}$ is nonincreasing. $\square$

The proof of the next theorem is omitted since it follows from the similar arguments as in Theorem 4.1.

Theorem 4.2

Let $\{\mathbf{x }^k\}$ be the sequence generated by RInDCA$_\text {n}$ and $\gamma \in [0,{\bar{\sigma }}/2)$, where ${\bar{\sigma }} = \sigma _1(1-t) + \sigma _2 -\lambda \sigma _2/t$ with $\lambda \in (0,1)$, $t\in (0,1]$. Then the following statements hold:

• (i) $\lim \limits _{k\rightarrow \infty }{\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert = 0}$;

• (ii) If $\{\mathbf{x }^k\}$ is bounded, then any limit point of $\{\mathbf{x }^k\}$ is a critical point of (P).

4.3 Some results on the sequences obtained by RInDCA

In this subsection, we provide some important results on the sequences obtained by RInDCA$_\text {e}$ and RInDCA$_\text {n}$.

Proposition 4.1

Suppose that the assumptions in Theorem 4.1 hold. Let $\{\mathbf{x }^k\}$ be the sequence generated by RInDCA$_\text {e}$ and let $\Omega _1$ be the set of the limit points of $\{\mathbf{x }^k\}$. If $\{\mathbf{x }^k\}$ is bounded, then we have

• (i) $\lim \limits _{k\rightarrow \infty } f(\mathbf{x }^k):= \zeta$ exists;

• (ii) $f \equiv \zeta$ on $\Omega _1$.

Proof

(i) Lemma 4.1 implies that the sequence $\{f(\mathbf{x }^k)+ \frac{\sigma _1+\sigma _2-\gamma }{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 \}$ is nonincreasing, combining the fact that this sequence is bounded below, thus it converges. On the other hand, (ii) of Theorem 4.1 implies that $\lim \limits _{k\rightarrow \infty } \Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 = 0$. Therefore, $\lim \limits _{k\rightarrow \infty } f(\mathbf{x }^k):=\zeta$ exists. (ii) Because $\Omega _1$ is nonempty, thus given any $\bar{\mathbf{x }}\in \Omega _1$, there exists a subsequence $\{\mathbf{x }^{k_i}\}$ such that $\lim \limits _{i\rightarrow \infty } \mathbf{x }^{k_i} = \bar{\mathbf{x }}$. Then, we get from $\mathbf{y }^{k_i} \in \partial f_2(\mathbf{x }^{k_i})$ and $\sigma _2$-convexity of $f_2$ that

$$\begin{aligned} f_2(\mathbf{x }^{k_i+1}) \ge f_2(\mathbf{x }^{k_i}) + \langle \mathbf{y }^{k_i} , \mathbf{x }^{k_i+1}-\mathbf{x }^{k_i} \rangle + \frac{\sigma _2}{2}\Vert \mathbf{x }^{k_i+1}-\mathbf{x }^{k_i}\Vert ^2. \end{aligned}$$

(18)

Similarly, we obtain as well from $\mathbf{y }^{k_i} + \gamma (\mathbf{x }^{k_i}-\mathbf{x }^{k_i-1}) \in \partial f_1(\mathbf{x }^{k_i+1})$ and $\sigma _1$-convexity of $f_1$ that

$$\begin{aligned} f_1(\bar{\mathbf{x }}) \ge f_1(\mathbf{x }^{k_i+1}) + \langle \mathbf{y }^{k_i} + \gamma (\mathbf{x }^{k_i}-\mathbf{x }^{k_i-1}),\bar{\mathbf{x }} - \mathbf{x }^{k_i+1} \rangle + \frac{\sigma _1}{2}\Vert \bar{\mathbf{x }} - \mathbf{x }^{k_i+1} \Vert ^2. \end{aligned}$$

(19)

Then we have

$$\begin{aligned} \zeta =&\lim \limits _{k\rightarrow \infty } f(\mathbf{x }^k) \\ =&\lim \limits _{i\rightarrow \infty } f_1(\mathbf{x }^{k_i+1})-f_2(\mathbf{x }^{k_i+1}) \\ \overset{{(18)}}{\le }&\limsup \limits _{i\rightarrow \infty } f_1(\mathbf{x }^{k_i+1})-\{f_2(\mathbf{x }^{k_i})+\langle \mathbf{y }^{k_i},\mathbf{x }^{k_i+1}-\mathbf{x }^{k_i} \rangle +\frac{\sigma _2}{2}\Vert \mathbf{x }^{k_i+1}-\mathbf{x }^{k_i}\Vert ^2\}\\ \overset{{(19)}}{\le }&\limsup \limits _{i\rightarrow \infty } f_1(\bar{\mathbf{x }}) -\langle \mathbf{y }^{k_i} +\gamma (\mathbf{x }^{k_i}-\mathbf{x }^{k_i-1}),\bar{\mathbf{x }}-\mathbf{x }^{k_i+1}\rangle - \frac{\sigma _1}{2}\Vert \mathbf{x }^{k_i+1}-\bar{\mathbf{x }}\Vert ^2\\&-f_2(\mathbf{x }^{k_i})-\langle \mathbf{y }^{k_i},\mathbf{x }^{k_i+1}-\mathbf{x }^{k_i}\rangle -\frac{\sigma _2}{2}\Vert \mathbf{x }^{k_i+1}-\mathbf{x }^{k_i}\Vert ^2 \\ =&\,f(\bar{\mathbf{x }}), \end{aligned}$$

where the last equality follows that $\lim \limits _{i\rightarrow \infty } \Vert \mathbf{x }^{k_i}-\mathbf{x }^{k_i-1}\Vert = 0$, $f_2$ is continuous over $\text {dom}f_1$, and $\{\mathbf{y }^{k_i}\}$ is bounded. On the other hand, because f is a closed function, then we have

$$\begin{aligned} f(\bar{\mathbf{x }})&= f_1(\bar{\mathbf{x }}) - f_2(\bar{\mathbf{x }}) \\&\le \liminf \limits _{i\rightarrow \infty } f_1(\mathbf{x }^{k_i}) - f_2(\mathbf{x }^{k_i})\\&= \liminf \limits _{i\rightarrow \infty } f(\mathbf{x }^{k_i}) =\zeta . \end{aligned}$$

Thus, we obtain that $f(\bar{\mathbf{x }}) = \zeta$ and conclude that $f\equiv \zeta$ on $\Omega _1$. $\square$

We can obtain a similar proposition for RInDCA$_\text {n}$ described as follows whose proof is omitted.

Proposition 4.2

Suppose that the assumptions in Theorem 4.2 hold. Let $\{\mathbf{x }^k\}$ be the sequence generated by RInDCA$_\text {n}$ and let $\Omega _2$ be the set of the limit points of $\{\mathbf{x }^k\}$. If $\{\mathbf{x }^k\}$ is bounded, then we have

• (i) $\lim \limits _{k\rightarrow \infty } f(\mathbf{x }^k):= {\widetilde{\zeta }}$ exists;

• (ii) $f \equiv {\widetilde{\zeta }}$ on $\Omega _2$.

5 Sequential convergence analysis

In this section, we will establish the sequential convergence of RInDCA. Let us consider the next auxiliary functions:

$$\begin{aligned}&E({ \mathbf{x },\mathbf{y },\mathbf{z }}) = f_1({ \mathbf{x }}) -\langle { \mathbf{x },\mathbf{y }}\rangle + f_2^*({ \mathbf{y }}) + \frac{\sigma _1- \gamma }{2}\Vert { \mathbf{x }-\mathbf{z }}\Vert ^2, \end{aligned}$$

(20)

$$\begin{aligned}&{\widetilde{E}}(\mathbf{x },\mathbf{y },\mathbf{z }) = f_1(\mathbf{x }) - \langle \mathbf{x },\mathbf{y }\rangle + f_2^*(\mathbf{y }) + \frac{{\bar{\sigma }}-\sigma _2-\gamma }{2}\Vert \mathbf{x }-\mathbf{z }\Vert ^2, \end{aligned}$$

(21)

where $f_1$ and $f_2$ are defined in problem (P) with the strong convexity parameters $\sigma _1$ and $\sigma _2$, $f_2^*$ is the conjugate function of $f_2$, and ${\bar{\sigma }}$ is defined in Lemma 4.2. Note that our construction of E and ${\widetilde{E}}$ is motivated by Liu et al. (2019), and our sequential convergence analysis follows similar arguments as in Attouch et al. (2013); Liu et al. (2019).

First, the following Proposition 5.1 establishes the non-increasing property of the sequence $\{E({ \mathbf{x }}^k,{ \mathbf{y }}^{k-1},{ \mathbf{x }}^{k-1})\}_{k\ge 1}$.

Proposition 5.1

Suppose that the assumptions in Theorem 4.1 hold. Let E be defined as in (20), ${ \{\mathbf{x }^k\}}$ be the sequence generated by RInDCA$_\text {e}$, and ${ \mathbf{y }^k} \in \partial f_2({ \mathbf{x }^k})$ for all $k\ge 0$. Then we have

• (i) For any $k\ge 1$,

  $$\begin{aligned} E({ \mathbf{x }}^{k+1},{ \mathbf{y }}^k,{ \mathbf{x }}^k) \le E({ \mathbf{x }}^k,{ \mathbf{y }}^{k-1},{ \mathbf{x }}^{k-1}) - \frac{\sigma _1+\sigma _2-2\gamma }{2}\Vert { \mathbf{x }}^k-{ \mathbf{x }}^{k-1}\Vert ^2; \end{aligned}$$

  (22)

• (ii) If $\{\mathbf{x }^k\}$ is bounded, let $\Upsilon$ be the set of all limit points of the sequence ${ \{(\mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1})\}}$. Then $\Upsilon$ is a nonempty compact set,

  $$\begin{aligned} \lim \limits _{k\rightarrow \infty } E({ \mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1})}:=\zeta \end{aligned}$$

  exists, and $E\equiv \zeta$ on $\Upsilon$.

Proof

(i) For any $k\ge 1$, $\mathbf{y }^{k-1}\in \partial f_2(\mathbf{x }^{k-1})$ together with $\sigma _2$-convexity of $f_2$ implies that

$$\begin{aligned} f_2(\mathbf{x }^k)\ge f_2(\mathbf{x }^{k-1})+\langle \mathbf{y }^{k-1},\mathbf{x }^k-\mathbf{x }^{k-1}\rangle + \frac{\sigma _2}{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2. \end{aligned}$$

(23)

Thus we have

$$\begin{aligned} \langle \mathbf{y }^{k-1},\mathbf{x }^k\rangle - f_2(\mathbf{x }^k) + \frac{\sigma _2}{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2&\overset{{(23)}}{\le } \langle \mathbf{y }^{k-1},\mathbf{x }^{k-1}\rangle - f_2(\mathbf{x }^{k-1}) \nonumber \\&\ = f_2^*(\mathbf{y }^{k-1}), \end{aligned}$$

(24)

where the equality is implied by $\mathbf{y }^{k-1}\in \partial f_2(\mathbf{x }^{k-1})$, and thus $\langle \mathbf{y }^{k-1},\mathbf{x }^{k-1}\rangle = f_2(\mathbf{x }^{k-1}) + f_2^*(\mathbf{y }^{k-1})$ (see Theorem 4.20 in Beck (2017)). Moreover, $\mathbf{y }^k +\gamma (\mathbf{x }^k-\mathbf{x }^{k-1}) \in \partial f_1(\mathbf{x }^{k+1})$ and $\sigma _1$-convexity of $f_1$ imply that

$$\begin{aligned} f_1(\mathbf{x }^k) \ge f_1(\mathbf{x }^{k+1}) +\langle \mathbf{y }^k +\gamma (\mathbf{x }^k-\mathbf{x }^{k-1}),\mathbf{x }^k-\mathbf{x }^{k+1} \rangle + \frac{\sigma _1}{2}\Vert \mathbf{x }^k-\mathbf{x }^{k+1}\Vert ^2. \end{aligned}$$

(25)

Next, we have

$$\begin{aligned}&E(\mathbf{x }^{k+1},\mathbf{y }^k,\mathbf{x }^k) \\ &\quad=f_1(\mathbf{x }^{k+1})-\langle \mathbf{x }^{k+1},\mathbf{y }^k\rangle + f_2^*(\mathbf{y }^k) + \frac{\sigma _1-\gamma }{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2 \\ &\quad\overset{{(25)}}{\le }f_1(\mathbf{x }^k) - \langle \mathbf{y }^k + \gamma (\mathbf{x }^k-\mathbf{x }^{k-1}),\mathbf{x }^k-\mathbf{x }^{k+1}\rangle -\frac{\sigma _1}{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2 \\&\qquad-\langle \mathbf{x }^{k+1},\mathbf{y }^k\rangle + f_2^*(\mathbf{y }^k) + \frac{\sigma _1-\gamma }{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2 \\ &\quad=f_1(\mathbf{x }^k) - \langle \mathbf{y }^k + \gamma (\mathbf{x }^k-\mathbf{x }^{k-1}),\mathbf{x }^k-\mathbf{x }^{k+1}\rangle -\frac{\sigma _1}{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2 \\&\qquad-\langle \mathbf{x }^{k+1},\mathbf{y }^{k}\rangle +\langle \mathbf{y }^k,\mathbf{x }^k\rangle -f_2(\mathbf{x }^k) + \frac{\sigma _1-\gamma }{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2 \\ &\quad=f_1(\mathbf{x }^k) - f_2(\mathbf{x }^k) - \langle \gamma (\mathbf{x }^k-\mathbf{x }^{k-1}),\mathbf{x }^k-\mathbf{x }^{k+1}\rangle -\frac{\gamma }{2}\Vert \mathbf{x }^{k+1}-\mathbf{x }^k\Vert ^2 \\ &\quad\le f_1(\mathbf{x }^k) - f_2(\mathbf{x }^k) + \frac{\gamma }{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 \\ &\quad \overset{{(24)}}{\le }f_1(\mathbf{x }^k) -\langle \mathbf{x }^k,\mathbf{y }^{k-1}\rangle + f_2^*(\mathbf{y }^{k-1}) + \frac{\gamma -\sigma _2}{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 \\ &\quad=E(\mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1}) - \frac{\sigma _1+\sigma _2-2\gamma }{2}\Vert \mathbf{x }^{k}-\mathbf{x }^{k-1}\Vert ^2, \end{aligned}$$

where the second equality is implied by $\mathbf{y }^k \in \partial f_2(\mathbf{x }^k)$, and thus $f_2(\mathbf{x }^k) + f_2^*(\mathbf{y }^k) = \langle \mathbf{x }^k,\mathbf{y }^k\rangle$; the second inequality follows from $\langle \mathbf{x }^k-\mathbf{x }^{k-1},\mathbf{x }^k-\mathbf{x }^{k+1}\rangle \ge -(\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 + \Vert \mathbf{x }^k-\mathbf{x }^{k+1}\Vert ^2)/2$.

(ii) The boundedness of $\{\mathbf{x }^k\}$ implies the boundedness of $\{\mathbf{y }^{k-1}\}$. Thus, the sequence $\{(\mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1})\}$ is bounded, yielding that $\Upsilon$ is a nonempty compact set. Let ${ (\bar{\mathbf{x }},\bar{\mathbf{y }},\bar{\mathbf{z }})} \in \Upsilon$, it is easy to see that $(\bar{\mathbf{x }},\bar{\mathbf{y }},\bar{\mathbf{z }}) \in \Upsilon$ implies $\bar{\mathbf{x }} = \bar{\mathbf{z }} \in \Omega _1$. For any $k\ge 1$, we have

$$\begin{aligned} E(\mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1})&= f_1({ \mathbf{x }^k}) -\langle { \mathbf{x }^k,\mathbf{y }^{k-1}}\rangle + f_2^*({ \mathbf{y }^{k-1}}) + \frac{\sigma _1- \gamma }{2}\Vert { \mathbf{x }^k-\mathbf{x }^{k-1}}\Vert ^2 \\&\ge f_1(\mathbf{x }^k) - f_2(\mathbf{x }^k) + \frac{\sigma _1- \gamma }{2}\Vert { \mathbf{x }^k-\mathbf{x }^{k-1}}\Vert ^2 \\&\ge f^* + \frac{\sigma _1- \gamma }{2}\Vert { \mathbf{x }^k-\mathbf{x }^{k-1}}\Vert ^2, \end{aligned}$$

where the first inequality follows from $f_2(\mathbf{x }^k) + f_2^*(\mathbf{y }^{k-1}) \ge \langle \mathbf{x }^k,\mathbf{y }^{k-1}\rangle$ and $f^*$ is the lower bound of f. Thus, $\liminf \limits _{k\rightarrow \infty } E(\mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1}) \ge f^*$. Then, combining the fact that the sequence $\{E({ \mathbf{x }}^k,{ \mathbf{y }}^{k-1},{ \mathbf{x }}^{k-1})\}$ is nonincreasing (statement (i)), we obtain the existence of $\lim \limits _{k\rightarrow \infty } E({ \mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1})}$. Next, we prove the last part of (ii). Given any $(\bar{\mathbf{x }},\bar{\mathbf{y }},\bar{\mathbf{x }}) \in \Upsilon$, there exists a subsequence $(\mathbf{x }^{k_i},\mathbf{y }^{k_i-1},\mathbf{x }^{k_i-1})$ such that

$$\begin{aligned} \lim \limits _{i\rightarrow \infty } \Vert (\mathbf{x }^{k_i},\mathbf{y }^{k_i-1},\mathbf{x }^{k_i-1})-(\bar{\mathbf{x }},\bar{\mathbf{y }},\bar{\mathbf{x }})\Vert = 0. \end{aligned}$$

Then we have

$$\begin{aligned}&\lim \limits _{k\rightarrow \infty } E(\mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1}) \\ &\quad=\lim \limits _{i\rightarrow \infty } E(\mathbf{x }^{k_i+1},\mathbf{y }^{k_i},\mathbf{x }^{k_i}) \\ &\quad=\lim \limits _{i\rightarrow \infty } f_1(\mathbf{x }^{k_i+1}) - \langle \mathbf{x }^{k_i+1},\mathbf{y }^{k_i}\rangle +f_2^*(\mathbf{y }^{k_i}) + \frac{\sigma _1-\gamma }{2}\Vert \mathbf{x }^{k_i+1}-\mathbf{x }^{k_i}\Vert ^2 \\ &\quad=\lim \limits _{i\rightarrow \infty } f_1(\mathbf{x }^{k_i+1}) - \langle \mathbf{x }^{k_i+1},\mathbf{y }^{k_i}\rangle - f_2(\mathbf{x }^{k_i}) + \langle \mathbf{y }^{k_i},\mathbf{x }^{k_i}\rangle + \frac{\sigma _1-\gamma }{2}\Vert \mathbf{x }^{k_i+1}-\mathbf{x }^{k_i}\Vert ^2 \\ &\quad\le\limsup \limits _{i\rightarrow \infty } f_1(\mathbf{x }^{k_i}) -\langle \mathbf{y }^{k_i} +\gamma (\mathbf{x }^{k_i}-\mathbf{x }^{k_i-1}),\mathbf{x }^{k_i}-\mathbf{x }^{k_i+1}\rangle - \frac{\sigma _1}{2}\Vert \mathbf{x }^{k_i+1}-\mathbf{x }^{k_i}\Vert ^2 \\&\qquad- \langle \mathbf{x }^{k_i+1},\mathbf{y }^{k_i}\rangle - f_2(\mathbf{x }^{k_i}) + \langle \mathbf{y }^{k_i},\mathbf{x }^{k_i}\rangle + \frac{\sigma _1-\gamma }{2}\Vert \mathbf{x }^{k_i+1}-\mathbf{x }^{k_i}\Vert ^2 \\ &\quad=\limsup \limits _{i\rightarrow \infty } f(\mathbf{x }^{k_i}) -\gamma \langle \mathbf{x }^{k_i}-\mathbf{x }^{k_i-1},\mathbf{x }^{k_i}-\mathbf{x }^{k_i+1}\rangle - \frac{\gamma }{2}\Vert \mathbf{x }^{k_i+1}-\mathbf{x }^{k_i}\Vert ^2\\ &\quad=\limsup \limits _{i\rightarrow \infty } f(\mathbf{x }^{k_i}) \\ &\quad=\zeta \\ &\quad=\,f(\bar{\mathbf{x }}) \le E(\bar{\mathbf{x }},\bar{\mathbf{y }},\bar{\mathbf{x }}), \end{aligned}$$

where the third equality follows from $\mathbf{y }^{k_i} \in \partial f_2(\mathbf{x }^{k_i})$ and thus $f_2(\mathbf{x }^{k_i}) + f_2^*(\mathbf{y }^{k_i}) = \langle \mathbf{y }^{k_i},\mathbf{x }^{k_i}\rangle$; the first inequality is implied by $\mathbf{y }^{k_i} + \gamma (\mathbf{x }^{k_i}-\mathbf{x }^{k_i-1}) \in \partial f_1(\mathbf{x }^{k_i+1})$ and $\sigma _1$-convexity of $f_1$; the fifth equality follows from $\lim \limits _{i\rightarrow \infty } \Vert \mathbf{x }^{k_i}-\mathbf{x }^{k_i-1}\Vert =0$. On the other hand, the closedness of E implies that $E(\bar{\mathbf{x }},\bar{\mathbf{y }},\bar{\mathbf{x }}) \le \zeta .$ Thus, we obtain that $E(\bar{\mathbf{x }},\bar{\mathbf{y }},\bar{\mathbf{x }}) = \zeta$ and conclude that $E\equiv \zeta$ on $\Upsilon$. $\square$

Next, we start to create the sequential convergence of RInDCA$_\text {e}$ based on the KL property of E and Proposition 5.1. Note that the KL property of E can be implied by the KL property of f (see Liu et al. 2019).

Theorem 5.1

Suppose that the assumptions in Proposition 5.1 hold. Let E defined in (20) be a KL function, ${ \{\mathbf{x }^k\}}$ be the sequence generated by RInDCA$_\text {e}$, and ${ \mathbf{y }^k} \in \partial f_2({ \mathbf{x }^k})$ for all $k\ge 0$. Then we have

• (i) There exists $D >0$ such that $\forall k\ge 1$,

  $$\begin{aligned} { \text {dist}}({ \mathbf{0 }},\partial E({ \mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1})}) \le D(\Vert { \mathbf{x }^k-\mathbf{x }^{k-1}}\Vert +\Vert { \mathbf{x }^{k-1}-\mathbf{x }^{k-2}}\Vert ). \end{aligned}$$

  (26)

• (ii) If ${ \{\mathbf{x }^k\}}$ is bounded, then ${ \{\mathbf{x }^k\}}$ converges to a critical point of problem (P).

Proof

(i) Note that the subdifferential of E at $\mathbf{w }^k :=(\mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1})$ is:

$$\begin{aligned} \partial E(\mathbf{w }^k) = \begin{bmatrix} \partial f_1(\mathbf{x }^k)-\mathbf{y }^{k-1} + \frac{\gamma -\sigma _2}{2}(\mathbf{x }^k-\mathbf{x }^{k-1}) \\ -\mathbf{x }^k + \partial f_2^*(\mathbf{y }^{k-1}) \\ -\frac{\gamma -\sigma _2}{2}(\mathbf{x }^k-\mathbf{x }^{k-1}) \\ \end{bmatrix}. \end{aligned}$$

Because $\mathbf{y }^{k-1}\in \partial f_2(\mathbf{x }^{k-1})$, thus $\mathbf{x }^{k-1} \in \partial f_2^*(\mathbf{y }^{k-1})$; besides, we have $\mathbf{y }^{k-1} + \gamma (\mathbf{x }^{k-1}-\mathbf{x }^{k-2}) \in \partial f_1(\mathbf{x }^k)$. Combining these relations, we have

$$\begin{aligned} \begin{bmatrix} \gamma (\mathbf{x }^{k-1}-\mathbf{x }^{k-2}) + \frac{\gamma -\sigma _2}{2}(\mathbf{x }^k-\mathbf{x }^{k-1}) \\ -\mathbf{x }^k + \mathbf{x }^{k-1} \\ -\frac{\gamma -\sigma _2}{2}(\mathbf{x }^k-\mathbf{x }^{k-1}) \\ \end{bmatrix} \in \partial E(\mathbf{w }^k). \end{aligned}$$

Thus, it is easy to see that there exists $D >0$ such that $\forall k\ge 1$,

$$\begin{aligned} \text {dist}(\mathbf{0 },\partial E(\mathbf{x }^k,\mathbf{y }^{k-1},\mathbf{x }^{k-1})) \le D(\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert +\Vert \mathbf{x }^{k-1}-\mathbf{x }^{k-2}\Vert ). \end{aligned}$$

(ii) It is sufficient to prove that $\sum _{k=1}^{\infty } \Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert < \infty$. If there exists $N_0 \ge 1$ such that $E(\mathbf{w }^{N_0})=\zeta _1$, then the inequality (22) implies that $\mathbf{x }^k = \mathbf{x }^{N_0}, \forall k\ge N_0$; naturally, the sequence $\{\mathbf{x }^{k}\}$ is convergent. Thus, we can assume that

$$\begin{aligned} E(\mathbf{w }^k) > \zeta , \forall k\ge 1. \end{aligned}$$

Then, it follows from $\Upsilon$ is a compact set, $\Upsilon \subseteq \text {dom}\partial E$ and $E\equiv \zeta$ on $\Upsilon$ that there exists $\varepsilon >0$, $\eta >0$ and $\varphi \in \Xi _{\eta }$ such that

$$\begin{aligned} \varphi '(E(\mathbf{x },\mathbf{y },\mathbf{z })-\zeta ) \text {dist}(\mathbf{0 },\partial E(\mathbf{x },\mathbf{y },\mathbf{z })) \ge 1 \end{aligned}$$

for all $(\mathbf{x },\mathbf{y },\mathbf{z }) \in U$ with

$$\begin{aligned} U =\{(\mathbf{x },\mathbf{y },\mathbf{z }):\text {dist}((\mathbf{x },\mathbf{y },\mathbf{z }),\Upsilon )<\varepsilon \} \cap \{(\mathbf{x },\mathbf{y },\mathbf{z }):\zeta<E(\mathbf{x },\mathbf{y },\mathbf{z })<\zeta +\eta \}. \end{aligned}$$

Moreover, it is easy to derive from $\lim \limits _{k\rightarrow \infty }\text {dist}(\mathbf{w }^k,\Upsilon ) = 0$ and $\lim \limits _{k\rightarrow \infty }E(\mathbf{w }^k) = \zeta$ that there exists $N\ge 1$ such that $\mathbf{w }^k \in U, \forall k\ge N$. Thus,

$$\begin{aligned} \varphi '(E(\mathbf{w }^k)-\zeta ) \text {dist}(\mathbf{0 },\partial E(\mathbf{w }^k) \ge 1,~ \forall k\ge N. \end{aligned}$$

Using the concavity of $\varphi$, we see that $\forall k\ge N$,

$$\begin{aligned}&[\varphi (E(\mathbf{w }^k)-\zeta )-\varphi (E(\mathbf{w }^{k+1})-\zeta )] \text {dist}(\mathbf{0 },\partial E(\mathbf{w }^k))\nonumber \\ &\quad\ge\,\varphi '(E(\mathbf{w }^k)-\zeta ) \text {dist}(\mathbf{0 },\partial E(\mathbf{w }^k)) (E(\mathbf{w }^k)-E(\mathbf{w }^{k+1}))\nonumber \\ &\quad\ge \, E(\mathbf{w }^k)-E(\mathbf{w }^{k+1}). \end{aligned}$$

(27)

Let $\Delta _k := \varphi (E(\mathbf{w }^k)-\zeta )-\varphi (E(\mathbf{w }^{k+1})-\zeta )$ and $C:= \frac{\sigma _1+\sigma _2-2\gamma }{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2$. Then combining (27), (26) and (i) of Proposition 4.2, we have

$$\begin{aligned} \Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert ^2 \le \frac{D}{C}\Delta _k(\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert +\Vert \mathbf{x }^{k-1}+\mathbf{x }^{k-2}\Vert ). \end{aligned}$$

Thus, taking square roots on both sides, we obtain

$$\begin{aligned} \Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert&\le \sqrt{\frac{2D}{C}\Delta _k} \sqrt{\frac{\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert +\Vert \mathbf{x }^{k-1}-\mathbf{x }^{k-2}\Vert }{2}} \\&\le \frac{D}{C}\Delta _k + \frac{1}{4}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert + \frac{1}{4}\Vert \mathbf{x }^{k-1}-\mathbf{x }^{k-2}\Vert , \end{aligned}$$

this yields

$$\begin{aligned} \frac{1}{2}\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert \le \frac{D}{C}\Delta _k + \frac{1}{4}\Vert \mathbf{x }^{k-1}-\mathbf{x }^{k-2}\Vert - \frac{1}{4}\Vert \mathbf{x }^k - \mathbf{x }^{k-1}\Vert . \end{aligned}$$

Considering also that $\sum _{k=1}^{\infty } \Delta _k < \infty$, thus the above inequality implies that $\sum _{k=1}^{\infty } \Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert < \infty$, which indicates that $\{\mathbf{x }^k\}$ is a Cauchy sequence, and thus convergent. The proof is completed. $\square$

The sequential convergence of RInDCA$_\text {n}$ can be similarly developed based on the KL property of ${\widetilde{E}}$, Proposition 4.2, and Proposition 5.1 for ${\widetilde{E}}$, thus the proof is omitted.

6 Numerical results

In this part, we conduct numerical simulations on testing copositivity of matrices (constrained case) and image denoising problem (unconstrained case). All experiments are implemented in Matlab 2019a on a 64-bit PC with an Intel(R) Core(TM) i5-6200U CPU (2.30GHz) and 8GB of RAM.

6.1 Checking copositivity of matrices

Recall that a symmetric matrix $\mathbf{A } \in \mathbb {R}^{n\times n}$ is called copositive if $\mathbf{x }^{\top }\mathbf{A }\mathbf{x } \ge 0$ for all $\mathbf{x }\ge 0$, and called non-copositive otherwise. Consider the next formulation

$$\begin{aligned} \min \quad&\frac{1}{2}\mathbf{x }^{\top }\mathbf{A }\mathbf{x } \\ \text {s.t.}\quad&\mathbf{x }\in \mathbb {R}_{+}^n. \end{aligned}$$

(COPO)

Clearly, $\mathbf{A }$ is copositive if and only if the optimal value of problem (COPO) is nonnegative, and problem (COPO) is equivalent to the next DC program

$$\begin{aligned} f(\mathbf{x }) = \underbrace{\frac{L}{2}\Vert \mathbf{x }\Vert ^2 + \delta _{\mathbb {R}_+^n}(\mathbf{x })}_{f_1(\mathbf{x })} - (\underbrace{\frac{L}{2}\Vert \mathbf{x }\Vert ^2 - \frac{1}{2}\mathbf{x }^{\top }\mathbf{A }\mathbf{x }}_{f_2(\mathbf{x })}),\qquad \qquad \qquad \qquad (DC_{copo}) \end{aligned}$$

where $L\ge \Vert \mathbf{A }\Vert$. In Dür and Hiriart-Urruty (2013), DCA applied for the above DC decomposition is used to check the copositivity of $\mathbf{A }$. For our experiments, the same instances of $\mathbf{A }$ as in Dür and Hiriart-Urruty (2013) will be used. A brief introduction about the instances is given as follows. Let $\mathbf{E }_n\in \mathbb {R}^{n\times n}$ be the matrix with all entries being one. The matrix $\mathbf{A }_{\text {cycle}} = (a_{ij})\in \mathbb {R}^{n\times n}$ is given component-wise by

$$\begin{aligned} a_{ij} := {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }\vert i-j\vert \in \{1,n-1\},\\ 0 &{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

It was known that the following matrix

$$\begin{aligned} \mathbf{Q }_n^{\mu } := \mu (\mathbf{E }_n-\mathbf{A }_{\text {cycle}}) - \mathbf{E }_n \in \mathbb {R}^{n\times n} \end{aligned}$$

is copositive for $\mu \ge 2$ and non-copositive for $\mu < 2$. When $\mu = 2$, $\mathbf{Q }_n^{\mu }$ is called Horn matrix, denoted as $\mathbf{H }_n$.

In order to apply DCA, InDCA$_\text {e}$, and RInDCA$_\text {e}$ for ($DC_{copo}$), we set $L = \Vert \mathbf{A }\Vert$ for DCA and $L = \Vert \mathbf{A }\Vert +1$ for InDCA$_\text {e}$ and RInDCA$_\text {e}$. The inertial ranges of InDCA$_\text {e}$ and RInDCA$_\text {e}$ are [0, 1/2) and $[0,(\Vert \mathbf{A }\Vert +2)/2)$, respectively. For InDCA$_\text {e}$, $\gamma = 0.499$ is set, while for RInDCA$_\text {e}$  we choose $\gamma = 0.499(\Vert \mathbf{A }\Vert +2)$. Moreover, the common initial point for all involved algorithms is randomly generated as follows: we first use the standard normal distribution to generate a point $\mathbf{y } \in \mathbb {R}^n$, then we obtain the initial point $\mathbf{x }^0 = (\mathbf{x }^0_j)$ by setting

$$\begin{aligned} \mathbf{x }^0_j = \frac{e^{\mathbf{y }_j}}{\sum _{j=1}^{n} e^{\mathbf{y }_j}} \end{aligned}$$

for $j = 1,\ldots ,n$. We report the number of iterations, the computational time, and the objective functions values. The bold values in Tables 1 and 2 highlight the best numerical results. The computational time presented is the average execution time (in seconds) over 10 runs.

Table 1 Performances of DCA, InDCA$_\text {e}$, and RInDCA$_\text {e}$ for checking the copositivity of $\mathbf{H }_n$ with $n \in \{500,1000,1500,2000\}$

First, we consider to check the copositivity of the Horn matrices. All algorithms are terminated when $\Vert \mathbf{x }^k-\mathbf{x }^{k-1}\Vert < 10^{-9}$. Table 1 describes the performances of DCA, InDCA$_\text {e}$, and RInDCA$_\text {e}$ for checking the copositivity of $\mathbf{H }_n$ with $n \in \{500,1000,1500,2000\}$. It is observed that DCA and InDCA$_\text {e}$ perform almost the same since the number of iterations of InDCA$_\text {e}$ is very close to that of DCA. We also observe that RInDCA$_\text {e}$ performs the best among the three algorithms, terminating with almost half of the number of iterations of DCA or InDCA$_\text {e}$, and with the smallest objective function values. The reason why InDCA$_\text {e}$ loses the inertial-force effect may be that 0.499 is much smaller than $0.499(\Vert \mathbf{A }\Vert +2)$ for the instance $\mathbf{H }_n$ when n is large.

Next, we check the non-copositivity of $\mathbf{Q }_n^{\mu }$ $(\mu = 1.9)$. Here, the stopping criterion for the involved algorithms DCA, InDCA$_\text {e}$, and RInDCA$_\text {e}$ is that $f(\mathbf{x }^{k}) \le -10^{-6}$. Once this condition is verified, then the non-copositivity of the involved matrix is determined. Table 2 shows the performances of DCA, InDCA$_\text {e}$, and RInDCA$_\text {e}$ for checking the copositivity of $\mathbf{Q }_n^{\mu }$ ($\mu = 1.9$) with $n \in \{500,1000,1500,2000\}$.

Table 2 Performances of DCA, InDCA$_\text {e}$, and RInDCA$_\text {e}$ for checking the copositivity of $\mathbf{Q }_n^{\mu }$ ($\mu = 1.9$) with $n \in \{500,1000,1500,2000\}$

It is also observed that among the involved algorithms RInDCA$_\text {e}$ performs the best, hitting the stopping criterion $f(\mathbf{x }^{k}) \le -10^{-6}$ with about half of the number of iterations as well as the time of DCA or InDCA$_\text {e}$. The behavior of the algorithms for checking the noncopositivity almost coincides with the previous experiment.

The above experiments show that the effect of heavy-ball inertial-force may be lost if the strong convexity of the first DC component is not considered.

6.2 Image denoising problem

Consider a gray-scale image of $m\times n$ pixels and with entries in [0, 1], where 0 represents pure black and 1 represents pure white. The original image $\mathbf{X }\in \mathbb {R}^{m\times n}$ is assumed to be corrupted with a noise $\mathbf{B }$. Then, we obtain the observed image $\widetilde{\mathbf{X }} = \mathbf{X } +\mathbf{B }$, which is known to us. We aim to recover the original image $\mathbf{X }$ by solving the next problem

$$\begin{aligned} \min \bigg \{\frac{\mu }{2}\Vert \mathbf{X }- \widetilde{\mathbf{X }} \Vert ^2_{F} + \text {TV}_{\phi }(\mathbf{X }):\mathbf{X }\in \mathbb {R}^{m\times n} \bigg \}, \end{aligned}$$

(28)

where $\mu >0$ is a trade-off constant; $\widetilde{\mathbf{X }}$ is the observed image; $\Vert \cdot \Vert _F$ represents the Frobenius norm; $\phi :\mathbb {R}_{+} \rightarrow \mathbb {R}$ is a concave function and $\text {TV}_{\phi }$ is defined as:

$$\begin{aligned} \text {TV}_{\phi }(\mathbf{X }) = \sum _{i,j} \phi (\Vert \nabla \mathbf{X }_{i,j}\Vert ) \end{aligned}$$

with

$$\begin{aligned} \Vert \nabla \mathbf{X }_{i,j}\Vert = {\left\{ \begin{array}{ll} \vert \mathbf{X }_{i,j}-\mathbf{X }_{i,j+1}\vert &{}\quad i=m,j\ne n, \\ \vert \mathbf{X }_{i,j}-\mathbf{X }_{i+1,j}\vert &{}\quad i\ne m,j=n, \\ 0 &{}\quad i=m,j=n, \\ \sqrt{(\mathbf{X }_{i,j}-\mathbf{X }_{i+1,j})^2+(\mathbf{X }_{i,j}-\mathbf{X }_{i,j+1})^2}&{}\quad \text {otherwise}.\\ \end{array}\right. } \end{aligned}$$

When $\phi \equiv 1$, we denote $\text {TV}$ as $\text {TV}_{\phi }$. The model (28) with $\phi \equiv 1$ is convex. In (de Oliveira and Tcheou 2019), it has shown that the convex model ($\phi \equiv 1$) is not effective to preserve edges in the restoration process of piecewise-constant images than the model (28) with $\phi$ being concave, such as the $\phi$ described in Table 3. Moreover it has also shown how to derive the DC decomposition for $\text {TV}_{\phi }$. Concretely, $\text {TV}_{\phi }(\mathbf{X })$ has the following DC decomposition

$$\begin{aligned} \text {TV}_{\phi }(\mathbf{X }) = \text {TV}(\mathbf{X }) - (\text {TV}(\mathbf{X }) - \text {TV}_{\phi }(\mathbf{X })). \end{aligned}$$

Then, we get from (28) the next two equivalent DC programs

$$\begin{aligned} \min \{\underbrace{\frac{\mu }{2}\Vert \mathbf{X }- \widetilde{\mathbf{X }} \Vert ^2_{F} + \text {TV}(\mathbf{X })}_{f_1(\mathbf{X })} - (\underbrace{\text {TV}(\mathbf{X }) - \text {TV}_{\phi }(\mathbf{X })}_{f_2(\mathbf{X })}):\mathbf{X }\in \mathbb {R}^{m\times n} \}, \end{aligned}$$

(29)

and

$$\begin{aligned} \min \{\underbrace{\frac{\mu +\rho }{2}\Vert \mathbf{X }- \widetilde{\mathbf{X }} \Vert ^2_{F} + \text {TV}(\mathbf{X })}_{\widetilde{f_1}(\mathbf{X })} - (\underbrace{\frac{\rho }{2}\Vert \mathbf{X }- \widetilde{\mathbf{X }} \Vert ^2_{F} + \text {TV}(\mathbf{X }) - \text {TV}_{\phi }(\mathbf{X })}_{{\widetilde{f}}_2(\mathbf{X })})\}, \end{aligned}$$

(30)

where $\rho >0$.

Table 3 Some examples of concave function $\phi _{a}:\mathbb {R}_{+}\rightarrow \mathbb {R}$ parameterized by $a>0$

We will compare DCA, InDCA$_\text {e}$, RInDCA$_\text {e}$, and ADCA (Phan et al. 2018) (a DCA based algorithm using the Nesterov’s extrapolation). Note that DCA and ADCA are applied for (29), while InDCA$_\text {e}$ and RInDCA$_\text {e}$ are applied for (30). All of the involved algorithms require solving the convex subproblems in form of

$$\begin{aligned} \min \bigg \{ \frac{{\widetilde{t}}}{2}\Vert \mathbf{X }-\mathbf{Z }\Vert _F^2 + \text {TV}(\mathbf{X }):\mathbf{X }\in \mathbb {R}^{m\times n}\bigg \}, \end{aligned}$$

where ${\widetilde{t}}>0$ and $\mathbf{Z }\in \mathbb {R}^{m\times n}$, which can be efficiently solved by the fast gradient projection (FGP) method proposed in Beck and Teboulle (2009).

We use the gray-scale image checkerboard.png ($200\times 200$ pixels) for our experiments. White noise with variance 0.1 is added to the image to produce the observed image $\widetilde{\mathbf{X }}$ in both (29) and (30). Here, we use the same method as described in de Oliveira and Tcheou (2019) to generate the corrupted image. The original image and the corrupted image are shown in Fig. 2. To measure the quality of reconstruction images, we use the peak signal-to-noise ratio (PSNR) and the structural similarity (SSIM) index (see (Monga 2017)). In general, the larger PSNR means the better restoration, while the closer to 1 of SSIM indicates the better reconstruction quality. For all the involved algorithms, the observed images $\widetilde{\mathbf{X }}$ are set as the common initial point, whose convex subproblems are all solved by FGP with the stopping condition that the distance between two consecutive iterates is smaller than $10^{-4}$. It is also worth noting that for problems (29) and (30), another DCA based method with Nesterov’s extrapolation developed in Wen et al. (2018) reduces to DCA.

Fig. 2

Original and corrupted images

We test DCA and ADCA for (29), InDCA$_\text {e}$ and RInDCA$_\text {e}$ for (30). The parameter $\mu$ for both (29) and (30) ranges from 0.8 to 1.6, and we set $\phi = \phi _{\text {rat}}$ with $a=6$, moreover, the parameter $\rho$ in (30) is fixed as 1. The inertial step-size $\gamma$ in InDCA$_\text {e}$ is set as $0.5 \times \rho \times 99\% = 0.495$, and in RInDCA$_\text {e}$ as $0.5\times (\mu +2\rho )\times 99\% = 0.495\mu +0.99$. Besides, the parameter q in ADCA is set as 3. In Table 4, we present in detail the best objective values $f_{\text {best}}$ within 100 iterations and the corresponding values of PSNR and SSIM. The trends of the objective function values together with the values of PSNR and SSIM when $\mu = 1.2$ with respect to running time (average on 10 runs) are plotted in Fig 3. Moreover, the recovered images within 100 iterations are demonstrated in Fig 4. Here, we observes that RInDCA$_\text {e}$ always obtains the lowest objective function values, and almost always the best PSNR and SSIM. The benefit of enlarged inertial step-size is indicated by comparing InDCA$_\text {e}$ and RInDCA$_\text {e}$. Moreover, we also observe that ADCA performs better than DCA and InDCA$_\text {e}$. Finally, by comparing DCA and InDCA$_\text {e}$, we observe that adding a strong convexity term to the original DC program (29) degrades the effectiveness of DCA-based algorithm, which can not be offset by the benefit of inertial-force.

As a conclusion, for the image denoising problem, our method RInDCA$_\text {e}$ is a promising approach, which outperforms the other tested algorithms.

Table 4 Restoration of the corrupted checkerboard image

Fig. 3

The trends of the objective function values together with PSNR and SSIM

Fig. 4

Image reconstructions where a, b, c, d is respectively the resulting image by DCA, InDCA$_\text {e}$, RInDCA$_\text {e}$, and ADCA

7 Conclusion and perspective

In this paper, based on the inertial DC algorithm (de Oliveira and Tcheou 2019) for DC programming, we propose a refined version with larger inertial step-size, for which we prove the subsequential convergence and the sequential convergence by further assuming the KL property. Numerical simulations on checking copositivity of matrices and image denoising problem show the good performance of our proposed methods and the benefit of larger step-size.

About the future works, the numerical test on RInDCA$_\text {n}$ will be investigated. We may also introduce non-heavy-ball and non-Nesterov acceleration to DC programming. Furthermore, the inertial-force procedure will be extended to the partial DC programming (Pham et al. 2021) in which the objective function f depends on two variables $\mathbf{x }$ and $\mathbf{y }$ where $f(\mathbf{x },.)$ and $f(.,\mathbf{y })$ are both DC functions.