1 Introduction

In this note, we introduce two new methods for inverse wave scattering in one and two dimensional domains. This problem appears very naturally in various applications including acoustics (Colten et al. 2000), quantum mechanics (Lagaris and Evangelakis 2011; Sacks and Jaemin 2009), nondestructive testing of materials (Jamil et al. 2013), magnetic resonance imaging (Fessler 2010), and optics (Belai et al. 2008).

It is well-known that this class of problems are highly ill-posed (Colten and Kress 1991) and various methods have been developed to overcome it. These methods include singular value decomposition (Capozzoli et al. 2017), direct sampling methods (Kang et al. 2020), inexact Newton method (Desmal and Bağci 2015), multiple forward method (Tadi et al. 2011), meshless method (2006) (Jin and Zheng 2006), level set method (2008) (Irishina et al. 2008), dual reciprocity (Marin et al. 2006), generalized inverse , proper solution space (Hamad and Tadi 2019), and iterative methods which treats the integral formulation of the scattering problem (Barcelo et al. 2016) and (Novikov 2015). Although this problem has been approached by a number of researchers (Mueller and Siltanen 2012) (also references therein), the research in developing computational algorithms is still underway due to the complexity of the problem (Klibanov and Romanov 2015).

For this particular problem in one dimension, recent results include (Bugarija et al. 2020) where the unknown function is assumed to be piecewise constant Thanh and Klibanov (2020) where a globally convergent numerical method is presented, and Klibanov et al. (2018) where a one-dimensional model is used for land-mind detection. The purpose of this paper is to develop two numerical methods. One method is based on using a set of sampling functions to formulate a moment problem. We have developed this method to solve a Cauchy problem that appears in stable operation of Tadi (2019). In this paper, We develop this method for one-dimensional and two-dimensional domains. For the one-dimensional domain, only the boundary of the domain is accessible for collecting measurements. For the two-dimensional domain, the external boundary of the domain is used to collect the data. When applying the sampling function method to a 2-D domain, the effect of noise in the data becomes crucial. In this paper, we also develop a new tailored filtering technique that is very effective in eliminating the noise in the data. This filtering technique has it’s roots in an inversion method based on proper solution space (Tadi 2017).

The second method uses a perturbation technique, i.e., (Eshkuvatov 2018) to relate the unknown function directly to the measurements provided for the inversion. Using this method, it is also possible to include the effect of nonlinear term that appears in the equation for the error field.

In Sect. 2, we present the method based on the use of sampling functions. In Sect. 3, we present the direct formulation. In Sect. 4, we present the sampling method for 2-D Helmholtz equation. In Sect. 5, we present the new tailored filtering technique, and in Sect. 6, we choose a specific set of sampling functions and develop the direct method for 2-D Helmholtz equation. In Sect. 7 we use a number of numerical results to study the applicability of the present methods.

Notation For the one dimensional problems, Sects. 2 and 3, the domain is a straight line \(\varOmega =[0,1]\) where the outer point at \(x=0\) is accessible. In order to impose non-reflecting boundary condition it is extended to \(\varOmega =[-1,2]\). For Sects. 4, 5, and 6, \(\varOmega ({\mathbf{x}})\) is a closed bounded 2-dimensional domain. Subscript \(()_x\) denotes differentiation with respect to x (in 1-D case). Subscript \(()_n\) denotes the outward normal derivative for 2-D domains. In Sects. 2 and 3, the field is a complex quantity and \({\mathfrak {R}}()\) and \({\mathfrak {I}}()\) denote the real and imaginary part of a complex quantity. We use the notation \(()|_{x=}\) to denote the value of the quantity at x. We use bold letters to denote vectors and matrices.

2 A moment problem

Consider the wave propagation in a one dimensional domain \(x\in \varOmega =[-1,2]\) given by

$$\begin{aligned} u_{xx}+k^2p(x)u=\delta (x-x_0), \end{aligned}$$
(1)

where, u(x) is the electric field, k is the wave number and the unknown function, p(x), represents the material property. The function p(x) is unknown for \(x\in [0,1]\), and is assumed to be equal to a nominal value (here, \(p(x)=1\)) for \(x\in [-1,0]\cup [1,2]\). The domain is excited by the source \(\delta (x-x_0)\) with \(x_0\in [-1,0)\). Non-reflecting boundary conditions are imposed at the boundaries, i.e.

$$\begin{aligned} u_x(-1)+iku(-1)=0,\quad u_x(2)-iku(2)=0, \quad u(0)=g, \end{aligned}$$
(2)

where \(i=\sqrt{-1}\), and \(u(0)=g\) is the collected measurement. The inverse problem of interest is the evaluation of the unknown function p(x) for \(x\in [0,1]\) based on the measurement collected at \(x=0\) which is the accessible point of the domain.

One can start with an initial guess \(\hat{p}(x)\) and obtain a background field given by

$$\begin{aligned} \hat{u}_{xx}+k^2\hat{p}(x)\hat{u}=\delta (x-x_0). \end{aligned}$$
(3)

The error field, \(e(x)=u(x)-{\hat{u}}(x)\), is then given by

$$\begin{aligned} e_{xx}+k^2p(x)u-k^2\hat{p}(x)\hat{u}=0. \end{aligned}$$
(4)

The actual unknown is related to the assumed value according to \(p(x)={\hat{p}}(x)+q(x)\), and the above equation leads to

$$\begin{aligned} e_{xx}+k^2{\hat{p}}e +\underbrace{k^2qe}+k^2q{\hat{u}}=0.,(e_x+ike)|_{x=-1}=0,(e_x-ike)_{x=2}=0. \end{aligned}$$
(5)

The error field is required to satisfy additional condition given by

$$\begin{aligned} e(0)=u(0)-{\hat{u}}(0)= g-{\hat{u}}(0)=\hat{g}. \end{aligned}$$
(6)

The under braced term in Eq. (5) is the nonlinear term involving the two unknowns, i.e., q(x) and e(x). This term is the product of two correction terms. In fact, \(q=0\) for \(x\in [-1,0]\cup [1,2]\), and is only nonzero (and unknown) for \(x\in [0,1]\). We first develop the formulation without this term. We can later on show that the contribution from this term can be included in the form of a series.

Consider a sampling function that is the solution of the differential equation given by

$$\begin{aligned} \psi _{xx}+k^2{\hat{p}}\psi =0.,\psi |_{x=-1}=\psi _0,(\psi _x-ik\psi )_{x=2}=0. \end{aligned}$$
(7)

Multiplying Eq. (5) by \(\psi (x)\) and integrating the product over the region \(x\in [0,2]\) leads to

$$\begin{aligned} \int _0^2\psi \left[ e_{xx}+k^2{\hat{p}}e +k^2q{\hat{u}}\right] dx=0. \end{aligned}$$
(8)

Integrating by parts twice and using Eqs. (7) and (5) leads to

$$\begin{aligned} k^2\int _0^2\psi {\hat{u}}q dx= (\psi e_x)|_{x=0}-(\psi _x e)|_{x=0}=\gamma . \end{aligned}$$
(9)

The quantities on the right hand side, denoted by \(\gamma \) for simplicity, are known. If the measurements are collected for a range of frequencies, i.e., \(k_1,k_2,\ldots ,k_\ell \), then we can write the above equation for each measurement according to

$$\begin{aligned} \int _0^2\psi _\ell {\hat{u}}q dx=\gamma _\ell /k_\ell ^2,\quad \ell =1,\ldots ,L. \end{aligned}$$
(10)

The above equation is the classical moment problem for the unknown function q(x) (Ang et al. 2002). It is easy to note that the functions \(\psi _\ell \) form a linearly independent set.

Remark 1 For i and j, with \(i\ne j\), the functions \(\psi _i(x)\) and \(\psi _j(x)\) are linearly independent for \(x\in [0:2]\). To see that these functions are linearly independent one can consider two sampling functions \(\psi _i(x)\) and \(\psi _j(x)\) that satisfy Eq. (7). Multiplying the equation for \(\psi _i(x)\) by \(\psi _j(x)\), and the equation for \(\psi _j(x)\) by \(\psi _i(x)\), integrating by parts and subtracting them leads to

$$\begin{aligned} (k_i^2-k_j^2)\int _0^2{\hat{p}}(x)\psi _i(x)\psi _j(x)dx=0, \end{aligned}$$

for \(\psi _i(0)=\psi _j(0)=0\). If \(\psi _i(x)=\kappa \psi _j(x)\) for a constant \(\kappa \), then \(k_i=k_j\) which is a contradiction.

The unknown function q(x) is only nonzero within \(x\in [0,1]\). Assuming an expansion of the form \(q(x)=\sum _{j=1}^Nc_j(x)\tau _j\)

$$\begin{aligned} \int _0^1\psi _\ell {\hat{u}}\sum _{j=1}^Nc_j(x)\tau _j dx=\gamma _\ell /k_\ell ^2,\quad \ell =1,2,\ldots ,L. \end{aligned}$$
(11)

placing the unknown values \(\tau _j\) in a vector \(\varvec{\tau }\), and the terms on the right hand side in a vector \(\varvec{\gamma }\) leads to a matrix equation given by

$$\begin{aligned} {\mathbf{A}}\varvec{\tau }= \varvec{\gamma },A_{\ell j}=\left[ \int _0^1{\hat{u}}(x)\psi _\ell (x)c_j(x)dx\right] ,\ell =1,2,\ldots ,L,j=1,2,\ldots ,N. \end{aligned}$$
(12)

Least-square solution of the above linear system can be solved after introducing Tikhonov regularization according to

$$\begin{aligned} \underbrace{ \left[ \begin{array}{c} {\mathbf{A}}\\ \beta \varvec{\varGamma }\end{array}\right] }_{\mathbf{B}}\varvec{\tau }=\underbrace{\left[ \begin{array}{c}\varvec{\gamma }\\ 0\end{array}\right] }_{\varvec{\eta }},\quad \varvec{\tau }=\left[ \mathbf{B}^T\mathbf{B}\right] ^{-1}\mathbf{B}^T\varvec{\eta }, \end{aligned}$$
(13)

where, the parameter \(\beta \) is the weight for the Tikhonov regularization, and \(\varvec{\varGamma }\) is the matrix representing the first derivative operator. Once the above linear system is solved for \(\varvec{\tau }\), then the assumed value can be updated according to \({\hat{p}}(x) = {\hat{p}}(x)+q(x)\). We next formulate a different algorithm that can lead to a similar linear system for the correction term.

3 A direct formulation

Consider the error equation given in Eq. (5)

$$\begin{aligned} e_{xx}+k^2{\hat{p}}e +k^2qe+k^2q{\hat{u}}=0.,(e_x+ike)|_{x=-1}=0,(e_x-ike)_{x=2}=0. \end{aligned}$$

Instead of the above equation, an approximate solution can be obtained by considering a homotopy-perturbation approximation given by

$$\begin{aligned} e^0_{xx}+k^2e^0-e_{xx}-k^2e={\mathcal {H}}\left[ e^0_{xx}+k^2e^0+k^2({\bar{p}}+q)e+k^2q{\hat{u}}\right] \end{aligned}$$
(14)

where, \({\bar{p}}(x)={\hat{p}}(x)-1\), and for \({\mathcal {H}}=1\) we recover Eq. (5). Seeking a solution in the form of \(e=e^0+{\mathcal {H}}e^1+{\mathcal {H}}^2e^2+\ldots \), leads to

$$\begin{aligned}&{\mathcal {H}}^0: e^0_{xx}+k^2e^0=-k^2q{\hat{u}},(e^0_x+ike^0)|_{x=-1}=0,(e^0_x-ike^0)|_{x=2}=0 \end{aligned}$$
(15)
$$\begin{aligned}&{\mathcal {H}}^1: e^1_{xx}+k^2e^1=-k^2({\bar{p}}+q)e^0,e^1|_{x=-1}=e^1|_{x=2}=0, \end{aligned}$$
(16)
$$\begin{aligned}&{\mathcal {H}}^2: e^2_{xx}+k^2e^2=-k^2({\bar{p}}+q)e^1,e^2|_{x=-1}=e^2|_{x=2}=0,\dots \end{aligned}$$
(17)

Using variation of parameters, the zeroth order solution is given by

$$\begin{aligned} e^0=\frac{ik}{2}e^{ik(2-x)}\int _{-1}^2q(\eta ){\hat{u}}(\eta )e^{ik(\eta -2)}d\eta + k\int _{-1}^xq(\eta ){\hat{u}}(\eta )\sin k(\eta -x)d\eta , \end{aligned}$$
(18)

and, the first order solution is given by

$$\begin{aligned}&e^1=-\frac{k\sin k(x+1)}{\sin 3k}\int _{-1}^2({\bar{p}}+q)e^0(\eta )\sin k(\eta -2)d\eta \nonumber \\&\qquad +k\int _{-1}^x({\bar{p}}+q)e^0(\eta )\sin k(\eta -x)d\eta . \end{aligned}$$
(19)

Higher order terms can also be computed in a similar way. Note that the zeroth order solution depends on q, linearly. The first order solution depends on q, quadratically, and so on.

Evaluating the zeroth-order solution, i.e. Eq. (18), at \(x=0\) leads toFootnote 1

$$\begin{aligned} e(0)=e^0(0)=\frac{ik}{2}e^{2ik}\int _{-1}^2q(\eta ){\hat{u}}(\eta )e^{ik(\eta -2)}d\eta =\hat{g}. \end{aligned}$$
(20)

The second integral drops because \(q=0\) for \(x\in [-1,0]\). Assuming a similar expansion for the unknown q leads to

$$\begin{aligned}&\frac{ik}{2}e^{2ik}\int _{-1}^2\left[ \sum _{j=1}^Nc_j(\eta )\tau _j\right] {\hat{u}}(\eta )e^{ik(\eta -2)}d\eta =\hat{g}, \text {or},\quad \sum _{j=1}^N\mu _j\tau _j=\hat{g}, \nonumber \\&\quad \text {where},\quad \mu _j= \frac{ik}{2}e^{2ik}\int _{-1}^2c_j(\eta ){\hat{u}}(\eta )e^{ik(\eta -2)}d\eta . \end{aligned}$$
(21)

For the range of frequencies \(k_1,k_2,\ldots ,k_\ell \), the above equation leads to

$$\begin{aligned} \mathbf{E}\varvec{\tau }=\hat{\varvec{\gamma }},\quad E_{\ell j}= \frac{ik_\ell }{2}e^{2ik_\ell }\int _{-1}^2c_j(\eta ){\hat{u}}(\eta )e^{ik_\ell (\eta -2)}d\eta ,\end{aligned}$$
(22)

for \(\ell =1,2,\ldots ,L\) and \(j=1,2,\ldots ,N\). Also, the right-hand-side quantities \(\hat{g}\) are stored in \(\hat{\varvec{\gamma }}\). Similar to Eq. (12), the coefficient matrix \(\mathbf{E}\) is rank deficient. A least-square solution can be obtained after introducing Tikhonov regularization.

We can similarly include the higher-order terms. Taking the first two terms, i.e., \(e=e^0+e^1\) leads to

$$\begin{aligned} e_{x=0}=\frac{ik}{2}e^{2ik}\int _{-1}^2q(\eta ){\hat{u}}(\eta )e^{ik(\eta -2)}d\eta -\frac{k\sin k}{\sin 3k}\int _{-1}^2({\bar{p}}+q)e^0(\eta )\sin k(\eta -2)d\eta . \end{aligned}$$

Replacing \(e^0\) in the above equation according to Eq. (18), leads to a quadratic system of equations for q, (or, \(\varvec{\tau }\)). However, it would be easier to set up an iteration. One can first use the zeroth order solution and, using Eq. (22), obtain \(e^0(x)\). Denoting this solution with \(\epsilon ^0\), the above equation leads to

$$\begin{aligned}&\int _{-1}^2\left[ \frac{ik}{2}e^{2ik}{\hat{u}}(\eta )e^{ik(\eta -2)} -\frac{k\sin k}{\sin 3k}\epsilon ^0(\eta )\sin k(\eta -2)\right] q(\eta )d\eta \nonumber \\&=\quad \hat{g}+\frac{k\sin k}{\sin 3k}\int _{-1}^2{\bar{p}}\epsilon ^0(\eta )\sin k(\eta -2)d\eta . \end{aligned}$$
(23)

Assuming a similar expansion for q(x) according to \(q(x)=\sum _{j=1}^Nc_j(x)\tau _j\) leads to a similar linear system given by,

$$\begin{aligned} \mathbf{F}\varvec{\tau }=\varvec{\nu },\nu _\ell =\hat{g}_\ell +\frac{k_\ell \sin k_\ell }{\sin 3k_\ell }\int _{-1}^2{\bar{p}}\epsilon ^0(\eta )\sin k_\ell (\eta -2)d\eta , \end{aligned}$$
(24)

where the entries in the matrix \(\mathbf{F}\) are given by

$$\begin{aligned} F_{\ell j}=\int _{-1}^2\left[ \frac{ik_\ell }{2}e^{2ik_\ell }{\hat{u}}(\eta )e^{ik_\ell (\eta -2)} -\frac{k_\ell \sin k_\ell }{\sin 3k_\ell }\epsilon ^0(\eta )\sin k_\ell (\eta -2)\right] c_j(\eta )d\eta , \end{aligned}$$
(25)

where, Eq. (23) is used for a sequences of frequencies, \(k_1,k_2,\ldots ,k_\ell \). Similar to Eq. (13), least-square solution can be obtained after introducing Tikhonov regularization.

4 Moment method for 2-D Helmholtz equation

We next apply the method developed in Sect. refs2 to a 2-D Helmholtz equation. For this problem we assume that all of the boundary is accessible for collecting measurements. Let \(\varOmega \in R^2\) be a closed bounded set. Consider a 2-D Helmholtz equation given by

$$\begin{aligned} \varDelta u({\mathbf{x}})+k^2p({\mathbf{x}})u({\mathbf{x}})=0\quad {\mathbf{x}}\in \varOmega \subset R^2, \end{aligned}$$
(26)

where Dirichlet and Neumann boundary conditions are given at the boundary of \(\varOmega \), denoted by \({\partial }\varOmega \).

$$\begin{aligned} u({\mathbf{x}})= \sigma ({\mathbf{x}}),\quad \nabla _nu({\mathbf{x}})=\vartheta ({\mathbf{x}}),\quad {\mathbf{x}}\in {\partial }\varOmega . \end{aligned}$$
(27)

Measurements in the form of normal derivative at the boundaries can be collected and provided for the purpose of inversion. One can assume an initial value for the unknown function, i.e., \(\hat{p}({\mathbf{x}})\) and, using the Dirichlet boundary conditions, obtain the background field satisfying the system

$$\begin{aligned} \varDelta \hat{u}+k^2\hat{p}({\mathbf{x}})\hat{u}=0,\quad {\mathbf{x}}\in \varOmega ,\quad \hat{u}({\mathbf{x}})= \sigma ({\mathbf{x}}),\quad {\mathbf{x}}\in {\partial }\varOmega . \end{aligned}$$
(28)

Subtracting the background field from Eq. (26), one can obtain the error field, \(e({\mathbf{x}})=u({\mathbf{x}})-\hat{u}({\mathbf{x}})\), given by

$$\begin{aligned} \varDelta e+k^2\left[ p({\mathbf{x}})u-\hat{p}({\mathbf{x}})\hat{u}\right] =0,\quad {\mathbf{x}}\in \varOmega . \end{aligned}$$
(29)

Since the background field satisfies the Dirichlet boundary condition, the boundary conditions for the error field are given by \(e=0,\forall {\mathbf{x}}\in {\partial }\varOmega \), and \(\nabla _ne=\nabla _nu-\nabla _n\hat{u}\), where \(\nabla _n\) denotes the normal derivative. A linearized version of the above equation is given by

$$\begin{aligned} \varDelta e +k^2\hat{p}({\mathbf{x}})e+k^2q({\mathbf{x}}){\hat{u}}=0,\quad {\mathbf{x}}\in \varOmega . \end{aligned}$$
(30)

We can now consider a sampling function that is the solution to the Helmholtz equation given by

$$\begin{aligned} \varDelta \xi +k^2\hat{p}({\mathbf{x}})\xi =0,\quad {\mathbf{x}}\in \varOmega ,\quad \xi ({\mathbf{x}})=\varpi ({\mathbf{x}}),\quad \forall {\mathbf{x}}\in {\partial }\varOmega , \end{aligned}$$
(31)

where \(\varpi ({\mathbf{x}})\) is an arbitrary boundary condition. Using Green’s second identity leads to

$$\begin{aligned}&\int _\varOmega \left[ \xi \varDelta e-e\varDelta \xi \right] dA =\oint \left[ \xi \nabla _n e-e\nabla _n\xi \right] ds,\text {or} \end{aligned}$$
(32)
$$\begin{aligned}&\int _\varOmega \left[ \xi {\hat{u}}({\mathbf{x}})\right] qdA =-\frac{1}{k^2}\oint \left[ \varpi \nabla _n e\right] ds=\mu , \end{aligned}$$
(33)

where the right-hand-side is known. Similar to Eq. (9), Eq. (33) constitute a moment problem. Choosing a set of linearly independent functions for the boundary conditions \(\varpi _\ell \) leads to

$$\begin{aligned} \int _\varOmega \left[ \xi _\ell {\hat{u}}({\mathbf{x}})\right] qdA =-\frac{1}{k^2}\oint \underbrace{\left[ \varpi _\ell \nabla _n e\right] }ds=\mu _\ell ,\ell =1,2,\ldots ,L, \end{aligned}$$
(34)

where the kernels \({\hat{u}}({\mathbf{x}})\xi _\ell \) are linearly indenpendentFootnote 2. Note that the under braced term includes the data which may often be noisy. Therefore, the right-hand-side requires that we integrate functions that are contaminated with noise. In the next section we develop a method that can filter out the noise. Assuming a similar expansion for the correction term \(q({\mathbf{x}})\), according to \(q=\sum _{j=1}\zeta _j({\mathbf{x}})\tau _j\) leads to

$$\begin{aligned} \mathbf{D}\varvec{\tau }=\varvec{\mu },\quad D_{\ell j}= \int _\varOmega \left[ \xi _\ell ({\mathbf{x}}){\hat{u}}({\mathbf{x}})\zeta _j({\mathbf{x}})\right] dA. \end{aligned}$$
(35)

As is expected the coefficient matrix is non-square and rank deficient. Similar to Eq. (13), after introducing Tikhonov regularization, we can obtain a stable least-square solution for \(\varvec{\tau }\). We next develop a method that can effectively filter out the noise in the data.

5 Tailored filtering

The moment problem in Eq. (34) for the 2-D helmholtz equation requires the integration of the given data that maybe noisy. The data is given in the form of the normal derivative at the boundary in Eq. (27). Therefore, in the present iterative algorithm, the given data appear as the additional boundary condition for the error equation given in Eq. (30). We repeat this equation here for clarity

$$\begin{aligned} \varDelta e +k^2\hat{p}({\mathbf{x}})e+k^2q({\mathbf{x}}){\hat{u}}=0,\quad {\mathbf{x}}\in \varOmega ,\quad e({\mathbf{x}})=0, \quad {\mathbf{x}}\in {\partial }\varOmega . \end{aligned}$$

Additional condition for this equation is given by \(\nabla _ne=\underbrace{\nabla _nu}-\nabla _n\hat{u}\) for \({\mathbf{x}}\in {\partial }\varOmega \), where it includes the under braced term which is the noisy data. To formulate a tailored filter for the above equation we note that both \(q({\mathbf{x}})=0\) and \(e({\mathbf{x}})=0\) for \({\mathbf{x}}\in {\partial }\varOmega \). Since, \(k^2q({\mathbf{x}}){\hat{u}}({\mathbf{x}})=\sum _{j=1}^N\chi _j({\mathbf{x}})\vartheta _j\) where \(\chi _j({\mathbf{x}})=0\) for \({\mathbf{x}}\in {\partial }\varOmega \) with \(\vartheta _j\) being unknown. We can conclude that the error field has an expansion given by \(e({\mathbf{x}})=\sum _{j=1}^N\varepsilon _j({\mathbf{x}})\epsilon _j\) where \(\epsilon _j\) are unknowns and the functions \(\varepsilon _j({\mathbf{x}})\) satisfy the Helmholtz equations given byFootnote 3

$$\begin{aligned} \varDelta \varepsilon _j+k^2\hat{p}({\mathbf{x}})\varepsilon _j+\chi _j({\mathbf{x}})=0,\quad {\mathbf{x}}\in \varOmega ,\quad \varepsilon _j({\mathbf{x}})=0,\quad {\mathbf{x}}\in {\partial }\varOmega . \end{aligned}$$
(36)

Choosing a set of linearly independent functions \(\chi _j({\mathbf{x}})\), leads to a set of linearly independent solutions \(\varepsilon _j({\mathbf{x}})\). It is then reasonable to expect that the given boundary condition for the error field \(\nabla _n e({\mathbf{x}})\) live in the space generated by \(\nabla _n\varepsilon _j({\mathbf{x}})\), \(j=1,2,\ldots ,N\). In other words,

$$\begin{aligned} \sum _{j=1}^N\nabla _n\varepsilon _j({\mathbf{x}})\varrho _j=\nabla _n e,\quad {\mathbf{x}}\in {\partial }\varOmega , \end{aligned}$$
(37)

where the functions \(\varepsilon _j({\mathbf{x}})\) are computed, and \(\nabla _n e\) is the known noisy function. Multiplying the above equation by \(\varepsilon _i({\mathbf{x}})\) and computing the appropriate interproduct leads to a linear system given by

$$\begin{aligned} \int _{{\partial }\varOmega }\left[ \varepsilon _i({\mathbf{x}}) \sum _{j=1}^N\nabla _n\varepsilon _j({\mathbf{x}})\right] d{\mathbf{x}}\varrho _j= \int _{{\partial }\varOmega }\varepsilon _i({\mathbf{x}})\nabla _n ed{\mathbf{x}}\end{aligned}$$
(38)

Using singular-value-decomposition (Lay et al. 2016), the above linear system can be solved for the coefficients \(\varrho _j\). In the actual calculations, we can use the filtered data, \(\sum _{j=1}^N\nabla _n\varepsilon _j({\mathbf{x}})\varrho _j\) instead of the noisy data \(\nabla _n e\).

6 A direct formulation using sampling functions

In this section we use a specific set sampling functions to formulate a direct method that does not require integration of the data at the boundary. Consider a sampling function that is the solution to the Helmholtz equation given by

$$\begin{aligned} \varDelta \xi _\ell +k^2\hat{p}({\mathbf{x}})\xi =\delta ({\mathbf{x}}-{\mathbf{x}}_{0}),\quad {\mathbf{x}}\in \varOmega ,\quad \xi ({\mathbf{x}})=0,\quad \forall {\mathbf{x}}\in {\partial }\varOmega \end{aligned}$$
(39)

where \(\delta ({\mathbf{x}}-{\mathbf{x}}_0)\) is the delta function centered at \({\mathbf{x}}_0\). The above equation is the Green’s function for the variable wave number Helmholtz equation. We use an approximate method to obtain the solution which is presented in the appendix. Applying the Green’s second identity to the above equation and using Eq. (30) leads to

$$\begin{aligned} \int _\varOmega \left[ e\varDelta \xi _\ell -\xi _\ell \varDelta e\right] d{\mathbf{x}}= \oint \left[ e\nabla _n\xi _\ell -\xi _\ell \nabla _n e\right] ds. \end{aligned}$$
(40)

Using the property of the delta function and the boundary conditions, the above equation leads to the value of the error at \({\mathbf{x}}_{0}\) according to

$$\begin{aligned} e({\mathbf{x}}_0)=-k^2\int _\varOmega \xi ({\mathbf{x}}) q({\mathbf{x}}){\hat{u}}({\mathbf{x}})d{\mathbf{x}}. \end{aligned}$$
(41)
Fig. 1
figure 1

On-sided first-derivative finite-difference nodes at a boundary

Full size image

Now, consider domain close to a boundary as depicted in Fig. 1. One can use a third-order one-sided first-derivative of the error at the boundary according to

$$\begin{aligned} e_x=\frac{1}{6dx}\left[ -11e(x_1)+18e(x_2)-9e(x_3)+2e(x_4)\right] , \end{aligned}$$
(42)

where dx is the equal spacing between the points. Using Eq. (41), one can relate the unknown \(q({\mathbf{x}})\) to the gradient of the error at the boundary according to

$$\begin{aligned} e_x=-\frac{k^2}{6dx} \int _\varOmega \left[ 18\xi (x_2)-9\xi (x_3)+2\xi (x_4)\right] q({\mathbf{x}}){\hat{u}}({\mathbf{x}})d{\mathbf{x}}. \end{aligned}$$
(43)

The above equation relates the unknown correction term \(q({\mathbf{x}})\) to the known quantity which is the gradient of the error field at the boundary. Note that the error at the boundary is equal to zero, i.e., \(e(x_0)=0\). Evaluating the above equation for L locations (i.e., \(\ell =1,2,\ldots ,L\)) on the boundary, and assuming a similar expansion for the correction term \(q=\sum _{j=1}\zeta _j({\mathbf{x}})\tau _j\) leads to

$$\begin{aligned}&\mathbf{F}\varvec{\tau }=\varvec{\varkappa },\quad F_{\ell j} =-\frac{k^2}{6dx}\int _\varOmega \varUpsilon _{\ell }({\mathbf{x}})\zeta _j({\mathbf{x}}){\hat{u}}({\mathbf{x}})d{\mathbf{x}},\text {where} \nonumber \\&\varUpsilon _\ell =\left[ 18\xi _\ell (x_2)-9\xi _\ell (x_3)+2\xi _\ell (x_4)\right] , \end{aligned}$$
(44)

and the gradient of the error \(\nabla _n e({\mathbf{x}})\), \({\mathbf{x}}\in {\partial }\varOmega \) at the boundaries are placed in the vector \(\varvec{\varkappa }\) on the right hand side. Similar to Eq. (13), the above equation can now be solved after the introduction of Tikhonov regularization through least-square minimization.

7 Numerical examples and implementations

So far, we have introduced two computational algorithms to study inverse wave scattering. We have presented two methods for the one-dimensional inverse wave scattering. For the one-dimensional case, the measurements are collected at one point on the boundary. For the one-dimensional cases the noise in the data is introduced using a random number generator. Since the data is a scalar value, one can collect a few measurement for the same frequency and average the value. We are introducing 1% noise for the numerical results involving one-dimensional case. For the 2-D problems, measurements are in the form of functions and filtering out the noise will be crucial. We are introducing a new method to filter out the noise. We first consider the one-dimensional problem.

We can divide the domain \(\varOmega =[-1,2]\) into equal intervals and use a second order finite difference approximation to solve various working equations. The point \(x=0\) is accessible, and is used to collect data. The excitation \(\delta (x-x_0)\) is placed at \(x_0=-0.5\). To excite the system, we can use \(L=20\) different values of frequencies, starting with \(k_1=1.2\), and with increments \(\varDelta k=0.14\).

7.1 Example 1

Assume that the interest is to recover the unknown function given by

$$\begin{aligned} p(x)= 1+7\exp \left[ -\frac{(x-0.25)^4}{0.00002}\right] + 7\exp \left[ -\frac{(x-0.65)^4}{0.00002}\right] . \end{aligned}$$
(45)

The unknown function is equal to the background outside the region of interest, i.e., \(p(x)=1\) for \(x\in [-1,0]\cup [1,2]\) and unknown for \(x\in [0,1]\). One can start with a nominal value for \({\hat{p}}(x)=1\), obtain the background fields, and obtain the errors \(e(0)=g_0\) for all frequencies. Boundary conditions for the sampling functions are given by \(\psi _j(-1)=(0.67k_\ell ,-(\ell /0.8))\), for \(\ell =1,2,\ldots ,L\). This choice is arbitrary. We just need to generate a set of sampling functions, \(\psi _j(x)\), that are linearly independent. Once the sampling functions are computed, then the right-hand-side in Eq. (10) can be computed. The correction to the assumed value is the unknown, and an appropriate finite dimensional approximation is given by \(q=\sum _{j=1}^N c_j(x)\tau _j\) where \(c_j(x)=sin(j\pi x)\), for \(j=1,2,\ldots ,N\). Choosing \(N=20\), one can compute the coefficient matrix in the linear system in Eq. (12). As is expected this matrix is rank deficient. Figure 2 presents the normalized eigenvalues of the symmetric matrix \([\mathfrak {R}(\mathbf{A})^T\mathfrak {R}(\mathbf{A})+\mathfrak {I}(\mathbf{A})^T\mathfrak {I}(\mathbf{A})]\). We can also check the performance of the direct method in Sect. refs3, by considering the rank of the coefficient matrix in Eq. (22). Figure 2 also presents the normalized eigenvalues of the symmetric matrix \([\mathfrak {R}(\mathbf{E})^T\mathfrak {R}(\mathbf{E})+\mathfrak {I}(\mathbf{E})^T\mathfrak {I}(\mathbf{E})]\).

Fig. 2
figure 2

Normalized eigenvalues of the linear part for the two methods

Full size image

Combining the two linear systems, we can solve the linear system after the introduction of Tikhonov regularization through the use of Least-square minimization. Figure 3 shows the recovered function when \(\beta =0.5E-4\) with 1% noise. It also show the recovered function when the first-order nonlinear term is included in the direct method, i.e., Eq. (24). Figure 4 presents the reduction in the error as a function of the number of iterations. The inclusion of the first-order nonlinear term improves the rate of the reduction in the error.

Fig. 3
figure 3

Actual and the recovered unknown function for example 1 with linear formulation. It also presents the results where the first-order nonlinear term is included

Full size image
Fig. 4
figure 4

Error as a function of the number of iterations for example 1

Full size image

7.2 Example 2

we next consider the evaluation of an unknown function given by

$$\begin{aligned} p(x)=1+7\exp \left[ \frac{-(x-.16)^4}{0.00001}\right] + 7\exp \left[ \frac{-(x-.42)^4}{0.00001}\right] + 3.5\exp \left[ \frac{-(x-.72)^4}{0.00001}\right] . \end{aligned}$$

Using both formulations and including the first-order term from the nonlinear contribution, Fig. 5 presents the recovered function and Fig. 6 shows the \(\beta =.6E-4\). This example involves three targets, and the combined methods can recover a close estimate of it. For both examples, the accuracy of the recovered function is better for the region that is closer to the accessible point of the domain.

Fig. 5
figure 5

Actual and the recovered unknown function for example 2. It also presents the recovered function after intermediate iterations, \(\beta =.6E-4\)

Full size image

7.3 Example 3

We next consider a 2-D domain \(\varOmega =[0,1]\times [0,1]\) and study the inverse evaluation of a wave function, given in Eq. (26). Assume that the unknown function is given by

$$\begin{aligned}&p(x,y)=1+g(x)f(y)+f(x)g(y),\nonumber \\&g(s)=exp\left[ \frac{-(s-.23)^4}{.00002}\right] , f(s)=exp\left[ \frac{-(s-.77)^4}{.00002}\right] . \end{aligned}$$
(46)

The boundary can be exposed to an incoming wave given by

$$\begin{aligned}&u(x,0)=\cos (k(x \cos (\theta ))),\quad u(x,1)=\cos (k(x \cos (\theta )+ \sin (\theta ))),\quad \nonumber \\&u(0,y)=\cos (k(y \sin (\theta )),\quad u(1,y)=\cos (k(\cos (\theta ) + y \sin (\theta ))), \end{aligned}$$
(47)

where \(k=3\) and \(\theta =\frac{\pi }{3.4}\). One can generate the data. For this example, we assume that data can be collected with no noise (Creedon et al. 2011). In this section, we study the reduction in the error which is the difference between the given data and the calculated value at a given iteration.

$$\begin{aligned} \text {Error}=\int _{{\partial }\varOmega }\left[ \nabla _nu({\mathbf{x}})-\nabla _n\hat{u}({\mathbf{x}})\right] ^2d{\mathbf{x}}\quad \forall {\mathbf{x}}\in \partial \varOmega . \end{aligned}$$
(48)

To generate the sampling functions, \(\xi _\ell ({\mathbf{x}})\), given in Eq. (31), one needs to provide linearly independent set of functions for the boundary conditions \(\xi _\ell ({\mathbf{x}})=\varpi _\ell ({\mathbf{x}})\), for \({\mathbf{x}}\in {\partial }\varOmega \). We can use a combination of cubic-B splines (Tadi 2009), and (Christensen 2010). For the Bessel functions, we can use

$$\begin{aligned} J_n(\lambda _j z)=\frac{1}{\pi }\int _0^\pi \cos (n\theta -\lambda _jz\sin \theta ) d\theta ,n=1,2,\ldots ,5,j=1,2,\ldots ,10. \end{aligned}$$
(49)

Note that \(J_n(0)=0\), and the values of \(\lambda _j\) are obtained by imposing \(J_n(1)=0\). And, for \(n=0\), we can use the functions \((1-x)-J_0(x)\). Using combinations of cubic-B splines and Bessel functions we can generate the boundary conditions \(\varpi _\ell \) needed to generate the sampling functions \(\xi _\ell ({\mathbf{x}})\). In this example, we are using 121 linearly independent set of functions, \(\varpi _\ell \) for \(\ell =1,2,\ldots ,121\). To approximate the corrections term \(q({\mathbf{x}})\), we can again use sine functions according to

$$\begin{aligned}&\zeta _\ell ({\mathbf{x}})=sin(i\pi x)sin(j\pi y), \nonumber \\&\qquad \qquad i=1,2,\ldots ,M,\quad j=1,2,\ldots ,M,\quad \ell =(i-1)M+j, \end{aligned}$$
(50)

where, \(\zeta _\ell ({\mathbf{x}})=0\) \(\forall {\mathbf{x}}\in {\partial }\varOmega \), for \(\ell =1,2,\ldots ,N\), with \(L=M^2\). Note that the unknown wave number is considered to be known at the boundaries therefore, we have \(q({\mathbf{x}})=0,\forall {\mathbf{x}}\in \partial \varOmega \). For this example, we are using \(M=14\), which leads to \(L=196\). We can now proceed and generate the linear system given in Eq. (35). As is expected the coefficient matrix is non-square and rank deficient. Figure 6 shows the normalized eigenvalues of the symmetric matrix \(\mathbf{D}^T\mathbf{D}\). We are normalizing the eigenvalues with respect to the highest eigenvalue.

Fig. 6
figure 6

Normalized eigenvalues of the coefficient matrix

Full size image

For only one set of data, i.e., \(k_1=3\), there are about 20 significant eigenvalues out of 196. If we can provide additional measurements and augment the linear system in Eq. (35), the number of significant eigenvalues in this matrix can be increased. Providing data for 4 different frequencies, i.e., \(k_1=3\), \(k_2=4\), \(k_3=5\), \(k_4=6\), the linear matrix is Eq. (35) leads to

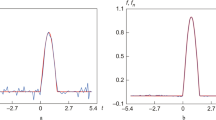
$$\begin{aligned} \left[ \begin{array}{c} \mathbf{D}_{k_1}\\ \mathbf{D}_{k_2}\\ \mathbf{D}_{k_3}\\ \mathbf{D}_{k_4}\end{array}\right] \varvec{\tau }=\left[ \begin{array}{c}\varvec{\mu }_{k_1}\\ \varvec{\mu }_{k_2}\\ \varvec{\mu }_{k_3}\\ \varvec{\mu }_{k_4}\end{array}\right] \end{aligned}$$
(51)

As we include the data for additional frequencies, the number of significant eigenvalues in this matrix increases. We next proceed to recover the unknown wave number. In order to obtain a stable inversion, we still need to introduce Tikhonov regularization, similar to Eq. (13). Figure 7 shows the actual unknown function and Fig. 8 shows the recovered function after 200 iteration. Figure 9 considers the cross-section along the line \(x+y=1\) and compares the actual function with the recovered function along this line.

Fig. 7
figure 7

The actual unknown function p(x, y)

Full size image
Fig. 8
figure 8

The recovered unknown function p(x, y)

Full size image
Fig. 9
figure 9

A cross-section of the recovered unknown function p(x, y) for \(y=1-x\)

Full size image

7.4 Example 4

Fig. 10
figure 10

Unknown function for example 4

Full size image

We next consider a case where the data is noisy and use the direct method presented in Sect. 6. We need to apply the tailored filter presented in Sect. 5. Consider the problem of recovering a wave number given by

$$\begin{aligned}&p(x,y)=1+g(x)f(y)+f(x)g(y), \nonumber \\&g(s)=exp\left[ \frac{-(s-.25)^4}{.000025}\right] , f(s)=exp\left[ \frac{-(s-.75)^4}{.000025}\right] , \end{aligned}$$
(52)

which is shown in Fig. 10. One can assume an initial guess, obtain background field and arrive at Eq. (30). The noisy data appears in the additional boundary condition given by \(\nabla _ne=\underbrace{\nabla _nu}-\nabla _n\hat{u}\) for \({\mathbf{x}}\in {\partial }\varOmega \). The proper space to project the noisy term, \(\nabla _ne\), can be obtained by first solving the set of Helmholtz equations given in Eq. (36) where \(\chi _j({\mathbf{x}})\), \(j=1,2,\ldots ,N\) is a set of linearly independent functions with \(\chi _j({\mathbf{x}})=0\) for \({\mathbf{x}}\in {\partial }\varOmega \). Using the same sine functions given in Eq. (50) with \(M=14\) leads to a set of linearly independent functions \(\varepsilon _j({\mathbf{x}})\), with \(j=1,2,\ldots ,156\). Therefore, the proper space to project the noisy term \(\nabla _ne({\mathbf{x}})\) is given by

$$\begin{aligned} \left[ \nabla _n\varepsilon _1({\mathbf{x}}),\nabla _n\varepsilon _2({\mathbf{x}}),\ldots ,\nabla _n\varepsilon _{156}({\mathbf{x}})\right] ,\quad {\mathbf{x}}\in {\partial }\varOmega . \end{aligned}$$
(53)

Consider the lower part of the boundary where \(y=0\) and \(x\in [0,1]\). The noisy boundary condition is given by \(\frac{{\partial }e}{{\partial }y}\) at \(x=0\). We can project this function according to

$$\begin{aligned} \frac{{\partial }e}{{\partial }y}|_{x=0}= \sum _{j=1}^N\left[ \frac{{\partial }\varepsilon _j}{{\partial }y}|_{x=0}\right] \varrho _j \end{aligned}$$
(54)

Solving for the components \(\varrho _j\) leads to a linear system given by

$$\begin{aligned} \int _0^1\left[ \frac{{\partial }\varepsilon _i}{{\partial }y}|_{x=0}\right] \sum _{j=1}^N\left[ \frac{{\partial }\varepsilon _j}{{\partial }y}|_{x=0}\right] dx\varrho _j= \int _0^1 \left[ \frac{{\partial }\varepsilon _i}{{\partial }y}|_{x=0}\right] \frac{{\partial }e}{{\partial }y}|_{x=0}dx, \end{aligned}$$
(55)

where the coefficient matrix is symmetric and rank deficient. Singular value decomposition can be easily used to solve this system. Once we have the parameters \(\varrho _j\), then for the calculations we can use the filtered data according to Eq. (54).

Figure 11 shows the function \(\nabla _ne ({\mathbf{x}})\) for \(y=0\) and \(x\in [0:1]\), lower boundary, or \(\frac{{\partial }e(x,y)}{{\partial }y}|_{y=0}\) for \(x\in [0{:}1]\). The figure compares the uncorrupted data and the noisy data which has 3% noise added. It also presents the filtered data.

We next proceed to recover the unknown function using this filter. We can use a similar boundary condition given in Eq. (46). Using nine sets of data with \(k_1=3.\), \(k_2=3.4\), \(k_3=4.\), \(k_4=5.\), \(k_5=5.4\), \(k_6=5.8\), \(k_7=6.\), \(k_8=6.3\), and \(k_9=6.5\). We use three angles for the incoming waves given by \(\theta _1=\frac{\pi }{3.4}\), \(\theta _2=\frac{\pi }{4.4}\), and \(\theta _3=\frac{\pi }{6.9}\) to generate 9 sets of linearly independent boundary conditions. Figures 12, 13 shows the recovered function after 300 iterations and Fig. 14 shows a cross-section of the function. It compares the recovered function with the actual value along the long \(x+y=1\).

Fig. 11
figure 11

Noise free, Noisy, and filtered data \(\nabla _n e(x,0)\), for example 4

Full size image
Fig. 12
figure 12

Recovered function for example 4 with \(\beta =.2E-4\)

Full size image
Fig. 13
figure 13

Unknown function for example 4 with \(\beta =.2E-4\)

Full size image

7.5 Example 5

We next consider the recovering of an unknown function given by

$$\begin{aligned}&p(x,y)=1+f(x)g(y)+g(x)f(y), \nonumber \\&g(s)=exp\left[ \frac{-(s-.23)^2}{.008}\right] , f(s)=exp\left[ \frac{-(s-.77)^4}{.00002}\right] , \end{aligned}$$
(56)
Fig. 14
figure 14

Unknown function for example 5

Full size image
Fig. 15
figure 15

Recovered function for example 5 after 300 iterations, with \(\beta =.1E-4\)

Full size image
Fig. 16
figure 16

Recovered function for example 5 along a cross-section \(y=x\) after 300 iterations, with \(\beta =.1E-4\)

Full size image

which is shown in Fig. 15. Using the same number of collected data as in example 4, Fig. 16 shows the recovered function after 300 iterations, and Fig. 16 compares the recovered function over the cross-section \(x=y\).

Over-all the results can be improved by using higher frequencies, which in general requires finer mesh. We also need to investigate various sampling functions. The present method can also be naturally combined with our previous method based on proper solution space (Hamad and Tadi 2019), since both treat the linearized error field to obtain a correction term to an assumed initial guess for the unknown function. All of these issues will be addressed in our future work.

8 Conclusion

In this note we presented two methods for inverse wave scattering. We also presented a new method for filtering noisy data. For one dimensional problems the present method is able to recover a close estimate of the unknown function based on data collected at one point on the boundary. For two dimensional problems the presented method can recover a reasonable approximation of the unknown function with up to 3% noise. This method can be combined with our previous method. The accuracy of the recovered function can also be improved by introducing additional data and/or using finer computational mesh. All of these issues will be addressed in our future work.