A spectral approach using fractional Jaiswal functions to solve the mixed time-fractional Black-Scholes European option pricing model with error analysis

Abstract

In this paper, we propose a collocation scheme for efficiently solving the mixed time-fractional Black-Scholes (MTF-BS) model and obtaining the option price. Our approach involves deriving the mixed fractional Black-Scholes (MF-BS) partial differential equation (PDE) considering the delta hedging strategy and the mixed fractional Geometric Brownian motion (MFGBM) model. To simplify the problem, we transform the MTF-BS PDE into a modified Riemann-Liouville derivative form. Subsequently, a collocation method is employed to numerically solve the transformed equation, where the solution is represented as a series of fractional Jaiswal functions with unknown coefficients. By utilizing operational matrices and collocation points, we convert the problem into a linear system of equations, allowing for the examination of convergence and stability in the Sobolev spaces. Finally, we present four examples to demonstrate the method’s effectiveness and accuracy.

1 Introduction

Option pricing is a financial concept that involves determining the value of a financial contract known as an option [1]. The pricing of options is crucial for investors and traders in the financial markets as it helps them to make informed decisions about buying, selling, or holding these instruments. By understanding the value of options, market participants can assess the potential risks and rewards associated with their investment strategies. The Black-Scholes (BS) model, developed in the 1970s, is one of the prominent methodologies used for option pricing [2]. This model takes into consideration factors such as the asset price, the strike price, the expiration time, the expected volatility, interest rates, and dividends. By incorporating these variables, the model generates an estimated value for the option.

Financial models play an important role in option pricing because they help determine the fair value or theoretical price of an option contract [3, 4]. These models often use stochastic processes to incorporate uncertainty and randomness into their calculations. In recent years, various stochastic processes have been used in financial models. One of the most important ones is fractional Brownian motion (fBm) [5, 6]. The fBm was first introduced by Kolmogorov in 1940, and it is a stochastic process that is widely employed in financial modeling due to its ability to capture long-range dependence, self-similarity, and fractal nature in asset price movements over time [7]. Unlike the standard Brownian motion, which assumes independent and identically distributed increments, the fBm process incorporates memory effects, making it a suitable tool for modeling financial data with persistent autocorrelation. The process is parameterized by a Hurst exponent (H), which characterizes the level of dependence present in the data. If $H \in (\frac{1}{2}, 1)$, the process has long memory [8]. However, since the fBm process with $H \ne \frac{1}{2}$ is not a semimartingale, applying the related financial models creates arbitrage opportunities [9,10,11]. But Cheridito in 2001 studied the fBm models and showed how arbitrage can be removed from fBm models [12]. Moreover, he presented the mfBm, which combines the properties of both the fBm process and the Brownian motion, in 2009 as [13]:

$$\begin{aligned} M_t^H=\alpha B_t + \beta B_t^H, ~ H \in (0 , 1), ~and ~ t\ge 0, \end{aligned}$$

(1)

where $\alpha$ and $\beta$ are real constants. Cheridito showed that the mfBm process with $H \in (\frac{3}{4}, 1)$ is equivalent to a martingale, and applying the mixed fractional models for forecasting the stock price doesn’t create arbitrage opportunities [13]. After that, Zili in 2006 studied the process and presented some stochastic properties and characteristics of this process [14]. Cai et al. [15], Zhang et al. [16], and Xiao et al. [17] applied the process in different financial models and showed that the efficiency of the process is higher than the standard and fBms.

1.1 The methodology for determining the option price PDE

Here, we obtain the option price PDE under the MFGBM model. Let $\left( \Omega , \mathcal {F}, \mathbb {P} \right)$ be a probability space and the dynamic of the asset price satisfies the following equation:

$$\begin{aligned} dS(t) = \mu S(t) dt + \sigma S(t) dM(t), ~~~~~ t\ge 0, \end{aligned}$$

(2)

where $\mu$ and $\sigma$ are constants.

Lemma 1

Let $\mathcal {V}(S, t)$ denotes the value of the option on the underlying asset S at time t. Then, $\mathcal {V}(S, t)$ satisfies in

$$\begin{aligned} \frac{\partial \mathcal {V}}{\partial t}(S, t) +\frac{ \sigma _1^2(t)}{2} S(t)^2 \frac{\partial ^2 \mathcal {V}}{\partial S^2} (S, t) + r S(t) \frac{\partial \mathcal {V}}{\partial S}(S, t) -r\mathcal {V} (S, t) =0. \end{aligned}$$

(3)

where

$$\begin{aligned} \sigma _1^2(t)=2\sigma ^2\left( \beta ^2 \left( \frac{1}{2} + H t^{2H-1} \right) - \sqrt{\frac{2}{\pi }}\frac{k}{ \sigma } \sqrt{\frac{\beta ^2 + \beta ^2 (dt)^{2H-1}}{dt}} sign(\frac{\partial ^2\mathcal {V}}{\partial S^2})\right) . \end{aligned}$$

(4)

Proof

Let Y denotes a replicating portfolio with the call option $\mathcal {V}$ and sell $\Delta$ shares of the underlying stock S. Then, the portfolio’s price equation satisfies in:

$$\begin{aligned} Y(t)=\mathcal {V}(S, t) -\Delta (t) S(t), ~~ t \ge 0. \end{aligned}$$

(5)

By Proposition 2.9 and Theorem 2.10 from [18] for Y and $\mathcal {V}$, we deduce that

$$\begin{aligned} dY(t) =&~ d\mathcal {V}(S, t) - \Delta dS(t) - k|\nu _t|S_{t+\delta t} \nonumber \\ =&\Big [\frac{\partial {\mathcal {V}}}{\partial {t}} (S, t)+\mu S(t) \frac{\partial {\mathcal {V}}}{\partial {S}}(S, t) +\beta ^2 \left( \frac{1}{2} + Ht^{2H-1}\right) \nonumber \\&\sigma ^2 S(t)^2 \frac{\partial ^2{\mathcal {V}}}{{\partial {S}}^2}(S, t) -\mu S(t)\Delta (t)\Big ]dt \nonumber \\&+\sigma S(t)(\frac{\partial {\mathcal {V}}}{\partial {S}}(S, t)- \Delta (t))dM_t^H -k|\nu _t| S_{t+dt}. \end{aligned}$$

(6)

To derive the PDE, we remove the stochastic part of the (6). Thus, $\Delta =\frac{\partial \mathcal {V}}{\partial S}$ which this is the Delta Hedging assumption of Leland and Kabanov strategies [19, 20]. Therefore, we conclude that

$$\begin{aligned} dY(t)=&\Big [\frac{\partial {\mathcal {V}}}{\partial {t}} (S, t)+\mu S(t) \frac{\partial {\mathcal {V}}}{\partial {S}}(S, t)+ \beta ^2 \left( \frac{1}{2} + Ht^{2H-1}\right) \sigma ^2 S(t)^2 \frac{\partial ^2{\mathcal {V}}}{{\partial {S}}^2}(S, t) \nonumber \\&~~~~~~~~~~~~~~~~~~-\mu S(t)\Delta (t)\Big ]dt -k|\nu _t| S(t+dt), \end{aligned}$$

(7)

where $\nu _t=\Delta (t+dt) - \Delta (t)$ and $k=k_0 n^{\xi - 1/2}$ is the amount of transaction costs in which $k_0 >0$ and $\xi \in {[0,1/2]}$ are constant and n is the number of revisions. Also, we have

$$E(k|\nu _t|S(t+dt))=k|\frac{\partial ^2\mathcal {V}}{\partial S^2} |\sigma S(t) E\left( |d M(t)|S(t+dt)\right) +O(dt).$$

$$\begin{aligned} =\sqrt{\frac{2}{\pi } }k \sigma S(t)^2 \sqrt{\beta ^2 d t + \beta ^2 (dt)^{2H}} |\frac{\partial ^2\mathcal {V}}{\partial S^2}(S, t)| + O(dt). \end{aligned}$$

(8)

By removing the random part of the (7), the expected return of the Hedge portfolio is equal to the risk-free rate ( r). Thus, we deduce that

$$\begin{aligned} \mathbb {E}(d Y(t))= r Y(t) dt. \end{aligned}$$

(9)

Additionally, one has

$$\begin{aligned} \mathbb {E}(d Y(t))=&\left( \frac{\partial \mathcal {V}}{\partial t} (S, t) + \beta ^2 \left( \frac{1}{2} + H t^{2H-1} \right) \sigma ^2 S(t)^2 \frac{\partial ^2 \mathcal {V}}{\partial S^2} (S, t) \right) dt \nonumber \\&-\sqrt{\frac{2}{\pi }}k \sigma S(t)^2 \sqrt{\beta ^2 d t + \beta ^2 (dt)^{2H}} |\frac{\partial ^2\mathcal {V}}{\partial S^2} (S, t)| +O( d t). \end{aligned}$$

(10)

By (9) and (10), we deduce that

$$\begin{aligned} \frac{\partial \mathcal {V}}{\partial t} (S, t) +&\beta ^2 \left( \frac{1}{2} + H t^{2H-1} \right) \sigma ^2 S(t)^2 \frac{\partial ^2 \mathcal {V}}{\partial S^2} (S, t) + r S(t) \frac{\partial \mathcal {V}}{\partial S} (S, t) \nonumber \\&-\sqrt{\frac{2}{\pi }}k \sigma S(t)^2 \sqrt{\frac{\beta ^2 + \beta ^2 (dt)^{2H-1}}{dt}} |\frac{\partial ^2\mathcal {V}}{\partial S^2}(S, t)| -r\mathcal {V}(S, t) =0. \end{aligned}$$

(11)

Let us consider

$$\sigma _1^2(t)=2\sigma ^2\left( \beta ^2 \left( \frac{1}{2} + H t^{2H-1} \right) - \sqrt{\frac{2}{\pi }}\frac{k}{ \sigma } \sqrt{\frac{\beta ^2 + \beta ^2 (dt)^{2H-1}}{dt}} sign(\frac{\partial ^2\mathcal {V}}{\partial S^2})\right) .$$

Finally, we obtain

$$ \frac{\partial \mathcal {V}}{\partial t}(S, t) +\frac{ \sigma _1^2(t)}{2} S(t)^2 \frac{\partial ^2 \mathcal {V}}{\partial S^2} (S, t) + r S(t) \frac{\partial \mathcal {V}}{\partial S} (S, t) -r\mathcal {V} (S, t) =0.$$

1.2 Fractional model

In light of their vast range of applications, fractional partial differential equations (FPDEs) have sparked the interest of scientists from a variety of disciplines. Many articles have investigated fractional Black-Scholes models. Meihui Zhang et al. focused on a time-fractional option pricing model with asset-price-dependent variable order and a fast numerical technique to solve the time-fractional option pricing mode [21]. Fazlollah Soleymani and Shengfeng Zhu introduced a discretization scheme of $(2 - \alpha )$ order for the Caputo fractional derivative utilizing graded meshes along the time dimension to solve the time-fractional option price PDE [22]. Other methods are also provided for the numerical solution of the time-fractional option price PDE [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. H. Mesgarani et al. investigated the approximation of the solution u(x, t) for the temporal fractional Black-Scholes model, which involves the Caputo sense time derivative and is subject to initial and boundary conditions [31]. H. Mesgarani et al. introduced a novel fuzzy mathematical programming approach initially designed to address problems within the framework of linear programming (LP) models [32]. Y. Esmaeelzade Aghdam et al. combined the composition of orthogonal Gegenbauer polynomials (GB polynomials) and the approximation of the fractional derivative based on the Caputo derivative for estimating the fractional Black-Scholes model [33]. In the sequel, we consider the following equation,

$$\begin{aligned} \frac{\partial ^{\alpha } \mathcal {V}(S,\gamma )}{\partial \gamma ^{\beta }} +\frac{ \sigma _1^2(\gamma )}{2} S(\gamma )^2 \frac{\partial ^2 \mathcal {V}(S,\gamma )}{\partial S(\gamma )^2} + r S(\gamma ) \frac{\partial \mathcal {V}(S,\gamma )}{\partial S(\gamma )}-r\mathcal {V}(S,\gamma ) =0, \end{aligned}$$

(12)

where $\frac{\partial ^{\alpha } \mathcal {V}(S,\gamma )}{\partial \gamma ^{\beta }}$ is the modified Riemann-Liouville derivative

$$\begin{aligned} \frac{\partial ^{\alpha } \mathcal {V}(S,\gamma )}{\partial \gamma ^{\alpha }}=\frac{1}{\Gamma (1-\alpha )}\frac{d}{d\gamma }\int _{\gamma }^{T}\frac{\mathcal {V}(S,\psi )-\mathcal {V}(S,T)}{(\psi -\gamma )^{\alpha }}d\psi ,\qquad 0<\alpha <1. \end{aligned}$$

(13)

For this problem, we consider the initial and boundary conditions as

$$\begin{aligned}&\mathcal {V}(0,\gamma )=\mathcal {V}_1(\gamma ),\qquad \mathcal {V}(\infty ,\gamma )=\mathcal {V}_2(\gamma ),\end{aligned}$$

(14)

$$\begin{aligned}&\mathcal {V}(S,T)=\mathcal {V}_3(S). \end{aligned}$$

(15)

Assume, $S=e^x$, $\gamma =T-t$, and $\mathcal {J}(x,t)=\mathcal {V}(e^x,T-t)$. Then, we have

$$\begin{aligned}&\frac{\partial \mathcal {V}(S,\gamma )}{\partial S}=\frac{1}{S}\frac{\partial \mathcal {J}(x,t)}{\partial x},\\ {}&\frac{\partial ^2 \mathcal {V}(S,\gamma )}{\partial S^2}=-\frac{1}{S^2}\frac{\partial \mathcal {J}(x,t)}{\partial x}+\frac{1}{S^2}\frac{\partial ^2 \mathcal {J}(x,t)}{\partial x^2},\\ {}&\frac{\partial ^{\alpha } \mathcal {V}(S,\gamma )}{\partial \gamma ^{\alpha }}=-\frac{1}{\Gamma (1-\alpha )}\frac{d}{dt}\int _{0}^{T}\frac{\mathcal {V}(S,T-\psi )-\mathcal {V}(S,T)}{(T-\psi )^{\beta }}d\psi =-~^{C}_{0}D_{t}^{\alpha }\mathcal {J}(x,t), \end{aligned}$$

where

$$\begin{aligned} ^{C}_{0}D_{t}^{\alpha }\mathcal {J}(x,t)=\frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}(t-\sigma )^{-\alpha }\frac{\partial \mathcal {J}(x,\sigma )}{\partial \sigma }d\sigma . \end{aligned}$$

(16)

So that, we obtain

$$\begin{aligned}&^{C}_{0}D_{t}^{\alpha }\mathcal {J}(x,t)=p(t)\frac{\partial ^2\mathcal {J}(x,t)}{\partial x^2}+q(t)\frac{\partial \mathcal {J}(x,t)}{\partial x}-r\mathcal {J}(x,t),\qquad x\in \mathbb {R},~0\le t\le T,\end{aligned}$$

(17)

$$\begin{aligned}&\mathcal {J}(-\infty ,t)=\mathcal {J}_1(t),\qquad \mathcal {J}(\infty ,t)=\mathcal {J}_2(t),\end{aligned}$$

(18)

$$\begin{aligned}&\mathcal {J}(x,0)=\mathcal {J}_3(x). \end{aligned}$$

(19)

Remark 1

We restrict the domain of space to a finite interval [c, d] because of numerical limitations and to assess our numerical scheme with artificial exact solutions. We apply a source term $\mathcal {F}(x, t)$ to problem (17)–(19). As a result, we have the following problem:

$$\begin{aligned} ^{C}_{0}D_{t}^{\alpha }\mathcal {J}(x,t)=&p(t)\frac{\partial ^2\mathcal {J}(x,t)}{\partial x^2}+q(t)\frac{\partial \mathcal {J}(x,t)}{\partial x}\nonumber \\&-r\mathcal {J}(x,t)+\mathcal {F}(x,t),\quad x\in (c,d),~0\le t\le T,\end{aligned}$$

(20)

$$\begin{aligned} \mathcal {J}(c,t)=&\mathcal {J}_1(t),\qquad \mathcal {J}(d,t)=\mathcal {J}_2(t),\end{aligned}$$

(21)

$$\begin{aligned} \mathcal {J}(x,0)=&\mathcal {J}_3(x). \end{aligned}$$

(22)

Remark 2

In real-world problems, we have some limitations on the initial and boundary conditions. Since the price of the stock changes within a logical interval, we first obtain the stock price based on the financial model. As a result, we can determine the minimum and maximum values of the stock price. With these values, we derive the boundary conditions for the option price.

1.3 Spectral methods

Spectral methods are a technique used to find the solution to a differential equation by representing it as a series of well-defined and smooth functions. These methods, which have gained popularity, are now considered a valid alternative to finite difference and finite element methods when it comes to numerically solving partial differential equations. These methods are comprehensive approaches in which the calculation at any specific location is influenced not only by data from nearby locations but also by data from the entire region. They are also considered global because they utilize all the available function values to create the required approximations. Different approaches used for solving partial differential equations using polynomial spectral methods are the Galerkin, tau, and collocation method.

1.4 Contribution and structure of the paper

As far as the authors are aware, the numerical solution of the problem (12)–(15) has not been investigated until now, and this study is the first attempt. We intend to propose a polynomial collocation scheme based on Jaiswal polynomials to solve the problem (20)–(22). To overcome this issue, let the solution to the problem be considered as a series of Jaiswal polynomials with unknown coefficients. By doing so, we will approximate the problem, and by collocating the resulting equations, we obtain a linear system of equations. The unknown coefficients are obtained by solving the resulting system, and the numerical solution of the problem is constructed. The convergence of the introduced scheme is studied in the Sobolev space. Some instances are provided to demonstrate the significance of the method.

In the following, the paper’s main contributions is presented:

• Introducing a fast collocation method to solve the model numerically.

• Introducing fractional form of Jaiswal polynomials.

• Computing operational matrices of the fractional jaiswal polynomials.

• Studied error analysis in the Sobolev space.

• Provided test problems with artificial and non-artificial exact solutions.

The continuation of the article is as follows: In Section 2, we introduce the Jaiswal polynomials and their fractional form and obtain the operational matrix of these polynomials. Section 3 is devoted to constructing a numerical scheme to address problem (20)–(22). An analysis of the suggested scheme is discussed in Section 4. Section 5 includes some examples to demonstrate how well the approach works. Finally, Section 6 concludes the article.

2 Jaiswal polynomials

In this part, we generate fractional Jaiswal functions by employing Jaiswal polynomials, which were initially proposed by D.V. Jaiswal in 1974 [40]. Jaiswal polynomials can be defined by the following explicit formula.

$$\begin{aligned} \mathcal {A}_n(y)=\sum _{i=0}^{\lfloor {\frac{n-1}{3}}\rfloor }\frac{(-1)^i(n-1-2i)!}{i!(n-1-3i)!}(2y)^{n-1-3i},\hspace{0.2cm}n\ge 1. \end{aligned}$$

(23)

For every $n\ge 0$, the subsequent relationship is true

$$\begin{aligned} y^{n}=\frac{1}{2^n}\sum _{t=0}^{\lfloor {\frac{n}{3}}\rfloor }\frac{n!(n-3t+1)}{t!(n-t)!(n-t+1)}\mathcal {A}_{n-3t+1}(y). \end{aligned}$$

(24)

The process of defining fractional Jaiswal functions involves applying a transformation $y\rightarrow y^{h},h\in \mathbb {R}^{+}$ to (23), in the following manner.

$$\begin{aligned} \mathcal {A}_n^h(y)=\sum _{i=0}^{\lfloor {\frac{n-1}{3}}rfloor}\frac{(-1)^i2^{n-1-3i}(n-1-2i)!}{i!(n-1-3i)!}y^{(n-1-3i)h},\hspace{0.2cm}n\ge 1. \end{aligned}$$

(25)

Moreover, we have

$$\begin{aligned} y^{nh}=\frac{1}{2^n}\sum _{t=0}^{\lfloor {\frac{n}{3}}\rfloor }\frac{n!(n-3t+1)}{t!(n-t)!(n-t+1)}\mathcal {A}_{n-3t+1}^h(y). \end{aligned}$$

(26)

We can represent a continuous function $\mathcal {J}(x,t)$ by utilizing fractional Jaiswal functions, as demonstrated below.

$$\begin{aligned} \mathcal {J}(x,t)=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }b_{i+1,j+1} \mathcal {A}_{i+1}^{h_1}(x) \mathcal {A}_{j+1}^{h_2}(t), \end{aligned}$$

(27)

where $h_1,h_2\in \mathbb {R}$. We use the truncated series of (27) in order to approximate $\mathcal {J}(x,t)$ as follows:

$$\begin{aligned} \mathcal {J}_{\mathcal {N}_x}^{\mathcal {N}_t}(x,t)=\sum _{i=0}^{\mathcal {N}_x}\sum _{j=0}^{\mathcal {N}_t}b_{i+1,j+1} \mathcal {A}_{i+1}^{h_1}(x) \mathcal {A}_{j+1}^{h_2}(t)=A_{\mathcal {N}_x}^{h_1}(x)^{T}\mathcal {M}A_{\mathcal {N}_t}^{h_2}(t), \end{aligned}$$

(28)

where

$$\begin{aligned} \mathcal {M}= \begin{bmatrix} m_{11}&{}m_{12}&{}\ldots &{}m_{1\mathcal {N}_t+1}\\ m_{21}&{}m_{22}&{}\ldots &{}m_{2\mathcal {N}_t+1}\\ \vdots &{}\vdots &{}\ldots &{}\vdots \\ m_{\mathcal {N}_x+11}&{}m_{\mathcal {N}_x+12}&{}\ldots &{}m_{\mathcal {N}_x+1\mathcal {N}_t+1} \end{bmatrix} \end{aligned}$$

and

$$A_{\mathcal {N}_x}^{h_1}(x)=[\mathcal {A}_0^{h_1}(x),\dots ,\mathcal {A}_{\mathcal {N}_x+1}^{h_1}(x)]^{T},\hspace{0.2cm} A_{\mathcal {N}_t}^{h_2}(t)=[\mathcal {A}_0^{h_2}(t),\dots ,\mathcal {A}_{\mathcal {N}_t+1}^{h_2}(t)]^{T}.$$

Furthermore, (28) can be expressed in an equivalent manner as provided below:

$$\begin{aligned} \mathcal {J}_{\mathcal {N}_x}^{\mathcal {N}_t}(x,t)=(\mathcal {Z}_x\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t), \end{aligned}$$

(29)

where $\mathcal {Z}_{x}$ and $\mathcal {Z}_{t}$ are as follows

$$\begin{aligned} (z_{i,j})= {\left\{ \begin{array}{ll} \left( {\begin{array}{c}i-2\lfloor {\frac{i-j}{3}}\rfloor \\ \lfloor {\frac{i-j}{3}}\rfloor \end{array}}\right) (-1)^{\lfloor {\frac{i-j}{3}}\rfloor }2^{i-3\lfloor {\frac{i-j}{3}}\rfloor },\hspace{0.2cm} if \hspace{0.1cm}i\ge j,\hspace{0.1cm}i\equiv j\pmod 3,\\ 0,\hspace{1cm} otherwise, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \mathcal {T}_{\mathcal {N}_x}^{h_1}(x)=[1,x^{h_1},\dots ,x^{\mathcal {N}_xh_1}]^{T},\quad \mathcal {T}_{\mathcal {N}_t}^{h_2}(t)=[1,t^{h_2},\dots ,t^{\mathcal {N}_th_2}]^{T}. \end{aligned}$$

3 Methodology

In this section, we develop a numerical technique using operational matrices to estimate the (20)–(22). It should be noted that there is not any non-linearity in (4). In fact $sign(\frac{\partial ^2 \mathcal {V}}{\partial S^2})$ is equal $\pm 1$. After collocating the approximated model, this term will be a constant number. To begin, we make an estimation of the Caputu fractional derivative.

$$\begin{aligned} ^{C}_{0}D_{t}^{\alpha }\mathcal {J}(x,t)&\approx ~ ^{C}_{0}D_{t}^{\alpha }\mathcal {J}_{\mathcal {N}_x}^{\mathcal {N}_t}(x,t) =~^{C}_{0}D_{t}^{\alpha }(\mathcal {Z}_x\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)\nonumber \\ {}&=(\mathcal {Z}_x\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t~^{C}_{0}D_{t}^{\beta }\mathcal {T}_{\mathcal {N}_t}^{h_2}(t). \end{aligned}$$

(30)

Next, we calculate the expression $^{C}_{0}D_{t}^{\alpha }\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)$.

$$\begin{aligned} ^{C}_{0}D_{t}^{\alpha }\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)&=\begin{bmatrix} ^{C}_{0}D_{t}^{\alpha }1\\ ^{C}_{0}D_{t}^{\alpha }t^{h_2}\\ \vdots \\ ^{C}_{0}D_{t}^{\alpha }t^{\mathcal {N}_th_2} \end{bmatrix}=\begin{bmatrix} 0\\ \frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}(t-\sigma )^{-\alpha }h_2t^{h_2-1}d\sigma \\ \vdots \\ \frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}(t-\sigma )^{-\alpha }\mathcal {N}_th_2t^{\mathcal {N}_th_2-1}d\sigma \end{bmatrix}\nonumber \\ {}&=\begin{bmatrix} 0\\ \frac{\Gamma (h_2+1)}{\Gamma (h_2+1-\alpha )}t^{h_2-\alpha }\\ \vdots \\ \frac{\Gamma (\mathcal {N}_th_2+1)}{\Gamma (\mathcal {N}_th_2+1-\alpha )}t^{h_2-\alpha } \end{bmatrix}=\mathcal {D}^{\alpha }\mathcal {T}_{\mathcal {N}_t}^{h_2}(t), \end{aligned}$$

(31)

where

$$\begin{aligned} \mathcal {D}^{\beta }=t^{-\alpha }\begin{pmatrix} 0&{}0&{}\dots &{}0\\ 0&{}\frac{\Gamma (h_2+1)}{\Gamma (h_2+1-\alpha )}&{}\dots &{}0\\ \vdots &{}\vdots &{}\ldots &{}0\\ 0&{}0&{}\dots &{}\frac{\Gamma (\mathcal {N}_th_2+1)}{\Gamma (\mathcal {N}_th_2+1-\alpha )} \end{pmatrix}. \end{aligned}$$

We have obtained by substituting (31) for (30)

$$\begin{aligned} ^{C}_{0}D_{t}^{\alpha }\mathcal {J}(x,t)\approx (\mathcal {Z}_x\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {D}^{\alpha }\mathcal {T}_{\mathcal {N}_t}^{h_2}(t). \end{aligned}$$

(32)

Now, we attempt to approximate the first and second derivatives of $\mathcal {J}(x,t)$.

$$\begin{aligned} \mathcal {J}'(x,t)\approx \mathcal {J'}_{\mathcal {N}_x}^{\mathcal {N}_t}(x,t)&=(\mathcal {Z}_x\mathcal {T'}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)\nonumber \\&=(\mathcal {T'}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {Z}_x^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)\nonumber \\&=\begin{bmatrix} 0\\ h_1x^{h_1-1}\\ \vdots \\ \mathcal {N}_xh_1x^{\mathcal {N}_xh_1-1} \end{bmatrix}\mathcal {Z}_x^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)\nonumber \\ {}&=(\mathcal {D}^{1}\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t), \end{aligned}$$

(33)

where

$$\begin{aligned} \mathcal {D}^{1}=\frac{1}{x}\begin{pmatrix} 0&{}0&{}\dots &{}0\\ 0&{}h_1&{}\dots &{}0\\ \vdots &{}\vdots &{}\ldots &{}0\\ 0&{}0&{}\dots &{}\mathcal {N}_xh_1 \end{pmatrix}. \end{aligned}$$

likewise, one has

$$\begin{aligned} \mathcal {J}''(x,t)\approx \mathcal {J'}_{\mathcal {N}_x}^{\mathcal {N}_t}(x,t)&=(\mathcal {Z}_x\mathcal {T''}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)\nonumber \\&=(\mathcal {T''}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {Z}_x^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)\nonumber \\ {}&=\begin{bmatrix} 0\\ h_1(h_1-1)x^{h_1-2}\\ \vdots \\ \mathcal {N}_xh_1(\mathcal {N}_xh_1-1)x^{\mathcal {N}_xh_1-2} \end{bmatrix}\mathcal {Z}_x^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)\nonumber \\ {}&=(\mathcal {D}^{2}\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t), \end{aligned}$$

(34)

where

$$\begin{aligned} \mathcal {D}^{2}=\frac{1}{x^2}\begin{pmatrix} 0&{}0&{}\dots &{}0\\ 0&{}h_1(h_1-1)&{}\dots &{}0\\ \vdots &{}\vdots &{}\ldots &{}0\\ 0&{}0&{}\dots &{}N_xh_1(\mathcal {N}_xh_1-1) \end{pmatrix}. \end{aligned}$$

Using (32)–(34), we obtain

$$\begin{aligned} \begin{aligned} \mathcal {I}_1(x,t)&=(\mathcal {Z}_x\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {D}^{\alpha }\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)-p(t)(\mathcal {D}^{2}\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)\\&-q(t)(\mathcal {D}^{1}\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)+r(\mathcal {Z}_x\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)\\&-\mathcal {F}(x,t)\approx 0. \end{aligned} \end{aligned}$$

(35)

Similarly, (21) and (22) can also be estimated as

$$\begin{aligned}&\mathcal {I}_2(x,t)=(\mathcal {Z}_x\mathcal {T}_{\mathcal {N}_x}^{h_1}(c))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)-\mathcal {J}_1(t)\approx 0,\end{aligned}$$

(36)

$$\begin{aligned}&\mathcal {I}_3(x,t)=(\mathcal {Z}_x\mathcal {T}_{\mathcal {N}_x}^{h_1}(d))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(t)-\mathcal {J}_2(t)\approx 0,\end{aligned}$$

(37)

$$\begin{aligned}&\mathcal {I}_4(x,t)=(\mathcal {Z}_x\mathcal {T}_{\mathcal {N}_x}^{h_1}(x))^{T}\mathcal {M}\mathcal {Z}_t\mathcal {T}_{\mathcal {N}_t}^{h_2}(0)-\mathcal {J}_3(t)\approx 0. \end{aligned}$$

(38)

Therefore, using the points $x_i=\frac{i+1}{\mathcal {N}_x}$ and $t_j=\frac{j}{\mathcal {N}_t}$, we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {I}_1(x_i,t_j)=0\hspace{0.4cm}i=0,(1),\mathcal {N}_x-2,\hspace{0.2cm} j=0,(1),\mathcal {N}_t-1,\\ \mathcal {I}_2(t_j)=0\hspace{1cm}i=0,(1),\mathcal {N}_t-1, \\ \mathcal {I}_3(t_j)=0\hspace{1cm}j=0,(1),\mathcal {N}_t-1, \\ \mathcal {I}_4(x_i)= 0\hspace{1cm}j=0,(1),\mathcal {N}_x. \end{array}\right. } \end{aligned}$$

(39)

By solving (39) and finding the value of matrix $\mathcal {M}$, we achieve the numerical solution for (20)–(22). Algorithm 1 outlines the fundamental steps required to implement the suggested approach.

Algorithm 1

 .

Theorem 1

Let $\mathcal {J}_{N_x}^{N_t}(x,t)=B^T\mathcal {A}_{N_xN_t}^{h_1h_2}(x,t)$ and $\tilde{\mathcal {J}}_{N_x}^{N_t}(x,t)=\tilde{B}^T\mathcal {A}_{N_xN_t}^{h_1h_2}(x,t)$ be, respectively, the exact and numerical solutions of (35), in which

$$\begin{aligned}&B=[b_{11},\dots ,b_{1N_t+1},b_{21},\dots ,b_{2N_t+1},\dots ,b_{N_x1},\dots ,b_{N_x+1N_t+1}]^{T},\\ {}&\mathcal {A}_{N_xN_t}^{h_1h_2}(x,t)=[\mathcal {A}_{0}^{h_1}\mathcal {A}_{0}^{h_2},\dots ,\mathcal {A}_{0}^{h_1}\mathcal {A}_{N_t}^{h_2},\dots ,\mathcal {A}_{N_x}^{h_1}\mathcal {A}_{1}^{h_2},\dots ,\mathcal {A}_{N_x}^{h_1}\mathcal {A}_{N_t}^{h_2}]^{T}. \end{aligned}$$

Then, we have

$$\begin{aligned} ||&\mathcal {J}_{N_x}^{N_t}(x,t)-\tilde{\mathcal {J}}_{N_x}^{N_t}(x,t)||_2\le C_3||B-\tilde{B}||_2^2\sum _{i=0}^{N_x}\sum _{j=0}^{N_t}\bigg (\sum _{r=0}^{\lfloor {\frac{i}{3}}\rfloor }\frac{(-1)^{r}2^{i-3r}(i-2r)!}{r!(i-3r)!}\bigg )^2\\&\bigg (\sum _{r=0}^{\lfloor {\frac{j}{3}}\rfloor }\frac{(-1)^{r}2^{j-3r}(j-2r)!}{r!(j-3r)!}\bigg )^2, \end{aligned}$$

in which $C_3$ is a constant.

Proof

The inequality of Cauchy-Schwarz enables us to acquire

$$\begin{aligned} ||{} & {} \mathcal {J}_{N_x}^{N_t}(x,t)-\tilde{\mathcal {J}}_{N_x}^{N_t}(x,t)||_2^2=\int _{0}^{T}\int _{c}^{d}|\mathcal {J}_{N_x}^{N_t}(x,t)-\tilde{\mathcal {J}}_{N_x}^{N_t}(x,t)|^2dxdt\\{} & {} =\int _{0}^{T}\int _{c}^{d}\bigg |\sum _{i=0}^{N_x}\sum _{j=0}^{N_t}(b_{i+1,j+1}-\tilde{b}_{i+1,j+1})\mathcal {A}_{i+1}^{h_1}(x)\mathcal {A}_{j+1}^{h_2}(t)\bigg |^2dxdt\\{} & {} \le \int _{0}^{T}\int _{c}^{d}\bigg (\sum _{i=0}^{N_x}\sum _{j=0}^{N_t}|b_{i+1,j+1}-\tilde{b}_{i+1,j+1}|^2\bigg )\bigg (\sum _{i=0}^{N_x}\sum _{j=0}^{N_t}|\mathcal {A}_{i+1}^{h_1}(x)\mathcal {A}_{j+1}^{h_2}(t)|^2\bigg )dxdt\\{} & {} =\sum _{i=0}^{N_x}\sum _{j=0}^{N_t}|b_{i+1,j+1}-\tilde{b}_{i+1,j+1}|^2\sum _{i=0}^{N_x}\sum _{j=0}^{N_t}\int _{0}^{T}\int _{c}^{d}|\mathcal {A}_{i+1}^{h_1}(x)\mathcal {A}_{j+1}^{h_2}(t)|^2dxdt\\{} & {} =||B-\tilde{B}||_2^2\sum _{i=0}^{N_x}\sum _{j=0}^{N_t}\int _{0}^{T}\int _{c}^{d}\bigg |\sum _{r=0}^{\lfloor {\frac{i}{3}}\rfloor }\frac{(-1)^{r}2^{i-3r}(i-2r)!}{r!(i-3r)!}x^{(i-3r)h_1}\bigg |^2\bigg |\sum _{r=0}^{\lfloor {\frac{j}{3}}\rfloor }\frac{(-1)^{r}2^{j-3r}(j-2r)!}{r!(j-3r)!}t^{(j-3r)h_2}\bigg |^2dxdt\\{} & {} \le C_1C_2||B-\tilde{B}||_2^2\sum _{i=0}^{N_x}\sum _{j=0}^{N_t}\int _{0}^{T}\int _{c}^{d}\bigg (\sum _{r=0}^{\lfloor {\frac{i}{3}}\rfloor }\frac{(-1)^{r}2^{i-3r}(i-2r)!}{r!(i-3r)!}\bigg )^2\bigg (\sum _{r=0}^{\lfloor {\frac{j}{3}}\rfloor }\frac{(-1)^{r}2^{j-3r}(j-2r)!}{r!(j-3r)!}\bigg )^2dxdt\\{} & {} =(d-c)TC_1C_2||B-\tilde{B}||_2^2\sum _{i=0}^{N_x}\sum _{j=0}^{N_t}\bigg (\sum _{r=0}^{\lfloor {\frac{i}{3}}\rfloor }\frac{(-1)^{r}2^{i-3r}(i-2r)!}{r!(i-3r)!}\bigg )^2\bigg (\sum _{r=0}^{\lfloor {\frac{j}{3}}\rfloor }\frac{(-1)^{r}2^{j-3r}(j-2r)!}{r!(j-3r)!}\bigg )^2\\{} & {} =C_3||B-\tilde{B}||_2^2\sum _{i=0}^{N_x}\sum _{j=0}^{N_t}\bigg (\sum _{r=0}^{\lfloor {\frac{i}{3}}\rfloor }\frac{(-1)^{r}2^{i-3r}(i-2r)!}{r!(i-3r)!}\bigg )^2\bigg (\sum _{r=0}^{\lfloor {\frac{j}{3}}\rfloor }\frac{(-1)^{r}2^{j-3r}(j-2r)!}{r!(j-3r)!}\bigg )^2. \end{aligned}$$

This completes the theorem’s proof. $\square$

4 Convergence analysis

Therein, we examine the convergence of the suggested approach on the Sobolev space. Our aim is to demonstrate that as the number of basis functions derived from the fractional Jaiswal functions increases, the approximate solution gradually approaches the exact value. Additionally, we define our function space and present several essential theorems to support our findings. In $\Omega =(c,d)\times (0,T)$ for $n\ge 1$ the Sobolev norm is defined [41]

$$\begin{aligned} ||\mathcal {J}||_{H^{n}}(\Omega )=\bigg (\sum _{j=0}^{n}\sum _{i=1}^{2}||D_{i}^{(j)}\mathcal {J}||^2_{L^2(\Omega )}\bigg )^{\frac{1}{2}}, \end{aligned}$$

(40)

where $D_{i}^{(j)}\mathcal {J}$ stand for the jth derivative of $\mathcal {J}$ with respect to ith variable. The semi-norm $|\mathcal {J}|_{H^{n;N}}(\Omega )$ are given by [41]

$$\begin{aligned} |\mathcal {J}|_{H^{n;N}}(\Omega )=\bigg (\sum _{j=\min (n,N+1)}^{n}\sum _{i=1}^{2}||D_{i}^{(j)}\mathcal {J}||^2_{L^2(\Omega )}\bigg )^{\frac{1}{2}}. \end{aligned}$$

(41)

Due to brevity, we will assume that $h_1=h_2=h$ and $N_x=N_t=N$.

Theorem 2

[42] Let $\mathcal {J}(x,t)\in H^{n}(\Omega )$ with $n\ge 1$. Assume $\mathcal {P}_{N}^{h}\mathcal {J}(x,t)=\sum _{i=0}^{N}\sum _{j=0}^{N}b_{i+1,j+1} \mathcal {A}_{i+1}^{h}(x)\mathcal {A}_{j+1}^{h}(t)$ be the best approximation of $\mathcal {J}$. Then,

$$\begin{aligned} ||\mathcal {J}(x,t)-\mathcal {P}_{N}^{h}\mathcal {J}(x,t)||_{L^2(\Omega )}\le \mathcal {C}h^{1-n}N^{1-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega ), \end{aligned}$$

(42)

and for $1\le s\le n$,

$$\begin{aligned} ||\mathcal {J}(x,t)-\mathcal {P}_{N}^{h}\mathcal {J}(x,t)||_{H^s(\Omega )}\le \mathcal {C}h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega ), \end{aligned}$$

(43)

where

$$\begin{aligned} \eta (s)={\left\{ \begin{array}{ll} 0,\quad \quad \quad s=0,\\ 2s-\frac{1}{2},\quad s\ge 0, \end{array}\right. } \end{aligned}$$

in which $\mathcal {C}$ depends on N and is a positive constant.

Theorem 3

Assume $\mathcal {J}(x,t)\in H^{n}(\Omega )$,$n>0$. Then, for $1\le s\le n$

$$\begin{aligned}&||^{C}_{0}D_{t}^{\alpha }\mathcal {J}(x,t)-~^{C}_{0}D_{t}^{\alpha }(\mathcal {P}_{N}^{h}\mathcal {J}(x,t))||_{L^2(\Omega )}\nonumber \\&\le \frac{\mathcal {C}(d-c)T^{1-\alpha }h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega )}{\Gamma (2-\alpha )}. \end{aligned}$$

(44)

Proof

Using Young’s convolution inequality

$$\begin{aligned} ||g_1*g_2||_{L^2(\Omega )}\le ||g_1||_{L^1(\Omega )}||g_2||_{L^2(\Omega )}, \end{aligned}$$

we gain

$$\begin{aligned} ||^{C}_{0}D_{t}^{\alpha }\mathcal {J}(x,t)-~^{C}_{0}D_{t}^{\alpha }(\mathcal {P}_{N}^{h}\mathcal {J}(x,t))||_{L^2(\Omega )}&=||I^{1-\alpha }(^{C}_{0}D_{t}^{1}\mathcal {J}(x,t)-~^{C}_{0}D_{t}^{1}(\mathcal {P}_{N}^{h}\mathcal {J}(x,t)))||_{L^2(\Omega )}\\ {}&=||\frac{t^{-\alpha }}{\Gamma (1-\alpha )}*(^{C}_{0}D_{t}^{1}\mathcal {J}(x,t)-~^{C}_{0}D_{t}^{1}(\mathcal {P}_{N}^{h}\mathcal {J}(x,t)))||_{L^2(\Omega )}\\ {}&\le \frac{(d-c)T^{1-\alpha }}{\Gamma (2-\alpha )}||^{C}_{0}D_{t}^{1}\mathcal {J}(x,t)-~^{C}_{0}D_{t}^{1}(\mathcal {P}_{N}^{h}\mathcal {J}(x,t))||_{L^2(\Omega )}\\ {}&\le \frac{(d-c)T^{1-\alpha }}{\Gamma (2-\alpha )}||\mathcal {J}(x,t)-\mathcal {P}_{N}^{h}\mathcal {J}(x,t)||_{H^{s}(\Omega )}. \end{aligned}$$

Using Theorem 2, we derive

$$\begin{aligned} ||^{C}_{0}D_{t}^{\alpha }\mathcal {J}(x,t)-~^{C}_{0}D_{t}^{\alpha }(\mathcal {P}_{N}^{h}\mathcal {J}(x,t))||_{L^2(\Omega )}\le \frac{\mathcal {C}(d-c)T^{1-\beta }h^{\eta (l)-n}N^{\eta (l)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega )}{\Gamma (2-\beta )}. \end{aligned}$$

Theorem 4

Consider that the previous theorem’s assumptions are true. Then,

$$\begin{aligned}&||\mathcal {J}_x(x,t)-(\mathcal {P}_{N}^{h}\mathcal {J}(x,t))_x||_{L^2(\Omega )}\le \mathcal {C}h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega ),\\ {}&||\mathcal {J}_{xx}(x,t)-(\mathcal {P}_{N}^{h}\mathcal {J}(x,t))_{xx}||_{L^2(\Omega )}\le \mathcal {C}h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega ). \end{aligned}$$

Proof

Theorem 3 naturally leads to the proof. In fact

$$\begin{aligned} ||\mathcal {J}_x(x,t)-(\mathcal {P}_{N}^{h}\mathcal {J}(x,t))_x||_{L^2(\Omega )}\le ||\mathcal {J}_x(x,t)-(\mathcal {P}_{N}^{h}\mathcal {J}(x,t))_x||_{H^s(\Omega )}, \end{aligned}$$

and

$$\begin{aligned} ||\mathcal {J}_{xx}(x,t)-(\mathcal {P}_{N}^{h}\mathcal {J}(x,t))_{xx}||_{L^2(\Omega )}\le ||\mathcal {J}_{xx}(x,t)-(\mathcal {P}_{N}^{h}\mathcal {J}(x,t))_{xx}||_{H^s(\Omega )}. \end{aligned}$$

Theorem 5

Assume that, $|p(t)|\le m_1$, $|q(t)|\le m_2$ and $\mathcal {J}(x,t)\in H^n(\Omega )$ with $n\ge 1$. For $1\le s\le n$, the following inequality is hold

$$\begin{aligned} ||\mathcal {X}(x,t)||_{L^2(\Omega )}&\le \frac{\mathcal {C}(d-c)T^{1-\beta }h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega )}{\Gamma (2-\beta )}+m_1\mathcal {C}h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega )\nonumber \\ {}&+m_2\mathcal {C}h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega )+r\mathcal {C}h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega ), \end{aligned}$$

(45)

where $\mathcal {X}(x,t)$ is the perturbation term.

Proof

The perturbation term satisfies the following equation

$$\begin{aligned} ^{C}_{0}D_{t}^{\alpha }\mathcal {P}_{N}^{h}\mathcal {J}(x,t)=&p(t)\frac{\partial ^2\mathcal {P}_{N}^{h}\mathcal {J}(x,t)}{\partial x^2}+q(t)\frac{\partial \mathcal {P}_{N}^{h}\mathcal {J}(x,t)}{\partial x}\nonumber \\&-r\mathcal {P}_{N}^{h}\mathcal {J}(x,t)+\mathcal {F}(x,t)+\mathcal {X}(x,t). \end{aligned}$$

(46)

According to (20)

$$\begin{aligned} ^{C}_{0}D_{t}^{\alpha }(\mathcal {J}(x,t)-\mathcal {P}_{N}^{h}\mathcal {J}(x,t))=&p(t)(\frac{\partial ^2\mathcal {J}(x,t)}{\partial x^2}-\frac{\partial ^2\mathcal {P}_{N}^{h}\mathcal {J}(x,t)}{\partial x^2})\\&+q(t)(\frac{\partial \mathcal {J}(x,t)}{\partial x}-\frac{\partial \mathcal {P}_{N}^{h}\mathcal {J}(x,t)}{\partial x})\\&-r(\mathcal {J}(x,t)-\mathcal {P}_{N}^{h}\mathcal {J}(x,t))-\mathcal {X}(x,t). \end{aligned}$$

Due to Theorems 2-4, we have

$$\begin{aligned} ||\mathcal {X}(x,t)||_{L^2(\Omega )}&\le ||p(t)(\frac{\partial ^2\mathcal {J}(x,t)}{\partial x^2}-\frac{\partial ^2\mathcal {P}_{N}^{h}\mathcal {J}(x,t)}{\partial x^2})||_{L^2(\Omega )} +||q(t)(\frac{\partial \mathcal {J}(x,t)}{\partial x}-\frac{\partial \mathcal {P}_{N}^{h}\mathcal {J}(x,t)}{\partial x})||_{L^2(\Omega )}\\ {}&+ ||r(\mathcal {J}(x,t)-\mathcal {P}_{N}^{h}\mathcal {J}(x,t))||_{L^2(\Omega )}+||^{C}_{0}D_{t}^{\alpha }(\mathcal {J}(x,t)-\mathcal {P}_{N}^{h}\mathcal {J}(x,t))||_{L^2(\Omega )}\\ {}&\le m_1||(\frac{\partial ^2\mathcal {J}(x,t)}{\partial x^2}-\frac{\partial ^2\mathcal {P}_{N}^{h}\mathcal {J}(x,t)}{\partial x^2})||_{L^2(\Omega )} +m_2||(\frac{\partial \mathcal {J}(x,t)}{\partial x}-\frac{\partial \mathcal {P}_{N}^{h}\mathcal {J}(x,t)}{\partial x})||_{L^2(\Omega )}\\ {}&+|r|||(\mathcal {J}(x,t)-\mathcal {P}_{N}^{h}\mathcal {J}(x,t))||_{L^2(\Omega )} +||^{C}_{0}D_{t}^{\alpha }(\mathcal {J}(x,t)-\mathcal {P}_{N}^{h}\mathcal {J}(x,t))||_{L^2(\Omega )}\\ {}&\le \frac{\mathcal {C}(d-c)T^{1-\alpha }h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega )}{\Gamma (2-\beta )}+m_1\mathcal {C}h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega )\\ {}&+m_2\mathcal {C}h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega )+r\mathcal {C}h^{\eta (s)-n}N^{\eta (s)-n}|\mathcal {J}|_{H^{n;Nh}}(\Omega ). \end{aligned}$$

$\square$

The approximation error can be reduced by selecting the number of basis functions suitably, as seen by the right-hand side of inequality (45). We also need to select the parameters $h_1$ and $h_2$. properly in order to decrease the method’s error. However, there is generally no way to select these parameters. So, we can apply the trial-and-error approach. Typically, parameters $h_1$ and $h_2$ can be taken like $\frac{1}{a}$ and $\frac{1}{b}$ so long as the $\mathcal {J}(x^{a},t^{b})$ be smooth enough. This can speed up the convergence rate, as demonstrated in theorem 4.1 of reference [44].

5 Test problems

In this part, we provide four examples for various types of exact solutions to demonstrate the novel method’s applications and computational performance. MATLAB 2020 is used to perform the computations. In all examples, the following error norm is applied to obtain numerical results.

$$\begin{aligned} ||e||_\infty =\max _{0\le i\le \mathcal {N}_x} |\mathcal {J}(x_i,T)- \mathcal {J}_{N_x}^{N_t}(x_i,T)|. \end{aligned}$$

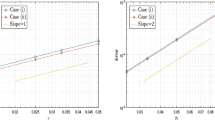
In order to validate the theoretical results, we choose a fix $\mathcal {N}_x$ properly and increase the number of basis functions in time direction. In fact, let $\mathcal {J}^{\mathcal {N}_t}(x,t)=\sum _{i=0}^{\infty }b_{\mathcal {N}_x+1,j+1}\mathcal {A}_{\mathcal {N}_x+1}^{h_1}(x)\mathcal {A}_{j+1}^{h_2}(t)$ and $\hat{\mathcal {J}}^{\mathcal {N}_t}(x,t)=\sum _{i=0}^{\mathcal {N}_t}b_{\mathcal {N}_x+1,j+1}\mathcal {A}_{\mathcal {N}_x+1}^{h_1}(x)$ $\mathcal {A}_{j+1}^{h_2}(t)$, then we estimate the following error norm

$$\begin{aligned} E^{\mathcal {N}_t}=||\mathcal {J}^{\mathcal {N}_t}(x,t)-\hat{\mathcal {J}}^{\mathcal {N}_t}(x,t)||_2. \end{aligned}$$

A bound similar to reference [45] can be found for the aforementioned error norm.

The convergence rate of the numerical approach was not obtained in the previous section; nevertheless, it has been experimentally computed in the numerical examples. An estimate of the convergence rate is calculated as [43]

$$\begin{aligned} CR=-\frac{\log (E_{\mathcal {N}_t})-\log (E_{\mathcal {N}_t+1})}{\log (\mathcal {N}_t)-\log (\mathcal {N}_{t}+1)}. \end{aligned}$$

Example 1

In the third example, we have chosen the following problem with exact solution $\mathcal {J}(x,t)=x^4t^{\alpha }$ on domain $\Omega =[0,1]^2$

$$\begin{aligned} ^{C}_{0}\mathcal {D}_{t}^{\alpha }\mathcal {J}(x,t)=p(t)\frac{\partial ^2\mathcal {J}(x,t)}{\partial x^2}+q(t)\frac{\partial \mathcal {J}(x,t)}{\partial x}-r\mathcal {J}(x,t)+\mathcal {F}(x,t), \end{aligned}$$

where $0<\beta <1$,  $r=0.5$, $p(t)=t^2$, $q(t)=t$ and

$$\begin{aligned} \mathcal {F}(x,t)=\Gamma (\beta +1)x^4-t^{\alpha }\bigg [p(t)(12x^2)+q(t)(4x^3)-rx^4\bigg ]. \end{aligned}$$

Absolute errors at sample point $(x_i,t_i)=(0,0),(\frac{1}{6},\frac{1}{6}), (\frac{1}{3},\frac{1}{3}),(\frac{1}{2},\frac{1}{2}),(\frac{2}{3},\frac{2}{3}),(\frac{5}{6},$ $\frac{5}{6}),(1,1)$ for different value of $\beta$ are collected in Table 1. We choose $\mathcal {N}_x=6$, $\mathcal {N}_t=3$, $h_1=1$, and $h_2=\alpha$. It is apparent that the absolute errors are approximately zero. The norm of errors, rate of convergence, and CPU time are provided in Table 2. This table demonstrates that we get better and better results that validate our theoretical analysis when we fix $\mathcal {N}_t$ by an appropriate number of basis functions in the time direction and increase $\mathcal {N}_x$. Also, the CPU time indicates the procedure is fast and efficient. The plot of error function depicted in Fig. 1. This picture illustrates how selecting appropriate values for $h_1$ and $h_2$ may reduce the absolute errors between numerical and exact solutions. The behavior of solutions at $T=1$ for $\alpha =0.2,0.4,0.8,0.9$ are illustrated in Fig. 2. Also, the surface of exact and numerical solutions is portrayed in Fig. 3. We can see that the two solutions are almost equal.

Table 1 Absolute errors and CPU time for $\beta =0.2,0.5,0.8$ and $\mathcal {N}_x=6, \mathcal {M}_t=3$ with $h_1=1,h_2=\alpha$

Table 2 Maximum absolute errors and convergence rate with $\mathcal {N}_t=3$, $\alpha =0.5$, and $h_1=1,h_2=\alpha$ for Example 1

Example 2

In this example, we consider the model as follows:

$$\begin{aligned} \frac{\partial ^{\alpha } \mathcal {V}(s,t)}{\partial t^{\alpha }} +\frac{ \sigma _1^2(t)}{2} s(t)^2 \frac{\partial ^2 \mathcal {V}(s,t)}{\partial s^2} + r s(t) \frac{\partial \mathcal {V}(s,t)}{\partial s}-r\mathcal {V}(s,t) =0, \end{aligned}$$

with terminal and boundary conditions

$$\begin{aligned}&\mathcal {V}(s_{\min },t)=0,\qquad \mathcal {V}(s_{max},t)=s_{\max }-Ke^{-r(T-t)},\quad 0\le t\le T,\\ {}&\mathcal {V}(s,T)=\max \{s-K,0\},\quad \qquad \qquad \hspace{1.5cm} s_{\min }\le s\le s_{\max }. \end{aligned}$$

where

$$\sigma _1^2(t)=2\sigma ^2\left( \beta ^2 \left( \frac{1}{2} + H t^{2H-1} \right) - \sqrt{\frac{2}{\pi }}\frac{k}{ \sigma } \sqrt{\frac{\beta ^2 + \beta ^2 (dt)^{2H-1}}{dt}} \right) .$$

Fig. 1

Surface of error function for $\alpha =0.5$ with $(\mathcal {N}_x,\mathcal {N}_t)=(4,4)$ for (Example 1)

Fig. 2

The behavior solutions with $(\mathcal {N}_x,\mathcal {N}_t)=(6,3)$ and $(h_1,h_2)=(1,\alpha )$ when $\alpha =0.2,0.5,0.8,$ and $\alpha = 0.9$ for (Example 1)

Fig. 3

The behavior of solutions for $(\mathcal {N}_x,\mathcal {N}_t)=(6,3)$ and $(h_1,h_2)=(1,\alpha )$ when $\alpha =0.5$ for (Example 1)

The parameters value are, $\sigma =0.4$, $r=0.1$, $K=5$, $k=0.01$, $H=0.8$, $\beta =0.5$, $\alpha =0.5$, $dt=0.001$, $s_{\min }=0.1$, $s_{\max }=33.33$, and $T=1$. Changes in the stock price and the time to maturity can have significant implications for the option value. The stock price directly impacts the value of a call option. As the stock price increases, the likelihood of the option being profitable also rises, resulting in a higher option value. Conversely, a decrease in the stock price diminishes the probability of the option becoming profitable, leading to a lower option value. Also, the time to maturity plays a crucial role in determining the option value. As the time to expiration decreases, the option has less time to move in a favorable direction, resulting in a lower probability of the option being profitable and consequently reducing its value. Conversely, a longer time to maturity provides more opportunity for the underlying stock price to fluctuate favorably, increasing the likelihood of profitability and driving up the option value. Moreover, when $\alpha \longrightarrow 1$, the MTF-BS equation convergences to the MF-BS equation. Because the exact solution is unknown, we follow the procedure of reference [30, 36] and estimate error of numerical scheme using the following relation

$$\begin{aligned} E_{\mathcal {N}_t}=||\mathcal {J}_{\mathcal {N}_x^*}^{\mathcal {N}_t}(x,t)-\mathcal {J}_{\mathcal {N}_x^*}^{\mathcal {\mathcal {N}}_{t+1}}(x,t)||_{L_2}, \end{aligned}$$

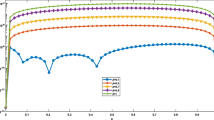
for a fixed value of $\mathcal {N}_x^{*}$. In Table 3, norm of errors, rate of convergence, and CPU time provided. It is clear that by selecting $\mathcal {N}_x$ suitably as $\mathcal {N}_t$ is increased, the numerical value of $\mathcal {J}(x,t)$ within the domain converge to the exact values. This table exhibits how the suggested method can generate precise numerical solutions even with a limited number of basis functions. The experimentally determined convergence rate of the approach indicates that our results are in good accord with the theoretical results. The graph of call option prices for European call option with $\alpha =0.5,0.6,0.7,0.8,0.9,1$ is depicted in Fig. 4. Figure 5 shows the surface of numerical solution for $\alpha =0.5$ with $(\mathcal {N}_x,\mathcal {N}_t)=(10,5)$. The graphs in this example demonstrate the efficacy and usefulness of the numerical method.

Table 3 Norm of errors, convergence rate, and CPU time for $h_1=1,h_2=\alpha$ at time $t=1$ for Example 2

Fig. 4

Call option prices of European call option with $\alpha =0.5,0.6,0.7,0.8,0.9,1$ for (Example 2)

Fig. 5

Surface of Numerical solution for $\alpha =0.5$ with $(\mathcal {N}_x,\mathcal {N}_t)=(10,5)$ for (Example 2)

Example 3

In this example, we consider the model as follows:

$$\begin{aligned} ^{C}_{0}\mathcal {D}_{t}^{\alpha }\mathcal {J}(s,t)-\frac{1}{2}\sigma ^2\frac{\partial ^2\mathcal {J}(s,t)}{\partial s^2}-\bigg (r-\frac{1}{2}\sigma ^2\bigg )\frac{\partial \mathcal {J}(s,t)}{\partial s}+r\mathcal {J}(s,t)=0,\quad (s,t)\in (-Y,Y)\times [0,T], \end{aligned}$$

with initial and boundary conditions

$$\begin{aligned}&\mathcal {J}(-Y,t)=Ke^{-rt},\qquad \mathcal {J}(Y,t)=0,\quad 0\le t\le T,\\ {}&\mathcal {J}(s,0)=\max \{K-Ke^s,0\},\quad \quad -Y\le s\le Y, \end{aligned}$$

with $0<\alpha <1$, $\sigma =0.1$, $r=0.01$, $T=1$, $K=50$, and $Y=2$. Since an exact solution for this problem is not easily accessible, we estimate the error of the numerical scheme by the following relation

$$\begin{aligned} E_{\mathcal {N}_t}=||\mathcal {J}_{\mathcal {N}_x^*}^{\mathcal {N}_t}(x,t)-\mathcal {J}_{\mathcal {N}_x^*}^{\mathcal {\mathcal {N}}_{t+1}}(x,t)||_{L_2}, \end{aligned}$$

for a fixed value of $\mathcal {N}_x^{*}$. The norm of errors, convergence rate, and CPU time of the numerical scheme are provided in Table 4 for $\alpha =0.2,0.8$. The error of the collocation scheme decreases as $\mathcal {N}_t$ increases, illustrating the accuracy of the proposed methodology. The accuracy of the method can be improved further by using suitable parameters. The surface plot of European put option prices computed by the presented scheme for $\alpha =0.5$, $(\mathcal {N}_x,\mathcal {N}_t)=(8,5)$, and $(h_1,h_2)=(1,\alpha )$ is demonstrated in Fig. 6. Our findings in this example show that the suggested approach can solve the problem effectively.

Table 4 Norm of errors, convergence rate, and CPU time for $h_1=1,h_2=\alpha$ at time $t=1$ for Example 3

Fig. 6

Surface of Numerical solution for $\alpha =0.5$ with $(\mathcal {N}_x,\mathcal {N}_t)=(8,5)$ and $(h_1,h_2)=(1,\alpha )$ for (Example 3)

Example 4

In the last example, we consider the model as follows:

$$\begin{aligned} ^{C}_{0}\mathcal {D}_{t}^{\alpha }\mathcal {J}(s,t)&-\frac{1}{2}\sigma _1^2(t)\frac{\partial ^2\mathcal {J}(s,t)}{\partial s^2}-\bigg (r-\frac{1}{2}\sigma _1^2(t)\bigg )\frac{\partial \mathcal {J}(s,t)}{\partial s}\\&~~~~+r\mathcal {J}(s,t)=0,\quad (s,t)\in (-Y,Y)\times [0,T], \end{aligned}$$

where

$$\sigma _1^2(t)=2\sigma ^2\left( \beta ^2 \left( \frac{1}{2} + H t^{2H-1} \right) - \sqrt{\frac{2}{\pi }}\frac{k}{ \sigma } \sqrt{\frac{\beta ^2 + \beta ^2 (dt)^{2H-1}}{dt}}\right) ,$$

together initial and boundary conditions

$$\begin{aligned}&\mathcal {J}(-Y,t)=Ke^{-rt},\qquad \mathcal {J}(Y,t)=0,\quad 0\le t\le T,\\ {}&\mathcal {J}(s,0)=\max \{K-Ke^s,0\},\quad \quad -Y\le s\le Y, \end{aligned}$$

with $0<\alpha <1$, $\sigma =0.1$, $r=0.01$, $k=0$, $H=0.8$, $\beta =0.5$, $dt=0.001$, $T=1$, $K=50$, and $Y=2$.

We estimate the error of the numerical scheme by the following relation

$$\begin{aligned} E_{\mathcal {N}_t}=||\mathcal {J}_{\mathcal {N}_x^*}^{\mathcal {N}_t}(x,t)-\mathcal {J}_{\mathcal {N}_x^*}^{\mathcal {\mathcal {N}}_{t+1}}(x,t)||_{L_2}, \end{aligned}$$

for a fixed value of $\mathcal {N}_x^{*}$. In this test problem, the volatility is not a constant. In order to obtain the numerical results, we fix $\mathcal {N}_x=4$. For different value of $\mathcal {N}_t$ norm of errors, convergence rate, and CPU time for $h_1=1,h_2=\alpha$ at time $t=1$ are presented in Table 5. This table demonstrates how, by selecting the proper number of basis functions, the method’s error tends to be zero. Based on the data in this table, it can be concluded that the approach used in this study solves the given problem with remarkable precision. The plot of put option values is demonstrated in Fig. 7. Overall, these findings show that the mixed time-fractional Black-Scholes European option pricing model can be solved accurately and effectively using the suggested collocation method.

Table 5 Norm of errors, convergence rate, and CPU time for $h_1=1,h_2=\alpha$ at time $t=1$ for Example 4

Fig. 7

Surface of Numerical solution for $\alpha =0.6$ with $(\mathcal {N}_x,\mathcal {N}_t)=(4,6)$ and $(h_1,h_2)=(1,\alpha )$ for (Example 4)

6 Conclusion

In the paper, we obtained the option price under the MTF-BS model where the stock price dynamic follows the MFGBM model. The model added the long memory property in which the feature is compatible with the real word data behavior. We considered the fractional form of the problem in the sense of Riemann-Liouville derivative. Since the option price PDE is non-linear, thus we apply the collocation method to treat the model numerically. We used the Jaiswal functions as a basis to construct the numerical scheme. We reduced the problem into an algebraic linear system of equations. Moreover, the convergence of the method is fully discussed in the Sobolev space framework. An error bound was found for the perturbation term, demonstrating that the exact solution tends to the exact solution by selecting the number of basis functions properly. In order to speed up the convergence rate, selecting parameters $h_1$ and $h_2$ are discussed. To demonstrate how effective the approach is, we provided four test problems and found the option price in different states. For examples where the exact solution was unknown, the norm of the difference between numerical solutions for two consecutive $\mathcal {N}_t$ is calculated. Also, the method can be used for problems with non-smooth solutions.