An improved numerical approach for solving shape optimization problems on convex domains

Abstract

This work is devoted to show the efficiency of a new numerical approach in solving geometrical shape optimization problems constrained to partial differential equations, on a family of convex domains. More precisely, we are interested to an improved numerical optimization process based on the new shape derivative formula, using the Minkowski deformation of convex domains, recently established in Boulkhemair and Chakib (J. Convex Anal. 21($\text {n}^{\circ }1$), 67–87 2014), Boulkhemair (SIAM J. Control Optim. 55($\text {n}^{\circ }1$), 156–171 2017). This last formula allows to express the shape derivative by means of the support function, in contrast to the classical one expressed in term of vector fields Henrot and Pierre 2005, Delfour and Zolésio 2011, Sokolowski and Zolesio 1992. This avoids some of the disadvantages related to the classical shape derivative approach, when one use the finite elements discretization for approximating the auxiliary boundary value problems in shape optimization processes Allaire 2007. So, we investigate here the performance of the proposed shape optimization approach through the numerical resolution of some shape optimization problems constrained to boundary value problems governed by Laplace or Stokes operator. Notably, we carry out a comparative numerical study between its resulting numerical optimization process and the classical one. Finally, we give some numerical results showing the efficiency of the proposed approach and its ability in producing good quality solutions and in providing better accuracy for the optimal solution in less CPU time compared to the classical approach.

1 Introduction

The shape optimization is a classical and ubiquitous field of research whose study becomes popular in academic researches and industry due to its increasingly wide applications in the field of computer science and engineering [14, 20, 30], structural mechanics [1, 20], optimal control [1, 24, 38], acoustics [42, 43], electromagnetics [19, 20] and chemical reactions [44]. The difficulty to dealing with this type of problems is to obtain analytically the optimal shapes which is usually impossible, notably in the usual case where the optimal shape design problems are constrained to partial differential equations (PDEs). So, a variety of numerical approaches and techniques find their powers to localize (approximate) optimal shapes with the help of the efficient PDEs discretization methods and modern optimization processes [5, 17, 25, 27].

In this respect, several questions arise when one deals with the study of a shape optimization problem. Notably, the existence of an optimal shape, its regularity as well as its geometrical property. On the other hand, the numerical investigation of shape optimization problems using the gradient optimization process is based on the study of the first variation of the cost functional, and in particular on the computation of its gradient or what one call the shape derivative. This notion of derivation with respect to domains was intensively studied in the 1980s by several authors. The first result concerning the differentiability with respect to perturbations of a geometrical domain was obtained by Hadamard in 1907 for solving an eigenvalue shape optimization problem [18]. Then, the shape derivative was introduced by Céa [8,9,10,11] and developed later by Murat and Simon [31, 36, 37] and extensively investigated in more recent works [15, 16, 40, 41], as well as in the books [1, 7, 14, 24, 38]. Also, different approaches, were applied to solve many problems in shape optimization, see, for example, the books [1, 14, 24, 34, 38] and the references therein. Finally, let us also mention that recent discussions on the so-called pre-shape derivative methods, based on the volume representation of the shape derivative, which enables to perform mesh and shape optimization approaches at the same time, are done in [28, 29].

This work is devoted to show the efficiency of a new numerical shape optimization approach, based on the shape derivative formula, involving the Minkowski deformation on a family of convex domains, recently established in [2, 3], in solving geometrical shape optimization problems. More precisely, we are interested to an improved numerical shape optimization process, based on this shape derivative formula allowing us to establish its expression by means of the support function, in contrast to the classical shape derivative expressed in term of vector fields [14, 24, 38]. In this context, we precise that the classical approach presents some difficulties from both theoretical and numerical point of view. For example, when one wants to connect the set of admissible domains with vector fields, one has to suppose high smoothness conditions on the initial data in order to differentiate functions depending on the domain. Note also that to solve a conditional shape optimization problem by this method is yet more complicated and usually requires to reduce it to a non conditional problem (for example, by Lagrange’s multipliers method). Moreover, we believe that the numerical optimization processes involving the classical shape derivative presents some disadvantages. We refer here to [1], for example, for explanations about the issues that arise when implementing numerically the gradient optimization algorithm using the classical shape derivative. Briefly, when one uses the deformation by vector fields, we have to extend the vector field (obtained only on the boundary) to the whole domain or to re-mesh the domain, at each iteration, and both tasks are expensive. In order to avoid a part of the above issues, we define and use another way of variation of domains, a way that is linked to the convexity context and based on the Minkowski sum. Recall that for any convex bounded domain the support function of this domain is a continuous convex and positive homogeneous function. Conversely, it is known that each continuous convex and positive homogeneous function is the support function of a convex bounded set (sub-differential of this function at the origin). Using this fact, the variation of domains is clearly characterized by the variation of the corresponding support function. Then, when solving optimal shape design problems numerically using an optimization process based the new shape derivative formula, one gets a support function at each step of the implementation, the domain being recovered as the sub-differential of this support function. So in order to show the efficiency of this approach, which is successfully applied for solving concrete problems in [4, 5] using boundary element method, we investigate here its numerical comparative study with the classical one, in solving some shape optimization problems of minimizing appropriate cost functionals constrained to elliptic boundary value problems. In this respect, let us mention that a first numerical comparative result for solving a simple shape optimization problem of minimizing only a least-square cost functional of the velocity, solution of the state Stokes problem, was stated in a short communication [6]. We deal here with the numerical study of more complicated situations for different shape optimization problems of minimizing various cost functional constrained to Laplace or Stokes Operator. For this, we provide a detailed description of the new approach and investigate the numerical shape optimization algorithms using different shape derivative approaches performed by the finite element method for approximating the auxiliary boundary value problems in the shape optimization processes. Finally, we give some numerical experiments including comparison results which confirm our expectation. Mainly the proposed approach using the new shape derivative formula converges to solutions of good quality and offer better accuracy for the optimal shape as well as the associated reconstructed solution in less CPU time compared to the one using the classical approach.

The remainder of this paper is organized as follows: in Sect. 2, we present a brief survey on the classical shape sensitivity analysis based the Hadamard approaches and summarized its resulting numerical shape optimization process. We propose the new numerical shape optimization approach based on the shape derivative formula involving the Minkowski deformation and present its numerical algorithm. Then, we propose the discretization of this shape optimization approach using the finite element method and suggest the discrete numerical optimization process. The Sect. 3 is devoted to the application of both approaches for solving some shape optimization problems of minimizing some appropriate cost functionals subjected to some elliptic boundary value problems governed by Laplace or Stokes equation. Notably, we give some numerical experiments including comparison results showing the efficiency of the new shape optimization approach compared to the classical one.

2 Shape sensitivity approaches and resulting algorithms

The numerical investigation of shape optimization problems is based on the study of the first variation of a shape functional, and in particular, on the computation of its gradient with respect to domains. So in this section, we present a short survey on the notion of differentiability with respect to domains or the so-called the shape derivative. The first part is devoted to introduce the Hadamard’s shape derivative approaches extensively studied in the literature (see, for example,  [1, 14, 24, 30, 38]) and summarized the resulting numerical algorithm for solving shape optimization problems. Then, we present the new shape derivative approach introduced in [2, 3] for convex domains and suggest its resulting numerical shape optimization process.

In all what follows, let us consider a typical shape optimization problem:

$$\begin{aligned} \min _{\Omega \in \mathcal {U}}\mathcal {F}(\Omega ,u_{\Omega },\nabla u_{\Omega }) \end{aligned}$$

(2.1)

where $\mathcal {F}$ is a shape cost functional and $\mathcal {U}$ is a family of admissible open smooth enough subsets of D, a large and a smooth set of $\mathbb {R}^d$ $(d\ge 2)$, and $u_{\Omega }$ is the solution of boundary value problem on $\Omega$ called the state problem.

2.1 Hadamard’s shape sensitivity based approaches

In order to carry out the sensitivity analysis of shape cost functionals $\Omega \rightarrow J(\Omega )$, one needs to introduce a family of perturbations $\{\Omega _\epsilon \}_\epsilon$ of a given domain $\Omega _0\subset \mathbb {R}^d$ for $0\le \epsilon < 1$. Thereby one can construct a family of transformations $T_\epsilon :\mathbb {R}^d\rightarrow \mathbb {R}^d$ for some $\epsilon \in [0,1[$ and $T_\epsilon$ maps $\Omega$ onto $\Omega _\epsilon .$ The family of domains $\{\Omega _\epsilon \}_\epsilon$ is then defined by $\Omega _\epsilon =T_\epsilon (\Omega )$, such that $T_\epsilon$ satisfies appropriate regularity assumptions. More precisely, in the case of enough smooth domains, one can use the transformation of domains introduced by Hadamard in 1907 in his famous memory on elastic plates [18] to compute the derivative of a shape functional $\Omega \rightarrow J(\Omega )$ by considering the normal perturbations of the boundary. This is the basic idea in the notion of shape derivative in a topological context developed later by several authors. This approach can be briefly described as follows, if $\Omega _0$ is domain of class $\mathcal {C}^\infty$, its outward unit normal vector $\nu _0$ on $\Gamma _0:=\partial \Omega _0$ is in $\mathcal {C}(\Gamma _0,\mathbb {R}^d)$. Let $g\in \mathcal {C}^{\infty }(\Gamma _0)$ be a given function, since $\Gamma _0$ is assumed to be compact, then there exists $\delta >0$ such that for any $\epsilon \in ]-\delta ,\delta [$, we have that

$$ \Gamma _\epsilon =\Gamma +\epsilon g\nu =\{y\,\,|\,\,y=x+\epsilon g(x)\nu _0(x)\,\,\text {for}\,\,x\in \Gamma _0\} $$

is the boundary of the domain $\Omega _\epsilon$ which is of class $\mathcal {C}^{\infty }$. Consider an extension $\mathcal {N}_0$ to $\mathbb {R}^d$ of the normal vector field $\nu _0$ defined on $\Gamma _0$, $\mathcal {N}_0\in \mathcal {C}^{\infty }(\mathbb {R}^d,\mathbb {R}^d)$, we can define the transformation $T_\epsilon =\text {Id}_{\mathbb {R}^{d}}+\epsilon g_0\mathcal {N}_0$, where $g_0$ denotes an extension in $\mathcal {C}^{\infty }(\mathbb {R}^d)$ of $g\in \mathcal {C}^{\infty }(\Gamma )$.

Then, this approach was widely developed by many authors, see, for example, [14, 24, 30, 31, 38] and the references therein. Notably, there are two variants of the Hadamard’s method of shape differentiation. We will present here the more extensively used:

The first one is introduced by Murat and Simon [31, 36, 37] and based on the variation of domains by the transformation $T_{\theta }:=\text {Id}_{\mathbb {R}^{d}}+\theta$, such that

$$\begin{aligned} \Omega _{\theta }:=T_{\theta }(\Omega _0)=\{x+\theta (x)\,\,|\,\, x\in \Omega _0\}, \end{aligned}$$

(2.2)

where $\Omega _0$ is an element of a family of domains $\mathcal {U}$ and $\theta \in W^{1,\infty }(\mathbb {R}^d,\mathbb {R}^d)$.

So assume that there exists $\epsilon \in ]0,1[$ such that $\Omega _{\theta }\in \mathcal {U}\,\,\,\forall \theta \in B_{{W^{1,\infty }}}(0,\epsilon ),$ where $B_{{W^{1,\infty }}}(0,\epsilon )$ is the ball of center 0 and radius $\epsilon$ in $W^{1,\infty }(\mathbb {R}^d,\mathbb {R}^d).$ Then, the shape derivative of a cost functional $\Omega \rightarrow J(\Omega )$ at $\Omega _0$ is defined as the Fréchet derivative at 0 in $W^{1,\infty }(\mathbb {R}^d,\mathbb {R}^d)$ of $\theta \in B_{{W^{1,\infty }}}(0,\epsilon ) \mapsto J((\text {Id}_{\mathbb {R}^{d}}+\theta )(\Omega _0))\in \mathbb {R}$.

Note that when $\theta \in W^{1,\infty }(\mathbb {R}^d,\mathbb {R}^d)$, such that $\Vert \theta \Vert _{W^{1,\infty }}\le \epsilon$ (for $\epsilon \in [0,1[$), the function $\text {Id}_{\mathbb {R}^{d}}+\theta$ called the perturbation of the identity [13] is a diffeomorphism, which is the main fact used for the existence of the shape derivative with respect to domains.

The second approach is the so-called speed method, introduced by Zolésio et al. [15, 16, 40, 41], and summarized as follows: for a given vector field $V \in \mathcal {C}^{1}(\mathbb {R} \times \mathbb {R}^{d};\mathbb {R}^{d})$, consider the solution of the following ordinary differential equation

$$\begin{aligned} \Phi _{V}(0,x)=x \quad \text {and}\quad \frac{d\Phi _{V}(\epsilon ,x)}{d \epsilon }=V(\epsilon ,\Phi _{V}(\epsilon ,x)),\quad x\in \Omega _0. \end{aligned}$$

(2.3)

and define the domain

$$ \Omega _\epsilon = T_{\epsilon }(V)(\Omega _0) =\{T_{\epsilon }(V)(x)\,\,|\,\,x\in \Omega _0\},\quad T_{\epsilon }(V)(\Omega _0):=\Phi _{V}(\epsilon ,\Omega _0). $$

Then,

(i):

$\text {the Eulerian derivative of}$ $J(\Omega )$ at $\Omega _0$:

$$\begin{aligned} dJ(\Omega _0)(V):=\lim _{\epsilon \rightarrow 0} \frac{J(T_{\epsilon }(V)(\Omega _0))-J(\Omega _0)}{\epsilon } \end{aligned}$$

(2.4)

exists for all $V\in \mathcal {C}(]0,\epsilon [,\mathcal {C}^k(D,\mathbb {R}^d))$ $(k\in \mathbb {N})$ and for $|\epsilon |<1$.

(ii):

the mapping $V\rightarrow dJ(\Omega _0,V)$ is linear and continuous from $\mathcal {C}(]0,\epsilon [,\mathcal {C}^k(D,\mathbb {R}^d))$ into $\mathbb {R}$.

Note that, using the Taylor expansions for $T_{\epsilon }(V)$ with respect to $\epsilon$, we can write:

$$\begin{aligned} T_{\epsilon }(V)=\Phi _{V}(\epsilon ,x)&=\Phi _{V}(0,x) + \epsilon \left. \frac{d\Phi _{V}(\epsilon ,x)}{d \epsilon }\right| _{\epsilon =0} + \epsilon ^2\left. \frac{d^2\Phi _{V}(\epsilon ,x)}{d\epsilon ^2}\right| _{\epsilon =0}\\&=x+\epsilon V(0,x)+\frac{\epsilon ^2}{2}\nabla V (0,x)V (0,x)+ o(\epsilon ^2). \end{aligned}$$

So $T_{\epsilon }(V)$ can be approximated by the diffeomorphism $\text {Id}_{\mathbb {R}^{d}}+ \epsilon V (0,.)$ on a neighborhood of x, which is the frequently used deformation in the literature for the variation of domains in the shape derivative approach [1, 7, 14, 24, 38].

2.1.1 Identification shape optimization process

In order to introduce a gradient method for minimizing the shape optimization problem (3.1), let us consider here the frequent variations of a given domain $\Omega _0\in \mathcal {U}$ defined by the transformation $\epsilon \rightarrow \text {Id}_{\mathbb {R}^{d}}+ \epsilon V$ where $V: \mathbb {R}^d\rightarrow \mathbb {R}^d$ is a smooth vector field and $\text {Id}_{\mathbb {R}^{d}}$ is the identity mapping in $\mathbb {R}^d$, such that $\Omega _\epsilon = (\text {Id}_{\mathbb {R}^{d}}+ \epsilon V)(\Omega _0),$ $t\in [0,1[$. So, let us assume that the functional $\epsilon \rightarrow \mathcal {F}(\Omega _{\epsilon },u_{\Omega _\epsilon },\nabla u_{\Omega _\epsilon })$ is differentiable at $\epsilon =0$. Then, according to the fundamental result called "structure theorem" established by Hadamard and rigorously considered later by Zolésio [14], which plays a crucial role in shape optimization tools both from numerical and theoretical point of view, one can write the shape derivative of $\mathcal {F}$ in the direction of V,  denoted by $\delta \mathcal {F}(\Omega _0)[V]$, as follows:

$$\begin{aligned} \delta \mathcal {F}(\Omega _0)[V]:=\int _{\partial \Omega _0} g_0(u_{\Omega _0},\psi _{\Omega _0}) \langle V,\nu _0\rangle d\sigma \end{aligned}$$

(2.5)

where $g_0(\cdot ,\cdot )$ is an integrable function on $\partial \Omega _0$, $\psi _{\Omega _0}$ is the solution of an appropriate adjoint state problem, $\nu _0$ denotes the outward unit normal vector to $\partial \Omega _0$ and $\langle .,.\rangle$ designates the inner product in $\mathbb {R}^d$.

This formula known as the canonical form in the shape optimization theory provides a descent direction for the gradient method which can be given by the vector field $V=-g_0\nu _0$. Then, we can update the shape $\Omega _0$ by $\Omega _\epsilon =(\text {Id}_{\mathbb {R}^{d}}+\epsilon V)(\Omega )$. So we get

$$\begin{aligned} \mathcal {F}(\Omega _\epsilon ,u_{\Omega _\epsilon },\nabla u_{\Omega _\epsilon })=\mathcal {F}(\Omega _0,u_{\Omega _0},\nabla u_{\Omega _0})-\epsilon \int _{\partial \Omega _0} g_0^2\,\langle \nu _0,\nu _0\rangle \,d\sigma + o(\epsilon ^2). \end{aligned}$$

(2.6)

This ensures the decrease of the cost functional. However, the vector field V is defined only on the boundary $\partial \Omega _0$ and must be extended to the whole domain $\Omega _0$. So we can extend it accordingly to the structure theorem [27], as the unique solution in $[H^1(\Omega _0)]^d$ of the following variational problem:

$$\begin{aligned} \int _{\Omega _0}\nabla V:\nabla \Psi dx+\int _{\Omega _0}V\cdot \Psi dx=- \delta \mathcal {F}(\Omega _0)[\Psi ],\,\,\forall \Psi =(\Psi ^{(1)},...,\Psi ^{(d)})\in [H^1(\Omega _0)]^d \end{aligned}$$

(2.7)

where $\displaystyle \nabla V:\nabla \Psi = \sum _{k, j=1}^d \frac{\partial V^{(k)}}{\partial x_j} \frac{\partial \Psi _i^{(k)}}{\partial x_j}$ with $V=(V^{(1)},...,V^{(d)})$.

In fact, we can find more details about the choice of the descent direction for example in [1]. We note also that for the choice of the step size $\rho ,$ for the gradient method, one can opt for the approach inspired from the Armijo-Goldstein strategy in [26] as follows:

$$\begin{aligned} \rho =\alpha \frac{\mathcal {F}(\Omega ,u_{\Omega },\nabla u_{\Omega })}{\Vert V\Vert _{H^{1}(\Omega )}^2},\,\,\text {for some}\,\,\alpha \in ]0,1[. \end{aligned}$$

(2.8)

Thereby, we have

$$\begin{aligned} \mathcal {F}(\Omega _\rho ,u_{\Omega _\rho },\nabla u_{\Omega _\rho })\simeq & {} \mathcal {F}(\Omega _{0},u_{\Omega _0},\nabla u_{\Omega _0})+\rho \delta \mathcal {F}(\Omega _0)[V] +O(\rho ^2)\\= & {} \mathcal {F}(\Omega _{0},u_{\Omega _0},\nabla u_{\Omega _0})+\alpha \frac{\mathcal {F}(\Omega _{0},u_{\Omega _0},\nabla u_{\Omega _0})}{\Vert V\Vert _{H^{1}(\Omega )}^2}\delta \mathcal {F}(\Omega _0)[V]+O(\rho ^2) \\= & {} (1-\alpha )\mathcal {F}(\Omega _{0},u_{\Omega _0},\nabla u_{\Omega _0})+O(\rho ^2). \end{aligned}$$

Then, the vector fields $\rho V$ defines a descent direction for $\alpha \in ]0, 1[$. Moreover, we note that when the step size parameter is such that $\alpha >1$, the vector fields $\rho V$ still define a descent direction. This last choice of the parameters $\alpha$ is illustrated in some numerical tests in the numerical results section.

Hence, the numerical gradient algorithm for solving the shape optimization problem (2.1) is summarized as follows:

Algorithm 1

Numerical optimization algorithm based on the classical formula.

2.2 Shape derivative via minkowski deformation

The shape derivative approach presented in the previous section presents some difficulties from both theoretical and numerical point of view. For example, when one wants to connect the set of admissible domains with vector fields, one has to suppose high smoothness conditions on the initial data in order to differentiate functions depending on the domain and we have to extend the vector fields (obtained only on the boundary) to the whole domain or to re-mesh the domain, at each iteration, and both tasks are expensive. In order to avoid a part of the above issues, we define and use another way of variation of domains, a way that is linked to the convexity context and based on the Minkowski sum. This allows to define a novel concept of computing the derivative with respect to domains using the so called support functions in convex analysis.

In order to be more precise, let D be a fixed smooth convex and bounded open subset of $\mathbb {R}^{d}$, let us consider the set of admissible domains $\mathcal {U}$ given by

$$ \mathcal {U}=\{\Omega \subset D\,\,/\,\, \Omega \text { is open, convex and of class } {C}^{2} \} $$

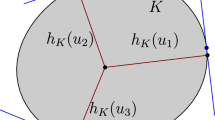
and let us recall that a support function $P_\Omega$ of a bounded convex domain $\Omega$ is given by

$$ P_\Omega (x)=\sup _{y\in \Omega }\langle x,y\rangle =\sup _{y\in \overline{\Omega }}\langle x,y\rangle \,, $$

where $\langle x,y\rangle$ denotes the standard scalar product of x and y in $\mathbb {R}^{d}$.

So, let us define the shape derivative approach based on the variation of domains using the Minkowski sum. Let $\Omega _0\in \mathcal {U}$ and $\Omega$ be a convex domain. The deformed domain denoted by $\Omega _\epsilon$ is given by the Minkowski sum as follows:

$$ \Omega _\epsilon =\Omega _0+\epsilon \Omega :=\{x+\epsilon y\,\,|\,\,x\in \Omega _0,\,\,y\in \Omega \},\,\, \epsilon \in [0,1]. $$

Consider a real-valued shape function $J:\Lambda \in \mathcal {U}\longmapsto J(\Lambda )\in \mathbb {R}$ defined on a family $\mathcal {U}$ of subsets of $\mathbb {R}^{d}$. The shape functional J is called shape differentiable at $\Omega _0$ in the direction of $\Omega$, if the eulerian derivative

$$ \delta J(\Omega _0)[\Omega ]:= \lim _{\epsilon \rightarrow 0^+}\frac{J(\Omega _\epsilon )-J(\Omega _0)}{\epsilon }. $$

exists for all convex domain $\Omega$. Then, the expression $\delta J(\Omega _0)[\Omega ]$ is called the shape derivative of J at $\Omega _0$ in the direction of $\Omega$.

In this context, let us precise that the shape derivative of a volume functional J defined on $\mathcal {U}$ by

$$ \Lambda \rightarrow J(\Lambda )=\int _{\Lambda }fdx,\,\, \text { where } \,\,f\,\,\text { is a fixed function defined in } \mathbb {R}^{d}, $$

using a convex deformation of kind:

$$ (1-\epsilon )\Omega _0+\epsilon \Omega , \quad \,\,\text {for}\,\,\Omega _0,\Omega \in \mathcal {U}\,\,\text{ and }\,\, \epsilon \in [0,1] $$

was first established by A. A. Niftiyev and Y. Gasimov [32], for the function f is of class $C^1$. More precisely they show that

$$\begin{aligned} \delta J(\Omega _0)[\Omega ]:= \lim _{\epsilon \rightarrow 0^+} \frac{J((1-\epsilon )\Omega _0+\epsilon \Omega ) - J(\Omega _0)}{\epsilon }=\int _{\partial {\Omega _0}} f(x)\,\left( P_{\Omega }(\nu _0(x))-P_{\Omega _0}(\nu _0(x))\right) \,d\sigma (x), \end{aligned}$$

(2.9)

where $\nu _0(x)$ denotes the outward unit normal vector to $\partial \Omega _0$ at x, and $P_{\Omega _0}$, $P_{\Omega }$ are the support functions of the domains ${\Omega _0}$, ${\Omega }$, respectively.

Recently, A. Boulkhemair and A. Chakib [3] extended this formula to the case where f is in the space $W^{1,1}_{loc}(\mathbb {R}^n)$. Then, based on the Brunn-Minkowski theory (see, for example, R. Schneider, [35]), they also proposed a similar shape derivative formula to (2.9) by considering the Minkowski deformation

$$ \Omega _0+\epsilon \Omega ,\quad \,\,\text {for}\,\,\Omega _0,\Omega \in \mathcal {U},\,\,\text {and}\,\, \epsilon \in [0,1], $$

that is,

$$\begin{aligned} \lim _{\epsilon \rightarrow 0^+} \frac{J(\Omega _0+\epsilon \Omega ) - J(\Omega _0)}{\epsilon }=\int _{\partial {\Omega _0}} f(x)\,P_{\Omega }(\nu _0(x))\,d\sigma (x), \end{aligned}$$

(2.10)

where $\nu _0(x)$ denotes the outward unit normal vector to $\partial \Omega _0$ at x, and $P_{\Omega }$ is the support function of the domain ${\Omega }$.

In fact, this formula holds true for bounded convex domains, see [2]. Moreover, according to this work, there is an equivalence between the formulas (2.9) and (2.10) of shape derivative with respect to respectively convex and Minkowski deformations. So depending on what it is needed, we use one of the two deformations and consequently investigate the associated shape derivative formula. In this context, we mention that numerical optimization processes based on the gradient method involving these shape derivative formulas are successfully applied for solving concrete problems in [4, 5], using boundary element method for approximating the auxiliary boundary value problems.

We note also that the above formulas allow us to express the shape derivative of the cost functional by means of support functions, and when solving numerically problems one gets a support function at each step of the implementation, then the domain can be recovered as the sub-differential of the support function. Thereby, during the numerical process, we get at each step support functions instead of domains. From this fact, we believe that, in the context of convexity and the numerical implementation, the use of these formulas involving the support functions is more advantageous than the classical shape derivative formula expressed in term of vectors fields. So the aim of this paper is to prove numerically these expectations by a comparative numerical study between the two approaches through the resolution of some shape optimization problems constrained to boundary value problems governed by elliptic operators.

2.2.1 New numerical optimization process involving support function

In this section, we will describe the numerical process adopted to solve numerically the problem (3.1), using the shape derivative formulas (2.10) and (2.9). Let us first recall that when one assumes that $\Omega$ is strongly convex, according to [3], the domains $\Lambda _\epsilon =\Omega _0+\epsilon \Omega$ for small enough $\epsilon$ can be considered as deformations of the domain $\Omega _0$ by the following explicit vector field V defined by $V(0)=0$ and

$$\begin{aligned} V(x)=J_{\Omega _{0}}(x)\,\nabla P_{\Omega }\left( \nu _0\left( \frac{x}{J_{\Omega _{0}}(x)}\right) \right) ,\,\,\, x\in \mathbb {R}^d,x\ne 0 \end{aligned}$$

(2.11)

where $P_{\Omega }$ is the support function of $\Omega$, $\nu _0$ is the outward unit normal vector to $\partial \Omega _0$ and $J_{\Omega _{0}}$ is the gauge function associated to $\Omega$ which is defined by $J_{\Omega _0}(x)=\inf \{\lambda ;\lambda >0 ,\, x\in \lambda \Omega _0\}.$ Thereby $\Lambda _{\epsilon }=(\text {Id}_{\mathbb {R}^{d}}+\epsilon V)(\Omega _{0})$ for small enough $\epsilon$. Furthermore, since $\Omega _0$ and $\Omega$ are of class $\mathcal {C}^2$, then $V \in W^{1,\infty }(\mathbb {R}^d,\mathbb {R}^d)\cap \mathcal {C}^1$. Therefore, if $\epsilon \rightarrow F(\Omega _\epsilon ,u_{\Lambda _{\epsilon }},\nabla u_{\Lambda _{\epsilon }})$ is differentiable at $0^+$, using the formula (2.5), we get

$$\begin{aligned} \delta \mathcal {F}(\Omega _0)[\Omega ]:=\langle g_0(u_{\Omega _0},\psi _{\Omega _0}),\langle V,\nu _0\rangle \rangle _{L^{2}(\partial \Omega _0)}, \end{aligned}$$

where $g_0(u_{\Omega _0},\psi _{\Omega _0})$ is an integrable function on $\partial \Omega _0$, $\psi _{\Omega _0}$ is the solution of an appropriate adjoint state problem. It follows from Lemma 4.1 of [3] that $\langle V,\nu _{0}\rangle = P_{\Omega }(\nu _{0})$ on $\partial \Omega _{0}$, so that

$$\begin{aligned} \delta \mathcal {F}(\Omega _0)[\Omega ]=\langle g_0(u_{\Omega _0},\psi _{\Omega _0}),P_{\Omega }(\nu _{0}) \rangle _{L^{2}(\partial \Omega _0)}. \end{aligned}$$

(2.12)

So the numerical optimization algorithm for solving the shape optimal design problem (3.1), based on the shape derivative formula (2.12) is summarized in the following algorithm.

Algorithm 2

Numerical optimization algorithm involving support function.

We note that the problem (2.13) admits a solution $\widehat{p}\in \mathcal {P}.$ Since the functional $j:p\in \mathcal {P}\rightarrow j(p)=\langle g_{\partial \Omega _0},p\circ \nu _{0}\rangle _{L^{2}(\partial \Omega )}$ is continuous on a compact set $\mathcal {P}$ of $\mathcal {C}(\overline{D})$. Indeed, let $p\in \mathcal {P}$, so it is the support function of a unique convex bounded open set which is its sub-differential at 0, that is, $p= P_{\partial p(0)}$ (see, for example, [33, 39]). So, for all $x,y\in \overline{D}$, using the fact that a support function is sub-linear and homogenous of degree 1 and $p\le P_D$, we get

$$\begin{aligned} \forall x,y\in \overline{D},\,\,\forall p\in \mathcal {P}\,\,|p(x)-p(y)|= & {} |P_{\partial p(0)}(x)-P_{\partial p(0)}(y)|\\\le & {} \sup _{w\in \mathbb {S}^{n-1}}P_{\partial p(0)}(w)\Vert x-y\Vert \\\le & {} \sup _{w\in \mathbb {S}^{n-1}}P_{D}(w)\Vert x-y\Vert . \end{aligned}$$

which implies that the family $\mathcal {P}$ is equicontinuous. On the other hand, it is clear that j is linear, and moreover, it is continuous since:

$$ \forall p,q\in \mathcal {P}\,\,\,\,|j(p)|\le |\!|g_{\partial \Omega _0}|\!|_{L^{1}(\partial \Omega _0)}|\!|p|\!|_{\infty ,D}. $$

So it follows from the Ascoli-Arzela theorem’s that $\mathcal {P}$ is relatively compact in $\mathcal {C}(\overline{D})$. Then, it is easy to check that it is closed in $(\mathcal {C}(\overline{D}),|\!|\cdot |\!|_{\infty ,D})$ and then it is compact in $(\mathcal {C}(\overline{D}),|\!|\cdot |\!|_{\infty ,D})$.

We note also that, the shape derivative of a general class of shape functionals $J(\Omega )$ in direction of a vector field V has the generic form:

$$\begin{aligned} \delta J(\Omega )[V] = \int _{\partial {\Omega }} g\langle V(x),\nu (x)\rangle d\sigma (x) =: \langle g_{\mid \Gamma }, \langle V(x),\nu (x)\rangle \rangle _{L^{2}(\partial {\Omega })}. \end{aligned}$$

(2.13)

where the scalar function $g: \partial {\Omega } \rightarrow \mathbb {R}$ is the shape gradient of J with respect to the $L^{2}(\partial {\Omega })$ inner product. In the case of convex domains, using the shape derivative formulas (2.10) and (2.9), this formula becomes

$$\begin{aligned} \delta g(\Omega )[\Theta ] : =\int _{\partial {\Omega }} g_{\partial {\Omega }}(x) P_{\Theta }(\nu (x))d\sigma (x)=\langle g_{\partial {\Omega }}, P_{\Theta }(\nu ) \rangle _{L^{2}(\partial {\Omega })}. \end{aligned}$$

(2.14)

Here, $\delta J(\Omega )[\Theta ]$ depends only on the normal component of $P_{\Theta }$ on the boundary $\partial \Omega .$ This expression allows to easily to deduce the direction of descent, as it was summarized in the above algorithm. Indeed, the sequence of domains $(\Omega _{k}) _ {k \in \mathbb {N}}$ must be constructed in such a way that $(J(\Omega _{k})) _ {k \in \mathbb {N}}$ is decreasing. So let $k \in \mathbb {N}^{*}$, then for a small $\rho \in ]0,1[$, we have

$$\begin{aligned} J(\Omega _{k+1})- J(\Omega _{k})= J(\Omega _k +\rho \Theta _{k})- J(\Omega _{k}) =\rho \left( \int _{\partial \Omega _{k}} g_{k}P_{\Theta _{k}}\circ \nu _{k} d\sigma \right) +O(\rho ^2). \end{aligned}$$

Thus, if we take $\displaystyle P_{\Theta _{k}}= \widehat{P}_{k}$ the solution of $\displaystyle \text {arg}\min _{p\in \mathcal {E}}\Lambda _{k}(p)$, we get

$$ \Lambda _{k}(\widehat{P}_{k})=\int _{\partial \Omega _{k}}g_{{k}}P_{\Theta _{k}}\circ \nu _{k} d\sigma \le \Lambda _{k}(0)=0. $$

This ensures the decrease of the objective functional J. Consequently $\widehat{\Omega }_{k}=\partial \widehat{P}_{k}(0)$ defines a descent direction for J.

2.3 Discretization of the proposed shape optimization process

In what follows, we suppose that $d=2$. Let $\Omega _0\in \mathcal {U}_{ad}$ and let $X=(x_k)^{N}_{k=1}$ be a partition of $\Gamma _0:=\partial \Omega _0$, such that N is the number of the nodes located at the boundary $\Gamma _0$ and $x_k=(x_k^{(1)}, x_k^{(2)})$. Let us also consider the family $\zeta =(\xi _k)^{N}_{k=1}$, with $\xi _k=(\xi _k^{(1)}, \xi _k^{(2)})$ is the centroid of the boundary elements $C_i=[x_i, x_{i+1}]$ which is also a partition of $\Gamma _0$. Let us also denote by $\mathcal {T}_h$ a regular mesh of $\Omega _0$ (see [12]) and by $N_{mn}$ the number of the freedom degrees generated from the mesh of the domain limited by the N boundary elements.

So the discrete approximation of the gradient of $\mathcal {F}$, $\delta \mathcal {F}(\Omega _0)[\Omega ]$ reads:

$$\begin{aligned} \delta \mathcal {F}_0(P)=\sum _{k=1}^{N-1}\int _{x_k}^{x_{k+1}}\,g\,P(\nu )=\sum _{k=1}^{N} \ell _k\, g_k\, P_k \end{aligned}$$

(2.15)

where $\ell _k=\Vert x_{k+1}-x_k\Vert$; $P=(P_k=P(\nu _k)^{N}_{k=1})$; $\nu _k=\nu (\xi _k)$ is the outward unit normal vector to the boundary elements $[x_k, x_{k+1}]$ that can be computed explicitly by the relation $\nu (\xi _k)=((x_{k+1}^{(2)}-x_{k}^{(2)})/\ell _k, (-x_{k+1}^{(1)}+x_{k}^{(1)})/\ell _k)$, $g=g(u_0,\psi _0)$ is the shape gradient which depends on $u_0$ the solution of the state problem and $\psi _0$ the solution of an appropriate adjoint state problem and $g_k$ is the approximate value of the shape gradient function g at the node $x_k$, using finite element discretization of the state and adjoint state problems.

Then, the next step is to deal with the discretization of the problem (2.13). For this purpose based on the polygonal shape of the discretized boundary $\Gamma =\cup _{k=1}^{N-1}[x_k,x_{k+1}]$, we derive some equations using the fact that the support function is sub-linear and homogeneous of degree 1. So, let B(0, R) be a large ball which contains D,  the space of the admissible support function is discretized as follows [5]:

$$ \begin{array}{ll} {\mathcal P} = \left\{ P = (P_1,\cdots ,P_{N}) \in \mathbb {R}^{N} / P \quad \text {satisfies equations}~(2.17)\,\,\text {and}\,\,(2.18)\, \right\} \end{array} $$

where

$$\begin{aligned} r=r\Vert \nu (\xi _k)\Vert =P_{B(0,r)}(\nu (\xi _k)) \le P_k \le P_{D}(\nu (\xi _k))\le P_{B(0,R)}(\nu (\xi _k))=R\Vert \nu (\xi _k)\Vert =R \quad \text {for}\quad k=1,\,\dots \,,N. \end{aligned}$$

(2.16)

and

$$\begin{aligned} {\left\{ \begin{array}{ll}\,\, P_{1}\,\le \,(1-\lambda _{1})\,P_{N}+ \lambda _{1}\,P_{2},\\ \,\,P_{k}\,\le \,(1-\lambda _{k})\,P_{k-1}+ \lambda _{k}\,P_{k+1},\,\, \text {for}\,\, k=2,\,\dots \,,N-1\\ \,\,P_{N}\,\le \,(1-\lambda _{N})\,P_{N-1}+ \lambda _{N}\,P_{1} \end{array}\right. } \end{aligned}$$

(2.17)

with

$$\begin{aligned} \lambda _1= & {} \displaystyle \frac{\Vert \nu (\xi _{1})-\nu (\xi _N)\Vert }{\Vert \nu (\xi _{2})-\nu (\xi _{N})\Vert }, \quad \lambda _i=\displaystyle \frac{\Vert \nu (\xi _{i})-\nu (\xi _{i-1})\Vert }{\Vert \nu (\xi _{i+1})-\nu (\xi _{i-1})\Vert } \quad \text {for} \,\,i=2,\,\dots ,\,N-1;\\ \lambda _N= & {} \displaystyle \frac{\Vert \nu (\xi _{N})-\nu (\xi _{N-1})\Vert }{\Vert \nu (\xi _{1})-\nu (\xi _{N-1})\Vert }. \end{aligned}$$

The final step is to identify the boundary of the shape $\Omega _{k+1}$, at each iteration $k\ge 0,$ defined by the following: $\Omega _{k+1}= \Omega _{k}+\epsilon \,\partial {\widehat{P}}_{k}\left( 0 \right) .$ For this, let $\widehat{P}_{k}$ be the solution of the problem (2.13) and let us consider its sub-differential at 0, $\partial {\widehat{P}}_{k}\left( 0 \right) ,$ which is a bounded convex domain [33]. Based on Lemma 4.7. of [3], for all $\delta >0$, the domain $\partial {\widehat{P}}_{k}\left( 0 \right)$ can be approximated by strongly convex sub-domains denoted by $\Omega ^{(k)}$, such that

$$\begin{aligned} d^{H}(\partial {\widehat{P}}_{k}\left( 0 \right) ,\overline{\Omega ^{(k)}}) \le \delta . \end{aligned}$$

(2.18)

On the other hand, according to [3], we can connect the two shapes $\Omega _{k}$ and $\Omega ^{(k)}$, by an explicit vector fields as follows:

$$ \Omega _{k}+\epsilon \,\Omega ^{(k)}=(\text {Id}_{\mathbb {R}^{d}}+\epsilon \Xi _k)(\Omega _{k})\,\,\text {and}\,\, \partial (\Omega _{k}+\epsilon \,\Omega ^{(k)})=(\text {Id}_{\mathbb {R}^{d}}+\epsilon \Xi _k)(\partial \Omega _{k}) $$

where $\Xi _k$ is the vector field defined by

$$ \Xi _k(0)=0 \text { and } \Xi _k(x)=J_{\Omega _k}(x)\nabla P_{\Omega ^{(k)}} \left( \nu _{\partial \Omega _{k}}\left( \frac{x}{J_{\Omega _k}(x)}\right) \right) ,\,\, x\in \mathbb {R}^2,x\ne 0 $$

such that $\Xi _k$ satisfies the following properties:

$$\begin{aligned} P_{\Omega ^{(k)}}(\nu _{\partial \Omega _{k}})=\langle \Xi _k,\nu _{\partial \Omega _{k}}\rangle \,\,\text {and}\,\, \nu _{\partial \Omega ^{(k)}}(\Xi _k)=\nu _{\partial \Omega _{k}}. \end{aligned}$$

(2.19)

where $\nu _{\partial \Omega ^{(k)}}$ and $\nu _{\partial \Omega _{k}}$ denotes the outward vectors normal to $\partial \Omega ^{(k)}$ and $\partial \Omega _{k}$ respectively. Moreover, from equation (2.19), by using the properties of Hausdorff distance on convex domains (see, for example, [35, 39]), we get

$$ d^{H}(\Omega _{k+1},\Omega _{k}+\epsilon \,\Omega ^{(k)})= d^{H}(\Omega _{k},\Omega _{k})+\epsilon \,d^{H}(\partial {\widehat{P}}_{k}\left( 0 \right) ,\overline{\Omega ^{(k)}})\le \epsilon \delta . $$

So, we can approach $\Omega _{k+1}$ by the set $(\text {Id}_{\mathbb {R}^{d}}+\epsilon \Xi _k)(\Omega _{k}).$

Now, let us determine $\Gamma _{k+1}$, using the partition $\Gamma _{k}=\bigcup _{i=1}^{N-1} C_i$. This is equivalent to compute the set $\Xi _k(\Gamma _{k})$. For this, we can use the equation (2.20) and the family $(P_{i})_{i}$ (solution of the problem (2.13)) to get an approximation of the family $(\Xi _k(\xi _i)=\nabla P_{\Omega ^{(k)}}(\nu _{\partial \Omega _{k}}(\xi _i)))_i$, or we can use the properties in (2.20) to get $(\Xi _k(\xi _i))_i$ as the solution of the following systems (see [5, 32]). So denote by $\Xi _k(\xi _i)=l_i=(l_i^{(1)},l_i^{(2)})$, we have that $l_i -\xi _i$ is collinear to $\nu (\xi _i)=\nu _{\partial \Omega _{k}}(\xi _i)=(\nu ^{(1)}(\xi _i),\nu ^{(2)}(\xi _i))$, i.e.,

$$\begin{aligned} \nu ^{(1)}(\xi _i)\,l_i^{(2)}-\nu ^{(2)}(\xi _i)\,l_i^{(1)}= \nu ^{(1)}(\xi _i)\,\xi _i^{(2)}-\nu ^{(2)}(\xi _i)\,\xi _i^{(1)} \quad \text {for}\,\, i=1,\,\dots ,\,N. \end{aligned}$$

(2.20)

On the other hand, we have

$$\begin{aligned} \nu ^{(1)}(\xi _i)\,l_i^{(1)}+\nu ^{(2)}(\xi _i)\,l_i^{(2)}={\widehat{P}}_i \quad \text{ for }\,\, i=1,\,\dots ,\,N. \end{aligned}$$

(2.21)

We are now ready to provide a precise sketch of the discrete shape optimization algorithm accordingly to the previous considerations.

Algorithm 3

Discrete algorithmic description of the optimization process.

We note that the problem (2.23) can be read as follows:

$$\begin{aligned} \arg \min \limits _{P=(P_i)_i} j_k(P):= & {} \sum _{i=1}^{N} \ell _i\,\mathcal {G}_i\,P_i \end{aligned}$$

(2.22)

$$\begin{aligned} \text {with}\,\,\,\ell _i= & {} \Vert x_{i+1}-x_i\Vert ,\quad i=1,...,N \nonumber \\ \text {subject to} \end{aligned}$$

(2.24)

$$\begin{aligned} \mathcal {A}P\le & {} \mathcal {B}:=\mathcal {B}=(b_i)_{i=1}^{3N}\,\,\,\text {where}\nonumber \end{aligned}$$

(2.25)

$$\begin{aligned} \mathcal {A}= & {} \begin{bmatrix} A\\ -\textrm{I}_N\\ \textrm{I}_N \end{bmatrix}\,\,\text {where}\,\, A= \begin{bmatrix} 1 &{} -\lambda _{1} &{} 0 &{} \dots &{} 0 &{}(\lambda _{1}-1) \\ (\lambda _{2}-1) &{} 1 &{} -\lambda _{2} &{} \dots &{} 0 &{} 0 \\ 0 &{} (\lambda _{3}-1) &{} 1 &{} -\lambda _{3} &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \ddots &{} \vdots \\ -\lambda _{N} &{} 0 &{} 0 &{} \dots &{} (\lambda _{N}-1) &{} 1 \end{bmatrix};\\ b_i= & {} {\left\{ \begin{array}{ll} 0,\,\,\,\text {for}\,\,\, i=1,...,N \\ -r,\,\,\,\text {for}\,\,\, i=N+1,...,2N \\ R,\,\,\,\text {for}\,\,\,i=2N,...,3N \end{array}\right. } \end{aligned}$$

with   

$$\begin{aligned} \lambda _1= & {} \displaystyle \frac{\Vert \nu (\xi _{1})-\nu (\xi _N)\Vert }{\Vert \nu (\xi _{2})-\nu (\xi _{N})\Vert },\quad \lambda _i=\displaystyle \frac{\Vert \nu (\xi _{i})-\nu (\xi _{i-1})\Vert }{\Vert \nu (\xi _{i+1})-\nu (\xi _{i-1})\Vert } \quad \text {for} \,\,i=2,\,\dots ,\,N-1; \\ \lambda _N= & {} \displaystyle \frac{\Vert \nu (\xi _{N})-\nu (\xi _{N-1})\Vert }{\Vert \nu (\xi _{1})-\nu (\xi _{N-1})\Vert } \end{aligned}$$

and $\textrm{I}_N$ denotes the matrix identity in $\mathbb {R}^{N\times N}$.

We note that this linear optimization problem can be solved using for example the simplex method.

3 Application for solving some classical shape optimization problems

In this section, we test the efficiency of the proposed approach through the resolution of some shape optimization problems. Especially, we propose a comparative numerical study between this proposed shape gradient approach and the classical one.

3.1 Statement of the shape optimization problems

The first considered shape optimization problems consist in minimizing a generic volume cost functional constrained to a Laplace-Dirichlet or Laplace-Neumann boundary value problems and the second one is a fluid mechanics shape optimal design problem which aims to minimize appropriate cost functional constrained to Stokes boundary value problem. So, let D be a large smooth domain in $\mathbb {R}^2$ and let us denote the set of admissible shapes by

$$ \mathcal {U}=\{\Theta \subset D \,\,/\,\,\Theta \,\text {is open},\,\,\,\Theta \in \mathcal {C}^{2}\cap \mathcal {K}\}, $$

where $\mathcal {K}$ denotes the set of all convex domains and $\mathcal {C}^{2}$ denotes the space of domains with boundaries of class $C^{2}$. We will solve numerically the following models:

Model 1: Shape optimization problems for classical elliptic operator

Let us consider the following shape optimization problem:

$$\begin{aligned} \min _{\Omega \in \mathcal {U}}\mathcal {F}(\Omega ,u_{\Omega },\nabla u_{\Omega }) \text {where} \mathcal {F}(\Omega ,u_{\Omega },\nabla u_{\Omega }):=\varpi |\!|u_{\Omega }-\varphi _1|\!|^2_{L^{2}(\Omega )}+\beta |\!|\nabla u_{\Omega }-\varphi _2|\!|^2_{L^{2}(\Omega )} \end{aligned}$$

(3.1)

and   $u_{\Omega }$    satisfies the following state problem:

$$\begin{aligned} -\mu \Delta u +\lambda u= & {} f\quad \text {in}\quad \Omega ,\end{aligned}$$

(3.2)

$$\begin{aligned} \eta \partial _{\nu } u +\gamma u= & {} g \quad \text {on}\quad \Gamma :=\partial \Omega , \end{aligned}$$

(3.3)

where $\varphi _{1}$, $\varphi _{2}$, f and g are given functions, $\varpi ,$ $\beta$, $\mu$, $\eta$ and $\gamma$ are given constants that satisfy appropriate assumptions allowing the existence and the uniqueness of the solution of the boundary value problem (3.2)-(3.3) and $\partial _{\nu }u=\langle \nabla u|_{\Gamma }, \nu \rangle$, with $\nu$ is the outward unit normal vector to $\Gamma$ and $\langle \cdot , \cdot \rangle$ denotes the scalar product in $\mathbb {R}^2$.

Model 2: Shape optimization problems in fluid dynamics

Let us consider a fluid mechanics shape optimization problem constrained to Stokes equation:

$$\begin{aligned} \min _{\Omega \in \mathcal {U}}\mathcal {S}(\Omega ,w_{\Omega },D w_{\Omega }) \,\,\, \text {where} \,\,\, \mathcal {S}(\Omega ,w_{\Omega },\nabla w_{\Omega }):= \rho \int _{\Omega }|\!|w_{\Omega }-\phi _1|\!|^2dx+ \sigma \int _{\Omega }|\!|\nabla w_{\Omega }-\phi _2|\!|^2 dx \end{aligned}$$

(3.4)

and   $(w_{\Omega },p_{\Omega })$   is solution of the Stokes system:

$$\begin{aligned} \left\{ \begin{array}{lll} -\kappa \Delta w +\nabla p = h &{}\text { in }&{}\Omega \\ \text {div} w =0 &{}\text { in }&{} \Omega \\ w =0 &{}\text { on } &{}\Gamma :=\partial \Omega \end{array}\right. \end{aligned}$$

(3.5)

where $\Omega$ is the domain occupied by a fluid, $\kappa >0$ is the viscosity coefficient, $w=(w_\ell )_{\ell =1}^2$ represents the fluid velocity, p is the associated pressure, $\phi _1$ is the target velocity, $\phi _2$ is a given function and h is a source term. The norm $|\!|\nabla w|\!|$ is associated to the usual Frobenius inner product given by the following: $\displaystyle \nabla w:\nabla w=\sum _{k,\ell =1}^{2}\frac{\partial w_\ell }{\partial x_k} \frac{\partial w_\ell }{\partial x_k}.$

In the sequel, in order to test the validity and the efficiency of the proposed approach summarized in the Algorithm 2 involving the new shape derivative formula, we propose its numerical comparative study with the classical approach based on the Algorithm 1 in terms of computation time (time CPU) and the accuracy of the obtained optimal solutions by dealing with numerical resolution of the problem (3.1) constrained to (3.2)-(3.3) for different values of the constants $\varpi ,$ $\beta$, $\mu$ and $\gamma$. Then, we deal with the numerical approximation of the shape optimization problem in fluid dynamics (3.4), by minimizing the cost functional $\mathcal {S}$ for different values of $\rho$ and $\sigma$, constrained to the Stokes problem (3.5).

3.2 Numerical results for shape optimization problems

The numerical algorithms are implemented using the programming software $\textrm{FreeFem}++$ [21], so in order to increase the mesh quality, notably its uniformness and regularity, the “adapt-mesh” tool can be used if necessary. The numerical experiments is done on a workstation with an Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz. For all the numerical test the target shape is taken as the disc of center 0 and radius 1 and the stopping criterion precision is chosen the same for the two algorithms. Also the considered initial domain can be chosen as follows:

• case 1: square $[-2,2]^2;$

• case 2: disk $\{(x,y) | x=3 \cos (t),\,\,\, y= 3 \sin (t), t\in [0,2\pi ]\};$

• case 3: ellipse $\{(x,y) | x=2.5\,\cos (t),\,\,\, y=3\,\sin (t), t\in [0,2\pi ]\}.$

In order to perform a numerical comparative study between the two approaches based on the gradient method, let us first start by analyzing the sensitivity and the influence of the choice of the step size parameter on the convergence performance of these algorithms.

Fig. 1

The computed error of the solution in optimal domain using Algorithm 1 (above) and Algorithm 2 (below) for different cases

3.2.1 Influence of the step size on the shape optimization processes

In this section, we deal with the numerical analysis of the sensitivity of the two shape optimization processes with respect to the step size parameter through the numerical resolution of the shape optimization problem (3.1) of minimizing the cost functional $\mathcal {F}$ with $\varpi =\frac{1}{2}$ and $\beta =0$:

$$\begin{aligned} \mathcal {F}(\Omega ,u_{\Omega },\nabla u_{\Omega })= \frac{1}{2}\,|\!|u_{\Omega }-u_{ex}|\!|_{L^{2}(\Omega )}^2, \end{aligned}$$

(3.6)

where $u_{\Omega }$ is the solution of the Dirichlet boundary value state problem associated to the parameters $\mu =1,$ $\lambda =1,$ $\eta =0$ and $\gamma =1$. The shape gradient of this functional at $\Omega _0\in \mathcal {U}$, for the two shape derivative formulas, is given by the following:

$$\begin{aligned} \left. \left( |u_{\Omega _0}-u_{ex}|^2+\frac{\partial u_{\Omega _0} }{\partial \nu _0}\frac{\partial \psi _0}{\partial \nu _0}\right) \right| _{\partial \Omega _0}, \end{aligned}$$

(3.7)

where $\psi _0$ is the solution of the adjoint state problem:

$$\begin{aligned} -\Delta \psi _0 + \psi _0 =(u_{\Omega _0}-u_{ex})\,\,\, \text {in} \,\,\Omega _0, \quad \displaystyle \psi _0 =0 \,\,\, \text {on} \,\, \partial \Omega _0 \end{aligned}$$

(3.8)

The aim of the following numerical tests is to reconstruct the target shape and the exact solution of the state problem, which is taken to be $u_{ex}=x^2+y^2-1$, using both algorithms for different initial shapes. Thereby, we propose first to compare the two algorithms using a fixed optimal steps size (the best ones allowing a rapid convergence of the algorithms). Then, we compare the Algorithm 2 (Algorithm of the new method “NM”) using a fixed optimal step size and the Algorithm 1 (Algorithm of the classical method “CM”) performed with updated step size by Armijo-Goldstein strategy (2.8), for different values of $\alpha$.

Fig. 2

Comparison of the convergence histories of the objective functional using Algorithms 1 and 2 for different cases

Table 1 Numerical comparison between Algorithms 1 and 2 for different cases

Shape optimization processes with fixed optimal step-size

The implementation of the two algorithms is done using the number of elements $N=36$ and by choosing fixed step size parameters allowing rapid convergence of the two algorithms. In this respect, we note that these parameters are chosen in an optimal way, such that, if we take greater values of these parameters than the chosen ones, the two algorithms diverges. So the optimal step size parameters used respectively for both algorithms and for different initial shapes are taken such that, in case 1 ($\rho$=0.1 for Algorithm 2 and $\rho$=0.052 for Algorithm 1), in case 2 ($\rho$=0.9 for Algorithm 2 and $\rho$=0.043 for Algorithm 1) and in case 3 ($\rho$=0.79 for Algorithm 2 and $\rho$=0.034 for Algorithm 1). Thereby, in Fig. 1, we present the errors $(u-u_{\text {ex}})$ in the optimal domains obtained by the finite element discretization for different initial domains: case 1, case 2, and case 3. The variation of the objective or cost functionals with respect to the number of iterations are shown respectively in Fig. 2 for different cases. These results shows that the Algorithm 2 converges faster to more accurate optimal solutions than the Algorithm 1, for different initial shapes. This expectation is confirmed in Table 1, where we present the CPU-time, the final objective cost, the iteration numbers and the time reduction for both approaches. We observe that the proposed approach converges in less number of iterations compared to the classical one and the CPU execution time is reduced by at least 93%. These numerical tests show the efficiency of the Algorithm 2 in terms of CPU time execution and the accuracy of optimal solutions compared to Algorithm 1, when one use fixed optimal step size parameters.

Fig. 3

Comparison of the convergence histories of the objective functional using Algorithms 1 and 2 for different values of $\alpha$: case 1

Fig. 4

Comparison of the convergence histories of the objective functional using Algorithms 1 and 2 for different values of $\alpha$: case 3

In the sequel, in order to improve the performance of the Algorithm 1, we propose to update the step size parameter using the Armijo-Goldstein strategy (2.8), for different values of $\alpha$.

Algorithm 2 with fixed step size and Algorithm 1 performed with Armijo-Goldstein step size

In this case, the number of elements is taken $N=36$ and the Algorithm 2 is implemented using only a fixed optimal step size parameter, while the Algorithm 1 is performed using the Armijo-Goldstein strategy (2.8) for different values of $\alpha$, including its optimal value denotes $\alpha _{opt}$ allowing a rapid convergence of this algorithm and chosen such that if we take greater value of it the algorithm diverges. Thereby, the variation of the objective with respect to the number of iterations for different values of $\alpha$ is presented in Figs. 3 and 4, respectively, for the case 1 and case 3. The CPU-time, the final objective functional, the iteration numbers and the time reduction for both approaches are illustrated in Tables 2 and 3, for the different initial shapes. We observe in this case also that the proposed approach converges in less number of iterations to accurate solutions compared to the classical one and the CPU execution time is reduced by at least (90.84% for case 1) and (90.13% for case 3), which decrease when the parameters $\alpha$ increase to reaches there optimal values, and the CPU time reduction in this case reaches (47% for case 1) and (46% for case 3). These numerical tests show the efficiency of the Algorithm 2, using only a fixed optimal step size parameter, in terms of CPU time execution and the accuracy of optimal solutions compared to Algorithm 1 performed with the Armijo-Goldstein strategy, for different values of $\alpha$.

Table 2 Numerical comparison between Algorithms 1 and 2 for different values of $\alpha$: case 1

Table 3 Numerical comparison between Algorithms 1 and 2 for different values of $\alpha$: case 3

Fig. 5

Comparisons on the reconstructed shape using Algorithm 1 (above) and Algorithm 2 (below): case 1

Fig. 6

The computed error of the solution in optimal domain using Algorithm 1 (above) and Algorithm 2 (below): case 1

From these numerical results, we conclude that the Algorithm 2 with only a fixed optimal step size parameter is more efficient than the Algorithm 1 performed with the Armijo-Goldstein strategy for optimal value of $\alpha$, in terms of CPU time execution and the accuracy of optimal solutions. This is due to the fact that the classical approach requires, at each iteration, the resolution of the state and the adjoint state problems as well as the extension boundary value problem of the vector fields to the whole domain (2.7), which are of size $N_{mn}$ the number of the nodes generated from the mesh of the domain limited by the N boundary elements (which is such that $N_{mn}\gg N$), in contrast to the proposed approach which requires in addition to the resolution of the state and the adjoint state problems, to minimize only a linear optimization problem (2.13) of size N.

Fig. 7

The computed error of the solution in optimal domain using Algorithm 1 (above) and Algorithm 2 (below): case 2

Fig. 8

The computed error of the solution in optimal domain using Algorithm 1 (above) and Algorithm 2 (below): case 3

Fig. 9

Comparison of the convergence histories of the objective functional using Algorithms 1 and 2: case 1

Fig. 10

Comparison of the convergence histories of the objective functional using Algorithms 1 and 2: cases 2

Fig. 11

Comparison of the convergence histories of the objective functional using Algorithms 1 and 2: cases 3

Table 4 Numerical comparison between Algorithms 1 and 2: case 2

In the sequel, in order to show the performance of the proposed approach, we will present more numerical tests for different values of boundary elements N using the Algorithm 2 with fixed optimal step size parameter and the Algorithm 1 performed with the Armijo-Goldstein strategy.

Numerical examples tests for different values of boundary elements

For these tests, the initial shape is taken to be the square. Let us first illustrate the convergence of the two algorithms, for the number of elements $N=28.$ So, we present in Fig. 5, the successive and optimal shapes for both approaches. The obtained optimal shapes are reached after 35 and 39 iteration respectively for the Algorithm 2 and the Algorithm 1. We observe that the numerical optimal shape obtained by Algorithm 2 is of good quality compared to the one obtained by Algorithm 1 which presents four singular corner points appearing on its boundary. Then, the errors on the solutions in the optimal domains obtained by the finite element method for different initial domains case 1, case 2, and case 3 and for different N $(N \in \left\{ 28, 48, 80 \right\} )$ are presented respectively in Figs. 6, 7, and 8. Also the variation of the objective or cost functionals with respect to the number of iterations are presented respectively in Figs. 9, 10, and 11. These results shows that the new Algorithm 2 converges faster to more accurate optimal solutions than the Algorithm 1 for different initial shapes and different values of N. This expectation is confirmed in Table 4 where we present the CPU-time, the final objective cost, the iteration numbers and the time reduction for both approaches, when we use the initial shape of case 2. We observe that the proposed approach converges in less number of iterations compared to the classical one and the CPU execution time is reduced by at least 50% which increases with the number of elements N to reaches 58%. In the Table 5, we illustrate the CPU-time, the final objective cost and the time reduction, for $N=28$ and different initial shapes, for both approaches. We see that the time reduction obtained by using the square as an initial shape is very important (71%) compared to the one obtained by using the disk as an initial shape (47%), which is obvious due to singular points of the square (see Fig. 5).

Table 5 Numerical comparison between Algorithms 1 and 2 for different cases and for $N=28$

Fig. 12

Comparisons on the reconstructed shape using Algorithm 1 (above) and Algorithm 2 (below)

3.2.2 Shape optimization problems of minimizing $L^2-$gradient and $H^1$ norms constrained to Dirichlet boundary value problem

In this section, we consider the numerical approximation of shape optimization problems, constrained to Laplace-Dirichlet boundary value state problem, of minimizing cost functionals involving the $L^2-$norm of the gradient and the $H^1$-norm of the solution of the state problem. For all the numerical tests the exact solution is taken $u_{ex}=x^2+y^2-1$.

Our main objective is to propose a comparative numerical study between the Algorithm 2 and the Algorithm 1 in terms of computation time (time CPU) and the accuracy of the obtained optimal solutions for different initial domains associated to the three considered cases.

Fig. 13

The computed error of the solution in optimal shape using Algorithm 1 (left) and Algorithm 2 (right)

Cost functional involving the $L^2-$norm of the gradient of the state problems solution’s

Fig. 14

Comparison of the convergence histories of the objective functional using Algorithms 1 and 2

Fig. 15

Comparison of the reconstructed solution using Algorithm 1 (above) and Algorithm 2 (below): case 1

We perform now a comparison numerical result between the Algorithm 2 and the Algorithm 1 for solving the shape optimization problem (3.1) of minimizing the cost functional $\mathcal {F}$, for $\varpi =0$ and $\beta =\displaystyle \frac{1}{2}$:

$$\begin{aligned} \mathcal {F}(\Omega ,u_{\Omega },\nabla u_{\Omega })=\frac{1}{2}|\!|\nabla u_{\Omega }-\nabla u_{ex}|\!|_{L^{2}(\Omega )}^2. \end{aligned}$$

(3.9)

where $u_{\Omega }$ is the solution of the following Dirichlet state problem:

$$ (PE_2) \left\{ \begin{array}{lll} -\Delta u + u = f_{ex} &{}\text { in }&{}\mathcal {D}\\ u =g_{ex} &{}\text { on } &{} \partial \mathcal {D}. \end{array}\right. $$

Table 6 Numerical comparison between Algorithms 1 and 2

Fig. 16

Comparison of the reconstructed solution using Algorithm 1 (above) and Algorithm 2 (below): case 3

Fig. 17

The computed errors of the solutions in the optimal domain using Algorithm 1 (above) and Algorithm 2 (below): case 1

So, the expression of the gradient at $\Omega _0\in \mathcal {U}$, for the two shape derivative formulas, is given by the following:

$$ \left. \left( \displaystyle \frac{\partial u_{\Omega _0}}{\partial \nu _0} \frac{\partial p_0}{\partial \nu _0} + \displaystyle \frac{1}{2} \left( |\nabla u_{ex}|^2 - \displaystyle [\frac{\partial u_{\Omega _0}}{\partial \nu _0}]^2 \right) \right) \right| _{\partial \Omega _0}, $$

where $p_0$ is the solution of the adjoint state problem $(PE_2)$ with $f=\Delta u_{ex}-\Delta u$.

Fig. 18

Comparison of the convergence histories of the objective functional using Algorithm 1 and Algorithm 2: case 1

Fig. 19

Comparison of the convergence histories of the objective functionals using Algorithm 1 and Algorithm 2: case 3

In this example, we choose the initial shape as the square given in case 1 and we set the number of elements $N=36$ for both approaches. The successive and optimal shape is plotted in Fig. 12. The computed errors of the solutions in the optimal shape are presented in Fig. 13. Then, the convergence history for the objective functional is plotted in Fig. 14, which shows that the proposed approach converges faster for more accurate optimal solution than the classical one with the same precision of the stopping criterion. This is confirmed in Table 6 where we present the CPU-time, the number of iteration, the final cost functional and the CPU-time reduction. In this case the CPU time for the proposed approach is reduced by 58% compared to the classical one.

Fig. 20

Comparison of the reconstructed shapes using Algorithm 1 (above) and Algorithm 2 (below): case 3

Fig. 21

Comparison of the reconstructed solutions using Algorithm 1 (above) and Algorithm 2 (below): case 1

Fig. 22

The computed error of the solution in the optimal shape for ellipse as initial shape (first row) and square as initial shape (second row) using Algorithm 1 (left) and Algorithm 2 (right)

Fig. 23

Comparison of the convergence histories of the objective functional using Algorithms 1 and 2 for both Cases

Cost functional involving the $H^1$-norm of the state problems solution’s

We deal here with the numerical approximation of the shape optimization problem (3.1) of minimizing the cost functional $\mathcal {F}$, for $\varpi =\frac{1}{2}$ and $\beta =\frac{1}{2}$:

$$\begin{aligned} \mathcal {F}(\Omega ,u_{\Omega },\nabla u_{\Omega })=\frac{1}{2}|\!|u_{\Omega }-v_1|\!|_{L^{2}(\Omega )}^2+\frac{1}{2} |\!|\nabla u_{\Omega }- \nabla v_2|\!|_{L^{2}(\Omega )}^2 \end{aligned}$$

(3.10)

where $v_1=v_2=u_{ex}$ and $u_{\Omega }$ is the solution of the Dirichlet state problem. The shape gradient of this functional at $\Omega _0\in \mathcal {U}$, for the two shape derivative formulas, is given by the following:

$$\begin{aligned} \left. \left( \displaystyle \frac{\partial u_{\Omega _0}}{\partial \nu _0} \frac{\partial p_0}{\partial \nu _0} + \frac{1}{2} \left( |\nabla v_2| - \left[ \frac{\partial u_{\Omega _0}}{\partial \nu _0}\right] ^2 \right) + \frac{1}{2} \left| u_{\Omega _0}-v_1\right| ^2 \right) \right| _{\partial \Omega _0}. \end{aligned}$$

(3.11)

where $p_0$ is the solution of the adjoint state problem:

$$\begin{aligned} -\Delta p_0 + p_0 =(\Delta v_2-\Delta u)+(u-v1)\,\,\, \text {in} \,\,\Omega _0, \quad \displaystyle p_0 =0 \,\,\, \text {on} \,\, \partial \Omega _0 \end{aligned}$$

(3.12)

Table 7 Numerical comparison between Algorithms 1 and 2: case 1

Table 8 Numerical comparison between Algorithms 1 and 2: case 3

For this example we take $N=80$, so in Figs. 15 and 16, we plot the successive and the final reconstructed solutions respectively for initial shapes the square (case 1) and the ellipse (case 3). The computed errors of the solutions in the optimal shapes are shown in Fig. 17 for the initial shape is square. The comparison of the convergence history of the objective functional for both approaches and for different initial shapes are presented in Figs. 18 and 19. In Tables 7 and 8, we give the final cost functional, the CPU time, the iterations number and the CPU time reduction for $N=36$, $N=48$ and $N=80.$ In this example, we deduce also that the proposed approach converges faster to more accurate optimal solutions in less number of iterations compared to the classical one for both initial shapes and for different values of N.

3.2.3 Shape optimization constrained to elliptic Neumann boundary value problem

We consider the shape optimization problem 2.1 of minimizing the cost functional $\mathcal {F}$ with $\varpi =1$ and $\beta =0$:

$$\begin{aligned} \mathcal {F}(\Omega ,u_{\Omega },\nabla u_{\Omega })= |\!|u_{\Omega }-u_{ex}|\!|_{L^{2}(\Omega )}^2, \end{aligned}$$

(3.13)

where $u_{ex}=x^2+y^2-1$ and $u_{\Omega }$ is the solution of the Neumann boundary value state problem associated to the parameters $\mu =1,$ $\lambda =1,$ $\eta =1$ and $\gamma =0$. The shape gradient of this functional at $\Omega _0\in \mathcal {U}$, for the two shape derivative formulas, is given by the following:

$$\begin{aligned} \left. \left( |u-u_{ex}|^2 + \nabla u . \nabla p + p(u-u_{ex}) \right) \right| _{\partial \Omega _0}, \end{aligned}$$

(3.14)

where p is the solution of the adjoint state problem:

$$\begin{aligned} -\Delta p + p =-2(u_{0}-u_{ex})\,\,\, \text {in} \,\,\Omega _0, \quad \displaystyle \frac{\partial p}{\partial \nu } =0 \,\,\, \text {on} \,\, \partial \Omega _0. \end{aligned}$$

(3.15)

In this example, we take $N=36$, so in Figs. 20 and 21, we plot the successive and the final reconstructed shapes respectively for initial shapes the ellipse (case 3) and the square (case 1). The computed errors of the solutions in the optimal shapes are shown in Fig. 22 for the initial shape is square and ellipse. The comparison of the convergence history of the objective cost functional for both approaches and for different initial shapes are presented in Fig. 23. Finally, in Table 9, we give the final cost functional, the CPU time, the iterations number and the CPU time reduction for different cases. In this example, we deduce also that the proposed approach converges faster to more accurate optimal solutions in less number of iterations compared to the classical one for both initial shapes.

Table 9 Numerical comparisons between Algorithms 1 and 2

3.2.4 Shape optimization constrained to elliptic Stokes flows equation

In this section, we deal with the numerical approximation of shape optimization problem (3.4) of minimizing different cost functionals constrained to Stokes equation, especially the functional of minimizing the $L^2-$norm of the solution of the state problem or the functional energy. So, the main objective is to achieve a comparative numerical study between the Algorithm 2 and the Algorithm 1 in terms of the CPU (s) time and the accuracy of the obtained optimal solutions, through the resolution of this class of problems for different initial domains associated the three above cases. For this, the Taylor-Hood finite element discretization $\mathbb {P}_2/\mathbb {P}_1$ is used with different number of boundary elements N for approximating respectively the fluid velocity and the associated pressure for the Stokes problem for the following data: the viscosity coefficient is given by $\kappa =0.01,$ the target velocity and pressure are respectively given by $u_{d}(x,y)=( -y\,(x^2+y^2-4), x\,(x^2+y^2-4)),$ $p_{ex}=x+y-1$ and $f_{ex} = (8 \, \kappa \, y +1, 1 - 8\, \kappa \, x).$

Fig. 24

Comparison of the reconstructed shapes using Algorithm 1 (above) and Algorithm 2 (below): case 1

Fig. 25

Comparison of the reconstructed shape using Algorithm 1 (above) and Algorithm 2 (below): case 3

Fig. 26

The computed error of the solution in the optimal domain using Algorithm 1 (above) and Algorithm 2 (below): case 1

Fig. 27

The computed error of the solution in the optimal domain using Algorithm 1 (above) and Algorithm 2 (below): case 2

Fig. 28

The computed error of the solution in the optimal domain using Algorithm 1 (above) and Algorithm 2 (below): case 3

Fig. 29

Comparison of the convergence histories of the objective functional using Algorithms 1 and 2: case 1

Fig. 30

Comparison of the convergence histories of the objective functional using Algorithms 1 and 2: case 2

Fig. 31

Comparisons of the convergence histories of the objective functional using Algorithms 1 and 2: case 3

Quadratic functional

We consider the shape optimization problem (3.4) of minimizing the cost functional $\mathcal {S}$ for $\rho =\frac{1}{2}$ and $\sigma =0$:

$$\begin{aligned} \Omega \in \mathcal {U} \longmapsto \mathcal {S}(\Omega ,w_{\Omega _0},\nabla w_{\Omega _0}):= \frac{1}{2}\int _{\Omega _0}|\!|w_{\Omega _0}-u_d|\!|^2dx, \end{aligned}$$

(3.16)

where $(\omega _{\Omega _0}, p_{\Omega _0})$ is solution of the problem (3.5) on $\Omega _0$. The shape gradient of this functional at $\Omega _0\in \mathcal {U}$, for the two shape derivative formulas, is given by the following:

$$\begin{aligned} \left. \left( \Vert w_{\Omega _0}-u_d\Vert + \nabla w_{\Omega _0}: \nabla \psi _0 \right) \right| _{\partial \Omega _0}, \end{aligned}$$

(3.17)

such that $(\psi _0, p_0)$ is the solution of the adjoint state stokes problem:

$$\begin{aligned} -\kappa \Delta \psi _0 +\nabla p_0 = u_0-u_d \,\,\, \text {in} \, \,\,\Omega _0, \quad \displaystyle \text {div} \psi _0 =0 \,\,\,\text { in } \,\,\, \Omega _0 \quad \displaystyle \psi _0 =0 \,\,\, \text {on} \,\, \partial \Omega _0. \end{aligned}$$

(3.18)

Table 10 Numerical comparison between Algorithms 1 and 2: case 1

Fig. 32

Comparison of the reconstructed shapes using Algorithm 1 (above) and Algorithm 2 (below)

Fig. 33

The computed error of the solution in the optimal domain using Algorithm 1 (above) and Algorithm 2 (below): case 1

Fig. 34

The computed error of the solution in the optimal domain using Algorithm 1 (above) and Algorithm 2 (below): case 3

Fig. 35

The computed error of the solution in the optimal domain using Algorithms 1 and 2: case 1

For the first test we take $N = 80,$ thereby the successive and optimal shape are plotted in Figs. 24 and 25 respectively for the initial shape is a square (case 1) and a disc (case 3). Then, the computed errors of the solutions in the optimal shape with the iso-value meshes are presented in Figs. 26, 27, and 28 for different number of element N and different initial shapes. The convergence history for the objective functional is plotted in Figs. 29, 30, and 31, which shows that the proposed approach converges faster for more accurate optimal solution than the classical one using the same precision of the stopping criterion. The performance of the proposed approach is confirmed in Table 10 where we present the CPU-time, the number of iteration, the final cost functional and the CPU-time reduction. In this case the CPU time of execution for this approach is reduced by 48% compared to that of the classical one

Fig. 36

The computed error of the solution in optimal domain using Algorithms 1 and 2: case 3

Energy functional

Now we consider the shape optimization problem (3.1) of minimizing the cost functional $\mathcal {F}$ for $\rho =0$ and $\sigma =\kappa$:

$$\begin{aligned} \Omega \in \mathcal {U} \longmapsto \mathcal {S}(\Omega ,w_{\Omega },\nabla w_{\Omega }):= \kappa \,\int _{\Omega }|\!|\nabla w_{\Omega }-\nabla u_d|\!|^2 dx. \end{aligned}$$

(3.19)

The shape gradient of this functional at $\Omega _0\in \mathcal {U}$, for the two shape derivative formulas, is given by the following:

$$ \left. ( \kappa \left[ (\nabla w_{\Omega _0}. \nu _0).(\nabla p_0. \nu _0) - |\!|\nabla w_{\Omega _0}. \nu _0|\!|^2 \right] ) \right| _{\partial \Omega _0}, $$

such that $(\psi _0,p_0)$ is the solution of the adjoint state stokes problem:

$$\begin{aligned} -\kappa \Delta \psi _0 +\nabla q_0 = \kappa \Delta ({w}_{\Omega _0}-u_d) \,\,\, \text {in} \, \,\,\Omega _0, \quad \displaystyle \text {div} \psi _0 =0 \,\,\,\text { in } \,\,\, \Omega _0 \quad \displaystyle \psi _0 =0 \,\,\, \text {on} \,\, \partial \Omega _0. \end{aligned}$$

(3.20)

For this example, the successive and optimal shape are plotted in Fig. 32 for the initial shape is ellipse case 3) and for $N = 100$. The computed optimal shapes are reached after 24 and 59 iteration respectively for the Algorithms 2 and 1. The errors on the solutions in the optimal domains obtained by the finite element method for different initial domains considered in case 1 and case 3 and for different values of N $(N \in \left\{ 28, 36, 48, 100 \right\} )$ are presented respectively in Figs. 33 and 34. Also the variation of the objective functionals with respect to the number of iterations are presented respectively in Figs. 35 and 36. These results shows that the new Algorithm 2 converges faster to more accurate optimal solutions than the Algorithm 1 for different values of N. This expectation is confirmed in Table 11 where we present the CPU-time, the final objective functional, the iteration numbers and the time reduction for both approaches, when we use the initial shape of case 3. We observe for this test also that the proposed approach converges in less number of iterations compared to the classical one and the CPU execution time is reduced by at least 50% which increases with the number of elements N to reaches 65%. This expectation is confirmed in Table 12 where we illustrate the CPU-time, the final objective functional and the time reduction, for $N = 28$ and different initial shapes, for both approaches.

Table 11 Numerical comparison between Algorithms 1 and 2: case 3

3.2.5 Discussions and concluding remarks on the numerical results

The comparative numerical study between the Algorithm 1 and the Algorithm 2 concerns the quality of optimal solutions and the CPU time reduction. In this regard, we note that for all the obtained numerical results, the Algorithm 2 reaches the optimal solutions on less number of iterations compared to the Algorithm 1. Moreover, we observe from these numerical results, that the difference between the numbers of iterations at convergence for the two algorithms and the CPU time reduction depend strongly on the choice of the step descent parameter in the gradient methods and the number of boundary elements discretization N as well as the type of the boundary condition in the state problems and the initial domains in the shape optimization processes. Indeed:

Table 12 Numerical comparison between Algorithms 1 and 2 for different cases and $N=28$

• Concerning the choice of the step descent parameter in the gradient methods, we have analyzed the sensitivity and the influence of the choice of the step size parameter on the convergence performance of the both algorithms. More precisely, we have compared first the two algorithms using a fixed optimal steps size (the best ones allowing a rapid convergence of the algorithms). Then, we compared the Algorithm 2 using a fixed optimal step size and the Algorithm 1 performed with updated step size by Armijo-Goldstein strategy (2.8). From the obtained numerical results, we conclude that the Algorithm 2 with only a fixed optimal step size parameter is more efficient than the Algorithm 1 performed with the Armijo-Goldstein strategy, in terms of CPU time execution and the accuracy of optimal solutions. This is due to the fact that the classical approach (Algorithm 1) requires, at each iteration, the resolution of the state and the adjoint state problems as well as the extension boundary value problem of the vector fields to the whole domain (2.8), which are of size $N_{mn}$ the number of the freedom degrees generated from the mesh of the domain limited by the N boundary elements (which is such that $N_{mn}\gg N$), in contrast to the proposed approach which requires in addition to the resolution of the state and the adjoint state problems, to minimize only a linear optimization problem  (2.13) of size N.

• Regarding the influence of the number of boundary elements N or its resulting number of the freedom degrees $N_{mn}$ on the reduction of the CPU time, we have observed from some example tests, that even if the difference between the iteration numbers of the two algorithms is not large, the CPU time reduction is very remarkable. This is due to the fact that the Algorithm 1 requires to solve more additional linear systems of size $N_{mn}$ (which are of number more greater than the iterations number of the Algorithm 2) compared to the Algorithm 2. This is in fact illustrated for example in Table 7 (last line for the case $N = 80$) where we remark that even if the difference between the iteration numbers of the two algorithms is just 7 iterations, the reduction of the CPU times reaches $69\%$, and for example in Table 8 (first line for the case $N = 36$) where the obtained CPU time reduction reaches $54\%$.

• We note also that the CPU time reduction is influenced by the geometrical regularity of the considered initial domains as well as on the type of the boundary condition (Dirichlet or Neumann condition) in the considered state problems. Indeed, when one consider the Dirichlet boundary value state problem on the square as initial shape, the shape optimization process requires a mesh refinement of the successive domains to overcome to the inconveniences due to the singularity of the corners points, thereby the number $N_{mn}$ may be too large ($N_{mn}\ggg N$) compared to the case where the initial shape is more regular, such as the ellipse or the disc. This means that the reduction in CPU time is more important, when the initial domain is a square, even if the difference between the number of iterations of the two algorithms is not large. This is due to the fact that the Algorithm 1 requires to solve some additional linear systems of size $N_{mn}$ (which are of number more greater than the iterations number of the Algorithm 2) compared to the Algorithm 2. This is in fact illustrated in the example tests in Table 5, where even if the difference between the iteration numbers of the two algorithms is not large, the CPU time reduction is remarkable and reaches $71\%$. This expectation is no longer true, when one consider the Neumann boundary value state problem on the square as initial shape, since the accuracy of the solutions of the state and adjoint state problems for both algorithms is affected by the discontinuity of the normal derivative on the corner points. This is in fact illustrated in Table 9, where the CPU time reduction for the example test where the initial shape is the ellipse is more important compared to the one where the initial shape is the square.

4 Conclusion

We conclude from this numerical study that the use of the shape derivative involving the support functions in the gradient shape optimization process is more advantageous than the one using the classical shape derivative involving vector fields, when the finite element method is used for the discretization of the auxiliary problems. This is illustrated through the comparative numerical results showing the efficiency of the resulting numerical process “Algorithm 2” of the proposed approach and its ability in producing good quality solutions and in providing better accuracy for the optimal solution in less CPU time compared to the classical approach “Algorithm 1,” even if this last algorithm is based on the gradient method performed with the optimal step strategy of Armijo-Goldstein [26], while the Algorithm 2 is accomplished with only a fixed step chosen once for all the iterations of the optimization process.