A high-order adaptive numerical algorithm for fractional diffusion wave equation on non-uniform meshes

Abstract 

In this work, our motivation is to design an impressive new numerical approximation on non-uniform grid points for the Caputo fractional derivative in time ${~}^{\mathrm {C}}_{0}\mathcal {D}_{t}^{\alpha }$ with the order α ∈ (1,2). An adaptive high-order stable implicit difference scheme is developed for the time-fractional diffusion wave equations (TFDWEs) by using estimation of order $\mathcal {O}(N_{t}^{\alpha -5})$ for the Caputo derivative in the time domain on non-uniform mesh and well-known second-order central difference approximation for estimating the spatial derivative on a uniform mesh. The designed algorithm allows one to build adaptive nature where the scheme is adjusted according to the behaviour of α in order to keep the numerical errors very small and converge to the solution very fast as compared to the previously investigated scheme. We rigorously analyze the local truncation errors, unconditional stability of the proposed method, and its convergence of (5 − α)-th order in time and second-order in space for all values of α ∈ (1,2). A reduced order technique is implemented by using moving mesh refinement and assemble with the derived scheme in order to improve the temporal accuracy at several starting time levels. Furthermore, the numerical stability of the derived adaptive scheme is verified by imposing random external noises. Some numerical tests are given to show that the numerical results are consistent with the theoretical results.

1 Introduction

The theory of non-integer derivatives is an emerging topic of applied mathematics, which attracted the attention of many researchers from various disciplines. The nonlocal properties of fractional operators attract a significant level of intrigue in the area of fractional calculus since it can give a superior way to deal with the complex phenomena in nature, such as biological systems [1], control theory [2], finance [3], signal and image processing [4, 5], sub-diffusion and super-diffusion process [6], viscoelastic fluid [7], electrochemical process [8], and so on. The main advantage of FDEs is that it provides a powerful tool for depicting the systems with memory, long-range interactions and hereditary properties of several materials as opposed to the classical differential equations in which such effects are difficult to incorporate [9, 10]. Some applications of FDEs in different fields of real-life problems are discussed in [11].

A wide range of relevant physical phenomena are characterize by time-fractional diffusion equations (TFDEs) or TFDWEs [12, 13]. TFDEs are derived by replacing the first-order time derivative of the standard diffusion equations with α-order (0 < α < 1) fractional derivative and TFDWEs are derived by replacing the second-order time derivative of the classical diffusion or wave equations with α-order (1 < α < 2) fractional derivative. It is popular that the behaviour of diffusion and wave equations are completely different according to their reaction to localized disturbance. The propagation speed of the disturbance in the process described by the diffusion equation is infinitely fast, whereas, in the case of wave equations, it is constant. From a specific perspective, these two distinct reactions are interconnected to compose TFDWEs and thus become popular and satisfactory for many physical applications.

Most of the non-integer derivatives express in the form of convolution type integro-differential equations whose kernels are generally of weakly singular type since kernel of these fractional derivatives (FDs) contained the power-law term (t − s)^−α. Due to which very few of FDEs have analytical solutions. A developing number of analysts have built up an interest in finding the analytical solution of FDEs. Usually, the analytical solutions of FDEs are investigated via the Laplace transform methods [14], homotopy analysis methods [15, 16], Adomian decomposition method [17], method of separation of variables [18], and the Green function method [19]. In general, analytic solutions to most of the FDEs cannot be obtained explicitly or given in terms of multinomial Mittag-Leffler functions, which are extremely complex and difficult to evaluate [14, 15, 20,21,22]. Therefore, it is of great importance to develop some efficient numerical methods for finding the approximate solutions of these models, especially for those cases where analytical solutions are either unavailable or extremely complex and difficult to evaluate. Some excellent numerical techniques have been developed in order to get approximate solution of different kind of fractional models, e.g., Galerkin spectral method (GSM) [23], finite volume methods [24], finite element methods [25,26,27], finite difference methods (FDM) [28, 29], and many more.

G. Gao et al. [30] solved distributed-order TFDWEs by using two difference schemes, N. H. Sweilam et al. [31] presented a weighted average FDM for solving fractional Cable equation and fractional reaction sub-diffusion equation, M. Dehghan et al. [32] applied the homotopy analysis method for solving the fractional wave, Burgers, KdV, KdV-Burgers, and Klein-Gordon equations. Authors of [33] used ADI and Galerkin method approach for getting the approximate solution of distributed-order TFDEW. Authors of [34] used spectral element procedure for simulating the neutral delay distributed-order fractional damped diffusion wave equation. In 2018, K. Shah and M. Akram [35] have used the shifted Jacobi operational matrices for the numerical solution of a class of multi-term FDEs. The main aim of [36] is to develop several schemes based on the FDM for 2D Schr$\ddot {\mathrm {o}}$dinger equation with Dirichlet’s boundary conditions.

In this article, the work focuses on developing a new and efficient adaptive difference scheme for solving the TFDWEs on a rectangular domain. The model problem considered here is the one-dimensional TFDWEs [37]:

$$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha} \mathcal{U}(x,t)&= \xi {\Delta}^{x} \mathcal{U} + f(x,t), \end{array}$$

(1.1)

$$\begin{array}{@{}rcl@{}} \mathcal{U}(x,0)=\phi(x),\qquad \frac{\partial \mathcal{U}}{\partial t}\bigg|_{t=0} = \psi(x),\qquad 0\leq x\leq \mathrm{L}, \end{array}$$

(1.2)

$$\begin{array}{@{}rcl@{}} \mathcal{U}(0,t)={\Phi}_{1}(t),\qquad \mathcal{U}(\mathrm{L},t)={\Phi}_{2}(t),\qquad t>0. \end{array}$$

(1.3)

Here, (1.2) and (1.3) are the initial and Dirichlet boundary conditions, respectively. ξ is a constant diffusion-wave coefficient, Δ^x is the spatial Laplacian operator, the fractional derivative ${~}^{\mathrm {C}}_{0}\mathcal {D}_{t}^{\alpha }$ is intended to be in the Caputo sense, 1 < α < 2, and (x,t) ∈Ω = [0,L] × [0,T].

1.1 Motivation and a brief description of the main results

There are many numerical methods available for the spatial domain, which can create efficient high-order numerical methods while high-order numerical methods are rarely available for time-fractional operators compared to spatial operators because of the weakly singular kernel of many FDs in the time domain. Moreover, from the computational methods prospective, the availability of numerical methods are much less for TFDWEs than TFDEs. In this context, let us now review some results that motivated us to design a new high-order difference algorithm for time-fractional operator ${~}^{\mathrm {C}}_{0}\mathcal {D}_{t}^{\alpha }$ on non-uniform meshes.

• M. Cui [38] have considered uniform meshes in space and time domain and used compact difference scheme to discretized the spatial operator ${\partial ^{2}_{x}}$ and Gr$\ddot {\mathrm {u}}$nwald-Letnikov difference scheme to discretized the Riemann–Liouville fractional derivative ${~}^{\text {RL}}_{0}\mathcal {D}_{t}^{1-\gamma }~ (0<\gamma <1)$ of order 1 − γ, respectively, for TFDEs. The detailed analysis of stability and local truncation error are done by using the Fourier method. Moreover, the designed scheme have shown fourth-order accuracy in the spatial domain and first-order accuracy in the time domain.

• Soori et al. [39] developed a new high-order numerical scheme of order (3 − α), 0 < α < 1, for TFDEs on a non-uniform mesh.

• M. Dehghan et al. [40] proposed GSM and compact FDM on uniform meshes for obtaining the approximate solution of multi-term TFDWEs and error analysis have been studied thoroughly concerning $L_{\infty }-$norm. It was proved that the developed method has fourth-order accuracy in spatial component and (3 − α)-th, 1 < α < 2, order accuracy in time variables, respectively.

• Various kinds of methods are discussed and developed by many researchers to get the numerical approximations of the FDs. The classical L1 method is suitable for the case 0 < α < 1 and the L2 and L2C methods are ideal for the case of 1 < α < 2.

• The L1 method for approximating the Caputo FD in time is:

  $$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha} u(\text{x},t)\bigg|_{t^{n}} \approx \frac{1}{\Gamma(1-\alpha)} \sum\limits_{k=0}^{n-1}\frac{u(\text{x},t^{k+1}) - u(\text{x},t^{k})}{\Delta t}{\int}_{t^{k}}^{t^{k+1}} (t^{n}-\eta)^{-\alpha} d\eta + \mathcal{R}_{n}, ~~0<\alpha<1, \end{array}$$

  (1.4)

  where $\mathcal {R}_{n}$ is the local truncation error and $0=t^{0}<t^{1}<{\dots } < t^{n}$. For uniform mesh, authors of [41] have shown that $\left | \mathcal {R}_{n} \right |=\mathcal {O}({\Delta } t^{2-\alpha })$, where ${\Delta } t= t^{k+1}-t^{k},~\forall ~ k=0,\dots ,n-1$.

• In case of 1 < α < 2,

  $$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha} u(\text{x},t)\bigg|_{t^{n}} \approx \frac{1}{\Gamma(2-\alpha)} \sum\limits_{k=0}^{n-1}\frac{u(\text{x},t^{n-k-1}) - 2u(\text{x},t^{n-k}) + u(\text{x},t^{n-k+1})}{\Delta t^{2}}{\int}_{t^{k}}^{t^{k+1}} \eta^{1-\alpha}d\eta +\mathcal{R}_{n}, \end{array}$$

  (1.5)

  and,

  $$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha} u(\text{x},t)\bigg|_{t^{n}} &&\approx \frac{1}{\Gamma(2-\alpha)} \displaystyle\sum\limits_{k=0}^{n-1}\frac{u(\text{x},t^{n-k-2}) - u(\text{x},t^{n-k-1}) + u(\text{x},t^{n-k+1}) - u(\text{x},t^{n-k})}{2{\Delta} t^{2}}{\int}_{t^{k}}^{t^{k+1}} \eta^{1-\alpha}d\eta \\ &&+\mathcal{R}_{n} , \end{array}$$

  (1.6)

  where (1.5) and (1.6) are the numerical approximation of the Caputo FD and obtained by using L2 and L2C methods, respectively. Moreover, L2 method converges with order $\mathcal {O}({\Delta } t^{3-\alpha })$ on uniform mesh (see [42]).

• To improve the accuracy of the L1 method, authors of [43] used L1 method on a particular type of non-uniform mesh and derived a semi-discrete scheme for TFDEs. The unconditional stability and second-order convergence of the scheme have shown for H¹ norm. Moreover, they introduced some fictitious points on each sub-interval and developed a moving refinement technique on that non-uniform mesh and demonstrated that the accuracy is improving further by using this technique.

• C. Li et al. [44] used a special kind of non-uniform mesh for a class of non-linear FDEs and detailed analysis are presented about error estimates, stability, and convergence. Besides, they verified that the proposed scheme has better accuracy by using a particular kind of non-uniform mesh as compared to the already existing scheme based on uniform mesh.

• V. E. Lynch et al. [45] have shown that L2C method gives more accurate result for α < 1.5, while L2 method provides the more precise result for α > 1.5, and both methods have similar behaviour around α = 1.5.

• M. M. Meerschaert et al. [46] presented a difference scheme for fractional advection-dispersion flow equations and shown that the implementation of standard Gr$\ddot {\mathrm {u}}$nwald-Letnikov approximation is making the scheme unstable while a consistent and unconditionally stable scheme is developed when shifted Gr$\ddot {\mathrm {u}}$nwald-Letnikov approximation is used in place of standard Gr$\ddot {\mathrm {u}}$nwald-Letnikov approximation.

• R. Du et al. [47] proposed a difference scheme to approximate the Caputo fractional derivative with convergence order $\mathcal {O}({\Delta } t^{4-\alpha }),~\alpha \in (1,2)$, and presented a difference scheme for fractional diffusion-wave equation on non-uniform mesh.

1.2 Purpose and contribution of the paper

Motivated by above achievements and combining with the moving refinement technique, we will present a high-order adaptive difference scheme by using a non-uniform mesh in the time domain which is based on the interpolation approximation for the TFDWEs. The significant contributions of this paper are as follows:

• Previous study has shown that the numerical approximations of FDs with non-uniform mesh have better accuracy than the uniform mesh and there are only very few numerical methods available with non-uniform mesh compare to uniform mesh for the case of 1 < α < 2. The main goal of this manuscript is to derive a new high-order approximation for Caputo FD in time ${~}^{\mathrm {C}}_{0}\mathcal {D}_{t}^{\alpha },~1<\alpha <2$ for a non-uniform mesh.

• In order to get the high-order approximation to Caputo FD, we first use linear Newton interpolation approximation (NIA) in the first subinterval [t⁰,t¹], quadratic NIA in second subinterval [t¹,t²], and for rest of the subintervals we apply cubic NIA on non-uniform meshes by using the points $(t^{k_{t}-3},\mathcal {U}(t^{k_{t}-3})),~(t^{k_{t}-2},\mathcal {U}(t^{k_{t}-2})),~(t^{k_{t}-1},\mathcal {U}(t^{k_{t}-1}))$, and $(t^{k_{t}},\mathcal {U}(t^{k_{t}}))$ for the integrand $\mathcal {U}(t)$ on each subinterval $[t^{k_{t}-1},t^{k_{t}}],~1\leq k_{t} \leq n$. While applying a special non-uniform mesh, a new high-order approximation to the Caputo FD of order $\mathcal {O}({N}_{t}^{\alpha -5}),~1<\alpha <2,$ is obtained.

• A high-order adaptive FDM for solving problem (1.1)–(1.3) is constructed by approximating the Caputo FD ${~}^{\mathrm {C}}_{0}\mathcal {D}_{t}^{\alpha }$ by using approximation of order $\mathcal {O}({N}_{t}^{\alpha -5})$ as it is for the case of 1 < α < 1.5, and for 1.5 ≤ α < 2, first we shift the mesh and then apply the approximation of order $\mathcal {O}({N}_{t}^{\alpha -5})$. Furthermore, for the spatial discretization of Laplacian operator Δ^x, the well-known second-order central difference formula is used.

• The solvability, unconditional stability, and convergence of the derived scheme are investigated thoroughly using $L_{\infty }$-norm.

• It is shown that the proposed scheme has accuracy of the order $\mathcal {O}(N_{t}^{\alpha -5}+\hslash ^{2})$, where N_t and $\hslash$ are discretization parameters.

• Numerical stability of the proposed scheme is also verified by introducing random external disturbances.

• To improve the accuracy in the temporal direction, we combine the moving mesh technique with our derived scheme.

• Numerical experiments with the inclusion of test functions are performed to validate the applicability and reliability of the method.

This manuscript is sectioned as follows:

• Section 2: Some basic definitions of different fractional operators are given.

• Section 3: New highly accurate approximation of Caputo’s time derivative and construction of high-order adaptive difference algorithm for TFDWEs are derived.

• Section 4: Stability and convergence analysis of the presented methods are rigorously investigated.

• Section 5: To verify the numerical stability and in support of our theoretical findings, numerical results are provided.

• Section 6: A conclusion and some future works are presented.

Notations

Throughout this paper, we denote C as a generic positive constant which might be dependent on the given data of the problem and regularity of exact solution, but independent from the discretization parameter $\hslash$ and N_t. Moreover, the set of integers and real numbers are represented by $\mathbb {Z}$ and $\mathbb {R}$, and set of non-negative integers and non-negative real numbers are represented by $\mathbb {Z}^{+}$ and $\mathbb {R}^{+}$, respectively. $\mathbb {N}$ denotes the set of natural numbers.

2 Preliminaries

Unlike the classical derivative, there are more than one definitions of FDs. Out of these definitions, most frequently used definitions are Riemann-Liouville and Caputo derivative. Here, we introduce some fractional-order derivatives.

Definition 1

(Gr$\ddot {\mathrm {u}}$nwald-Letnikov derivatives) The left and right Gr$\ddot {\mathrm {u}}$nwald-Letnikov derivatives with order α > 0 of the given function u(t), t ∈ (a,b) are defined as

$$\begin{array}{@{}rcl@{}} {~}^{\text{GL}}_{a}\mathcal{D}_{t}^{\alpha} u(t)= \lim\limits_{\substack{{h \rightarrow 0}\\ Nh=t-a}} h^{-\alpha} \sum\limits_{j=0}^{N}(-1)^{j} {\left(\begin{array}{c}\alpha\\j\end{array}\right)} u(t-jh), \end{array}$$

(2.1)

and

$$\begin{array}{@{}rcl@{}} {~}^{\text{GL}}_{t}\mathcal{D}_{b}^{\alpha} u(t)= \lim\limits_{\substack{{h \rightarrow 0}\\ Nh=b-t}} h^{-\alpha} \sum\limits_{j=0}^{N}(-1)^{j} {\left(\begin{array}{c}\alpha\\j\end{array}\right)} u(t+jh), \end{array}$$

(2.2)

respectively. For more information about the role of Gr$\ddot {\mathrm {u}}$nwald and Letnikov to derive the above formula (2.1) and (2.2) one can see [2].

Definition 2

(Riemann-Liouville fractional derivative) The left and right Riemann-Liouville FDs with order α > 0 of the given function u(t), t ∈ (a,b) are defined as

$$\begin{array}{@{}rcl@{}} {~}^{\text{RL}}_{a}\mathcal{D}_{t}^{\alpha} u(t)= \frac{1}{\displaystyle{\Gamma}(m-\alpha)} \frac{\mathrm{d}^{m}}{\mathrm{d}t^{m}} {{\int}_{a}^{t}}(t-s)^{(m-\alpha-1)} u(s) \mathrm{d}s, \end{array}$$

(2.3)

and

$$\begin{array}{@{}rcl@{}} {~}^{\text{RL}}_{t}\mathcal{D}_{b}^{\alpha} u(t)= \frac{(-1)^{m}}{\displaystyle{\Gamma}(m-\alpha)} \frac{\mathrm{d}^{m}}{\mathrm{d}t^{m}} {{\int}_{t}^{b}}(s-t)^{(m-\alpha-1)} u(s) \mathrm{d}s, \end{array}$$

(2.4)

respectively, where $m\in \mathbb {Z}^{+}$ satisfying m − 1 ≤ α < m.

Definition 3

(Caputo fractional derivative) The left and right Caputo FDs with order α > 0 of the given function u(t), t ∈ (a,b) are defined as

$$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{a}\mathcal{D}_{t}^{\alpha} u(t)= \frac{1}{\displaystyle{\Gamma}(m-\alpha)} {{\int}_{a}^{t}}(t-s)^{m-\alpha-1} u^{(m)}(s) \mathrm{d}s, \end{array}$$

(2.5)

and

$$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{t}\mathcal{D}_{b}^{\alpha} u(t)= \frac{(-1)^{m}}{\displaystyle{\Gamma}(m-\alpha)} {{\int}_{t}^{b}}(s-t)^{m-\alpha-1} u^{(m)}(s) \mathrm{d}s, \end{array}$$

(2.6)

respectively, where $m\in \mathbb {Z}^{+}$ satisfying m − 1 < α ≤ m.

Definition 4

(Riesz fractional derivative) The Riesz fractional derivative with order α > 0 of the given function u(t), t ∈ (a,b) is defined as

$$\begin{array}{@{}rcl@{}} {~}^{\text{RZ}}\mathcal{D}_{t}^{\alpha} u(t)= c_{\alpha} \left({~}^{\text{RL}}_{a}\mathcal{D}_{t}^{\alpha} u(t) + {~}^{\text{RL}}_{t}\mathcal{D}_{b}^{\alpha} u(t) \right) , \end{array}$$

(2.7)

where $c_{\alpha }=- \frac {1}{2\cos \limits (\alpha \pi /2)},~ \alpha \neq 2k+1,~ k=0,1,\dots .~{~}^{\text {RZ}}\mathcal {D}_{t}^{\alpha } u(t)$ is sometimes expressed as $\frac {\partial ^{\alpha } u(t)}{\partial |t|^{\alpha }}$.

3 Formulation and analysis of the newly design high-order approximation of Caputo-fractional derivative

For temporal discretization, we discretized the time domain [0,T] into N_t non-equal length subintervals with $0=t^{0}<t^{1}<\dots <t^{N_{t}}=\mathrm {T}$. We denote ${\Delta } t^{k_{t}}$ as temporal step-size and N_t as some positive integer such that ${\Delta } t^{k_{t}}=t^{{k_{t}}+1}-t^{k_{t}},$ where $k_{t} \in \mathbb {Z}_{[0,N_{t}-1]}$. Meanwhile, the spatial interval [0, L] is divided into N_x equal subintervals of length $\hslash = \frac {\text {L}}{N_{x}},$ where N_x is some positive integer. If the singularity is present at the origin, then the choice of the non-equidistant stepsizes should be non-decreasing, i.e., Δtⁱ ≤Δt^i+ 1 [44]. Let ${\Delta } t_{m+} = {\Delta } t^{0} +{\dots } + {\Delta } t^{m},~m\in \mathbb {Z}_{[0,N_{t}-1]}$, and Δt_(− 1)+ = 0, thus the temporal and spatial meshes are given by

$${\Omega}_{\Delta t}=\{t^{k_{t}}\in \mathbb{R} :~t^{k_{t}}= {\Delta} t_{(k_{t}-1)+},~k_{t}\in \mathbb{Z}_{[0,N_{t}]}\},~{\Omega}_{\hslash}=\{x^{k_{x}}\in \mathbb{R} :~x^{k_{x}}=k_{x} \hslash,~k_{x}\in \mathbb{Z}_{[0,N_{x}]}\}.$$

Then, the domain Ω = [0,L] × [0,T] is covered by ${\Omega }_{\hslash {\Delta } t} :={\Omega }_{\hslash }\times {\Omega }_{\Delta t}$. We denote ${V}(x^{k_{x}},t^{k_{t}})={V}^{k_{x}}_{k_{t}}$ and let $\{{V}^{k_{x}}_{k_{t}}:~k_{t}\in \mathbb {Z}_{[0,N_{t}]},~k_{x}\in \mathbb {Z}_{[0,N_{x}]}\}$ be the grid function space on ${\Omega }_{\hslash {\Delta } t}$. Moreover, we use the following finite difference notations:

$$\delta_{x} {V}^{k_{x}}=\frac{{V}^{k_{x}}-{V}^{k_{x}-1}}{\hslash},~~~~~~~ {\delta_{x}^{2}} {V}^{k_{x}}=\frac{\delta_{x} {V}^{k_{x}+1}-\delta_{x} {V}^{k_{x}}}{\hslash},~~~~~~~\delta_{t} {V}_{k_{t}}=\frac{{V}_{k_{t}}-{V}_{k_{t}-1}}{\Delta t^{k_{t}-1}}.$$

Define the discrete inner product and norm as:

$$\left\langle {U},{V} \right\rangle=\sum\limits_{k_{x}=1}^{N_{x}-1} \hslash {U}^{k_{x}} {V}^{k_{x}},~~~~~~~~\left\| {V} \right\|_{2}^{2}=\left\langle {V},{V} \right\rangle,~~~~~~~~\left\| {V}_{k_{t}} \right\|_{\infty}=\max_{x^{k_{x}}\in {\Omega}_{\hslash} } \left| {V}^{k_{x}}_{k_{t}} \right| .$$

3.1 Derivation of a new numerical formula for Caputo non-integer derivative on non-uniform meshes

The linear Newton interpolating polynomial of $\mathcal {U}(t)$ at points $(t^{k_{t}-1},~\mathcal {U}(t^{k_{t}-1}))~and~(t^{k_{t}},~\mathcal {U}(t^{k_{t}}))$ is given by

$$\begin{array}{@{}rcl@{}} {\Xi}^{1,k_{t}} \left(\mathcal{U}(t) \right) = \mathcal{U}_{k_{t}-1}~ \left(\frac{t^{k_{t}} - t}{\Delta t^{k_{t}-1}}\right) + \mathcal{U}_{k_{t}}~ \left(\frac{t- t^{k_{t}-1}}{\Delta t^{k_{t}-1}}\right). \end{array}$$

(3.1)

To increase the degree of interpolating polynomial upto cubic interpolation function, we need two more points $(t^{k_{t}-3},~\mathcal {U}(t^{k_{t}-3}))$ and $(t^{k_{t}-2}, ~\mathcal {U}(t^{k_{t}-2}))$. Firstly, we are constructing quadratic interpolation polynomial ${\Xi }^{2,k_{t}} \left (\mathcal {U}(t) \right )$ of $\mathcal {U}(t)$ by adding an additional point $(t^{k_{t}-2},~ \mathcal {U}(t^{k_{t}-2}))$, given as

$$\begin{array}{@{}rcl@{}} {\Xi}^{2,k_{t}} \left(\mathcal{U}(t) \right) &= {\Xi}^{1,k_{t}} \left(\mathcal{U}(t)\right) + \frac{1}{t^{k_{t}} - t^{k_{t}-2}}\left[ \frac{\mathcal{U}_{k_{t}} - \mathcal{U}_{k_{t}-1}}{t^{k_{t}} - t^{k_{t}-1}} - \frac{\mathcal{U}_{k_{t}-1} - \mathcal{U}_{k_{t}-2}}{t^{k_{t}-1} - t^{k_{t}-2} } \right] (t-t^{k_{t}}) (t-t^{k_{t}-1}), \\ &= {\Xi}^{1,k_{t}} \left(\mathcal{U}(t)\right) + \frac{1}{\Delta t^{k_{t}-1} + {\Delta} t^{k_{t}-2}} \left(\delta_{t} \mathcal{U}_{k_{t}} - \delta_{t} \mathcal{U}_{k_{t}-1} \right) (t-t^{k_{t}}) (t-t^{k_{t}-1}). \end{array}$$

(3.2)

For k_t ≥ 3, to increase one more degree of interpolating polynomial, we add one more point $(t^{k_{t}-3},~\mathcal {U}(t^{k_{t}-3}))$ and construct cubic interpolation function ${\Xi }^{3,k_{t}} \left (\mathcal {U}(t)\right )$ of $\mathcal {U}(t)$. Then, we have:

$$\begin{array}{@{}rcl@{}} {\Xi}^{3,k_{t}} \left(\mathcal{U}(t) \right) &&= {\Xi}^{2,k_{t}} \left(\mathcal{U}(t)\right) + \frac{1}{t^{k_{t}} - t^{k_{t}-3}}\left[ \frac{1}{t^{k_{t}} - t^{k_{t}-2} }\left(\frac{\mathcal{U}_{k_{t}} - \mathcal{U}_{k_{t}-1}}{t^{k_{t}} - t^{k_{t}-1}} - \frac{\mathcal{U}_{k_{t}-1} - \mathcal{U}_{k_{t}-2}}{t^{k_{t}-1} - t^{k_{t}-2}}\right) \right. \\ && \left. - \frac{1}{t^{k_{t}-1} - t^{k_{t}-3} }\left(\frac{\mathcal{U}_{k_{t}-1} - \mathcal{U}_{k_{t}-2}}{t^{k_{t}-1} - t^{k_{t}-2}} - \frac{\mathcal{U}_{k_{t}-2} - \mathcal{U}_{k_{t}-3}}{t^{k_{t}-2} - t^{k_{t}-3}}\right) \right] (t-t^{k_{t}}) (t-t^{k_{t}-1})(t-t^{k_{t}-2}), \\ &&= {\Xi}^{2,k_{t}} \left(\mathcal{U}(t)\right) + \frac{1}{\Delta t^{k_{t}-3} + {\Delta} t^{k_{t}-2} + {\Delta} t^{k_{t}-1}}\left[ \frac{1}{\Delta t^{k_{t}-2}+ {\Delta} t^{k_{t}-1} }\left(\delta_{t} \mathcal{U}_{k_{t}} - \delta_{t} \mathcal{U}_{k_{t}-1}\right) \right. \\ &&\left. - \frac{1}{\Delta t^{k_{t}-3}+ {\Delta} t^{k_{t}-2} }\left(\delta_{t} \mathcal{U}_{k_{t}-1} + \delta_{t} \mathcal{U}_{k_{t}-2} \right) \right] (t-t^{k_{t}})(t-t^{k_{t}-1})(t-t^{k_{t}-2}). \end{array}$$

(3.3)

For linear, quadratic and cubic interpolating polynomials, the following error estimates hold:

$$\begin{array}{@{}rcl@{}} \mathcal{U}(t) - {\Xi}^{1,k_{t}} \left(\mathcal{U}(t)\right)= \frac{ \mathcal{U}^{\prime\prime}(\xi^{k_{t}}_{1})}{2!} (t-t^{k_{t}-1})(t-t^{k_{t}}), ~ t\in [t^{k_{t}-1},t^{k_{t}}],~ \xi^{k_{t}}_{1}\in(t^{k_{t}-1},t^{k_{t}}),~ 1\leq k_{t} \leq n, \end{array}$$

(3.4)

$$\begin{array}{@{}rcl@{}} \mathcal{U}(t) - {\Xi}^{2,k_{t}} \left(\mathcal{U}(t)\right)= \frac{ \mathcal{U}^{\prime\prime\prime}(\xi^{k_{t}}_{2})}{3!} (t-t^{k_{t}-2})(t-t^{k_{t}-1})(t-t^{k_{t}}), ~ t\in [t^{k_{t}-1},t^{k_{t}}],\\ \xi^{k_{t}}_{2}\in(t^{k_{t}-2},t^{k_{t}}),~ 1\leq k_{t} \leq n, \end{array}$$

(3.5)

and

$$\begin{array}{@{}rcl@{}} \mathcal{U}(t) - {\Xi}^{3,k_{t}} \left(\mathcal{U}(t)\right)= \frac{ \mathcal{U}^{(\text{iv})}(\xi^{k_{t}}_{3})}{4!} (t-t^{k_{t}-3})(t-t^{k_{t}-2})(t-t^{k_{t}-1})(t-t^{k_{t}}), ~ t\in [t^{k_{t}-1},t^{k_{t}}],\\ \xi^{k_{t}}_{3}\in(t^{k_{t}-3},t^{k_{t}}),~ 1\leq k_{t} \leq n. \end{array}$$

(3.6)

For simplicity, we define:

$$\mathcal{A}^{2}_{t} \mathcal{U}_{k_{t}} = \frac{2}{\Delta t^{k_{t}-2} + {\Delta} t^{k_{t}-1}} \left(\delta_{t} \mathcal{U}_{k_{t}} - \delta_{t} \mathcal{U}_{k_{t}-1} \right),$$

and

$$\begin{array}{@{}rcl@{}} \mathcal{A}^{3}_{t} \mathcal{U}_{k_{t}} = \frac{1}{({\Delta} t^{k_{t}-3} + {\Delta} t^{k_{t}-2} + {\Delta} t^{k_{t}-1})}&\left[ \frac{1}{\Delta t^{k_{t}-2} + {\Delta} t^{k_{t}-1} } \left(\delta_{t} \mathcal{U}_{k_{t}} - \delta_{t} \mathcal{U}_{k_{t}-1}\right)\right.\\ &\left. - \frac{1}{\Delta t^{k_{t}-3}+ {\Delta} t^{k_{t}-2} }\left(\delta_{t} \mathcal{U}_{k_{t}-1} - \delta_{t} \mathcal{U}_{k_{t}-2} \right) \right]. \end{array}$$

For approximation of the Caputo FD in time ${~}^{\mathrm {C}}_{0}\mathcal {D}_{t}^{\alpha }$, we have taken linear interpolation in first sub-interval, quadratic in second, and then cubic for all next sub-intervals. As double derivative of the linear interpolation function vanishes causing more error, to avoid this computational error, we have taken interpolation of derivative function in the first sub-interval and derivative of interpolation function in all the next sub-intervals. Let $v(s)=\mathcal {U}^{\prime }(s)$, then

$$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha} \mathcal{U}(t)&&= \frac{1}{\Gamma(2-\alpha)} \sum\limits_{k_{t}=1}^{n} {\int}_{t^{k_{t}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}}{v^{\prime}(s)} \mathrm{d}s,\\ &&= \frac{1}{\Gamma(2-\alpha)} \left[ {\int}_{t^{0}}^{t^{1}} {(t^{n}-s)^{1-\alpha}}{v^{\prime}(s)} \mathrm{d}s + {\int}_{t^{1}}^{t^{2}} {(t^{n}-s)^{1-\alpha}}{v^{\prime}(s)} \mathrm{d}s \right.\\ &&\left. + \sum\limits_{{k_{t}}=3}^{n} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}}{v^{\prime}(s)} \mathrm{d}s\right], \end{array}$$

(3.7)

$$\begin{array}{@{}rcl@{}} &&\approx \frac{1}{\Gamma(2-\alpha)} \left[ {\int}_{t^{0}}^{t^{1}} {(t^{n}-s)^{1-\alpha}} \left({{\Xi}^{1,1} v(s)} \right)' \mathrm{d}s + {\int}_{t^{1}}^{t^{2}} {(t^{n}-s)^{1-\alpha}}{\left({{\Xi}^{2,2} \mathcal{U}(s)} \right)^{\prime\prime}} \mathrm{d}s \right.\\ &&\left. + \sum\limits_{{k_{t}}=3}^{n} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}}{\left({{\Xi}^{3,{k_{t}}} \mathcal{U}(s)} \right)^{\prime\prime}} \mathrm{d}s\right] ,\\ &&= \frac{1}{\Gamma(2-\alpha)} \left[ {\int}_{t^{0}}^{t^{1}} {(t^{n}-s)^{1-\alpha}} \left(\frac{\delta_{t} \mathcal{U}_{1} - \delta_{t} \mathcal{U}_{0}}{\Delta t^{0}}\right) \mathrm{d}s + {\int}_{t^{1}}^{t^{2}} {(t^{n}-s)^{1-\alpha}} \left(\mathcal{A}^{2}_{t} \mathcal{U}_{2} \right) \mathrm{d}s \right. \\ &&\left. + {\sum}_{{k_{t}}=3}^{n} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}}{\left[ \mathcal{A}^{2}_{t} \mathcal{U}_{k_{t}} + \mathcal{A}^{3}_{t} \mathcal{U}_{k_{t}} \left(6s - 2\left(t^{{k_{t}}-2}+t^{{k_{t}}-1}+t^{{k_{t}}} \right) \right) \right]} \mathrm{d}s\right] ,\\ &&= \frac{1}{\Gamma(2-\alpha)} \left[ \sum\limits_{{k_{t}}=1}^{n} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}} \left(\mathcal{A}^{2}_{t} \mathcal{U}_{k_{t}} \right) \mathrm{d}s \right. \\ &&\left. + \sum\limits_{{k_{t}}=3}^{n} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}}{\left[ \mathcal{A}^{3}_{t} \mathcal{U}_{k_{t}} \left(6s - 2\left(t^{{k_{t}}-2}+t^{{k_{t}}-1}+t^{{k_{t}}} \right) \right) \right]} \mathrm{d}s\right] . \end{array}$$

(3.8)

To remove the dummy point $\mathcal {U}_{-1}$, we use the initial condition ${\frac {\partial \mathcal {U}(x,t)}{\partial t}}\bigg |_{t=0} =\psi (x)$ and take Δt^− 1 = Δt⁰, therefore, $\mathcal {U}_{-1}=\mathcal {U}_{0} - {\Delta } t^{0} v_{0} = \phi (x) - {\Delta } t^{0} \psi (x)$. Noticing that

$$\begin{array}{@{}rcl@{}} \mathcal{H}^{1,n}_{k_{t}} &&= \frac{2}{\Gamma(2-\alpha)} {\int}_{t^{k_{t}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}}~\mathrm{d}s\\ &&= \frac{2}{\Gamma(3-\alpha)} \left[ \left(t^{n}- t^{k_{t}-1} \right)^{2-\alpha} - \left(t^{n}- t^{k_{t}} \right)^{2-\alpha} \right], \end{array}$$

(3.9)

and

$$\begin{array}{@{}rcl@{}} \mathcal{H}^{2,n}_{k_{t}} &&= \frac{1}{\Gamma(2-\alpha)} \frac{1}{\left({\Delta} t^{k_{t}-3} + {\Delta} t^{k_{t}-2} + {\Delta} t^{k_{t}-1}\right) } {\int}_{t^{k_{t}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}}{ \left(6s - 2\left(t^{k_{t}-2}+t^{k_{t}-1}+t^{k_{t}} \right) \right) } \mathrm{d}s\\ &&= \frac{1}{\Gamma(3-\alpha)} \frac{1}{\left({\Delta} t^{k_{t}-3} + {\Delta} t^{k_{t}-2} + {\Delta} t^{k_{t}-1}\right) } \left\lbrace \frac{6}{(3-\alpha) } \left[ \left(t^{n} - t^{k_{t}-1} \right)^{3-\alpha} - \left(t^{n} - t^{k_{t}} \right)^{3-\alpha}\right] \right.\\ &&\left. +\left[ \left(4t^{k_{t}-1}-2\left(t^{k_{t}-2} +t^{k_{t}} \right) \right) \left(t^{n} - t^{k_{t}-1} \right)^{2-\alpha} - \left(4t^{k_{t}}-2\left(t^{k_{t}-2} +t^{k_{t}-1} \right) \right) \left(t^{n} - t^{k_{t}} \right)^{2-\alpha} \right] \right\rbrace . \end{array}$$

(3.10)

Using (3.9) and (3.10) in (3.8), we get the following numerical formula for FD ${~}^{\mathrm {C}}_{0}\mathcal {D}_{t}^{\alpha } \mathcal {U}(t)$:

$$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha} \mathcal{U}(t) &&= \left[ {\sum}_{k_{t}=1}^{n} \mathcal{H}^{1,n}_{k_{t}} \left(\frac{ \delta_{t} \mathcal{U}_{k_{t}} - \delta_{t} \mathcal{U}_{{k_{t}}-1} }{\Delta t^{{k_{t}}-1} + {\Delta} t^{{k_{t}}-2}} \right) + {\sum}_{{k_{t}}=3}^{n} \mathcal{H}^{2,n}_{k_{t}} {\left(\frac{ \delta_{t} \mathcal{U}_{k_{t}} - \delta_{t} \mathcal{U}_{{k_{t}}-1} }{\Delta t^{{k_{t}}-1} + {\Delta} t^{{k_{t}}-2}} - \frac{ \delta_{t} \mathcal{U}_{{k_{t}}-1} - \delta_{t} \mathcal{U}_{{k_{t}}-2} }{\Delta t^{{k_{t}}-2} + {\Delta} t^{{k_{t}}-3}} \right)} \right] \\ &&= {\sum}_{{k_{t}}=1}^{n} \mathcal{H}^{1,n}_{k_{t}} \left(\frac{ \delta_{t} \mathcal{U}_{k_{t}} - \delta_{t} \mathcal{U}_{{k_{t}}-1} }{\Delta t^{{k_{t}}-1} + {\Delta} t^{{k_{t}}-2}} \right) + {\sum}_{{k_{t}}=3}^{n} \mathcal{H}^{2,n}_{k_{t}} \frac{ \delta_{t} \mathcal{U}_{k_{t}} - \delta_{t} \mathcal{U}_{{k_{t}}-1} }{\Delta t^{{k_{t}}-1} + {\Delta} t^{{k_{t}}-2}} - {\sum}_{{k_{t}}=2}^{n-1} \mathcal{H}^{2,n}_{{k_{t}}+1} \frac{ \delta_{t} \mathcal{U}_{{k_{t}}} - \delta_{t} \mathcal{U}_{{k_{t}}-1} }{\Delta t^{{k_{t}}-1} + {\Delta} t^{{k_{t}}-2}} \\ &&= {\sum}_{{k_{t}}=1}^{n} \mathcal{H}^{3,n}_{k_{t}} \left(\frac{ \delta_{t} \mathcal{U}_{k_{t}} - \delta_{t} \mathcal{U}_{{k_{t}}-1} }{\Delta t^{{k_{t}}-1} + {\Delta} t^{{k_{t}}-2}} \right), \end{array}$$

(3.11)

where ${\mathcal{H}}^{3,1}_{1}={\mathcal{H}}^{1,1}_{1}>0,$ ${\mathcal{H}}^{3,2}_{1}={\mathcal{H}}^{1,2}_{1}>0,$ and ${\mathcal{H}}^{3,2}_{2}={\mathcal{H}}^{1,2}_{2}>0.$ For n ≥ 3,

$$\begin{array}{@{}rcl@{}} \mathcal{H}^{3,n}_{k_{t}} = \left\{ \begin{array}{ll} \mathcal{H}^{1,n}_{k_{t}}, & \text{if}~ {k_{t}}=1,\\ \mathcal{H}^{1,n}_{k_{t}} - \mathcal{H}^{2,n}_{{k_{t}}+1}, & \text{if}~ {k_{t}}=2, \\ \mathcal{H}^{1,n}_{k_{t}} + \mathcal{H}^{2,n}_{{k_{t}}} - \mathcal{H}^{2,n}_{{k_{t}}+1}, & \text{if}~ 3\leq {k_{t}} \leq n-1, \\ \mathcal{H}^{1,n}_{n} + \mathcal{H}^{2,n}_{n}, & \text{if}~ {k_{t}}=n. \end{array} \right. \end{array}$$

(3.12)

In this manuscript, we have taken the following non-uniform mesh

$$\begin{array}{@{}rcl@{}} {\Delta} t^{n} = (n+1)\mu,~0\leq n \leq N_{t}-1, \end{array}$$

(3.13)

where $\mu =\frac {2\mathrm {T}}{N_{t} (N_{t}+1)}$. Properties of the coefficients ${\mathcal{H}}^{1,n}_{k_{t}},~{\mathcal{H}}^{2,n}_{k_{t}}$ and ${\mathcal{H}}^{3,n}_{k_{t}}$ have discussed in the following lemmas.

Lemma 3.1

For any α (1 < α < 2) and $\left \lbrace {\mathcal{H}}^{1,n}_{k_{t}} : 1\leq {k_{t}} \leq n, ~\text {and}~ 1\leq n \leq N_{t} \right \rbrace$ defined in (3.9), it holds that

$$\begin{array}{@{}rcl@{}} 0<\mathcal{H}^{1,n}_{1} < {\dots} < \mathcal{H}^{1,n}_{{k_{t}}-1} < \mathcal{H}^{1,n}_{k_{t}} < {\dots} < \mathcal{H}^{1,n}_{n-1} < \mathcal{H}^{1,n}_{n}. \end{array}$$

(3.14)

Proof

Making use of (3.9) and Fundamental theorem of calculus, one can get

$$\begin{array}{@{}rcl@{}} \mathcal{H}^{1,n}_{k_{t}} &&= \frac{2}{\Gamma(2-\alpha)} {\int}_{t^{k_{t}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}}~\mathrm{d}s,~1\leq k_{t} \leq n,~ 1\leq n \leq N_{t},\\ &&= \frac{2}{\Gamma(2-\alpha)} {\Delta} t^{k_{t}} (t^{n}- \zeta_{k_{t}})^{1-\alpha},~\zeta_{k_{t}} \in (t^{k_{t}-1}, t^{k_{t}}), \end{array}$$

where ${\Delta } t^{k_{t}} ~and~ (t^{n}- \zeta _{k_{t}})^{1-\alpha }$ are monotonic increasing function for 1 < α < 2. Hence, we get the result.

Lemma 3.2

For any α (1 < α < 2) and $\left \lbrace {\mathcal{H}}^{2,n}_{k_{t}} : 3\leq {k_{t}} \leq n, ~\text {and}~ 3\leq n \leq N_{t} \right \rbrace$ defined in (3.10), it holds that

$$\begin{array}{@{}rcl@{}} 0<\mathcal{H}^{2,n}_{3} < {\dots} < \mathcal{H}^{2,n}_{{k_{t}}-1} < \mathcal{H}^{2,n}_{k_{t}} < {\dots} < \mathcal{H}^{2,n}_{n-1} < \mathcal{H}^{2,n}_{n}. \end{array}$$

(3.15)

Proof

From (3.10), consider

$$\begin{array}{@{}rcl@{}} {\int}_{t^{k_{t}-1}}^{t^{k_{t}}} &&{(t^{n}-s)^{1-\alpha}}{ \left(6s - 2\left(t^{k_{t}-2}+t^{k_{t}-1}+t^{k_{t}} \right) \right) } \mathrm{d}s = \frac{6}{(2-\alpha)}\left[ {\int}_{t^{k_{t}-1}}^{t^{k_{t}}} ({t^{n}}-s)^{2-\alpha} ds \right.\\ &&\left. -\frac{1}{6} \left\lbrace \left(4t^{k_{t}}-2\left(t^{k_{t}-2} +t^{k_{t}-1} \right) \right) \left(t^{n} - t^{k_{t}} \right)^{2-\alpha} - \left(4t^{k_{t}-1}-2\left(t^{k_{t}-2} +t^{k_{t}} \right) \right) \left(t^{n} - t^{k_{t}-1} \right)^{2-\alpha} \right\rbrace \right]. \end{array}$$

The well-known Trapezoidal error estimate formula yields that

$$\begin{array}{@{}rcl@{}} {\int}_{t^{k_{t}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}}{ \left(6s - 2\left(t^{k_{t}-2}+t^{k_{t}-1}+t^{k_{t}} \right) \right) } \mathrm{d}s &&= -6\left(\frac{\Delta t^{k_{t}}}{12}\right) \left(({t^{n}}-s)^{2-\alpha}\right)^{\prime\prime}\bigg|_{s=\zeta_{k_{t}}},\\ &&=\frac{\Delta t^{k_{t}}}{2} (2-\alpha) (\alpha-1) ({t^{n}} - \zeta_{k_{t}})^{-\alpha},~ \zeta_{k_{t}}\in (t^{k_{t}-1}, t^{k_{t}}). \end{array}$$

It is easy to check that ${\mathcal{H}}^{2,n}_{k_{t}}>0$ and (tⁿ − s)^−α is a monotonic increasing function for every 1 < α < 2 on [0,T], consequently we get the required result.

Lemma 3.3

For any α (1 < α < 2) and $\left \lbrace {\mathcal{H}}^{3,n}_{k_{t}} : 1 \leq {k_{t}} \leq n, ~\text {and}~ 3\leq n \leq N_{t} \right \rbrace$ defined in (3.12), it holds that

• 1) ${\mathcal{H}}^{3,n}_{k_{t}}>0,$

• 2) ${\mathcal{H}}^{3,n}_{1} < {\dots } < {\mathcal{H}}^{3,n}_{{k_{t}}-1} < {\mathcal{H}}^{3,n}_{k_{t}} < {\dots } < {\mathcal{H}}^{3,n}_{n-1} < {\mathcal{H}}^{3,n}_{n}.$

Using the result of Lemma 3.1, Lemma 3.2, and definition of ${\mathcal{H}}^{3,n}_{k_{t}}$, one can prove the above result.

Now, detail analysis of the truncation errors of the formula defined in (3.11) is discussed in the following theorem:

Theorem 3.1

For any 1 < α < 2, and $\mathcal {U}(t)\in \mathrm {C}^{5}[0,t^{n}]$, it holds that

$$\begin{array}{@{}rcl@{}} \left| \hat{R} (\mathcal{U}(t^{1}))\right| &\leq& \frac{(\alpha -1) 2^{(2-\alpha)}}{\Gamma(4-\alpha)} \max_{t^{0}\leq t \leq t^{1}} \left| \mathcal{U}^{\prime\prime\prime}(t)\right| \text{T}^{3-\alpha} (N_{t} +1)^{\alpha-3}, \end{array}$$

(3.16)

$$\begin{array}{@{}rcl@{}} \left| \hat{R} (\mathcal{U}(t^{2}))\right| &\leq& \frac{(\alpha-1) }{\Gamma(2-\alpha)} \left\lbrace \frac{1}{2^{2\alpha}} \max_{t^{0}\leq t \leq t^{1}} \left| \mathcal{U}^{\prime\prime\prime}(t) \right| \text{T}^{3-\alpha} (N_{t} +1)^{\alpha-3} \right.\\ &&\left. + \left[ \frac{2^{6-2\alpha}}{3} \frac{1}{(2-\alpha)(3-\alpha)} \left(\frac{8-\alpha}{4-\alpha}\right) \right] \max_{t^{0}\leq t \leq t^{2}} \left| \mathcal{U}^{(\text{iv})} (t)\right| \text{T}^{4-\alpha} (N_{t} +1)^{\alpha-4} \right\rbrace,\\ \left| \hat{R} (\mathcal{U}(t^{n}))\right| &\leq& \frac{(\alpha-1) }{\Gamma(2-\alpha)} \left\lbrace \max_{t^{0}\leq t \leq t^{1}} \left| \mathcal{U}^{\prime\prime\prime} (t) \right| \text{T}^{3-\alpha} (N_{t}+1)^{\alpha-3} +16\max_{t^{0}\leq t \leq t^{2}} \left| \mathcal{U}^{(\text{iv})} (t)\right| \text{T}^{4-\alpha} (N_{t}+1)^{\alpha-4} \right. \end{array}$$

(3.17)

$$\begin{array}{@{}rcl@{}} &&\left. \left[ \left(\frac{2\alpha}{\alpha-1}\right) + \frac{2^{6-\alpha}}{24} \frac{1}{(2-\alpha)(3-\alpha)} \left(\frac{3(6-\alpha)}{(4-\alpha)(5-\alpha)} +1 \right) \right] \max_{t^{0}\leq t \leq t^{n}} \left| \mathcal{U}^{({\text{v}})}(t)\right| \text{T}^{5-\alpha} (N_{t}+1)^{\alpha-5} \right\rbrace . \end{array}$$

(3.18)

Proof

For n = 1, and from (3.4) and (3.7), one gets:

$$\begin{array}{@{}rcl@{}} \hat{R}(\mathcal{U}(t^{1})) &=& \frac{1}{\Gamma(2-\alpha)} {\int}_{t^{0}}^{t^{1}} {(t^{1}-s)^{1-\alpha}} \left[{v(s)}- {\Xi}^{1,1} v(s)\right]' \mathrm{d}s \\ &=& \frac{1}{\Gamma(2-\alpha)} \left[ \left(v(s) - {\Xi}^{1,1} v(s)\right) \left(t^{1} - s \right)^{1-\alpha} \bigg|_{s=t^{0}}^{t^{1}} + (1-\alpha) {\int}_{t^{0}}^{t^{1}} \left[ v(s) - {\Xi}^{1,1} v(s) \right] \left(t^{1} - s \right)^{-\alpha} \right] \\ &=& \frac{1}{\Gamma(2-\alpha)} \left[ -\frac{1}{2} v^{\prime\prime}({\xi^{1}_{1}}) (s-t^{0}) (t^{1}-s)^{2-\alpha}\bigg|_{s=t^{0}}^{t^{1}} + (\alpha-1) {\int}_{t^{0}}^{t^{1}} \frac{1}{2} v^{\prime\prime}({\xi^{1}_{1}}) (s-t^{0}) (t^{1}-s)^{1-\alpha} \right] \\ &=& \frac{(\alpha-1)2^{2-\alpha}}{\Gamma(4-\alpha)}~\mathcal{U}^{\prime\prime\prime}({\eta^{1}_{1}}) \mathrm{T}^{3-\alpha} (N_{t}+1)^{\alpha-3},~{\eta^{1}_{1}}\in (t^{0},t^{1}). \end{array}$$

(3.19)

If n = 2, then one can obtain the following result by using integration by parts and then substituting the values of (3.7) and (3.5):

$$\begin{array}{@{}rcl@{}} \hat{R}(\mathcal{U}(t^{2})) &&= \frac{1}{\Gamma(2-\alpha)} \left[ {\int}_{t^{0}}^{t^{1}} {(t^{2}-s)^{1-\alpha}} \mathrm{d} \left[{v(s)}- {\Xi}^{1,1} v(s)\right] + {\int}_{t^{1}}^{t^{2}} {(t^{2}-s)^{1-\alpha}} \mathrm{d} \left[{v(s)}- {\Xi}^{2,2} v(s)\right] \right] \\ &&=\frac{(1-\alpha)}{\Gamma(2-\alpha)} \left[ {\int}_{t^{0}}^{t^{1}} \left[ v(s) - {\Xi}^{1,1} v(s) \right] {(t^{2}-s)^{-\alpha}} \mathrm{d}s + {\int}_{t^{1}}^{t^{2}} \left[ v(s) - {\Xi}^{2,2} v(s) \right] {(t^{2}-s)^{-\alpha}} \mathrm{d}s \right], \end{array}$$

(3.20)

by (3.4), it follows

$$\begin{array}{@{}rcl@{}} \bigg| {\int}_{t^{0}}^{t^{1}} \left[ v(s) - {\Xi}^{1,1} v(s) \right] {(t^{2}-s)^{-\alpha}} \mathrm{d}s \bigg| &=& \bigg| {\int}_{t^{1}}^{t^{0}} \frac{v^{\prime\prime}({\xi^{1}_{1}})}{2} (s-t^{0}) (t^{1} - s) (t^{2} - s)^{-\alpha} \mathrm{d}s \bigg| \\ &\leq& \frac{1}{8}~ | \mathcal{U}^{\prime\prime\prime}({\eta^{1}_{1}}) | ~({\Delta} t^{0})^{2}~ \bigg| {\int}_{t^{1}}^{t^{0}} {(t^{2}-s)^{-\alpha}} \mathrm{d}s \bigg| \\ &=& \frac{1}{8}~ | \mathcal{U}^{\prime\prime\prime}({\eta^{1}_{1}}) |~\mu^{3}~2^{-\alpha} \mu^{-\alpha}, \end{array}$$

substituting the value of μ, we get

$$\begin{array}{@{}rcl@{}} \bigg| {\int}_{t^{0}}^{t^{1}} \left[ v(s) - {\Xi}^{1,1} v(s) \right] {(t^{2}-s)^{-\alpha}} \mathrm{d}s \bigg| &\leq \frac{1}{2^{2\alpha}}~ | \mathcal{U}^{\prime\prime\prime}({\eta^{1}_{1}}) | ~\mathrm{T}^{3-\alpha} (N_{t}+1)^{\alpha-3}, ~{\eta^{1}_{1}}\in (t^{0},t^{1}), \end{array}$$

(3.21)

and by (3.5) and definition of μ, it follows that

$$\begin{array}{@{}rcl@{}} \bigg| {\int}_{t^{1}}^{t^{2}} \left[ v(s) - {\Xi}^{2,2} v(s) \right] {(t^{2}-s)^{-\alpha}} \mathrm{d}s \bigg| &=& \bigg| {\int}_{t^{1}}^{t^{2}} \frac{v^{\prime\prime\prime}({\xi^{2}_{2}})}{6} (s-t^{0}) (s-t^{1}) (s-t^{2}) (t^{2} - s)^{-\alpha} \mathrm{d}s \bigg| \\ &\leq& \frac{1}{6} \frac{1}{(2-\alpha)(3-\alpha)} | \mathcal{U}^{(\text{iv})}({\eta^{2}_{2}}) | ~ \bigg| 2^{3-\alpha} \mu^{4-\alpha} + \frac{2^{5-\alpha}}{(4-\alpha)} \mu^{4-\alpha} \bigg| \\ &\leq& \frac{2^{6-2\alpha}}{3} \frac{1}{(2-\alpha)(3-\alpha)} | \mathcal{U}^{(\text{iv})}({\eta^{2}_{2}}) | \left(\frac{8-\alpha}{4-\alpha} \right) \mathrm{T}^{4-\alpha} (N_{t}+1)^{\alpha-4},\\ &&\qquad \qquad\qquad \qquad\qquad \qquad\qquad \qquad\qquad {\qquad\eta^{2}_{2}}\in (t^{0},t^{2}).\\ \end{array}$$

(3.22)

Using (3.21) and (3.22) in (3.20), we get the result for n = 2. Moreover, for n ≥ 3, from (3.4)–(3.7) and using integration by parts, we get:

$$\begin{array}{@{}rcl@{}} \hat{R}(\mathcal{U}(t^{n})) &=& \frac{1}{\Gamma(2-\alpha)} \left[ {\int}_{t^{0}}^{t^{1}} {(t^{n}-s)^{1-\alpha}} \mathrm{d} \left[{v(s)}- {\Xi}^{1,1} v(s)\right] + {\int}_{t^{1}}^{t^{2}} {(t^{n}-s)^{1-\alpha}} \mathrm{d} \left[{v(s)}- {\Xi}^{2,2} v(s)\right] \right. \\ &&+\left. \sum\limits_{{k_{t}}=3}^{n} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} {(t^{n}-s)^{1-\alpha}} \mathrm{d} \left[{v(s)}- {\Xi}^{3,{k_{t}}} v(s)\right] \right]\\ &=& \frac{1}{\Gamma(2-\alpha)} \left[ {\left[ {v(s)}- {\Xi}^{1,1} v(s) \right]\left(t^{n}-s \right)^{1-\alpha}\bigg|_{s=t^{0}}^{t^{1}}} + (1-\alpha) {\int}_{t^{0}}^{t^{1}} \left[ {v(s)}- {\Xi}^{1,1} v(s) \right]\left(t^{n}-s \right)^{-\alpha} \mathrm{d}s \right.\\ &&\left. + \left\lbrace {\left({v(s)}- {\Xi}^{2,2} v(s)\right) {\left(t^{n}-s \right)^{1-\alpha}}\bigg|_{s=t^{1}}^{t^{2}}} + (1-\alpha) {\int}_{t^{1}}^{t^{2}} \left({v(s)}- {\Xi}^{2,2} v(s)\right) {\left(t^{n}-s \right)^{-\alpha}} \mathrm{d}s \right\rbrace \right.\\ &&\left. + \sum\limits_{{k_{t}}=3}^{n} \left\lbrace {\left({v(s)}- {\Xi}^{3,{k_{t}}} v(s)\right) {\left(t^{n}-s \right)^{1-\alpha}}\bigg|_{s=t^{{k_{t}}-1}}^{t^{k_{t}}} } + (1-\alpha) {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} \left({v(s)}- {\Xi}^{3,{k_{t}}} v(s)\right) {\left(t^{n}-s \right)^{-\alpha}} \mathrm{d}s \right\rbrace \right] \\ &&= \frac{(1-\alpha)}{\Gamma(2-\alpha)} \left[ {\int}_{t^{0}}^{t^{1}} \left[{v(s)}- {\Xi}^{1,1} v(s)\right] {(t^{n}-s)^{-\alpha}} \mathrm{d}s + {\int}_{t^{1}}^{t^{2}} \left[{v(s)}- {\Xi}^{2,2} v(s)\right] {(t^{n}-s)^{-\alpha}} \mathrm{d}s \right. \\ &&\left. + \sum\limits_{{k_{t}}=3}^{n} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} \left[ {v(s)}- {\Xi}^{3,{k_{t}}} v(s) \right] {\left(t^{n}-s \right)^{-\alpha}} \mathrm{d}s \right], \end{array}$$

(3.23)

by (3.4), it follows

$$\begin{array}{@{}rcl@{}} \bigg|{\int}_{t^{0}}^{t^{1}} \left[{v(s)}- {\Xi}^{1,1} v(s)\right] {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg|&=&\bigg| {\int}_{t^{0}}^{t^{1}} \frac{v^{\prime\prime}({\xi^{1}_{1}})}{2!} (s -t^{0})(s -t^{1}) {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg| \\ & \leq& \frac{1}{8} ~ | \mathcal{U}^{\prime\prime\prime}({\eta^{1}_{1}}) |~({\Delta} t^{0})^{2}~ \bigg| {\int}_{t^{0}}^{t^{1}} {(t^{n}- s)^{-\alpha}} \mathrm{d}s \bigg| \\ & \leq& \frac{1}{8} ~ | \mathcal{U}^{\prime\prime\prime}({\eta^{1}_{1}}) |~({\Delta} t^{0})^{2}~ {(t^{n}- t^{1})^{-\alpha}} {\int}_{t^{0}}^{t^{1}} \mathrm{d}s \\ & \leq& | \mathcal{U}^{\prime\prime\prime}({\eta^{1}_{1}}) |~ \mathrm{T}^{3-\alpha} (N_{t} +1)^{\alpha - 3}, \end{array}$$

(3.24)

by making use of (3.5), we get

$$\begin{array}{@{}rcl@{}} \bigg|{\int}_{t^{1}}^{t^{2}} \left[{v(s)}- {\Xi}^{2,2} v(s)\right] {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg|&=&\bigg| {\int}_{t^{1}}^{t^{2}} \frac{v^{\prime\prime\prime}({\xi^{2}_{2}})}{3!} (s -t^{0})(s -t^{1}) (s -t^{2}) {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg| \\ & \leq& \frac{1}{24} ~ | \mathcal{U}^{(\text{iv})}({\eta^{2}_{2}}) |~({\Delta} t^{1})^{2}~({\Delta} t^{0} + {\Delta} t^{1}) \bigg| {\int}_{t^{1}}^{t^{2}} {(t^{n}- s)^{-\alpha}} \mathrm{d}s \bigg| \\ & \leq& \frac{1}{24} ~ | \mathcal{U}^{(\text{iv})} ({\eta^{2}_{2}}) |~({\Delta} t^{1})^{2} ({\Delta} t^{0}+ {\Delta} t^{1})~ {(t^{n}- t^{2})^{-\alpha}} {\int}_{t^{1}}^{t^{2}} \mathrm{d}s \\ & \leq &2^{4}~| \mathcal{U}^{(\text{iv})}({\eta^{2}_{2}}) |~ \mathrm{T}^{4-\alpha} (N_{t} +1)^{\alpha - 4}. \end{array}$$

(3.25)

Moreover, by (3.5), it follows

$$\begin{array}{@{}rcl@{}} \bigg| \sum\limits_{{k_{t}}=3}^{n-1} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} \left[{v(s)}- {\Xi}^{3,{k_{t}}} v(s)\right] {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg|&=&\bigg| \sum\limits_{{k_{t}}=3}^{n-1} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} \frac{v^{(\text{iv})}(\xi^{3}_{k_{t}})}{4!} (s -t^{{k_{t}}-3})(s -t^{{k_{t}}-2}) \\ && \qquad (s -t^{{k_{t}}-1}) (s -t^{k_{t}}) {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg|, ~ \xi^{3}_{k_{t}}\in (t^{{k_{t}}-3},t^{k_{t}}), \\ & \leq& \frac{1}{24} ~ | \mathcal{U}^{(\mathrm{v})}(\eta) |~ {\sum}_{{k_{t}}=3}^{n-1} \bigg| {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} (s -t^{{k_{t}}-3})(s -t^{{k_{t}}-2}) \\ && \qquad \qquad (s -t^{{k_{t}}-1}) (s -t^{k_{t}}) {(t^{n}- s)^{-\alpha}} \mathrm{d}s \bigg| \\ & \leq& \frac{1}{96} ~ | \mathcal{U}^{(\mathrm{v})} (\eta) |~ \left[ {\sum}_{{k_{t}}=3}^{n-1} \left[ ({\Delta} t^{{k_{t}}-1})^{2} ({\Delta} t^{{k_{t}}-2} + {\Delta} t^{{k_{t}}-1})\right.\right.\\ &&\left.\left. \qquad ({\Delta} t^{{k_{t}}-3}+{\Delta} t^{{k_{t}}-2} + {\Delta} t^{{k_{t}}-1})\right] {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} {(t^{n}- s)^{-\alpha}} \mathrm{d}s \right] \\ & \leq& \left(\frac{2\alpha}{\alpha - 1} \right) ~| \mathcal{U}^{(\mathrm{v})}(\eta) |~ \mathrm{T}^{5-\alpha} (N_{t} +1)^{\alpha - 5}, \end{array}$$

(3.26)

where η ∈ (t⁰,t^n− 1) and 3 ≤ k_t ≤ n − 1. In addition, for k_t = n

$$\begin{array}{@{}rcl@{}} \bigg| {\int}_{t^{n-1}}^{t^{n}} \left[{v(s)}- {\Xi}^{3,n} v(s)\right] {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg|&=&\bigg| {\int}_{t^{n-1}}^{t^{n}} \frac{v^{(\text{iv})}({\xi^{3}_{n}})}{4!} (s -t^{n-3})(s -t^{n-2}) \\ && \qquad (s -t^{n-1}) (s -t^{n}) {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg|, ~ {\xi^{3}_{n}}\in (t^{n-3},t^{n}), \\ & =&\bigg| \frac{1}{24} ~ \mathcal{U}^{(\mathrm{v})}(\eta_{n}) {\int}_{t^{n-1}}^{t^{n}} (s -t^{n-3})(s -t^{n-2}) \\ && \qquad \qquad (s -t^{n-1}) {(t^{n}-s)^{1-\alpha}} \mathrm{d}s \bigg|, \\ & \leq& \frac{2^{3-\alpha}}{(2-\alpha )(3-\alpha )} ~\left[ \left\lbrace \left(\frac{(6-\alpha)}{(4-\alpha)(5-\alpha)} + \frac{1}{3}\right) \mathrm{T}^{5-\alpha} \right\rbrace \right. \\ && \left. \qquad \qquad | \mathcal{U}^{(\mathrm{v})}(\eta_{n}) |~ \right] (N_{t} +1)^{\alpha - 5}, \end{array}$$

(3.27)

where η_n ∈ (t^n− 3,tⁿ).

remark 1

The inequality (3.22) can be evaluated as:

$$\begin{array}{@{}rcl@{}} \bigg| {\int}_{t^{1}}^{t^{2}} \left[ v(s) - {\Xi}^{2,2} v(s) \right] {(t^{2}-s)^{-\alpha}} \mathrm{d}s \bigg| &= &\bigg| {\int}_{t^{1}}^{t^{2}} \frac{v^{\prime\prime\prime}({\xi^{2}_{2}})}{6} (s-t^{0}) (s-t^{1}) (s-t^{2}) (t^{2} - s)^{-\alpha} \mathrm{d}s \bigg| \\ &=&\frac{1}{6} \bigg| \mathcal{U}^{(\text{iv})}({\eta^{2}_{2}}) \bigg| \bigg| {\int}_{t^{1}}^{t^{2}} (s-t^{0}) (s-t^{1}) (t^{2} - s)^{1-\alpha} \mathrm{d}s \bigg|. \end{array}$$

Apply integration by parts, we get:

$$\begin{array}{@{}rcl@{}} \bigg| {\int}_{t^{1}}^{t^{2}} \left[ v(s) - {\Xi}^{2,2} v(s) \right] {(t^{2}-s)^{-\alpha}} \mathrm{d}s \bigg| & = &\frac{1}{6} | \mathcal{U}^{(\text{iv})}({\eta^{2}_{2}})| \bigg| \left[ \underbrace{ (s-t^{0}) (s-t^{1}) \frac{-(t^{2} - s)^{2-\alpha}}{(2-\alpha)} \bigg|_{s=t^{1}}^{s=t^{2}} }_{=0} \right. \\ &&\left. + \frac{1}{(2-\alpha)} {\int}_{t^{1}}^{t^{2}} (2s-(t^{0}+t^{1}))(t^{2}-s)^{2-\alpha}ds \right] \bigg|.\\ \end{array}$$

Again apply integration by parts, we get:

$$\begin{array}{@{}rcl@{}} \bigg| {\int}_{t^{1}}^{t^{2}} \left[ v(s) - {\Xi}^{2,2} v(s) \right] {(t^{2}-s)^{-\alpha}} \mathrm{d}s \bigg| & =& \frac{1}{6} | \mathcal{U}^{(\text{iv})}({\eta^{2}_{2}})| \frac{1}{(2-\alpha)} \bigg| \left[ (2s-(t^{0}+t^{1}))\frac{-(t^{2}-s)^{3-\alpha}}{(3-\alpha)} \bigg|_{s=t^{1}}^{s=t^{2}}\right.\\ & &\left. + \frac{2}{(3-\alpha)} {\int}_{t^{1}}^{t^{2}} (t^{2}-s)^{3-\alpha} ds \right] \bigg|\\ &\leq& \frac{1}{6} \frac{1}{(2-\alpha)(3-\alpha)} | \mathcal{U}^{(\text{iv})}({\eta^{2}_{2}}) | ~ \bigg| {\Delta} t^{0} ({\Delta} t^{1})^{3-\alpha} + \frac{2}{(4-\alpha)} ({\Delta} t^{1})^{4-\alpha} \bigg|. \end{array}$$

Substituting the values of Δt⁰, Δt¹ from (3.13) and making use of definition of μ in above equation, we get the required result (3.22).

remark 2

The inequality (3.25) can be evaluated as:

$$\begin{array}{@{}rcl@{}} \bigg|{\int}_{t^{1}}^{t^{2}} \left[{v(s)}- {\Xi}^{2,2} v(s)\right] {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg|&=&\bigg| {\int}_{t^{1}}^{t^{2}} \frac{v^{\prime\prime\prime}({\xi^{2}_{2}})}{3!} (s -t^{0})(s -t^{1}) (s -t^{2}) {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg| \\ & \leq& \frac{1}{6}| \mathcal{U}^{(\text{iv})} ({\eta^{2}_{2}}) | \bigg| {\int}_{t^{1}}^{t^{2}} (s -t^{0})(s -t^{1}) (s -t^{2}) {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg| . \end{array}$$

(3.28)

Since, $\displaystyle \max \limits _{t^{0}\leq s \leq t^{n}} \bigg | (s -t^{1}) (s -t^{2}) \bigg | = \frac {({\Delta } t^{1})^{2}}{4}$ is obtained at $s=t^{1}+\frac {\Delta t^{1}}{2}$, so we have:

$$\begin{array}{@{}rcl@{}} (s -t^{0})(s -t^{1}) (s -t^{2})\leq \frac{({\Delta} t^{1})^{2}}{4} \left({\Delta} t^{0} + \frac{\Delta t^{1}}{2} \right)\leq \frac{({\Delta} t^{1})^{2}}{4} \left({\Delta} t^{0} + {\Delta} t^{1} \right). \end{array}$$

(3.29)

Substituting the value of (3.29) into (3.28), we get

$$\begin{array}{@{}rcl@{}} \bigg|{\int}_{t^{1}}^{t^{2}} \left[{v(s)}- {\Xi}^{2,2} v(s)\right] {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg|& \leq& \frac{1}{24} ~ | \mathcal{U}^{(\text{iv})} ({\eta^{2}_{2}}) |~({\Delta} t^{1})^{2} ({\Delta} t^{0}+ {\Delta} t^{1})~ {(t^{n}- t^{2})^{-\alpha}} {\int}_{t^{1}}^{t^{2}} \mathrm{d}s \\ &=&\frac{1}{24} ~ | \mathcal{U}^{(\text{iv})} ({\eta^{2}_{2}}) |~({\Delta} t^{1})^{3} ({\Delta} t^{0}+ {\Delta} t^{1})~ {(t^{n}- t^{2})^{-\alpha}} . \end{array}$$

(3.30)

Consider,

$$\begin{array}{@{}rcl@{}} t^{n}-t^{2}=\sum\limits_{m=2}^{n-1} {\Delta} t^{m} = \sum\limits_{m=2}^{n-1} (m+1)\mu = \frac{\mu}{2} (n-2)(n+3), \end{array}$$

(3.31)

where, (n − 2)^−α ≤ 1 and (n + 3)^−α ≤ 1, for n ≥ 3. Now, using (3.31) and (3.13) into (3.30), we get the required inequality (3.25).

remark 3

The inequality (3.26) can be evaluated as:

$$\begin{array}{@{}rcl@{}} \bigg| \sum\limits_{{k_{t}}=3}^{n-1} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} \left[{v(s)}- {\Xi}^{3,{k_{t}}} v(s)\right] {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg| &=&\bigg| \sum\limits_{{k_{t}}=3}^{n-1} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} \frac{v^{(\text{iv})}(\xi^{3}_{k_{t}})}{4!} (s -t^{{k_{t}}-3})(s -t^{{k_{t}}-2}) \\ && \qquad (s -t^{{k_{t}}-1}) (s -t^{k_{t}}) {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg|, ~ \xi^{3}_{k_{t}}\in (t^{{k_{t}}-3},t^{k_{t}}), \\ & \leq& \frac{1}{24} ~ | \mathcal{U}^{(\mathrm{v})}(\eta) |~ \sum\limits_{{k_{t}}=3}^{n-1} \bigg| {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} (s -t^{{k_{t}}-3})(s -t^{{k_{t}}-2}) \\ && \qquad \qquad (s -t^{{k_{t}}-1}) (s -t^{k_{t}}) {(t^{n}- s)^{-\alpha}} \mathrm{d}s \bigg|. \end{array}$$

(3.32)

Since, $\displaystyle \max \limits _{t^{0}\leq s \leq t^{n}} \bigg | (s -t^{k_{t} -1}) (s -t^{k_{t}}) \bigg | = \frac {({\Delta } t^{k_{t}-1})^{2}}{4}$ is obtained at $s=t^{k_{t}-1}+\frac {\Delta t^{k_{t}-1}}{2}$, so we have:

$$\begin{array}{@{}rcl@{}} (s -t^{{k_{t}}-3})(s -t^{{k_{t}}-2}) (s -t^{{k_{t}}-1}) (s -t^{k_{t}}) &\leq& \frac{({\Delta} t^{k_{t}-1})^{2}}{4} \left(t^{k_{t}-1} + \frac{\Delta t^{k_{t}-1}}{2} -t^{k_{t}-3}\right)\left(t^{k_{t}-1} + \frac{\Delta t^{k_{t}-1}}{2} -t^{k_{t}-2}\right) \\ &\leq &\frac{({\Delta} t^{k_{t}-1})^{2}}{4} \left({\Delta} t^{k_{t}-3} + {\Delta} t^{k_{t}-2} + {\Delta} t^{k_{t}-1}\right) \left({\Delta} t^{k_{t}-2} + {\Delta} t^{k_{t}-1}\right). \end{array}$$

(3.33)

Substituting the value of (3.33) into (3.32), we get

$$\begin{array}{@{}rcl@{}} \bigg| \sum\limits_{{k_{t}}=3}^{n-1} {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} \left[{v(s)}- {\Xi}^{3,{k_{t}}} v(s)\right] {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg| & \leq& \frac{1}{96} ~ | \mathcal{U}^{(\mathrm{v})} (\eta) |~ \left[ \sum\limits_{{k_{t}}=3}^{n-1} \left[ ({\Delta} t^{{k_{t}}-1})^{2} ({\Delta} t^{{k_{t}}-2} + {\Delta} t^{{k_{t}}-1})\right.\right.\\ &&\left.\left. \qquad ({\Delta} t^{{k_{t}}-3}+{\Delta} t^{{k_{t}}-2} + {\Delta} t^{{k_{t}}-1})\right] {\int}_{t^{{k_{t}}-1}}^{t^{k_{t}}} {(t^{n}- s)^{-\alpha}} \mathrm{d}s \right] \\ & \leq& \frac{1}{96} ~ | \mathcal{U}^{(\mathrm{v})} (\eta) |~ \left[ \sum\limits_{{k_{t}}=3}^{n-1} \left[ ({\Delta} t^{{k_{t}}-1})^{3} ({\Delta} t^{{k_{t}}-2} + {\Delta} t^{{k_{t}}-1})\right.\right.\\ &&\left.\left. \qquad ({\Delta} t^{{k_{t}}-3}+{\Delta} t^{{k_{t}}-2} + {\Delta} t^{{k_{t}}-1})\right] {(t^{n}- t^{k_{t}})^{-\alpha}} \right] . \end{array}$$

(3.34)

Consider,

$$\begin{array}{@{}rcl@{}} t^{n}-t^{k_{t}}=\sum\limits_{m=k_{t}}^{n-1} {\Delta} t^{m} = \sum\limits_{m=k_{t}}^{n-1} (m+1)\mu = \frac{\mu}{2} (n-k_{t})(n+k_{t}+1), \end{array}$$

(3.35)

where, (n + k_t + 1)^−α ≤ 1, for all n ≥ 3, and

$$\begin{array}{@{}rcl@{}} \sum\limits_{k_{t}=3}^{n-1} (n-k_{t})^{-\alpha}&=1+\sum\limits_{k_{t}=3}^{n-2}\frac{1}{{k_{t}}^{\alpha}}\leq 1+\sum\limits_{k_{t}=3}^{\infty}\frac{1}{{k_{t}}^{\alpha}}\leq\left(\frac{\alpha}{\alpha-1}\right) . \end{array}$$

(3.36)

Now, using (3.35), (3.36), and (3.13) into (3.34), we get the required inequality (3.26).

remark 4

The inequality (3.27) can be evaluated as:

$$\begin{array}{@{}rcl@{}} {\int}_{t^{n-1}}^{t^{n}} (s -t^{n-3})(s -t^{n-2}) (s -t^{n-1}) {(t^{n}-s)^{1-\alpha}} \mathrm{d}s &=& \frac{1}{(2-\alpha)(3-\alpha)} \left[ \left(t^{n-1} - t^{n-2} \right) \left(t^{n-1} - t^{n-3} \right) ({\Delta} t^{n-1})^{3-\alpha}\right. \\ &&+ \frac{1}{(4-\alpha)} \left\{ \left(2 (t^{n-1} - t^{n-2}) + 2(t^{n-1} - t^{n-3}) \right) ({\Delta} t^{n-1})^{4-\alpha} \right.\\ &&\left.\left. + \frac{6}{(5-\alpha)}({\Delta} t^{n-1})^{5-\alpha} \right\} \right] \\ &=&\frac{1}{(2-\alpha)(3-\alpha)} \left[ {\Delta} t^{n-2} \left({\Delta} t^{n-3} + {\Delta} t^{n-2} \right) ({\Delta} t^{n-1})^{3-\alpha}\right. \\ &&+ \frac{2}{(4-\alpha)} \left\{ \left(2{\Delta} t^{n-2} + {\Delta} t^{n-3} \right) ({\Delta} t^{n-1})^{4-\alpha}\right. \\ &&\left.\left.+ \frac{3}{(5-\alpha)} ({\Delta} t^{n-1})^{5-\alpha} \right\} \right] \\ &=& \frac{1}{(2-\alpha)(3-\alpha)} \left[ (n-1) (2n-3) n^{3-\alpha} \mu^{5-\alpha}\right. \\ &&\left. + \frac{2}{(4-\alpha)} \left\lbrace 3(n-1) n^{4-\alpha} \mu^{5-\alpha} + \frac{3}{(5-\alpha)} n^{5-\alpha} \mu^{5-\alpha} \right\rbrace \right],\\ \end{array}$$

(3.37)

by using (3.37), it follows that

$$\begin{array}{@{}rcl@{}} \bigg| {\int}_{t^{n-1}}^{t^{n}} \left[{v(s)}- {\Xi}^{3,n} v(s)\right] && {(t^{n}-s)^{-\alpha}} \mathrm{d}s \bigg| \leq \frac{1}{24} ~ | \mathcal{U}^{(\mathrm{v})}(\eta_{n}) | \frac{1}{(2-\alpha)(3-\alpha)} \left[ N_{t} ~ 2 N_{t} ~ {N_{t}}^{3-\alpha} \frac{2^{5-\alpha}~ \mathrm{T}^{5-\alpha}}{{N_{t}}^{5-\alpha} (N_{t}+1)^{5-\alpha}} \right.\\ && \left. + \frac{2}{(4-\alpha)} \left\lbrace 3N_{t}~ {N_{t}}^{4-\alpha} \frac{2^{5-\alpha}~ \mathrm{T}^{5-\alpha}}{{N_{t}}^{5-\alpha} (N_{t}+1)^{5-\alpha}} + \frac{3}{(5-\alpha)} {N_{t}}^{5-\alpha} \frac{2^{5-\alpha}~ \mathrm{T}^{5-\alpha}}{{N_{t}}^{5-\alpha} (N_{t}+1)^{5-\alpha}} \right\rbrace \right],\\ \end{array}$$

(3.38)

after simplification of (3.38), we get (3.27).

3.2 Fully discrete difference scheme for fractional-diffusion wave equation on non-uniform meshes

In the current subsection, a high-order fully discrete difference scheme is derived for the proposed one-dimensional TFDWEs (1.1)–(1.3). V. E. Lynch et al. (2003) verify that one will get a better result from L2C method in comparison with L2 method for 1 < α < 1.5, while the reverse happens in the case of 1.5 < α < 2. Motivated with the work of [45, 46, 48], we develop a scheme that depends on two cases of α. For 1 < α < 1.5, we use (3.11) in (1.1)–(1.3) as it is, while for the case of 1.5 ≤ α < 2, first we shift the non-uniform mesh (3.13) and then apply (3.11) on the problem (1.1)–(1.3).

Case-1

When 1 < α < 1.5.

$$\begin{array}{@{}rcl@{}} \sum\limits_{k_{t}=1}^{n} \mathcal{H}^{3,n}_{k_{t}} \left(\frac{ \delta_{t} \mathcal{U}^{k_{x}}_{k_{t}} - \delta_{t} \mathcal{U}^{k_{x}}_{{k_{t}}-1} }{\Delta t^{{k_{t}}-1} + {\Delta} t^{{k_{t}}-2}} \right)=\xi {\Delta}^{x} \mathcal{U} (x^{k_{x}},t^{n}) + f^{k_{x}}_{n} +(R_{t})^{k_{x}}_{n}. \end{array}$$

(3.39)

Furthermore, we have

$$\begin{array}{@{}rcl@{}} {\Delta}^{x} \mathcal{U} (x^{k_{x}},t^{n})=\frac{\mathcal{U}^{{k_{x}}+1}_{n} - 2\mathcal{U}^{k_{x}}_{n} + \mathcal{U}^{{k_{x}}-1}_{n}}{\hslash^{2}} + (R_{x})^{k_{x}}_{n}, \end{array}$$

where $| (R_{x})^{k_{x}}_{n} | = \mathcal {O} (\hslash ^{2})$. Then, we can obtain the following scheme:

$$\begin{array}{@{}rcl@{}} \sum\limits_{{k_{t}}=1}^{n} \mathcal{H}^{3,n}_{k_{t}} \left(\frac{ \delta_{t} \mathcal{U}^{k_{x}}_{k_{t}} - \delta_{t} \mathcal{U}^{k_{x}}_{{k_{t}}-1} }{\Delta t^{{k_{t}}-1} + {\Delta} t^{{k_{t}}-2}} \right)=\xi \frac{\mathcal{U}^{{k_{x}}+1}_{n} - 2\mathcal{U}^{k_{x}}_{n} + \mathcal{U}^{{k_{x}}-1}_{n}}{\hslash^{2}} + f^{k_{x}}_{n} + R^{k_{x}}_{n}, \end{array}$$

(3.40)

where $R^{k_{x}}_{n} = (R_{t})^{k_{x}}_{n} + \mathcal {O} (\hslash ^{2})$. For non-uniform mesh (3.13), it holds that

$$\begin{array}{@{}rcl@{}} | R^{k_{x}}_{n} | = \mathcal{O} ({N_{t}}^{\alpha-5} + \hslash^{2}) , \quad 1\leq {k_{x}} \leq N_{x}, \quad 1 \leq n \leq N_{t}. \end{array}$$

(3.41)

Replacing $\mathcal {U}^{k_{x}}_{k_{t}}$ with its numerical approximation $\mathrm {U}^{k_{x}}_{k_{t}}$, we get the following difference scheme:

$$\begin{array}{@{}rcl@{}} \sum\limits_{{k_{t}}=1}^{n} \mathcal{H}^{3,n}_{k_{t}} \left(\frac{ \delta_{t} {\mathrm{U}}^{k_{x}}_{k_{t}} - \delta_{t} {\mathrm{U}}^{k_{x}}_{{k_{t}}-1} }{\Delta t^{{k_{t}}-1} + {\Delta} t^{{k_{t}}-2}} \right)=\xi {\delta^{2}_{x}} \mathrm{U}^{k_{x}}_{n} + f^{k_{x}}_{n}, \quad 1\leq {k_{x}} \leq {N_{x}}, \quad 1 \leq n \leq N_{t}. \end{array}$$

(3.42)

Case-2

For 1.5 ≤ α < 2, shift the non-uniform mesh (3.13), i.e., Δtⁿ = (n + 2)μ, 0 ≤ n ≤ N_t − 1. Now, apply (3.42), we get the value of $\mathrm {U}_{1}, {\dots } ,\mathrm {U}_{N_{t}-1}, \mathrm {U}_{N_{t}+1}$ (Fig. 1).

Fig. 1

Distribution of mesh after shifting

To evaluate the value at final time T, we use

$$\begin{array}{@{}rcl@{}} \mathrm{U}^{k_{x}}_{N_{t}} = \frac{\nu_{1} \mathrm{U}^{k_{x}}_{N_{t}-1} + \nu_{2} \mathrm{U}^{k_{x}}_{N_{t}+1}}{\nu_{1} + \nu_{2}}, \end{array}$$

(3.43)

where $\nu _{1}= \mathrm {T}- t^{N_{t}-1}$ and $\nu _{2}= t^{N_{t}+1} - \mathrm {T}$.

3.3 Matrix representations of the derived scheme

If we write (3.42) at each grid point and set $\textrm {\textbf {U}}_{\textbf {n}}=[\mathrm {U}_{n}^{1},~\mathrm {U}_{n}^{2}, \dots , \mathrm {U}_{n}^{{N_{x}}-1}]^{T}$, we can obtain the following matrix–vector form of the proposed method

$$\begin{array}{@{}rcl@{}} \left\{ \begin{array}{ll} {\textbf{A}}_{\textbf{1}} {\textbf{U}}_{\textbf{1}} &= \frac{2 ({\Delta} t^{0})^{-\alpha}}{\Gamma(3-\alpha)} {\textbf{U}}_{\textbf{0}} + {\textbf{F}}_{\textbf{1}}, \\ {\textbf{A}}_{\textbf{2}} {\textbf{U}}_{\textbf{2}} &= -\frac{\mathcal{H}^{1,2}_{1}}{2{\Delta} t^{0}} [ \delta_{t} {\textbf{U}}_{\textbf{1}} - \delta_{t} {\textbf{U}}_{\textbf{0}} ] + \frac{\mathcal{H}^{1,2}_{2}}{ ({\Delta} t^{1} + {\Delta} t^{0})} \delta_{t} {\textbf{U}}_{\textbf{1}} + \frac{\mathcal{H}^{1,2}_{2}}{\Delta t^{1} ({\Delta} t^{1} + {\Delta} t^{0})} {\textbf{U}}_{\textbf{1}} + {\textbf{F}}_{\textbf{2}}, \\ {\textbf{A}} {\textbf{U}}_{\textbf{n}} &= - \displaystyle{\sum}_{k_{t}=1}^{n-1} \frac{\mathcal{H}^{3,n}_{k_{t}}}{\Delta t^{k_{t}-1} + {\Delta} t^{k_{t}-2}} [ \delta_{t} {\textbf{U}}_{\textbf{k}_{\textbf{t}}} - \delta_{t} {\textbf{U}}_{\textbf{k}_{\textbf{t}}-\textbf{1}} ] + \frac{\mathcal{H}^{1,n}_{n} + \mathcal{H}^{2,n}_{n}}{ ({\Delta} t^{n-1} + {\Delta} t^{n-2})} \delta_{t}{\textbf{U}}_{\textbf{n-1}} \\ &+ \frac{\mathcal{H}^{1,n}_{n} + \mathcal{H}^{2,n}_{n}}{ {\Delta} t^{n-1}({\Delta} t^{n-1} + {\Delta} t^{n-2})} {\textbf{U}}_{\textbf{n-1}} + {\textbf{F}}_{\textbf{n}}, \quad n=3, {\dots} , N_{t}. \end{array} \right. \end{array}$$

(3.44)

In which

$$\begin{array}{@{}rcl@{}} {\textbf{A}}_{\textbf{1}} &= \text{tri} \left[ -\frac{\xi}{\hslash^{2}}, \quad \left(\frac{({\Delta} t^{0})^{-\alpha}}{\Gamma(3-\alpha)} + \frac{2\xi}{\hslash^{2}}\right), \quad - \frac{\xi}{\hslash^{2}} \right]_{({N_{x}}-1) \times ({N_{x}}-1)} , \end{array}$$

(3.45)

$$\begin{array}{@{}rcl@{}} {\textbf{A}}_{\textbf{2}} &= \text{tri} \left[ -\frac{\xi}{\hslash^{2}}, \quad \left(\frac{\mathcal{H}^{1,2}_{2}}{({\Delta} t^{1} + {\Delta} t^{0}){\Delta} t^{1}} + \frac{2\xi}{\hslash^{2}}\right), \quad - \frac{\xi}{\hslash^{2}} \right]_{({N_{x}}-1) \times ({N_{x}}-1)} , \end{array}$$

(3.46)

$$\begin{array}{@{}rcl@{}} {\textbf{A}} &= \text{tri} \left[ -\frac{\xi}{\hslash^{2}}, \quad \left(\frac{\mathcal{H}^{1,n}_{n} + \mathcal{H}^{2,n}_{n}}{({\Delta} t^{1} + {\Delta} t^{0}){\Delta} t^{1}} + \frac{2\xi}{\hslash^{2}}\right), \quad - \frac{\xi}{\hslash^{2}} \right]_{({N_{x}}-1) \times ({N_{x}}-1)} , \end{array}$$

(3.47)

and

$$\begin{array}{@{}rcl@{}} {\textbf{F}}_{\textbf{1}}= \begin{bmatrix} {f^{1}_{1}} + (\phi^{1} - {\Delta} t^{0} \psi^{1})\frac{(\Delta t^{0})^{-\alpha}}{\Gamma (3-\alpha)}+\frac{\xi}{h^{2}}U_{1}^{0}\\ f_{1}^{2}+(\phi^{2}-\Delta t^{0} \psi^{2})\frac{(\Delta t^{0})^{-\alpha}}{\Gamma (3-\alpha)}\\\vdots\\ \vdots\\ f_{1}^{N_{x}-2}+(\phi^{N_{x}-2}-\Delta t^{0} \psi^{N_{x}-2})\frac{(\Delta t^{0})^{-\alpha}}{\Gamma (3-\alpha)}\\ f^{{N_{x}}-1}_{1} + (\phi^{{N_{x}}-1} - {\Delta} t^{0} \psi^{{N_{x}}-1})\frac{(\Delta t^{0})^{-\alpha}}{\Gamma (3-\alpha)}+\frac{\xi}{h^{2}}U_{1}^{N_{x}} \end{bmatrix}_{({N_{x}}-1)\times 1},~{\textbf{F}}_{\textbf{n}}= \begin{bmatrix} {f^{1}_{n}}+\frac{\xi}{h^{2}}U_{n}^{0}\\f^{2}_{n}\\ \vdots\\ \vdots\\ f_{n}^{N_{x}-2}\\f^{{N_{x}}-1}_{n}+\frac{\xi}{h^{2}}U^{N_{x}}_{n} \end{bmatrix}_{({N_{x}}-1)\times 1},\quad n=2,\dots, N_{t}. \end{array}$$

(3.48)

Proof

The matrix-vector forms

4 Analysis of difference scheme

4.1 Solvability

We use Gershgorin circle theorem to show the solvability of our scheme (3.42).

Theorem 4.1

The difference scheme (3.42) is uniquely solvable.

of the difference scheme (3.42) are given in (3.44). By the Gershgorin circle theorem, the matrices A₁, A₂ and A are invertible. These invertibility guarantee the solvability of proposed scheme.

4.2 Stability and convergence analysis

Theorem 4.2

The difference scheme (3.42) is unconditionally stable.

Proof

To analyze the stability of the present difference algorithm (3.42), first, we mention some crucial notions. Suppose $\tilde {\text {U}}$ be an estimation of the numerical scheme (3.42), and define

$$\rho_{n}^{k_{x}}=\mathcal{U}^{k_{x}}_{n}-\tilde{\text{U}}^{k_{x}}_{n},~0\leq {k_{x}} \leq {N_{x}},~ 1\leq n \leq N_{t}.$$

Let $\rho _{n}=({\rho _{n}^{0}},~{\rho _{n}^{1}},\dots , \rho _{n}^{N_{x}})^{T},$ and use the norm

$$\left\| \rho_{n} \right\|_{\infty} = \displaystyle\max_{0\leq {k_{x}} \leq N_{x}} \left| \rho_{n}^{k_{x}}\right| = \left| {\rho_{n}^{j}}\right| .$$

It follows from (3.42) that

$$\begin{array}{@{}rcl@{}} \mathcal{H}^{3,n}_{n} \left(\frac{ \delta_{t} {\mathrm{U}}^{k_{x}}_{n} - \delta_{t} {\mathrm{U}}^{k_{x}}_{n-1} }{\Delta t^{n-1} + {\Delta} t^{n-2}} \right) + \sum\limits_{k_{t}=1}^{n-1} \mathcal{H}^{3,n}_{k_{t}} \left(\frac{ \delta_{t} {\mathrm{U}}^{k_{x}}_{k_{t}} - \delta_{t} {\mathrm{U}}^{k_{x}}_{k_{t}-1} }{\Delta t^{k_{t}-1} + {\Delta} t^{k_{t}-2}} \right)&=\xi {\delta^{2}_{x}} \mathrm{U}^{k_{x}}_{n} + f^{k_{x}}_{n}, \quad 1\leq {k_{x}} \leq {N_{x}}, \quad 1 \leq n \leq N_{t}. \end{array}$$

After simplification of terms, we have

$$\begin{array}{@{}rcl@{}} \frac{ {\mathrm{U}}^{k_{x}}_{n} - {\mathrm{U}}^{k_{x}}_{n-1} }{\Delta t^{n-1} } - \frac{ {\mathrm{U}}^{k_{x}}_{n-1} - {\mathrm{U}}^{k_{x}}_{n-2} }{\Delta t^{n-2} } &=&\frac{\xi}{\tilde{\mathcal{H}}^{3,n}_{n}} {\delta^{2}_{x}} \mathrm{U}^{k_{x}}_{n} + \frac{f^{k_{x}}_{n}}{\tilde{\mathcal{H}}^{3,n}_{n}} - \frac{1}{\tilde{\mathcal{H}}^{3,n}_{n}} \sum\limits_{k_{t}=1}^{n-1} \frac{\tilde{\mathcal{H}}^{3,n}_{k_{t}}}{\Delta t^{k_{t}-1}} \left({\mathrm{U}}^{k_{x}}_{k_{t}} - {\mathrm{U}}^{k_{x}}_{k_{t}-1} \right) \\ &&+ \frac{1}{\tilde{\mathcal{H}}^{3,n}_{n}} \sum\limits_{k_{t}=1}^{n-1} \frac{\tilde{\mathcal{H}}^{3,n}_{k_{t}}}{\Delta t^{k_{t}-2}} \left({\mathrm{U}}^{k_{x}}_{k_{t}-1} - {\mathrm{U}}^{k_{x}}_{k_{t}-2} \right), \\ \mathcal{K} \mathrm{U}^{{k_{x}}+1}_{n} + \left(\frac{1}{\Delta t^{n-1}} - 2\mathcal{K}\right) \mathrm{U}^{{k_{x}}}_{n} + \mathcal{K} \mathrm{U}^{{k_{x}}-1}_{n} &=& \frac{-1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \sum\limits_{k_{t}=1}^{n-1} {\upbeta}^{n}_{1,k_{t}} \left(\mathrm{U}^{{k_{x}}}_{k_{t}} - \mathrm{U}_{k_{t}-1}^{{k_{x}}} \right) + \frac{1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \sum\limits_{k_{t}=1}^{n-1} {\upbeta}^{n}_{2,k_{t}} \left(\mathrm{U}_{k_{t}-1}^{{k_{x}}} - \mathrm{U}_{k_{t}-2}^{{k_{x}}} \right) \\ &&+\frac{\text{U}_{n-1}^{k_{x}}}{\Delta t^{n-1}} + \frac{\text{U}_{n-1}^{k_{x}} - \text{U}_{n-2}^{k_{x}} }{\Delta t^{n-2}} + \frac{f^{k_{x}}_{n}}{ \tilde{\mathcal{H}}^{3,n}_{n} }, \end{array}$$

(4.1)

where $\tilde {{\mathcal{H}}}^{3,n}_{k_{t}}=\frac {{{\mathcal{H}}}^{3,n}_{k_{t}}}{\Delta t^{k_{t}-1}+{\Delta } t^{k_{t}-2}},~{\upbeta }^{n}_{1,k_{t}}= \frac {\tilde {{\mathcal{H}}}^{3,n}_{k_{t}}}{\Delta t^{k_{t}-1}},~ {\upbeta }^{n}_{2,k_{t}}=\frac {\tilde {{\mathcal{H}}}^{3,n}_{k_{t}}}{\Delta t^{k_{t}-2}},$ and $\mathcal {K}=\frac {-\xi }{\tilde {{\mathcal{H}}}^{3,n}_{k_{t}} \hslash ^{2}}$.

After some simple calculations, one can get

$$\begin{array}{@{}rcl@{}} \frac{-1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \sum\limits_{k_{t}=1}^{n-1} {\upbeta}^{n}_{1,k_{t}} \left(\mathrm{U}_{k_{t}}^{{k_{x}}} - \mathrm{U}_{k_{t}-1}^{{k_{x}}} \right) + \frac{\text{U}_{n-1}^{k_{x}}}{\Delta t^{n-1}}&=\frac{1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \sum\limits_{k_{t}=0}^{n-1} \left({\upbeta}^{n}_{1,{k_{t}+1}} - {\upbeta}^{n}_{1,{k_{t}}} \right) \text{U}_{k_{t}}^{k_{x}}, \end{array}$$

(4.2)

and,

$$\begin{array}{@{}rcl@{}} \frac{1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \sum\limits_{k_{t}=1}^{n-1} {\upbeta}^{n}_{2,k_{t}} \left(\mathrm{U}_{k_{t}-1}^{{k_{x}}} - \mathrm{U}_{k_{t}-2}^{{k_{x}}} \right) + \frac{\text{U}_{n-1}^{k_{x}} - \text{U}_{n-2}^{k_{x}}}{\Delta t^{n-2}}&=\frac{-1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \sum\limits_{k_{t}=0}^{n} \left({\upbeta}^{n}_{2,{k_{t}+1}} - {\upbeta}^{n}_{2,{k_{t}}} \right) \text{U}_{k_{t}-1}^{k_{x}}. \end{array}$$

(4.3)

Inserting (4.2) and (4.3) into (4.1), one can get

$$\begin{array}{@{}rcl@{}} \mathcal{K} \mathrm{U}_{n}^{{k_{x}}+1} + \left(\frac{1}{\Delta t^{n-1}} - 2\mathcal{K}\right) \mathrm{U}_{n}^{{k_{x}}} + \mathcal{K} \mathrm{U}_{n}^{{k_{x}}-1} &&= \frac{1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \left[ \sum\limits_{k_{t}=0}^{n-1} \left({\upbeta}^{n}_{1,{k_{t}+1}} - {\upbeta}^{n}_{1,k_{t}} \right) \mathrm{U}_{k_{t}}^{{k_{x}}} - \sum\limits_{k_{t}=0}^{n} \left({\upbeta}^{n}_{2,{k_{t}+1}} - {\upbeta}^{n}_{2,{k_{t}}} \right) \mathrm{U}_{k_{t}-1}^{{k_{x}}} \right] \\ &&+ \frac{f_{n}^{k_{x}}}{ \tilde{\mathcal{H}}^{3,n}_{n} }, \end{array}$$

(4.4)

By making use of (4.4), one can obtain the following roundoff error equation

$$\begin{array}{@{}rcl@{}} \mathcal{K} \rho_{n}^{{k_{x}}+1} + \left(\frac{1}{\Delta t^{n-1}} - 2\mathcal{K}\right) \rho_{n}^{{k_{x}}} + \mathcal{K} \rho_{n}^{{k_{x}}-1} &= \frac{1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \left[ \sum\limits_{k_{t}=0}^{n-1} \left({\upbeta}^{n}_{1,{k_{t}+1}} - {\upbeta}^{n}_{1,k_{t}} \right) \rho_{k_{t}}^{{k_{x}}} - \sum\limits_{k_{t}=0}^{n} \left({\upbeta}^{n}_{2,{k_{t}+1}} - {\upbeta}^{n}_{2,{k_{t}}} \right) \rho_{k_{t}-1}^{{k_{x}}} \right]. \end{array}$$

(4.5)

For simplicity of the formulas in our further consideration, we define

$$\begin{array}{@{}rcl@{}} \mathcal{L}_{1}(\rho_{n}^{k_{x}})&=\mathcal{K} \rho_{n}^{{k_{x}}+1} + \left(\frac{1}{\Delta t^{n-1}} - 2\mathcal{K}\right) \rho_{n}^{{k_{x}}} + \mathcal{K} \rho_{n}^{{k_{x}}-1}, \end{array}$$

(4.6)

$$\begin{array}{@{}rcl@{}} \mathcal{L}_{2}(\rho_{n-1}^{k_{x}})&=\frac{1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \left[ \sum\limits_{k_{t}=0}^{n-1} \left({\upbeta}^{n}_{1,{k_{t}+1}} - {\upbeta}^{n}_{1,k_{t}} \right) \rho_{k_{t}}^{{k_{x}}} - \sum\limits_{k_{t}=0}^{n} \left({\upbeta}^{n}_{2,{k_{t}+1}} - {\upbeta}^{n}_{2,{k_{t}}} \right) \rho_{k_{t}-1}^{{k_{x}}} \right]. \end{array}$$

(4.7)

Grouping (4.6) and (4.7) with (4.5), then (4.5) can be re-written as:

$$\begin{array}{@{}rcl@{}} \mathcal{L}_{1}(\rho_{n}^{k_{x}})=\mathcal{L}_{2}(\rho_{n-1}^{k_{x}}). \end{array}$$

Consider,

$$\begin{array}{@{}rcl@{}} \left| \mathcal{L}_{2}(\rho_{n-1}^{k_{x}}) \right| &&\leq \frac{1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \left| \rho_{n-1}^{k_{x}} \right| \sum\limits_{k_{t}=0}^{n-1} \left| \left({\upbeta}^{n}_{1,{k_{t}+1}} - {\upbeta}^{n}_{1,k_{t}} \right) \right| + \frac{1}{ \tilde{\mathcal{H}}^{3,n}_{n} } \left| \rho_{n-1}^{k_{x}} \right| \sum\limits_{k_{t}=0}^{n-1} \left| \left({\upbeta}^{n}_{2,{k_{t}+1}} - {\upbeta}^{n}_{2,{k_{t}}} \right) \right| ,\\ &&\leq C \left| \rho_{n-1}^{k_{x}}\right|, \end{array}$$

(4.8)

where $\left | \rho _{n-1}^{k_{x}}\right | = \displaystyle \max \limits _{0\leq k_{t} \leq n-1} \left | \rho _{k_{t}}^{k_{x}} \right |$. Using (4.6) and (4.8), we get

$$\begin{array}{@{}rcl@{}} \left\| \rho_{n}\right\|_{\infty} \leq {C}\left\| \rho_{0} \right\|_{\infty},~ 1\leq n \leq N_{t}, \end{array}$$

(4.9)

which is the required result for unconditional stability of proposed scheme.

Theorem 4.3

Let TFDWEs (1.1)–(1.3) has smooth solution $\mathcal {U}(x, t) \in C^{2,5}_{x,t},$ and (3.42) have the approximate solution $\{\text {U}_{n}^{k_{x}}|~0 \leq {k_{x}} \leq N_{x},~ 1 \leq n \leq N_{t}\}$, where, the non-uniform mesh defined by (3.13) is taken for temporal domain discretization. Then,

$$\begin{array}{@{}rcl@{}} \left\| \mathcal{U}(x^{k_{x}},t^{n}) - \text{U}_{n}^{k_{x}} \right\|_{\infty} \leq C ({N_{t}}^{\alpha-5} + \hslash^{2}), ~ 1 \leq n \leq N_{t}. \end{array}$$

(4.10)

Proof

Suppose $E^{k_{x}}_{n}=\mathcal {U}(x^{k_{x}},t^{n})-\text {U}^{k_{x}}_{n},~~0\leq k_{x}\leq N_{x},~0\leq n \leq N_{t}.$ Now, subtracting (3.42) from (3.40), one can obtain

$$\mathcal{L}_{1} E^{k_{x}}_{n}= \mathcal{L}_{2} E^{k_{x}}_{n-1} + R^{k_{x}}_{n},~~1\leq k_{x} \leq N_{x} -1,~~1\leq n \leq N_{t},$$

and from initial and boundary conditions given in (1.2)–(1.3), we get

$${E^{0}_{n}}=E^{N_{x}}_{n}=0,~~1\leq n \leq N_{t},$$

$$E^{k_{x}}_{1}=0,~~0\leq k_{x} \leq N_{x}.$$

Consider,

$$\left\|E_{n}\right\|_{\infty}= \max_{0\leq {k_{x}} \leq N_{x}} \left|E^{k_{x}}_{n}\right|=\left|E^{k_{j}}_{n}\right|.$$

Then,

$$\begin{array}{@{}rcl@{}} \left\|E_{n}\right\|_{\infty}=\left|E^{k_{j}}_{n}\right|=\left|\mathcal{L}_{1}E^{k_{j}}_{n}\right|&&=\left|\mathcal{L}_{2}E^{k_{j}}_{n-1} + R^{k_{j}}_{n}\right|,\\ &&\leq \left|\mathcal{L}_{2} E^{k_{j}}_{n-1}\right|+\left|R^{k_{j}}_{n}\right|,\\ &&\leq \left\|E_{n-1}\right\|_{\infty} + R_{max}, \end{array}$$

where, $R_{max}=\displaystyle \max \limits _{n, k_{j}}\left |R^{k_{j}}_{n}\right |$. For n = 1, we have

$$\left\|E_{1}\right\|_{\infty}\leq \left\|E_{0}\right\|_{\infty}+R_{max}=R_{max}.$$

Hence,

$$\left\|E_{n}\right\|_{\infty}\leq R_{max},~~1\leq n \leq N_{t}.$$

(4.11)

Now, inserting the value of (3.18) in (4.11), we get the required result (4.10).

From Theorem 4.3, we conclude that our derived scheme (3.44) has (5 − α)-th order global accuracy in the time domain for all time levels n and second-order global accuracy in the spatial direction. It is seen from the analysis part of local truncation error (in Theorem 3.1) that the (5 − α)-th order accuracy in time direction has achieved for a sufficiently large value of n. Although a little larger errors are obtained at starting time levels (when n is small), the impacts of these errors caused on the accompanying time levels are more fragile and more vulnerable with the end goal so that they can be overlooked when the value of n is sufficiently large. Consequently, we can presume that the convergence rate will be better when n is large enough, which is confirmed by the numerical investigations in the upcoming Section 5.

5 Numerical experiments

In the current section, we will test some problems to verify the theoretical results and numerical stability of our proposed adaptive algorithm. The following formulas demonstrate the effectiveness of the algorithm:

$$\mathcal{E}(N_{x},N_{t})_{L_{j}}=\left\| \mathcal{U}- \bar{\mathcal{U}} \right\|_{L_{j}}=\left\{ \begin{array}{ll} \sqrt{ \displaystyle\sum\limits_{k_{x}=1}^{N_{x}-1} \hslash \left| \mathcal{U}(x^{k_{x}},t^{N_{t}}) - \bar{\mathcal{U}}_{N_{t}}^{k_{x}} \right|^{2} },~~~~~~~~~~~~~~~\text{for}~j=2,\\ \displaystyle\max_{0\leq k_{x} \leq N_{x}} \left| \mathcal{U}(x^{k_{x}},t^{N_{t}}) - \bar{\mathcal{U}}_{N_{t}}^{k_{x}} \right| ,~~~~~~~~~~~~~~~~~~\text{for}~j=\infty. \end{array} \right.$$

(5.1)

To calculate the temporal and spatial convergence orders, we utilize the following computational order formula:

$$(\text{Order})_{L_{j}}=\left\{ \begin{array}{ll} \frac{\log \frac{\left\| \mathcal{E}{(N_{x_{1}}, N_{t})}\right\|_{j} }{\left\|\mathcal{E}{(N_{x_{2}}, N_{t})}\right\|_{j} }}{{\log\frac{N_{x_{1}}}{N_{x_{2}}}}},~~~~\text{for space} ,\\ \frac{\log \frac{\left\| \mathcal{E}{(N_{x},N_{t_{1}})}\right\|_{j} }{\left\|\mathcal{E}{(N_{x},N_{t_{2}})}\right\|_{j} }}{{\log \frac{N_{t_{1}}}{N_{t_{2}}}}},~~~~\text{for time}. \end{array} \right.$$

(5.2)

From Theorem 4.3 and Theorem 3.1, we conclude that the rate of convergence of our developed scheme is of order $\mathcal {O}({N_{t}}^{\alpha -5} + \hslash ^{2})$ for sufficient large value of n and errors obtained at starting time levels are little larger, respectively. In order to improve the accuracy and efficiency of our scheme, moving refinement approach has been introduced on our non-uniform mesh (3.13) by inserting some fictitious points $t_{(k_{t})}^{1},~t_{(k_{t})}^{2},...,t_{(k_{t})}^{J_{k_{t}}}$ in the subinterval $[t^{k_{t}-1},t^{k_{t}}],$ and let $\varpi _{k_{t}}=\frac {2{\Delta } t^{k_{t}}}{(J_{k_{t}} +1)(J_{k_{t}}+2)},$

$$\begin{array}{@{}rcl@{}} t_{(k_{t})}^{j+1}=t_{(k_{t})}^{j} + (J_{k_{t}} +1-j)\varpi_{k_{t}},~1\leq j\leq J_{k_{t}} -1, \end{array}$$

where,

$$\begin{array}{@{}rcl@{}} t_{(k_{t})}^{1}= t^{k_{t}-1} + (J_{k_{t}}+1)\varpi_{k_{t}} \end{array}$$

To improve the accuracy of the proposed scheme at initial time levels, we upgrade the proposed adaptive scheme by inserting the following process, where $\text {U}_{k_{t}}$ denotes the numerical approximation on the time level $t^{k_{t}}$:

• Step 1: Firstly evaluate U₁ by using initial value U₀ and proposed scheme (3.44) on the grid $t^{0}<t_{(1)}^{1}<t_{(1)}^{2}<\dots <t_{(1)}^{J_{1}}<t^{1}$.

• Step 2: With the help of U₁ and scheme (3.44) compute U₂ on $t^{0}<t^{1}<t_{(2)}^{1}<t_{(2)}^{2}<\dots <t_{(2)}^{J_{2}}<t^{2}$.

• Step 3: After receiving U₁ and U₂ from above two steps, we proceed the following process for further time levels:

  • Case-I For 1 < α < 1.5, evaluate $\{\text {U}_{l}\}_{l=3}^{n}$ by scheme (3.44) on the non-uniform grid $t^{0}<t^{1}<t^{2}<\dots <t^{n}.$

  • Case-II For 1.5 ≤ α < 2, evaluate $\{\text {U}_{l}\}_{l=3}^{n-1,n+1}$ by using scheme (3.44) on non-uniform refined mesh $t^0<t^1<\dots<t^{n-2}<t_{(n-1)}^1<\dots<t_{(n-1)}^{J_{n-1}}<t^{n-1}<t_{\left(n\right)}^1<t_{\left(n\right)}^2<\dots<t_{\left(n\right)}^{J_n}<t^{n+1}.$  

We now analyze the stability of the modified Adaptive Algorithm 2. Theorem 3.1 shows that the Adaptive Algorithm 1 has rate of convergence of order (3 − α) and (4 − α) for starting time levels n = 1 and n = 2, respectively. When we compute U₁ on a new time grid from Step 1, it follows from Theorem 3.1 that $\left | \hat {R}(\mathcal {U}(t^{1})) \right |=\mathcal {O}(5-\alpha )$, since there are only J₁ additional node points in new time grid which is generated with the help of ${\Delta } t^{k_{t}}$ and $\varpi _{k_{t}}$. Similarly, when we compute U₂ on new time grid from Step 2, we get $\left | \hat {R}(\mathcal {U}(t^{2})) \right |=\mathcal {O}(5-\alpha )$. Thus, by mathematical induction method, one can easily obtained the stability of upgraded Adaptive Algorithm 2.

Based on developed numerical scheme (3.44) and moving refinement technique, we now present two adaptive algorithms for the approximate solutions of proposed problem (1.1)–(1.3) (Fig. 2):

Fig. 2

Flowchart of the proposed adaptive algorithm

Test Problem 5.1

[49] We consider the 1D problem (1.1)–(1.3) with an exact analytic solution $\mathcal {U}(x,t)=t^{3}\sin \limits (\pi x)$ in the domain Ω = [0,1] × [0,1]. Corresponding forcing term and initial and boundary conditions are:

$$f(x,t)=\pi^{2} t^{3} \sin(\pi x)+\frac{6t^{3-\alpha}\sin(\pi x)}{\Gamma (2-\alpha) ~(6-5\alpha+\alpha^{2})},~\phi(x)=\psi(x)=0,~{\Phi}_{1}(t)={\Phi}_{2}(t)=0.$$

Recently, above problem has been solved in [49] by using finite difference method on uniform mesh and achieved the convergence order $\mathcal {O}(\tau ^{3-\alpha })$ in the time domain. After implementation of proposed high-order adaptive Algorithm 1 and Algorithm 2, the numerical outcomes on non-uniform mesh are described in detail as below:

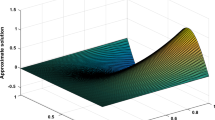
• Exact and numerical solutions obtained by proposed Algorithm 1 for N_x = 100, N_t = 20, and α = 1.2 are given in Figs. 3 and 4, respectively. Good similarity of both the figures ensure that the proposed numerical scheme work effectively.

• To test the absolute errors and convergence orders on a non-uniform mesh concerning $L_{\infty }$ and L₂ discrete error norms in the time domain, allowing N_t to change and fixing N_x = 1000 adequately large to avoid contamination of the spatial errors. Tables 1, 2, and 3 give the results at time T = 1 and $J_{1}=5,~J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10$. These tables clearly show that the adaptive algorithm 2 improve the accuracy of numerical solutions as compare to the numerical solutions obtained by adaptive algorithm 1. Moreover, from Tables 1, 2, and 3 we can conclude that the upgraded adaptive algorithm 2 gets (5 − α)-th order temporal accuracy with respect to $L_{\infty }$ and L₂ discrete error norms, respectively.

• A comparative results is demonstrated in Tables 1 and 2. From the results of both the tables, it can be seen that our adaptive scheme on non-uniform mesh giving far better result than the scheme discussed in [49] on uniform mesh.

• The outcomes of Table 3 verify the stability and accuracy of the proposed adaptive scheme when $\alpha \rightarrow 1$ or $\alpha \rightarrow 2$. We can see that the upgraded adaptive algorithm 2 has (5 − α)-th order accuracy in temporal direction when $\alpha \rightarrow 1$ or $\alpha \rightarrow 2$.

• A similar process is also done in Tables 4 and 5 by using adaptive algorithm 1 for analyze the behavior of numerical solution in spatial domain. The outcomes of both the tables shown that the adaptive numerical scheme has second-order accuracy in spatial direction with respect to $L_{\infty }$ and L₂ discrete error norms, respectively.

• The numerical results obtained in Tables 1–5 for different values of α verify our theoretical findings discussed in Section 4.

Fig. 3

Graph of exact solution of Test Problem 5.1 for N_x = 100, N_t = 20, J₁ = 5, J₂ = 5, and α = 1.2 at different time level without any noisy data

Fig. 4

Graph of numerical solution of Test Problem 5.1 for N_x = 100, N_t = 20, J₁ = 5, J₂ = 5, and α = 1.2 at different time level without any noisy data

Table 1 $\text {L}_{\infty }-$ errors and temporal orders at T = 1, $N_{x}=1000,~J_{1}=5,~J_{2}=5,~J_{N_{t}-1}=10,~J_{N_{t}}=10$, and different values of α for Test Problem 5.1

Table 2 L₂ − errors and temporal orders at T = 1, $N_{x}=1000,~J_{1}=5,~J_{2}=5,~J_{N_{t}-1}=10,~J_{N_{t}}=10$, and different values of α for Test Problem 5.1

Table 3 $\text {L}_{\infty }$ and L₂ − errors and temporal orders with T = 1, $N_{x}=1000,~J_{1}=5,~J_{2}=5,~J_{N_{t}-1}=10,~J_{N_{t}}=10$, and different α for Test Problem 5.1

Table 4 $\text {L}_{\infty }-$ errors and spatial orders with T = 1, N_t = 1000, and different values of α for Test Problem 5.1

Table 5 L₂ − errors and spatial orders with T = 1, N_t = 1000, and different values of α for Test Problem 5.1

Test Problem 5.2

[49] We consider the problem (1.1)

$$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha} \mathcal{U}(x,t)&= {\Delta}^{x} \mathcal{U} + f(x,t),~(x,t)={\Omega}\in[0,1]\times[0,1],~1<\alpha<2, \end{array}$$

with an exact analytic solution $\mathcal {U}(x,t)=t^{3}x^{1+\alpha }(1-x)$. It can be checked that the corresponding initial and boundary conditions are ϕ(x) = ψ(x) = 0 and Φ₁(t) = Φ₂(t) = 0, respectively, and value of forcing term is:

$$f(x,t)=2(1+\alpha)t^{3}x^{\alpha} - \alpha(1+\alpha) t^{3} (1-x) x^{\alpha-1} - \frac{6t^{3-\alpha} (x-1) x^{1+\alpha}}{\Gamma(2-\alpha) ~(6-5\alpha+\alpha^{2})}.$$

This problem has been considered in [49] and solved numerically by finite difference method on uniform mesh. We analyze the behavior of numerical solution of same problem by a newly design adaptive numerical scheme based on finite difference method on a non-uniform mesh. The detail outcomes are pointed as:

• Behavior of exact and numerical solutions for discretization parameter N_x = 100, N_t = 20, J₁ = 5, J₂ = 5, and α = 1.4 are shown in Figs. 5 and 6, respectively. It clearly shows that, the approximate solutions are in good agreement with the exact solutions at each time level.

• To verify the computational performance and convergence order in temporal direction of our adaptive algorithm, first we set up the value of N_x = 1000 in Tables 6 and 7 to ensure that the computational errors in spacial direction are small enough and do not affect the temporal computational errors. After that varying the temporal discretization parameter N_t to observe the $L_{\infty }$ and L₂ errors and convergence order in time domain for different values of α. Results of both the tables shown that the better result obtained from modified adaptive algorithm 2 as compare to the adaptive algorithm 1. Furthermore, we can see that the developed difference scheme on non-uniform mesh has (5 − α)-th order accuracy in time direction.

• Moreover, Tables 6 and 7 demonstrate the comparison of our proposed numerical scheme and the method discussed in [49] with respect to $L_{\infty }$ and L₂ discrete error norms, respectively. From the results of both the tables, one can conclude that the scheme presented in this paper is far superior than the scheme considered in [49].

• Numerical results of our adaptive algorithm 1 for spatial direction are discussed in Tables 8 and 9, respectively. Specifically, we take N_t = 1000 and varying the values of N_x then we get second-order spatial accuracy for different values of α.

• All the numerical results of Tables 6–9 are supported our theoretical results obtained in Section 4.

Fig. 5

Graph of exact solution of Test Problem 5.2 for N_x = 100, N_t = 20, J₁ = 5,J₂ = 5, and α = 1.4 at different time level without any noisy data

Fig. 6

Graph of numerical solution of Test Problem 5.2 for N_x = 100, N_t = 20,J₁ = 5, J₂ = 5, and α = 1.4 at different time level without any noisy data

Table 6 $\text {L}_{\infty }-$ errors and temporal orders at T = 1, $N_{x}=1000,~J_{1}=5,~J_{2}=5,~J_{N_{t}-1}=10,~J_{N_{t}}=10$, and different values of α for Test Problem 5.2

Table 7 L₂ − errors and temporal orders with T = 1, $N_{x}=1000,~J_{1}=5,~J_{2}=5,~J_{N_{t}-1}=10,~J_{N_{t}}=10$, and different α for Test Problem 5.2

Table 8 $\text {L}_{\infty }-$ errors and spatial orders with T = 1, N_t = 1000, and different α for Test Problem 5.2

Table 9 L₂ − errors and spatial orders with T = 1, N_t = 1000, and different α for Test Problem 5.2

Test Problem 5.3

[21, 50] Consider the time fractional wave equation

$$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{3/2} u(x,t)&= {\Delta}^{x} u,~(x,t)={\Omega}\in(0,1]\times(0,1], \end{array}$$

subject to the initial conditions

$$\begin{array}{@{}rcl@{}} u(x,0)=\sin(x), \qquad\qquad u_{t}(x,0)=-\sin(x), \end{array}$$

and boundary conditions

$$\begin{array}{@{}rcl@{}} u(0,t)=0, \qquad\qquad u(1,t)=\sin(1)(E_{3/2,1}(-t^{3/2} ) - tE_{3/2,2}(-t^{3/2})). \end{array}$$

Momani et al. [21] showed that its exact solution is $E_{3/2,1}(-t^{3/2} )\sin \limits (x) - tE_{3/2,2}(-t^{3/2})\sin \limits (x)$, where $E_{{\upbeta }_{1},{\upbeta }_{2}}(z)$ is the two parameters Mittag–Lefller function defined by:

$$E_{{\upbeta}_{1},{\upbeta}_{2}}(z)=\sum\limits_{n=0}^{\infty}\frac{z^{n}}{\Gamma({\upbeta}_{1} n + {\upbeta}_{2})}.$$

Table 10 presents the $L_{\infty }$ and L₂ errors obtained by our proposed adaptive algorithms at time $T=1,~\alpha =1.5,~N_{x}=1000,~J_{1}=5,~J_{2}=5,~J_{N_{t}-1}=10,~J_{N_{t}}=10$ for the Test Problem 5.3. Also, Table 10 illustrates that theoretical results are closed to computational orders in the temporal direction.

Table 10 $\text {L}_{\infty }$ and L₂ − errors and temporal orders at T = 1, $N_{x}=1000,~J_{1}=5,~J_{2}=5,~J_{N_{t}-1}=10,~J_{N_{t}}=10$, and α = 1.5 for Test Problem 5.3

Test Problem 5.4

The considered problem (1.1)

$$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha} \mathcal{U}(x,t)&= {\Delta}^{x} \mathcal{U}(x,t) + f(x,t),~(x,t)={\Omega}\in[0,1]\times[0,1],~1<\alpha<2, \end{array}$$

with an exact analytic solution $\mathcal {U}(x,t)=e^{t}\sin \limits (x)$. The initial and boundary conditions are $\phi (x)=\psi (x)=\sin \limits (x)$ and ${\Phi }_{1}(t)=0,~ {\Phi }_{2}(t)=e^{t}\sin \limits (1)$, respectively, and value of forcing term f(x,t) can be obtained from the exact solution for different choices of α. After implementation of proposed schemes, the numerical outcomes on non-uniform mesh are described in detail as below:

• Outcomes of $L_{\infty }$ and L₂ errors and computational orders for different values of α, discretization parameter $N_{x}=1000,~J_{N_{t}}=J_{N_{t}-1}=10,$ and J₁ = J₂ = 5 are given in Table 11. It clearly shows that the proposed adaptive algorithm 2 achieves (5 − α)-th order accuracy in temporal direction with respect to $L_{\infty }$ and L₂ discrete error norms, respectively.

• To test the behavior of numerical solution and convergence rates in spatial direction, allowing N_x to change and fixing N_t = 1000. Tables 12–13 demonstrate that adaptive algorithm 1 achieve second-order accuracy in spatial direction with respect to $L_{\infty }$ and L₂ discrete error norms, respectively.

• All the numerical results of Tables 11–13 are supported our theoretical results obtained in Section 4.

Table 11 $\text {L}_{\infty }$ and L₂ − errors and temporal orders with T = 1, $N_{x}=1000,~J_{1}=5,~J_{2}=5,~J_{N_{t}-1}=10,~J_{N_{t}}=10$, and different α for Test Problem 5.4

Table 12 $\text {L}_{\infty }-$ errors and spatial orders with T = 1, N_t = 1000, and different α for Test Problem 5.4

Table 13 L₂ − errors and spatial orders with T = 1, N_t = 1000, and different α for Test Problem 5.4

5.1 Numerical stability

In this part, we investigate the numerical stability of our proposed numerical scheme. For this aim, we have added some random noises to the linear source term and given initial data of the problem (1.1)–(1.3) according as [51].

In the above Test Problems 5.1 and 5.2, initial data and source term without any noisy inputs are represented as ϕ(x), ψ(x), and f(x,t) respectively; while noisy initial data and source terms are denoted by ϕ^𝜖(x), ψ^𝜖(x), and f^𝜖(x,t), respectively. The noisy profiles ϕ^𝜖(x), ψ^𝜖(x), and f^𝜖(x,t) are obtained by introducing a random noise 𝜖 to f(x,t), ϕ(x), and ψ(x), respectively. To control the upper limit of the input noises, we have used two parameters m and δ_i, where $m\in \mathbb {R}^{+}$ is adjusted according to the test problems and δ_i ∈ [− 1,1] such that $\phi ^{\epsilon }(x^{k_{x}})=\phi (x^{k_{x}})+\epsilon \delta _{i},$ $\psi ^{\epsilon }(x^{k_{x}})=\psi (x^{k_{x}})+\epsilon \delta _{i}$, and $f^{\epsilon }(x^{k_{x}},\text {T})= f(x^{k_{x}},\text {T}) + \epsilon \delta _{i},$ where $x^{k_{x}}=k_{x} \hslash ,~k_{x}=0,\dots , N^{\prime }\hslash$, $N^{\prime }\hslash =\text {L}$, and $\displaystyle \max \limits _{0\leq k_{x} \leq N^{\prime }} \left | \phi ^{\epsilon }(x^{k_{x}}) - \phi (x^{k_{x}}) \right | \leq \epsilon$, $\displaystyle \max \limits _{0\leq k_{x} \leq N^{\prime }} \left | \psi ^{\epsilon }(x^{k_{x}}) - \psi (x^{k_{x}}) \right | \leq \epsilon$, and $\displaystyle \max \limits _{0\leq k_{x} \leq N^{\prime }} \left | f^{\epsilon }(x^{k_{x}}, \text {T}) - f(x^{k_{x}}, \text {T}) \right | \leq \epsilon$.

In order to demonstrate the efficiency and numerical stability of the schemes, we have imposed two different kind of random noises, namely, 𝜖_i as 𝜖₁ = 0 and $\epsilon _{2}= m \% ~\text {of} ~\sigma _{N^{\prime }}$, where $\sigma _{N^{\prime }}$ are average deviation given in (5.2) for j = 2 case.

The point-wise absolute errors are evaluated by

$$\left| \mathcal{U}- \bar{\mathcal{U}} \right| = \left| \mathcal{U}(x^{k_{x}},t^{k_{t}}) - \bar{\mathcal{U}}_{k_{t}}^{k_{x}} \right|,~k_{x}\in\mathbb{Z}_{[0,N_{x}]},~ k_{t}\in\mathbb{Z}_{[0,N_{t}]}.$$

(5.3)

Remark 5.1

In all figures given below ${u^{i}_{j}},~{U^{i}_{j}}$ and ${E^{i}_{j}},~i=1,\dots ,3;~j=1,\dots ,9,$ represent the exact solutions, approximate solutions, and absolute errors at various time level T, respectively.

For Test Problem 5.1

Following facts about Figs. 7, 8, 9, 10, and 11 that characterize the numerical stability of the Test Problem 5.1 should be noticed:

• For labeling the graph in Fig. 7, we scale the graph as ${u^{1}_{j}}=10^{-2} \times \mathcal {U}(x^{k_{x}},\text {T}) + 0.0(j-1),~ j=1, \dots , 9;~u^{2}_{j-9}=3\times 10^{-2} \times \mathcal {U}(x^{k_{x}},\text {T}) + 0.0(j-10),~j=10,\dots ,18;~u^{3}_{j-18}=50\times 10^{-2} \times \mathcal {U}(x^{k_{x}},\text {T}) + 0.0(j-19),~j=19,\dots ,27,$ and $k_{x}=0,\dots ,N_{x}.$ In similar way, we label the graph in Fig. 8 as ${U^{1}_{j}}=10^{-2} \times \bar {\mathcal {U}}(x^{k_{x}},\text {T}) + 0.0(j-1),~ j=1, \dots , 9;~U^{2}_{j-9}=3\times 10^{-2} \times \bar {\mathcal {U}}(x^{k_{x}},\text {T}) + 0.0(j-10),~j=10,\dots ,18;~U^{3}_{j-18}=50\times 10^{-2} \times \bar {\mathcal {U}}(x^{k_{x}},\text {T}) + 0.0(j-19),~j=19,\dots ,27,$ and $k_{x}=0,\dots ,N_{x}.$ To label the graph in Fig. 9, we multiply ${E^{2}_{j}}=4\times \left | \mathcal {U}- \bar {\mathcal {U}} \right |$ and ${E^{3}_{j}}=10^{2}\times \left | \mathcal {U}- \bar {\mathcal {U}} \right |,~j=1,\dots ,9.$

• Figures 7 and 8 show a good similarity between exact and approximate solutions of Test Problem 5.1 for different values of α at different time level T when we fixed the discretization parameter $N_{x}=N_{t}=100,~J_{1}=J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10,$ and add a noise 𝜖₁ in given initial data and linear source term.

• Figure 7 shows the absolute errors between exact and approximate solution obtained by the proposed adaptive numerical algorithm for the noise 𝜖₁ in initial data and linear source term when we fix the discretization parameter $N_{x}=N_{t}=100,~J_{1}=J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10$.

• For $N^{\prime }=100, ~\alpha =1.2,~ N_{x}=100,~N_{t}=20,~J_{1}=J_{2}=5,$ and m = 20, the absolute errors between exact and approximate solutions at different time levels are shown in Fig. 10 when we force noise 𝜖₂ in linear source term.

• Figure 11 reflects the absolute errors between exact and approximate solutions when we add noise 𝜖₂ in both initial data and linear source term for the parameters $N^{\prime }=100, ~\alpha =1.2,~ N_{x}=100,~N_{t}=20,~J_{1}=J_{2}=5,$ and m = 20.

• From the error Figs. 7, 8, 9, 10, and 11 it is evident that the effect of noises 𝜖₁ and 𝜖₂ in given initial data and source term are almost negligible and hence it can be concluded that the proposed method is numerically stable.

Fig. 7

Graph of exact solutions of Test Problem 5.1 for different value of α at different time levels T with noise 𝜖₁ in initial data and linear source term when $N_{x}=N_{t}=100,~J_{1}=J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10$

Fig. 8

Graph of numerical solutions of Test Problem 5.1 for different value of α at different time levels T with noise 𝜖₁ in initial data and linear source term when $N_{x}=N_{t}=100,~J_{1}=J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10$

Fig. 9

Graph of absolute errors of Test Problem 5.1 without any noisy data for different values of α at different time levels T with noise 𝜖₁ in initial data and linear source term when $N_{x}=N_{t}=100,~J_{1}=J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10$

Fig. 10

Graph of absolute errors of Test Problem 5.1 for N_x = 100, N_t = 20, J₁ = J₂ = 5, and α = 1.2 at different time levels with noisy data in linear source term

Fig. 11

Graph of absolute errors of Test Problem 5.1 for N_x = 100, N_t = 20, J₁ = J₂ = 5, and α = 1.2 at different time levels with noisy inputs in initial data and linear source term

For Test Problem 5.2

Following facts about Figs. 12, 13, 14, 15, and 16 that characterize the numerical stability of the Test Problem 5.2 should be noticed:

• For labeling the graph in Fig. 12, we scale the graph as ${u^{2}_{j}}=3 \times \mathcal {U}(x^{k_{x}},\text {T});~{u^{3}_{j}}=50\times \mathcal {U}(x^{k_{x}},\text {T}),~j=1,\dots ,9,$ and $k_{x}=0,\dots ,N_{x}.$ In similar way, we label the graph in Fig. 13 as ${U^{2}_{j}}=3\times \bar {\mathcal {U}}(x^{k_{x}},\text {T});~{U^{3}_{j}}=50\times \bar {\mathcal {U}}(x^{k_{x}},\text {T}),~j=1,\dots ,9,$ and $k_{x}=0,\dots ,N_{x}.$ To label the graph in Fig. 14, we multiply ${E^{2}_{j}}=5\times \left | \mathcal {U}- \bar {\mathcal {U}} \right |$ and ${E^{3}_{j}}=10^{2}\times \left | \mathcal {U}- \bar {\mathcal {U}} \right |,~j=1,\dots ,9.$

• Figures 12, 13 show a good similarity between exact and approximate solutions of Test Problem 5.2 for different values of α at different time level T when we fixed the discretization parameter $N_{x}=N_{t}=100,~J_{1}=J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10,$ and add a noise 𝜖₁ in given initial data and linear source term.

• Figure 14 shows the absolute errors between exact and approximate solution obtained by the proposed adaptive numerical algorithm for the noise 𝜖₁ in initial data and linear source term when we fix the discretization parameter $N_{x}=N_{t}=100,~J_{1}=J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10$.

• For $N^{\prime }=100, ~\alpha =1.4,~ N_{x}=100,~N_{t}=20,~J_{1}=J_{2}=5,$ and m = 40, the absolute errors between exact and approximate solutions at different time levels are shown in Fig. 15 when we force noise 𝜖₂ in linear source term.

• Figure 16 reflects the absolute errors between exact and approximate solutions when we add noise 𝜖₂ in both initial data and linear source term for the parameters $N^{\prime }=100, ~\alpha =1.4,~ N_{x}=100,~N_{t}=20,~J_{1}=J_{2}=5,$ and m = 40.

• From the error Figs. 12, 13, 14, 15, and 16, it is evident that the effect of noises 𝜖₁ and 𝜖₂ in given initial data and source term are almost negligible and hence it can be concluded that the proposed adaptive numerical scheme is numerically stable.

Fig. 12

Graph of exact solutions of Test Problem 5.2 for different values of α at different time levels T when $N_{x}=N_{t}=100,~J_{1}=J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10$

Fig. 13

Graph of numerical solutions of Test Problem 5.2 for different values of α at different time levels T when $N_{x}=N_{t}=100,~J_{1}=J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10$

Fig. 14

Graph of absolute errors of Test Problem 5.2 without any noisy data for different values of α at different time levels T when $N_{x}=N_{t}=100,~J_{1}=J_{2}=5,~J_{N_{t}-1}=J_{N_{t}}=10$

Fig. 15

Graph of absolute errors of Test Problem 5.2 for N_x = 100, N_t = 20, J₁ = J₂ = 5, and α = 1.4 at different time levels with noisy data in linear source term

Fig. 16

Graph of absolute errors of Test Problem 5.2 for N_x = 100, N_t = 20, J₁ = J₂ = 5, and α = 1.4 at different time levels with noisy inputs in initial data and linear source term both

6 Concluding remarks and future work

Most of the existing numerical schemes for the time-fractional Caputo derivative ${~}^{\mathrm {C}}_{0}\mathcal {D}_{t}^{\alpha }$ with order α ∈ (1,2) have convergence rate (3 − α) and based on uniform mesh. There are very less study on numerical methods which have convergence rate more than (3 − α), and especially for the case of non-uniform mesh as compare to the uniform mesh till now. So develop some high convergence rate schemes based on the non-uniform mesh are really a challenging and interesting task. This investigation proposes a new convergent approximation for the Caputo fractional derivative with convergence rate (5 − α) on a non-uniform mesh. Using this approximation of Caputo derivative in the time direction and second-order central difference discretization in the spatial direction, we proposed a high-order adaptive numerical algorithm to solve the TFDWEs numerically. Setup of the designed algorithm is such that the algorithm changes its behavior automatically according to the value of α. A detailed analysis of the local truncation error of the scheme is given in Theorem 3.1, and stability and convergence analysis of the numerical methods are given in Theorem 4.2 and 4.3, respectively. Optimal error bounds of the numerical methods show that the proposed scheme has (5 − α)-th order accuracy in the time direction and second-order accuracy in the spatial direction. To improve the temporal error accuracy of the numerical solutions, we assemble a moving mesh technique with our proposed scheme. Moreover, the numerical stability of the proposed scheme is verified by imposing some random noises in the initial data and non-homogeneous source term (see: Figs. 7, 8, 9, 10, 11, 12, 13, 14, 15, and 16). From error tables, we can see that our proposed numerical scheme based on non-uniform mesh gives better convergence rate as compare to the numerical scheme based on uniform mesh given in [49] (see: Tables 1–3, 6–7, 10–11). Finally, our derived numerical method has the advantage over previous works that the rate of convergence is far better as compared to the numerical methods based on uniform mesh.

6.1 Future work

Now, we proposed some future works for the readers which is based on the scheme presented in this manuscript:

• Extend the developed adaptive algorithm for more complex boundary conditions [52]:

  $$\begin{array}{@{}rcl@{}} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha} u(x,t)- {\Delta}^{x} u(x,t) = h(t)f(x), ~~x\in {\Omega},~t\in(0,T) \end{array}$$

  (6.1)

  with initial and boundary conditions:

  $$\begin{array}{@{}rcl@{}} u(x,0)&&=u_{0}(x),~~x\in{\Omega},\\ u_{t}(x,0)&&=v_{0}(x),~~x\in{\Omega},\\ u(x,t)&&=0,~~~(x,t)\in{\Gamma}_{D}\times(0,T),\\ -{~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha} u(x,t)-\triangledown u(x,t).{\nu}&&=\sigma(x,t) ,~(x,t)\in{\Gamma}_{D}\times(0,T), \end{array}$$

  (6.2)

  where $\alpha \in (1,2),~{\Omega }\subset \mathbb {R}^{d}$ is bounded with the Lipschitz boundary Γ, T > 0, ${\Gamma }_{D}\cap {\Gamma }_{N}=\emptyset ,~\bar {{\Gamma }_{D}}\cup \bar {{\Gamma }_{N}}={\Gamma },~|{\Gamma }_{D}|>0$, ν is a outer normal vector on Γ, and Γ_N is the dynamical boundary conditions.

• Extension of the proposed method for non-linear problem in higher dimension. Consider the problem [53]:

  $$\begin{array}{@{}rcl@{}} \sum\limits_{k=1}^{K} {~}^{\mathrm{C}}_{0}\mathcal{D}_{t}^{\alpha_{k}} u(x,y,t)&=\sum\limits_{s=1}^{S} \left(\frac{\partial^{{\upbeta}_{s}}}{\partial|x|^{{\upbeta}_{s}}}+ \frac{\partial^{{\upbeta}_{s}}}{\partial|y|^{{\upbeta}_{s}}}\right) u(x,y,t)+f(x,y,t,u(x,y,t)), \end{array}$$

  (6.3)

  with initial and boundary conditions:

  $$\begin{array}{@{}rcl@{}} u(x,y,0)=\phi(x),~~u_{t}(x,y,0)={\Phi}(x),~~(x,y)\in\bar{\Omega}, \end{array}$$

  (6.4)
  $$\begin{array}{@{}rcl@{}} u(x,y,t)=0,~(x,y)\in\partial{\Omega},~0<t\leq T, \end{array}$$

  (6.5)

  where, Ω = (0,L_x) × (0,L_y), ∂Ω, and $\bar {\Omega }$ are the boundary and closure of Ω, respectively. f(x,y,t,u) is a nonlinear function of unknown u, and satisfies the Lipschitz condition with respect to u. ϕ(x,y) and Φ(x,y) are known sufficiently smooth functions. Furthermore, K and S are two integers, $1<\alpha _{K}\leq \alpha _{K-1}\leq \dots \leq \alpha _{2}\leq \alpha _{1}<2$ and $1<{\upbeta }_{S}\leq {\upbeta }_{S-1}\leq \dots \leq {\upbeta }_{2}\leq {\upbeta }_{1}<2$.

• Analysis of the derived scheme proposed for sufficiently smooth solution. Extension of the current work for non-smooth solution will be a work for readers.