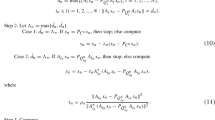Self-adaptive algorithms for solving split feasibility problem with multiple output sets

Abstract

In this paper, we study the split feasibility problem with multiple output sets in Hilbert spaces. For solving the aforementioned problem, we propose two new self-adaptive relaxed CQ algorithms which involve computing of projections onto half-spaces instead of computing onto the closed convex sets, and it does not require calculating the operator norm. We establish a weak and a strong convergence theorems for the proposed algorithms. We apply the new results to solve some other problems. Finally, we present some numerical examples to show the efficiency and accuracy of our algorithm compared to some existing results. Our results extend and improve some existing methods in the literature.

1 Introduction

Let H₁ and H₂ be two real Hilbert spaces. Let C and Q be nonempty, closed, and convex subsets of H₁ and H₂, respectively. Let A : H₁ → H₂ be a nonzero bounded linear operator and let A^∗ : H₂ → H₁ be its adjoint. The split feasibility problem (SFP) is formulated to find a point x^∗∈ H₁ satisfying

$$ x^{*}\in C \text{ such that } Ax^{*}\in Q. $$

(1)

The SFP was first introduced in 1994 by Censor and Elfving [1] in finite-dimensional Hilbert spaces for modeling certain inverse problems and has received a great attention since then. This is because the SFP can be used to model several inverse problems arising from, for example, phase retrievals and in medical image reconstruction [1, 2], intensity-modulated radiation therapy (IMRT) [3,4,5], gene regulatory network inference [6], just to mention but few, for more details one can, see, e.g., [7,8,9,10,11,12,13,14] and the references therein. In the span of the last twenty five years, focusing on real world applications, several iterative methods for solving the SFP (1) have been introduced and analyzed. Among them, Byrne [2, 9] introduced the first applicable and most celebrated method called the well-known CQ-algorithm as follows: for x₀ ∈ H₁;

$$ x_{n+1}:=P_{C}(x_{n}-\tau_{n}A^{*}(I-P_{Q})Ax_{n})), $$

(2)

where P_C and P_Q are the metric projections onto C and Q, respectively, and the stepsize $\tau _{n}\in \left (0, \frac {2}{\|A\|^{2}}\right )$ where ∥A∥² is the spectral radius of the matrix A^∗A.

The CQ algorithm proposed by Byrne [2, 9], requires the computation of metric projection onto the sets C and Q (in some cases, it is impossible or is too expensive to exactly compute the metric projection). In addition, the determination of the stepsize depends on the operator norm which computation (or at least estimate) is not easy task. In practical applications, the sets C and Q are usually the level sets of convex functions which are given by

$$ C:=\{x\in H_{1}:c(x)\leq 0\} \text{ and } Q=\{y\in H_{2}:q(y)\leq 0\}, $$

(3)

where $c:H_{1}\rightarrow \mathbb {R}$ and $q:H_{2}\rightarrow \mathbb {R}$ are convex and subdifferentiable functions on H₁ and H₂, respectively, and that subdifferentials ∂c(x) and ∂q(y) of c and q, respectively, are bounded operators (i.e., bounded on bounded sets).

Later, in 2004, Yang [12] generalized the CQ method to the so-called relaxed CQ algorithm, needing computation of the metric projection onto (relaxed sets) half-spacesC_n and Q_n, where

$$ C_{n}:=\{x\in H_{1}:c(x_{n})\leq\langle\xi_{n},x_{n}-x\rangle\}, $$

(4)

where ξ_n ∈ ∂c(x_n) and

$$ Q_{n}:=\{y\in H_{2}:q(Ax_{n})\leq\langle\eta_{n},Ax_{n}-y\rangle\}, $$

(5)

where η_n ∈ ∂q(Ax_n). It is easy to see that $C\subseteq C_{n}$ and $Q\subseteq Q_{n}$ for all n ≥ 1. Moreover, it is known that projections onto half-spaces C_n and Q_n have closed forms. In what follows, define

$$ f_{n}(x_{n}):=\frac{1}{2}\|(I-P_{Q_{n}})Ax_{n}\|^{2}, $$

(6)

where Q_n is given as in (5). f_n is a convex and differentiable function with its gradient ∇f_n defined by

$$ \nabla f_{n}(x_{n}):=A^{*}(I-P_{Q_{n}})Ax_{n}. $$

(7)

More precisely, Yang [12] introduced the following relaxed CQ algorithm for solving the SFP (1) in a finite-dimensional Hilbert space: for x₀ ∈ H₁;

$$ x_{n+1}:=P_{C_{n}}(x_{n}-\tau_{n}\nabla f_{n}(x_{n})), $$

(8)

where $\tau _{n}\in \left (0, \frac {2}{\|A\|^{2}}\right )$. Since $P_{C_{n}}$ and $P_{Q_{n}}$ are easily calculated, this method appears to be very practical. However, to compute the norm of A turns out to be complicated and costly. To overcome this difficulty, in 2012, López et al. [15] introduced a relaxed CQ algorithm for solving the SFP (1) with a new adaptive way of determining the stepsize sequence τ_n defined as follows:

$$ \tau_{n}:=\frac{\rho_{n}f_{n}(x_{n})}{\|\nabla f_{n}(x_{n})\|^{2}}, $$

(9)

where ρ_n ∈ (0,4),∀n ≥ 1 such that $\liminf _{n\rightarrow \infty }\rho _{n}(4-\rho _{n})>0$. It was proved that the sequence {x_n} generated by (8) with τ_n defined by (9) converges weakly to a solution of the SFP (1). That is, their algorithm has only weak convergence in the framework of infinite-dimensional Hilbert spaces. But, in the infinite-dimensional spaces norm (strong) convergence is more desirable than the weak convergence for solving our problems. In this regard, many authors proposed algorithms that generate a sequence {x_n}, converges strongly to a point in the solution set of the SFP (1), see, e.g., [15,16,17,18,19]. In particular, López et al. [15] proposed a Halpern's iterative scheme for solving the SFP (1) in the setting of infinite-dimensional Hilbert spaces as follows: for u,x₀ ∈ H₁;

$$ x_{n+1}:=\alpha_{n}u+(1-\alpha_{n})P_{C_n}\left( x_{n}-\tau_{n}\nabla f_{n}(x_{n})\right), \forall n\geq 1, $$

(10)

where {α_n}⊂ (0,1), and ∇f_n(x_n) and τ_n are given by (7) and (9), respectively. In 2013, He et al. [16] also introduced a new relaxed CQ algorithm for solving the SFP (1) such that strong convergence is guaranteed in infinite-dimensional Hilbert space. Their algorithm generates a sequence {x_n} by the following manner: for u,x₀ ∈ H₁;

$$ x_{n+1}:= P_{C_{n}}\left( \alpha_{n}u+(1-\alpha_{n})\big(x_{n}-\tau_{n}\nabla g_{n}(x_{n})\big)\right), $$

(11)

where C_n and τ_n are given as in (4) and (9), respectively, and {α_n}⊂ (0,1) such that $\lim _{n\rightarrow \infty } \alpha _{n}=0$ and $\sum _{n=1}^{\infty }\alpha _{n}=+\infty$. Under some standard conditions, it was shown that the sequence {x_n} generated by (10) and (11) converges strongly to p^∗ = P_Ω(u) ∈Ω = {p ∈ H₁ : p ∈ C such that Ap ∈ Q} of the SFP (1). Both schemes (10) and (11) do not require any prior knowledge of the operator norm and compute the projections onto the half-spaces C_n and Q_n (which have closed-form), and thus both are easily implementable.

Some generalizations of the SFP have also been studied by many authors. We mention, for instance, the multiple-sets SFP (MSSFP) [3, 20,21,22,23,24,25,26,27,28,29,30,31,32,33,34], the split common fixed point problem (SFPP) [35, 36], the split variational inequality problem (SVIP) [37], and the split common null point problem (SCNPP) [38,39,40,41,42].

Very recently, Reich et al. [43] considered and studied the following split feasibility problem with multiple output sets in real Hilbert spaces.

Let $H, H_{i}, i=1, 2, \dots , N,$ be real Hilbert spaces and let $A_{i}: H\to H_{i}, i=1, 2, \dots , N,$ be bounded linear operators. Let C and $Q_{i}, i=1, 2, \dots , N,$ be nonempty, closed, and convex subsets of H and $H_{i}, i=1, 2, \dots , N$, respectively. Given H,H_i, and A_i as above, the split feasibility problem with multiple output sets (SFPMOS, for short) is to find an element p^∗ such that

$$ p^{*}\in{\Omega}:=C\cap \left( \cap_{i=1}^{N} A^{-1}_{i}(Q_{i})\right) \ne\emptyset. $$

(12)

That is p^∗∈ C and A_ip^∗∈ Q_i for each $i=1, 2, \dots , N$.

In 2020, Reich et al. [43] introduced the following two methods for solving the SFPMOS (12).

For any given points, x₀,y₀ ∈ H, {x_n}, and {y_n} are sequences generated by

$$ x_{n+1}:=P_{C}\left( x_{n}-\lambda_{n}{\sum}_{i=1}^{N}A^{*}_{i}(I-P_{Q_{i}})A_{i}x_{n}\right), $$

(13)

$$ y_{n+1}:=\alpha_{n}f(y_{n})+(1-\alpha_{n}) P_{C}\left( y_{n}-\lambda_{n}{\sum}_{i=1}^{N}A^{*}_{i}(I-P_{Q_{i}})A_{i}y_{n}\right), $$

(14)

where f : C → C is a strict contraction mapping of H into itself with the contraction constant $\theta \in [0, 1),~\lambda _{n}\subset (0, \infty )$ and {α_n}⊂ (0,1). It was proved that if the sequence {λ_n} satisfies the condition:

$$0<a\leq\lambda_{n}\leq b<\frac{2}{N\max_{i=1, 2, \dots, N}\{\|A_{i}\|^{2}\}}$$

for all n ≥ 1, then the sequence {x_n} generated by (13) converges weakly to a solution point p^∗∈Ω of the SFPMOS (12). Furthermore, if the sequence {α_n} satisfies the conditions:

$$ \lim_{n\rightarrow \infty}\alpha_{n}=0 \text{ ~ and ~} {\sum}_{n=1}^{\infty}\alpha_{n}=\infty, $$

then the sequence {y_n} generated by (14) converges strongly to a solution point p^∗∈Ω of the SFPMOS (12), which is a unique solution of the variational inequality

$$ \langle (I-f)p^{*}, x-p^{*} \rangle \geq 0~\forall x\in{\Omega}. $$

An important observation here is that the iterative methods (Scheme (13) and Scheme (14)) introduced by Reich et al. [43] requires to compute the metric projections on to the sets C and Q_i. Moreover, it needs to compute the operator norm. Due to this reason, the following question naturally arises. Question: Can we design two new iterative algorithms (a weakly convergent and strongly convergent methods, different from Scheme (13) and Scheme (14)) for solving the SFPMOS (12) which mainly involves a self-adaptive step-size and requires to compute the projections onto half-spaces so that the algorithm is easily implementable?.

We have a positive answer for the above question which is motivated by the iterative schemes (13) and (14) proposed by Reich et al. [43] for solving the SFPMOS (12), the Halpern’s-type iterative schemes (10) and (11) proposed by López et al. [15] and He et al. [16], respectively, to solve the SFP (1). In this paper, we propose two new self-adaptive relaxed CQ algorithms for solving the SFPMOS (12) in infinite-dimensional Hilbert spaces.

In the next section, we recall some necessary tools which are used in establishing our main results. In Section 3, we propose self-adaptive relaxed CQ algorithms for solving the SFPMOS (12), and we establish and analyze weak and strong convergence theorems for the proposed algorithms. In the same section, we also present some newly derived results for solving the SFP (1). In Section 4, we present the application of our methods to solve the generalized split feasibility problem (another generalization of the SFP). Finally, in the last section, we provide several numerical examples to illustrate the implementation of our algorithms compared to some existing results.

2 Preliminaries

In this section, we recall some definitions and basic results which are needed in the sequel. Let H be a real Hilbert space with the inner product 〈.,.〉, and induced norm ∥.∥. Let I stands for the identity operator on H. Let the symbols “$\rightharpoonup$” and “→”, denote the weak and strong convergence, respectively. For any sequence {x_n}⊂ H, $\omega _{w}(x_{n})=\{x\in H:\exists \{x_{n_{k}}\}\subset \{x_{n}\} \text { such that } x_{n_{k}}\rightharpoonup x\}$ denotes the weak w-limit set of {x_n}.

Definition 1

([44]) Let C be a nonempty closed convex subset of H. Let $T:C\rightarrow H$ be a given operator. Then, T is called

(1):

Lipschitz continuous with constant λ > 0 on C if

$$ \|Tx-Ty\|\leq \lambda\|x-y\|,\forall x,y \in C; $$

(15)

(2):

nonexpansive on C if

$$ \|Tx-Ty\|\leq\|x-y\|, \forall x,y \in C; $$

(16)

(3):

firmly nonexpansive on C if

$$ \|Tx-Ty\|^{2}\leq \|x-y\|^{2}-||(I-T)x-(I-T)y\|^{2}, \forall x,y\in C , $$

(17)

which is equivalent to

$$ \|Tx-Ty\|^{2}\leq \langle Tx-Ty,x-y\rangle, \forall x,y\in C; $$

(18)

(4):

averaged if there exists a number λ ∈ (0,1) and a nonexpansive operator $F:C\rightarrow H$ such that

$$ T=\lambda F+(1-\lambda)I, \text{ where } I \text{ is the identity operator}. $$

(19)

In this case, we say that T is λ-averaged.

Definition 2

([44]) Let C ⊂ H be a nonempty, closed and convex set. For every element x ∈ H, there exists a unique nearest point in C, denoted by P_C(x) such that

$$ \|x-P_{C}(x)\|=\min\{\|x-y\|:y\in{C}\}. $$

(20)

The operator P_C (mapping $P_{C} : H\rightarrow {C}$) is called a metric projection of H onto C and it has the following well-known properties.

Lemma 1

([44, 45]) Let C ⊂ H be a nonempty, closed and convex set. Then, the following assertions hold for any x,y ∈ H and z ∈ C :

(1):

〈x − P_C(x),z − P_C(x)〉≤ 0;

(2):

∥P_C(x) − P_C(y)∥≤∥x − y∥;

(3):

∥P_C(x) − P_C(y)∥² ≤〈P_C(x) − P_C(y),x − y〉;

(4):

∥P_C(x) − z∥² ≤∥x − z∥² −∥x − P_C(x)∥².

We see from Lemma 1 that the metric projection mapping is firmly nonexpansive and nonexpansive. Moreover, it is not hard to show that I − P_C is also firmly nonexpansive and nonexpansive.

Lemma 2

For all x,y ∈ H and for all $\alpha \in \mathbb {R}$, we have

• ∥x + y∥² ≤∥x∥² + 2〈y, x + y〉;

• ∥x + y∥² = ∥x∥² + ∥y∥² + 2〈x, y〉;

• $\langle x,y\rangle =\frac {1}{2}\|x\|^{2}+\frac {1}{2}\|y\|^{2}-\frac {1}{2}\|x-y\|^{2};$

• ∥αx + (1 − α)y∥² = α∥x∥² + (1 − α)∥y∥² − α(1 − α)∥x − y∥².

Fejér-monotone sequences are very useful in the analysis of optimization iterative algorithms.

Definition 3

([44]) Let C be a nonempty subset of H and let {x_n} be a sequence in H. Then, {x_n} is Fejér monotone with respect to C if

$$ \|x_{n+1}-z\|\leq \|x_{n}-z\|,~\forall z\in C. $$

It is easy to see that a Fejér monotone sequence {x_n} is bounded and the limit $\lim _{n\rightarrow \infty }\|x_{n}-z\|$ exists.

Lemma 3

(Demiclosedness principle of nonexpansive mappings [44]) Let C be a closed convex subset of H, T : C → C be a nonexpansive mapping with nonempty fixed point sets. If {x_n} is a sequence in C converging weakly to x and {(I − T)x_n} converges strongly to y, then (I − T)x = y. In particular, if y = 0, then x = Tx.

Lemma 4

([44, 46, 47]) Let C be a nonempty, closed, and convex subset of a real Hilbert space H and let {x_n} be a sequence in H satisfying the properties:

(1):

$\lim _{n\rightarrow \infty }\|x_{n}-x^{*}\|$ exists for every x^∗∈ C;

(2):

ω_w(x_n) ⊂ C.

Then, there exists a point $\hat {x}\in C$ such that {x_n} converges weakly to $\hat {x}$.

Definition 4

Let $f: H\rightarrow \mathbb {R}$ be a function and λ ∈ [0,1]. Then,

(1):

f is convex if

$$ f(\lambda x+(1-\lambda)y)\leq \lambda f(x)+(1-\lambda)f(y), \forall x,y\in H. $$

(2):

A vector ξ ∈ H is a subgradient of f at a point x if

$$ f(y)\geq f(x)+\langle \xi, y-x\rangle,~\forall y\in H. $$

(3):

The set of all subgradients of a convex function $f:H\rightarrow \mathbb {R}$ at x ∈ H, denoted by ∂f(x), is called the subdifferential of f, and is defined by

$$ \partial f(x)=\{\xi\in H:f(y)\geq f(x)+\langle \xi,y-x \rangle, ~\text{for each } y\in H\}. $$

(4):

If ∂f(x)≠∅, f is said to be subdifferentiable at x. If the function f is continuously differentiable then ∂f(x) = {∇f(x)}. The convex function is subdifferentiable everywhere [44].

(5):

f is called weakly lower semicontinuous at x₀ if for a sequence {x_n} weakly converging to x₀ one has

$$ f(x_{0})\leq \liminf_{n\rightarrow\infty}f(x_{n}). $$

A function which is weakly lower semicontinuous at each point of H is called weakly lower semicontinuous on H.

Lemma 5

([48]) Let H₁ and H₂ be real Hilbert spaces and $f:H_{1}\rightarrow \mathbb {R}$ is given by $f(x)=\frac {1}{2}\|(I-P_{Q})Ax\|^{2}$ where Q is a nonempty, closed convex subset of H₂ and $A:H_{1}\rightarrow H_{2}$ be a bounded linear operator. Then, the following assertions hold:

(1):

f is convex and differentiable;

(2):

f is weakly lower semicontinuous on H₁;

(3):

∇f(x) = A^∗(I − P_Q)Ax, for x ∈ H₁;

(4):

∇f is ∥A∥²-Lipschitz, i.e., ∥∇f(x) −∇f(y)∥≤∥A∥²∥x − y∥,∀x,y ∈ H₁.

Lemma 6

([49]) Let {Λ_n} be a sequence of real numbers that does not decrease at infinity. Also consider the sequence of integers $\{\varphi (n)\}_{n\geq n_{0}}$ defined by

$$ \varphi(n)=\max\{m\in\mathbb{N}:m\leq n,{\Lambda}_{m}\leq {\Lambda}_{m+1}\}. $$

Then, $\{\varphi (n)\}_{n\geq n_{0}}$ is a nondecreasing sequence verifying $\lim _{n\rightarrow \infty }\varphi (n)=\infty$, and for all n ≥ n₀, the following two estimates hold:

$$ {\Lambda}_{\varphi(n)}\leq {\Lambda}_{\varphi(n)+1} \text{ and }{\Lambda}_{n}\leq {\Lambda}_{\varphi(n)+1}. $$

Lemma 7

([50]) Let {s_n} be a sequence of nonnegative real numbers satisfying the following relation:

$$ s_{n+1}\leq (1-{\varrho}_{n})s_{n}+{\varrho}_{n}\mu_{n}+\theta_{n}, n\geq 1, $$

where {ϱ_n}, {μ_n} and {𝜃_n} satisfying the conditions:

(1):

{ϱ_n}⊂ [0,1], ${\sum }_{n=1}^{\infty }{\varrho }_{n}=\infty ;$

(2):

$\limsup _{n\rightarrow \infty }\mu _{n}\leq 0;$

(3):

𝜃_n ≥ 0, ${\sum }_{n=1}^{\infty }\theta _{n}<\infty$.

Then, $\lim _{n\rightarrow \infty }s_{n}=0$.

3 The iterative algorithms for solving SFPMOS

In this section, we propose new self-adaptive relaxed iterative methods for solving the SFPMOS (12) in the infinite-dimensional Hilbert spaces, and we prove a weak and strong convergence theorems of the proposed methods.

The relaxed projection methods use metric projections onto half-spaces instead of projections onto the original closed convex sets. In what follows, we consider a general case of the SFPMOS (12), where the nonempty, closed and convex sets C and $Q_{i}(i=1, 2, \dots , N)$ are given by level sets of convex functions defined as follows:

$$ C:=\{x\in H:c(x)\leq 0\} \text{ and } Q_{i}:=\{y\in H_{i}:q_{i}(y)\leq 0\} $$

(21)

where, $c:H\rightarrow \mathbb {R}$ and $q_{i}:H_{i}\rightarrow \mathbb {R}$, $i=1, 2, \dots , N$ are lower semicontinuous convex functions. We assume that both c and each q_i are subdifferentiable on H and H_i, respectively, with subdifferential ∂c and ∂q_i, respectively. Moreover, assume that for any x ∈ H a subgradient ξ ∈ ∂c(x) can be calculated, and for any y ∈ H_i and for each $i\in \{1, 2, \dots , N\}$, a subgradient η_i ∈ ∂q_i(y) can be calculated. Again, assume that both ∂c and $\partial q_{i}(i=1, 2, \dots , N)$ are bounded operators (i.e., bounded on bounded sets). The subdifferentials ∂c and ∂q_i are defined by

$$ \partial c(x):=\{\xi\in H:c(z)\geq c(x)+\langle \xi,z-x \rangle, ~\forall z\in H\} $$

for all x ∈ C and

$$ \partial q_{i}(y):=\{\eta_{i}\in H_{i}:q_{i}(u)\geq q_{i}(y)+\langle \eta_{i},u-y \rangle, ~\forall u\in H_{i}\} $$

for all y ∈ Q_i, $i=1, 2, \dots , N$.

In this situation, the projections onto C and Q_i are not easily implemented in general. To avoid this difficulty, we introduce a relaxed projection gradient methods, in which the projections onto the half-spaces are adopted in stead of the projections onto C and Q_i. In particular for $n\in \mathbb {N}$, we define the relaxed sets (half-spaces) C_n and ${Q^{n}_{i}}(i=1, 2, \dots , N)$ of C and Q_i, respectively, at x_n as follows:

$$ C_{n}:=\{x\in H:c(x_{n})\leq \langle \xi_{n},x_{n}-x\rangle\}, $$

(22)

where ξ_n ∈ ∂c(x_n) is subgradient of c at x_n and

$$ {Q^{n}_{i}}:=\{y\in H_{i}:q_{i}(A_{i}x_{n})\leq \langle {\eta^{n}_{i}},A_{i}x_{n}-y\rangle\}, $$

(23)

where ${\eta ^{n}_{i}}\in \partial q_{i}(A_{i}x_{n})$. By the definition of the subgradient, it is easy to see that $C\subseteq C_{n}$ and $Q_{i}\subseteq {Q^{n}_{i}}$ (see [51]), and the metric projections onto C_n and ${Q_{i}^{n}}$ can be directly calculated (since the projections onto C_n and ${Q_{i}^{n}}$ have closed-form expressions), for example, for ξ_n ∈ ∂c(x_n)

$$ P_{C_{n}}(x_{n})= \left\{\begin{array}{l} x_{n}-\frac{c(x_{n})}{\|\xi_{n}\|^{2}}\xi_{n},~~~\text{if}\quad \xi_{n}\ne 0,\\ x_{n}, \qquad\qquad\text{ otherwise }. \end{array}\right. $$

Now, we present the following easily implementable algorithms.

3.1 Weak convergence theorems

In this subsection, we propose a new self-adaptive relaxed iterative method for solving the SFPMOS (12) in the infinite-dimensional Hilbert spaces, and we prove a weak convergence theorem of the proposed method.

Theorem 1

Assume that the SFPMOS (12) is consistent (i.e., Ω≠∅). Suppose the sequences $\{{\rho _{1}^{n}}\}$ and $\{{\rho _{2}^{n}}\}$ in Algorithm 1 are in (0,1) such that $0<a_{1}\leq {\rho _{1}^{n}}\leq b_{1}<1$ and $0<a_{2}\leq {\rho _{2}^{n}}\leq b_{2}<1$, respectively. Then, the sequence {x_n} generated by Algorithm 1 converges weakly to a solution p^∗∈Ω of the SFPMOS (12).

Proof

For convenience, we set the following notations first (for $i=1, 2, \dots , N$)

$$ f_{C_{n}}^{n}:=\left( I-P_{C_{n}}\right)x_{n},~~f_{{Q_{i}^{n}}}^{n}:=\left( I-P_{{Q_{i}^{n}}}\right)A_{i}x_{n}. $$

(25)

Consequently, the step-size τ_n given by (??) can be written as

$$ \tau_{n}: = \frac{{\rho_{2}^{n}}{\sum}_{i=1}^{N}\vartheta_{i}\|f_{{Q_{i}^{n}}}^{n}\|^{2}}{\bar{\tau}_{n}^{2}} $$

(26)

where

$$ \bar{\tau}_{n}: = \max\left\{\|{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\|, ~\beta\right\}. $$

Then, the iterative sequence {x_n} in Algorithm 1 can be rewritten as follows:

$$ x_{n+1}=x_{n}-{\rho_{1}^{n}}f_{C_{n}}^{n} -\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}. $$

(27)

Let p^∗∈Ω (Ω is the solution set of the SFPMOS (12)). By (27), we have

$$ \begin{array}{@{}rcl@{}} &&\|x_{n+1}-p^{*}\|^{2} =\|x_{n}-{\rho_{1}^{n}}f_{C_{n}}^{n}-\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}-p^{*}\|^{2}\\ &{}=&\|x_{n}-p^{*}\|^{2}-2\left\langle x_{n}-p^{*},{\rho_{1}^{n}}f_{C_{n}}^{n}+\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right\rangle\\&+&\|{\rho_{1}^{n}}f_{C_{n}}^{n}+\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\|^{2}\\ &{}=&\|x_{n}-p^{*}\|^{2}-2\left\langle x_{n}-p^{*},{\rho_{1}^{n}}f_{C_{n}}^{n}\right\rangle-2\left\langle x_{n}-p^{*},\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right\rangle\\&+&\|{\rho_{1}^{n}}f_{C_{n}}^{n}\|^{2}+\|\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\|^{2}+2\left\langle {\rho_{1}^{n}}f_{C_{n}}^{n}, \tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n} \right\rangle\\ &{}\leq&\|x_{n}-p^{*}\|^{2}-2\left\langle x_{n}-p^{*},{\rho_{1}^{n}}f_{C_{n}}^{n}\right\rangle-2\left\langle x_{n}-p^{*},\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right\rangle\\&+&\|{\rho_{1}^{n}}f_{C_{n}}^{n}\|^{2}+\|\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\|^{2}+2\|{\rho_{1}^{n}}f_{C_{n}}^{n}\| \|\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\|\\ &{}\leq&\|x_{n}-p^{*}\|^{2}-2\left\langle x_{n}-p^{*},{\rho_{1}^{n}}f_{C_{n}}^{n}\right\rangle-2\left\langle x_{n}-p^{*},\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right\rangle\\&+&2\|{\rho_{1}^{n}}f_{C_{n}}^{n}\|^{2}+2{\tau_{n}^{2}}\|{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\|^{2}. \end{array} $$

(28)

Using Lemma 1 (1), we obtain the following two estimations.

$$ \begin{array}{@{}rcl@{}} \left\langle x_{n}-p^{*}, {\rho_{1}^{n}}f_{C_{n}}^{n}\right\rangle &=&{\rho_{1}^{n}}\left\langle x_{n}-p^{*}, f_{C_{n}}^{n}\right\rangle\\ &=&{\rho_{1}^{n}}(\langle x_{n}-P_{C_{n}}(x_{n}), f_{C_{n}}^{n}\rangle+\langle P_{C_{n}}(x_{n})-p^{*}, f_{C_{n}}^{n}\rangle)\\ &=&{\rho_{1}^{n}}(\langle f_{C_{n}}^{n}, f_{C_{n}}^{n}\rangle+\langle P_{C_{n}}(x_{n})-p^{*}, f_{C_{n}}^{n}\rangle)\\ &\geq&{\rho_{1}^{n}}\|f_{C_{n}}^{n}\|^{2}. \end{array} $$

(29)

$$ \begin{array}{@{}rcl@{}} \left\langle x_{n} - p^{*}, \tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right\rangle & = &\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}\left\langle x_{n}-p^{*}, A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right\rangle\\ & = &\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}\left\langle A_{i}x_{n}-A_{i}p^{*}, f_{{Q_{i}^{n}}}^{n}\right\rangle\\ & = &\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}\left( \left\langle f_{{Q_{i}^{n}}}^{n}, f_{{Q_{i}^{n}}}^{n}\right\rangle+\left\langle P_{{Q_{i}^{n}}}(A_{i}x_{n})-A_{i}p^{*}, f_{{Q_{i}^{n}}}^{n}\right\rangle\right)\\ &\!\geq\!&\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}. \end{array} $$

(30)

Substituting (29) and (30) into (28) and since $\|{\sum }_{i=1}^{N}\vartheta _{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\|\leq \bar {\tau }_{n}$, we obtain that

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p^{*}\|^{2} &\leq&\|x_{n}-p^{*}\|^{2}-2{\rho_{1}^{n}}\|f_{C_{n}}^{n}\|^{2}-2\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}\\&&+2\|{\rho_{1}^{n}}f_{C_{n}}^{n}\|^{2}+2{\tau_{n}^{2}}\|{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\|^{2}\\ &\leq&\|x_{n}-p^{*}\|^{2}-2{\rho_{1}^{n}}\left( 1-{\rho_{1}^{n}}\right)\|f_{C_{n}}^{n}\|^{2}-2\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}+2{\tau_{n}^{2}}\bar{\tau}_{n}^{2}\\ &=&\|x_{n}-p^{*}\|^{2}-2{\rho_{1}^{n}}\left( 1-{\rho_{1}^{n}}\right)\|f_{C_{n}}^{n}\|^{2}\\ &&-2\left( \frac{{\rho_{2}^{n}}{\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}}{\bar{\tau}_{n}^{2}}\right){\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}+2\left( \frac{{\rho_{2}^{n}}{\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}}{\bar{\tau}_{n}^{2}}\right)^{2}\bar{\tau}_{n}^{2}\\ &=&\|x_{n}-p^{*}\|^{2}-2{\rho_{1}^{n}}\left( 1-{\rho_{1}^{n}}\right)\|f_{C_{n}}^{n}\|^{2}-2{\rho_{2}^{n}}\left( 1-{\rho_{2}^{n}}\right)\frac{\left( {\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}\right)^{2}}{\bar{\tau}_{n}^{2}}. \end{array} $$

(31)

Since $0<a_{1}\leq {\rho _{1}^{n}}\leq b_{1}<1$ and $0<a_{2}\leq {\rho _{2}^{n}}\leq b_{2}<1$, we have from (31) that

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p^{*}\|^{2} &\leq&\|x_{n}-p^{*}\|^{2}. \end{array} $$

Therefore, the sequence {x_n} is Fejér-monotone with respect to Ω. As a consequence, $\lim _{n\rightarrow \infty }\|x_{n}-p^{*}\|$ exists. That is, {x_n} is bounded, and hence the sequence $\{A_{i}x_{n}\}_{i=1}^{N}$ is also bounded.

Noticing that ${\rho _{1}^{n}}\in [a_{1}, b_{1}]\subset (0, 1)$, we can obtain from (31) that

$$ \begin{array}{@{}rcl@{}} 2a_{1}(1-b_{1})\|f_{C_{n}}^{n}\|^{2} &\leq&2{\rho_{1}^{n}}\left( 1-{\rho_{1}^{n}}\right)\|f_{C_{n}}^{n}\|^{2}\\ &\leq&\|x_{n}-p^{*}\|^{2}-\|x_{n+1}-p^{*}\|^{2}. \end{array} $$

(32)

Since {x_n} is bounded and $f_{C_{n}}^{n}$ is 1-Lipschitz continuous, there exists a real number R > 0 such that $\|f_{C_{n}}^{n}\|^{2}\leq R$. Thus, we can obtain from (32) that

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\|f_{C_{n}}^{n}\|^{2}=0. \end{array} $$

(33)

Hence, we obtain from (33)

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\|f_{C_{n}}^{n}\|=0. \end{array} $$

(34)

Noticing that ${\rho _{2}^{n}}\in [a_{2}, b_{2}]\subset (0, 1)$, we can obtain from (31) that

$$ \begin{array}{@{}rcl@{}} 2a_{2}(1-b_{2})\frac{\left( {\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}\right)^{2}}{\bar{\tau}_{n}^{2}} &\leq&2{\rho_{2}^{n}}\left( 1-{\rho_{2}^{n}}\right)\frac{\left( {\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}\right)^{2}}{\bar{\tau}_{n}^{2}}\\ &\leq&\|x_{n}-p^{*}\|^{2}-\|x_{n+1}-p^{*}\|^{2}. \end{array} $$

(35)

Letting $n\rightarrow \infty$ on both sides of (35), we have

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\frac{\left( {\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}\right)^{2}}{\bar{\tau}_{n}^{2}}=0. \end{array} $$

(36)

Since the iterative sequence {x_n} is bounded and by the Lipschitz continuity of $f_{{Q_{i}^{n}}}^{n}$, the sequence $\left \{\left \|{\sum }_{i=1}^{N}\vartheta _{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right \|\right \}_{n=1}^{\infty }$ is bounded and so the sequence $\{\bar {\tau }_{n}\}$ is bounded too. Therefore, we can get from (36) that

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\|f_{{Q_{i}^{n}}}^{n}\|=0 ~\text{ for } i=1, 2, \dots, N. \end{array} $$

(37)

Next, we will prove that ω_w(x_n) ⊂Ω. For each $i=1, 2, \dots , N$, since ∂q_i is bounded on bounded sets, there exists a constant γ > 0 such that $\|{\eta _{i}^{n}}\|\leq \gamma$, where ${\eta _{i}^{n}}\in \partial q_{i}(A_{i}x_{n})$. Then, for $i=1, 2, \dots , N$, notice that $P_{{Q_{i}^{n}}}(A_{i}x_{n})\in {Q_{i}^{n}}$, we have

$$ \begin{array}{@{}rcl@{}} q_{i}(A_{i}x_{n}) &\leq&\langle {\eta_{i}^{n}}, A_{i}x_{n}-P_{{Q_{i}^{n}}}(A_{i}x_{n}) \rangle\\ &\leq&\|{\eta_{i}^{n}}\|\|A_{i}x_{n}-P_{{Q_{i}^{n}}}(A_{i}x_{n})\|\\ &\leq&\gamma\|\left( I-P_{{Q_{i}^{n}}}\right)A_{i}x_{n}\|. \end{array} $$

(38)

By (37), we have for any $i=1, 2, \dots , N,$ that

$$ \begin{array}{@{}rcl@{}} \limsup_{n\rightarrow\infty}q_{i}(A_{i}x_{n})\leq 0. \end{array} $$

(39)

Let $\hat {p}\in \omega _{w}(x_{n})$, there exists a subsequence $\{x_{n_{m}}\}\subset \{x_{n}\}$ such that $x_{n_{m}}\rightharpoonup \hat {p}$ as $m\to \infty$. By the weak lower semicontinuity of the function q_i and (39), we get

$$ \begin{array}{@{}rcl@{}} q_{i}(A_{i}\hat{p})\leq \liminf_{m\rightarrow\infty}q_{i}(A_{i}x_{n_{m}})\leq 0, \end{array} $$

(40)

which means that $A_{i}\hat {p}\in Q_{i}$ for $i=1, 2, \dots , N$.

Since ∂c is bounded, there exists a constant δ > 0 such that ∥ξ_n∥≤ δ, where ξ_n ∈ ∂c(x_n). Then, notice that $P_{C_{n}}(x_{n})\in C_{n}$, we have

$$ \begin{array}{@{}rcl@{}} c(x_{n}) &\leq&\langle \xi_{n}, x_{n}-P_{C_{n}}(x_{n}) \rangle\\ &\leq&\|\xi_{n}\|\|x_{n}-P_{C_{n}}(x_{n})\|\\ &\leq&\delta\|\left( I-P_{C_{n}}\right)x_{n}\|. \end{array} $$

(41)

By (34), we have that

$$ \begin{array}{@{}rcl@{}} \limsup_{n\rightarrow\infty}c(x_{n})\leq 0. \end{array} $$

(42)

By the weak lower semicontinuity of the convex function c and (42), we obtain

$$ \begin{array}{@{}rcl@{}} c(\hat{p})\leq \liminf_{m\rightarrow\infty}c(x_{n_{m}})\leq 0. \end{array} $$

(43)

Consequently, $\hat {p}\in C$. Therefore, $\hat {p}\in {\Omega }$.

Notice that for any p^∗∈Ω, $\lim _{n\rightarrow \infty }\|x_{n}-p^{*}\|$ exists and ω_w(x_n) ⊂Ω. Therefore, applying Lemma 4, we conclude that the iterative sequence {x_n} converges weakly to a solution of the SFPMOS (12). This completes the proof. □

For N = 1, we note the following iterative method for solving the SFP (1).

As an immediate consequence of Theorem 1, we obtain the following corollary.

Corollary 1

Assume that the SFP (1) is consistent. Suppose the sequences $\{{\rho _{1}^{n}}\}$ and $\{{\rho _{2}^{n}}\}$ in Algorithm 2 are in (0,1) such that $0<a_{1}\leq {\rho _{1}^{n}}\leq b_{1}<1$ and $0<a_{2}\leq {\rho _{2}^{n}}\leq b_{2}<1$, respectively. Then, the sequence {x_n} generated by Algorithm 2 converges weakly to a solution p^∗∈Ω = {p ∈ H₁ : p ∈ C such that Ap ∈ Q}.

3.2 Strong convergence theorem

In this subsection, we propose a new iterative method for solving the SFPMOS (12) in the infinite-dimensional Hilbert spaces, and we prove a strong convergence theorem of the proposed method.

Theorem 2

Assume that the SFPMOS (12) is consistent (i.e., Ω≠∅). Suppose the sequences $\{{\rho _{1}^{n}}\}$, $\{{\rho _{2}^{n}}\}$, and {α_n} in Algorithm 3 are in (0,1) such that $0<a_{1}\leq {\rho _{1}^{n}}\leq b_{1}<1$ and $0<a_{2}\leq {\rho _{2}^{n}}\leq b_{2}<1$, and $\lim _{n\rightarrow \infty }\alpha _{n}=0$ and ${\sum }_{n=0}^{\infty } \alpha _{n}=\infty$. Then, the sequence {x_n} generated by Algorithm 3 converges strongly to the point p^∗∈Ω, where p^∗ = P_Ωu.

Proof

For simplicity, the same as we did in the proof of Theorem 1, we introduce some notations first.

$$ f_{C_{n}}^{n}:=\left( I-P_{C_{n}}\right)x_{n}, ~~f_{{Q_{i}^{n}}}^{n}:=\left( I-P_{{Q_{i}^{n}}}\right)A_{i}x_{n} ~\text{ for } i=1, 2, \dots, N, $$

$$ y_{n}=x_{n}-{\rho_{1}^{n}}f_{C_{n}}^{n} -\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}, $$

where τ_n is the stepsize given in the Algorithm 3 and can be defined as

$$ \tau_{n}: = \frac{{\rho_{2}^{n}}{\sum}_{i=1}^{N}\vartheta_{i}\|f_{{Q_{i}^{n}}}^{n}\|^{2}}{\bar{\tau}_{n}^{2}} $$

(46)

where

$$ \bar{\tau}_{n}: = \max\left\{\left\|{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right\|, ~\beta\right\}. $$

Then, the iterative sequence {x_n} in Algorithm 3 can be rewritten as follows:

$$ x_{n+1}=\alpha_{n}u+(1-\alpha_{n})y_{n}. $$

(47)

Let p^∗∈Ω. Using Lemma 2 (1) and by (47), we have that

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p^{*}\|^{2} &{} = &\|\alpha_{n}u + (1-\alpha_{n})y_{n}-p^{*}\|^{2}\\ &{} = &\|\alpha_{n}u + (1-\alpha_{n})y_{n}-p^{*} + \alpha_{n}p^{*} - \alpha_{n}p^{*}\|^{2}\\ &{} = &\|\alpha_{n}(u-p^{*}) + (1-\alpha_{n})(y_{n}-p^{*})\|^{2}\\ &{} \leq &(1-\alpha_{n})^{2}\|y_{n}-p^{*}\|^{2} + 2\langle \alpha_{n}(u-p^{*}), ~ x_{n+1}-p^{*}\rangle\\ &{} \leq &(1-\alpha_{n})\|y_{n}-p^{*}\|^{2} + 2\alpha_{n}\langle u-p^{*}, ~ x_{n+1}-p^{*}\rangle. \end{array} $$

(48)

From (31), we have

$$ \begin{array}{@{}rcl@{}} \|y_{n}-p^{*}\|^{2}&\leq&\|x_{n}-p^{*}\|^{2}-2{\rho_{1}^{n}}\left( 1-{\rho_{1}^{n}}\right)\|f_{C_{n}}^{n}\|^{2}-2{\rho_{2}^{n}}\left( 1-{\rho_{2}^{n}}\right)\frac{\left( {\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}\right)^{2}}{\bar{\tau}_{n}^{2}}. \end{array} $$

(49)

From (48) and (49), we obtain

$$ \begin{array}{@{}rcl@{}} &&\|x_{n+1}-p^{*}\|^{2} \leq(1-\alpha_{n})\|x_{n}-p^{*}\|^{2}+2\alpha_{n}\langle u-p^{*}, x_{n+1}-p^{*}\rangle-\\ &{}&(1-\alpha_{n})\left[2{\rho_{1}^{n}}\left( 1-{\rho_{1}^{n}}\right)\|f_{C_{n}}^{n}\|^{2}+2{\rho_{2}^{n}}\left( 1-{\rho_{2}^{n}}\right)\frac{\left( {\sum}_{i=1}^{N}\vartheta_{i}\|f_{{Q_{i}^{n}}}^{n}\|^{2}\right)^{2}}{\bar{\tau}_{n}^{2}}\right]. \end{array} $$

(50)

Now, we prove the sequence {x_n} is bounded. Indeed, using the assumptions imposed on $\{{\rho _{1}^{n}}\}$, $\{{\rho _{2}^{n}}\}$ and {α_n}, we have from (50) that

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p^{*}\|^{2} &\leq&(1-\alpha_{n})\|x_{n}-p^{*}\|^{2}\|+2\alpha_{n}\langle u-p^{*}, x_{n+1}-p^{*}\rangle\\ &\leq&(1-\alpha_{n})\|x_{n}-p^{*}\|^{2}\|+4\alpha_{n}\|u-p^{*}\|^{2}+\frac{1}{4}\alpha_{n}\|x_{n+1}-p^{*}\|^{2}. \end{array} $$

Consequently,

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-p^{*}\|^{2} &\leq&\frac{1-\alpha_{n}}{1-\frac{1}{4}\alpha_{n}}\|x_{n}-p^{*}\|^{2}+ \frac{\frac{3}{4}\alpha_{n}}{1-\frac{1}{4}\alpha_{n}}\frac{16}{3}\|u-p^{*}\|^{2}\\ &\leq&\max\left\{\|x_{n}-p^{*}\|,\frac{16}{3}\|u-p^{*}\|\right\}\\ &\vdots&\\ &\leq&\max\left\{\|x_{0}-p^{*}\|,\frac{16}{3}\|u-p^{*}\|\right\}. \end{array} $$

(51)

This shows that the sequence {x_n} is bounded, and {y_n} and $\{A_{i}x_{n}\}_{i=1}^{N}$ as well.

Next, with no loss of generality, we may assume that there exist σ₁,σ₂ > 0 such that $2{\rho _{1}^{n}}\left (1-{\rho _{1}^{n}}\right )(1-\alpha _{n})\geq \sigma _{1}$ and $2{\rho _{2}^{n}}\left (1-{\rho _{2}^{n}}\right )(1-\alpha _{n})\geq \sigma _{2}$ for all n.

Setting s_n = ∥x_n − p^∗∥², we get from (50) that

$$ \begin{array}{@{}rcl@{}} s_{n+1}-(1-\alpha_{n})s_{n}+\sigma_{1}\|f_{C_{n}}^{n}\|^{2}+\frac{\sigma_{2}\left( {\sum}_{i=1}^{N}\vartheta_{i}\|f_{{Q_{i}^{n}}}^{n}\|^{2}\right)^{2}}{\bar{\tau}_{n}^{2}}&\leq&2\alpha_{n}\langle u-p^{*}, x_{n+1}-p^{*}\rangle\\ &\leq&2\alpha_{n}\|u-p^{*}\|\|x_{n+1}-p^{*}\|. \end{array} $$

(52)

Now, we prove s_n → 0 by distinguishing two cases. Case 1: Assume that {s_n} is eventually decreasing. That is, there exists k ≥ 0 such that s_n+ 1 < s_n holds for all n ≥ k. In this case, {s_n} must be convergent, and from (52) it follows that

$$ \begin{array}{@{}rcl@{}} \Bigg(\sigma_{1}\|f_{C_{n}}^{n}\|^{2}+\frac{\sigma_{2}\left( {\sum}_{i=1}^{N}\vartheta_{i}\|f_{{Q_{i}^{n}}}^{n}\|^{2}\right)^{2}}{\bar{\tau}_{n}^{2}}\Bigg)&\leq&\alpha_{n}K+(s_{n}-s_{n+1}), \end{array} $$

(53)

where K > 0 is a constant such that 2∥u − p^∗∥∥x_n+ 1 − p^∗∥≤ K for all $n\in \mathbb {N}$. Since σ₁,σ₂ > 0, and α_n → 0 as $n\to \infty$, we have from (53) that

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\|f_{C_{n}}^{n}\|^{2}=0 \Rightarrow\lim_{n\rightarrow\infty}\|f_{C_{n}}^{n}\|=0\Rightarrow\lim_{n\rightarrow\infty}\|\left( I-P_{C_{n}}\right)x_{n}\|=0, \end{array} $$

(54)

and

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\frac{\left( {\sum}_{i=1}^{N}\vartheta_{i}\left\| f_{{Q_{i}^{n}}}^{n}\right\|^{2}\right)^{2}}{\bar{\tau}_{n}^{2}}=0. \end{array} $$

(55)

Next, we show that $\left \{f_{{Q_{i}^{n}}}^{n}\right \}\to 0$. To do so, it suffices to verify that $\left \{ \|{\sum }_{i=1}^{N}\vartheta _{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\|^{2}\right \}$ is bounded. Since p^∗∈Ω, we note that $A^{*}_{i}\left (I-P_{{Q_{i}^{n}}}\right )A_{i}p^{*}=0$. Hence, it follows from Lemma 5 that

$$ \begin{array}{@{}rcl@{}} \|A^{*}_{i}\left( I-P_{{Q_{i}^{n}}}\right)A_{i}x_{n}-A^{*}_{i}\left( I-P_{{Q_{i}^{n}}}\right)A_{i}p^{*}\|\leq \left( \max_{1\leq i\leq N}\|A_{i}\|^{2}\right)\|x_{n}-p^{*}\| \end{array} $$

(56)

and since {x_n} is bounded, for all $i=1, 2, \dots , N$, we have the sequence $\left \{\left \|A_{i}^{*}\left (I-P_{{Q^{n}_{i}}}\right )A_{i}x_{n}\right \|\right \}_{n=1}^{\infty }$ is bounded. This implies that the sequence $\left \{\left \|{\sum }_{i=1}^{N}\vartheta _{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right \|\right \}_{n=1}^{\infty }$ is also bounded. Consequently, $\{\bar {\tau }_{n}\}$ is bounded too. Therefore, we can get from (55) that

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\|f_{{Q_{i}^{n}}}^{n}\|=0\Rightarrow\lim_{n\rightarrow\infty}\|\left( I-P_{{Q_{i}^{n}}}\right)A_{i}x_{n}\|=0 \end{array} $$

(57)

for i= 1, 2, …, N.

Next, we verify that ω_w(x_n) ⊂Ω. For each $i=1, 2, \dots , N$, since ∂q_i is bounded on bounded sets, there exists a constant δ > 0 such that $\|{\eta _{i}^{n}}\|\leq \delta$ for all n ≥ 0, where ${\eta _{i}^{n}}\in \partial q_{i}(A_{i}x_{n})$. Then, from the fact that $P_{{Q_{i}^{n}}}(A_{i}x_{n})\in {Q_{i}^{n}}$ and (23), it follows (for $i=1, 2, \dots , N$) that

$$ \begin{array}{@{}rcl@{}} q_{i}(A_{i}x_{n}) &\leq&\langle {\eta_{i}^{n}}, A_{i}x_{n}-P_{{Q_{i}^{n}}}(A_{i}x_{n}) \rangle\\ &\leq&\|{\eta_{i}^{n}}\|\|A_{i}x_{n}-P_{{Q_{i}^{n}}}(A_{i}x_{n})\|\\ &\leq&\delta \|\left( I-P_{{Q_{i}^{n}}}\right)A_{i}x_{n}\|. \end{array} $$

(58)

Let $\hat {p}\in \omega _{w}(x_{n})$, there exists a subsequence $\{x_{n_{m}}\}$ of {x_n} such that $x_{n_{m}}\rightharpoonup \hat {p}$ as $m\to \infty$. Then, the weak lower semicontinuity of q_i and (58) imply that

$$ \begin{array}{@{}rcl@{}} q_{i}(A_{i}\hat{p})\leq \liminf_{m\rightarrow\infty}q_{i}(A_{i}x_{n_{m}})\leq 0. \end{array} $$

(59)

It turns out that $A_{i}\hat {p}\in Q_{i}$ for $i=1, 2, \dots , N$. Next, we turn to prove that $\hat {p}\in C$. Since ∂c is bounded, there exists a constant γ > 0 such that ∥ξ_n∥≤ γ for all n ≥ 0, where ξ_n ∈ ∂c(x_n). Then, from that trivial fact that $P_{C_{n}}(x_{n})\in C_{n}$ and (22), it follows that

$$ \begin{array}{@{}rcl@{}} c(x_{n}) &\leq&\langle \xi_{n}, x_{n}-P_{C_{n}}(x_{n}) \rangle\\ &\leq&\|\xi_{n}\|\|x_{n}-P_{C_{n}}(x_{n})\|\\ &\leq&\gamma\|\left( I-P_{C_{n}}\right)x_{n}\|. \end{array} $$

(60)

The weak lower semicontinuity of c then implies that

$$ \begin{array}{@{}rcl@{}} c(\hat{p})\leq \liminf_{m\rightarrow\infty}c(x_{n_{m}})\leq 0. \end{array} $$

(61)

Consequently, $\hat {p}\in C$. Therefore, $\hat {p}\in {\Omega }$. Hence, ω_w(x_n) ⊂Ω.

Moreover, we have the following estimation

$$ \begin{array}{@{}rcl@{}} \|x_{n}-x_{n+1}\| &=&\left\|x_{n}-\left[\alpha_{n}u+(1-\alpha_{n})\left( x_{n}-{\rho_{1}^{n}}f_{C_{n}}^{n} -\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right)\right]\right\|\\ &=&\left\|\alpha_{n}(x_{n}-u)+(1-\alpha_{n})\left( {\rho_{1}^{n}}f_{C_{n}}^{n} +\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}f_{{Q_{i}^{n}}}^{n}\right)\right\|\\ &\leq&\alpha_{n}\|x_{n}-u\|+(1-\alpha_{n})\left( {\rho_{1}^{n}}\|f_{C_{n}}^{n}\| +\frac{{\rho_{2}^{n}}{\sum}_{i=1}^{N}\vartheta_{i}\|f_{{Q_{i}^{n}}}^{n}\|^{2}}{\bar{\tau}_{n}}\right),\\ \end{array} $$

since {x_n} is bounded and $\lim _{n\rightarrow \infty }\alpha _{n}=0$, we have that $\lim _{n\rightarrow \infty }\alpha _{n}\|x_{n}-u\|=0$. Noting that $\{\|A_{i}^{*}(I-P_{{Q^{n}_{i}}})A_{i}x_{n}\|\}_{n=1}^{\infty }$ is bounded, (57) together with the conditions $0<a_{1}\leq {\rho _{1}^{n}}\leq b_{1}<1$ and $0<a_{2}\leq {\rho _{2}^{n}}\leq b_{2}<1$, we have that

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}(1-\alpha_{n})\left( {\rho_{1}^{n}}\|f_{C_{n}}^{n}\| +\frac{{\rho_{2}^{n}}{\sum}_{i=1}^{N}\vartheta_{i}\|f_{{Q_{i}^{n}}}^{n}\|^{2}}{\bar{\tau}_{n}}\right)=0, \end{array} $$

which implies that

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\|x_{n}-x_{n+1}\|=0. \end{array} $$

(62)

Furthermore, due to Lemma 1 (1), we get

$$ \begin{array}{@{}rcl@{}} \limsup_{n\rightarrow\infty}\langle u-p^{*}, x_{n}-p^{*} \rangle=\max_{z\in\omega_{w}(x_{n})}\langle u-P_{\Omega}(u), z-P_{\Omega}(u) \rangle\leq 0. \end{array} $$

(63)

Taking into account of (52), we have

$$ \begin{array}{@{}rcl@{}} s_{n+1}\leq(1-\alpha_{n})s_{n}+2\alpha_{n}\langle u-p^{*}, x_{n+1}-p^{*}\rangle. \end{array} $$

(64)

Applying Lemma 7 to (64), we obtain s_n = ∥x_n − p^∗∥² → 0.

Case 2: Assume that {s_n} is not eventually decreasing. That is, we can find an integer n₀ such that $s_{n_{0}}\leq s_{n_{0}+1}$. Now we define

$$ \begin{array}{@{}rcl@{}} M_{n}:=\left\{n_{0}\leq m\leq n: s_{m}\leq s_{m+1}\right\}, n>n_{0}. \end{array} $$

(65)

It is easy to see that M_n is nonempty and satisfies $M_{n}\subseteq M_{n+1}$. Let

$$ \begin{array}{@{}rcl@{}} \phi(n):=\max {M_{n}},n>n_{0}. \end{array} $$

(66)

It is clear that $\phi (n)\to \infty$ as $n\to \infty$ (otherwise, {s_n} is eventually decreasing). It is also clear that s_ϕ(n) ≤ s_ϕ(n)+ 1 for all n > n₀. Moreover,

$$ \begin{array}{@{}rcl@{}} s_{n}\leq s_{\phi(n)+1},~ n>n_{0}. \end{array} $$

(67)

In fact, if ϕ(n) = n, then (67) is trivial: if ϕ(n) < n, from (66), there exists some $j\in \mathbb {N}$ such that ϕ(n) + j = n, we deduce that

$$ \begin{array}{@{}rcl@{}} s_{n}=s_{\phi(n)+j} < {\dots} < s_{\phi(n)+2} < s_{\phi(n)+1}, \end{array} $$

(68)

and (67) holds again. Since s_ϕ(n) < s_ϕ(n)+ 1 for all n > n₀, it follows from (53) that

$$ \begin{array}{@{}rcl@{}} \left( \sigma_{1}\|f_{C_{\phi(n)}}^{\phi(n)}\|^{2}+\frac{\sigma_{2}({\sum}_{i=1}^{N}\vartheta_{i}\|f_{Q_{i}^{\phi(n)}}^{\phi(n)}\|^{2})^{2}}{\bar{\tau}_{\phi(n)}^{2}}\right)\leq\alpha_{\phi(n)}K\to 0, \end{array} $$

(69)

so that

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\|f_{C_{\phi(n)}}^{\phi(n)}\|=0\Rightarrow\lim_{n\rightarrow\infty}\|(I-P_{C_{\phi(n)}})x_{\phi(n)}\|=0, \end{array} $$

(70)

and

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\frac{({\sum}_{i=1}^{N}\vartheta_{i}\| f_{Q_{i}^{\phi(n)}}^{\phi(n)}\|^{2})^{2}}{\bar{\tau}_{\phi(n)}^{2}}=0. \end{array} $$

(71)

Noting that $\left \{\left \|A_{i}^{*}(I-P_{Q^{\phi (n)}_{i}})A_{i}x_{\phi (n)}\right \|\right \}_{n=1}^{\infty }$ is bounded, for $i=1, 2, \dots , N$, we also have that

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\left\|f_{Q_{i}^{\phi(n)}}^{\phi(n)}\right\|=0\Rightarrow\lim_{n\rightarrow\infty}\left\|(I-P_{Q_{i}^{\phi(n)}})A_{i}x_{\phi(n)}\right\|=0. \end{array} $$

(72)

By the same argument to the proof in Case 1, we have ω_w(x_ϕ(n)) ⊂Ω.

Furthermore, by the same argument to the proof in Case 1, from (62), we have that

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow\infty}\|x_{\phi(n)}-x_{\phi(n)+1}\|=0. \end{array} $$

(73)

Thus, one can deduce that

$$ \begin{array}{@{}rcl@{}} \limsup_{n\rightarrow\infty}\langle u-p^{*}, x_{\phi(n)+1}-p^{*} \rangle&=&\limsup_{n\rightarrow\infty}\langle u-p^{*}, x_{\phi(n)}-p^{*} \rangle\\ &=&\max_{z\in\omega_{w}(x_{\phi(n)})}\langle u-P_{\Omega}(u), z-P_{\Omega}(u)\rangle\\&\leq&0. \end{array} $$

(74)

Since s_ϕ(n) ≤ s_ϕ(n)+ 1, it follows from (52) that

$$ \begin{array}{@{}rcl@{}} s_{\phi(n)} \leq2 \langle u-p^{*}, x_{\phi(n)+1}-p^{*}>, ~n>n_{0}. \end{array} $$

(75)

(74) and (75) together gives

$$ \begin{array}{@{}rcl@{}} \limsup_{n\rightarrow\infty}s_{\phi(n)}\leq 0. \end{array} $$

(76)

Hence, $\lim _{n\rightarrow \infty }s_{\phi (n)}=0$, which together with (73)

$$ \begin{array}{@{}rcl@{}} \sqrt{s_{\phi(n)+1}}&\leq&\|x_{\phi(n)+1}-p^{*}\|\\ &=&\|(x_{\phi(n)}-p^{*})+(x_{\phi(n)+1}-x_{\phi(n)})\|\\ &\leq&\|x_{\phi(n)}-p^{*}\|+\|x_{\phi(n)+1}-x_{\phi(n)}\|\\ &=&\sqrt{s_{\phi(n)}}+\|x_{\phi(n)+1}-x_{\phi(n)}\|\to 0, \end{array} $$

(77)

which, together with (67), in turn implies that s_n → 0, that is, x_n → p^∗. Therefore, the full iterative sequence {x_n} converges strongly to the solution p^∗ = P_Ω(u) of SFPMOS (12). This completes the proof. □

Corollary 2

Assume that the SFPMOS (12) is consistent (i.e., Ω≠∅). Let x₀ ∈ H be an arbitrary initial point, and set n = 0. Let {x_n} be a sequence generated via the manner

$$ x_{n+1}=\alpha_{n}x_{0}+(1-\alpha_{n})\left( x_{n}-{\rho_{1}^{n}} \left( I-P_{C_{n}}\right)x_{n}-\tau_{n}{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}\left( I-P_{{Q^{n}_{i}}}\right)A_{i}x_{n}\right) $$

s where the step-size τ_n is updated self-adaptively as

$$ \tau_{n}: = \frac{{\rho_{2}^{n}}{\sum}_{i=1}^{N}\vartheta_{i}\|(I-P_{{Q^{n}_{i}}})A_{i}x_{n}\|^{2}}{\bar{\tau}_{n}^{2}} $$

(78)

where for a constant β > 0

$$\bar{\tau}_{n}: = \max\left\{\|{\sum}_{i=1}^{N}\vartheta_{i}A^{*}_{i}\left( I-P_{{Q^{n}_{i}}}\right)A_{i}x_{n}\|, ~\beta\right\},$$

and C_n and ${Q_{i}^{n}}$ are the half-spaces given as in (22) and (23), respectively. Suppose the parameters $\{{\rho _{1}^{n}}\}, \{{\rho _{2}^{n}}\}, \{\alpha _{n}\}$ are in (0,1) satisfying the conditions in Theorem 2, and $\{\vartheta _{i}\}_{i=1}^{N}>0$. Then, the sequence {x_n} converges strongly to the point p^∗∈Ω, where p^∗ = P_Ω(x₀).

Similarly as in Subsection 3.1, for N = 1, we again obtain the following strongly convergent result regarding the SFP (1).

As an immediate consequence of Theorem 2, we obtain the following corollary.

Corollary 3

Assume that the SFP (1) is consistent. Suppose the sequences $\{{\rho _{1}^{n}}\}$, $\{{\rho _{2}^{n}}\}$ and {α_n} in Algorithm 4 are in (0,1) such that $0<a_{1}\leq {\rho _{1}^{n}}\leq b_{1}<1$ and $0<a_{2}\leq {\rho _{2}^{n}}\leq b_{2}<1$, and $\lim _{n\rightarrow \infty }\alpha _{n}=0$ and ${\sum }_{n=0}^{\infty } \alpha _{n}=\infty$. Then, the sequence {x_n} generated by Algorithm 4 converges strongly to the point p^∗ = P_Ω(u) ∈Ω = {p ∈ H₁ : p ∈ C such that Ap ∈ Q}.

4 Application to the generalized split feasibility problem

In this section, we present an application of Theorems 1 and 2 for solving generalized split feasibility problem (another generalization of the SFP) in Hilbert spaces. We recall the generalized split feasibility problem first.

In 2020, Reich and Tuyen [52] first introduced and studied the following generalized split feasibility problem (GSFP).

Let $H_{i}, i=1, 2, \dots , N,$ be real Hilbert spaces and $C_{i},~i=1, 2, \dots , N,$ be closed and convex subsets of H_i, respectively. Let $B_{i}: H_{i}\to H_{i+1},~i=1, 2, \dots , N-1,$ be bounded linear operators such that

$$ S:=C_{1}\cap B^{-1}_{1} (C_{2})\cap\dots\cap B^{-1}_{1} \left( B^{-1}_{2}\dots\left( B^{-1}_{N-1}(C_{N})\right)\right)\ne\emptyset. $$

(80)

Given H_i, C_i and A_i as above, the generalized SFP (GSFP)([52]) is to

$$ \text{ find an element }p^{*}\in S. $$

(81)

That is $p^{*}\in C_{1}, B_{1}p^{*}\in C_{2},\dots , B_{N-1}B_{N-2}{\dots } B_{1}p^{*}\in C_{N}$. In [52], Reich and Tuyen proved a strong convergence theorem for a modification of the CQ method which solves the GSFP (81). For more details on the GSFP (81), one can read the paper [52].

Remark 1

([43, Remark 1.1]) Letting H = H₁,C = C₁,Q_i = C_i+ 1,1 ≤ i ≤ N − 1, $A_{1}=B_{1}, A_{2}=B_{2}B_{1}, \dots ,$ and $A_{N-1}=B_{N-1}B_{N-2}B_{N-3} {\dots } B_{2}B_{1}$, then the SFPMOS (12) becomes the GSFP (81).

From Theorem 1 and Remark 1, we note the following theorem for solving the GSFP (81).

Theorem 3

Let H = H₁,C = C₁,Q_i = C_i+ 1,1 ≤ i ≤ N − 1, $A_{1}=B_{1}, A_{2}=B_{2}B_{1}, \dots ,$ and $A_{N-1}=B_{N-1}B_{N-2}B_{N-3} {\dots } B_{2}B_{1}$. Assume that the GSFP (81) is consistent (i.e., S≠∅). Let x₀ ∈ C₁ be an arbitrary initial point and set n = 0. Let {x_n} be the sequence generated by

$$ x_{n+1}=x_{n}-{\rho_{1}^{n}} \left( I-P_{{C^{n}_{1}}}\right)x_{n}-\tau_{n}{\sum}_{i=1}^{N-1}\vartheta_{i}A^{*}_{i}\left( I-P_{C^{n}_{i+1}}\right)A_{i}x_{n} $$

(82)

where ${C^{n}_{1}}$ and $C^{n}_{i+1}$ are half-spaces of C₁ and C_i+ 1 (at the nth iterate ), respectively,

$$ \tau_{n}: = \frac{{\rho_{2}^{n}}{\sum}_{i=1}^{N-1}\vartheta_{i}\left\|\left( I-P_{C^{n}_{i+1}}\right)A_{i}x_{n}\right\|^{2}}{\bar{\tau}_{n}^{2}} $$

where for a constant β > 0

$$\bar{\tau}_{n}: = \max\left\{\left\|{\sum}_{i=1}^{N-1}\vartheta_{i}A^{*}_{i}\left( I-P_{C^{n}_{i+1}}\right)A_{i}x_{n}\right\|, ~\beta\right\},$$

and the sequences $\{{\rho _{1}^{n}}\}$, $\{{\rho _{2}^{n}}\}\subset (0, 1)$ such that $0<a_{1}\leq {\rho _{1}^{n}}\leq b_{1}<1$ and $0<a_{2}\leq {\rho _{2}^{n}}\leq b_{2}<1$, and the parameter $\{\vartheta _{i}\}_{i=1}^{N}>0$. Then, the sequence {x_n} generated by the iterative scheme (82) converges weakly to a solution p^∗∈ S.

Again, using Theorem 2 and Remark 1, we note the following result to solve the GSFP (81).

Theorem 4

Let H = H₁,C = C₁,Q_i = C_i+ 1,1 ≤ i ≤ N − 1, $A_{1}=B_{1}, A_{2}=B_{2}B_{1}, \dots ,$ and $A_{N-1}=B_{N-1}B_{N-2}B_{N-3} {\dots } B_{2}B_{1}$. Assume that the GSFP (81) is consistent (i.e., S≠∅). Let u ∈ C₁ be a fixed point and x₀ ∈ C₁ is an arbitrary initial point, and set n = 0. Let {x_n} be the sequence generated by

$$ x_{n+1}=\alpha_{n}u+(1-\alpha_{n})\left( x_{n}-{\rho_{1}^{n}} \left( I-P_{{C^{n}_{1}}}\right)x_{n}-\tau_{n}{\sum}_{i=1}^{N-1}\vartheta_{i}A^{*}_{i}\left( I-P_{C^{n}_{i+1}}\right)A_{i}x_{n}\right) $$

(83)

where ${C^{n}_{1}}$ and $C^{n}_{i+1}$ are half-spaces of C₁ and C_i+ 1, respectively,

$$ \tau_{n}: = \frac{{\rho_{2}^{n}}{\sum}_{i=1}^{N-1}\vartheta_{i}\left\|\left( I-P_{C^{n}_{i+1}}\right) A_{i}x_{n}\right\|^{2}}{\bar{\tau}_{n}^{2}} $$

where for a constant β > 0 and

$$\bar{\tau}_{n}: = \max\left\{\left\|{\sum}_{i=1}^{N-1}\vartheta_{i}A^{*}_{i}\left( I-P_{C^{n}_{i+1}}\right)A_{i}x_{n}\right\|, ~\beta\right\},$$

the sequences $\{{\rho _{1}^{n}}\}$, $\{{\rho _{2}^{n}}\},\{\alpha _{n}\}\subset (0, 1)$ such that $0<a_{1}\leq {\rho _{1}^{n}}\leq b_{1}<1$, $0<a_{2}\leq {\rho _{2}^{n}}\leq b_{2}<1$, $\lim _{n\rightarrow \infty }\alpha _{n}=0$ and ${\sum }_{n=0}^{\infty } \alpha _{n}=\infty$, and the parameter $\{\vartheta _{i}\}_{i=1}^{N}>0$. Then, the sequence {x_n} generated by the iterative scheme (83) converges strongly to the solution p^∗∈ S, where p^∗ = P_S(u).

5 Numerical results

In this section, we present some numerical examples to illustrate the implementation and efficiency of our proposed methods compared to some existing results by solving some problems. The numerical results are completed on a standard FUJITSUNOTEBOOK laptop with 11th Gen Intel(R) Core(TM) i7-1165G7 @ 2.80GHz 2.80 GHz with memory 16GB. The code is implemented in MATLAB R2022a. In our numerical experiments, Iter. (n) stands for the number of iterations and CPU(s) for the Elapsed time-run in seconds.

Example 1

([43]) Consider $H=\mathbb {R}^{10}$, $H_{1}=\mathbb {R}^{20}$, $H_{2}=\mathbb {R}^{30}$ and $H_{3}=\mathbb {R}^{40}$. Find a point $p^{*}\in \mathbb {R}^{10}$ such that

$$ p^{*}\in{\Omega}:=C\cap A^{-1}_{1}(Q_{1})\cap A^{-1}_{2}(Q_{2})\cap A^{-1}_{3}(Q_{3})\ne\emptyset, $$

(84)

where the sets C and Q_i, and the linear bounded operators A_i are defined by

$$ \begin{array}{lr} C=\left\{x\in\mathbb{R}^{10}: \|x-\textbf{c}\|^{2}\leq \textbf{r}^{2}\right\},\\ Q_{1}=\left\{A_{1}x\in\mathbb{R}^{20}:\|A_{1}x-\textbf{c}_{1}\|^{2}\leq\textbf{r}^{2}_{1}\right\},\\ Q_{2}=\left\{A_{2}x\in\mathbb{R}^{30}:\|A_{2}x-\textbf{c}_{2}\|^{2}\leq\textbf{r}^{2}_{2}\right\},\\ Q_{3}=\left\{A_{3}x\in\mathbb{R}^{40}:\|A_{3}x-\textbf{c}_{3}\|^{2}\leq \textbf{r}^{2}_{3}\right\}. \end{array} $$

(85)

where $\textbf {c}\in \mathbb {R}^{10}$, $\textbf {c}_{1}\in \mathbb {R}^{20}$, $\textbf {c}_{2}\in \mathbb {R}^{30}$, $\textbf {c}_{3}\in \mathbb {R}^{40}$, $\textbf {r}, \textbf {r}_{1}, \textbf {r}_{2}, \textbf {r}_{3}\in \mathbb {R}$, and $A_{1}:\mathbb {R}^{10}\to \mathbb {R}^{20}$, $A_{2}:\mathbb {R}^{10}\to \mathbb {R}^{30}$, $A_{3}:\mathbb {R}^{10}\to \mathbb {R}^{40}$. In this case, for any $x\in \mathbb {R}^{10}$ we have c(x) = ∥x −c∥² −r² and $q_{i}(A_{i}x)=\|A_{i}x-\textbf {c}_{i}\|^{2}-\textbf {r}^{2}_{i}$ for i = 1,2,3. According to (22) and (23), the half-spaces C_n and ${Q^{n}_{i}}$ (i = 1,2,3), respectively of the sets C and Q_i are determined at a point x_n and A_ix_n, respectively as follows:

$$ \begin{array}{lr} C_{n}=\{x\in\mathbb{R}^{10}:\|x_{n}-\textbf{c}\|^{2}-\textbf{r}^{2}\leq 2\langle x_{n}-\textbf{c}, x_{n}-x\rangle\},\\ {Q^{n}_{1}}=\{y\in\mathbb{R}^{20}:\|A_{1}x_{n}-\textbf{c}_{1}\|^{2}-\textbf{r}^{2}_{1}\leq 2\langle A_{1}x_{n}-\textbf{c}_{1}, A_{1}x_{n}-y\rangle\},\\ {Q^{n}_{2}}=\{y\in\mathbb{R}^{30}:\|A_{2}x_{n}-\textbf{c}_{2}\|^{2}-\textbf{r}^{2}_{2}\leq 2\langle A_{2}x_{n}-\textbf{c}_{2}, A_{2}x_{n}-y\rangle\},\\ {Q^{n}_{3}}=\{y\in \mathbb{R}^{40}:\|A_{3}x_{n}-\textbf{c}_{3}\|^{2}-\textbf{r}^{2}_{3}\leq 2\langle A_{3}x_{n}-\textbf{c}_{3}, A_{3}x_{n}-y\rangle\}. \end{array} $$

(86)

Then, the metric projections onto the half-spaces C_n and ${Q^{n}_{i}}$ (i = 1,2,3), can be easily calculated. The elements of the representing matrices A_i are randomly generated in the closed interval [− 5,5], the coordinates of the centers c,c₁,c₂,c₃ are randomly generated in the closed interval [− 1,1], and the radii r,r₁,r₂,r₃ are randomly generated in the closed intervals [10,20], [20,40], [30,60] and [40,80], respectively. For simplicity, denote $e_{1}=(1, 1, \dots , 1)^{T}\in \mathbb {R}^{10}$.

In this example, we examine the convergence of the sequence {x_n} which is defined by Algorithms 1 and 3 by solving problem (84) compared to the recently introduced iterative methods for solving the SFPMOS (12) given by Scheme (13), Scheme (14), and with the following viscosity approximation an optimization approach method proposed by Reich et al. [53] for solving the SFPMOS (12). For any given point x₀ ∈ H, {x_n} is a sequence generated by the iterative method

$$ x_{n+1}:=\alpha_{n}f(x_{n})+(1-\alpha_{n}) P_{C}\left( x_{n}-\lambda_{n}{\sum}_{i\in I(x_{n})}\gamma_{i,n}A^{*}_{i}\left( I-P_{Q_{i}}\right)A_{i}x_{n}\right), $$

(87)

where f : C → C is a strict contraction mapping of H into itself with the contraction constant 𝜃 ∈ [0,1), {α_n}⊂ (0,1), $I(x_{n}) = \left \{i : \left \|A_{i}x_{n}-P_{Q_{i}}A_{i}x_{n}\right \|\right .$ $\left .=\max \limits _{i=1, 2, \dots , N}\left \|A_{i}x_{n}-P_{Q_{i}}A_{i}x_{n}\right \|\right \}$, γ_i,n ≥ 0 for all i ∈ I(x_n) with ${\sum }_{i\in I(x_{n})}\gamma _{i,n}=1$, and for $\{\rho _{n}\}\subset [\bar {a}, \bar {a}]\subset (0, 2)$ $\{\lambda _{n}\}\subset [0, \infty )$ such that

$$ \lambda_{n} = \left\{\begin{array}{l} \rho_{n}\frac{(\max_{i=1, 2, \dots, N}\|A_{i}x_{n}-P_{Q_{i}}A_{i}x_{n}\|)^{2}}{\|{\sum}_{i\in I(x_{n})}\gamma_{i,n}A^{*}_{i}(I-P_{Q_{i}})A_{i}x_{n}\|^{2}}, \text{ if }~\|{\sum}_{i\in I(x_{n})}\gamma_{i,n}A^{*}_{i}(I-P_{Q_{i}})A_{i}x_{n}\|>0,\\ 0, \qquad\qquad\qquad\qquad\qquad\qquad \text{ otherwise }. \end{array}\right. $$

(88)

For comparison purpose, we consider the values of the parameters appeared in the methods as follows. For Algorithms 1 and 3, we take β = 0.05, ${\rho ^{n}_{1}}=\frac {1}{10^{4}n+1}={\rho ^{n}_{2}}$ and $\vartheta _{i}=\frac {i}{12}, i=1,2,3$. For Algorithm 3, Scheme (14), and Scheme (87) $\alpha _{n}=\frac {1}{n+1}$. For Scheme (13) and Scheme (14), we take λ_n = 0.00005. For Scheme (14) and Scheme (87), we take f(x) = 0.975x. Moreover, for Scheme (87), we take $\gamma _{1,n}=\frac {1}{6}$, $\gamma _{2,n}=\frac {1}{3}$, $\gamma _{3,n}=\frac {1}{2}$ and $\rho _{n}=\frac {1}{10^{4}n+1}$. Using E_n = ∥x_n+ 1 − x_n∥² < 10^− 8 as stopping criteria, for different choices of the fixed point u and the initial point x₀, the results of numerical experiments are reported in Table 1 and Fig. 1.

Table 1 Comparison of Algorithms 1 and 3 with Scheme (13), Scheme (14), and Scheme (87) for different choices of u and x₀

Fig. 1

Comparison of Algorithm 1 and Algorithm 3 with Scheme (13), Scheme (14), and Scheme (87) for different choices of u and x₀

It can be observed from Table 1 and Fig. 1 that for each choices of (u,x₀), our proposed methods Algorithms 1 and 3 have better performance interms of the iteration numbers (Iter. (n)) and comparatively the CPU-run time in seconds (CPU(s)) than of the compared methods. More precisely, Algorithms 1 and 3 have less number of iterations and take small CPU-time to run than of the iterative methods given by Scheme (13), Scheme (14), and Scheme (87).

Example 2

Let H₁ = H₂ = L₂([0,2π]) with the inner product 〈.〉 defined by

$$ \quad \langle x, y\rangle = {\int}_{0}{\!}^{2\pi}x(t)y(t)dt,~~ \forall x, y \in L_{2}([0, 2\pi]) $$

and with the norm ∥.∥ defined by

$$ \|x||_{2}: = \sqrt{{\int}_{0}{\!}^{2\pi} |x(t)|^{2}dt},~~~\forall x, y \in L^{2}([0, 2\pi]). $$

Furthermore, we consider the following half-spaces

$$ C: = \left\{x\in L_{2}([0, 2\pi]): {\int}_{0}{\!}^{2\pi}x(t)dt \leq 1 \right\} \text{ and } Q: = \left\{y\in L_{2}([0, 2\pi]): {\int}_{0}{\!}^{2\pi}|y(t)-sin(t)|^{2}dt \leq 16 \right\}. $$

In addition, we consider a linear continuous operator A : L₂([0,2π]) → L₂([0,2π]), where (Ax)(t) = x(t). Then, (A^∗x)(t) = x(t) and ∥A∥ = 1. That is, A is an identity operator. The metric projection onto C and Q have an explicit formula [54]. We can also write the projections onto C and the projections onto Q as follows:

$$ P_{C}(x(t))=\left\{ \begin{array}{ll} x(t)+\frac{1-{\int}_{0}{\!}^{2\pi}x(t)dt}{4 {\pi}^{2}}, \text{ if } {\int}_{0}{\!}^{2\pi} x(t)dt > 1,\\ x(t), \text{ if } {\int}_{0}{\!}^{2\pi} x(t)dt \leq 1. \end{array}\right. $$

$$ P_{Q}(y(t))= \left\{\begin{array}{ll} sin(t)+\frac{4(y(t)-sin(t))}{\sqrt{{\int}_{0}{\!}^{2\pi}|y(t)-sin(t)|^{2}dt}},&\quad\qquad\text{if }~~{\int}_{0}{\!}^{2\pi}|y(t)-sin(t)|^{2}dt > 16,\\ y(t),&\quad\qquad\text{if }~~{\int}_{0}{\!}^{2\pi}|y(t)-sin(t)|^{2}dt \leq 16. \end{array}\right. $$

Now, we solve the following problem

$$ \text{ find } p^{*}\in C \text{ such that } Ap^{*}\in Q. $$

(89)

In this example, we examine the numerical behaviour of our proposed method: Algorithm 4 and compare it with the strongly convergent iterative algorithms given by Scheme (10) and Scheme (11) by solving problem (89). For comparison purpose, we take the following data: For Algorithm 4, we take, β = 0.05, ${\rho _{1}^{n}}={\rho _{2}^{n}}=\frac {n}{n+1}$ and $\alpha _{n}=\frac {1}{n+1}$. For Schemes (10) and (11), we take $\rho _{n}=\frac {n}{n+1}$ and $\alpha _{n}=\frac {1}{n+1}$.

Now, using E_n = ∥x_n+ 1 − x_n∥ < 10^− 4 as stopping criteria for all methods, for different choices of the fixed point u and the initial point x₀, the outcomes of the numerical experiments of the compared methods are reported in Table 2 and Fig. 2.

Table 2 Comparison of Algorithm 4 with Scheme (10) and Scheme (11) for different choices of u and x₀

Fig. 2

Comparison of Algorithm 4 with Scheme (10) and Scheme (11) for different choices of u, x₀

It can be observed from Table 2 and Fig. 2 that for each choices of u and x₀, Algorithm 4 is faster in terms of less number of iterations (Iter. (n)) and CPU-run time in seconds (CPU(s)) than the compared algorithms.

Example 3

The problem of computing sparse solutions (i.e., solutions where only a very small number of entries are nonzero) to linear inverse problems arises in a large number of application areas, for instance, in image restoration [55], channel equalization [56], echo cancellation [57], and stock market analysis [58]. The linear inverse problem consists of computing sparse solutions of a vector that has been digitized and has been degraded by an additive noise. Without loss of generality, for a vector x ∈ H₁ and an observed vector y ∈ H₂, a model including an additive noise can be written as

$$ y=Ax+\eta, $$

where A is a bounded linear operator between the two Hilbert spaces H₁ and H₂ and η ∈ H₂ denotes the additive noise.

Suppose that H₁ = H₂ = L²([0,1]) with norm $\|x\|:=\left ({{\int \limits }_{0}{\!}^{1}}|x(t)|^{2}dt\right )^{\frac {1}{2}}$ and inner product $\langle x, y\rangle :={{\int \limits }_{0}{\!}^{1}}x(t)y(t)dt$, x,y ∈ L²([0,1]). Define the Volterra integral operator $A:L^{2}([0,1])\rightarrow L^{2}([0,1])$ by

$$ Ax(t):={{\int}_{0}{\!}^{t}}x(s)ds, \forall x\in L^{2}([0,1]), t\in [0,1]. $$

Then, A is bounded linear monotone and $\|A\|=\frac {2}{\pi }$ (see [59, Problem 188, p100; Solution 188, p300]). Using Algorithm 4, we develop an iterative algorithm to recover the solution of the linear equation Ax = y − η. Furthermore, we compare the performance of our proposed Algorithm 4 and Scheme (10).

We are interested in solutions x^∗∈{x ∈ C : Ax ∈ Q}, where C is the cone of functions x(t) that are negative for t ∈ [0,0.25] and positive for t ∈ [0.25,1] and Q = [a(t),b(t)] := {y(t) : a(t) ≤ y(t) ≤ b(t),0 ≤ t ≤ 1} is a box delimited by the functions a(t) and b(t). The metric projection P_Q can be computed by formula:

$$ P_{Q}(y) :=max\{a, min\{y, b\}\}. $$

For some problems, the solution is almost sparse. To ensure the existence of the solution of the consider problem, K-sparse vector x^∗(t) is generated randomly in C. Taking y(t) = Ax^∗(t) and a(t) = y(t) − 0.01, b(t) = y(t) + 0.01, we have Q = [a(t),b(t)]. We take K = 30, K = 55 and K = 70 (see Fig. 3). The problem of interest is to find x ∈ C such that Ax ∈ Q.

Fig. 3

x^∗∈ C (left) and Ax^∗∈ Q (right) for K = 30,55,70

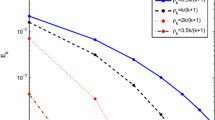
We compare the behavior of Algorithm 4 and Scheme (10) for the same initial point $x_{0}=e^{4t^{2}}$ and same fixed point u = t². Set ${\rho _{1}^{n}}=\frac {2n}{3n+1}={\rho _{2}^{n}}$ and $\alpha _{n}=\frac {1}{n}$ in Algorithm 4 and $\rho _{n}=\frac {2n}{3n+1}$ and $\alpha _{n}=\frac {1}{n}$ in Scheme (10). In the implementation, we take E_n < ε = 10^− 4 as the stopping criterion, where

$$ E_{n}=\|x-P_{C} x\|^{2}+\|Ax-P_{Q} Ax\|^{2}. $$

In Table 3, we present our numerical results with different K-sparse (K = 30, 55, 70). Table 3 shows the number of iterations and the time of execution in seconds (CPU(s)) of Algorithm 4 and Scheme (10). In Fig. 4, we report the behavior of Algorithm 4 and Scheme (10) for K = 30, 55, 70. Furthermore, Fig. 4 presents error value versus the iteration numbers. It can be seen that Algorithm 4 is significantly faster than Scheme (10). This shows the effectiveness of our proposed algorithms.

Table 3 Numerical results with different K-sparse

Fig. 4

Number of iterations and error estimate for Algorithm 4 and Scheme (10)