A second-order finite difference scheme for the multi-dimensional nonlinear time-fractional Schrödinger equation

Abstract

This paper is concerned with a linearized second-order finite difference scheme for solving the nonlinear time-fractional Schrödinger equation in d (d = 1,2,3) dimensions. Under a weak assumption on the nonlinearity, the optimal error estimate of the numerical solution is established without any restriction on the grid ratio. Besides the standard energy method, the key tools for analysis include the mathematical induction method, several inverse Sobolev inequalities, and a discrete fractional Gronwall-type inequality. The convergence rate of the proposed scheme is of O(τ² + h²) with time step τ and mesh size h. Numerical results are carried out to confirm the theoretical analysis.

1 Introduction

In this paper, we consider the d-dimensional (d = 1,2,3) nonlinear time-fractional Schrödinger (NTFS) equation

$$ \begin{array}{@{}rcl@{}} & i {}^{\mathcal{C}}_{0}\mathcal{D}_{t}^{\alpha} u + {\Delta} u + f(|u|^{2})u = 0, \quad {\text{x}} \in {\Omega}, 0 < t \leq T, \end{array} $$

(1.1)

with initial condition

$$ \begin{array}{@{}rcl@{}} & u({\text{x}}, 0) = u_{0}(\text{x}), \quad {\text{x}} \in \overline{\Omega}, \end{array} $$

(1.2)

and boundary condition

$$ \begin{array}{@{}rcl@{}} & u({\text{x}}, t) = 0, \quad {\text{x}} \in \partial {\Omega}, 0 \le t \le T, \end{array} $$

(1.3)

where $i = \sqrt {-1}$ is the imaginary unit, t is time variable, x is coordinate in $\mathbb {R}^{d}$, ${\Omega } \subset \mathbb {R}^{d}$ is a bounded computational domain, u = u(x,t) is the unknown complex-valued wave function, $f \in C^{1}(\mathbb {R}^{+})$ is a given real-valued function, u₀ is a given complex-valued function, and ${}^{\mathcal {C}}_{0}\mathcal {D}_{t}^{\alpha }$ with α ∈ (0,1) represents the Caputo fractional derivative defined by

$$^{\mathcal{C}}_{0}\mathcal{D}_{t}^{\alpha} u({\textbf{x}}, t) = \frac{1}{\Gamma(1-\alpha)} {{\int}_{0}^{t}} \frac{\partial u({\textbf{x}}, s)}{\partial s} \frac{1}{(t - s)^{\alpha}} ds. $$

(1.4)

Here Γ(⋅) denotes the standard gamma function ${\Gamma }(z)={\int \limits }_{0}^{\infty }t^{z-1}e^{-t} d t$. the NTFS equation is a widely used model for plenty of nature phenomena in physics [19, 38, 44, 46]. In recent years, extensive numerical studies have been carried out in the literature for solving time-fractional PDEs. As α tends to 1, the NTFS equation reduces to the famous nonlinear Schrödinger (NLS) equation. For numerical methods on solving NLS equation, we refer to [3, 5,6,7, 12, 16, 17, 26, 27, 31, 39, 40, 42, 43, 45, 47, 50, 52] and references therein.

In recent years, extensive numerical studies have been carried out in the literature for solving fractional partial differential equations. Those numerical methods can be roughly divided into two types, indirect ones and direct ones. The indirect methods [10, 11, 36, 37, 54] consider reformulating the time-fractional differential equations into integro-differential equations, while the direct methods [1, 4, 8, 9, 13, 15, 18, 20,21,22,23,24,25, 30, 32, 34, 35, 48, 49, 51] directly consider approximating the fractional derivative via some numerical schemes. From the practical implementation perspective, the direct methods are much easier to implement than the indirect methods. Most of the direct methods use finite difference method or finite element method in spatial direction which are of little difference from the numerical schemes of integro-differential equations.

In [33, 41], an L1 approximation to the Caputo fractional derivative was presented, where the truncation error of the time-fractional derivative is merely of O(τ^2−α). In order to improve the accuracy, an L1-2 formula [14] and an L2-1_σ formula [2] were proposed to approximate the Caputo fractional derivative with truncation error of O(τ^3−α). In fact, for the integer NLS equation, the L1-2 formula reduces to the famous second-order backward differentiation formula, and the L2-1_σ formula reduces to the famous Crank-Nicolson differentiation formula.

Though extensive numerical studies for time-fractional partial differential equations have been carried out in literature, few numerical methods are proposed for the multi-dimensional nonlinear time-fractional Schrödinger equation. In [25], Li, Wang and Zhang proposed a linearized L1-Galerkin finite element method to solve the nonlinear time-fractional Schrödinger equation in multi-dimensions. By a temporal-spatial error-splitting method and a fractional Gronwall-type inequality, they obtained the optimal error estimate of the numerical scheme without any grid ratio condition, and the convergence order is proved to be of O(τ^2−α + h^k) with time step τ and mesh size h. In [48], to improve the temporal accuracy, Wang et al. adopted the L2-1_σ method to approximate the Caputo time-fractional derivative and utilized the Galerkin finite element method in space to derive two numerical methods with second-order accuracy in time direction, then they established the optimal error estimates by using similar method in [25]. However, as far as we know, there is few analysis on finite difference scheme of the NTFS equation. Hence, we derive an accurate finite difference scheme for NTFS equation and establish the optimal error estimate in this work. In summary, the main contributions of this paper are threefold:

• (1) A linearized L2-1_σ finite difference scheme for the NTFS (1.1) with second-order accuracy in time is proposed;

• (2) The optimal error estimate of the proposed scheme is established without any restriction on the grid ratio. Meanwhile, a new analysis for an iterative procedure to obtain the numerical solution at the first time level is given.

• (3) A novel and concise analysis method is introduced to establish the optimal error estimate by combining the standard energy method, the mathematical induction method, inverse Sobolev inequalities, and a fractional Gronwall-type inequality. In fact, by using this new analysis method, one can avoid estimating the semi-H¹ norm or the semi-H² norm of the “error” function, which not only makes the new analysis method rather concise than the existing ones in the literature but also merely requires $f \in C^{1}(\mathbb {R}^{+})$ instead of $f \in C^{3}(\mathbb {R}^{+})$ required in existing works.

The rest of this paper is organized as follows. In Section 2, a linearized fully discrete numerical scheme is proposed and the main convergence result is stated. In Section 3, a time-fractional Gronwall-type inequality for L2-1_σ approximation is introduced and the L² error estimate of the numerical solution is established without any restriction on the grid ratio. In Section 4, several numerical examples are provided to verify our theoretical results. Finally, conclusions and future perspectives are drawn in Section 5.

2 An accurate finite difference scheme and main result

For simplicity, we here only consider the NTFS equation in two dimensions with computation domain Ω = (a,b) × (c,d). The extension to three-dimensional cases is straightforward with minor modification. The initial-boundary value problem of the two-dimensional NTFS equation reads

$$ \begin{array}{@{}rcl@{}} && i {}^{\mathcal{C}}_{0}D_{t}^{\alpha} u + {\Delta} u + f(|u|^{2})u = 0, \qquad\qquad (x,y) \in {\Omega}, 0 < t \le T, \end{array} $$

(2.1)

$$ \begin{array}{@{}rcl@{}} && u(x,y,t) = 0, \qquad\qquad\qquad\qquad {\kern26pt} (x,y) \in \partial {\Omega}, 0 < t \le T, \end{array} $$

(2.2)

$$ \begin{array}{@{}rcl@{}} && u(x,y,0) = u_{0}(x,y), \qquad\qquad\qquad{\kern16pt} (x,y) \in \overline{\Omega}. \end{array} $$

(2.3)

For a positive integer N, choose time step τ = T/N and denote time steps t_n = nτ, n = 0,1,2,⋯ ,N, where $0<T<T_{\max \limits }$ with $T_{\max \limits }$ the maximal existing time of the solution. Choose mesh sizes h₁ = (b − a)/J, h₂ = (d − c)/K with two positive integers J and K;let $h = \max \limits \{h_{1},h_{2}\}$ and $\tilde {h} = \min \limits \{h_{1},h_{2}\}$ satisfy $h \leq C_{0}\tilde {h}$ with C₀ a positive constant; and denote grid points (x_j,y_k) = (a + jh₁,c + kh₂) for j = 0,1,2,⋯ ,J,k = 0,1,2,⋯ ,K.

Introduce three index sets

$$ \begin{array}{@{}rcl@{}} \mathcal{T}_{h}^{0} &:=& \{(j,k) | j = 0,1,2,\cdots,J, \ k = 0,1,2,\cdots,K\},\\ \mathcal{T}_{h} &:=& \{(j,k) | j = 1,2,\cdots,J-1, \ k = 1,2,\cdots,K-1\},\\ {\Gamma}_{h} &:=& \mathcal{T}_{h}^{0}\backslash\mathcal{T}_{h}= \{(j,k) | (j,k)\in\mathcal{T}_{h}^{0}{,} (j,k)\notin\mathcal{T}_{h}\}, \end{array} $$

and three corresponding grid sets

$$ \overline{\Omega}_{h} := \big\{(x_{j},y_{k})| (j,k) \in \mathcal{T}_{h}^{0}\big\}, \quad {\Omega}_{h} := \big\{(x_{j},y_{k})| (j,k) \in \mathcal{T}_{h} \big\}, \quad \partial {\Omega}_{h} := \big\{(x_{j},y_{k})| (j,k) \in {\Gamma}_{h} \}. $$

From the notations of above index sets and corresponding grid sets, we can easily see that

$$ (j,k) \in \mathcal{T}_{h}^{0}{\Longleftrightarrow}(x_{j},y_{k})\in\overline{\Omega}_{h}, \quad (j,k) \in \mathcal{T}_{h}{\Longleftrightarrow}(x_{j},y_{k})\in{\Omega}_{h}, \quad (j,k) \in {\Gamma}_{h}{\Longleftrightarrow}(x_{j},y_{k})\in\partial {\Omega}_{h}. $$

For simplicity, we define a space of grid functions defined on $\overline {\Omega }_{h}$ as

$$ X_{h} := \{u_{h}=\{u_{j,k}\} |{u_{j,k}\in\mathbb{C} \text{ for }} (j,k) \in \mathcal{T}_{h}^{0} {\text{and}} u_{j,k} = 0 {\text{when}} (j,k) \in {\Gamma}_{h}\}. $$

We denote by $U_{j,k}^{n}$ and $u_{j,k}^{n}$ as the numerical approximation and the exact value of u at the point (x_j,y_k,t_n), respectively. For a grid function ωⁿ ∈ X_h, we introduce the L2-1_σ formula given in [2] to approximate the Caputo derivative, i.e.,

$$ \begin{array}{@{}rcl@{}} D_{\sigma}^{\alpha} \omega^{n} = \frac{1}{\mu}\bigg[C_{0}^{\sigma} \omega^{n+1} - \sum\limits_{s=1}^{n} (C_{n-s}^{\sigma} - C_{n-s+1}^{\sigma}) \omega^{s} - C_{n}^{\sigma} \omega^{0}\bigg] = \frac{1}{\mu} \sum\limits_{s=0}^{n} C_{n-s}^{\sigma} (\omega^{s+1} - \omega^{s}), \end{array} $$

where μ = τ^αΓ(2 − α), σ = 1 − α/2, and

$$ C_{l}^{\sigma} = \begin{cases} a_{0}^{\sigma} + b_{1}^{\sigma}, & \text{if } l = 0,\\ a_{l}^{\sigma} + b_{l+1}^{\sigma} - b_{l}^{\sigma}, & \text{if } l = 1,2,\cdots, n-1,\\ a_{n}^{\sigma} -b_{n}^{\sigma}, & \text{if } l = n, \end{cases} $$

with

$$ \begin{array}{@{}rcl@{}} a_{0}^{\sigma} &=&\sigma^{1-\alpha},\quad a_{l}^{\sigma} = (l+\sigma)^{1-\alpha} - (l+\sigma-1)^{1-\alpha}, \quad l \geq 1,\\ b_{l}^{\sigma} &=&\frac{1}{2-\alpha} \left[(l+\sigma)^{2-\alpha} - (l+\sigma-1)^{2-\alpha}\right] - \frac{1}{2} \left[(l+\sigma)^{1-\alpha} + (l+\sigma-1)^{1-\alpha}\right], \quad l \geq 1. \end{array} $$

Remark 2.1

Because L2 − 1_σ formula uses a linear interpolation at the last temporal layer which is different with the quadratic interpolation at other temporal layers, $C_{l}^{\sigma }$ depends on n, which means that $C_{l}^{\sigma }$ is different in every layers.

For a function v ∈ C³([0,T]), the local truncation error between $D_{\sigma }^{\alpha } v(t_{n})$ and ${}^{\mathcal {C}}_{0} D_{t}^{\alpha } v(t_{n+\sigma })$ satisfies [2]

$$ \left|D_{\sigma}^{\alpha} v(t_{n}) -{}^{\mathcal{C}}_{0} D_{t}^{\alpha} v(t_{n+\sigma})\right| = O(\tau^{3-\alpha}), $$

(2.4)

where t_n+σ = (n + σ)τ.

As usual, for any grid function ωⁿ ∈ X_h, we introduce the following finite difference quotient operators/notations,

$$ \begin{array}{@{}rcl@{}} && \delta_{x}^{+} \omega_{j,k}^{n} = \frac{1}{h_{1}} (\omega_{j+1,k}^{n} - \omega_{j,k}^{n}), \qquad\qquad\qquad\qquad \delta_{y}^{+} \omega_{j,k}^{n} = \frac{1}{h_{2}} (\omega_{j,k+1}^{n} - \omega_{j,k}^{n}),\\ && \delta_{x}^{2} \omega_{j,k}^{n} = \frac{1}{{h_{1}^{2}}} (\omega_{j-1,k}^{n} - 2\omega_{j,k}^{n} + \omega_{j+1,k}^{n}), \qquad\qquad{} \delta_{y}^{2} \omega_{j,k}^{n} = \frac{1}{{h_{2}^{2}}} (\omega_{j,k-1}^{n} - 2\omega_{j,k}^{n} + \omega_{j,k+1}^{n}),\\ && {\Delta}_{h} \omega_{j,k}^{n} = ({\delta_{x}^{2}} + {\delta_{y}^{2}}) \omega_{j,k}^{n}, \qquad\qquad\qquad\qquad\qquad \hat{\omega}_{j,k}^{n+\sigma} = (1+\sigma) \omega_{j,k}^{n} - \sigma \omega_{j,k}^{n-1},\\ && \omega_{j,k}^{n+\sigma} = (1-\sigma) \omega_{j,k}^{n}+ \sigma \omega_{j,k}^{n+1}. \end{array} $$

For any grid functions w,v ∈ X_h, we define discrete inner products and discrete norms over X_h as

$$ \begin{array}{@{}rcl@{}} &&\langle{w,v}\rangle := h_{1} h_{2} \sum\limits_{j=1}^{J-1} \sum\limits_{k=1}^{K-1} w_{j,k} \overline{v_{j,k}}, \quad \langle{\delta_{x}^{+} w,\delta_{x}^{+} v}\rangle_{0} := h_{1} h_{2} \sum\limits_{j=0}^{J-1} \sum\limits_{k=1}^{K-1} \delta_{x}^{+} w_{j,k}\delta_{x}^{+} \overline{v_{j,k}},\\ &&\langle{\delta_{y}^{+} w,\delta_{y}^{+} v}\rangle_{0} := h_{1} h_{2} \sum\limits_{j=1}^{J-1} \sum\limits_{k=0}^{K-1} \delta_{y}^{+} w_{j,k}\delta_{y}^{+} \overline{v_{j,k}},\quad \|w\| := \langle{w,w}\rangle^{\frac{1}{2}}, \\ && |w|_{1} := \left[\langle{\delta_{x}^{+} w, \delta_{x}^{+} w}\rangle_{0} + \langle{\delta_{y}^{+} w, \delta_{y}^{+} w}\rangle_{0}\right]^{\frac{1}{2}}, \quad |w|_{2} := \langle{{\Delta}_{h} w, {\Delta}_{h} w}\rangle^{\frac{1}{2}},\\ &&\|w\|_{1} := (\|w\|^{2} + |w|_{1}^{2})^{\frac{1}{2}}, \quad \|w\|_{2} \!:=\! (\|w\|_{1}^{2} + |w|_{2}^{2})^{\frac{1}{2}}, \quad \|w\|_{\infty} := \max_{(j,k)\in\mathcal{T}_{h}} |w_{j,k}|, \end{array} $$

where $\overline {\nu }$ is the complex conjugate of ν, |w|₁ and |w|₂ are semi-norms of the grid function w ∈ X_h, and ∥w∥,∥w∥₁,∥w∥₂ are norms of the grid function w ∈ X_h.

Throughout the paper, we denote C as a generic positive constant which depends on the regularity of the exact solutions and the given data but is independent of the time step τ and the grid size h.

2.1 Finite difference scheme

Now, we give the following finite difference scheme to solve the problem (2.1)–(2.3) as

$$ \begin{array}{@{}rcl@{}} &&\textit{i} D_{\sigma}^{\alpha} U_{j,k}^{n} + {\Delta}_{h} {U}_{j,k}^{n+\sigma} + f(|\hat{U}_{j,k}^{n+\sigma}|^{2})\hat{U}_{j,k}^{n+\sigma} = 0, \quad (j,k) \in \mathcal{T}_{h},\\ && \qquad\textit{n}=1,2,\cdots,{N-1}, \end{array} $$

(2.5)

$$ \begin{array}{@{}rcl@{}} && U_{j,k}^{n}= 0,\quad(j,k)\in {\Gamma}_{h}, n=1,2,\cdots,{N}, \end{array} $$

(2.6)

$$ \begin{array}{@{}rcl@{}} && U_{j,k}^{0}=u_{0}(x_{j},t_{n}), \quad(j,k)\in\mathcal{T}_{h}^{0}. \end{array} $$

(2.7)

Due to the local extrapolation used in approximating the nonlinear term, the above scheme is not self-starting. In order to start it, we introduce the following iterative algorithm to obtain $U^{1}=U^{1,m_{\alpha }}\in {X_{h}}$:

$$ \begin{array}{@{}rcl@{}} &&i \frac{\sigma^{1-\alpha}}{\mu} ({U}_{j,k}^{1,s} - U_{j,k}^{0}) + {\Delta}_{h} {W}_{j,k}^{1,s} + f(|{W}_{j,k}^{1,s-1}|^{2}) {W}_{j,k}^{1,s-1} = 0,\quad (j,k)\in\mathcal{T}_{h},\\ &&\qquad s = 1,2,\cdots,m_{\alpha}, \end{array} $$

(2.8)

$$ \begin{array}{@{}rcl@{}} && {U}_{j,k}^{1}=0,\quad {U}_{j,k}^{1,s}=0,\quad(j,k)\in {\Gamma}_{h}, s = 1,2,\cdots,m_{\alpha}, \end{array} $$

(2.9)

$$ \begin{array}{@{}rcl@{}} &&{U}_{j,k}^{1,0} = U_{j,k}^{0}, \quad (j,k)\in\mathcal{T}_{h}^{0}, \end{array} $$

(2.10)

where $m_{\alpha }:=\left [\frac {1}{\alpha } + \frac {1}{2}\right ]$ and W^1,s = (1 − σ)U⁰ + σU^1,s for s = 0,1,2,⋯ ,m_α.

Remark 2.2

For the integer NLS equation (α = 1), the above iterative algorithm reduces to a two-level linearized implicit scheme in which the approximations of the linear terms and the nonlinear terms are implicit and explicit, respectively.

2.2 Main result

In this paper, we assume that the exact solution satisfies

$$ \begin{array}{@{}rcl@{}} &\|u\|_{C^{2}([\varepsilon,T];W^{2,\infty}({\Omega}))} + \|u\|_{C([\varepsilon,T];W^{4,\infty}({\Omega}))} + \|u\|_{C^{3}([\varepsilon,T];L^{2}({\Omega}))} \leq {C}, \end{array} $$

(2.11)

with positive number ε arbitrarily small.

Remark 2.3

In order to deal with the singularity of the time-fractional derivative (1.4) at time t = 0, we give a particular two-level scheme (i.e., the scheme (2.8)–(2.10)) to solve the numerical solution at the first level. And we can see from the analysis of the local truncation error and convergence rate of the two-level scheme, we just need to require that the exact solution u at the initial time interval [0,τ] satisfies ${\int \limits }_{0}^{\tau } \|u_{t}(\cdot , cdot, \theta \tau )\| d\theta \leq C$.

We now state our main theoretical result in the following theorem.

Theorem 2.1

Suppose that the system (2.1)–(2.3) has a unique solution u = u(x,y,t) satisfying (2.11), then the scheme (2.5)–(2.10) has a unique solution Uⁿ ∈ X_h for n = 0,1,2,⋯ ,N satisfying

$$ \begin{array}{@{}rcl@{}} &\|u^{n} - U^{n}\| \leq C (\tau^{2} + h^{2}), \quad \|U^{n}\|_{\infty} \leq C, \quad n=1,2,\cdots,N, \end{array} $$

(2.12)

where uⁿ ∈ X_h with $u_{j,k}^{n}=u(x_{j},y_{k},t_{n})$.

3 Error analysis

In this section, we aim to prove the optimal error estimate given in Theorem 2.1. At first, let us introduce several lemmas which will be frequently used in our analysis.

Lemma 3.1

[28, 29, 48] Suppose that the nonnegative sequences {ωⁿ,gⁿ|n = 0,1,2,⋯} satisfy and

$$ \begin{array}{@{}rcl@{}} D_{\sigma}^{\alpha} \omega^{0} &\leq& \lambda_{1} \omega^{1} + \lambda_{2} \omega^{0} + g^{0}, \end{array} $$

(3.1)

$$ \begin{array}{@{}rcl@{}} D_{\sigma}^{\alpha} \omega^{n} &\leq& \lambda_{1} \omega^{n+1} + \lambda_{2} \omega^{n} + \lambda_{3} \omega^{n-1} + g^{n}, \end{array} $$

(3.2)

where λ₁ > 0,λ₂ > 0,λ₃ > 0 are given constants independent of τ. Then there exists a positive constant τ^∗ suchthat,when0 <τ ≤ τ^∗, there is

$$ \omega^{n} \leq \left( 6 \omega^{0} + \frac{12 t_{n}^{\alpha}}{\Gamma(1+\alpha)} \underset{0 \leq {l} \leq n}{\max} g^{l}\right) E_{\alpha}(2 \lambda t_{n}^{\alpha}), \quad {n}\geq{1}. $$

(3.3)

Here, $E_{\alpha }(z) = {\sum }_{k=0}^{\infty } \frac {z^{k}}{\Gamma (1+k\alpha )}$ is the Mittag-Leffler function, and $\lambda = 6 \lambda _{1} + \frac {C_{0}^{\sigma } \lambda _{2}}{C_{0}^{\sigma } - C_{1}^{\sigma }} + \frac {C_{0}^{\sigma } \lambda _{3}}{C_{1}^{\sigma } - C_{2}^{\sigma }}$.

The time-fractional Gronwall inequality given in Lemma 3.1 plays a crucial role in our analysis work, and we give another different and direct proof of the inequality in the Appendix section.

Remark 3.1

Under some particular condition, the time-fractional Gronwall inequality given in Lemma 3.1 can be viewed as a spatial case of the one given in [29] where the nonuniform time step is allowed, and they proved it by using the discrete convolution method. This also means that our proposed scheme can be generalized to the nonuniform time stepping case, and the convergence results can be proved similarly by using our analysis method together with the time-fractional Gronwall inequality given in [29].

Lemma 3.2

[53] For any grid function v ∈ X_h, there is

$$ \|v\|_{\infty} \le C \|v\|^{\frac{1}{2}} (\|v\| + |v|_{2})^{\frac{1}{2}}{.} $$

(3.4)

Lemma 3.3

For any grid function v ∈ X_h, there is

$$ \begin{array}{@{}rcl@{}} & \|v\|_{\infty} \le C_{0}h^{-1}\|v\|, \end{array} $$

(3.5)

where C₀ is the constant used to limit the mesh ratio in both directions of space.

Proof

From the definition of the maximum norm and the discrete L² norm, we have

$$ \begin{array}{@{}rcl@{}} & \|v\|_{\infty}^{2}\leq{h}_{1}^{-1}{h}_{2}^{-1}\|v\|^{2}\leq{\tilde{h}}^{-2}\|v\|^{2}\leq{(C_{0})}^{2}{h}^{-2}\|v\|^{2}, \end{array} $$

where $h\leq {C_{0}} {\tilde {h}}$ was used. This immediately gives (3.5). □

Lemma 3.4 (Lemma 3 in 48)

For any grid function ωⁿ ∈ X_h, there are

$$ \begin{array}{@{}rcl@{}} &&{\text{Im}} {\langle} {\Delta}_{h} \omega^{n+\sigma}, \omega^{n+\sigma} {\rangle}= 0,\quad n=0,1,2,\cdots,N-1, \end{array} $$

(3.6)

$$ \begin{array}{@{}rcl@{}} &&{\text{Re}} {\langle} D_{\sigma}^{\alpha} \omega^{n}, \omega^{n+\sigma} {\rangle}\ge \frac{1}{2} D_{\sigma}^{\alpha} \|\omega^{n}\|,\quad n=0,1,2,\cdots,N-1, \end{array} $$

(3.7)

where Im(ν) and Re(ν) denote the imaginary part and the real part of ν, respectively.

Lemma 3.5

For any grid function ωⁿ ∈ X_h, there is

$$ \begin{array}{@{}rcl@{}} & ||D_{\sigma}^{\alpha} \omega^{n}||\leq {C}\tau^{-\alpha}\sqrt{\sum\limits_{s=0}^{n+1}||\omega^{s}||^{2}},\quad n=1,2,\cdots, N-1. \end{array} $$

(3.8)

Proof

Combining $C_{0}^{\sigma } \geq C_{1}^{\sigma } \geq {\cdots } \ge C_{N-1}^{\sigma } \geq 0$ with

$$ \begin{array}{@{}rcl@{}} C_{0}^{\sigma} &=& a_{0}^{\sigma} + b_{1}^{\sigma} \\ &=& \sigma^{1-\alpha} + \frac{1}{2-\alpha} \big[(1+\sigma)^{2-\alpha} - \sigma^{2-\alpha}\big] - \frac{1}{2}\big[(1+\sigma)^{1-\alpha} + \sigma^{1-\alpha}\big]\\ &=& \frac{1}{2-\alpha} \big[ (1+\sigma)^{2-\alpha} - \sigma^{2-\alpha}\big]-\frac{1}{2} \big[(1+\sigma)^{1-\alpha} - \sigma^{1-\alpha}\big]\\ &\leq& \frac{1}{2-\alpha} \big[ (1+\sigma)^{2-\alpha} - \sigma^{2-\alpha}\big] = {{\int}_{0}^{1}} (\sigma + z)^{1-\alpha}dz \leq 2 \end{array} $$

gives

$${0}\leq{C}_{l}^{\sigma} \leq 2,\quad l=0,1,2\cdots,N-1.$$

Then, by using Cauchy-Schwarz inequality, we have

$$ \begin{array}{@{}rcl@{}} \|D_{\sigma}^{\alpha} \omega^{n}\|^{2} &=& h_{1} h_{2} \sum\limits_{j=1}^{J-1} \sum\limits_{k=1}^{K-1} \frac{1}{\mu^{2}} \bigg[C_{0}^{\sigma} \omega_{j,k}^{n+1} - \sum\limits_{s=1}^{n} (C_{n-s}^{\sigma} - C_{n-s+1}^{\sigma}) \omega_{j,k}^{s} - C_{n}^{\sigma} \omega_{j,k}^{0}\bigg]^{2}\\ &\leq& \frac{3}{\mu^{2}} {h_{1} h_{2}}\sum\limits_{j=1}^{J-1} \sum\limits_{k=1}^{K-1} \bigg[\big|C_{0}^{\sigma} \omega_{j,k}^{n+1}\big|^{2} + \Big|\sum\limits_{s=1}^{n} (C_{n-s}^{\sigma} - C_{n-s+1}^{\sigma}) \omega_{j,k}^{s}\Big|^{2} + \big|C_{n}^{\sigma} \omega_{j,k}^{0}\big|^{2}\bigg]\\ &\leq& \frac{3}{\mu^{2}} {h_{1} h_{2}}\sum\limits_{j=1}^{J-1} \sum\limits_{k=1}^{K-1} \bigg[ \big|C_{0}^{\sigma} \big|^{2} \big|\omega_{j,k}^{n+1} \big|^{2} + \sum\limits_{s=1}^{n} \big|C_{n-s}^{\sigma} - C_{n-s+1}^{\sigma} \big|^{2} \sum\limits_{s=1}^{n} \big|\omega_{j,k}^{s} \big|^{2} + \big|C_{n}^{\sigma} \big|^{2} \big|\omega_{j,k}^{0} \big|^{2} \bigg]\\ &\leq& \frac{6}{\mu^{2}} {h_{1} h_{2}}\sum\limits_{j=1}^{J-1} \sum\limits_{k=1}^{K-1} \bigg[C_{0}^{\sigma} \big|\omega_{j,k}^{n+1}\big|^{2} + \sum\limits_{s=1}^{n} (C_{n-s}^{\sigma} - C_{n-s+1}^{\sigma}) \sum\limits_{s=1}^{n} \big|\omega_{j,k}^{s}\big|^{2} + C_{n}^{\sigma} \big|\omega_{j,k}^{0}\big|^{2}\bigg]\\ &=& \frac{6}{\mu^{2}} {h_{1} h_{2}} \sum\limits_{j=1}^{J-1} \sum\limits_{k=1}^{K-1} \bigg[C_{0}^{\sigma} \big|\omega_{j,k}^{n+1}\big|^{2} + (C_{0}^{\sigma} - C_{n}^{\sigma}) \sum\limits_{s=1}^{n} \big|\omega_{j,k}^{s}\big|^{2} + C_{n}^{\sigma}\big|\omega_{j,k}^{0}\big|^{2}\bigg]\\ &\leq& \frac{6C_{0}^{\sigma}}{\mu^{2}} {h_{1} h_{2}} \sum\limits_{s=0}^{n+1} \sum\limits_{j=1}^{J-1} \sum\limits_{k=1}^{K-1} |\omega_{j,k}^{s}|^{2}\leq \frac{12}{\mu^{2}} \sum\limits_{s=0}^{n+1} \|\omega^{s}\|^{2}. \end{array} $$

It follows that

$$ \begin{array}{@{}rcl@{}} &\|D_{\sigma}^{\alpha} \omega^{n}\|\leq\frac{\sqrt{12}}{\mu}\sqrt{ \sum\limits_{s=0}^{n+1} \|\omega^{s}\|^{2}} \leq{C}{\tau^{-\alpha}}\sqrt{ \sum\limits_{s=0}^{n+1} \|\omega^{s}\|^{2}}. \end{array} $$

This completes the proof of Lemma 3.5. □

3.1 Local truncation error

We define the local truncation errors $P^{n+\sigma }\in {X_{h}}, {P}^{\sigma ,s}\in {X_{h}}$ of the scheme (2.5)–(2.10) as follows,

$$ \begin{array}{@{}rcl@{}} &&P_{j,k}^{n+\sigma}:= i D_{\sigma}^{\alpha} u_{j,k}^{n} + {\Delta}_{h} u_{j,k}^{n+\sigma}+ f(|\hat{u}_{j,k}^{n+\sigma}|^{2})\hat{u}_{j,k}^{n+\sigma},\quad (j,k)\in\mathcal{T}_{h}, \\ && \qquad n = 1,2,\cdots,N-1, \end{array} $$

(3.9)

$$ \begin{array}{@{}rcl@{}} && {P}_{j,k}^{\sigma,s}:= i D_{\sigma}^{\alpha{u}_{j,k}{0}} + {\Delta}_{h} u_{j,k}^{\sigma} + f(|u_{j,k}^{\sigma}|^{2})u_{j,k}^{\sigma} ,\quad (j,k)\in\mathcal{T}_{h}, \\ && \qquad s=0,1,2,\cdots,m_{\alpha}, \end{array} $$

(3.10)

Noticing the initial-boundary value problem (2.1)–(2.3), one can see that

$$ \begin{array}{@{}rcl@{}} P_{j,k}^{n+\sigma} &=&i\left[D_{\sigma}^{\alpha} u_{j,k}^{n} - {}^{\mathcal{C}}_{0}D_{t}^{\alpha}u(x_{j},y_{k},t_{n+\sigma})\right] + {\Delta}_{h} u_{j,k}^{n+\sigma} - {\Delta} u(x_{j},y_{k},t_{n+\sigma})+ f\left( |\hat{u}_{j,k}^{n+\sigma}|^{2}\right)\hat{u}_{j,k}^{n+\sigma}\\ && - f\left( |u(x_{j},y_{k},t_{n+\sigma})|^{2}\right)u(x_{j},y_{k},t_{n+\sigma}),\quad (j,k)\in\mathcal{T}_{h}, n = 1,2,\cdots,N-1, \end{array} $$

(3.11)

$$ \begin{array}{@{}rcl@{}} {P}_{j,k}^{\sigma,s} &=& i\left( D_{\sigma}^{\alpha{u}{j,k}^{0}} - {}^{\mathcal{C}}_{0}D_{t}^{\alpha} u(x_{j},y_{k},t_{\sigma}) \right) + {\Delta}_{h} u_{j,k}^{\sigma} - {\Delta} u(x_{j},y_{k},t_{\sigma})+ f\left( |u_{j,k}^{\sigma}|^{2}\right)u_{j,k}^{\sigma}\\ && - f(|u(x_{j},y_{k},t_{\sigma})|)u(x_{j},y_{k},t_{\sigma}), \quad (j,k)\in\mathcal{T}_{h}, s=0,1,2,\cdots,m_{\alpha}-1. \end{array} $$

(3.12)

Under assumption (2.11), one can use the standard Taylor’s expansion to obtain that

$$ \begin{array}{@{}rcl@{}} &&D_{\sigma}^{\alpha} u_{j,k}^{n} = {}^{\mathcal{C}}_{0} D_{t}^{\alpha} u(x_{j},y_{k},t_{n+\sigma}) + O(\tau^{3-\alpha}),\quad {\Delta}_{h} u_{j,k}^{n} = {\Delta} u(x_{j},y_{k},t_{n}) + O(h^{2}),\\ && u_{j,k}^{n+\sigma} = u(x_{j},y_{k},t_{n+\sigma}) + O(\tau^{2}),\quad \hat{u}_{j,k}^{n+\sigma} = u(x_{j},y_{k},t_{n+\sigma}) + O(\tau^{2}),\\ &&f(|\hat{u}_{j,k}^{n+\sigma}|^{2})\hat{u}_{j,k}^{n+\sigma} = f(|u(x_{j},y_{k},t_{n+\sigma})|^{2})u(x_{j},y_{k},t_{n+\sigma})+ O(\tau^{2}),\\ && f(|u_{j,k}^{\sigma}|^{2})u_{j,k}^{\sigma} = f(|u(x_{j},y_{k},t_{\sigma})|)u(x_{j},y_{k})+ O(\tau^{2}). \end{array} $$

Substituting the above equations into (3.11)–(3.12) gives

Lemma 3.6

Under assumption (2.11), we have the following estimates of the local truncation errors:

$$ \begin{array}{@{}rcl@{}} &&\|{P}^{n+\sigma}\| \le C (h^{2} + \tau^{2}), \quad \textit{n} =0, 1,2,\cdots,N-1, \end{array} $$

(3.13)

$$ \begin{array}{@{}rcl@{}} &&\|{P}^{\sigma,s}\| \le C (h^{2} + \tau^{2}), \quad \textit{s} = 0,1,2,\cdots,m_{\alpha}. \end{array} $$

(3.14)

3.2 Proof of the main result

This subsection aims to give the proof of Theorem 2.1. For simplicity of notations, we define the “error” functions e^1,s ∈ X_h, eⁿ ∈ X_h for n = 0,1,⋯ ,N as

$$ e_{j,k}^{1,s} = u_{j,k}^{1} - U_{j,k}^{1,s}, \quad e_{j,k}^{n} = u_{j,k}^{n} - U_{j,k}^{n}, \quad (j,k)\in\mathcal{T}_{h}^{0}, s=0,1,2,\cdots,m_{\alpha}. $$

(3.15)

Then we obtain the following “error” equations by subtracting (2.5)–(2.10) from (3.10)–(3.9),

$$ \begin{array}{@{}rcl@{}} &&\textit{i} D_{\sigma}^{\alpha} e_{j,k}^{n} + {\Delta}_{h} e_{j,k}^{n+\sigma}+ {R}_{j,k}^{n+\sigma} = P_{j,k}^{n+\sigma},\quad (j,k)\in\mathcal{T}_{h}, \\ &&\textit{n} =0, 1,2,\cdots,N-1, \end{array} $$

(3.16)

$$ \begin{array}{@{}rcl@{}} &&\textit{i} \frac{\sigma^{1-\alpha}}{\mu} {e}_{j,k}^{1,s} + \sigma{\Delta}_{h} e_{j,k}^{1,s}+ {R}_{j,k}^{1,s-1} = P_{j,k}^{\sigma,s},\quad (j,k)\in\mathcal{T}_{h}, \textit{s} = 1,2,\cdots,m_{\alpha},\\ \end{array} $$

(3.17)

where

$$ \begin{array}{@{}rcl@{}} && {R}_{j,k}^{n+\sigma} = f(|\hat{u}_{j,k}^{n+\sigma}|^{2})\hat{u}_{j,k}^{n+\sigma} - f(|\hat{U}_{j,k}^{n+\sigma}|^{2})\hat{U}_{j,k}^{n+\sigma}, \quad n = 1,2,\cdots, N - 1, \end{array} $$

(3.18)

$$ \begin{array}{@{}rcl@{}} && {R}_{j,k}^{1,s-1} = f(|u_{j,k}^{\sigma}|^{2})u_{j,k}^{\sigma} - f(| {W}_{j,k}^{1,s-1}|^{2}) {W}_{j,k}^{1, s-1}, \quad s=1,2,\cdots,m_{\alpha}. \end{array} $$

(3.19)

Lemma 3.7

Under assumption (2.11), we have the following estimates of the “error” functions e^1,s,

$$ \begin{array}{@{}rcl@{}} \| {e}^{1,s}\| &\le& {C}\tau^{(s-\frac{1}{2})\alpha} (h^{2} +\tau), \quad \textit{s} = 1,2,\cdots,m_{\alpha}, \end{array} $$

(3.20)

$$ \begin{array}{@{}rcl@{}} | {e}^{1,s}|_{2} &\le& {C}\tau^{(s-\frac{3}{2})\alpha} (h^{2}+\tau), \quad \textit{s} = 1,2,\cdots,m_{\alpha}. \end{array} $$

(3.21)

Proof

Here we use mathematical induction method to prove this lemma in three steps.

Step 1. when s = 0, we obtain from (3.15) and (2.10) that

$$ \begin{array}{@{}rcl@{}} &&{e}_{j,k}^{1,0} = u_{j,k}^{1} - {u}_{j,k}^{0}={\tau{\int}_{0}^{1}}u_{t}(x_{j},y_{k},\theta\tau)d\theta, \end{array} $$

(3.22)

which together with (2.11) gives

$$ \begin{array}{@{}rcl@{}} &&\| {e}^{1,0}\| \leq {C}\tau. \end{array} $$

(3.23)

Step 2. when s = 1, we have

$$ \begin{array}{@{}rcl@{}} {R}_{j,k}^{1,0} &=&f(|u_{j,k}^{\sigma}|^{2})u_{j,k}^{\sigma}- f(| {u}_{j,k}^{0}|^{2}){u}_{j,k}^{0}\\ &=&[f(|u_{j,k}^{\sigma}|^{2})- f(| {u}_{j,k}^{0}|^{2})]{u}_{j,k}^{\sigma}+ f(| {u}_{j,k}^{0}|^{2})({u}_{j,k}^{\sigma}-{u}_{j,k}^{0})\\ &=&[f(|u_{j,k}^{\sigma}|^{2})- f(| {u}_{j,k}^{0}|^{2})]{u}_{j,k}^{\sigma}+ {\sigma}f(| {u}_{j,k}^{0}|^{2})({u}_{j,k}^{1}-{u}_{j,k}^{0})\\ &=&f^{\prime}(\xi){\sigma}\left[\overline{u_{j,k}^{\sigma}}e_{j,k}^{1,0}+((1-\sigma)u_{j,k}^{0} + \sigma u_{j,k}^{1,s-1})\overline{e_{j,k}^{1,0}}\right]{u}_{j,k}^{\sigma}\\ &&+ {\sigma}f(|{u}_{j,k}^{0}|^{2}){e}_{j,k}^{1,0}, \end{array} $$

(3.24)

where ξ is some number between $|{u}_{j,k}^{0}|^{2}$ and $|{u}_{j,k}^{\sigma }|^{2}$. This together with $f \in C^{1}(\mathbb {R}^{+})$ gives

$$ \begin{array}{@{}rcl@{}} ||{R}^{1,0}||\leq & C ||{e}^{1,0}||. \end{array} $$

(3.25)

For s = 1 in (3.17), computing the inner product of (3.17) with e^1,1, and taking the imaginary part, we arrive at

$$ \begin{array}{@{}rcl@{}} \|e^{1,1}\| &\le&\frac{\mu}{\sigma^{1-\alpha}} \left( \|{R}^{1,0}\| + \|{P}^{\sigma,0}\|\right) \le C {\Gamma}(2-\alpha) \sigma^{\alpha-1} \tau^{\alpha} \left( h^{2} +\tau\right)\\ &\leq& C \tau^{\left( s-\frac{1}{2}\right) \alpha} \left( h^{2} + \tau\right), \end{array} $$

(3.26)

where (3.14) and (3.23) were used. In order to estimate |e^1,1|₂, we rewrite (3.17) with s = 1 into

$$ \begin{array}{@{}rcl@{}} {\Delta}_{h} {e}_{j,k}^{1,1} = -\frac{i \sigma^{-\alpha}}{\mu} {e}_{j,k}^{1,1} - \sigma^{-1} {R}_{j,k}^{1,0} + \sigma^{-1}{P}_{j,k}^{\sigma,0}, \end{array} $$

(3.27)

then taking the discrete L² norm of both sides of (3.27), we have

$$ \begin{array}{@{}rcl@{}} | {e}^{1,1}|_{2} &\leq& \frac{\sigma^{-\alpha}}{\mu} \| {e}^{1,1}\| + \sigma^{-1} \| {R}^{1,0}\| + \sigma^{-1} \| {P}^{\sigma,0}\|\\ &\leq& {C} \sigma^{-1} (h^{2} + \tau) + {C} \sigma^{-1} \tau + {C} \sigma^{-1} (h^{2} + \tau^{2})\\ &\leq& C \sigma^{-1} (h^{2} +\tau)\\ &\leq& C \tau^{(s-\frac{3}{2}) \alpha} (h^{2} + \tau), \end{array} $$

(3.28)

where (3.14), (3.23) and (3.25) were used. Therefore, (3.20) and (3.21) hold for s = 1.

Step 3. With mathematical induction method, we suppose that (3.20) holds for s ≤ m − 1 with 2 ≤ m ≤ m_α, i.e.,

$$ \begin{array}{@{}rcl@{}} \| {e}^{1,s}\| &\leq& C \tau^{(s-\frac{1}{2})\alpha}(h^{2}+\tau),\\ | {e}^{1,s}|_{2} &\leq& C \tau^{(s-\frac{3}{2})\alpha} (h^{2}+\tau), s = 1,2,\cdots, m-1, \end{array} $$

(3.29)

this together with Lemma 3.2 gives

$$ \begin{array}{@{}rcl@{}} \|{e}^{1,s}\|_{\infty} &\leq& C \|{e}^{1,s}\|^{\frac{1}{2}} (\|{e}^{1,s}\| + |{e}^{1,s}|_{2})^{\frac{1}{2}} \leq C \tau^{(s-1)\alpha} (h^{2} +\tau)\\ &\le& C (h^{2} +\tau),\quad \textit{s} = 1,2,\cdots, m-1. \end{array} $$

(3.30)

Hence, for sufficiently small τ and h, we have

$$ \begin{array}{@{}rcl@{}} \|{U}^{1,s}\|_{\infty} \leq \|{u}^{1}\|_{\infty} + \|{e}^{1,s}\|_{\infty} \leq C,\quad s = 1,2,\cdots, m-1. \end{array} $$

(3.31)

Noting $f\in C^{1}(\mathbb {R}^{+})$ and using differential mean value theorem, we obtain

$$ \begin{array}{@{}rcl@{}} {R}_{j,k}^{1,m-1} & = &f(|u_{j,k}^{\sigma}|^{2})u_{j,k}^{\sigma} - f(|(1 - \sigma){u}_{j,k}^{0} + \sigma{U}_{j,k}^{1,m-1}|^{2})((1-\sigma){u}_{j,k}^{0}+\sigma{U}_{j,k}^{1,m-1})\\ &=&[f(|u_{j,k}^{\sigma}|^{2})- f(|(1-\sigma){u}_{j,k}^{0}+\sigma{U}_{j,k}^{1,m-1}|^{2})]{u}_{j,k}^{\sigma}\\ &&+ {\sigma}f(|(1-\sigma){u}_{j,k}^{0}+\sigma{U}_{j,k}^{1,m-1}|^{2})({u}_{j,k}^{1}-{U}_{j,k}^{1,m-1})\\ &=&f^{\prime}(\xi){\sigma}\left[\overline{u_{j,k}^{\sigma}}e_{j,k}^{1,m-1}+((1-\sigma)u_{j,k}^{0} + \sigma {U}_{j,k}^{1,m-1})\overline{e_{j,k}^{1,m-1}}\right]{u}_{j,k}^{\sigma}\\ &&+{\sigma}f(|(1-\sigma){u}_{j,k}^{0}+\sigma{U}_{j,k}^{1,m-1}|^{2})\overline{{e}_{j,k}^{1,m-1}}, \end{array} $$

(3.32)

where ξ is some number between $|(1-\sigma ){u}_{j,k}^{0}+\sigma {u}_{j,k}^{1}|^{2}$ and $|(1-\sigma ){u}_{j,k}^{0}+\sigma {U}_{j,k}^{1,m-1}|^{2}$. Combining (3.32) together with assumption (2.11) and (3.31) gives

$$ \begin{array}{@{}rcl@{}} ||{R}^{1,m-1} || \leq&{C} \sigma ||{e}^{1,m-1}||. \end{array} $$

(3.33)

Next, we will show that (3.20) and (3.21) hold for s = m. To do this, for s = m in (3.17), by computing the inner product of (3.17) with e^1,m and taking the imaginary part of the result, we have

$$ \frac{\sigma^{1-\alpha}}{\mu} \|{e}^{1,m}\|^{2} = -{\text{Im}}{\langle} {R}^{1,m-1}, {e}^{1,m}{\rangle} + {\text{Im}}{\langle} {P}^{1,m-1}, {e}^{1,m}{\rangle}, $$

(3.34)

which implies

$$ \begin{array}{@{}rcl@{}} \|{e}^{1,m}\| &\leq& \frac{\mu}{\sigma^{1-\alpha}} (\|{R}^{1,m-1}\| + \|{P}^{1,m-1}\|) \\ &\leq& C {\Gamma}(2-\alpha) \sigma^{\alpha-1} \tau^{\alpha} \tau^{(m-2)\alpha}(h^{2} +\tau)\\ &\leq& C \tau^{(m-\frac{3}{2})\alpha}(h^{2}+\tau) \le C \tau^{\frac{\alpha}{2} }(h^{2}+\tau), \end{array} $$

(3.35)

where (3.14), (3.29) and (3.33) where used. In order to estimate $\|{e}^{1,m}\|_{\infty }$, we rewrite (3.17) with s = m into the following form:

$$ \begin{array}{@{}rcl@{}} {\Delta}_{h} {e}_{j,k}^{1,m} = -\frac{i \sigma^{-\alpha}}{\mu} {e}_{j,k}^{1,m} - \sigma^{-1} {R}_{j,k}^{1,m-1} + \sigma^{-1}{P}_{j,k}^{\sigma,m-1}, \end{array} $$

(3.36)

then taking the discrete L² norm of both sides of (3.36), we have

$$ \begin{array}{@{}rcl@{}} | {e}^{1,m}|_{2} &\leq& \frac{\sigma^{-\alpha}}{\mu} \| {e}^{1,m}\| + \sigma^{-1} \| {R}^{1,m-1}\| + \sigma^{-1} \| {P}^{\sigma,m-1}\|\\ &\leq& C\left( \sigma^{-1} \tau^{(m-2)\alpha}\left( h^{2} +\tau\right) + \tau^{\left( m-\frac{3}{2}\right)\alpha}\left( h^{2} +\tau\right) + \sigma^{-1}\left( h^{2}+\tau^{2}\right)\right)\\ &\leq& C \tau^{\left( m-\frac{3}{2}\right)\alpha}\left( \tau+h^{2}\right) \leq C \tau^{\frac{\alpha}{2}}\left( \tau+h^{2}\right). \end{array} $$

(3.37)

where (3.14), (3.29), (3.33) and (3.35) were used. This completes the proof of Lemma 3.7. □

Lemma 3.8

Suppose that the system (2.1)–(2.3) has a unique solution u satisfying (2.11), then the scheme (2.6) has a unique solution $U_{j,k}^{1}$, and there exists $\tau _{1}^{*} > 0$ such that when ${0<}\tau \leq \tau _{1}^{*}$, there is

$$ \begin{array}{@{}rcl@{}} \|e^{1}\| \leq {C} \tau (h^{2}+\tau),\quad |e^{1}|_{2} \leq {C}\tau^{1-\alpha}(h^{2}+\tau), \quad \|U^{1}\|_{\infty} \leq {C}. \end{array} $$

(3.38)

Proof

Taking s = m_α in Lemma 3.7 and using Lemma 3.2 immediately give (3.38). □

We now turn back to the proof of Theorem 2.1.

Proof

From Lemma 3.8, we know that Theorem 2.1 holds for n = 1. By using the mathematical induction method, we assume that (2.12) holds for n ≤ l with l ≤ N − 1, i.e.,

$$ \begin{array}{@{}rcl@{}} &\|e^{n}\| \leq C (\tau^{2} + h^{2}), \quad \|U^{n}\|_{\infty} \leq C, \quad n=1,2,\cdots,l. \end{array} $$

(3.39)

Direct calculation gives that

$$ \begin{array}{@{}rcl@{}} R_{j,k}^{l+\sigma} =& f^{\prime}(\xi) \Big(\hat{e}_{j,k}^{l+\sigma} \overline{\hat{u}_{j,k}^{l+\sigma}} + \hat{U}_{j,k}^{l+\sigma} \overline{\hat{e}_{j,k}^{l+\sigma}} \Big) \hat{u}_{j,k}^{l+\sigma} + f(|\hat{U}_{j,k}^{l+\sigma}|^{2}) \hat{e}_{j,k}^{l+\sigma}, \end{array} $$

(3.40)

where ξ is some number between $|\hat {u}_{j,k}^{l+\sigma }|^{2}$ and $|\hat {U}_{j,k}^{l+\sigma }|^{2}$ and then it satisfies |ξ|≤ C. This together with (3.39) gives

$$ \begin{array}{@{}rcl@{}} \|R^{l+\sigma}\| \leq C\|\hat{e}^{l+\sigma}\| \leq C \big((1+\sigma) \|e^{l}\| + \sigma \|e^{l-1}\| \big). \end{array} $$

(3.41)

Next, we are going to prove that (2.12) hold for n = l + 1. Let n = l in (3.16), then by taking the inner product of (3.16) with $e_{j,k}^{l+\sigma }$ and then taking the imaginary part of the result, we arrive at

$$ \begin{array}{@{}rcl@{}} {\text{Re}}(D_{\sigma}^{\alpha} e^{l}, e^{l+\sigma}) &=& - {\text{Im}}\big(R^{l+\sigma}, e^{l+\sigma}\big) + {\text{Im}}\big(P^{l+\sigma}, e^{l+\sigma}\big) \\ &\leq& \|e^{l+\sigma}\|^{2} + \frac{1}{2} \|R^{l+\sigma}\|^{2} + \frac{1}{2} \|P^{l+\sigma}\|^{2} \\ &\leq& C\big(\|e^{l+1}\|^{2} +\|e^{l}\|^{2} +\|e^{l-1}\|^{2}\big)+C (h^{2}+ \tau^{2}), \end{array} $$

(3.42)

where Lemmas 3.4 and 3.6 were used. This together with (3.7) gives

$$ \begin{array}{@{}rcl@{}} D_{\sigma}^{\alpha} \|e^{l}\|^{2} \leq & C\left( \|e^{l+1}\|^{2} +\|e^{l}\|^{2} +\|e^{l-1}\|^{2}\right)+C(h^{2}+ \tau^{2} ). \end{array} $$

(3.43)

By using Theorem 3.1, there exists a positive constant τ^∗ such that when τ < τ^∗, there is

$$ \|e^{l+1}\| \leq C \left( h^{2}+ \tau^{2}\right). $$

(3.44)

In order to get the bound of $||U^{l+1}||_{\infty }$, we rewrite (3.16) with n = l into the following form,

$$ {\Delta}_{h} e_{j,k}^{l+\sigma} = -i D_{\sigma}^{\alpha} e^{l} - R_{j,k}^{l+\sigma} + P_{j,k}^{l+\sigma}, $$

(3.45)

then taking the discrete L² norm of both sides of (3.45), we have

$$ \begin{array}{@{}rcl@{}} |e^{l+\sigma}|_{2} &\leq& \|D_{\sigma}^{\alpha} e^{l}\| + \|R^{l+\sigma}\| + \|P^{l+\sigma}\| \\ &\leq& {C}\tau^{-\alpha}\sqrt{\sum\limits_{m=0}^{l+1}\|e^{m}\|^{2} }+ \|R^{l+\sigma}\| + \|P^{l+\sigma}\| \\ &\leq& {C}\tau^{-\left( \frac{1}{2}+\alpha\right)} \left( h^{2}+\tau^{2}\right) + {C}\left( \|e^{l+1}\| + \|e^{l}\|\right) + C\left( h^{2}+\tau^{2}\right)\\ &\leq& {C}\tau^{-\left( \frac{1}{2}+\alpha\right)} \left( h^{2}+\tau^{2}\right), \end{array} $$

(3.46)

where Lemma 3.5 was used. Noting that $\sigma =1-\frac {\alpha }{2}>\frac {1}{2}>1-\sigma =\frac {\alpha }{2}$ with 0 < α < 1, then by using Minkowski inequality, we obtain

$$ \begin{array}{@{}rcl@{}} \sigma |e^{l+1}|_{2}- \sigma |e^{l}|_{2} \leq \sigma |e^{l+1}|_{2}- (1-\sigma) |e^{l}|_{2}\leq |e^{l+\sigma}|_{2}, \end{array} $$

(3.47)

this together with (3.46) gives

$$ \begin{array}{@{}rcl@{}} |e^{l+1}|_{2}-|e^{l}|_{2}\leq {C}\tau^{-\left( \frac{1}{2}+\alpha\right)} \left( h^{2}+\tau^{2}\right). \end{array} $$

(3.48)

Summing (3.48) up for l from 1 to m, then replacing m by l, we obtain

$$ \begin{array}{@{}rcl@{}} |e^{l+1}|_{2} &\leq& |e^{1}|_{2}+C\sum\limits_{m=1}^{l+1}\tau^{-\left( \frac{1}{2}+\alpha\right)}\left( h^{2}+\tau^{2}\right)\\ &\leq& C \tau^{-{\alpha}} \left( h^{2}+\tau^{2}\right)+C \tau^{-\left( \frac{3}{2}+\alpha\right)} \left( h^{2}+\tau^{2}\right)\\ &\leq& C\tau^{-\left( \frac{3}{2}+\alpha\right)} \left( h^{2}+\tau^{2}\right), \end{array} $$

(3.49)

where Lemma 3.8 was used. This together with Lemma 3.2 gives

$$ \begin{array}{@{}rcl@{}} ||e^{l+1}||_{\infty} \leq {C}||e^{l+\sigma}||^{\frac{1}{2}}\big(||e^{l+\sigma}||+|e^{l+\sigma}|_{2}\big)^{\frac{1}{2}} \leq {C}\tau^{-\left( \frac{3}{4}+\frac{\alpha}{2}\right)}\left( h^{2}+\tau^{2}\right). \end{array} $$

(3.50)

On the other hand, by using Lemma 3.3, we obtain

$$ \begin{array}{@{}rcl@{}} ||e^{l+1}||_{\infty} \leq {C_{0}} {h}^{-1} ||e^{l+1}|| \leq C{h}^{-1}\left( h^{2}+\tau^{2}\right), \end{array} $$

(3.51)

where (3.44) was used. Combining (3.50) with (3.51) gives

$$ \begin{array}{@{}rcl@{}} \|{e}^{l+1}\|_{\infty}\leq{C}\min\left\{\tau^{-(\frac{3}{4}+\frac{\alpha}{2})}, {h^{-1}}\right\} \left( \tau^{2} + h^{2}\right). \end{array} $$

(3.52)

Hence, for both the case h ≤ τ and the case τ ≤ h, we always have

$$ \begin{array}{@{}rcl@{}} \|{U}^{l+1}\|_{\infty} \leq \|{u}^{l+1}\|_{\infty} + \|{e}^{l+1}\|_{\infty} \leq C. \end{array} $$

(3.53)

Therefore, (3.20) and (3.21) hold for n = l + 1. This completes the proof of Theorem 2.1. □

Remark 3.2

The numerical method can be generalized to solve the initial-boundary value problem of the time-fractional Gross-Pitaevskii equation (TFGPE) in d dimensions. For simplicity, we here still take the two-dimensional TFGPE as an example, i.e.,

$$ \begin{array}{@{}rcl@{}} && i {}^{\mathcal{C}}_{0}D_{t}^{\alpha} u = \left[-\frac{1}{2} {\Delta}+V(x,y)+\beta|u|^{2}\right]u , {\kern20pt} (x,y) \in {\Omega}, 0 < t \leq T, \quad\qquad \end{array} $$

(3.54)

$$ \begin{array}{@{}rcl@{}} && u(x,y,t) = 0, {\kern128pt} (x,y) \in \partial {\Omega}, 0 < t \leq T, \end{array} $$

(3.55)

$$ \begin{array}{@{}rcl@{}} && u(x,y,0) = u_{0}(x,y), {\kern98pt} (x,y) \in \overline{\Omega}, \end{array} $$

(3.56)

where V = V (x,y) is a given real-valued function and β is a given real constant. The extension of the linearized second-order finite difference scheme to solve the initial-boundary value problem (3.54)–(3.56) reads

$$ \begin{array}{@{}rcl@{}} &&i D_{\sigma}^{\alpha} U_{j,k}^{n} +\frac{1}{2}{\Delta}_{h} {U}_{j,k}^{n+\sigma} -V_{j,k}{U}_{j,k}^{n+\sigma}-\beta|\hat{U}_{j,k}^{n+\sigma}|^{2}\hat{U}_{j,k}^{n+\sigma} = 0, \quad (j,k)\in\mathcal{T}_{h}, 1\leq{n}<{N},\\ && \end{array} $$

(3.57)

$$ \begin{array}{@{}rcl@{}} && U_{j,k}^{n}= 0,\quad(j,k)\in {\Gamma}_{h}, n=1,2,\cdots,{N}, \end{array} $$

(3.58)

$$ \begin{array}{@{}rcl@{}} && U_{j,k}^{0}=u_{0}(x_{j},t_{n}), \quad(j,k)\in\mathcal{T}_{h}^{0}, \end{array} $$

(3.59)

where V_j,k = V (x_j,y_k) for $(j,k)\in \mathcal {T}_{h}^{0}$. To start the scheme (3.57)–(3.59), we compute $U^{1}=U^{1,m_{\alpha }}\in {X_{h}}$ by the following two-level scheme

$$ \begin{array}{@{}rcl@{}} &&i \frac{\sigma^{1-\alpha}}{\mu} ({U}_{j,k}^{1,s} - U_{j,k}^{0}) + \frac{1}{2} {\Delta}_{h} {W}_{j,k}^{1,s} -V_{j,k}{W}_{j,k}^{1,s}-\beta |{W}_{j,k}^{1,s-1}|^{2} {W}_{j,k}^{1,s-1} = 0,\quad (j,k)\in\mathcal{T}_{h},\\ &&\qquad s = 1,2,\cdots,m_{\alpha}, \end{array} $$

(3.60)

$$ \begin{array}{@{}rcl@{}} && {U}_{j,k}^{1}=0,\quad {U}_{j,k}^{1,s}=0,\quad(j,k)\in {\Gamma}_{h}, s = 1,2,\cdots,m_{\alpha}, \end{array} $$

(3.61)

$$ \begin{array}{@{}rcl@{}} &&{U}_{j,k}^{1,0} = U_{j,k}^{0}, \quad (j,k)\in\mathcal{T}_{h}^{0}, \end{array} $$

(3.62)

where $m_{\alpha }:=\left [\frac {1}{\alpha } + \frac {1}{2}\right ]$ and W^1,s = (1 − σ)U⁰ + σU^1,s for s = 0,1,2,⋯ ,m_α.

4 Numerical experiments

In this section, we carry out several numerical results to show the performance of the proposed scheme for solving the NTFS equation.

Example 4.1

Consider the following 1D cubic NTFS equation

$$ \begin{array}{@{}rcl@{}} &i {}^{\mathcal{C}}_{0}\mathcal{D}_{t}^{\alpha} u + \partial_{xx} u + |u|^{2} u = 0, \quad x \in (a,b), t\in(0,T], \end{array} $$

(4.1)

with initial condition

$$ \begin{array}{@{}rcl@{}} &u(x,0) = e^{-x^{2}},\quad x \in [a,b], \end{array} $$

(4.2)

and boundary condition

$$ \begin{array}{@{}rcl@{}} &u(a,t) =u(b,t)=0,\quad t\in(0,T], \end{array} $$

(4.3)

where a = − 10,b = 10,T = 1.

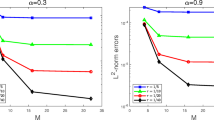
To test the convergence order of the proposed scheme, we choose sufficiently fine time step τ and mesh size h (here we choose h = 10^− 3,τ = 10^− 3) to get a numerically “exact” solution. The L²-errors at time T = 1 and convergence rates of the proposed scheme in computing Example 4.1 with different α are listed in Tables 1 and 2. One can observe from the two tables that the proposed scheme has an accuracy of O(τ² + h²). As verifies the convergence results given in Theorem 2.1.

Table 1 L²-errors and convergence rates of the time with different α in solving Example 4.1

Table 2 L²-errors and convergence rates of the space with different α in solving Example 4.1

In order to test the influence of α to the evolution of the total mass and energy of the NTFS equation, we draw the total mass and energy of the 1D NTFS equation computed by the proposed scheme in Fig. 2, and draw the approximation of |u| in Fig. 2. From Figs. 1 and 2, we can see that the nonlinear integer Schrödinger equation is dispersive but the NTFS equation is dissipative, and the smaller the parameter α is, the faster the mass and energy dissipate.

Fig. 1

Evolution of the mass and energy of the 1D NTFS (4.1) with different α

Fig. 2

Evolution of |u| of the 1D NTFS (4.1) with different α

Example 4.2

Consider the following non-homogeneous 2D NTFS equation with different nonlinearities

$$ i {}^{\mathcal{C}}_{0}\mathcal{D}_{t}^{\alpha} u + {\Delta} u + f(|u|^{2}) u = g, \quad (x,y) \in [0,1]^{2}, t\in(0,1], $$

(4.4)

where the function g, the initial and boundary conditions are determined by the exact solution

$$ u = (2+i) e^{t} {\sin}(2\pi x) {\sin}(2\pi y). $$

The nonlinear term f(s) is selected for three cases:

$$ \begin{array}{@{}rcl@{}} \text{Case I.}&& \quad f(s) = s;\\ \text{Case II.}&& \quad f(s) = ln(1+s);\\ \text{Case III.}&& \quad f(s) = 1 - e^{-s}. \end{array} $$

In Example 4.2, we test the convergence order of the proposed scheme in computing the 2D NTFS equation. In order to reduce the computational cost and memory, we choose h₁ = h₂ = τ and investigate the temporal convergence and spatial convergence together by refining τ and h simultaneously. The L²-errors at time T = 1 and convergence rates with different α’s are listed in Tables 3, 4 and 5. One can observe again that the accuracy of the proposed scheme is of O(τ² + h²), which verifies again the error estimate results given in Theorem 2.1.

Table 3 L²-errors and convergence rates of the proposed scheme with different α in case I

Table 4 L²-errors and convergence rates of the scheme with different α in case II

Table 5 L²-errors and convergence rates of the scheme with different α in case III

5 Conclusion

In this paper, we proposed a linearized finite difference scheme to solve the NTFS equation in d (d = 1,2,3) dimensions, and introduced a novel and concise analysis method to establish the optimal error estimate of the numerical solution. Under a weaker requirement of the coefficient function f than the literature, we introduced a new analysis technique to prove that the proposed scheme is unconditionally convergent with L² convergence order O(h² + τ²). Our analysis methods can be adopted to relax the requirement of the coefficient function f for the Galerkin FEMs given in [25, 48]. Numerical results of the NTFS equation with several different types of nonlinear terms were carried out to illustrate our theoretical results. Furthermore, if the exact solution is smooth enough, one can use some high accurate method to improve the spatial accuracy, e.g., one can consider adopting the compact finite difference method or Pseudo-spectral method to discretize the spatial derivatives to achieve higher order accuracy in the space. Applying the analysis method used in this paper, one can obtain the optimal error estimate of the high-order accurate scheme without any restrictions on the grid ratio. In our future works, we will discuss a nonlinear finite difference scheme, which can start by itself for solving the NTFS equation, and introduce a concise analysis method to establish the optimal error estimate without any restriction on the grid ratio.

Appendix. Proof of the time-fractional Gronwall inequality given in Lemma 3.1

In this appendix, we present two useful lemmas which are main tools used for proving Lemma 3.1.

Lemma A.1

Let {p_n} be a sequence defined by

$$ p_{0} = \frac{1}{C_{0}^{\sigma}}, \quad p_{n} = \frac{1}{C_{0}^{\sigma}} \sum\limits_{j=1}^{n} (C_{j-1}^{\sigma} - C_{j}^{\sigma}) p_{n-j}, \quad n \ge 1. $$

(A.1)

Then it holds that

$$ \begin{array}{@{}rcl@{}} &&\text{(i)}\quad 0\le p_{n} \le \frac{1}{C_{0}^{\sigma}}, \quad \sum\limits_{j=k}^{n+1} p_{n-j+1} C_{j-k}^{\sigma} = 1, \quad 1 \le k \le n; \end{array} $$

(A.2)

$$ \begin{array}{@{}rcl@{}} &&\text{(ii)}\quad{\Gamma}(2-\alpha) \sum\limits_{j=0}^{n} p_{n-j} \le \frac{(n+1)^{\alpha}}{\Gamma(1+\alpha)}; \end{array} $$

(A.3)

$$ \begin{array}{@{}rcl@{}} &&\text{(iii)}\quad\frac{\Gamma(2-\alpha)}{\Gamma(1+(m-1)\alpha)} \sum\limits_{j=1}^{n} p_{n-j+1} j^{(m-1)\alpha}\\ &&\qquad \leq \frac{(n+1)^{m\alpha}}{\Gamma(1+m\alpha)}, \quad m=1,2,\cdots. \end{array} $$

(A.4)

Proof

(i) Since $C_{0}^{\sigma } \geq C_{1}^{\sigma } \geq {\cdots } \geq C_{j}^{\sigma } \ge 0$ for j ≥ 0, it is easy to verify inductively from (A.1) that $0 \leq p_{n} \leq 1/C_{0}^{\sigma } \ (n \geq 1)$ by mathematical induction. Moreover, we have

$$ {\Phi}_{n} = \sum\limits_{j=1}^{n+1} p_{n-j+1} C_{j-1}^{\sigma} = \sum\limits_{j=0}^{n} p_{n-j} C_{j}^{\sigma} = \sum\limits_{j=1}^{n} p_{n-j} C_{j-1}^{\sigma} = {\Phi}_{n-1}, \qquad n \ge 1. $$

(A.5)

This implies ${\Phi }_{n} = {\Phi }_{0} = p_{0} C_{0}^{\sigma } = 1$ for n ≥ 1. Substituting j = l + k − 1, we further find

$$ \sum\limits_{j=k}^{n+1} p_{n-j+1} C_{j-k}^{\sigma} = \sum\limits_{l=1}^{n-k+2} p_{n-k+2-l} C_{l-1}^{\sigma} = {\Phi}_{n-k+1} = {\Phi}_{n} = 1, \qquad 1 \leq k \leq n. $$

(A.6)

The equality (A.2) is proved.

(ii) To prove (A.3) and (A.4), we introduce an auxiliary function q(t) = t^mα/Γ(1 + mα) for m ≥ 1. Then for j ≥ 1, we have

$$ {\int}_{0}^{j+\sigma} \frac{(j+\sigma-s)^{-\alpha} q^{\prime}(s)}{\Gamma(1-\alpha)} ds = \frac{B(1-\alpha, m\alpha) (j+\sigma)^{(m-1)\alpha}}{\Gamma(1-\alpha) {\Gamma}(m\alpha)} = \frac{(j+\sigma)^{(m-1)\alpha}}{\Gamma(1+(m-1)\alpha)}. $$

(A.7)

Let Q(t) be a quadratic interpolation of q(t) using the points (s − 1,q(s − 1)), (s,q(s)), (s + 1,q(s + 1)) for 1 ≤ s ≤ j, and a linear interpolation of q(t) using the points (j,q(j)), (j + 1,q(j + 1)). We define the approximation error by

$$ \begin{array}{@{}rcl@{}} &&{\int}_{0}^{j+\sigma} \frac{q^{\prime}(s) - Q^{\prime}(s)}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &=& \sum\limits_{k=1}^{j} {\int}_{k-1}^{k} \frac{q^{\prime}(s) - Q^{\prime}(s)}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds + {\int}_{j}^{j+\sigma} \frac{q^{\prime}(s) - Q^{\prime}(s)}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &:=& \sum\limits_{k=1}^{j} {R_{k}^{j}} + R_{\sigma}^{j}, \end{array} $$

(A.8)

where

$$ \begin{array}{@{}rcl@{}} {R_{k}^{j}} &=& {\int}_{k-1}^{k} \frac{q^{\prime}(s) - Q^{\prime}(s)}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &=& -\frac{\alpha}{\Gamma(1-\alpha)} {\int}_{k-1}^{k} \frac{q(s) - Q(s)}{(j+\sigma-s)^{\alpha+1}} ds \\ &=& -\frac{\alpha}{\Gamma(1-\alpha)} {\int}_{k-1}^{k} \frac{ \frac{1}{6} q^{\prime\prime\prime}(\xi_{s}) (s-(k-1))(s-k)(s-(k+1)) }{(j+\sigma-s)^{\alpha+1}} ds, \quad\\ && 1 \leq k \leq j, \end{array} $$

(A.9)

$$ \begin{array}{@{}rcl@{}} R_{\sigma}^{j} &=& {\int}_{j}^{j+\sigma} \frac{q^{\prime}(s) - Q^{\prime}(s)}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &=& {\int}_{j}^{j+\sigma} \frac{q^{\prime}(s) - q(j+\frac{1}{2}) + q(j+\frac{1}{2}) - Q^{\prime}(s)}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &=& {\int}_{j}^{j+\sigma} \frac{2q^{\prime\prime}(j+\frac{1}{2})(s-(j+\frac{1}{2})) + q^{\prime\prime\prime}(\xi_{s})(s-(j+\frac{1}{2}))^{2}}{2{\Gamma}(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &&- {\int}_{j}^{j+\sigma} \frac{q^{\prime\prime\prime}(\xi_{s})}{24{\Gamma}(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &=& {\int}_{j}^{j+\sigma} \frac{q^{\prime\prime\prime}(\xi_{s})(s-(j+\frac{1}{2}))^{2}}{2{\Gamma}(1-\alpha)(j+\sigma-s)^{\alpha}} ds\\ &&- {\int}_{j}^{j+\sigma} \frac{q^{\prime\prime\prime}(\xi_{s})}{24{\Gamma}(1-\alpha)(j+\sigma-s)^{\alpha}} ds. \end{array} $$

(A.10)

Combining (A.7) and (A.8) yields

$$ \frac{(j+\sigma)^{(m-1)\alpha}}{\Gamma(1+(m-1)\alpha)} = \frac{1}{\Gamma(2-\alpha)} \sum\limits_{k=0}^{j} C_{j-k}^{\sigma} (q(k+1) - q(k)) + \sum\limits_{k=1}^{j} {R_{k}^{j}} + R_{\sigma}^{j}. $$

(A.11)

Noting that $q^{\prime \prime \prime }(t) \geq 0$ for m = 1, we have ${R_{k}^{j}} \leq 0$ and

$$ \begin{array}{@{}rcl@{}} R_{\sigma}^{j} &\leq& \frac{q^{\prime\prime\prime}(\xi)}{24{\Gamma}(1-\alpha)} {\int}_{j}^{j+\sigma} \frac{12(s-(j+\frac{1}{2}))^{2} - 1}{(j+\sigma-s)^{\alpha}} ds \\ &=&\frac{q^{\prime\prime\prime}(\xi)}{24{\Gamma}(1-\alpha)} \frac{4(\sigma-1)}{(2\sigma+1)\sigma(2\sigma-1)} \leq 0, \end{array} $$

(A.12)

so we have

$$ \begin{array}{@{}rcl@{}} \frac{1}{\Gamma(2-\alpha)} \sum\limits_{k=0}^{j} C_{j-k}^{\sigma} (q(k+1) - q(k)) \geq 1. \end{array} $$

(A.13)

Multiplying (A.13) by Γ(2 − α)p_n−j and summing it over for j from 0 to n, we have

$$ \begin{array}{@{}rcl@{}} {\Gamma}(2-\alpha) \sum\limits_{j=0}^{n} p_{n-j} &\leq& \sum\limits_{j=0}^{n} p_{n-j} \sum\limits_{k=1}^{j+1} C_{j-k+1}^{\sigma} (q(k) - q(k-1))\\ &= & \sum\limits_{k=1}^{n+1} (q(k) - q(k-1)) \sum\limits_{j=k-1}^{n} p_{n-j} C_{j-k+1}^{\sigma} \\ &= & \sum\limits_{k=1}^{n+1} (q(k) - q(k-1)) \sum\limits_{j=k}^{n+1} p_{n-j+1} C_{j-k}^{\sigma} \\ &= & \sum\limits_{k=1}^{n+1} (q(k) - q(k-1))\\ &= & \frac{(n+1)^{\alpha}}{\Gamma(1+\alpha)}, \end{array} $$

(A.14)

where we the equality (A.2) was used.

(iii) Consider of (A.11), we have

$$ \begin{array}{@{}rcl@{}} \frac{j^{(m-1)\alpha}}{\Gamma(1+(m-1)\alpha)} &\leq &\frac{(j+\sigma)^{(m-1)\alpha}}{\Gamma(1+(m-1)\alpha)} \\ &=&\frac{1}{\Gamma(2-\alpha)} \sum\limits_{k=0}^{j} C_{j-k}^{\sigma} (q(k+1) - q(k)) \\ &&+ \sum\limits_{k=1}^{j} {R_{k}^{j}} + R_{\sigma}^{j}. \end{array} $$

(A.15)

We multiply (A.15) by Γ(2 − α)p_n−j+ 1 and sum the resulting inequality for j from 1 to n to obtain

$$ \begin{array}{@{}rcl@{}} &&\frac{\Gamma(2-\alpha)}{\Gamma(1+(m-1)\alpha)} \sum\limits_{j=1}^{n} p_{n-j+1} j^{(m-1)\alpha}\\ &&\leq \sum\limits_{j=1}^{n} p_{n-j+1} \sum\limits_{k=0}^{j} C_{j-k}^{\sigma}\left( q(k+1) - q(k)\right) \\ &&\quad + {\Gamma}(2-\alpha) \sum\limits_{j=1}^{n} p_{n-j+1} \left( \sum\limits_{k=1}^{j} {R_{k}^{j}} + R_{\sigma}^{j}\right). \end{array} $$

(A.16)

If 1 ≤ m ≤ 1/α, $q^{\prime \prime \prime }(t) \geq 0$, then ${R_{k}^{j}} \leq 0$ and $R_{\sigma }^{j} \le 0$, so (A.4) follows immediately from the above estimate. If m ≥ 1/α, by (A.8), we have

$$ \begin{array}{@{}rcl@{}} {R_{k}^{j}} &=& {\int}_{k-1}^{k} \frac{q^{\prime}(s) - Q^{\prime}(s)}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &=& {\int}_{k-1}^{k} \frac{q^{\prime}(s) - [q(k)-q(k-1) + (q(k-1) - 2q(k) + q(k+1))(s-(k-\frac{1}{2}))]}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &=& {\int}_{k-1}^{k} \frac{q^{\prime}(s) - (q(k)-q(k-1))}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ && + {\int}_{k-1}^{k} \frac{(s-(k-\frac{1}{2}))[(q(k)-q(k-1)) - (q(k+1) - q(k))]}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &=& {\int}_{k-1}^{k} \frac{(j+\sigma-s)^{-\alpha}}{\Gamma(1-\alpha)} {\int}_{k-1}^{k} {\int}_{\mu}^{s} q^{\prime\prime}(\eta) d\eta d\mu ds \\ &&+ {\int}_{k-1}^{k} \frac{s-(k-\frac{1}{2})}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} {\int}_{k-1}^{k} q^{\prime}(\mu) d\mu ds \\ && - {\int}_{k-1}^{k} \frac{s-(k-\frac{1}{2})}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} {\int}_{k}^{k+1} q^{\prime}(\mu) d\mu ds \\ &\leq& {\int}_{k-1}^{k} \frac{(j+\sigma-s)^{-\alpha}}{\Gamma(1-\alpha)} {\int}_{k-1}^{k} {\int}_{\mu}^{k} q^{\prime\prime}(\eta) d\eta d\mu ds\\ && + {\int}_{k-1}^{k} \frac{s-(k-\frac{1}{2})}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} {\int}_{k-1}^{k} q^{\prime}(\mu) d\mu ds \\ && - {\int}_{k-1}^{k} \frac{s-(k-\frac{1}{2})}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} {\int}_{k}^{k+1} q^{\prime}(\mu) d\mu ds \\ &=& \frac{a_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k-1}^{k} {\int}_{\mu}^{k} q^{\prime\prime}(\eta) d\eta d\mu + \frac{b_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k-1}^{k} q^{\prime}(\mu) d\mu \\ && - \frac{b_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k}^{k+1} q^{\prime}(\mu) d\mu \end{array} $$

$$ \begin{array}{@{}rcl@{}} &=& \frac{a_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k-1}^{k} \frac{k^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu + \frac{b_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k-1}^{k} \frac{\mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu \\ && - \frac{b_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k}^{k+1} \frac{\mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu \\ &=& \frac{a_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k-1}^{k} \frac{k^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu - \frac{b_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k-1}^{k} \frac{k^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu \\ &&+ \frac{b_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k}^{k+1} \frac{k^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu \\ &\leq& \frac{a_{j-k+1}^{\sigma} - b_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k-1}^{k} \frac{k^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu \\ && + \frac{b_{j-k+1}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{k}^{k+1} \frac{(k+1)^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu \end{array} $$

(A.17)

and

$$ \begin{array}{@{}rcl@{}} R_{\sigma}^{j} &=& {\int}_{j}^{j+\sigma} \frac{q^{\prime}(s) - Q^{\prime}(s)}{\Gamma(1-\alpha)(j+\sigma-s)^{\alpha}} ds \\ &=&{\int}_{j}^{j+\sigma} \frac{(j+\sigma-s)^{-\alpha}}{\Gamma(1-\alpha)} {\int}_{j}^{j+1} q^{\prime}(s) - q^{\prime}(\mu) d\mu ds \\ &\leq& \frac{a_{0}^{\sigma}}{\Gamma(2-\alpha)} {\int}_{j}^{j+1} \frac{(j+1)^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu, \end{array} $$

(A.18)

so that

$$ \sum\limits_{k=1}^{j}{R_{k}^{j}} + R_{\sigma}^{j} \leq \sum\limits_{k=0}^{j} C_{j-k}^{\sigma} {\int}_{k}^{k+1} \frac{(k+1)^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu. $$

(A.19)

Because of

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{j=1}^{n} p_{n-j+1} \sum\limits_{k=0}^{j} C_{j-k}^{\sigma} (q(k+1) - q(k)) \\ &=& \sum\limits_{k=0}^{n}(q(k+1)-q(k)) \sum\limits_{j=k}^{n} p_{n-j+1} C_{j-k}^{\sigma} - p_{n+1} c_{0}^{\sigma} (q(1)-q(0)) \\ &\leq&\sum\limits_{k=0}^{n} (q(k+1) - q(k)) \sum\limits_{j=k}^{n+1} p_{n-j+1} C_{j-k}^{\sigma} \\ &=& \frac{(n+1)^{m\alpha}}{\Gamma(1+m\alpha)}, \end{array} $$

(A.20)

and

$$ \begin{array}{@{}rcl@{}} &&{\Gamma}(2-\alpha) \sum\limits_{j=1}^{n} p_{n-j+1} \left( \sum\limits_{k=1}^{j} {R_{k}^{j}} + R_{\sigma}^{j}\right) \\ &\leq&\sum\limits_{j=1}^{n} p_{n-j+1} \sum\limits_{k=0}^{j} C_{j-k}^{\sigma} {\int}_{k}^{k+1} \frac{(k+1)^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu \\ &=& \sum\limits_{k=0}^{n} {\int}_{k}^{k+1} \frac{(k+1)^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu \sum\limits_{j=k}^{n} p_{n-j+1} C_{j-k}^{\sigma} - p_{n+1} C_{0}^{\sigma} {{\int}_{0}^{1}} \frac{1-\mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu \\ &\leq& \sum\limits_{k=0}^{n} {\int}_{k}^{k+1} \frac{(k+1)^{m\alpha-1} - \mu^{m\alpha-1}}{\Gamma(m\alpha)} d\mu \sum\limits_{j=k}^{n+1} p_{n-j+1} C_{j-k}^{\sigma} \\ &=& \sum\limits_{k=0}^{n} \frac{(k+1)^{m\alpha-1}}{\Gamma(m\alpha)} - \frac{(n+1)^{m\alpha}}{\Gamma(1+m\alpha)} \\ &\leq& \frac{(n+1)^{m\alpha}}{\Gamma(1+m\alpha)} - \frac{(n+1)^{m\alpha}}{\Gamma(1+m\alpha)} \\ &=& 0, \end{array} $$

(A.21)

one can immediately get (A.4), and the proof of Lemma A.1 is completed. □

Lemma A.2

Let $\vec {e} = (1,1,\cdots ,1)^{T} \in R^{n+1}$ and

$$ J = 2 {\Gamma}(2-\alpha) \lambda \tau^{\alpha} \begin{bmatrix} 0 & p_{1} & {\cdots} & p_{n-1} & p_{n} \\ 0 & 0 & {\cdots} & p_{n-2} & p_{n-1} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} & {\vdots} \\ 0 & 0 & {\cdots} & 0 & p_{1} \\ 0 & 0 & {\cdots} & 0 & 0 \end{bmatrix}_{(n+1) \times (n+1)} $$

(A.22)

Then, it holds that

$$ \begin{array}{@{}rcl@{}} &&\text{(i)} \quad J^{l} = 0, \quad l \geq n+1; \end{array} $$

(A.23)

$$ \begin{array}{@{}rcl@{}} &&\text{(ii)} \quad J^{m} \vec{e} \le \frac{1}{\Gamma(1+m\alpha)} \left( (2\lambda t_{n+1}^{\alpha})^{m}, (2\lambda t_{n}^{\alpha})^{m}, \cdots, (2\lambda t_{1}^{\alpha})^{m} \right)^{T}, \quad \\ &&\qquad m = 0,1,2,\cdots; \end{array} $$

(A.24)

$$ \begin{array}{@{}rcl@{}} &&\text{(iii)} \quad \sum\limits_{j=0}^{l} J^{j} \vec{e} = \sum\limits_{j=0}^{n} J^{j} \vec{e} \leq \left( E_{\alpha}(2\lambda t_{n+1}^{\alpha}), E_{\alpha}(2\lambda t_{n}^{\alpha}), \cdots, E_{\alpha}(2\lambda t_{1}^{\alpha}) \right)^{T}, \quad \\ &&\qquad l \geq n+1. \end{array} $$

(A.25)

Proof

The proof is similar to that of Lemma 3.3 in [24], and we here omit it for brevity. □

We now turn back to the proof of Lemma 3.1

Proof Proof of Lemma 3.1

By the definition of $D_{\sigma }^{\alpha }$, we get

$$ \sum\limits_{k=0}^{j} C_{j-k}^{\sigma} (\omega^{k+1} - \omega^{k}) \le {\Gamma}(2-\alpha)\tau^{\alpha} (\lambda_{1} \omega^{j+1} + \lambda_{2} \omega^{j} + \lambda_{3} \omega^{j-1}) + {\Gamma}(2-\alpha)\tau^{\alpha} g^{j}, \quad j \geq 1. $$

(A.26)

Multiplying inequality (A.26) by p_n−j and summing over for j from 1 to n, we have

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{j=1}^{n} p_{n-j} \sum\limits_{k=1}^{j+1} C_{j-k+1}^{\sigma} (\omega^{k} - \omega^{k-1}) \\ &&\leq {\Gamma}(2-\alpha)\tau^{\alpha} \sum\limits_{j=1}^{n} p_{n-j} (\lambda_{1} \omega^{j+1} + \lambda_{2} \omega^{j} + \lambda_{3} \omega^{j-1}) \\ && \quad + {\Gamma}(2-\alpha)\tau^{\alpha} \sum\limits_{j=1}^{n} p_{n-j} g^{j}. \end{array} $$

(A.27)

By using the result (A.2) in Lemma A.1, we obtain

$$ \begin{array}{@{}rcl@{}} && \sum\limits_{j=1}^{n} p_{n-j} \sum\limits_{k=1}^{j+1} C_{j-k+1}^{\sigma} (\omega^{k} - \omega^{k-1}) \\ &=&\sum\limits_{k=1}^{n+1} (\omega^{k} - \omega^{k-1}) {\sum}_{j=k+1}^{n} p_{n-j} C_{j-k+1}^{\sigma} - p_{n} C_{0}^{\sigma} (\omega^{1} - \omega^{0}) \\ &=&\sum\limits_{k=1}^{n+1} (\omega^{k} - \omega^{k-1}) - p_{n} C_{0}^{\sigma} (\omega^{1} - \omega^{0}) \\ &=&\omega^{n+1} - \omega^{0} - p_{n} C_{0}^{\sigma} (\omega^{1} - \omega^{0}), \quad n \geq 1. \end{array} $$

(A.28)

It follows that

$$ \begin{array}{@{}rcl@{}} \omega^{n+1} &\leq&\omega^{0} + p_{n} C_{0}^{\sigma} (\omega^{1} - \omega^{0}) + {\Gamma}(2-\alpha)\tau^{\alpha} \sum\limits_{j=1}^{n} p_{n-j} g^{j} \\ &&+ {\Gamma}(2-\alpha)\tau^{\alpha} \sum\limits_{j=1}^{n} p_{n-j} \left( \lambda_{1} \omega^{j+1} + \lambda_{2} \omega^{j} + \lambda_{3} \omega^{j-1}\right). \end{array} $$

(A.29)

Because of

$$ \frac{a_{0}^{\sigma}}{\Gamma(2-\alpha)\tau^{\alpha}} \left( \omega^{1} - \omega^{0}\right) = D_{\sigma}^{\alpha} \omega^{0} \leq \lambda_{1} \omega^{1} + \lambda_{2} \omega^{0} + g^{0} $$

and

$$ \frac{C_{0}^{\sigma}}{a_{0}^{\sigma}} = \frac{a_{0}^{\sigma} + b_{1}^{\sigma}}{a_{0}^{\sigma}} \leq 6, $$

we get

$$ \begin{array}{@{}rcl@{}} \omega^{n+1} &\leq& \omega^{0} + 6{\Gamma}(2-\alpha)\tau^{\alpha} p_{n} (\lambda_{1} \omega^{1} + \lambda_{2} \omega^{0} + g^{0}) + {\Gamma}(2-\alpha)\tau^{\alpha} \sum\limits_{j=1}^{n} p_{n-j} g^{j} \\ && + {\Gamma}(2-\alpha)\tau^{\alpha} \sum\limits_{j=1}^{n} p_{n-j} (\lambda_{1} \omega^{j+1} + \lambda_{2} \omega^{j} + \lambda_{3} \omega^{j-1}) \\ &=& {\Gamma}(2-\alpha) \lambda_{1} \tau^{\alpha} p_{0} \omega^{n+1} + (1 + 6{\Gamma}(2-\alpha) \lambda_{2} \tau^{\alpha} p_{n} + {\Gamma}(2-\alpha)\lambda_{3} \tau^{\alpha} p_{n-1}) \omega^{0} \\ && + 6{\Gamma}(2-\alpha) \tau^{\alpha} p_{n} g^{0} + {\Gamma}(2-\alpha)\tau^{\alpha} {\sum}_{j=1}^{n} p_{n-j} g^{j} \\ && + 6{\Gamma}(2-\alpha) \lambda_{1} \tau^{\alpha} p_{n} \omega^{1} + {\Gamma}(2-\alpha) \lambda_{1} \tau^{\alpha} \sum\limits_{j=1}^{n-1} p_{n-j} \omega^{j+1} \\ && + {\Gamma}(2-\alpha) \lambda_{2} \tau^{\alpha} \sum\limits_{j=1}^{n} p_{n-j} \omega^{j} + {\Gamma}(2-\alpha) \lambda_{3} \tau^{\alpha} \sum\limits_{j=2}^{n} p_{n-j} \omega^{j-1}. \end{array} $$

(A.30)

It follows that

$$ \begin{array}{@{}rcl@{}} \omega^{n+1} & \leq& 6 \omega^{0} + 12 {\Gamma}(2-\alpha) \tau^{\alpha} \sum\limits_{j=0}^{n} p_{n-j} g^{j} + 12 {\Gamma}(2-\alpha) \lambda_{1} \tau^{\alpha} \sum\limits_{j=0}^{n-1} p_{n-j} \omega^{j+1} \\ && + 2 {\Gamma}(2-\alpha) \lambda_{2} \tau^{\alpha} \sum\limits_{j=1}^{n} p_{n-j} \omega^{j} \\ && + 2 {\Gamma}(2-\alpha) \lambda_{3} \tau^{\alpha} \sum\limits_{j=2}^{n} p_{n-j} \omega^{j-1}, \quad n \geq 1, \end{array} $$

(A.31)

when τ ≤ τ^∗. By using the result (A.3) in Lemma A.1, we obtain

$$ \begin{array}{@{}rcl@{}} {\Gamma}(2-\alpha) \tau^{\alpha} \sum\limits_{j=0}^{n} p_{n-j} g^{j} &\leq& {\Gamma}(2-\alpha) \tau^{\alpha} \max_{0\le j\le n} g^{j} \sum\limits_{j=0}^{n} p_{n-j} \\ &\leq& \frac{t_{n+1}^{\alpha}}{\Gamma(1+\alpha)} \max_{0\leq j\le n} g^{j}, \quad n \geq 1. \end{array} $$

(A.32)

It follows that

$$ \omega^{n+1} \leq {\Psi}_{n} + {\Gamma}(2-\alpha) \left( 12 \lambda_{1} \tau^{\alpha} \sum\limits_{j=0}^{n-1} p_{n-j} \omega^{j+1} + 2 \lambda_{2} \tau^{\alpha} \sum\limits_{j=1}^{n} p_{n-j} \omega^{j} + 2 \lambda_{3} \tau^{\alpha} \sum\limits_{j=2}^{n} p_{n-j} \omega^{j-1} \right), $$

(A.33)

where

$$ {\Psi}_{n} = 6 \omega^{0} + \frac{12t_{n+1}^{\alpha}}{\Gamma(1+\alpha)} \underset{0\leq j\leq n}{\max} g^{j}, $$

(A.34)

and it is easy to get that Ψ_n ≥Ψ_k for n ≥ k ≥ 1. Let V = (ω^n+ 1,ωⁿ,⋯ ,ω¹)^T, then (A.33) can be written in a vector form by

$$ V \leq {\Psi}_{n} \vec{e} + (6\lambda_{1} J_{1} + \lambda_{2} J_{2} + \lambda_{3} J_{3}) V, $$

(A.35)

where

$$ \begin{array}{@{}rcl@{}} J_{1} = 2 {\Gamma}(2-\alpha) \tau^{\alpha} \begin{bmatrix} 0 & p_{1} & {\cdots} & p_{n-1} & p_{n} \\ 0 & 0 & {\cdots} & p_{n-2} & p_{n-1} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} & {\vdots} \\ 0 & 0 & {\cdots} & 0 & p_{1} \\ 0 & 0 & {\cdots} & 0 & 0 \end{bmatrix}_{(n+1)\times(n+1)}, \end{array} $$

(A.36)

$$ \begin{array}{@{}rcl@{}} J_{2} = 2 {\Gamma}(2-\alpha) \tau^{\alpha} \begin{bmatrix} 0 & p_{0} & {\cdots} & p_{n-2} & p_{n-1} \\ 0 & 0 & {\cdots} & p_{n-3} & p_{n-2} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} & {\vdots} \\ 0 & 0 & {\cdots} & 0 & p_{0} \\ 0 & 0 & {\cdots} & 0 & 0 \end{bmatrix}_{(n+1)\times(n+1)}, \end{array} $$

(A.37)

$$ \begin{array}{@{}rcl@{}} J_{3} = 2 {\Gamma}(2-\alpha) \tau^{\alpha} \begin{bmatrix} 0 & 0 & {\cdots} & p_{n-3} & p_{n-2} \\ 0 & 0 & {\cdots} & p_{n-4} & p_{n-3} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} & {\vdots} \\ 0 & 0 & {\cdots} & 0 & 0 \\ 0 & 0 & {\cdots} & 0 & 0 \end{bmatrix}_{(n+1)\times(n+1)}. \end{array} $$

(A.38)

By (A.1), we have

$$ \begin{array}{@{}rcl@{}} p_{i} \leq \frac{C_{0}^{\sigma}}{C_{0}^{\sigma} - C_{1}^{\sigma}} p_{i+1}, \qquad p_{1} \leq \frac{C_{0}^{\sigma}}{C_{1}^{\sigma} - C_{2}^{\sigma}} p_{i+2}, \end{array} $$

(A.39)

therefore,

$$ J_{2} V \leq \frac{C_{0}^{\sigma}}{C_{0}^{\sigma} - C_{1}^{\sigma}} \frac{1}{\lambda} J V, \qquad J_{2} V \leq \frac{C_{0}^{\sigma}}{C_{1}^{\sigma} - C_{2}^{\sigma}} \frac{1}{\lambda} JV, $$

(A.40)

which shows that

$$ V \leq J V + {\Psi}_{n} \vec{e}, $$

(A.41)

where J is defined in (A.22) with $\lambda = 6 \lambda _{1} + \frac {C_{0}^{\sigma } \lambda _{2}}{C_{0}^{\sigma } - C_{1}^{\sigma }} + \frac {C_{0}^{\sigma } \lambda _{3}}{C_{1}^{\sigma } - C_{2}^{\sigma }}$. As a result, we see that

$$ \begin{array}{@{}rcl@{}} V &\leq& JV + {\Psi}_{n} \vec{e} \leq J(JV + {\Psi}_{n} \vec{e}) + {\Psi}_{n} \vec{e} = J^{2}{V} + {\Psi}_{n} \sum\limits_{j=0}^{1} J^{j} \vec{e} \\ &\leq& {\cdots} \leq J^{n+1} V + {\Psi} \sum\limits_{j=0}^{n} J^{j} \vec{e}. \end{array} $$

(A.42)

This together with Lemma A.2 completes the proof. □