Unconditional optimal error estimates of linearized backward Euler Galerkin FEMs for nonlinear Schrödinger-Helmholtz equations

Abstract

In this paper, we establish unconditionally optimal error estimates for linearized backward Euler Galerkin finite element methods (FEMs) applied to nonlinear Schrödinger-Helmholtz equations. By using the temporal-spatial error splitting techniques, we split the error between the exact solution and the numerical solution into two parts which are called the temporal error and the spatial error. First, by introducing a time-discrete system, we prove the uniform boundedness for the solution of this time-discrete system in some strong norms and derive error estimates in temporal direction. Second, by the above achievements, we obtain the boundedness of the numerical solution in $L^{\infty }$-norm. Then, the optimal L² error estimates for r-order FEMs are derived without any restriction on the time step size. Numerical results in both two- and three-dimensional spaces are provided to illustrate the theoretical predictions and demonstrate the efficiency of the methods.

1 Introduction

In this paper, we focus on error estimates for linearized backward Euler Galerkin FEMs applied to the generalized nonlinear Schrödinger-Helmholtz equations defined by

$$ \begin{array}{lllll} \textmd{i} \frac{\partial u}{\partial t}+{\Delta} u+\psi f(|u|)u=0, \end{array} $$

(1)

$$ \begin{array}{lllll} \alpha \psi-{\upbeta}^{2}{\Delta}\psi=f(|u|)|u|^{2}, \end{array} $$

(2)

for x ∈Ω and t ∈ [0,T], where Ω is a bounded and convex (or smooth) domain in $\mathbb {R}^{d} ~(d=2,3)$. The initial and boundary conditions are taken to be

$$ \begin{array}{lllll} &u(x,0)=u_{0}(x), ~~\textmd{for} ~x\in{\Omega},\\ &u(x,t)=\psi(x,t)=0, ~~\textmd{for} ~x\in\partial{\Omega},~t\in [0,T]. \end{array} $$

(3)

Here $\textmd {i}=\sqrt {-1}$, α, β are real nonnegative constants with α + β≠ 0, and $f:~\mathbb {R}\rightarrow \mathbb {R}$ and $u_{0}:~{\Omega }\rightarrow \mathbb {C}$ are given functions. The complex-valued function u(x,t) stands for the single particle wave function, ψ(x,t) is a real-valued function which denotes the potential. The above system may describe many different physical phenomena in optics, quantum mechanics, and plasma physics. The system (1)–(3) defines the Schrödinger-Poisson model [7, 18, 22, 27, 28, 30] when α = 0. When β = 0, the system (1)–(3) reduces to a generalized nonlinear Schrödinger (GNLS) equation [3, 33, 34]. The other Schrödinger system such as the Schrödinger-Poisson-Slater model can found in [5, 37, 44].

In the past several decades, there are numerous works devoted to the theoretical analysis for various Schrödinger type equations (see, e.g., [6, 38] and the references therein). We refer to [30, 37] for the existence and uniqueness of solutions of the Schrödinger-Poisson type equations in $\mathbb {R}^{d}~(d=2,3)$. In [11], Cao et al. proved the local and global existence of a unique solution of the Schrödinger-Helmholtz equations. Numerical methods and analysis for the nonlinear Schrödinger type equations can be found in [4, 9, 29, 35, 40] for finite difference methods, in [2, 7, 36, 45] for FEMs, and in [8, 12] for spectral methods. In [2], Akrivis obtained optimal L² error estimates of the Crank-Nicolson Galerkin FEMs for the GNLS equation by a classical energy method. But this optimal L² error estimates required the time step condition $\tau =\mathcal {O}(h^{d/4})~(d=2,3)$ for both linearized and nonlinear schemes, where τ and h denote the time step size and the mesh width, respectively, and d represents the dimension of space. In [42], Tourigny obtained optimal H¹ error estimates of the implicit backward Euler and Crank-Nicolson Galerkin finite element schemes for the GNLS equation by using a nonlinear stability theory, which required the time step conditions $\tau =\mathcal {O}(h^{d/2})$ and $\tau =\mathcal {O}(h^{d/4})$ (d = 1,2,3) for the two schemes, respectively. In addition, optimal error estimates of finite difference schemes under certain time step conditions can be found in [5, 36]. In [39], Sun and Wang established two linearized Crank-Nicolson finite difference schemes for coupled cubic Schrödinger equation in three-dimensional space, and derived optimal L² error estimates of the schemes unconditionally.

In the practical computations of solving nonlinear partial differential equations, linearized schemes are usually more efficient since at each time step, the schemes only require solving a linear system. However, they typically suffer from the time step restriction conditions. In order to derive the optimal error estimates of linearized backward Euler Galerkin FEMs, one usually needs to prove the boundedness of numerical solutions in $L^{\infty }$-norm. For this purpose, by using the induction method with an inverse inequality, one has

$$ \begin{array}{lllll} \|{U_{h}^{n}}\|_{L^{\infty}} &\leq \|R_{h}u^{n}\|_{L^{\infty}}+\|R_{h}u^{n}-{U_{h}^{n}}\|_{L^{\infty}}\\ &\leq C\|u^{n}\|_{H^{2}}+Ch^{-\frac{d}{2}}\|R_{h}u^{n}-{U_{h}^{n}}\|_{L^{2}}\\ &\leq C\|u^{n}\|_{H^{2}}+Ch^{-\frac{d}{2}}(\tau+h^{r+1})\\ &\leq C, \end{array} $$

where ${U_{h}^{n}}$ and uⁿ are the numerical solution and the exact solution, respectively; R_h is a Ritz projection operator; r is the degree of the Galerkin FEMs; and C is a generic positive constant. However, the above inequality leads to a time step condition $\tau =\mathcal {O}(h^{\frac {d}{2}})$ (see [13, 14, 19, 31] for more details). This condition may lead to the use of an unnecessarily small time steps and make the computations much more time-consuming in practice. Recently, a new method was proposed by Li and Sun [23, 24] to derive unconditional stability and convergence of a linearized backward Euler Galerkin FEM for the time-dependent Joule heating equations. Moreover, this method was used in [25] for a nonlinear equation from incompressible miscible flows in porous media, in [16] for the Landau-Lifshitz equation, in [17] for the time-dependent Ginzburg-Landau equations, and in [43] for the generalized nonlinear Schrödinger equation. This new method is based upon an error splitting technique by introducing a corresponding time-discrete system. After deriving a priori estimates for the solution of the time-discrete system, one has

$$ \begin{array}{lllll} \|{U_{h}^{n}}\|_{L^{\infty}} &\leq \|R_{h}U^{n}\|_{L^{\infty}}+\|R_{h}U^{n}-{U_{h}^{n}}\|_{L^{\infty}}\\ &\leq \|R_{h}U^{n}\|_{L^{\infty}}+Ch^{-\frac{d}{2}}\|R_{h}U^{n}-{U_{h}^{n}}\|_{L^{2}}\\ &\leq C+Ch^{2-\frac{d}{2}}\\ &\leq C, \end{array} $$

where Uⁿ is the solution of the time-discrete system. Therefore, the boundedness of ${U_{h}^{n}}$ in $L^{\infty }$-norm can be obtained without time step restriction.

In this paper, applying the error splitting technique proposed in [23,24,25,26], we study two linearized backward Euler schemes with r-order Galerkin FEMs (r ≥ 1) for the time-dependent nonlinear Schrödinger-Helmholtz equations (1)–(3). The first scheme is semi-decoupled, and at each time step, one needs to solve for ${\Psi }_{h}^{n+1}$ firstly, and then to solve for $U_{h}^{n+1}$. The second scheme is fully decoupled, which is presented in numerical experiments. At each time step, it allows us to solve for ${\Psi }_{h}^{n+1}$ and $U_{h}^{n+1}$ in parallel. We only consider the theoretical analysis of the first scheme since it can be easily extended to the second one. However, the efficiency of the second method is verified in numerical experiments. In our analysis, by introducing a corresponding iterated time-discrete system, we prove the uniform boundedness for the solution of this system in some strong norms and derive error estimates in temporal direction. Next, we split the finite element error into two parts, the error in the temporal direction plus the error in the spatial direction, and derive the boundedness of the numerical solution in $L^{\infty }$-norm. Then, the optimal L² error estimates for r-order FEMs (r ≥ 1) are derived without any restriction on the time step size. Numerical results in both two- and three-dimensional space are presented to illustrate the theoretical predictions and demonstrate the efficiency of the method.

The rest of the paper is organized as follows. In Section 2, a linearized backward Euler Galerkin FEM for the nonlinear Schrödinger-Helmholtz equations (1)–(3) is presented. We split the error function as a temporal error function and a spatial error function by introducing a corresponding time-discrete system. Section 3 provides a priori estimates for the temporal error and suitable regularity for the solution of the time-discrete system. In Section 4, we obtain the τ-independent spatial error estimates in L²-norm. In Section 5, we derive the uniform boundedness of numerical solutions in $L^{\infty }$-norm and establish unconditional optimal L² error estimates of the r-order (r ≥ 1) Galerkin FEMs. In Section 6, we present the fully decoupled linearized backward Euler Galerkin FEM and provide some numerical examples for both two- and three-dimensional models to illustrate our theoretical analysis. Finally, conclusions are given in Section 7.

2 Preliminaries

Before presenting the schemes, we introduce some notations, definitions, and preliminary lemmas which will be used in the analysis. Let Ω be an open, bounded convex polygonal domain in $\mathbb {R}^{2}$ or polyhedral domain in $\mathbb {R}^{3}$ with Lipschitz continuous boundary ∂Ω. Let $W^{k,p}({\Omega })~(k\in \mathbb {N},1\leq p\leq +\infty )$ denote the standard Sobolev space equipped with the norm $\|\cdot \|_{W^{k,p}}$ [1]. The space H^k(Ω) is the standard Hilbertian Sobolev space of order k with norm $\|\cdot \|_{H^{k}}$ [1]. All other norms will be clearly labeled.

Following the classical finite element theory [10], we define $\tau _{h}=\{\mathcal {K}\}$ to be a quasi-uniform partition of Ω into triangular (in $\mathbb {R}^{2}$) or tetrahedral (in $\mathbb {R}^{3}$), let $h=\max \limits _{\forall \mathcal {K}\in \tau _{h}}\{\textmd {diam}\mathcal {K}\}$ and 0 < h < 1. For every $\mathcal {K}\in \tau _{h}$ and a nonnegative integer l , $P_{l}(\mathcal {K})$ is the space of the l th-order polynomial on $\mathcal {K}$. With these notations, we introduce the following finite element space

$$ V_{h}=\{v_{h}\in \mathcal{C}(\bar{\Omega}): ~v_{h}\in P_{r}(\mathcal{K})~ \textmd{and} ~v_{h}=0 ~ \textmd{on}~\partial{\Omega},~~\forall \mathcal{K}\in \tau_{h}\}, $$

where r ≥ 1 is a fixed integer. Let 0 = t₀ < t₁ < ⋅⋅⋅ < t_N = T be a uniform partition of the time interval [0,T] with time step size τ = T/N, t_n = nτ and uⁿ = u(⋅,t_n), ψⁿ = ψ(⋅,t_n) for 0 ≤ n ≤ N. For any sequence of functions $\{f^{n}\}_{n=0}^{N}$, we define

$$ D_{\tau} f^{n+1} =\frac{f^{n+1}- f^{n}}{\tau}~~\textmd{for}~ n=0,1,2,\cdot\cdot\cdot, N-1. $$

For any two complex functions u, v ∈ L²(Ω), the L² inner product is defined as follows:

$$ (u,v)={\int}_{\Omega} u(x)\cdot \bar{v}(x)dx, $$

where $\bar {v}$ denotes the complex conjugate of v.

Let $R_{h}:~{H_{0}^{1}}({\Omega })\rightarrow V_{h}$ be a Ritz projection operator defined by

$$ \big(\nabla(v-R_{h} v), \nabla w\big)=0,~~\textmd{for}~~w\in V_{h}. $$

By the classical finite element theory [10, 41], we know

$$ \begin{array}{lllll} &\|v-R_{h} v\|_{L^{2}}+h\|\nabla(v-R_{h} v)\|_{L^{2}}\leq Ch^{s}\|v\|_{H^{s}}, \end{array} $$

(4)

and

$$ \begin{array}{lllll} &\|R_{h} v\|_{W^{1,p}}\leq C\|v\|_{W^{1,p}},~~~\forall p>1, \end{array} $$

(5)

for any $v\in H^{s}({\Omega })\cap {H_{0}^{1}}({\Omega })$, 1 ≤ s ≤ r + 1.

With above notations, a linearized backward Euler Galerkin FEM is to find $U_{h}^{n+1},~\psi _{h}^{n+1}\in V_{h}$ such that

$$ \textmd{i} (D_{\tau} U_{h}^{n+1}, v)-(\nabla U_{h}^{n+1},\nabla v)+\big({\Psi}_{h}^{n+1} f(|{U_{h}^{n}}|)U_{h}^{n+1},v\big)=0,~~\forall v\in V_{h}, $$

(6)

$$ \alpha({\Psi}_{h}^{n+1},\varphi)+\beta^{2}(\nabla{\Psi}_{h}^{n+1},\nabla\varphi)=\big(f(|{U_{h}^{n}}|)|{U_{h}^{n}}|^{2},\varphi\big),~~\forall \varphi\in V_{h}, $$

(7)

with the initial value ${U_{h}^{0}}=R_{h} u_{0}$ and ${{\Psi }_{h}^{0}}$ satisfies

$$ \alpha({{\Psi}_{h}^{0}},\varphi)+\beta^{2}({\nabla{\Psi}_{h}^{0}},\nabla\varphi)=\big(f(|u_{0}|)|u_{0}|^{2},\varphi\big),~~\forall \varphi\in V_{h}. $$

(8)

Multiplying (6) by $U_{h}^{n+1}$ and integrating it over Ω to get

$$ \textmd{i} \frac{\|U_{h}^{n+1}\|_{L^{2}}^{2}}{\tau}-\frac{\textmd{i}}{\tau}({U_{h}^{n}},U_{h}^{n+1}) -\|\nabla U_{h}^{n+1}\|_{L^{2}}^{2}+{\Psi}_{h}^{n+1} f(|{U_{h}^{n}}|)\|U_{h}^{n+1}\|_{L^{2}}^{2}=0. $$

Taking the imaginary parts of the above equation yields

$$ \|U_{h}^{n+1}\|_{L^{2}}^{2}=\textmd{Re}({U_{h}^{n}},U_{h}^{n+1})\leq \|{U_{h}^{n}}\|_{L^{2}}\|U_{h}^{n+1}\|_{L^{2}}, $$

and then, we have

$$ \|U_{h}^{n+1}\|_{L^{2}}\leq \|{U_{h}^{0}}\|_{L^{2}}~~\textmd{for}~n=0,1,\cdot\cdot\cdot,N-1. $$

(9)

For analyzing the linearized scheme (6)–(7), we introduce a time-discrete system corresponding it as follows:

$$ \textmd{i} D_{\tau} U^{n+1}+{\Delta} U^{n+1}+{\Psi}^{n+1} f(|U^{n}|)U^{n+1}=0, $$

(10)

$$ \alpha{\Psi}^{n+1}-\beta^{2}{\Delta}{\Psi}^{n+1}=f(|U^{n}|)|U^{n}|^{2}, $$

(11)

with the initial and boundary conditions

$$ \begin{array}{lllll} &U^{0}=u_{0}, ~~\textmd{in}~{\Omega},\\ &U^{n+1}=0,~~{\Psi}^{n+1}=0,~~\textmd{on} ~\partial{\Omega}, \end{array} $$

(12)

for n = 0,1,⋅⋅⋅,N − 1, where ${\Psi }^{0}=\psi ^{0}$ satisfies (2) at t = t₀. The homogeneous Dirichlet boundary condition ψ = 0 is imposed on ∂Ω; thus, the classical regularity theory of PDEs [15] shows the boundedness of $\|{\Psi }^{0}\|_{H^{2}}$. In addition, it is easy to see that U^n+ 1 satisfies the following estimate

$$ \|U^{n+1}\|_{L^{2}}\leq \|U^{0}\|_{L^{2}}=\|u_{0}\|_{L^{2}},~~\textmd{for}~~0\leq n\leq N-1. $$

(13)

The main idea to our proof in this paper is the error splitting technique proposed in [23,24,25,26]; by this technique, we separate the errors into the temporal error and the spatial error as

$$ \begin{array}{lllll} &\|u^{n+1}-U_{h}^{n+1}\|_{L^{2}}\leq \|u^{n+1}-U^{n+1}\|_{L^{2}}+\|U^{n+1}-U_{h}^{n+1}\|_{L^{2}},\\ &\|\psi^{n+1}-{\Psi}_{h}^{n+1}\|_{L^{2}}\leq \|\psi^{n+1}-{\Psi}^{n+1}\|_{L^{2}}+\|{\Psi}^{n+1}-{\Psi}_{h}^{n+1}\|_{L^{2}}. \end{array} $$

With the splitting, we can prove that the temporal error is $\mathcal {O}(\tau )$ and the spatial error is $\mathcal {O}(h^{2})$, from which and the inverse inequality, we can obtain the uniform boundedness of numerical solutions $U_{h}^{n+1}$ and ${\Psi }_{h}^{n+1}$ in $L^{\infty }$-norm. Then, the optimal error estimates can be easily obtained.

In the remaining of this paper, we assume that $f^{(l)}:~\mathbb {R}\rightarrow \mathbb {R}~(l=0,1)$ are locally Lipschitz continuous, i.e., for any r₁, r₂ ∈ [−M^∗,M^∗],

$$ |f^{(l)}(r_{1})-f^{(l)}(r_{2})|\leq L_{M^{*}}|r_{1}-r_{2}|, $$

(14)

where $L_{M^{*}}$ is the Lipschitz constant depended on M^∗ and f^(l) denotes the l th-order derivative of f. We also assume that the solution to the initial and boundary value problem (1)–(3) exists and satisfies

$$ \begin{array}{lllll} &\|u_{0}\|_{H^{r+1}}+\|u\|_{L^{\infty}((0,T);H^{r+1})}+\|u_{t}\|_{L^{\infty}((0,T);H^{r+1})}\\ &\quad+\|u_{tt}\|_{L^{2}((0,T);H^{1})}+\|\psi\|_{L^{\infty}((0,T);H^{r+1})}\leq M. \end{array} $$

(15)

The discrete Gronwall’s lemma plays an important role in the analysis; we recall from [21] as follows:

Lemma 1

(Discrete Gronwall’s inequality) Let Δt,H and a_n,b_n,c_n,d_n (for integers n ≥ 0) be nonnegative numbers such that

$$ a_{l}+{\Delta} t\sum\limits_{n=0}^{l} b_{n}\leq {\Delta} t\sum\limits_{n=0}^{l}d_{n}a_{n}+{\Delta} t\sum\limits_{n=0}^{l} c_{n}+H~ \textmd{for} ~l\in \mathbb{N}, $$

Suppose that Δtd_n < 1, for all n, and set σ_n = (1 −Δtd_n)^− 1, then

$$ a_{l}+{\Delta} t\sum\limits_{n=0}^{l} b_{n}\leq \exp\bigg({\Delta} t\sum\limits_{n=0}^{l}\sigma_{n}d_{n}\bigg)\bigg({\Delta} t\sum\limits_{n=0}^{l} c_{n}+H\bigg)~ \textmd{for} ~l\in \mathbb{N}. $$

Remark 1

If the first sum on the right-hand side of (1) extends only up to l − 1, then estimate (1) holds for all Δt > 0 with σ_n = 1.

In our analysis, we need the following lemma and we refer to [15] for the details of the proof.

Lemma 2

Let m be a nonnegative integer, and assume g ∈ H^m(Ω) and ∂Ω is C^m+ 2. Suppose that $v\in {H_{0}^{1}}({\Omega })$ is the unique solution of the boundary value problem

$$ \begin{array}{lllll} &\alpha v-\beta^{2}{\Delta} v=g ~~\textmd{in} ~~{\Omega},\\ &v=0 ~~\textmd{on}~~\partial{\Omega}. \end{array} $$

Then v ∈ H^m+ 2(Ω) and the following estimate holds

$$ \|v\|_{H^{m+2}}\leq \tilde{C}\|g\|_{H^{m}}, $$

where $\tilde {C}$ depending on m, Ω and α, β.

Remark 2

Lemma 2 is also valid for convex domains when m = 0.

We recall the Gagliardo-Nirenberg inequality [1, 32] in the following lemma which will be frequently used in our proofs.

Lemma 3

(Gagliardo-Nirenberg inequality) Let u be a function defined on Ω and ∂^su be any partial derivative of u of order s, then

$$ \|\partial^{j} u\|_{L^{p}}\leq C\|\partial^{m} u\|_{L^{r}}^{a}\| u\|_{L^{q}}^{1-a}+C\| u\|_{L^{q}}, $$

for 0 ≤ j < m and $\frac {j}{m}\leq a\leq 1$ with

$$ \frac{1}{p}=\frac{j}{d}+a\big(\frac{1}{r}-\frac{m}{d}\big)+(1-a)\frac{1}{q}, $$

except $1<r<\infty$ and $m-j-\frac {d}{r}$ is a non-negative integer, in which case the above estimate holds for $\frac {j}{m}\leq a <1$.

Since the triangulations τ_h is assumed to be regular, for each v_h ∈ V_h, the following inverse inequality holds [10]:

$$ \begin{array}{lllll} &\|v_{h}\|_{L^{\infty}}\leq Ch^{-\frac{d}{2}}\|v_{h}\|_{L^{2}} ~~\textmd{for}~~d=2,~3. \end{array} $$

(16)

For the simplicity of notations, we denote by C₀ a constant dependent upon α, β, f, and M given in (15). We denote by C a generic positive constant involved in some classical inequalities, such as the Gagliardo-Nirenberg inequality and inequalities for Ritz projection, which depend upon the domain Ω and the shape regularity parameter of the mesh. Also we denote by C_M a generic positive constant independent of n, h, and τ and can absorb the constants C₀ and C, which could be taken different values in different places.

3 Temporal error estimates

In this section, we will estimate the error functions u^n+ 1 − U^n+ 1 and ψ^n+ 1 −Ψ^n+ 1 and establish the boundedness of the time-discrete solutions in some norms.

Under the regularity assumption (15), we define

$$ M_{0}:=\max_{0\leq n\leq N}\|u^{n}\|_{L^{\infty}}+\|u^{1}\|_{L^{\infty}}+1, $$

which is a positive constant dependent on M and independent of τ, h, and n. Let

$$ e^{n+1}=u^{n+1}-U^{n+1},~~\eta^{n+1}=\psi^{n+1}-{\Psi}^{n+1}. $$

The system (1)–(2) at t = t_n+ 1 can be rewritten as

$$ \begin{array}{lllll} \textmd{i} D_{\tau} u^{n+1}+{\Delta} u^{n+1}+\psi^{n+1} f(|u^{n}|)u^{n+1}=\mathcal{R}^{n+1}, \end{array} $$

(17)

$$ \begin{array}{lllll} \alpha \psi^{n+1}-\beta^{2}{\Delta}\psi^{n+1}=f(|u^{n}|)|u^{n}|^{2}+\mathcal{Q}^{n+1}, \end{array} $$

(18)

where

$$ \begin{array}{lllll} &\mathcal{R}^{n+1}=\textmd{i} D_{\tau} u^{n+1}-\textmd{i} u_{t}(t_{n+1})+\psi^{n+1} f(|u^{n}|)u^{n+1}-\psi^{n+1} f(|u^{n+1}|)u^{n+1},\\ &\mathcal{Q}^{n+1}=f(|u^{n+1}|)|u^{n+1}|^{2}-f(|u^{n}|)|u^{n}|^{2}. \end{array} $$

Subtracting (10)–(11) from (17)–(18) leads to

$$ \begin{array}{lllll} &\textmd{i}D_{\tau} e^{n+1}+{\Delta} e^{n+1}+\mathcal{R}_{1}^{n+1}=\mathcal{R}^{n+1}, \end{array} $$

(19)

$$ \begin{array}{lllll} &\alpha \eta^{n+1}-\beta^{2}{\Delta} \eta^{n+1}=\mathcal{Q}_{1}^{n+1}+\mathcal{Q}^{n+1}, \end{array} $$

(20)

where

$$ \begin{array}{lllll} &\mathcal{R}_{1}^{n+1}=\psi^{n+1}f(|u^{n}|)u^{n+1}-{\Psi}^{n+1}f(|U^{n}|)U^{n+1},\\ &\mathcal{Q}_{1}^{n+1}=f(|u^{n}|)|u^{n}|^{2}-f(|U^{n}|)|U^{n}|^{2}. \end{array} $$

By Taylor formulation, (14), and the regularity assumption (15), it is easy to see that

$$ \|\mathcal{Q}^{n+1}\|_{L^{2}}+\left( \sum\limits_{n=0}^{N-1}\tau\|\mathcal{R}^{n+1}\|_{L^{2}}^{2}\right)^{\frac{1}{2}}\leq C_{0}\tau. $$

(21)

Theorem 1

Suppose that the system (1)–(3) has a unique solution u, ψ satisfying (15). Then, there exists positive constants $\tau _{0}^{*}$ such that when $\tau <\tau _{0}^{*}$, the time-discrete system (10)–(12) has unique solutions U^m+ 1, Ψ^m+ 1, m = 0,1,⋅⋅⋅,N − 1, and there holds

$$ \|e^{m+1}\|_{L^{2}}+\|\eta^{m+1}\|_{L^{2}}+\|e^{m+1}\|_{H^{1}}+\tau^{\frac{1}{2}}\|e^{m+1}\|_{H^{2}} +\|\eta^{m+1}\|_{H^{2}}\leq C_{0}^{*}\tau, $$

(22)

$$ \|U^{m+1}\|_{H^{2}}+\|{\Psi}^{m+1}\|_{H^{3}}+\left( \sum\limits_{m=0}^{N-1}\tau\|D_{\tau} U^{m+1}\|_{H^{2}}^{2}\right)^{\frac{1}{2}}\leq C_{0}^{+}, $$

(23)

where $C_{0}^{*},~C_{0}^{+}$ are two positive constants dependent on M and independent of m, h, τ.

Proof

System (10)–(12) are linear elliptic equations, and following the classical theory of elliptic PDEs and the bound (13), we can find the solution of system (10)–(12) exists and is unique. Before proving (22) and (23), we use mathematical induction to prove the following estimate

$$ \|U^{m+1}\|_{L^{\infty}}\leq M_{0},~~\textmd{for}~~m=0,1,\cdot\cdot\cdot,N-1. $$

(24)

We first prove that the above estimate holds for m = 0. Choosing n = 0 in (19), we have

$$ \begin{array}{lllll} &\textmd{i}D_{\tau} e^{1}+{\Delta} e^{1}+\mathcal{R}_{1}^{1}=\mathcal{R}^{1}, \end{array} $$

(25)

$$ \begin{array}{lllll} &\alpha \eta^{1}-\beta^{2}{\Delta} \eta^{1}=\mathcal{Q}^{1}. \end{array} $$

(26)

From (11) and Lemma 2, we have

$$ \|{\Psi}^{1}\|_{H^{2}}\leq \tilde{C}\|f(|u_{0}|)|u_{0}|^{2}\|_{L^{2}}\leq C_{0}\|u_{0}\|_{L^{4}}^{2}\leq C_{M}. $$

By the embedding $H^{2}({\Omega })\hookrightarrow L^{\infty }({\Omega })$, we have

$$ \|{\Psi}^{1}\|_{L^{\infty}}\leq C\|{\Psi}^{1}\|_{H^{2}}\leq C_{M}. $$

(27)

From (26), (21), and Lemma 2, we have

$$ \|\eta^{1}\|_{L^{2}}\leq \|\eta^{1}\|_{H^{2}}\leq \tilde{C}\|\mathcal{Q}^{1}\|_{L^{2}}\leq C_{0}\tau. $$

(28)

Noticing that

$$ \begin{array}{lllll} \mathcal{R}_{1}^{1} &=\psi^{1}f(|u_{0}|)u^{1}-{\Psi}^{1}f(|u_{0}|)U^{1} =\eta^{1}f(|u_{0}|)u^{1}+{\Psi}^{1}f(|u_{0}|)e^{1}, \end{array} $$

and using (27) and (28), we have

$$ \begin{array}{@{}rcl@{}} \|\mathcal{R}_{1}^{1}\|_{L^{2}} &\leq&\|\eta^{1}f(|u_{0}|)u^{1}\|_{L^{2}} +\|{\Psi}^{1}f(|u_{0}|)e^{1}\|_{L^{2}}\\ &\leq& C_{0}\|\eta^{1}\|_{L^{2}} +C_{0}\|{\Psi}^{1}\|_{L^{\infty}}\|e^{1}\|_{L^{2}}\\ &\leq& C_{M}(\|\eta^{1}\|_{L^{2}}+\|e^{1}\|_{L^{2}})\\ &\leq& C_{M}(\|e^{1}\|_{L^{2}}+\tau). \end{array} $$

(29)

Testing (25) by $\bar {e}^{1}$ and taking the imaginary part of the resulting equation to get

$$ \begin{array}{@{}rcl@{}} \| e^{1}\|_{L^{2}}^{2} &=&-\tau\textmd{Im}(\mathcal{R}_{1}^{1},e^{1})+\tau\textmd{Im}(\mathcal{R}^{1},e^{1})\\ &\leq&\tau\|\mathcal{R}_{1}^{1}\|_{L^{2}}\|e^{1}\|_{L^{2}}+\tau\|\mathcal{R}^{1}\|_{L^{2}}\|e^{1}\|_{L^{2}}. \end{array} $$

By (29) and (21), we get

$$ \| e^{1}\|_{L^{2}}\leq C_{M}\tau, $$

(30)

when $\tau \leq \tau _{1}=\min \limits \{\frac {1}{2C_{M}},(\frac {C_{M}}{C_{0}})^{2}\}$. From (25), (29), and (30), we know

$$ \|{\Delta} e^{1}\|_{L^{2}}\leq \frac{\| e^{1}\|_{L^{2}}}{\tau}+\|\mathcal{R}_{1}^{1}\|_{L^{2}} +\|\mathcal{R}^{1}\|_{L^{2}}\leq C_{M}+C_{M}\tau+C_{0}\tau^{\frac{1}{2}}\leq 3C_{M}, $$

(31)

when τ ≤ τ₁. Next, we estimate $\|e^{1}\|_{L^{\infty }}\leq CC_{M}\tau ^{\frac {1}{4}}$ for d = 3 and d = 2, respectively. For d = 3, by the Gagliardo-Nirenberg inequality in Lemma 3, (30), and (31), we have

$$ \|e^{1}\|_{L^{\infty}}\leq C\|e^{1}\|_{H^{2}}^{\frac{3}{4}}\|e^{1}\|_{L^{2}}^{\frac{1}{4}}+C\|e^{1}\|_{L^{2}}\leq CC_{M}\tau^{\frac{1}{4}}. $$

(32)

Similarly, for d = 2, we know

$$ \|e^{1}\|_{L^{\infty}}\leq C\|e^{1}\|_{H^{2}}^{\frac{1}{2}}\|e^{1}\|_{L^{2}}^{\frac{1}{2}}+C\|e^{1}\|_{L^{2}}\leq CC_{M}\tau^{\frac{1}{2}}\leq CC_{M}\tau^{\frac{1}{4}}. $$

(33)

Therefore,

$$ \begin{array}{@{}rcl@{}} \|U^{1}\|_{L^{\infty}} &\leq&\|u^{1}\|_{L^{\infty}}+\|e^{1}\|_{L^{\infty}}\\ &\leq& \|u^{1}\|_{L^{\infty}}+CC_{M}\tau^{\frac{1}{4}}\\ &\leq& M_{0}, \end{array} $$

when $\tau \leq \tau _{2}=\frac {1}{(CC_{M})^{4}}$. Thus, (24) holds for m = 0. Now, by mathematical induction, we assume (24) holds for m ≤ n − 1. Then, from (11), we have

$$ \begin{array}{@{}rcl@{}} \|{\Psi}^{n+1}\|_{H^{2}} &\leq& \tilde{C}\|f(|U^{n}|)|U^{n}|^{2}\|_{L^{2}}\\ &\leq& C_{0}\|U^{n}\|_{L^{4}}^{2}\leq C_{0}C\|U^{n}\|_{L^{\infty}}^{2}\leq C_{M}. \end{array} $$

(34)

Noticing that

$$ \mathcal{Q}_{1}^{n+1}=\big(f(|u^{n}|)-f(|U^{n}|)\big)|u^{n}|^{2} +f(|U^{n}|)\big(|u^{n}|+|U^{n}|\big)\big(|u^{n}|-|U^{n}|\big), $$

we have

$$ \begin{array}{@{}rcl@{}} \|\mathcal{Q}_{1}^{n+1}\|_{L^{2}}&\leq&\|\!\big(f(|u^{n}|) - f(|U^{n}|)\big)|u^{n}|^{2}\|_{L^{2}} + \|f(|U^{n}|)\big(|u^{n}| + |U^{n}|\big)\big(|u^{n}| - |U^{n}|\big)\!\|_{L^{2}}\\ &\leq& C_{M}\|e^{n}\|_{L^{2}}, \end{array} $$

(35)

here, (14), (15), and the induction assumption are used.

From (20), (21), (35), and Lemma 2, we know that

$$ \begin{array}{@{}rcl@{}} \|\eta^{n+1}\|_{L^{2}}&\leq&\|\eta^{n+1}\|_{H^{2}} \leq \tilde{C}(\|\mathcal{Q}_{1}^{n+1}\|_{L^{2}}+\|\mathcal{Q}^{n+1}\|_{L^{2}})\\ &\leq& C_{M}(\|e^{n}\|_{L^{2}}+\tau). \end{array} $$

(36)

We rewrite $\mathcal {R}_{1}^{n+1}$ as

$$ \mathcal{R}_{1}^{n+1}=\eta^{n+1}f(|u^{n}|)u^{n+1}+{\Psi}^{n+1}\big(f(|u^{n}|)-f(|U^{n}|)\big)u^{n+1} +{\Psi}^{n+1}f(|U^{n}|)e^{n+1}, $$

(37)

and then we have

$$ \begin{array}{@{}rcl@{}} \|\mathcal{R}_{1}^{n+1}\|_{L^{2}} &\leq&\|\eta^{n+1}f(|u^{n}|)u^{n+1}\|_{L^{2}} +\|{\Psi}^{n+1}\big(f(|u^{n}|)-f(|U^{n}|)\big)u^{n+1}\|_{L^{2}}\\ &&+\|{\Psi}^{n+1}f(|U^{n}|)e^{n+1}\|_{L^{2}},\\ &\leq& C_{M}\big(\|\eta^{n+1}\|_{L^{2}}+\|e^{n+1}\|_{L^{2}}+\|e^{n}\|_{L^{2}}\big)\\ &\leq& C_{M}\big(\|e^{n+1}\|_{L^{2}}+\|e^{n}\|_{L^{2}}\big)+C_{M}\tau, \end{array} $$

(38)

here, (34) and (36) are used.

Next, we prove that (24) holds for m = n. Testing (19) by $\bar {e}^{n+1}$ and taking the imaginary part of the resulting equation to derive

$$ \begin{array}{@{}rcl@{}} \frac{1}{2\tau}\big(\|e^{n+1}\|_{L^{2}}^{2}-\|e^{n}\|_{L^{2}}^{2}\big) &\leq& -\textmd{Im}(\mathcal {R}_{1}^{n+1},e^{n+1})+\textmd{Im}(\mathcal {R}^{n+1},e^{n+1})\\ &\leq& \|\mathcal {R}_{1}^{n+1}\|_{L^{2}}\|e^{n+1}\|_{L^{2}}+\|\mathcal {R}^{n+1}\|_{L^{2}}\|e^{n+1}\|_{L^{2}}\\ &\leq& C_{M}\big(\|e^{n+1}\|_{L^{2}}^{2}+\|e^{n}\|_{L^{2}}^{2}\big)+C_{M}\tau^{2}+C_{M}\|\mathcal {R}^{n+1}\|_{L^{2}}^{2}, \end{array} $$

where (38) is used. Summing up the above inequality and using the discrete Gronwall’s inequality and (21), we know that there exists τ₃ > 0 such that

$$ \begin{array}{lllll} \|e^{n+1}\|_{L^{2}}\leq C_{M}\tau, \end{array} $$

(39)

when τ ≤ τ₃. The above estimate shows that

$$ \|D_{\tau} e^{n+1}\|_{L^{2}}\leq C_{M}, $$

with which and (19) and (21), we have

$$ \begin{array}{@{}rcl@{}} \|{\Delta} e^{n+1}\|_{L^{2}}&\leq& \| D_{\tau} e^{n+1}\|_{L^{2}}+\|\mathcal{R}_{1}^{n+1}\|_{L^{2}} +\|\mathcal{R}^{n+1}\|_{L^{2}}\\ &\leq& C_{M}+C_{M}\tau+C_{0}\tau^{\frac{1}{2}}\leq 3C_{M}, \end{array} $$

(40)

when τ ≤ τ₁. By the same techniques used in the proof of estimates (32) and (33), one has

$$ \|e^{n+1}\|_{L^{\infty}} \leq CC_{M}\tau^{\frac{1}{4}}. $$

Thus, we have

$$ \begin{array}{@{}rcl@{}} \|U^{n+1}\|_{L^{\infty}} &\leq&\|u^{n+1}\|_{L^{\infty}}+\|e^{n+1}\|_{L^{\infty}}\\ &\leq& \|u^{n+1}\|_{L^{\infty}}+CC_{M}\tau^{\frac{1}{4}}\\ &\leq& M_{0}, \end{array} $$

(41)

when τ ≤ τ₂. Thus, (24) holds for m = n. The induction is completed.

From (36) and (39), we can easily obtain

$$ \begin{array}{lllll} \|e^{n+1}\|_{L^{2}}+\|\eta^{n+1}\|_{L^{2}}+\|\eta^{n+1}\|_{H^{2}}\leq C_{0}^{*}\tau. \end{array} $$

(42)

From (34) and (40), we have

$$ \begin{array}{lllll} &\|{\Psi}^{n+1}\|_{H^{2}}\leq C_{0}^{+},\\ &\|U^{n+1}\|_{H^{2}}\leq \|u^{n+1}\|_{H^{2}}+\|e^{n+1}\|_{H^{2}}\leq \|u^{n+1}\|_{H^{2}}+C\|{\Delta} e^{n+1}\|_{L^{2}}\leq C_{0}^{+}. \end{array} $$

(43)

Furthermore, by (43), (11), and Lemma 2, we arrive at

$$ \begin{array}{@{}rcl@{}} \|{\Psi}^{n+1}\|_{H^{3}} &\leq& \tilde{C}\|f(|U^{n}|)|U^{n}|^{2}\|_{H^{1}}\\ &\leq& \tilde{C}\|f^{\prime}(|U^{n}|)\nabla U^{n} |U^{n}|^{2}\|_{L^{2}}+\tilde{C}\|2f(|U^{n}|)|U^{n}|\nabla U^{n}\|_{L^{2}}\\ &\leq& C_{0}\|\nabla U^{n}\|_{L^{2}}\|U^{n}\|_{L^{\infty}}^{2}+C_{0}\|U^{n}\|_{L^{\infty}}\|\nabla U^{n}\|_{L^{2}}\\ &\leq& C_{M}. \end{array} $$

(44)

Testing (19) by ${\Delta } \bar {e}^{n+1}$ and taking the real parts of the resulting equation lead to

$$ \begin{array}{@{}rcl@{}} \|{\Delta} e^{n+1}\|_{L^{2}}^{2} &=&-\textmd{Re}(\mathcal{R}_{1}^{n+1},{\Delta} e^{n+1})+\textmd{Re}(\mathcal{R}^{n+1},{\Delta} e^{n+1})\\ &\leq& \|\mathcal{R}_{1}^{n+1}\|_{L^{2}}\|{\Delta} e^{n+1}\|_{L^{2}}+\|\mathcal{R}^{n+1}\|_{L^{2}}\|{\Delta} e^{n+1}\|_{L^{2}}\\ &\leq& \frac{1}{2}\|{\Delta} e^{n+1}\|_{L^{2}}^{2}+\|\mathcal{R}_{1}^{n+1}\|_{L^{2}}^{2}+\|\mathcal{R}^{n+1}\|_{L^{2}}^{2}, \end{array} $$

which shows that

$$ \tau\|{\Delta} e^{n+1}\|_{L^{2}}^{2}\leq 2\tau(\|\mathcal{R}_{1}^{n+1}\|_{L^{2}}^{2}+\|\mathcal{R}^{n+1}\|_{L^{2}}^{2}). $$

Summing the above inequality from n = 0 to n = N − 1 and using (21), (38), and (39), we have

$$ {\sum}_{n=0}^{N-1}\tau\|{\Delta} e^{n+1}\|_{L^{2}}^{2}\leq 2{\sum}_{n=0}^{N-1}\tau\|\mathcal{R}_{1}^{n+1}\|_{L^{2}}^{2}+2{\sum}_{n=0}^{N-1}\tau\|\mathcal{R}^{n+1}\|_{L^{2}}^{2}\leq C_{M}\tau^{2}. $$

From above inequality, we can easily get

$$ \begin{array}{@{}rcl@{}} {\sum}_{n=0}^{N-1}\tau\|D_{\tau} U^{n+1}\|_{H^{2}}^{2} &\leq& {\sum}_{n=0}^{N-1}\tau\|D_{\tau} u^{n+1}\|_{H^{2}}^{2} +{\sum}_{n=0}^{N-1}\tau\| D_{\tau} e^{n+1}\|_{H^{2}}^{2}\\ &\leq& {\sum}_{n=0}^{N-1}\tau\|D_{\tau} u^{n+1}\|_{H^{2}}^{2} +\frac{C_{M}}{\tau^{2}}\big({\sum}_{n=0}^{N-1}\tau\| {\Delta} e^{n+1}\|_{L^{2}}^{2}\big)\\ &\leq& C_{M}. \end{array} $$

(45)

For proving the remaining estimates, we need to bound $\|\mathcal {R}_{1}^{n+1}\|_{H^{1}}$. From (37), one has

$$ \begin{array}{@{}rcl@{}} \|\mathcal{R}_{1}^{n+1}\|_{H^{1}}&\leq&\|\eta^{n+1}f(|u^{n}|)u^{n+1}\|_{H^{1}} +\|{\Psi}^{n+1}\big(f(|u^{n}|)-f(|U^{n}|)\big)u^{n+1}\|_{H^{1}}\\ &&+\|{\Psi}^{n+1}f(|U^{n}|)e^{n+1}\|_{H^{1}}\\ &=&\mathcal {I}_{1}+\mathcal {I}_{2}+\mathcal {I}_{3}, \end{array} $$

(46)

where

$$ \begin{array}{@{}rcl@{}} \mathcal {I}_{1}&\leq&\|\nabla\eta^{n+1}f(|u^{n}|)u^{n+1}\|_{L^{2}}+\|\eta^{n+1}f^{\prime}(|u^{n}|)\nabla u^{n} u^{n+1}\|_{L^{2}}\\&&+\|\eta^{n+1}f(|u^{n}|)\nabla u^{n+1}\|_{L^{2}}\\ &\leq& C_{M}\|\nabla\eta^{n+1}\|_{L^{2}}, \end{array} $$

$$ \begin{array}{@{}rcl@{}} \mathcal {I}_{3}&\leq& \|\nabla{\Psi}^{n+1}f(|U^{n}|)e^{n+1}\|_{L^{2}}+\|{\Psi}^{n+1}f^{\prime}(|U^{n}|)\nabla U^{n} e^{n+1}\|_{L^{2}}\\&&+\|{\Psi}^{n+1}f(|U^{n}|)\nabla e^{n+1}\|_{L^{2}}\\ &\leq& C_{0}\|\nabla{\Psi}^{n+1}\|_{L^{3}}\|e^{n+1}\|_{L^{6}}+C_{0}\|{\Psi}^{n+1}\|_{L^{\infty}}\|\nabla U^{n}\|_{L^{3}} \|e^{n+1}\|_{L^{6}}\\&&+C_{0}\|{\Psi}^{n+1}\|_{L^{\infty}}\|\nabla e^{n+1}\|_{L^{2}}\\ &\leq& C_{M}\|\nabla e^{n+1}\|_{L^{2}}, \end{array} $$

$$ \begin{array}{@{}rcl@{}} \mathcal {I}_{2}&\leq&\|\nabla{\Psi}^{n+1}\big(f(|u^{n}|)-f(|U^{n}|)\big)u^{n+1}\|_{L^{2}} \\&&+\|{\Psi}^{n+1}\big(f^{\prime}(|u^{n}|)\nabla u^{n}-f^{\prime}(|U^{n}|)\nabla U^{n} \big)u^{n+1}\|_{L^{2}}\\ &&+\|{\Psi}^{n+1}\big(f(|u^{n}|)-f(|U^{n}|)\big)\nabla u^{n+1}\|_{L^{2}}\\ &=&\mathcal {I}_{2}^{1}+\mathcal {I}_{2}^{2}+\mathcal {I}_{2}^{3}, \end{array} $$

here,

$$ \begin{array}{@{}rcl@{}} &&\mathcal {I}_{2}^{1}\leq C_{0}\|\nabla{\Psi}^{n+1}e^{n} u^{n+1}\|_{L^{2}}\\ &\leq& C_{0}\|\nabla{\Psi}^{n+1}\|_{L^{3}}\|e^{n}\|_{L^{6}} \|u^{n+1}\|_{L^{\infty}}\\ &\leq& C_{0}C\|{\Psi}^{n+1}\|_{H^{2}}\|\nabla e^{n}\|_{L^{2}} \|u^{n+1}\|_{H^{2}}\\ &\leq& C_{M}\|\nabla e^{n}\|_{L^{2}},\\ &&\mathcal {I}_{2}^{2} \leq \|{\Psi}^{n+1}\big(f^{\prime}(|u^{n}|)-f^{\prime}(|U^{n}|)\big)\nabla u^{n} u^{n+1}\|_{L^{2}} +\|{\Psi}^{n+1}f^{\prime}(|U^{n}|)\nabla e^{n} u^{n+1}\|_{L^{2}}\\ &\leq& C_{0}\|{\Psi}^{n+1}e^{n}\nabla u^{n} u^{n+1}\|_{L^{2}} +C_{0}\|{\Psi}^{n+1}\nabla e^{n} u^{n+1}\|_{L^{2}}\\ &\leq& C_{M}\|\nabla e^{n}\|_{L^{2}},\\ &&\mathcal {I}_{2}^{3}\leq C_{M}\|\nabla e^{n}\|_{L^{2}}. \end{array} $$

Combining estimates $\mathcal {I}_{1}$, $\mathcal {I}_{2}$, and $\mathcal {I}_{3}$ into (46), and using (42), we have

$$ \begin{array}{lllll} \|\mathcal{R}_{1}^{n+1}\|_{H^{1}}&\leq C_{M}(\|\nabla e^{n+1}\|_{L^{2}}+\|\nabla e^{n}\|_{L^{2}})+C_{M}\tau. \end{array} $$

(47)

Testing (19) by − D_τe^n+ 1 leads to

$$ \begin{array}{lllll} &-\textmd{i}\|D_{\tau} e^{n+1}\|_{L^{2}}^{2}+(\nabla e^{n+1},D_{\tau} \nabla e^{n+1})-(\mathcal{R}_{1}^{n+1},D_{\tau} e^{n+1})=-(\mathcal{R}^{n+1},D_{\tau} e^{n+1}), \end{array} $$

(48)

Taking the real parts of above inequality, we have

$$ \begin{array}{lllll} &\frac{1}{2\tau}(\|\nabla e^{n+1}\|_{L^{2}}^{2}-\|\nabla e^{n}\|_{L^{2}}^{2})\leq |\textmd{Re}(\mathcal{R}_{1}^{n+1},D_{\tau} e^{n+1})|+|\textmd{Re}(\mathcal{R}^{n+1},D_{\tau} e^{n+1})|, \end{array} $$

(49)

Testing (19) by $\mathcal {R}_{1}^{n+1}$ and taking the imaginary parts of the resulting equation, we have

$$ \begin{array}{lllll} \textmd{Re}(D_{\tau} e^{n+1},\mathcal{R}_{1}^{n+1})-\textmd{Im}(\nabla e^{n+1},\nabla\mathcal{R}_{1}^{n+1})=\textmd{Im}(\mathcal{R}^{n+1},\mathcal{R}_{1}^{n+1}). \end{array} $$

(50)

By (38), (39), (47), and the Young’s inequality, we obtain

$$ \begin{array}{@{}rcl@{}} |\textmd{Re}(D_{\tau} e^{n+1},\mathcal{R}_{1}^{n+1})| &\leq&|\textmd{Im}(\nabla e^{n+1},\nabla\mathcal{R}_{1}^{n+1})|+|\textmd{Im}(\mathcal{R}^{n+1},\mathcal{R}_{1}^{n+1})|\\ &\leq&\|\nabla e^{n+1}\|_{L^{2}}\|\nabla\mathcal{R}_{1}^{n+1}\|_{L^{2}}+\|\mathcal{R}^{n+1}\|_{L^{2}}\|\mathcal{R}_{1}^{n+1}\|_{L^{2}}\\ &\leq&\frac{1}{2}\|\nabla e^{n+1}\|_{L^{2}}^{2} + \frac{1}{2}\|\nabla\mathcal{R}_{1}^{n+1}\|_{L^{2}}^{2} + \frac{1}{2}\|\mathcal{R}^{n+1}\|_{L^{2}}^{2} \!+\frac{1}{2}\|\mathcal{R}_{1}^{n+1}\|_{L^{2}}^{2}\\ &\leq& C_{M}(\|\nabla e^{n+1}\|_{L^{2}}^{2}+\|\nabla e^{n}\|_{L^{2}}^{2})+\frac{1}{2}\|\mathcal{R}^{n+1}\|_{L^{2}}^{2} +C_{M}\tau^{2}. \end{array} $$

(51)

Meanwhile, we write the second term on the right-hand side of inequality (49) as

$$ \begin{array}{@{}rcl@{}} &&|\textmd{Re}\big(\mathcal{R}^{n+1},D_{\tau} e^{n+1})|\\ &=&\big|\textmd{Re}(\textmd{i} D_{\tau} u^{n+1}-\textmd{i} u_{t}(t_{n+1})+\psi^{n+1} f(|u^{n}|)u^{n+1}\\&&-\psi^{n+1} f(|u^{n+1}|)u^{n+1},D_{\tau} e^{n+1}\big)\big|\\ &\leq&\big|\big(D_{\tau} u^{n+1}-u_{t}(t_{n+1}),D_{\tau} e^{n+1}\big)\big|+\big|\big(\psi^{n+1} f(|u^{n}|)u^{n+1}\\&&-\psi^{n+1} f(|u^{n+1}|)u^{n+1},D_{\tau} e^{n+1}\big)\big| \end{array} $$

(52)

Testing (19) by D_τu^n+ 1 − u_t(t_n+ 1) leads to

$$ \begin{array}{lllll} &\textmd{i}\big(D_{\tau} e^{n+1},D_{\tau} u^{n+1}-u_{t}(t_{n+1})\big)-\big(\nabla e^{n+1},\nabla(D_{\tau} u^{n+1}-u_{t}(t_{n+1}))\big)\\ &\quad+\big(\mathcal{R}_{1}^{n+1},D_{\tau} u^{n+1}-u_{t}(t_{n+1})\big)=\big(\mathcal{R}^{n+1},D_{\tau} u^{n+1}-u_{t}(t_{n+1})\big). \end{array} $$

By (38), (39), and the Young’s inequality, we can obtain

$$ \begin{array}{@{}rcl@{}} &&\big|\big(D_{\tau} e^{n+1},D_{\tau} u^{n+1}-u_{t}(t_{n+1})\big)\big|\\ &\leq& \frac{1}{2}\|\nabla e^{n+1}\|_{L^{2}}^{2}+\frac{1}{2}\|D_{\tau} u^{n+1}-u_{t}(t_{n+1})\|_{H^{1}}^{2}\\ &&+\|D_{\tau} u^{n+1}-u_{t}(t_{n+1})\|_{L^{2}}^{2}+\frac{1}{2}\|\mathcal{R}_{1}^{n+1}\|_{L^{2}}^{2} +\frac{1}{2}\|\mathcal{R}^{n+1}\|_{L^{2}}^{2}\\ &\leq& \frac{1}{2}\|\nabla e^{n+1}\|_{L^{2}}^{2}+C_{M}\|D_{\tau} u^{n+1}-u_{t}(t_{n+1})\|_{H^{1}}^{2}+\frac{1}{2}\|\mathcal{R}^{n+1}\|_{L^{2}}^{2}+C_{M}\tau^{2}. \end{array} $$

(53)

Testing (19) by ψ^n+ 1f(|uⁿ|)u^n+ 1 − ψ^n+ 1f(|u^n+ 1|)u^n+ 1 yields

$$ \begin{array}{@{}rcl@{}} &&\textmd{i}\big(D_{\tau} e^{n+1},\psi^{n+1} f(|u^{n}|)u^{n+1}-\psi^{n+1} f(|u^{n+1}|)u^{n+1}\big)\\ &&-\big(\nabla e^{n+1},\nabla(\psi^{n+1} f(|u^{n}|)u^{n+1}-\psi^{n+1} f(|u^{n+1}|)u^{n+1})\big)\\ &&+\big(\mathcal{R}_{1}^{n+1},\psi^{n+1} f(|u^{n}|)u^{n+1}-\psi^{n+1} f(|u^{n+1}|)u^{n+1}\big)\\ &=&\big(\mathcal{R}^{n+1},\psi^{n+1} f(|u^{n}|)u^{n+1}-\psi^{n+1} f(|u^{n+1}|)u^{n+1}\big). \end{array} $$

Thanks to the above equation, (38), (39), (14), and (15), we have

$$ \begin{array}{@{}rcl@{}} &&\big|\big(D_{\tau} e^{n+1},\psi^{n+1} f(|u^{n}|)u^{n+1}-\psi^{n+1} f(|u^{n+1}|)u^{n+1}\big)\big|\\ &\leq&\frac{1}{2}\|\nabla e^{n+1}\|_{L^{2}}^{2}+C_{M}\|u^{n+1}-u^{n}\|_{H^{1}}^{2}+\frac{1}{2}\|\mathcal{R}_{1}^{n+1}\|_{L^{2}}^{2} +\frac{1}{2}\|\mathcal{R}^{n+1}\|_{L^{2}}^{2}\\ &\leq&\frac{1}{2}\|\nabla e^{n+1}\|_{L^{2}}^{2}+\frac{1}{2}\|\mathcal{R}^{n+1}\|_{L^{2}}^{2}+C_{M}\tau^{2}. \end{array} $$

(54)

Combining estimates (51), (52), (53), and (54) into (49), we have

$$ \begin{array}{@{}rcl@{}} \|\nabla e^{n+1}\|_{L^{2}}^{2}-\|\nabla e^{n}\|_{L^{2}}^{2} &\leq& C_{M}\tau (\|\nabla e^{n+1}\|_{L^{2}}+\|\nabla e^{n}\|_{L^{2}})+3\tau\|\mathcal{R}^{n+1}\|_{L^{2}}^{2}\\ &&+C_{M}\tau \|D_{\tau} u^{n+1}-u_{t}(t_{n+1})\|_{H^{1}}^{2}+C_{M}\tau^{2}. \end{array} $$

Summing the above inequality up and applying the discrete Gronwall’s inequality, (15) and (21), we know that there exists τ₄ > 0 such that

$$ \|\nabla e^{n+1}\|_{L^{2}}\leq C_{M}\tau, $$

(55)

when τ ≤ τ₄. Testing (19) by Δe^n+ 1 and taking the real parts to arrive at

$$ \begin{array}{@{}rcl@{}} \!\!\!\!&&\|{\Delta} e^{n+1}\|_{L^{2}}^{2}\\ \!\!\!\!&=&-\frac{1}{\tau}\textmd{Im}(\nabla e^{n},\nabla e^{n+1})+\textmd{Re}(\mathcal{R}_{1}^{n+1},{\Delta} e^{n+1})+\textmd{Re}(\mathcal{R}^{n+1},{\Delta} e^{n+1})\\ \!\!\!\!&\leq&\frac{1}{2\tau}(\|\nabla e^{n+1}\|_{L^{2}}^{2} + \|\nabla e^{n}\|_{L^{2}}^{2}) + \frac{1}{2}\|{\Delta} e^{n+1}\|_{L^{2}}^{2}+\|\mathcal{R}_{1}^{n+1}\|_{L^{2}}^{2}+\|\mathcal{R}^{n+1}\|_{L^{2}}^{2}. \end{array} $$

(56)

Thanks to (21), (47), (39), and (55), we have

$$ \begin{array}{lllll} \|e^{n+1}\|_{H^{2}}\leq C_{M} \tau^{\frac{1}{2}}. \end{array} $$

(57)

Taking $\tau _{0}^{*}=\min \limits \{\tau _{1},\tau _{2},\tau _{3},\tau _{4}\}$, and combining (42), (55), (57), (45), (43), and (44), the proof of Theorem 1 is completed. □

4 Spatial error estimates

In this section, we will derive the τ-independent estimates for $U^{n+1}-U_{h}^{n+1}$ and ${\Psi }^{n+1}-{\Psi }_{h}^{n+1}$ in L²-norm.

By Sobolev embedding inequalities and (5), we know

$$\|R_{h} U^{n}\|_{L^{\infty}}\leq C\|R_{h} U^{n}\|_{W^{1,6}}\leq C\|U^{n}\|_{W^{1,6}}\leq C\|U^{n}\|_{H^{2}},~~n=0,~1,\cdot\cdot\cdot,N.$$

Similarly, $\|R_{h} {\Psi }^{n}\|_{L^{\infty }}\leq C\|{\Psi }^{n}\|_{H^{2}},~~n=0,~1,\cdot \cdot \cdot ,N$. With these estimates, we can define

$$ \begin{array}{lllll} &M_{1}=\max_{0\leq n\leq N-1}\|R_{h} U^{n+1}\|_{L^{\infty}}+\|R_{h} U^{0}\|_{L^{\infty}}+1,\\ &M_{2}=\max_{0\leq n\leq N-1}\|R_{h} {\Psi}^{n+1}\|_{L^{\infty}}+\|R_{h} {\Psi}^{0}\|_{L^{\infty}}+1, \end{array} $$

where M₁ and M₂ are two positive constants dependent on M and independent on τ, h, and n.

Let $e_{h}^{n+1}=U_{h}^{n+1}-R_{h}U^{n+1},~~\eta _{h}^{n+1}={\Psi }_{h}^{n+1}-R_{h}{\Psi }^{n+1}$. From the full discrete scheme (6)–(7) and the time-discrete scheme (10)–(11), we have the following error equations:

$$ \textmd{i} (D_{\tau} e_{h}^{n+1},v)-(\nabla e_{h}^{n+1},\nabla v)-(\mathcal {R}_{2}^{n+1},v) =\textmd{i} \big(D_{\tau} (U^{n+1}-R_{h}U^{n+1}),v\big),~~\forall v\in V_{h}, $$

(58)

$$ \begin{array}{@{}rcl@{}} &&\alpha(\eta_{h}^{n+1},\varphi)+\beta^{2}(\nabla\eta_{h}^{n+1},\nabla\varphi)=-(\mathcal {Q}_{2}^{n+1},\varphi)+\alpha({\Psi}^{n+1}-R_{h}{\Psi}^{n+1},\varphi)\\ &+&\beta^{2}\big(\nabla({\Psi}^{n+1}-R_{h}{\Psi}^{n+1}),\nabla\varphi\big),~~\forall \varphi\in V_{h}, \end{array} $$

(59)

where

$$ \begin{array}{lllll} &\mathcal{R}_{2}^{n+1}={\Psi}^{n+1}f(|U^{n}|)U^{n+1}-{\Psi}_{h}^{n+1}f(|{U_{h}^{n}}|)U_{h}^{n+1},\\ &\mathcal{Q}_{2}^{n+1}=f(|U^{n}|)|U^{n}|^{2}-f(|{U_{h}^{n}}|)|{U_{h}^{n}}|^{2}. \end{array} $$

Theorem 2

Assume that the unique solution u, ψ of system (1)–(3) satisfies (15). Then the full discrete system (6)–(7) has unique solution $U_{h}^{m+1},~{\Psi }_{h}^{n+1}$, m = 0,1,⋅⋅⋅,N − 1, and there exists $\tau _{0}^{\prime }>0$, $h_{0}^{\prime }>0$ such that when $\tau \leq \tau _{0}^{\prime }$, $h\leq h_{0}^{\prime }$,

$$ \|e_{h}^{m+1}\|_{L^{2}}+\|\eta_{h}^{m+1}\|_{L^{2}}\leq C_{0}^{\prime}h^{2}, $$

(60)

$$ \|\nabla e_{h}^{m+1}\|_{L^{2}}+\|\nabla\eta_{h}^{m+1}\|_{L^{2}}\leq C_{0}^{\prime}h, $$

(61)

where $C_{0}^{\prime }$ is a positive constant dependent on $C_{0}^{*},~C_{0}^{+}$, M, and independent of m, h, τ.

Proof

The existence and uniqueness of solution of (6) follows the uniform bound (9). Since the coefficient matrix of (7) is symmetric and positive definite, thus the existence and uniqueness of solution of (7) is ensured. Now, we prove the error estimate (60) by mathematical induction. Since ${U_{h}^{0}}=R_{h}u_{0}$, by using (4) and (15), we obtain

$$ \begin{array}{lllll} \|{e_{h}^{0}}\|_{L^{2}} = \|{U_{h}^{0}}-R_{h}U^{0}\|_{L^{2}}\!\leq\! \|{U_{h}^{0}}-u_{0}\|_{L^{2}}+\|{U_{h}^{0}}-u_{0}\|_{L^{2}}\!\leq\! Ch^{2}\|u_{0}\|_{H^{2}}\!\leq\! C_{M}h^{2}. \end{array} $$

(62)

From (8) and (2) at t = 0, we have

$$ \alpha({\Psi}^{0}-{{\Psi}_{h}^{0}},\varphi)+\beta^{2}\big(\nabla({\Psi}^{0}-{{\Psi}_{h}^{0}}),\nabla\varphi\big)=0,~~\forall \varphi\in V_{h}. $$

(63)

When β = 0, from (4), (15), and (63), we obtain

$$ \|{{\Psi}_{h}^{0}}-R_{h}{\Psi}^{0}\|_{L^{2}}\leq \|{\Psi}^{0}-R_{h}{\Psi}^{0}\|_{L^{2}}\leq Ch^{2}\|{\Psi}^{0}\|_{H^{2}}\leq C_{M} h^{2}. $$

(64)

When β≠ 0, from (4), (15), and (63), we have

$$ \|\nabla({{\Psi}_{h}^{0}}-R_{h}{\Psi}^{0})\|_{L^{2}}\leq C_{M} h. $$

(65)

For deriving the estimate $\|{\Psi }^{0}-{{\Psi }_{h}^{0}}\|_{L^{2}}$, we will use the Aubin-Nitsche techniques. Let g ∈ L²(Ω), take $\phi \in H^{2}({\Omega })\cap {H_{0}^{1}}({\Omega })$ as the solution of

$$ \alpha \phi-\beta^{2}{\Delta} \phi=g~~\textmd{in}~~{\Omega}, ~~\textmd{with}~~\phi=0 ~~\textmd{on} ~~\partial{\Omega}. $$

From Lemma 2, we know $\|\phi \|_{H^{2}}\leq \tilde {C}\|g\|_{L^{2}}$. Choosing $g={\Psi }^{0}-{{\Psi }_{h}^{0}}$, one has

$$ \begin{array}{@{}rcl@{}} \|{\Psi}^{0}-{{\Psi}_{h}^{0}}\|_{L^{2}}^{2} &=&\alpha ({\Psi}^{0}-{{\Psi}_{h}^{0}},\phi-P_{h}\phi)+\beta^{2}\big(\nabla({\Psi}^{0}-{{\Psi}_{h}^{0}}),\nabla(\phi-P_{h}\phi)\big)\\ &\leq& Ch^{2}\|{\Psi}^{0}-{{\Psi}_{h}^{0}}\|_{L^{2}}\|\phi\|_{H^{2}}+Ch\|\nabla({\Psi}^{0}-{{\Psi}_{h}^{0}})\|_{L^{2}}\|\phi\|_{H^{2}}\\ &\leq& C\tilde{C}h^{2}\|{\Psi}^{0}-{{\Psi}_{h}^{0}}\|_{L^{2}}^{2}+C\tilde{C}h\|\nabla({\Psi}^{0}-{{\Psi}_{h}^{0}})\|_{L^{2}}\|{\Psi}^{0}-{{\Psi}_{h}^{0}}\|_{L^{2}}. \end{array} $$

Where P_hϕ is the elliptic projection of ϕ. Choosing $h_{1}=(2C\tilde {C})^{-\frac {1}{2}}$, when h ≤ h₁, the above estimate along with (4) and (65) implies that

$$ \|{\Psi}^{0}-{{\Psi}_{h}^{0}}\|_{L^{2}}\leq C_{M} h^{2}, $$

(66)

with which and (4) shows that

$$ \|{{\Psi}_{h}^{0}}-R_{h}{\Psi}^{0}\|_{L^{2}}\leq\|{{\Psi}_{h}^{0}}-{\Psi}^{0}\|_{L^{2}}+\|{\Psi}^{0}-R_{h}{\Psi}^{0}\|_{L^{2}}\leq C_{M} h^{2}. $$

(67)

Combining estimates (62), (64), and (67), and applying the inverse inequality (16), we have

$$ \begin{array}{lllll} &\|{U_{h}^{0}}\|_{L^{\infty}}\leq \|R_{h}U^{0}\|_{L^{\infty}}+\|{U_{h}^{0}}-R_{h}U^{0}\|_{L^{\infty}} \leq \|R_{h}U^{0}\|_{L^{\infty}}+Ch^{-\frac{d}{2}}C_{M}h^{2}\leq M_{1},\\ &\|{{\Psi}_{h}^{0}}\|_{L^{\infty}}\leq \|R_{h}{\Psi}^{0}\|_{L^{\infty}}+\|{{\Psi}_{h}^{0}}-R_{h}{\Psi}^{0}\|_{L^{\infty}} \leq\|R_{h}{\Psi}^{0}\|_{L^{\infty}}+Ch^{-\frac{d}{2}}C_{M}h^{2}\leq M_{2}, \end{array} $$

when $h\leq h_{2}=(CC_{M})^{-\frac {2}{4-d}}$. We rewrite $\mathcal {Q}_{2}^{1}$ as

$$ \begin{array}{lllll} &\mathcal{Q}_{2}^{1}=(f(|U^{0}|)-f(|{U_{h}^{n}}|))|U^{0}|^{2}+f(|{U_{h}^{0}}|)(|U^{0}|+|{U_{h}^{0}}|)(|U^{0}|-|{U_{h}^{0}}|), \end{array} $$

and then we have

$$ \begin{array}{lllll} \|\mathcal{Q}_{2}^{1}\|_{L^{2}}&\leq C_{0}\|U^{0}-{U_{h}^{0}}\|_{L^{2}}\|U^{0}\|_{L^{\infty}}^{2}+C_{0}(\|U^{0}\|_{L^{\infty}}+\|{U_{h}^{0}}\|_{L^{\infty}})\|U^{0}-{U_{h}^{0}}\|_{L^{2}} \\ &\leq C_{M}\|U^{0}-{U_{h}^{0}}\|_{L^{2}}\leq C_{M}h^{2}. \end{array} $$

(68)

When β = 0, from (59), it is obvious to see that

$$ \begin{array}{lllll} \|{\Psi}^{1}-{{\Psi}_{h}^{1}}\|_{L^{2}}\leq C_{M}(\|{e_{h}^{0}}\|_{L^{2}}+h^{2})\leq C_{M}h^{2}. \end{array} $$

(69)

When β≠ 0, after choosing $\varphi ={\eta _{h}^{1}}$ and n = 0 in (59), and using (4), we have

$$ \begin{array}{lllll} \|\nabla({\Psi}^{1}-{{\Psi}_{h}^{1}})\|_{L^{2}}\leq C_{M}(\|{e_{h}^{0}}\|_{L^{2}}+h)\leq C_{M}h. \end{array} $$

(70)

Subtracting (7) from (11) with n = 0, we obtain

$$\alpha({\Psi}^{1}-{{\Psi}_{h}^{1}},\varphi)+\beta^{2}\big(\nabla({\Psi}^{1}-{{\Psi}_{h}^{1}}),\nabla\varphi\big) =(\mathcal {Q}_{2}^{1},\varphi),~~\forall \varphi\in V_{h}. $$

Now, we use the Aubin-Nitsche techniques again. Choosing $g={\Psi }^{1}-{{\Psi }_{h}^{1}}$ in (2), we find

$$ \begin{array}{@{}rcl@{}} &&\|{\Psi}^{1}-{{\Psi}_{h}^{1}}\|_{L^{2}}^{2}\\ &=&\alpha ({\Psi}^{1}-{{\Psi}_{h}^{1}},\phi-P_{h}\phi)+\beta^{2}\big(\nabla({\Psi}^{1}-{{\Psi}_{h}^{1}}),\nabla(\phi-P_{h}\phi)\big) \\&&-(\mathcal {Q}_{2}^{1},\phi-P_{h}\phi)+(\mathcal {Q}_{2}^{1},\phi)\\ &\leq& Ch^{2}\|{\Psi}^{1}-{{\Psi}_{h}^{1}}\|_{L^{2}}\|\phi\|_{H^{2}}+Ch\|\nabla({\Psi}^{1}-{{\Psi}_{h}^{1}})\|_{L^{2}}\|\phi\|_{H^{2}} \\&&+Ch^{2}\|\mathcal {Q}_{2}^{1}\|_{L^{2}}\|\phi\|_{H^{2}}+\|\mathcal {Q}_{2}^{1}\|_{L^{2}}\|\phi\|_{L^{2}}\\ &\leq& C\tilde{C}h^{2}\|{\Psi}^{1}-{{\Psi}_{h}^{1}}\|_{L^{2}}^{2}+C\tilde{C}\|{\Psi}^{1}-{{\Psi}_{h}^{1}}\|_{L^{2}} (h\|\nabla({\Psi}^{1}-{{\Psi}_{h}^{1}})\|_{L^{2}}+\|\mathcal {Q}_{2}^{1}\|_{L^{2}}). \end{array} $$

where h ≤ h₁, and by (68) and (70), we have

$$ \begin{array}{lllll} \|{\Psi}^{1}-{{\Psi}_{h}^{1}}\|_{L^{2}}\leq C_{M} h^{2}. \end{array} $$

(71)

Combining (69) and (71), and using the inverse inequality and (4), we have

$$ \begin{array}{lllll} \|{{\Psi}_{h}^{1}}\|_{L^{\infty}} &\leq \|R_{h}{\Psi}^{1}\|_{L^{\infty}}+\|R_{h}{\Psi}^{1}-{{\Psi}_{h}^{1}}\|_{L^{\infty}}\\ &\leq \|R_{h}{\Psi}^{1}\|_{L^{\infty}}+Ch^{-\frac{d}{2}}\|R_{h}{\Psi}^{1}-{{\Psi}_{h}^{1}}\|_{L^{2}}\\ &\leq \|R_{h}{\Psi}^{1}\|_{L^{\infty}}+CC_{M}h^{2-\frac{d}{2}}\leq M_{2}, \end{array} $$

when $h\leq h_{2}=(CC_{M})^{-\frac {2}{4-d}}$. Noticing that

$$ \mathcal {R}_{2}^{1}=({\Psi}^{1}-{{\Psi}_{h}^{1}})f(|U^{0}|)U^{1}+{{\Psi}_{h}^{1}}(f(|U^{0}|)-f(|{U_{h}^{0}}|))U^{1} +{{\Psi}_{h}^{1}}f(|{U_{h}^{0}}|)(U^{1}-{U_{h}^{1}}), $$

and from (4), (62), and (71), we have

$$ \begin{array}{@{}rcl@{}} \|\mathcal {R}_{2}^{1}\|_{L^{2}}&\leq& C_{0}\|{\Psi}^{1}-{{\Psi}_{h}^{1}}\|_{L^{2}}\|U^{1}\|_{L^{2}}+C_{0}\|{{\Psi}_{h}^{1}}\|_{L^{\infty}}\|U^{0}-{U_{h}^{0}}\|_{L^{2}}\|U^{1}\|_{L^{\infty}}\\ &&+C_{0}\|{{\Psi}_{h}^{1}}\|_{L^{\infty}}\|U^{1}-{U_{h}^{1}}\|_{L^{2}}\\ &\leq& C_{M}(\|{\Psi}^{1}-{{\Psi}_{h}^{1}}\|_{L^{2}}+\|{e_{h}^{1}}\|_{L^{2}}+h^{2})\\ &\leq& C_{M}(\|{e_{h}^{1}}\|_{L^{2}}+h^{2}). \end{array} $$

(72)

We choose $v={e_{h}^{1}}$ and n = 0 in (58)

$$ \begin{array}{@{}rcl@{}} &&\textmd{i} (\|{e_{h}^{1}}\|_{L^{2}}^{2}-\|{e_{h}^{0}}\|_{L^{2}}^{2}+\|{e_{h}^{1}}-{e_{h}^{0}}\|_{L^{2}}^{2})-2\tau\|\nabla {e_{h}^{1}}\|_{L^{2}}^{2}-2\tau(\mathcal {R}_{2}^{1},{e_{h}^{1}})\\ &=&2\textmd{i} (U^{1}-R_{h}U^{1},{e_{h}^{1}})-2\textmd{i} (U^{0}-R_{h}U^{0},{e_{h}^{1}}). \end{array} $$

Taking the imaginary parts of the above equation and applying (4) and (72), one has

$$ \begin{array}{@{}rcl@{}} &&\|{e_{h}^{1}}\|_{L^{2}}^{2}\\ &\leq& \|{e_{h}^{0}}\|_{L^{2}}^{2}+2\tau \big|\textmd{Im}(\mathcal {R}_{2}^{1},{e_{h}^{1}})\big|+2\big|\textmd{Re} (U^{1}-R_{h}U^{1},{e_{h}^{1}})\big|+2\textmd{Re} \big|(U^{0}-R_{h}U^{0},{e_{h}^{1}})\big|\\ &\leq& \|{e_{h}^{0}}\|_{L^{2}}^{2} + 2\tau \|\mathcal {R}_{2}^{1}\|_{L^{2}}\|{e_{h}^{1}}\|_{L^{2}} + 2\|U^{1} - R_{h}U^{1}\|_{L^{2}}\|{e_{h}^{1}}\|_{L^{2}} + 2\|U^{0} - R_{h}U^{0}\|_{L^{2}}\|{e_{h}^{1}}\|_{L^{2}}\\ &\leq& C_{M} h^{4}+2C_{M}\tau(\|{e_{h}^{1}}\|_{L^{2}}+h^{2})\|{e_{h}^{1}}\|_{L^{2}}+\frac{1}{2}\|{e_{h}^{1}}\|_{L^{2}}^{2} +4\|U^{1}-R_{h}U^{1}\|_{L^{2}}^{2} \\ &&+4\|U^{0}-R_{h}U^{0}\|_{L^{2}}^{2}\\ &\leq& C_{M} h^{4}+\frac{7}{8}\|{e_{h}^{1}}\|_{L^{2}}^{2}, \end{array} $$

when $\tau \leq \tau _{5}=\frac {1}{8C_{M}}$. Then, combining (69), (71), and (4), we find

$$ \begin{array}{lllll} \|{e_{h}^{1}}\|_{L^{2}}+\|{\eta_{h}^{1}}\|_{L^{2}}\leq C_{M} h^{2}, \end{array} $$

which shows that (60) holds for m = 0.

We assume that

$$ \|e_{h}^{m+1}\|_{L^{2}}\leq C_{0}^{\prime}h^{2}, $$

(73)

holds for m ≤ n − 1. By the inverse inequality (16) and the induction assumption (73), we can obtain

$$ \begin{array}{@{}rcl@{}} \|U_{h}^{m+1}\|_{L^{\infty}} &\leq& \|R_{h}U^{m+1}\|_{L^{\infty}}+\|R_{h}U^{m+1}-U_{h}^{m+1}\|_{L^{\infty}}\\ &\leq& \|R_{h}U^{m+1}\|_{L^{\infty}}+Ch^{-\frac{d}{2}}\|R_{h}U^{m+1}-U_{h}^{m+1}\|_{L^{2}}\\ &\leq& \|R_{h}U^{m+1}\|_{L^{\infty}}+CC_{0}^{\prime}h^{2-\frac{d}{2}}\leq M_{1}, \end{array} $$

for m ≤ n − 1, and $h\leq h_{2}=(CC_{0}^{\prime })^{-\frac {2}{4-d}}$. By the same techniques used in the proof of estimates (69) and (71), we can obtain

$$ \begin{array}{lllll} \|{\Psi}^{n+1}-{\Psi}_{h}^{n+1}\|_{L^{2}}\leq C_{M}(\|{e_{h}^{n}}\|_{L^{2}}+h^{2})\leq C_{M}C_{0}^{\prime}h^{2}, \end{array} $$

(74)

from which and the inverse inequality (16), we can derive that

$$ \begin{array}{@{}rcl@{}} \|{\Psi}_{h}^{n+1}\|_{L^{\infty}} &\leq& \|R_{h}{\Psi}^{n+1}\|_{L^{\infty}}+\|R_{h}{\Psi}^{n+1}-{\Psi}_{h}^{n+1}\|_{L^{\infty}}\\ &\leq& \|R_{h}{\Psi}^{n+1}\|_{L^{\infty}}+Ch^{-\frac{d}{2}}\|R_{h}{\Psi}^{n+1}-{\Psi}_{h}^{n+1}\|_{L^{2}}\\ &\leq& \|R_{h}{\Psi}^{n+1}\|_{L^{\infty}}+CC_{M}C_{0}^{\prime}h^{2-\frac{d}{2}}\leq M_{2}, \end{array} $$

when $h\leq h_{3}=(CC_{M}C_{0}^{\prime })^{-\frac {2}{4-d}}$. Noticing that

$$ \begin{array}{@{}rcl@{}} \mathcal {R}_{2}^{n+1}&=&({\Psi}^{n+1}-{\Psi}_{h}^{n+1})f(|U^{n}|)U^{n+1}+{\Psi}_{h}^{n+1}(f(|U^{n}|)-f(|{U_{h}^{n}}|))U^{n+1}\\ &&+{\Psi}_{h}^{n+1}f(|{U_{h}^{n}}|)(U^{n+1}-U_{h}^{n+1}), \end{array} $$

and from (74), we have

$$ \begin{array}{lllll} \|\mathcal {R}_{2}^{n+1}\|_{L^{2}} &\leq C_{M}(\|{\Psi}^{n+1}-{\Psi}_{h}^{n+1}\|_{L^{2}}+\|e_{h}^{n+1}\|_{L^{2}}+h^{2})\\ &\leq C_{M}(\|e_{h}^{n+1}\|_{L^{2}}+h^{2}). \end{array} $$

(75)

Next, we will prove that (60) also holds for m = n. Choosing $v=e_{h}^{n+1}$ in (58) and taking the imaginary parts of the resulting equation yield

$$ \begin{array}{lllll} &\frac{1}{2\tau} (\|e_{h}^{n+1}\|_{L^{2}}^{2}-\|{e_{h}^{n}}\|_{L^{2}}^{2}+\|e_{h}^{n+1}-{e_{h}^{n}}\|_{L^{2}}^{2}) -\textmd{Im}(\mathcal {R}_{2}^{n+1},e_{h}^{n+1})\\ &=\textmd{Re}\big(D_{\tau} (U^{n+1}-R_{h}U^{n+1}),e_{h}^{n+1}\big). \end{array} $$

Summing up the above equation and applying (4), (75), and the induction assumption (73), we have

$$ \begin{array}{@{}rcl@{}} &&\|e_{h}^{n+1}\|_{L^{2}}^{2}\\ &\leq&\! C_{M}\tau{\sum}_{m=0}^{n}\|e_{h}^{m+1}\|_{L^{2}}^{2}+\tau{\sum}_{m=0}^{n}\|D_{\tau} (U^{n+1}-R_{h}U^{n+1})\|_{L^{2}}\|e_{h}^{n+1}\|_{L^{2}}+C_{M}h^{4}\\ &\leq&\! C_{M}\tau{\sum}_{m=0}^{n}\|e_{h}^{m+1}\|_{L^{2}}^{2}+\tau{\sum}_{m=0}^{n}\|D_{\tau} (U^{n+1}\! - R_{h}U^{n+1})\|_{L^{2}}^{2} + \tau\!{\sum}_{m=0}^{n}\|e_{h}^{n+1}\|_{L^{2}}^{2} + C_{M}h^{4}\\ &\leq&\! C_{M}\tau{\sum}_{m=0}^{n}\|e_{h}^{m+1}\|_{L^{2}}^{2}+\tau{\sum}_{m=0}^{n}h^{4}\|D_{\tau} U^{n+1}\|_{H^{2}}^{2}+C_{M}h^{4}. \end{array} $$

By the discrete Gronwall’s inequality and Theorem 1, there exists τ₆ > 0, such that

$$ \|e_{h}^{n+1}\|_{L^{2}}\leq C_{M}h^{2}, $$

with which and (4) and (74), we have

$$ \|e_{h}^{n+1}\|_{L^{2}}+\|\eta_{h}^{n+1}\|_{L^{2}}\leq C_{0}^{\prime}h^{2}. $$

Thus, (60) holds for m = n. Since the τ-independent property of estimates in (60), we can obtain the H¹ error estimate by the inverse inequality:

$$ \|\nabla e_{h}^{n+1}\|_{L^{2}}\leq Ch^{-1}\| e_{h}^{n+1}\|_{L^{2}}\leq C_{M} h,~~\|\nabla \eta_{h}^{n+1}\|_{L^{2}}\leq Ch^{-1}\| \eta_{h}^{n+1}\|_{L^{2}}\leq C_{M} h. $$

Thus, taking $\tau _{0}^{\prime }=\min \limits \{\tau _{0}^{*},\tau _{5},\tau _{6}\}$, $h_{0}^{\prime }=\min \limits \{h_{1},h_{2},h_{3}\}$, we complete the proof of this theorem. □

5 L ² optimal error estimates

In this section, we will derive L² optimal error estimates for the r-order (r ≥ 1) Galerkin FEM by using the results in the above sections.

From (4), (22), and (60)–(61), we have optimal error estimates for the linear Galerkin FEM (r = 1) as follows.

Corollary 1

Under the assumptions of Theorem 2, the full discrete system (6)–(7) has unique solution $U_{h}^{m+1},~{\Psi }_{h}^{n+1}$, m = 0,1,⋅⋅⋅,N − 1, and there exists $\tau _{0}^{\prime }>0$, $h_{0}^{\prime }>0$ such that when $\tau \leq \tau _{0}^{\prime }$, $h\leq h_{0}^{\prime }$,

$$ \|u^{m+1}-U_{h}^{m+1}\|_{L^{2}}+\|\psi^{m+1}-{\Psi}_{h}^{m+1}\|_{L^{2}}\leq C_{1}^{\prime}(\tau+h^{2}), $$

(76)

$$ \|\nabla (u^{m+1}-U_{h}^{m+1})\|_{L^{2}}+\|\nabla(\psi^{m+1}-{\Psi}_{h}^{m+1})\|_{L^{2}}\leq C_{1}^{\prime}(\tau+h), $$

(77)

where $C_{1}^{\prime }$ is a positive constant dependent on $C_{0}^{*},~C_{0}^{+}$, $C_{0}^{\prime }$, M, and independent of m, h, τ.

For r > 1, the above estimates are not optimal for the r-order Galerkin FEM. However, we can derive the uniform bounds of the numerical solutions in $L^{\infty }$-norm from Theorem 2 as:

$$ \|U_{h}^{n+1}\|_{L^{\infty}} \leq \|R_{h}U^{m}\|_{L^{\infty}}+Ch^{-\frac{d}{2}}\|R_{h}U^{n+1}-U_{h}^{n+1}\|_{L^{2}}\leq M_{1}, $$

(78)

$$ \|{\Psi}_{h}^{n+1}\|_{L^{\infty}} \leq \|R_{h}{\Psi}^{n+1}\|_{L^{\infty}}+Ch^{-\frac{d}{2}}\|R_{h}{\Psi}^{n+1}-{\Psi}_{h}^{n+1}\|_{L^{2}}\leq M_{2}, $$

(79)

for n = 0,1,⋅⋅⋅,N − 1 when $\tau \leq \tau _{0}^{\prime }$, $h\leq h_{0}^{\prime }$. By the above uniform bounds, we can obtain optimal L² error estimates given in the following theorem.

Theorem 3

Assume that the system (1)–(3) has a unique solution u, ψ satisfying (15). Then the full discrete system (6)–(7) has unique solution $U_{h}^{m+1},~{\Psi }_{h}^{n+1}$, m = 0,1,⋅⋅⋅,N − 1, and there exists $\tau _{0}^{\prime \prime }>0$, $h_{0}^{\prime }>0$ such that when $\tau \leq \tau _{0}^{\prime \prime }$, $h\leq h_{0}^{\prime }$,

$$ \|u^{m+1}-U_{h}^{m+1}\|_{L^{2}}+\|\psi^{m+1}-{\Psi}_{h}^{m+1}\|_{L^{2}}\leq C^{*}(\tau+h^{r+1}), $$

(80)

where C^∗ is a positive constant dependent on $C_{0}^{*},~C_{0}^{+}$, $C_{0}^{\prime }$, $C_{1}^{\prime }$, M, and independent of m, h, τ.

Proof

The exact solutions u and ψ at t = t_n+ 1 satisfy

$$ \textmd{i} (u_{t}(t_{n+1}),v)-(\nabla u^{n+1},\nabla v)+\big(\psi^{n+1} f(|u^{n+1}|)u^{n+1},v\big)=0,~~\forall v\in V_{h}, $$

(81)

$$ \alpha(\psi^{n+1},\varphi)+\beta^{2}(\nabla\psi^{n+1},\nabla\varphi)=\big(f(|u^{n+1}|)|u^{n+1}|^{2},\varphi\big),~~\forall \varphi\in V_{h}. $$

(82)

Subtracting (6)–(7) from the two above equations, the error functions $\tilde {e}_{h}^{n+1}=U_{h}^{n+1}-R_{h} u^{n+1}$, $\tilde {\eta }_{h}^{n+1}={\Psi }_{h}^{n+1}-R_{h} \psi ^{n+1}$ satisfy

$$ \textmd{i} (D_{\tau} \tilde{e}_{h}^{n+1},v)-(\nabla \tilde{e}_{h}^{n+1},\nabla v)-(\mathcal {R}_{3}^{n+1},v) =-\textmd{i} \big(D_{\tau} R_{h}u^{n+1}-u_{t}(t_{n+1}),v\big),~~\forall v\in V_{h}, $$

(83)

$$ \begin{array}{@{}rcl@{}} &&\alpha(\tilde{\eta}_{h}^{n+1},\varphi)+\beta^{2}(\nabla\tilde{\eta}_{h}^{n+1},\nabla\varphi)=-(\mathcal {Q}_{3}^{n+1},\varphi)+\alpha(\psi^{n+1}-R_{h}\psi^{n+1},\varphi)\\ &+&\beta^{2}\big(\nabla(\psi^{n+1}-R_{h}\psi^{n+1}),\nabla\varphi\big),~~\forall \varphi\in V_{h}, \end{array} $$

(84)

where

$$ \begin{array}{@{}rcl@{}} \mathcal{R}_{3}^{n+1}&=&\psi^{n+1}f(|u^{n+1}|)u^{n+1}-{\Psi}_{h}^{n+1}f(|{U_{h}^{n}}|)U_{h}^{n+1}\\ &=&\psi^{n+1}\big(f(|u^{n+1}|)-f(|u^{n}|)\big)u^{n+1}+(\psi^{n+1}-{\Psi}_{h}^{n+1})f(|u^{n}|)u^{n+1}\\ &&+{\Psi}_{h}^{n+1}\big(f(|u^{n}|)-f(|{U_{h}^{n}}|)\big)U^{n+1}+{\Psi}_{h}^{n+1}f(|{U_{h}^{n}}|)(u^{n+1}-U_{h}^{n+1}) \end{array} $$

$$ \begin{array}{@{}rcl@{}} \mathcal{Q}_{3}^{n+1}&=&f(|u^{n+1}|)|u^{n+1}|^{2}-f(|{U_{h}^{n}}|)|{U_{h}^{n}}|^{2}\\ &=&\big(f(|u^{n+1}|)-f(|u^{n}|)\big)|u^{n+1}|^{2}+f(|u^{n}|)(|u^{n+1}|+|u^{n}|)(|u^{n+1}|-|u^{n}|)\\ &&+\big(f(|u^{n}|)-f(|{U_{h}^{n}}|)\big)|u^{n}|^{2}+f(|{U_{h}^{n}}|)(|u^{n}|+|{U_{h}^{n}}|)(|u^{n}|-|{U_{h}^{n}}|). \end{array} $$

By (4), (14), (15), and (78), we can derive

$$ \begin{array}{lllll} \|\mathcal{Q}_{3}^{n+1}\|_{L^{2}}&\leq C_{M}(\|u^{n+1}-u^{n}\|_{L^{2}}+\|u^{n}-{U_{h}^{n}}\|_{L^{2}})\\ &\leq C_{M}(\tau+h^{r+1}+\|\tilde{e}_{h}^{n}\|_{L^{2}}). \end{array} $$

By the same techniques used in the proof of estimates (69) and (71), we can obtain

$$ \begin{array}{lllll} \|{\Psi}^{n+1}-{\Psi}_{h}^{n+1}\|_{L^{2}}\leq C_{M}\|\tilde{e}_{h}^{n}\|_{L^{2}}+C_{M}(\tau+h^{r+1}), \end{array} $$

(85)

from which and (79), we find

$$ \begin{array}{lllll} \|\mathcal{R}_{3}^{n+1}\|_{L^{2}}&\leq C_{M}(\|\tilde{e}_{h}^{n+1}\|_{L^{2}}+\|\tilde{e}_{h}^{n}\|_{L^{2}}+\tau+h^{r+1}). \end{array} $$

(86)

Thanks to (4) and (15), one has

$$ \begin{array}{@{}rcl@{}} \|\tilde{e}_{h}^{0}\|_{L^{2}}&=&\|{U_{h}^{0}}-R_{h}u_{0}\|_{L^{2}}\leq \|{U_{h}^{0}}-u_{0}\|_{L^{2}}+\|u_{0}-R_{h}u_{0}\|_{L^{2}}\\ &\leq& Ch^{r+1}\|u_{0}\|_{r+1}\leq C_{M}h^{r+1}, \end{array} $$

(87)

and

$$ \begin{array}{@{}rcl@{}} &&\tau\sum\limits_{m=0}^{n}\|D_{\tau} R_{h} u^{m+1}-u_{t}(t_{n+1})\|_{L^{2}}^{2}\\ &\leq& 2\tau\sum\limits_{m=0}^{n}\|D_{\tau} R_{h} u^{m+1}-D_{\tau} u^{m+1}\|_{L^{2}}^{2} +2\tau\sum\limits_{m=0}^{n}\|D_{\tau} u^{m+1}-u_{t}(t_{n+1})\|_{L^{2}}^{2}\\ &\leq& C\tau h^{2(r+1)}\sum\limits_{m=0}^{n}\|D_{\tau} u^{m+1}\|_{H^{r+1}}^{2}+2\tau^{2}\|u_{tt}\|_{L^{2}((0,T);L^{2})}^{2}\\ &\leq& C_{M}(\tau^{2}+h^{2(r+1)}). \end{array} $$

(88)

Choosing $v=\tilde {e}_{h}^{n+1}$ in (83) and taking the imaginary parts of the resulting equation to arrive at

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{2\tau} (\|\tilde{e}_{h}^{n+1}\|_{L^{2}}^{2}-\|\tilde{e}_{h}^{n}\|_{L^{2}}^{2}+\|\tilde{e}_{h}^{n+1} -\tilde{e}_{h}^{n}\|_{L^{2}}^{2}) -\textmd{Im}(\mathcal {R}_{3}^{n+1},\tilde{e}_{h}^{n+1})\\ &=&-\textmd{Re}\big(D_{\tau} R_{h}u^{n+1}-u_{t}(t_{n+1}),\tilde{e}_{h}^{n+1}\big). \end{array} $$

Summing up the above equation and using the Cauchy-Schwarz inequality, (86), (87), and (88) lead to

$$ \begin{array}{lllll} \|\tilde{e}_{h}^{n+1}\|_{L^{2}}^{2} &\leq \|\tilde{e}_{h}^{0}\|_{L^{2}}^{2} +2\tau\sum\limits_{m=0}^{n}\|\mathcal {R}_{3}^{n+1}\|_{L^{2}}\|\tilde{e}_{h}^{n+1}\|_{L^{2}}\\ &\quad+2\tau\sum\limits_{m=0}^{n}\|D_{\tau} R_{h}u^{n+1}-u_{t}(t_{n+1})\|_{L^{2}}\|\tilde{e}_{h}^{n+1}\|_{L^{2}}\\ &\leq \|\tilde{e}_{h}^{0}\|_{L^{2}}^{2} +C_{M}\tau\sum\limits_{m=0}^{n}\|\tilde{e}_{h}^{n+1}\|_{L^{2}}^{2}+C_{M}\tau\sum\limits_{m=0}^{n}\|\mathcal {R}_{3}^{n+1}\|_{L^{2}}^{2}\\ &\quad+C_{M}\tau\sum\limits_{m=0}^{n}\|D_{\tau} R_{h}u^{n+1}-u_{t}(t_{n+1})\|_{L^{2}}^{2}\\ &\leq C_{M}\tau\sum\limits_{m=0}^{n}\|\tilde{e}_{h}^{n+1}\|_{L^{2}}^{2}+C_{M}(\tau^{2}+h^{2(r+1)}). \end{array} $$

By the discrete Gronwall’s inequality, there exists τ₇ > 0, such that

$$ \|\tilde{e}_{h}^{n+1}\|_{L^{2}}\leq C_{M}(\tau+h^{r+1}), $$

when τ ≤ τ₇, with which and (4) and (85), one has

$$ \|u^{m+1}-U_{h}^{m+1}\|_{L^{2}}+\|\psi^{m+1}-{\Psi}_{h}^{m+1}\|_{L^{2}}\leq C_{M}(\tau+h^{r+1}). $$

Let $\tau _{0}^{\prime \prime }=\min \limits \{\tau _{7},\tau _{0}^{\prime }\}$ and $h\leq h_{0}^{\prime }$, we finish the proof of Theorem 3. □

6 Numerical experiments

In this section, we provide numerical experiments to illustrate our theoretical analysis in the previous sections. All computations are performed with the public finite element software package Freefem++ [20]. In our tests, we choose the unit square Ω = [0,1]² as a two-dimensional domain, and the unit cube Ω = [0,1]³ as a three-dimensional domain. For the unit square, a uniform triangular partition with K + 1 nodes in both horizontal and vertical directions is made and the mesh width $h=\frac {\sqrt {2}}{K}$. For the unit cube, a uniform tetrahedra partition with K + 1 nodes is used in each direction, where the mesh width $h=\frac {\sqrt {3}}{K}$.

We also test the fully decoupled linearized backward Euler Galerkin FEM, which is under an explicit treatment of the nonlinear terms, the scheme is to seek $U_{h}^{n+1},\psi _{h}^{n+1}\in V_{h}$ such that

$$ \textmd{i} (D_{\tau} U_{h}^{n+1}, v)-(\nabla U_{h}^{n+1},\nabla v)+\big({{\Psi}_{h}^{n}} f(|{U_{h}^{n}}|)U_{h}^{n+1},v\big)=0,~~\forall v\in V_{h}, $$

(89)

$$ \alpha({\Psi}_{h}^{n+1},\varphi)+\beta^{2}(\nabla{\Psi}_{h}^{n+1},\nabla\varphi)=\big(f(|{U_{h}^{n}}|)|{U_{h}^{n}}|^{2},\varphi\big),~~\forall \varphi\in V_{h}, $$

(90)

with the initial value ${U_{h}^{0}}=R_{h} u_{0}$ and ${{\Psi }_{h}^{0}}$ satisfies (8).

The scheme (6)–(7) can be seen as a semi-decoupled scheme. At each time step, we need to solve (7) for ${\Phi }_{h}^{n+1}$ firstly, and then to solve (6) for $U_{h}^{n+1}$. However, the second scheme (89)–(90) is fully decoupled. At each time step, we only need to solve the two systems for $U_{h}^{n+1}$ and ${\Phi }_{h}^{n+1}$ in parallel. In this paper, we only give out error estimates for the linearized scheme (6)–(7). The analysis presented in this paper can be easily extended to the second linearized scheme (89)–(90), which will be confirmed numerically in this section.

Example 6.1

Firstly, we consider the following Schrödinger-Helmholtz equation

$$ \begin{array}{lllll} &\textmd{i} \frac{\partial u}{\partial t}+{\Delta} u+\psi u=f_{1}~~\textmd{in} ~{\Omega}\times [0,T]\\ &\alpha \psi-\beta^{2}{\Delta}\psi=|u|^{2}+f_{2} ~~\textmd{in} ~{\Omega}\times [0,T],\\ &u(x,0)=u_{0}(x)~~\textmd{in} ~{\Omega},\\ &u=\psi=0 ~~\textmd{on} ~\partial{\Omega}\times [0,T], \end{array} $$

(91)

where Ω = [0,1]². In our computations, the right-hand side functions f₁ and f₂ and the initial condition u₀ are determined by the following analytical solution

$$ \begin{array}{lllll} &u=\textmd{e}^{(i+1)t}\sin(x)\sin(y)\sin(\pi x)\sin(\pi y),\\ &\psi=\textmd{e}^{t+x+y}(1-x)(1-y)\sin(x)\sin(y). \end{array} $$

Choosing α = β = 1, we solve system (91) by the linearized backward Euler scheme (6)–(7) and the full decoupled scheme (89)–(90) with a linear finite element approximation and a quadratic finite element approximation, respectively. To confirm the optimal convergence rate in the L²-norm, we choose τ = h² for the linear finite element approximation and τ = h³ for the quadratic finite element approximation, respectively. We present numerical results in Tables 1, 2, 3, and 4 at time t = 0.5,1 and 2. From Tables 1, 2, 3, and 4, we can see that the errors in L²-norm are proportional to h^r+ 1, r = 1,2, which agrees with the theoretical analysis and indicates that both schemes are optimal convergence in L²-norm.

Table 1 L² errors and convergence rates of scheme (6)–(7) for the linear FEM with τ = h² (Example 6.1)

Table 2 L² errors and convergence rates of scheme (6)–(7) for the quadratic FEM with τ = h³ (Example 6.1)

Table 3 L² errors and convergence rates of scheme (89)–(90) for the linear FEM with τ = h² (Example 6.1)

Table 4 L² errors and convergence rates of scheme (89)–(90) for the quadratic FEM with τ = h³ (Example 6.1)

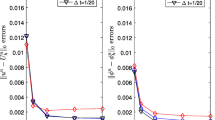
In Theorem 3, we obtain the optimal L² error estimate $\mathcal {O}(\tau +h^{r+1})$ unconditionally for r ≥ 1. In order to show the unconditional stability of the linearized backward Euler schemes (6)–(7) and (89)–(90), respectively, we solve problem (91) by using linear and quadratic FEMs with four different time step size τ = 0.2,0.1,0.05,0.01 on gradually refined meshes with K = 10j, j = 1,2,⋅⋅⋅,10. The L²-norm errors at t = 1 are presented in Figs. 1 and 3 for the linear FEM and in Figs. 2 and 4 for the quadratic FEM. From Figs. 1–4, we can observe that for a fixed τ, the L²-norm errors converge to a small constant when the mesh refine gradually, which shows that the two proposed schemes are unconditionally stable and the time step restriction is unnecessary.

Fig. 1

L²-norm errors for the linear FEM computed by scheme (6)–(7) (Example 6.1)

Fig. 2

L²-norm errors for the quadratic FEM computed by scheme (6)–(7) (Example 6.1)

Fig. 3

L²-norm errors for the linear FEM computed by scheme (89)–(90) (Example 6.1)

Fig. 4

L²-norm errors for the quadratic FEM computed by scheme (89)–(90) (Example 6.1)

Example 6.2

Next, we consider the following high order Schrödinger-Poisson-Slater system

$$ \begin{array}{lllll} &\textmd{i} \frac{\partial u}{\partial t}+{\Delta} u+\psi u+|u|^{4}u=f_{1}~~\textmd{in} ~{\Omega}\times [0,T]\\ &-{\Delta}\psi=|u|^{2}+f_{2} ~~\textmd{in} ~{\Omega}\times [0,T],\\ &u(x,0)=u_{0}(x)~~\textmd{in} ~{\Omega},\\ &u=\psi=0 ~~\textmd{on} ~\partial{\Omega}\times [0,T], \end{array} $$

(92)

where Ω = [0,1]². The exact solutions u and ϕ of above system are given as follows:

$$ \begin{array}{lllll} &u=2\textmd{e}^{it+(x+y)/5}(1+5t^{3})x(1-x)y(1-y),\\ &\phi=5(1+3t^{2}+\sin(t))\sin(\frac{x}{2})\sin(\frac{y}{2})(1-x)(1-y), \end{array} $$

and the right-hand side functions f₁ and f₂ and the initial condition u₀ are determined by the exact solution and system (92).

To show the unconditional stability (convergence) of the linearized backward Euler scheme (6)–(7), we solve problem (92) by using linear and quadratic FEMs with four different time step size τ = 0.2,0.1,0.05,0.01 on gradually refined meshes with K = 10j, j = 1,2,⋅⋅⋅,10. The numerical results at t = 1 are presented in Fig. 5 for the linear FEM and in Fig. 6 for the quadratic FEM. We can observe that for a fixed τ, L²-norm errors converge to a small constant when the mesh refine gradually, which also shows the unconditional stability of the proposed schemes.

Fig. 5

L²-norm errors for the linear FEM computed by scheme (6)–(7) (Example 6.2)

Fig. 6

L²-norm errors for the quadratic FEM computed by scheme (6)–(7) (Example 6.2)

Example 6.3

Finally, we consider the high order Schrödinger-Poisson-Slater system (92) in three-dimensional (3D) space with Ω = [0,1]³. The exact solutions are given as follows:

$$ \begin{array}{lllll} &u=10 \textmd{e}^{it+(x+y+z)/5}(1+5t^{3})x(1-x)y(1-y)z(1-z),\\ &\phi=10(1+3t^{2}+\sin(t))\sin(\frac{x}{2})\sin(\frac{y}{2})\sin(\frac{z}{2})(1-x)(1-y)(1-z). \end{array} $$

We solve the high-order Schrödinger-Poisson-Slater system (92) in 3D by the linearized backward Euler scheme (6)–(7) with a linear FEM. We present the numerical results at t = 1 in Fig. 7, which are obtained with four different time step size τ = 0.2,0.1,0.05,0.01 on gradually refined meshes with K = 4j, j = 1,2,⋅⋅⋅,7. Although some previous works give that the error estimates in 3D often required stronger time stepsize conditions than that in 2D, the results in Fig. 7 illustrate that the scheme (6)–(7) is unconditionally convergence for the 3D model.

Fig. 7

L²-norm errors for the linear FEM computed by scheme (6)–(7) (Example 6.3)

7 Conclusions and future works

In this paper, we have proved unconditionally optimal error estimates of the linearized backward Euler FEMs for the generalized nonlinear Schrödinger-Helmholtz equations. This optimal error estimate has no restriction on the time and spatial steps. Numerical results in both two- and three-dimensional space are presented to confirm the theoretical predictions and demonstrate clearly the unconditional stability of the proposed schemes. The analytic method in this paper can be considered to analyze other nonlinear physical models in future works.