Analysis of spectral Hamiltonian boundary value methods (SHBVMs) for the numerical solution of ODE problems

Abstract

Recently, the numerical solution of stiffly/highly oscillatory Hamiltonian problems has been attacked by using Hamiltonian boundary value methods (HBVMs) as spectral methods in time. While a theoretical analysis of this spectral approach has been only partially addressed, there is enough numerical evidence that it turns out to be very effective even when applied to a wider range of problems. Here, we fill this gap by providing a thorough convergence analysis of the methods and confirm the theoretical results with the aid of a few numerical tests.

1 Introduction

In recent years, the efficient numerical solution of Hamiltonian problems has been tackled via the definition of the energy-conserving Runge-Kutta methods named Hamiltonian boundary value methods (HBVMs) [10,11,12,13]. Such methods have been developed along several directions (see, e.g., [4, 14, 19]), including Hamiltonian BVPs [1] and Hamiltonian PDEs (see, e.g., [6]): we also refer to the monograph [7] and to the recent review paper [8] for further details.

More recently, HBVMs have been used as spectral methods in time for solving highly oscillatory Hamiltonian problems [18], as well as stiffly oscillatory Hamiltonian problems [9] emerging from the space semi-discretization of Hamiltonian PDEs. Their spectral implementation is justified by the fact that this family of methods performs a projection of the vector field onto a finite dimensional subspace via a least squares approach based on the use of Legendre orthogonal polynomials [13]. This spectral approach, supported by a very efficient nonlinear iteration technique to handle the large nonlinear systems needed to advance the solution in time (see [12], [7, Chapter 4] and [8]), proved to be very effective. However, a thorough convergence analysis of HBVMs, used as spectral methods, was still lacking. In fact, when using large stepsizes, as is required by the spectral strategy, the notion of classical order of a method is not sufficient to explain the correct asymptotic behavior of the solutions, so that a different analysis is needed, which is the main goal of the present paper. Moreover, the theoretical achievements will be numerically confirmed by applying the methods to a number of ODE-IVPs.

It is worth mentioning that early references where numerical methods were derived by projecting the vector field onto a finite dimensional subspace are, e.g., [2, 3, 27, 28] (a related reference is [36]). A similar technique, popular for solving oscillatory problems, is that of exponential/trigonometrically fitted methods and, more in general, functionally fitted methods [22,23,24, 26, 29,30,31,32,33, 35, 37].

With these premises, the structure of the paper is as follows: in Section 2, we analyze the use of spectral methods in time; in Section 3, we discuss the efficient implementation of the fully discrete method; in Section 4, we provide numerical evidence of the effectiveness of such an approach, confirming the theoretical achievements. At last, a few conclusions are reported in Section 5.

2 Spectral approximation in time

This section contains the main theoretical results regarding the spectral methods that we shall use for the numerical solution of ODE-IVPs which, without loss of generality, will be assumed in the form¹

$$ \dot y(t) = f(y(t)), \qquad y(0) = y_{0}\in\mathbb{R}^{m}. $$

(1)

Hereafter, f is assumed to be suitably smooth (in particular, we shall assume f(z) to be analytic in a closed complex ball centered at y₀). We consider the solution of problem (1) on the interval [0,h], where h stands for the time-step to be used by a one-step numerical method. The same arguments will be then repeated for the subsequent integration steps. According to [13], we consider the expansion of the right-hand side of (1) along the shifted and scaled Legendre polynomial orthonormal basis {P_j}_j≥ 0,

$$ P_{j}\in{\Pi}_{j}, \qquad {\int_{0}^{1}} P_{i}(x)P_{j}(x)\mathrm{d} x=\delta_{ij},\qquad i,j=0,1,\dots, $$

with π_j the set of polynomials of degree j and δ_ij the Kronecker delta. One then obtains:

$$ \dot y(ch) = f(y(ch)) \equiv \sum\limits_{j\ge 0} P_{j}(c)\gamma_{j}(y), \qquad c\in[0,1], $$

(2)

with the Fourier coefficients γ_j(y) given by

$$ \gamma_{j}(y)={\int_{0}^{1}} P_{j}(\tau)f(y(\tau h))\mathrm{d}\tau, \quad j=0,1,\dots. $$

(3)

We recall that:

$$ \|P_{j}\| := \max_{x\in[0,1]} |P_{j}(x)| = \sqrt{2j+1}, \qquad {\int_{0}^{1}} P_{j}(x) q(x)\mathrm{d} x = 0, \quad \forall q\in{\Pi}_{j-1}. $$

(4)

Let us now study the properties of the coefficients γ_j(y) defined at (3). To begin with, we report the following results.

Lemma 1

Let $g:[0,h]\rightarrow V$ , with V a vector space, admit a Taylor expansion at 0. Then,

$${\int_{0}^{1}}P_{j}(c) g(ch)\mathrm{d} c =O(h^{j}).$$

Proof

See [13, Lemma 1].

Corollary 1

The Fourier coefficients defined in (3) satisfy:γ_j(y) = O(h^j).

We now want to derive an estimate which generalizes the result of Corollary 1 to the case where the stepsize h is not small. For this purpose, hereafter we assume that the solution y(t) of (1) admits a complex analytic extension in a neighbourhood of 0. Moreover, we shall denote by $\mathcal {B}(0,r)$ the closed ball of center 0 and radius r in the complex plane, and $\mathcal {C}(0,r)$ the corresponding circumference. The following results then hold true.

Lemma 2

LetP_jbethejthshifted and scaled Legendre polynomial and, forρ > 1, letus define the function

$$ Q_{j}(\xi) = {\int_{0}^{1}} \frac{P_{j}(c)}{\xi-c}\mathrm{d} c, \qquad \xi\in\mathcal{C}(0,\rho). $$

(5)

Then,

$$ \|Q_{j}\|_{\rho} := \max_{\xi\in\mathcal{C}(0,\rho)}|Q_{j}(\xi)| \le {\sqrt{\frac{2}{j+1}}\frac{1}{(\rho-1)\rho^{j}}}. $$

(6)

Proof

One has, for |ξ| = ρ > 1, and taking into account (4):

$$ \begin{array}{@{}rcl@{}} Q_{j}(\xi) &=& {\int_{0}^{1}} \frac{P_{j}(c)}{\xi-c}\mathrm{d} c = \xi^{-1} {\int_{0}^{1}} \frac{P_{j}(c)}{1-\xi^{-1}c}\mathrm{d} c = \xi^{-1} {\int_{0}^{1}} P_{j}(c)\sum\limits_{\ell\ge0}\xi^{-\ell}c^{\ell} \mathrm{d} c\\ &=& \xi^{-1} \sum\limits_{\ell\ge j} \xi^{-\ell} {\int_{0}^{1}} P_{j}(c) c^{\ell} \mathrm{d} c = \xi^{-j-1} \sum\limits_{\ell\ge0}\xi^{-\ell} {\int_{0}^{1}} P_{j}(c)c^{\ell+j} \mathrm{d} c. \end{array} $$

Passing to norms, one has:

$$ \begin{array}{@{}rcl@{}} \left|{\int_{0}^{1}} P_{j}(c)c^{\ell+j} \mathrm{d} c\right|&\le& \|P_{j}\| {\int_{0}^{1}}c^{\ell+j}\mathrm{d} c = \frac{\sqrt{2j+1}}{j+\ell+1} \le \sqrt{\frac{2}{j+1}} ,\\ \left| \xi^{-j-1} \sum\limits_{\ell\ge0}\xi^{-\ell}\right| &\le& \rho^{-j-1} \sum\limits_{\ell\ge0}\rho^{-\ell} = \left[ (\rho-1)\rho^{j}\right]^{-1} , \end{array} $$

from which (6) follows.

Lemma 3

Letg(z) be analytic in theclosed ball$\mathcal {B}(0,r^{*})$of the complexplane, for a givenr^∗ > 0.Then, for all 0 < h≤ h^∗ < r^∗,

$$ g_{h}(\xi) := g(\xi h) $$

(7)

is analytic in $\mathcal {B}(0,\rho )$, with

$$ \rho \equiv \rho(h) := \frac{r^{*}}h {\ge \frac{r^{*}}{h^{*}}=:\rho^{*}} >1. $$

(8)

We are now in the position of stating the following result.²

Theorem 1

Assume that the function

$$ g(z):= f(y(z)) $$

(9)

and h in (2)–(3) satisfy the hypotheses of Lemma 3. Then, there exists κ = κ(h^∗) > 0, such that³

$$ |\gamma_{j}(y)| \le {\frac{\kappa}{\sqrt{j+1}}} \rho^{-j}. $$

(10)

Proof

By considering the function (7) corresponding to (9), and with reference to the function Q_j(ξ) defined in (5), one has that the parameter ρ, as defined in (8), is greater than 1 and, moreover, (see (3))

$$ \begin{array}{@{}rcl@{}} \gamma_{j}(y) &=& {\int_{0}^{1}}P_{j}(c)f(y(ch))\mathrm{d} c \equiv {\int_{0}^{1}} P_{j}(c) g_{h}(c)\mathrm{d} c\\ &=& {\int_{0}^{1}} P_{j}(c)\left[\frac{1}{2\pi \mathrm{i}}\int_{\mathcal{C}(0,\rho)} \frac{g_{h}(\xi)}{\xi-c}\mathrm{d} \xi\right] \mathrm{d} c \\ &=&\frac{1}{2\pi \mathrm{i}}\int_{\mathcal{C}(0,\rho)}g_{h}(\xi) \left[\int_{0}^{1} \frac{P_{j}(c)}{\xi-c}\mathrm{d} c\right] \mathrm{d} \xi \equiv \frac{1}{2\pi \mathrm{i}}\int_{\mathcal{C}(0,\rho)}g_{h}(\xi) Q_{j}(\xi) \mathrm{d} \xi. \end{array} $$

Then, passing to norms (see (6)),

$$|\gamma_{j}(y)|\le \rho\|g_{h}\|_{\rho} \|Q_{j}\|_{\rho}.$$

Moreover, observing that (see (9), (7), and (8)):

$$\|g_{h}\|_{\rho} := \max_{\xi\in \mathcal{C}(0,\rho)} \left|g_{h}\left( \xi\right)\right| \le \max_{\xi\in \mathcal{B}(0,\rho)} \left|g_{h}\left( \xi\right)\right| \equiv \max_{z\in \mathcal{B}(0,r^{*})} |g(z)|=:\|g\|,$$

and using (6), one has, (see (8)):

$$|\gamma_{j}(y)|\le \frac{ \|g\|} {(1-\rho^{-1})} \sqrt{\frac{2}{j+1}} \rho^{-j} \le \frac{ \|g\|} {(1-(\rho^{*})^{-1})} \sqrt{\frac{2}{j+1}} \rho^{-j},$$

from which (10) eventually follows.

Remark 1

It is worth mentioning that, in the bound (10), the dependence on h only concerns the parameter ρ > 1, via the expression (8), from which one infers that $\rho \sim h^{-1}$, for all 0 < h ≤ h^∗ < r^∗. This, in turn, is consistent with the result of Corollary 1, when $h\rightarrow 0$.

Let us now consider a polynomial approximation to (2),

$$ \dot\sigma(ch) = \sum\limits_{j=0}^{s-1} P_{j}(c) \gamma_{j}(\sigma),\qquad c\in[0,1], $$

(11)

where γ_j(σ) is defined according to (3) by formally replacing y by σ, i.e.,

$$ \gamma_{j}(\sigma)={\int_{0}^{1}} P_{j}(\tau)f(\sigma(\tau h))\mathrm{d}\tau, \quad j=0,1,\dots,s-1. $$

(12)

Integrating term by term (11), and imposing the initial condition in (1), provide us with the polynomial approximation of degree s:

$$ \sigma(ch) = y_{0} + h\sum\limits_{j=0}^{s-1} {\int_{0}^{c}} P_{j}(x)\mathrm{d} x \gamma_{j}(\sigma), \qquad c\in[0,1]. $$

(13)

We now want to assess the extent to which σ(ch) approximates y(ch), for c ∈ [0,1]. When $h\rightarrow 0$, it is known that y(h) − σ(h) = O(h^2s+ 1) (see, e.g., [7, 8, 13]). Nevertheless, we here discuss the approximation of σ to y, in the interval [0,h], when h is finite and only assuming that the result of Theorem 1 is valid. The following result then holds true.⁴

Theorem 2

Letybe thesolution of (1),σbedefined according to (13), and assume thatf(σ(z)) is analyticin$\mathcal {B}(0,r^{*})$, for agivenr^∗ > 0. Then,for all 0 < h≤ h^∗ < r^∗,there exist$M,\bar {M}>0$,$M=M(h^{*}), \bar {M}=\bar {M}(h^{*})$, andρ > 1,$\rho \sim h^{-1}$,such that:

• |σ(ch) − y(ch)|≤ chMρ^−s,c ∈ [0,1];

• $|\sigma (h)-y(h)| \le {h \bar {M} \rho ^{-2s}}$.

Proof

Let y(t,ξ,η) denote the solution of the problem

$$\dot y = f(y), \quad t\ge\xi, \qquad y(\xi)=\eta,$$

and Φ(t,ξ) be the solution of the associated variational problem,

$$\dot{\Phi}(t,\xi) = f^{\prime}(y(t,\xi,\eta)){\Phi}(t,\xi), \quad t\ge\xi,\qquad {\Phi}(\xi,\xi)=I,$$

having set $f^{\prime }$ the Jacobian of f. Without loss of generality, we shall assume that the function

$$ \hat{g}(z):= {\Phi}(h,z), $$

(14)

is also analytic in $\mathcal {B}(0,r^{*})$. We also recall the following well-known perturbation results:

$$\frac{\partial}{\partial\eta} y(t,\xi,\eta) = {\Phi}(t,\xi), \qquad \frac{\partial}{\partial\xi} y(t,\xi,\eta) = -{\Phi}(t,\xi)f(\eta).$$

Consequently, from (12) and (13), one has:

$$ \begin{array}{@{}rcl@{}} \sigma(ch)-y(ch)&=& y(ch,ch,\sigma(ch))-y(ch,0,\sigma(0)) = \int_{0}^{ch} \frac{\mathrm{d}}{\mathrm{d} t} y(ch,t,\sigma(t)) \mathrm{d} t\\ &=&\int_{0}^{ch} \left[\left.\frac{\partial}{\partial\xi} y(ch,\xi,\sigma(t))\right|_{\xi=t}+ \left.\frac{\partial}{\partial\eta} y(ch,t,\eta)\right|_{\eta=\sigma(t)}\dot\sigma(t)\right]\mathrm{d} t\\ &=&-h{\int_{0}^{c}}{\Phi}(ch,\tau h)\left[ f(\sigma(\tau h))-\dot\sigma(\tau h)\right]\mathrm{d} \tau\\ &=& -h {\int_{0}^{c}}{\Phi}(ch,\tau h)\left[ \sum\limits_{j\ge 0} P_{j}(\tau) \gamma_{j}(\sigma)-\sum\limits_{j=0}^{s-1}P_{j}(\tau)\gamma_{j}(\sigma)\right]\mathrm{d} \tau\\ &=&-h\sum\limits_{j\ge s} \left[\int_{0}^{c} P_{j}(\tau){\Phi}(ch,\tau h)\mathrm{d}\tau\right] \gamma_{j}(\sigma). \end{array} $$

(15)

From the result of Theorem 1 applied to g(z) := f(σ(z)), we know that there exist κ = κ(h^∗) and ρ > 1, $\rho \sim h^{-1}$, such that, for the Fourier coefficients defined in (12),

$$ |\gamma_{j}(\sigma)|\le {\frac{\kappa}{\sqrt{j+1}}} \rho^{-j}. $$

(16)

Moreover, (see (4)) $\|P_{j}\| = \sqrt {2j+1}$ and, considering that, for all h ∈ (0,h^∗],

$$\max_{x_{1},x_{2}\in[0,h]}|{\Phi}(x_{1},x_{2})| \le \max_{x_{1},x_{2}\in[0,{h^{*}}]}|{\Phi}(x_{1},x_{2})| =: \nu {\equiv \nu(h^{*})},$$

one has that

$$\left|{\int_{0}^{c}} P_{j}(\tau){\Phi}(ch,\tau h)\mathrm{d}\tau\right| \le c\nu\sqrt{2j+1}.$$

Consequently, the first statement follows from (15) by setting, with reference to the parameter ρ^∗ defined in (8),

$$M=\frac{\nu\kappa\sqrt{2}}{1-(\rho^{*})^{-1}},$$

since, for all c ∈ [0,1]:

$$ \begin{array}{@{}rcl@{}} |\sigma(ch)-y(ch)|&\le& ch \nu\kappa \sum\limits_{j\ge s} \sqrt{\frac{2j+1}{j+1}} \rho^{-j} \le ch \nu\kappa\sqrt{2} \sum\limits_{j\ge s} \rho^{-j}\\ &=& ch\nu\kappa\sqrt{2} \frac{\rho^{-s}}{1-\rho^{-1}} \le ch \frac{\nu\kappa\sqrt{2}}{1-(\rho^{*})^{-1}}\rho^{-s} \equiv chM\rho^{-s}. \end{array} $$

To prove the second statement (i.e., when c = 1), we observe that the result of Theorem 1 holds true also for the function (14) involved in the Fourier coefficients

$${\int_{0}^{1}} P_{j}(\tau){\Phi}(h,\tau h)\mathrm{d}\tau.$$

Consequently, there exist κ₁= κ₁(h^∗) > 0, such that

$$ \left|{\int_{0}^{1}} P_{j}(\tau){\Phi}(h,\tau h)\mathrm{d}\tau\right|\le {\frac{\kappa_{1}}{\sqrt{j+1}}} \rho^{-j}. $$

(17)

The second statement then follows again from (15) by setting

$$\bar{M}=\frac{\kappa_{1}\kappa}{1-(\rho^{*})^{-2}},$$

so that, by using same steps as above:

$$ \begin{array}{@{}rcl@{}} |\sigma(h)-y(h)|&\le& h \kappa_{1}\kappa \sum\limits_{j\ge s} \frac{\rho^{-2j}}{j+1} \le h \kappa_{1}\kappa \sum\limits_{j\ge s} \rho^{-2j}\\ &=& h \kappa_{1}\kappa \frac{\rho^{-2s}}{1-\rho^{-2}} \le h \frac{\kappa_{1}\kappa}{1-(\rho^{*})^{-2}}\rho^{-2s} \equiv h\bar{M}\rho^{-2s}. \end{array} $$

Let us now introduce the use of a finite precision arithmetic, with machine precision u, for approximating (2). Then, the best we can do is to consider the polynomial approximation (11)–(12)⁵

$$ \dot y(ch) \doteq \dot\sigma(ch) = \sum\limits_{j=0}^{s-1} P_{j}(c) \gamma_{j}(\sigma),\qquad c\in[0,1], $$

(18)

such that

$$ |\gamma_{s}(\sigma)| < \mathrm{tol} \cdot \max_{j<s} |\gamma_{j}(\sigma)|, \qquad \mathrm{tol}\sim u. $$

(19)

Integrating (18), and imposing that σ(0) = y₀, then brings back to (13). We observe that because of (16), (19) may be approximately recast as

$$ {\sqrt{\frac{1}{s+1}}} \rho^{-s} < \mathrm{tol} \sim u, $$

(20)

where $\rho \sim h^{-1}$. Consequently, choosing s such that (19) (or (20)) is satisfied, we obtain that:

• the polynomial σ(ch) defined by (18) and (13) provides a uniformly accurate approximation to y(ch), in the whole interval [0,h], within the possibility of the used finite precision arithmetic;

• σ(h) is a spectrally accurate approximation to y(h). Moreover, in light of the second point of the result of Theorem 2, one has that the criterion (19) can be conveniently relaxed. In fact, making the ansatz (see (16) and (17)) κ = κ₁, one has that

  $$ |\sigma(h)-y(h)| \lesssim \frac{h\kappa^{2}}{1-\rho^{-2}}\rho^{-2s} \approx \frac{h(s+1)}{1-\rho^{-2}} |\gamma_{s}(\sigma)|^{2}. $$

  (21)

  Imposing the approximate upper bound to be smaller than the machine epsilon u, one then obtains:

  $$ |\gamma_{s}(\sigma)| \lesssim {\sqrt{\frac{u(1-\rho^{-2})}{h(s+1)}}} \propto u^{1/2}, $$

  (22)

  which is generally much less restrictive than (19).⁶ Alternatively, by considering that the use of relatively large time-steps h is sought, one can use $\text {tol}\sim u^{1/2}$ in (19), that is,

  $$ |\gamma_{s}(\sigma)| < \mathrm{tol} \cdot \max_{j<s} |\gamma_{j}(\sigma)|, \qquad \mathrm{tol}\sim u^{1/2}, $$

  (23)

  In other words, (21) means that the method maintains the property of super-convergence, which is known to hold when $h\rightarrow 0$, also in the case where the time-step h is relatively large.

Remark 2

In particular, we observe that (19) (or (20) or (22)) can be fulfilled by varying the value of s, and/or that of the stepsize h, by considering that, by virtue of (8),

$$ \rho(h_\mathrm{new}) \approx \rho(h_\mathrm{old})\frac{h_\mathrm{old}}{h_\mathrm{new}}, $$

h_old and h_new being the old and new stepsizes, respectively.

It is worth mentioning that the result of Theorem 2 can be also used to define a stepsize variation, within a generic error tolerance tol, thus defining a strategy for the simultaneous order/stepsize variation.

We conclude this section mentioning that, to gain efficiency, the criterion (19) for the choice of s in (18) can be more conveniently changed to

$$ |\gamma_{s-1}(\sigma)| \le \mathrm{tol} \cdot \max_{j\le s-1} |\gamma_{j}(\sigma)|, \qquad \mathrm{tol} \sim \rho\cdot u. $$

(24)

Similarly, the less restrictive criterion (22) can be approximately modified as:

$$ |\gamma_{s-1}(\sigma)|\lesssim \rho\sqrt{\frac{u}{hs}} \propto u^{1/2}, $$

or, alternatively, one uses $\text {tol}\sim u^{1/2}$ in (24). As is clear, computing the norms of the coefficients γ_j(σ) permits to derive estimates for the parameters κ and ρ in (16), as we shall see later in the numerical tests.

3 SHBVMs

The approximation procedure studied in the previous section does not yet provide a numerical method, in that the integrals defining γ_j(σ), $j=0,\dots ,s-1$, in (12)–(13) need to be computed. For this purpose, one can approximate them to within machine precision through a Gauss-Legendre quadrature formula of order 2k (i.e., the interpolatory quadrature rule defined at the zeros of P_k) with k large enough. In particular, following the criterion used in [9, 18], for the double precision IEEE⁷, we choose

$$ k = \max\{ 20, s+2\}. $$

(25)

After that, we define the approximation to y(h) as

$$ y_{1} :=\sigma(h) \equiv y_{0}+h\gamma_{0}(\sigma). $$

(26)

In so doing, one eventually obtains a HBVM(k,s), which we sketch below. Hereafter, we shall refer to such a method as to spectral HBVM (in short, SHBVM), since its parameters s and k, respectively defined in (19) (or (20) or (22)) and (25), are aimed at obtaining a numerical solution which is accurate within the round-off error level of the used finite precision arithmetic.

For sake of completeness, let us now briefly sketch what a HBVM(k,s) is. In general, to approximate the Fourier coefficient γ_j(σ), and assuming for sake of simplicity that full machine accuracy is gained, we use the quadrature

$$ \gamma_{j}(\sigma) \doteq \sum\limits_{\ell=1}^{k} b_{\ell} P_{j}(c_{\ell})f(\sigma(c_{\ell} h)) =: \hat{\gamma}_{j},\qquad j=0,\dots,s-1, $$

(27)

where the polynomial σ is that defined in (13) by formally replacing γ_j(σ) with $\hat {\gamma }_{j}$, and (c_i,b_i) are the abscissae and weights of the Gauss-Legendre quadrature of order 2k on the interval [0,1].⁸ Setting Y_ℓ = σ(c_ℓh), from (27), one then obtains the stage equations

$$ \begin{array}{@{}rcl@{}} Y_{i} &=& y_{0} + h\sum\limits_{j=0}^{s-1} \int_{0}^{c_{i}} P_{j}(x)\mathrm{d} x \hat{\gamma}_{j}\\ &\equiv& y_{0} + h\sum\limits_{j=1}^{k} \underbrace{b_{j} \left[\sum\limits_{\ell=0}^{s-1} \int_{0}^{c_{i}}P_{\ell}(x)\mathrm{d} x P_{\ell}(c_{j})\right]}_{=: a_{ij}} f(Y_{j}), \quad i=1,\dots,k, \end{array} $$

(28)

with the new approximation given by (see (26))

$$ y_{1} = y_{0}+ h\hat{\gamma}_{0} \equiv y_{0}+h\sum_{i=1}^{k} b_{i} f(Y_{i}). $$

(29)

Consequently, with reference to (28), setting

$$ A = \left( a_{ij}\right)\in\mathbb{R}^{k\times k}, \qquad \boldsymbol{b} = (b_{i}), \boldsymbol{c}=(c_{i})\in\mathbb{R}^{k}, $$

(30)

one easily realizes that (28) and (29) define the k-stage Runge-Kutta method with Butcher tableau:

$$ \begin{array}{c|c} \boldsymbol{c} & A \\[-3mm] &\boldsymbol{b}^{\top} \end{array} . $$

From (28), one verifies that the Butcher matrix in (30) can be written as

$$ A = \mathcal{I}_{s}\mathcal{P}_{s}^{\top}\Omega, $$

(31)

with

$$ \mathcal{P}_{s} \!=\! \left( \begin{array}{ccc} P_{0}(c_{1})&\dots&P_{s-1}(c_{1})\\ \vdots & &\vdots\\ P_{0}(c_{k})&\dots&P_{s-1}(c_{k}) \end{array}\right), \mathcal{I}_{s} \!=\! \left( \begin{array}{ccc}\int_{0}^{c_{1}}P_{0}(x)\mathrm{d} x&\dots&\int_{0}^{c_{1}}P_{s-1}(x)\mathrm{d} x\\ \vdots & &\vdots\\ \int_{0}^{c_{k}}P_{0}(x)\mathrm{d} x&\dots&\int_{0}^{c_{k}}P_{s-1}(x)\mathrm{d} x \end{array}\right) \in\mathbb{R}^{k\times s}, $$

(32)

and

$$ {\Omega} = \left( \begin{array}{ccc}b_{1}\\ &\ddots\\ &&b_{k} \end{array}\right) \in\mathbb{R}^{k\times k}. $$

(33)

In fact, setting $\boldsymbol {e}_{i}\in \mathbb {R}^{k}$ the i th unit vector, and taking into account (31)–(33), one has

$$ \boldsymbol{e}_{i}^{\top} A\boldsymbol{e}_{j} =\boldsymbol{e}_{i}^{\top} \mathcal{I}_{s} \mathcal{P}_{s}^{\top} {\Omega}\boldsymbol{e}_{j} = \boldsymbol{e}_{i}^{\top} \mathcal{I}_{s} \left( \boldsymbol{e}_{j}^{\top} \mathcal{P}_{s} \right)^{\top} b_{j} \!=\!b_{j} \left[\sum\limits_{\ell=0}^{s-1} \int_{0}^{c_{i}}P_{\ell}(x)\mathrm{d} x P_{\ell}(c_{j})\right] \equiv a_{ij}, $$

as defined in (28). From well-known properties of Legendre polynomials (see, e.g., [7, Appendix A]), one has that

$$ \mathcal{I}_{s} = \mathcal{P}_{s+1}\hat X_{s} \equiv \left( \begin{array}{ccc}P_{0}(c_{1})&\dots&P_{s}(c_{1})\\ \vdots & &\vdots\\ P_{0}(c_{k})&\dots&P_{s}(c_{k}) \end{array}\right) \left( \begin{array}{cccc}\xi_{0} & -\xi_{1}\\ \xi_{1} &0 &\ddots\\ &\ddots & \ddots &-\xi_{s-1}\\ & &\xi_{s-1} &0\\ &&&\xi_{s} \end{array}\right), \quad \xi_{i} = \left( 2\sqrt{ |4i^{2}-1|}\right)^{-1}, $$

(34)

from which one easily derives the following property relating the matrices (32)–(33) (see, e.g., [7, Lemma 3.6]):

$$ \mathcal{P}_{s}^{\top}{\Omega}\mathcal{I}_{s} = \left( \begin{array}{cccc}\xi_{0} & -\xi_{1}\\ \xi_{1} &0 &\ddots\\ &\ddots & \ddots &-\xi_{s-1}\\ & &\xi_{s-1} &0 \end{array}\right) =: X_{s}\in\mathbb{R}^{s\times s}. $$

(35)

Remark 3

From (32)–(34), one has that the Butcher matrix (31) can be rewritten as

$$ A=\mathcal{P}_{s+1}\hat X_{s} \mathcal{P}_{s}^{\top}\Omega. $$

(36)

Considering that, when k = s, (see (35)) $\mathcal {P}_{s+1}\hat X_{s} = \mathcal {P}_{s}X_{s}$ and $\mathcal {P}_{s}^{\top }{\Omega } = \mathcal {P}_{s}^{-1}$, so that A reduces to $\mathcal {P}_{s} X_{s} \mathcal {P}_{s}^{-1}$, we observe that (36) can be also regarded as a generalization of the W-transformation in [25, Section IV.5].

At this point, we observe that the stage equation (28) can be cast in vector form, by taking into account (30)–(33), as

$$ Y \equiv \left( \begin{array}{cc} Y_{1}\\ \vdots \\ Y_{k} \end{array}\right) = \boldsymbol{e}\otimes y_{0} + h\mathcal{I}_{s}P_{s}^{\top}{\Omega} \otimes I_{m} \cdot f(Y), \qquad \boldsymbol{e}= \left( \begin{array}{cc}1\\ \vdots \\1 \end{array}\right) \in\mathbb{R}^{k}, $$

(37)

with an obvious meaning of f(Y ). On the other hand, the block vector of the coefficients in (27) turns out to be given by

$$ \hat{\boldsymbol{\gamma}} \equiv \left( \begin{array}{cc} \hat{\gamma}_{0} \\ \vdots \\ \hat{\gamma}_{s-1} \end{array}\right) = \mathcal{P}_{s}^{\top}{\Omega}\otimes I_{m}\cdot f(Y). $$

(38)

Consequently, from (37), one obtains

$$Y = \boldsymbol{e}\otimes y_{0} + h\mathcal{I}_{s}\otimes I_{m}\cdot \hat{\boldsymbol{\gamma}},$$

and then, from (38), one eventually derives the equivalent discrete problem

$$ F(\hat{\boldsymbol{\gamma}}) := \hat{\boldsymbol{\gamma}} - \mathcal{P}_{s}^{\top}{\Omega}\otimes I_{m}\cdot f\left( \boldsymbol{e}\otimes y_{0} + h\mathcal{I}_{s}\otimes I_{m}\cdot \hat{\boldsymbol{\gamma}}\right) = {\bf0}, $$

(39)

which has (block) dimension s, independently of k (compare with (37)). Once it has been solved, the new approximation is obtained (see (29)) as $y_{1}=y_{0}+h\hat {\gamma }_{0}$.

It is worth observing that the new discrete problem (39), having block dimension s independently of k, allows us to use arbitrarily high-order quadratures (see (25)), without affecting that much the computational cost.

In order to solve (39), one could in principle use a fixed-point iteration,⁹

$$ \hat{\boldsymbol{\gamma}}^{\ell+1} := \mathcal{P}_{s}^{\top}{\Omega}\otimes I_{m}\cdot f\left( \boldsymbol{e}\otimes y_{0} + h\mathcal{I}_{s}\otimes I_{m}\cdot \hat{\boldsymbol{\gamma}}^{\ell}\right), \qquad \ell=0,1,\dots,$$

which, though straightforward, usually implies restrictions on the choice of the stepsize h. For this reason, this approach is generally not useful when using the methods as spectral methods, where the use of relatively large stepsizes is sought. On the other hand, the use of the simplified Newton iteration for solving (39) reads, by virtue of (35),

$$ \text{solve: } \left[ I_{s}\otimes I_{m}-hX_{s}\otimes f^{\prime}(y_{0})\right] \boldsymbol{\delta}^{\ell} = -F(\hat{\boldsymbol{\gamma}}^{\ell}), \qquad \hat{\boldsymbol{\gamma}}^{\ell+1} := \hat{\boldsymbol{\gamma}}^{\ell}+\boldsymbol{\delta}^{\ell}, \qquad \ell=0,1,\dots. $$

(40)

However, the coefficient matrix in (40) has a dimension s times larger than that of the continuous problem (i.e., m) and, therefore, this can be an issue when large values of s are to be used, as in the case of SHBVMs. Fortunately, this problem can be overcome by replacing the previous iteration (40) with a corresponding blended iteration [7, 8, 12] (see also [5]). In more details, once one has formally computed the m × m matrix

$$ {\Sigma} = \left( I_{m}-h\rho_{s} f^{\prime}(y_{0})\right)^{-1}, \qquad \rho_{s} = \min_{\lambda\in\sigma(X_{s})}|\lambda|, $$

(41)

where σ(X_s) denotes, as is usual, the spectrum of matrix X_s, one iterates:

$$ \boldsymbol{\eta}^{\ell}:=F(\hat{\boldsymbol{\gamma}}^{\ell}),\quad \boldsymbol{\eta}_{1}^{\ell} := \rho_{s}X_{s}^{-1}\otimes I_{m}\boldsymbol{\eta}^{\ell}, \quad \hat{\boldsymbol{\gamma}}^{\ell+1} := \hat{\boldsymbol{\gamma}}^{\ell} +I_{s}\otimes {\Sigma} \left[ \boldsymbol{\eta}_{1}^{\ell} + I_{s}\otimes {\Sigma}\left( \boldsymbol{\eta}^{\ell}-\boldsymbol{\eta}_{1}^{\ell}\right)\right], \qquad \ell=0,1,\dots. $$

(42)

Consequently, one only needs to compute, at each time-step, the matrix ${\Sigma }\in \mathbb {R}^{m\times m}$ defined in (41),¹⁰ having the same size as that of the continuous problem. Moreover, it is worth mentioning that for semi-linear problems with a leading linear part, the Jacobian of f can be approximated with the (constant) linear part, so that Σ is computed once for all [6, 9, 18].

Remark 4

It must be stressed that it is the availability of the very efficient blended iteration (41)–(42) which makes the practical use of HBVMs as spectral methods in time possible, since relatively large values of s can be easily and effectively handled.

A thorough analysis of the blended iteration can be found in [15]. Contexts where it has been successfully implemented include stiff ODE-IVPs [16], linearly implicit DAEs up to index 3 [17] (see also the code BiMD in TestSet for IVP Solvers “https://archimede.dm.uniba.it/~testset/testsetivpsolvers/”), and canonical Hamiltonian systems (see the Matlab code HBVM, available at “http://web.math.unifi.it/users/brugnano/LIMbook/”), while its implementation in the solution of RKN methods may be found in [38].

4 Numerical tests

The aim of this section is twofold: firstly, to assess the theoretical analysis of SHBVMs made in Section 2; secondly, to compare such methods w.r.t. some well-known ones. All numerical tests, which concern different kinds of ODE problems, have been computed on a laptop with a 2.8-GHz Intel-i7 quad-core processor and 16GB of memory, running Matlab 2017b. For the SHBVM, the criteria (23) and (25) have been respectively used to determine its parameters s and κ.

4.1 The Kepler problem

We start considering the well-known Kepler problem (see, e.g., [7, Chapter 2.5]), which is Hamiltonian, with Hamiltonian function

$$ H(q,p) = \frac{1}2 \|p\|_{2}^{2} - \|q\|_{2}^{-1}, \qquad q,p\in\mathbb{R}^{2}. $$

(43)

Consequently, we obtain the equations

$$ \dot q = p, \qquad \dot p = -\|q\|_{2}^{-3}q, $$

(44)

which, when coupled with the initial conditions

$$ q(0) = \left( \begin{array}{ccc}1-\varepsilon,&0 \end{array}\right)^{\top}, \qquad p(0) = \left( \begin{array}{cc}0, & \sqrt{\frac{1+\varepsilon}{1-\varepsilon}} \end{array}\right)^{\top}, \qquad \varepsilon\in[0,1), $$

(45)

provide a periodic orbit of period T = 2π that, in the q-plane, is given by an ellipse of eccentricity ε. In particular, we choose the value ε = 0.5. The solution of this problem has two additional (functionally independent) invariants besides the Hamiltonian (43), i.e., the angular momentum and one of the nonzero components of the Lenz vector [7, page 64] (in particular, we select the second one):

$$ M(q,p) = q_{1}p_{2}-p_{1}q_{2}, \qquad L(q,p) = -p_{1}M(q,p)-q_{2}\|q\|_{2}^{-1}. $$

(46)

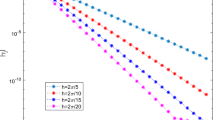
At first, we want to assess the result of Theorem 1. For this purpose, we apply the HBVM (20,16) for one step starting from the initial condition (45), and using time-steps h_i = 2π/(5 ⋅ 2^i− 1), $i=1,\dots ,5$. Figure 1 is the plot (see (27)) of $|\hat \gamma _{j}|$, for $j=0,1,\dots ,15$, (solid line with circles), which, according to (16), should behave as $\kappa \rho ^{-j}/\sqrt {j+1}$, due to the result of Theorem 1. A least squares approximation technique has been employed to estimate the two parameters (κ and ρ) appearing in the bound (16). These theoretical bounds are highlighted by the dashed line with asterisks in Fig. 1: evidently, they well fit the computed values, except those which are close to the round-off error level. Moreover, according to the arguments in the proof of Theorem 1, one also expects that the estimate of κ increases but is bounded, as $h\rightarrow 0$, whereas ρ should be proportional to h^− 1. This fact is confirmed by the results listed in Table 1.

Fig. 1

Behavior of $|\hat \gamma _{j}|$ for decreasing values of the time-step h for the Kepler problem (44)–(45) solved by the HBVM(20,16) with decreasing time-steps. The line with circles are the computed norms, whereas those with the asterisks are the estimated ones. Observe that for the smallest time-steps, the computed norms stagnate near the round-off error level

Table 1 Estimated values for the parameters κ and ρ for the Kepler problem (44)–(45), when using decreasing time-steps

Next, we compare the following methods for solving (44)–(45):

• the s-stage Gauss method (i.e., HBVM(s,s)), s = 1,2, which is symplectic and of order 2s. Consequently, it is expected to conserve the angular momentum M(q,p) in (46), which is a quadratic invariant [34];

• the HBVM(6, s) methods, s = 1,2, which, for the considered stepsizes is energy-conserving and of order 2s;

• the SHBVM method described above, where s and k are determined according to (23) and (25), respectively, with tol ≈ 10^− 8. This tolerance, in turn, should provide us with full accuracy, according to the result of Theorem 2, because of the super-convergence of the method, which is valid for any used step-size.¹¹

It is worth mentioning that the execution times that we shall list for the Gauss, HBVM, and SHBVM methods are perfectly comparable, since the same Matlab code has been used for all of them. This code, in turn, is a slight variant of the hbvm function available at the url “http://web.math.unifi.it/users/brugnano/LIMbook/”.

In Tables 2, 3, and 4, we list the obtained results when using a time-step h = 2π/n over 100 periods. In more details, we list the maximum errors, measured at each period, in the invariants (43) and (46), e_H,e_M,e_L, respectively, the solution error, e_y, and the execution times (in sec). As it is expected, the symplectic methods conserve the angular momentum (since it is a quadratic invariant), whereas the energy-conserving HBVMs conserve the Hamiltonian function.¹² On the other hand, the SHBVM conserves all the invariants and has a uniformly small solution error, by using very large stepsizes. Further, its execution time is the lowest one (less than 0.5 sec, when using h = 2π/5), thus confirming the effectiveness of the method.

Table 2 Numerical result for the s-stage Gauss method, s = 1,2, used for solving the Kepler problem (44)–(45), ε = 0.5, with stepsize h = 2π/n

Table 3 Numerical result for the HBVM(6, s) methods, s = 1,2, used for solving the Kepler problem (44)–(45), ε = 0.5, with stepsize h = 2π/n

Table 4 Numerical result for the SHBVM method used for solving the Kepler problem (44)–(45), ε = 0.5, with stepsize h = 2π/n

4.2 A Lotka-Volterra problem

We consider the following Poisson problem [20],

$$ \dot y = B(y) \nabla H(y), \qquad B(y)^{\top} = -B(y), $$

(47)

with $y\in \mathbb {R}^{3}$ and, for arbitrary real constants a,b,c,ν,μ,

$$ B(y) \!=\!\! \left( \!\begin{array}{ccc} 0 & c y_{1}y_{2} &bc y_{1}y_{3}\\ -c y_{1}y_{2} &0& -y_{2}y_{3}\\ -bc y_{1}y_{3} & y_{2}y_{3} &0 \end{array}\!\right)\!, \qquad H(y) \!=\! ab y_{1} + y_{2} -a y_{3} +\nu\ln y_{2} -\mu\ln y_{3}. $$

(48)

Moreover, assuming that abc = − 1, there is a further invariant besides the Hamiltonian H, i.e., the Casimir

$$ C(y) = ab\ln y_{1} -b\ln y_{2} +\ln y_{3}. $$

(49)

The solution turns out to be periodic, with period T ≈ 2.878130103817, when choosing

$$ a = -2, \quad b = -1, \quad c = -0.5, \quad \nu = 1, \quad\mu = 2, \quad y(0) = (1, 1.9, 0.5)^{\top}. $$

(50)

For this problem, the HBVM(k,s) is no more energy-conserving, as well as the s-stage Gauss method. As matter of fact, both exhibit a drift in the invariants and a quadratic error growth in the numerical solution. The obtained results for the SHBVM, with tol ≈ 10^− 8 in (23) for choosing s, κ given by (25), and using a stepsize h = T/n, are listed in Table 5, where it is reported the maximum Hamiltonian error, e_H, the Casimir error, e_C, and the solution error e_y, measured at each period, over 100 periods. In such a case, all the invariants turn out to be numerically conserved, and the solution error is uniformly very small. Moreover, the SHBVM using the largest time-step (i.e., h = T/5 ≈ 0.57) turns out to be the most efficient one. For comparison, in the table, we also list the results obtained by using the Matlab solver ode45 used with the default parameters, requiring 5600 integration steps and stepsizes approximately in the range [2.2 ⋅ 10^− 2,1.1 ⋅ 10^− 1], and the same solver used with parameters AbsTol= 1e-15, RelTol= 1e-10, now requiring 121760 integration steps, with stepsizes approximately in the range [10^− 3,4.2 ⋅ 10^− 3].

Table 5 Numerical result for the SHBVM method used for solving the Lotka-Volterra problem (47)–(50) with stepsize h = T/n

4.3 A stiff ODE-IVP

At last, we consider a stiff ODE-IVP,

$$ \dot y(t) = \left( \begin{array}{cccccc} -9999 & 1 & 1\\ 9900 & -100 & 1\\ 98 & 98 & -2 \end{array}\right) \left[ y(t) - g(t)\right] + \dot{g}(t), \qquad y(0) = g(0), $$

(51)

with g(t) a known function, having evidently solution y(t) = g(t). We choose

$$ g(t) = \left( \begin{array}{ccc}\cos 2\pi t, & \cos 4\pi t, &\cos 6\pi t \end{array}\right)^{\top}, $$

(52)

and consider the SHBVM with tol ≈ 10^− 8 in (23) for choosing s (as before, κ is chosen according to (25)), so that full accuracy is expected in the numerical solution. The time-step used is h = 100/n for n steps. The measured errors in the last point (coinciding with the initial condition), are then reported in Table 6. For comparison, also the results obtained by the Matlab solver ode15s, using its default parameters, are listed in the table. This latter solver requires 6006 steps, with time-steps approximately in the range [1.9 ⋅ 10^− 3,2 ⋅ 10^− 2].

Table 6 Numerical result for the SHBVM method used for solving the stiff problem (51)–(52) with stepsize h = 100/n, and ode15s with the default parameters

5 Conclusions

In this paper, we provide a thorough analysis of SHBVMs, namely HBVMs used as spectral methods in time, which further confirms their effectiveness. From the analysis, one obtains that the super-convergence of HBVMs is maintained also when using relatively large time-steps. SHBVMs become a practical method, due to the very efficient nonlinear blended iteration inherited from HBVMs. As a consequence, SHBVMs appear to be good candidates as general ODE solvers. This is indeed confirmed by a few numerical tests concerning a Hamiltonian problem, a Poisson (not Hamiltonian) problem, and a stiff ODE-IVP. The same tests show the numerical assessment of the theoretical achievements.