1 Introduction

Communication over the globe is becoming a basic need of populaces [1]. However, the inherent openness, dynamism, and complexity of the Internet frequently result in information leakage incidents, which makes it imperative to enhance the security level of sensitive information. The most direct method for the protection of information confidentiality is encryption, and various classic encryption algorithms, such as data encryption standard (DES) and advanced encryption standard (AES), have been proposed successively. Although these algorithms are easily available, extensively tested, and widely accepted for text data encryption, their application in image encryption is constrained due to the large amount of data, strong correlation between adjacent pixels, and high redundancy of image data.

Chaos is a central research topic of nonlinear theories. It exhibits distinctive properties, including initial state sensitivity, topological transitivity, and periodic orbit density [2]. These properties establish a natural connection between chaos and traditional cryptography, resulting in wide application in various fields such as S-box design [3, 4] and information hiding [5, 6]. At present, more than 32% of image encryption algorithms are designed based on chaos theory. Chaotic image encryption algorithms offer confidentiality protection for sensitive images in a variety of fields, such as e-medicine, military reconnaissance, remote sensing mapping, etc., thus avoiding the security risks associated with leaks of private information and misuse of data.

The fundamental prerequisite for the design of chaotic image encryption algorithms is the establishment of chaotic systems with excellent dynamic behavior. Chaotic systems are classified into two types: continuous chaotic systems and discrete chaotic systems. Currently, researchers mainly focus on continuous chaotic systems. For example, Yang et al. [7] designed a fractional-order hyperchaotic system based on the Lorenz system and analyzed the dynamical behavior of this system in detail using the Adomian decomposition method. Ma et al. [8] presented a multi-stable chaotic system with coexisting attractors by tuning the offset operation. However, continuous chaotic systems are inefficient due to the necessity of using time-consuming numerical analysis methods, like the Runge–Kutta method or the Adomian decomposition method, to generate chaotic sequences [9]. Discrete chaotic systems have proven to be more efficient than continuous chaotic systems, and a variety of classical chaotic maps, such as the Logistic map and the Tent map, have been successively introduced. However, Hua et al. [10] pointed out that the structure of these chaotic maps is relatively simple. In general, high-dimensional discrete chaotic systems are more likely to produce hyperchaotic attractors, which implies better chaotic properties. Choi et al. [11] constructed generalized high-dimensional Arnold systems using the Laplace theorem. Hua et al. [12] constructed high-dimensional discrete chaotic systems by composing classical low-dimensional discrete chaotic systems. Through rigorous theoretical analysis, Liu et al. [13] demonstrated that the third-order nonlinear filter can exhibit strong chaotic behavior if its system parameters are chosen appropriately. Unfortunately, the limited number of positive LE in the mentioned discrete chaotic systems is significantly lower than their dimensions, making them susceptible to chaotic degradation during digitization. To tackle this issue, Hua et al. [14] first discussed the internal relationship between the number of positive LE and the Arnold parameter matrix. Then, they presented a high-dimensional discrete chaotic system with an arbitrary number of positive LE. Wang et al. [15] and Zang et al. [16] designed non-degenerate discrete chaotic systems by using the chaotic inverse control method and the strict diagonal occupation matrix respectively. Liu et al. [17] also proposed a non-degenerate discrete chaotic system with uniform trajectories using nonlinear filters and the feed-forward and feed-back structure. Since the above discrete chaotic systems have a much greater number of positive LE compared to general chaotic systems, they are capable of displaying complex chaotic behavior. However, these systems do not exhibit multi-stability, which means that they are unable to switch freely between various steady states to meet diverse demands. Qin [18] pointed out that chaotic systems with more equilibrium points may contain more attractors, resulting in different coexisting attractors. Due to the inherent nonlinearity and periodicity of trigonometric functions, researchers have recently begun to investigate the design of multi-stable chaotic systems using them [19]. For example, Ali et al. [20] constructed a novel chaotic map using two sine functions with irrational frequency ratios but comparable amplitude and phase, and found coexisting attractors. Huang et al. [21] proposed a three-dimensional (3D) multi-stable hyperchaotic map with a concise symmetric structure. Furthermore, memristors are employed to enhance the dynamic behavior of multi-stable chaotic systems due to their distinctive nonlinear characteristics [22]. Ma et al. [23] designed a memristive chaotic system that has infinite equilibrium points and can exhibit seven different types of attractors. Liu et al. [24] and Marco et al. [25] proposed a class of discrete multi-stable chaotic systems using discrete memristors, respectively. However, these chaotic systems do not meet the non-degeneracy requirement and remain susceptible to chaotic degradation.

Chaos theory offers a plethora of beneficial insights for the design of image encryption algorithms. In 1989, Matthews et al. put forward the first chaotic image encryption algorithm using the Logistic map. Subsequently, Li et al. [26] constructed a key stream generator using the Tent map and applied it to the design of a stream cipher algorithm that is suitable for image confidentiality protection. Sang et al. [27] generated cipher images with excellent statistical features by scrambling plain images using the Logistic map and incorporating uniform distribution constraints to the training of deep auto-encoder. However, the above image encryption algorithms suffer from potential security risks due to the simple structure of the chaotic maps they use. In response to the above problem, Lai et al. [28] designed a novel neuron model with significant chaotic properties and applied it to the design of image encryption algorithms. Wang et al. [29] first designed a hyperchaotic system with complex chaotic behavior based on the Lorenz system and then proposed a color image encryption algorithm by combining the chaotic system and deoxyribonucleic acid (DNA) coding. Hua et al. [30] put forward an image encryption algorithm using a novel Logistic-Sine-coupling chaotic system. Javeed et al. [31] put forward an image encryption algorithm using the Rabinovich-Fabricant chaotic system. The above research has contributed to the research progress in the field of chaotic image encryption. However, none of the above chaotic systems are non-degeneracy, which may lead to security risks in image encryption algorithms due to chaotic degradation. To overcome this drawback, Wen et al. [32] and Wang et al. [33] proposed plaintext-related chaotic image encryption algorithms using non-degenerate discrete chaotic systems and the hash values of plain images, respectively. However, the derived key in the above algorithm is strongly linked to the hash values of plain images, making even a slight alteration in the hash value during transmission could result in decryption failure. Thus, how to securely transmit the hash value of a plain image limits the application of such image encryption algorithms.

Although chaotic cryptography has achieved several important research results after years of development, the existing chaotic systems are susceptible to chaotic degradation and generally do not exhibit multi-stability, and the current chaotic image encryption algorithms suffer from low efficiency in encryption and decryption and inadequate security measures. As such, existing research faces challenges in meeting the criteria for safeguarding the confidentiality of sensitive images In conclusion, there is still considerable research value in investigating non-degenerate multi-stable discrete chaotic systems and applying them to the design of effective image encryption algorithms.

The remainder of this paper is structured as follows. Section 2 presents a non-degenerate multi-stable discrete chaotic system that is analyzed through theoretical analysis and simulation experiments. In Sect. 3, we propose an image encryption algorithm based on non-degenerate multi-stable discrete chaos, and its performance is evaluated. Section 4 concludes this paper.

2 Non-degenerate multi-stable discrete chaotic system

In this section, we design a discrete chaotic system called NMDCS. Rigorous theoretical analyses and simulation experiments demonstrate that the NMDCS exhibits multi-stability and is not prone to chaotic degradation.

2.1 Mathematical expression of our discrete chaotic system

The mathematical model of N-dimensional NMDCS is described by Eq. (1), whose block diagram is shown in Fig. 1.

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{x_{1,t + 1}} = \sin \left( {\pi \cdot {x_{2,t}}} \right) }\\ \vdots \\ {{x_{N - 1,t + 1}} = \sin \left( {\pi \cdot {x_{N,t}}} \right) }\\ {{x_{N,t + 1}} = {x_{N,t}} + \sin \left( {\pi \cdot {x_{1,t}}} \right) - \frac{a}{\pi } \cdot \sin \left( {\frac{{\pi \cdot {x_{N,t}}}}{a}} \right) } \end{array}} \right. \end{aligned}$$
(1)
Fig. 1
figure 1

Block diagram of NMDCS

Full size image

where \(a = \frac{b}{{2 \cdot c}}\) is the system parameter, \(b,c \in \mathbb {Z} \backslash \left\{ 0 \right\} \) are coprime, \(\left| b \right| > 6 \cdot \left| c \right| \), \(\left\{ {{x_{1,t}},{x_{2,t}}, \cdots ,{x_{N-1,t}}} \right\} \in {I}\) and \({x_{N,t}} \in {I^*}\) are the chaotic state variables at moment t, \(I = \left[ { - 1,1} \right] \) and \({I^*} = \left[ { - 1 {+} k \cdot b {+} {\varepsilon _1},1 {+} k \cdot b {+} {\varepsilon _2}} \right] \) are the chaotic intervals, \(k \in \mathbb {Z}\), and the absolute values of \({\varepsilon _1}\) and \({\varepsilon _2}\) are far less than 1.

2.2 Theoretical analysis of our discrete chaotic system

In this section, we prove that the NMDCS system has unstable fixed points, and is not susceptible to chaotic degradation.

2.2.1 Fixed points analysis

According to Eq. (1), the fixed point equation of our NMDCS system can be derived as Eq. (2).

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{x_{1.t}} = \sin \left( {\pi \cdot {x_{2.t}}} \right) }\\ \vdots \\ {{x_{N - 1.t}} = \sin \left( {\pi \cdot {x_{N.t}}} \right) }\\ {{x_{N.t}} = {x_{N.t}} + \sin \left( {\pi \cdot {x_{1.t}}} \right) - \frac{a}{\pi } \cdot \sin \left( {\frac{{\pi \cdot {x_{N.t}}}}{a}} \right) } \end{array}} \right. \end{aligned}$$
(2)

Obviously, Eq. (2) has an infinite number of solutions. Therefore, the fixed points of the NMDCS system can be expressed as \(X = \left\{ {0,0, \cdots ,0,k \cdot b} \right\} \).

The Jacobian matrix of Eq. (2) at X is described by Eq. (3).

$$\begin{aligned} {{\textbf {J}}_t} = \left( {\begin{array}{*{20}{l}} 0&{}\pi &{}0&{} \cdots &{}0\\ 0&{}0&{}\pi &{} \cdots &{}0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{}0&{}0&{} \cdots &{}{\pi \cdot \cos \left( {\pi \cdot k \cdot b} \right) }\\ \pi &{}0&{}0&{} \cdots &{}0 \end{array}} \right) \end{aligned}$$
(3)

The characteristic polynomial of Eq. (3) is defined by Eq. (4).

$$\begin{aligned} g\left( {{\lambda _t}} \right) = \lambda _t^N + {\left( { - \pi } \right) ^N} \cdot \cos \left( {\pi \cdot k \cdot b} \right) \end{aligned}$$
(4)

According to Eq. (4), we can derive the eigenvalues as Eq. (5).

$$\begin{aligned} {\lambda _t} = - \pi \cdot {e^{\frac{{i \cdot \pi \cdot \left( {{k \cdot b} + 1} \right) }}{N}}} \end{aligned}$$
(5)

where \({i^2} = - 1\).

It is clear that there must be eigenvalues with zero or positive real parts, which means that the fixed point X may be critically stable or unstable.

2.2.2 Non-degenerate analysis

In this section, we analyze the trajectories of our NMDCS system using the following lemmas. Afterwards, we prove that the NMDCS system is a non-degenerate chaotic system using the above lemmas.

Lemma 1

If \({x_{n,0}}\) follows the uniform distribution in the interval I, the probability density function of \({x_{n,1}} = f\left( {{x_{n,0}}} \right) = \sin \left( {\pi \cdot {x_{n,0}}} \right) \) can be derived as \(p\left( {{x_{n,1}}} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{\pi \sqrt{1 - x_{n,1}^2} }},\mathrm{{ }}if\mathrm{{ }}{x_{n,1}} \in I}\\ {0,\mathrm{{ }}others} \end{array}} \right. \), where \(n \in \left\{ {1,2, \ldots ,N} \right\} \).

Proof

Since \({x_{n,0}}\) follows the uniform distribution in the interval I, its probability density function is \(p\left( {{x_{n,0}}} \right) = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{2},\mathrm{{ }}if \mathrm{{ }}{x_{n,0}} \in I}\\ {0,\mathrm{{ }}others} \end{array}} \right. \). Divide the interval I into a series of subintervals \({I_l} = \left[ {\frac{{l - 1}}{2},\frac{l}{2}} \right) \), where \(l \in \left\{ { - 1,0,1,2} \right\} \). Let \(h\left( {{x_{n,1}}} \right) \) be the inverse function of \(f\left( {{x_{n,0}}} \right) \), whose expression is shown in Eq. (6).

$$\begin{aligned} h\left( {{x_{n,1}}} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{\arcsin \left( {{x_{n,1}}} \right) }}{\pi },\mathrm{{ }}if\mathrm{{ }}{x_{n,0}} \in {I_0} \cup {I_1}}\\ { - \frac{{\arcsin \left( {{x_{n,1}}} \right) }}{\pi } \mp 1,\mathrm{{ }}if\mathrm{{ }}{x_{n,0}} \in {I_{ - 1}} \cup {I_2}}\\ {0,\mathrm{{ }}others} \end{array}} \right. \end{aligned}$$
(6)

According to Eq. (6), the probability density function of \({x_{n,1}} = f\left( {{x_{n,0}}} \right) \) can be derived as Eq. (7).

$$\begin{aligned} \begin{aligned} p\left( {{x_{n,1}}} \right)&= \left\{ {\begin{array}{*{20}{l}} {p\left( {h\left( {{x_{n,1}}} \right) } \right) \cdot \left| {{h^\prime }\left( {{x_{n,1}}} \right) } \right| ,\mathrm{{ }}if\mathrm{{ }}{x_{n,1}} \in I}\\ {0,\mathrm{{ }}others} \end{array}} \right. \\&{= \left\{ \begin{array}{l} \sum \nolimits _{l = - 1,0} {\frac{1}{2} \cdot \left| {{{\left( { - 1} \right) }^l} \cdot \frac{1}{{\pi \sqrt{1 - x_{n,1}^2} }}} \right| },\mathrm{{ }}if\mathrm{{ }}{x_{n,1}} \in {I_{ - 1}} \cup {I_0}\\ \sum \nolimits _{l = 1,2} {\frac{1}{2} \cdot \left| {{{\left( { - 1} \right) }^{l - 1}} \cdot \frac{1}{{\pi \sqrt{1 - x_{n,1}^2} }}} \right| },\mathrm{{ }}if\mathrm{{ }}{x_{n,1}} \in {I_1} \cup {I_2}\\ 0,\mathrm{{ }}others \end{array} \right. }\\&= \left\{ {\begin{array}{*{20}{c}} {\frac{1}{{\pi \sqrt{1 - x_{n,1}^2} }},\mathrm{{ }}if\mathrm{{ }}{x_{n,1}} \in I}\\ {0,\mathrm{{ }}others} \end{array}} \right. \end{aligned} \end{aligned}$$
(7)

Lemma 1 is thus proved. \(\square \)

Lemma 2

If \({x_{n,0}}\) follows the uniform distribution in the interval I, the probability density function of \({x_{n,2}} = {f}\left( {{f}\left( {{x_{n,0}}} \right) } \right) = \sin \left( {\pi \cdot \sin \left( {\pi \cdot {x_{n,0}}} \right) } \right) \) can be derived as \(p\left( {{x_{n,2}}} \right) = \left\{ \begin{array}{*{20}{lll}} \frac{1}{{\pi \sqrt{1 - x_{n,2}^2} }} \cdot \sum \nolimits _{i = 0, 1}\\ {\frac{1}{{\sqrt{{\pi ^2} - {{\left( {\arcsin \left| {{x_{n,2}}} \right| - i \cdot \pi } \right) }^2}} }}} ,\mathrm{{ }}if\mathrm{{ }}{x_{n,2}} \in I\\ {0,\mathrm{{ }}others} \end{array} \right. \), where \(n \in \left\{ {1,2, \ldots ,N} \right\} \).

Proof

Divide the interval I into a series of subintervals \({I_l} = \left[ {\frac{{l - 1}}{2},\frac{l}{2}} \right) \), where \(l \in \left\{ { - 1,0,1,2} \right\} \). Let \(h\left( {{x_{n,2}}} \right) \) be the inverse function of \(f\left( {{x_{n,1}}} \right) \), whose expression is listed in Eq. (8).

$$\begin{aligned} \begin{aligned} h\left( {{x_{n,2}}} \right) = \left\{ {\begin{array}{*{20}{c}} {\frac{{\arcsin \left( {{x_{n,2}}} \right) }}{\pi },\mathrm{{ }}if\mathrm{{ }}{x_{n,1}} \in {I_0} \cup {I_1}}\\ { - \frac{{\arcsin \left( {{x_{n,2}}} \right) }}{\pi } \mp 1,\mathrm{{ }}if\mathrm{{ }}{x_{n,1}} \in {I_{ - 1}} \cup {I_2}}\\ {0,\mathrm{{ }}others} \end{array}} \right. \end{aligned} \end{aligned}$$
(8)

From Eq. (8), the probability density function of \({x_{n,2}} = f\left( {{x_{n,1}}} \right) \) can be derived as Eq. (9).

$$\begin{aligned} \begin{aligned} p\left( {{x_{n,2}}} \right)&= \left\{ \begin{array}{*{20}{c}} {p\left( {h\left( {{x_{n,2}}} \right) } \right) \cdot \left| {{h^\prime }\left( {{x_{n,2}}} \right) } \right| ,\mathrm{{ }}if\mathrm{{ }}{x_{n,2}} \in I}\\ {0,\mathrm{{ }}others} \end{array} \right. \\&= \left\{ \begin{array}{*{20}{llll}} \sum \nolimits _{l = - 1,0} \frac{1}{{\pi \sqrt{1 - x_{n,1}^2} }} \cdot \\ \left| {{{\left( { - 1} \right) }^l} \cdot \frac{1}{{\pi \sqrt{1 - x_{n,2}^2} }}} \right| ,\mathrm{{ }}if\mathrm{{ }}{x_{n,2}} \in {I_{ - 1}} \cup {I_0}\\ \sum \nolimits _{l = 1,2} \frac{1}{{\pi \sqrt{1 - x_{n,1}^2} }} \cdot \\ \left| {{{\left( { - 1} \right) }^{l - 1}} \cdot \frac{1}{{\pi \sqrt{1 - x_{n,2}^2} }}} \right| ,\mathrm{{ }}if\mathrm{{ }}{x_{n,2}} \in {I_1} \cup {I_2}\\ {0,\mathrm{{ }}others} \end{array} \right. \\&= \left\{ \begin{array}{*{20}{llll}} \frac{1}{{\pi \sqrt{1 - x_{n,2}^2} }} \cdot \sum \nolimits _{l = - 1,0}\\ {\frac{1}{{\sqrt{{\pi ^2} - {{\left( {\arcsin \left( {{x_{n,2}}} \right) - l \cdot \pi } \right) }^2}} }}},\mathrm{{ }}if\mathrm{{ }}{x_{n,2}} \in {I_{ - 1}} \cup {I_0}\\ \frac{1}{{\pi \sqrt{1 - x_{n,2}^2} }} \cdot \sum \nolimits _{l = 1,2}\\ {\frac{1}{{\sqrt{{\pi ^2} - {{\left( {\arcsin \left( {{x_{n,2}}} \right) - \left( {l - 1} \right) \cdot \pi } \right) }^2}} }}},\mathrm{{ }}if\mathrm{{ }}{x_{n,2}} \in {I_1} \cup {I_2}\\ {0,\mathrm{{ }}others} \end{array} \right. \\&= \left\{ {\begin{array}{*{20}{c}} {\frac{1}{{\pi \sqrt{1 - x_{n,2}^2} }} \cdot \sum \nolimits _{i = 01} {\frac{1}{{\sqrt{{\pi ^2} - {{\left( {\arcsin \left| {{x_{n,2}}} \right| - i \cdot \pi } \right) }^2}} }}},\mathrm{{ }}if\mathrm{{ }}{x_{n,2}} \in I}\\ {0,\mathrm{{ }}others} \end{array}} \right. \end{aligned} \end{aligned}$$
(9)

Lemma 2 is thus proved. \(\square \)

Theorem 1

The NMDCS system is a non-degenerate discrete chaotic system.

Proof

From Eq. (1), the Jacobian matrix of the NMDCS system at moment t is shown in Eq. (10).

$$\begin{aligned} {{\textbf {J}}_t} = \left( {\begin{array}{*{20}{c}} 0&{}{f^\prime \left( {{x_{2,t}}} \right) }&{}0&{} \cdots &{}0\\ 0&{}0&{}{f^\prime \left( {{x_{3,t}}} \right) }&{} \cdots &{}0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{}0&{}0&{} \cdots &{}{f^\prime \left( {{x_{N,t}}} \right) }\\ {f^\prime \left( {{x_{1,t}}} \right) }&{}0&{}0&{} \cdots &{}{1 - \cos \left( {\frac{{\pi \cdot {x_{N,t}}}}{a}} \right) } \end{array}} \right) \nonumber \\ \end{aligned}$$
(10)

Where \(f^\prime \left( {{x_{n,t}}} \right) = \pi \cdot \cos \left( {\pi \cdot {x_{n,t}}} \right) \) and \(n \in \left\{ {1,2, \ldots ,N} \right\} \). The characteristic polynomial of (10) can be derived as (11).

$$\begin{aligned}{} & {} g\left( {{\lambda _t}} \right) = \lambda _t^{N - 1} \cdot \left( {{\lambda _t} - 1 + \cos \left( {\frac{{\pi \cdot {x_{N,t}}}}{a}} \right) } \right) \nonumber \\{} & {} + {\left( { - \pi } \right) ^N} \cdot \prod \nolimits _{n = 1}^N {\cos \left( {\pi \cdot {x_{n,t}}} \right) } \end{aligned}$$
(11)
Fig. 2
figure 2

Lyapunov exponent spectrum of our discrete chaotic system

Full size image
Fig. 3
figure 3

Coexisting attractors of our discrete chaotic system

Full size image

As is shown in Sect. 2.1, it is clear that \(\left| a \right| > 3\). Thus, we can derive Eq. (12) from Eq. (11).

$$\begin{aligned} g\left( {{\lambda _t}} \right) \approx \lambda _t^N + {\left( { - \pi } \right) ^N} \cdot \prod \nolimits _{n = 1}^N {\cos \left( {\pi \cdot {x_{n,t}}} \right) } \end{aligned}$$
(12)

According to Eq. (12), we can derive the eigenvalues as Eq. (13).

$$\begin{aligned} \left| {{\lambda _{n,t}}} \right| = \left| {\pi \cdot \cos \left( {\pi \cdot {x_{n,t}}} \right) } \right| \end{aligned}$$
(13)

From Eq. (13) and Lemma 2, we can derive the LE of our NMDCS system as \(\left\{ {L{E_1}, \cdots ,L{E_n}, \cdots ,L{E_N}} \right\} \), where \(L{E_n}\) is calculated by Eq. (14).

$$\begin{aligned} \begin{aligned} L{E_n}&= \int _{ - 1}^1 {\ln \left| {{\lambda _{n,t}}} \right| \cdot p\left( {{x_{n,t}}} \right) d{x_{n,t}}} \\&\approx \int _{ - 1}^1 {\ln \left| {{\lambda _{n,2}}} \right| \cdot p\left( {{x_{n,2}}} \right) d{x_{n,2}}} \\&= 0.6672 \end{aligned} \end{aligned}$$
(14)

In conclusion, the LE of the NMDCS system are all 0.6672, indicating that our NMDCS system is a non-degenerate discrete chaotic system. \(\square \)

2.3 Simulation experiments of our discrete chaotic system

This section demonstrates that our NMDCS system shows excellent chaotic behavior from the aspects of LE, coexisting attractors, Poincaré section, sensitive dependence on initial conditions, and iterative efficiency. Our experiments were conducted on a Windows machine running on an Intel Core i5-6300HQ and 12 GB RAM.

2.3.1 Lyapunov exponent spectrum

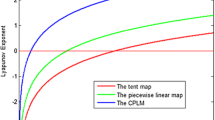
LE is always used to measure the rate of convergence or divergence of adjacent trajectories of a dynamical system. A positive LE means that the system stays in a chaotic state. If there are more than two positive LEs, the chaotic map becomes hyper-chaos and exhibits complex chaotic behavior in multiple dimensions. This section conducts simulation experiments to estimate the LE of the NMDCS, and the experimental results are shown in Fig. 2.

As is shown in Fig. 2, the number of positive LE of our NMDCS system is equal to its dimension, regardless of the selection of the system parameter a. Additionally, the LE values are all very close to the theoretical value of 0.6672 derived from Theorem 1. Therefore, the NMDCS system is a non-degenerate discrete chaotic system with stronger chaotic behavior than most of the existing chaotic systems, and is not prone to chaotic degradation during digitization.

Table 1 Efficiency comparison results
Full size table
Fig. 4
figure 4

Poincaré sections of our chaotic system

Full size image

2.3.2 Coexisting attractor analysis

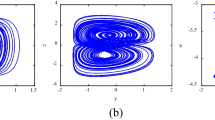
Due to the periodic properties of trigonometric functions, the position of the attractor of the NMDCS system depends on the initial state \({x_{N,0}}\), which means that our NMDCS system has coexisting attractors. This behavior is very interesting, and next we will draw the phase diagrams of the NMDCS system by selecting different \({x_{N,0}}\) to understand this phenomenon more intuitively. The simulation results are listed in Fig. 3.

From Fig. 3, it is obvious that the coexisting attractors of the NMDCS system are all square or cube, regardless of the initial state, which means that these coexisting attractors are all homogeneous. This is because although the initial states between different coexisting attractors are completely different, 2a and 4a are the period of the nonlinear term \(\sin \left( {\frac{{\pi \cdot {x_{N,t}}}}{a}} \right) \) in Eq. (1) respectively, so there will be no significant difference in the shape of the coexisting attractors.

2.3.3 Efficiency analysis

Efficiency is a crucial factor in assessing the practicality of chaotic systems. This section examines the effectiveness of chaotic systems through the symbol transfer rate. During the analysis, each chaotic system generated 320 Mbit of chaotic sequences. Table 1 shows the results of the efficiency analysis.

Fig. 5
figure 5

Initial state sensitivity of our chaotic system

Full size image
Fig. 6
figure 6

Block diagram of IEA-NMDCS

Full size image

As demonstrated in Table 1, the efficiency of our NMDCS exceeds that of the chaotic systems in [18, 34, 35]. This is because chaotic systems in [18, 34, 35] necessitate the utilization of time-consuming numerical analysis techniques, such as the Runge–Kutta method, throughout the iterative process. Although the efficiency of the NMDCS may not be on par with the chaotic systems described in [16, 24] due to the use of slightly time-consuming trigonometric function operations, it still achieves a symbol transmission rate of 53.2595 Mbps. Therefore, we can conclude that our NMDCS exhibits a commendable level of efficiency.

2.3.4 Poincaré section analysis

The Poincaré section is always used to analyze the dynamical behavior of multivariate autonomous systems. If there are only a few points on the Poincaré section, the motion is periodic. Otherwise, if there is a closed curve on the Poincaré section, the motion is determined to be quasi-periodic. When there are patches of dense points on the Poincaré section, the motion is assumed to be chaotic. This section sets various system parameters, and the Poincare section of our NMDCS system is shown in Fig. 4.

As is shown in Fig. 4, it can be seen that although the system parameters of the NMDCS are different, there are patches of dense points distributed on each Poincaré section. The above results further indicate that our NMDCS is chaotic.

2.3.5 Sensitivity to initial conditions

Initial condition sensitivity is the most essential property of chaotic systems, reflecting the inherent randomness of chaotic systems. Initial condition sensitivity refers to the fact that tiny differences between the initial states of a chaotic system will result in completely different trajectories, indicating that the long-term motion state of a chaotic system is unpredictable. In this section, different system parameters are selected to test the initial condition sensitivity of our NMDCS system, and the results are shown in Fig. 5.

As is shown in Fig. 5, it is obvious that slight changes between the initial values will cause our chaotic system to exhibit completely different trajectories. Therefore, our NMDCS system is highly sensitive to initial conditions and is particularly suitable for the design of cryptographic algorithms.

3 Image encryption algorithm based on non-degenerate multi-stable discrete chaos

Since our NMDCS system is not susceptible to chaotic degradation and has an infinite number of coexisting attractors, the chaotic system is used to design an efficient and secure image encryption algorithm.

3.1 Overall flow of the algorithm

Our image encryption algorithm based on non-degenerate multi-stable discrete chaos (IEA-NMDCS) mainly involves four steps of key derivation, pixel confusion, adaptive zigzag transformation, and cross-plane permutation, and its block diagram is shown in Fig. 6.

Fig. 7
figure 7

Schematic diagram of the adaptive zigzag transformation

Full size image

3.1.1 Key derivation

Our key derivation algorithm takes the 144-bit master key \(MK = M{K_1}||\) \(M{K_2}||M{K_3}\) as input to generate the derived keys \(S{K_1},S{K_2}\) for subsequent encryption and decryption operations, where the lengths of \(M{K_1},M{K_2},M{K_3}\) are all 48-bit, and || represents the link symbol. The procedure of the algorithm is shown in Algorithm 1.

  1. (1)

    It calculates the chaotic initial state \(IV = {\left\{ {I{V_i}} \right\} _{i \in \left\{ {1,2,3} \right\} }}\), where \(I{V_i} = \frac{{M{K_i}}}{{{2^{47}}}} - 1\).

  2. (2)

    It generates a chaotic sequence Q of size \(R \times C \times 3\) by iterating NMDCS according to IV.

  3. (3)

    It quantifies the chaotic sequence Q using Eq. (15).

    $$\begin{aligned} DQ = \mathrm{{floor}}\left( {Q \times {{10}^{15}}} \right) \end{aligned}$$
    (15)
  4. (4)

    It computes the confusion key \(S{K_1} = \left\{ {S{K_1}\left( {r,c,d} \right) } \right\} _{r \in \left\{ {1, \cdots ,R} \right\} ,c \in \left\{ {1, \cdots ,C} \right\} ,d \in \left\{ {1,2,3} \right\} }\), where \(S{K_1}\left( {r,c,d} \right) \) is computed using Eq. (16).

    $$\begin{aligned} S{K_1}\left( {r,c,d} \right) = \bmod \left( {DQ\left( {r,c,d} \right) ,256} \right) \end{aligned}$$
    (16)
  5. (5)

    It computes the cross-plane key \(S{K_2} = {\left\{ {S{K_2}\left( {r,c,d} \right) } \right\} _{r \in \left\{ {1, \cdots ,R} \right\} ,c \in \left\{ {1, \cdots ,C} \right\} ,d \in \left\{ {1,2} \right\} }}\), where \(S{K_2}\left( {r,c,d} \right) \) is computed using Eq. (17).

    $$\begin{aligned} S{K_2}\left( {r,c,d} \right) = \bmod \left( {DQ\left( {r,c,d} \right) ,D - d + 1} \right) + 1\nonumber \\ \end{aligned}$$
    (17)
Algorithm 1
figure a

Key derivation

Full size image
Fig. 8
figure 8

Schematic diagram of the cross-plane permutation

Full size image

3.1.2 Pixel confusion

Confusion is a nonlinear transformation that intricately disrupts the correlation between plain images and cipher images as well as between key and cipher images by changing pixels. In this section, the S-Box in [9] is used as the nonlinear confusion component to enhance the probabilistic statistical analysis resistance of our IEA-NMDCS algorithm, and the specific process is shown in Algorithm 2.

Algorithm 2
figure b

Pixel confusion

Full size image

3.1.3 Adaptive zigzag transformation

The correlation between neighboring pixels of a plain image can be effectively eliminated using the zigzag transformation. However, the initial position of the traditional zigzag transformation remains unaffected by the plain images, so minor alterations in a plain image will not transmit to the whole cipher image, resulting in its limited diffusion capability. To address the above problem, this section uses the mean value of the pixels and our NMDCS system to design a novel adaptive zigzag transformation that can improve the diffusion capability of our IEA-NMDCS algorithm while eliminating the correlation of neighboring pixels. The details are shown in Fig. 7.

  1. (1)

    It calculates the average value of the pixels in each plane of the cipher image and records them as \({\left\{ {{e_d}} \right\} _{d \in \left\{ {1,2,3} \right\} }}\).

  2. (2)

    It calculates the chaotic initial state \({\varvec{x}^0} = {\left\{ {x_d^0} \right\} _{d \in \left\{ {1,2,3} \right\} }}\) by Eq. (18).

    $$\begin{aligned} x_d^0 = \frac{{{e_d}}}{{128}} - 1 \end{aligned}$$
    (18)
  3. (3)

    It generates a chaotic sequence of length \(T + 2\) using the NMDCS system, and records the last two chaotic states as \({\varvec{x}^{T + 1}} = {\left\{ {x_d^{T + 1}} \right\} _{d \in \left\{ {1,2,3} \right\} }}\), and \({\varvec{x}^{T + 2}} = {\left\{ {x_d^{T + 2}} \right\} _{d \in \left\{ {1,2,3} \right\} }}\).

  4. (4)

    It calculates the initial coordinates of the rows and columns using Eqs. (19) and (20), and records them as \({\varvec{r}^0} = {\left\{ {r_d^0} \right\} _{d \in \left\{ {1,2,3} \right\} }}\) and \({\varvec{c}^0} = {\left\{ {c_d^0} \right\} _{d \in \left\{ {1,2,3} \right\} }}\) respectively.

    $$\begin{aligned} r_d^0 = mod\left( {floor\left( {x_d^{T + 1} \times {{10}^{15}}} \right) ,R} \right) + 1 \end{aligned}$$
    (19)
    $$\begin{aligned} c_d^0 = mod\left( {floor\left( {x_d^{T + 2} \times {{10}^{15}}} \right) ,C} \right) + 1 \end{aligned}$$
    (20)
  5. (5)

    It performs a zigzag transformation on the cipher image starting at \({\varvec{r}^0} = {\left\{ {r_d^0} \right\} _{d \in \left\{ {1,2,3} \right\} }}\) and \({\varvec{c}^0} = {\left\{ {c_d^0} \right\} _{d \in \left\{ {1,2,3} \right\} }}\) respectively.

3.1.4 Cross-plane permutation

Due to color images consisting of three planes of red, green, and blue, the cross-plane permutation algorithm must be developed to remove the correlation of pixels across different planes. Our IEA-NMDCS algorithm uses the cross-plane permutation key and the shuffling algorithm to blur the pixels between different planes of the image. The specific process is shown in Fig. 8 and Algorithm 3.

Algorithm 3
figure c

Cross-plane permutation

Full size image

3.2 Security and efficiency analysis

This section evaluates the performance of our IEA-NMDCS algorithm from the following aspects. The test images are all taken from the USC-SIPI database and the CVG-UGR database.

3.2.1 Key space analysis

Key space is an important indicator reflecting the resistance of encryption algorithms to brute force attacks. The larger the key space, the more difficult it is to obtain the correct key through brute forces. Typically, a key space of at least \(2 ^{100}\) possible secret keys is expected [36]. Since our IEA-NMDCS algorithm uses a 144-bit master key to generate derived subkeys, its key space is much larger than \(2^{100}\). The above results show that our IEA-NMDCS algorithm is sufficient to withstand brute force attacks.

3.2.2 NIST randomness test

The National Institute of Standards and Technology (NIST) provides a series of guidelines for statistical tests known as the NIST Test Suite 800-22. In this section, the randomness of the cipher images obtained using the IEA-NMDCS algorithm has been evaluated through the application of this test suite. The test results are shown in Table 2.

Table 2 NIST randomness test results
Full size table

It can be clearly seen from Table 2 that the P-value and proportions are all greater than 0.01 and 0.96 respectively. Therefore, the cipher images obtained using the IEA-NMDCS algorithm exhibit excellent randomness.

3.2.3 Histogram analysis

The histogram of an image can intuitively reflect the distribution of image pixels. In general, the histogram of a plaint image does not follow the uniform distribution, so it is susceptible to probabilistic statistical analysis. For an optimal encryption algorithm, the cipher images encrypted using the algorithm ought to conform to the uniform distribution. Figure 9 displays the histogram test results for the plain images and their cipher images encrypted with the IEA-NMDCS algorithm.

Fig. 9
figure 9

Histogram test results of the IEA-NMDCS algorithm

Full size image

As can be seen from Fig. 9, the histogram of the plaint image exhibits an uneven distribution, whereas the histogram of its cipher image is uniformly distributed, indicating that the cipher image does not leak any statistical information from the plain image.

To further demonstrate that the IEA-NMDCS algorithm can effectively withstand statistical analysis, we employ the chi-square test and the variance analysis to verify the uniformity of the histogram of the cipher images. The calculation methods for the chi-square test and the variance analysis are shown in Eq. (21) and [37], respectively.

$$\begin{aligned} {\chi ^2} = \sum \nolimits _{i = 1}^{256} {\frac{{{{\left( {{\eta _i} - \mu } \right) }^2}}}{\mu }} \end{aligned}$$
(21)

where \({\eta _i}\) and \(\mu \) represent the number of observations and the expected number of each pixel in the image, respectively. We set a significance level \(\alpha = 0.05\), and determine the following hypotheses using the chi-square test and the variance analysis. The analysis results are listed in Table 3.

\(H_0\): The cipher images encrypted using the IEA-NMDCS algorithm are uniformly distributed.

\(H_1\): The cipher images encrypted using the IEA-NMDCS algorithm are not uniformly distributed.

Table 3 Histogram analysis results
Full size table

From Table 3, the Chi-square test values for the cipher images encrypted with the IEA-NMDCS algorithm are all less than \(\chi _{0.05}^2\left( {255} \right) = 293.2478\). In addition, the histogram variance values of the \(512 \times 512 \times 3\) and \(256 \times 256 \times 3\) cipher images are approximately 3000 and 800, respectively. The above results indicate that the \(H_0\) assumption is correct. In conclusion, the cipher images generated by the IEA-NMDCS algorithm are uniformly distributed, so they can effectively resist statistical analysis.

3.2.4 Key sensitivity analysis

Key sensitivity refers to the fact that even minor alterations in the master key will produce an entirely different encryption or decryption result. A secure encryption algorithm must be sensitive to the master key. To test the key sensitivity of the IEA-NMDCS algorithm, we first randomly chose a master key \({K_1} = \mathrm{{c1e}}\underline{{\textbf {1}}} \mathrm{{bda054ebc9f6accfd2f7c5ca9783618}}\underline{{\textbf {2}}}\) of size 144-bit, and obtain the keys \({K_2} = \mathrm{{c1e1bda054ebc9f6a}} \mathrm{{ccfd2f7c5ca9783618}}\underline{{\textbf {0}}}\) and \({K_3} = \mathrm{{c1e}}\underline{{\textbf {0}}} \mathrm{{bda054ebc9f6acc}}\mathrm{{fd2f7c5ca97836182}}\) by randomly changing 1-bit of \(K_1\). Then,we encrypted and decrypted the images using \(K_1\), \(K_2\), and \(K_3\) respectively. The specific results are shown in Figs. 10 and 11.

Fig. 10
figure 10

Key sensitivity analysis during encryption

Full size image
Fig. 11
figure 11

Key sensitivity analysis during decryption

Full size image

Figure 10 demonstrates that although the plain images have specific statistical features, the cipher images encrypted with the IEA-NMDCS algorithm are similar to the random noise, and they are completely different when using different keys. Therefore, our IEA-NMDCS algorithm is sensitive to the master key during the encryption process.

Figure 11 clearly illustrates that only decrypting the cipher image with the correct key will obtain the corresponding plain image, while the images decrypted by incorrect keys are similar to random noises. Furthermore, the images decrypted by different wrong keys are completely different. Therefore, our IEA-NMDCS algorithm is responsive to the master key utilized in the decryption procedure.

3.2.5 Sensitivity analysis for plain images

Plaintext sensitivity refers to the capability of algorithms to withstand chosen plaintext attacks and differential attacks. Researchers commonly use the pixel change rate (NPCR) and normalized average change intensity (UACI) to assess the intensity of plaintext sensitivity. The calculation methods for these assessments are thoroughly described in [12]. The NPCR and UACI are anticipated to be 99.6094% and 33.4635% respectively. In addition, Wu et al. [38] have highlighted the necessity for NPCR values to surpass a defined threshold \({N_\alpha }\) and for UACI values to fall within the interval \(\left( {U_\alpha ^ -,U_\alpha ^ + } \right) \), where \({N_\alpha } = 99.5693\% \) and \(\left( {U_\alpha ^ -,U_\alpha ^ + } \right) = \left( {33.2824\%,33.6447\% } \right) \) for an image of size \(256 \times 256\), and \({N_\alpha } = 99.5893\% \) and \(\left( {U_\alpha ^ -,U_\alpha ^ + } \right) = \left( {33.3730\%,33.5541\% } \right) \) for an image of size \(512 \times 512\). The NPCR and UACI scores for the cipher images encrypted using the IEA-NMDCS algorithm are displayed in Tables 4 and 5 respectively.

As is evidenced by Tables 4 and 5, the NPCR and UACI scores for the cipher images encrypted using the IEA-NMDCS algorithm are all within the acceptable intervals, with values very close to 99.6094% and 33.4636% respectively. To further demonstrate the excellent plaintext sensitivity of our IEA-NMDCS algorithm, we use the ‘Lena’ as the plain image, and encrypt it using different image encryption algorithms. The NPCR and UACI comparison results can be found in Tables 6 and 7 respectively.

Table 4 NPCR scores of cipher images
Full size table
Table 5 UACI scores of cipher images
Full size table
Table 6 Comparison results of NPCR scores
Full size table
Table 7 Comparison results of UACI scores
Full size table

From Tables 6 and 7, the NPCR and UACI scores for the cipher images encrypted by different image algorithms are all within acceptable intervals, and the difference between them is very small, so they all achieve excellent plaintext sensitivity. However, the derived keys of the image encryption algorithms in [40, 41] associated with plain images, and how to securely transmit the information has become a critical security bottleneck that constrains the application of such image encryption algorithms. Therefore, it can be deduced that our IEA-NMDCS algorithm is capable of withstanding chosen plaintext attacks and differential attacks.

3.2.6 Relevance analysis

Generally, the adjacent pixels in a plain image are highly correlated with each other. An excellent image encryption algorithm should eliminate the correlation between adjacent pixels through substitution and permutation to enhance the pseudo-randomness of the cipher images. Consequently, the correlation between adjacent pixels becomes an essential indicator in the assessment of an algorithm’s security. The correlation coefficient R is calculated by Eq. (22).

$$\begin{aligned} \left\{ \begin{array}{l} E\left( X \right) = \frac{{\sum \nolimits _{i = 1}^n {{x_i}} }}{n}\\ D\left( X \right) = \frac{{\sum \nolimits _{i = 1}^n {{{\left( {{x_i} - E\left( X \right) } \right) }^2}} }}{n}\\ {\textrm{cov}} \left( {X,Y} \right) = \frac{{\sum \nolimits _{i = 1}^n {\left( {{x_i} - E\left( X \right) } \right) \left( {{Y_i} - E\left( Y \right) } \right) } }}{n}\\ R\left( {X,Y} \right) = \frac{{{\textrm{cov}} \left( {X,Y} \right) }}{{\sqrt{D\left( X \right) \times D\left( Y \right) } }} \end{array} \right. \end{aligned}$$
(22)

where X denotes the set consisting of image pixels, Y denotes the set consisting of adjacent pixels of pixels in X, and n is the number of pixels. The lower the correlation coefficient, the lower the correlation between adjacent pixels. In this section, we randomly select 12,000 pairs of adjacent pixels to calculate the correlation coefficients in the horizontal, vertical, and diagonal directions. The details are displayed in Fig. 12 and Table 8.

Fig. 12
figure 12

Diagram of correlation coefficients

Full size image
Table 8 Correlation coefficients of images
Full size table

As can be seen from Fig. 12 and Table 8, it is clear that the adjacent pixels of the plain images exhibit a high level of correlation, whereas the adjacent pixels of their cipher images display very low correlation. In addition, the correlation between the adjacent pixels of the cipher images encrypted using the IEA-NMDCS algorithm is very close to the ideal value of 0. To further prove that our algorithm can withstand statistical attacks, we performed correlation coefficient comparison tests for different image encryption algorithms. The comparison results are shown in Table 9.

Table 9 Correlation coefficient comparison results
Full size table
Table 10 Information entropy values of cipher images
Full size table

As illustrated in Table 9, the correlation coefficients of the cipher image encrypted with our IEA-NMDCS algorithm are closer to 0 than those of existing image encryption algorithms. The aforementioned results demonstrate that our image encryption algorithm is capable of effectively reducing the correlation among the adjacent pixels of images.

3.2.7 Information entropy

In this section, we evaluate the pseudo-randomness of the cipher images using information entropy. Each pixel of an image contains 8 bits of information, so the theoretical maximum value of its information entropy is 8. Table 10 displays the information entropy values of the plain images and their cipher images encrypted using the IEA-NMDCS algorithm.

From Table 10, it can be seen that although the information entropy of the plain images is far less than the ideal value of 8, the information entropy of the cipher images encrypted with the IEA-NMDCS algorithm is very close to 8, indicating that the cipher images are uniformly distributed and have excellent pseudo-randomness. To further evaluate the encryption effect of the IEA-NMDCS algorithm, we encrypted the Lena image using the existing image encryption algorithms as well as our algorithm, and the information entropy values of the cipher images are listed in Table 11.

From Table 11, the information entropy values of the cipher image encrypted with our IEA-NMDCS algorithm are 7.9993, 7.9994, and 7.9994 respectively, which are better than those of existing image encryption algorithms except [12, 41]. Thus, it can be concluded that our IEA-NMDCS algorithm can generate the cipher images with a uniform distribution that is highly resistant to probabilistic statistical analysis.

3.2.8 Efficiency analysis

Efficiency is a crucial factor in evaluating the practicality of image encryption algorithms. Because decryption is the reverse process of encryption, it has the same algorithmic efficiency as encryption, this section only lists the comparison results of the encryption efficiency between the IEA-NMDCS algorithm and existing image encryption algorithms in Table 12.

From Table 12, it can be seen that the IEA-NMDCS algorithm is more efficient in encryption than the existing image encryption algorithms. This is mainly because our IEA-NMDCS algorithm does not require time-consuming numerical analysis methods to generate pseudo-chaotic sequences. Furthermore, it possesses efficient substitution and permutation operations.

Table 11 Information entropy comparison results
Full size table
Table 12 Efficiency comparison results of image encryption algorithms
Full size table

4 Conclusion

This paper first designs a non-degenerate multi-stable discrete chaotic system that can be demonstrated to exhibit the properties of multi-stability and non-degeneracy through rigorous theoretical analysis. Simulation experiments demonstrate that our discrete chaotic system exhibits strong chaotic behavior and high efficiency in terms of Lyapunov exponents, coexisting attractors, Poincaré sections, sensitivity to initial conditions, and iterative efficiency. Then, an efficient image encryption algorithm is proposed by combining the aforementioned discrete chaotic system and an adaptive zigzag transformation method. Simulation experiments show that our image encryption algorithm offers superior performance in terms of encryption and decryption efficiency, as well as impressive security properties, including histogram, key sensitivity, plaintext sensitivity, correlation between adjacent pixels, and information entropy. The proposed image encryption algorithm provides a robust foundation for the confidentiality protection of sensitive images in key industries, including government agencies, healthcare systems and financial institutions. In the future, we will design chaotic image compression and encryption algorithms based on the compressed perception theory, which can reduce the storage and transmission costs of sensitive images as well as ensure their confidentiality.