A novel S-box generator using Frobenius automorphism and its applications in image encryption

Abstract

The goal of cryptography is to provide algorithms that safeguard sensitive information sent via unprotected networks. These methods encrypt the information, making it unintelligible even if adversaries manage to get it. The substitution box (S-box) structure is the most significant and nonlinear component of the Advanced Encryption Standard (AES) algorithm. In the algorithm, the S-box supplies the confusion or mixing process. A highly non-linearity-valued S-box significantly boosts defenses against a range of threats. Unfortunately, the achievable encryption throughput is constrained by the computationally costly nature of creating S-boxes. This emphasizes the necessity of creating new S-box generators with the best strength and minimum computing requirements to provide optimal security. We presented an efficient approach that uses the composition of Frobenius automorphism and Mobius transformation of $GF(2^{8})$. In this way, we got two highly nonlinear permutations that can produce millions of S-boxes with very strong cryptographic strength. The dynamic behavior of the proposed generator is analyzed by clarifying the requirements for generating distinct S-boxes and ensuring that the produced S-boxes have a uniform probability distribution. Our generator can produce S-boxes with robust cryptographic features, according to a thorough security study. Our novel generation method for building S-boxes efficiently combines the benefits of both algebraic modeling and chaotic mapping, providing a solid basis for building robust S-boxes. Our approach can guarantee that the produced S-boxes have strong variety and outstanding comprehensive performance by using the ergodicity of the chaotic system. Additionally, the experimental findings presented in this study validate that the dynamic S-boxes generated by our technique not only satisfy the criteria for creating encryption methods but also provide enhanced security for picture encryption. Furthermore, our approach generates S-boxes with good efficiency. Our technique has a wide range of possible applications in cryptography, including the creation of dynamic S-boxes for encryption algorithms and high-performance S-boxes for image security. In light of current security risks and computing demands, our theoretical and computational evaluations indicate that our S-box generator is a good contender for real-world applications.

1 Introduction

The field of cryptology encompasses the study of codes, which is divided into two main branches: Cryptography and Cryptanalysis. Cryptography concerns itself with developing encryption algorithms, whereas Cryptanalysis focuses on breaking these algorithms. The two main sub-fields of cryptography are symmetric and asymmetric cryptography. The former explores block ciphers and stream ciphers whereas the latter, also known as public key cryptography, encrypts and decrypts communications using a pair of mathematically linked keys, one public and one private, to provide a secure method of exchanging information over an insecure network. Block ciphers operate on fixed-length groups of blocks and transform them into ciphertext. The size of a block varies according to the specific cipher being used. Block sizes commonly used are 64 bits, 128 bits, or 256 bits. A block cipher makes use of a secret key to encrypt the input. The key is utilized to generate a sequence of sub-keys that are applied to the plaintext blocks in a series of iterations or rounds. Each round involves multiple operations that transform the plaintext block into ciphertext. Nowadays, various contemporary cryptosystems are in use, which are data encryption standard (DES) [1], international data encryption algorithm (IDEA) [2], and advanced encryption standard (AES) [3]. One of the primary advantages of block ciphers is their speed and efficiency, making them ideal for use in applications that require fast encryption and decryption of large amounts of data. Yet, they are vulnerable to specific assault types, such as well-known plaintext assaults, which if the attacker has access to both the decrypted text and the encrypted text, can jeopardize the security of the cipher. Therefore the development of strong and secure block ciphers is an ongoing area of research in the field of cryptology. A Substitution-box is a nonlinear constituent of a block cipher and its effectiveness determines the overall strength of the cipher. A well-designed S-box ought to have strong nonlinearity, resistance to differential and linear cryptanalysis, confusion, diffusion, bijectivity, algebraic complexity, and the absence of fixed points. As data traffic continues to grow, secure data transmission is becoming increasingly crucial, which is why the development of a robust S-box is the top priority of researchers.

1.1 Literature review

A range of methods, including the use of algebraic structures such as Galois fields, Galois rings, projective general and special linear groups, elliptic curves, coset diagrams, and Cayley graphs are being used to create effective S-boxes. The researchers used only primitive irreducible polynomials for the generation of the Galois field and then employed any bijective map for designing an S-box. The most used polynomial is $p(x)=x^{8}+x^{4}+x^{3}+x^{2}+1$. There are 16 primitive and 14 non-primitive irreducible polynomials of degree 8 over $\mathbb {Z}_{2}$ which can be used to design an S-box. [4] proposed an image encryption scheme using S-boxes based on Mobius transformation. [5] designed a novel scheme of image encryption using Mobius transformation on $GF(2^{8})$ and chaos. [6] used a novel irreducible polynomial to generate a robust S-box and used it to encrypt medical images. The authors used Mobius transformation to design a bijective S-box. A new S-box was proposed by [7] using I-Ching operators and the findings demonstrate that the S-box is well-suited for cryptography. A new S-box was proposed by [8] using cubic fractional transformation of the prime field to create a strong S-box. They used the composition of cubic polynomial and affine inversion map of $\mathbb {F}_{257}$. [9] examined the impact of nonlinearity on their findings by altering the basic irreducible polynomial that generates elements of the Galois field. They discovered that by selecting a specific irreducible polynomial could improve the effectiveness of S-boxes, developed based on the algebraic structure of the $GF(p^{n})$. Unfortunately, it was determined that their suggested S-box was non-bijective. A new design was proposed by [10] by employing a direct product of cyclic groups and the Galois field to formulate a robust S-box. They used a highly nonlinear inversion map of the Galois field rather than a fractional transformation. [11] designed a novel S-box using a chaotic map. They also introduced a technique that can adaptively enhance the probability of differential approximation for the S-box. A new approach was employed by [12] that uses coset diagrams to show how $PSL(2,\mathbb {Z})$ acts on the projective lines of $GF(2^{8})$. The Fibonacci sequence was additionally used by the authors to choose the coset diagram’s vertex positions. [13] describes a method for creating a useful S-box that combines the use of a logistic map with bacterial foraging optimization. [14] outlines a new algorithm that includes the composing of an inversion function with the action of the $S_{8}$ on the $GF(2^{8})$. It was shown that the resulting S-box is highly nonlinear and bijective. A relatively new approach based on 2-D Arnold’s Cat map was employed by [15] to generate dynamic S-boxes. The scheme produced efficient and nonlinear S-boxes but it does not provide any guarantee of bijectivity for every S-box. [16] developed a new chaotic system to formulate S-boxes, but the average nonlinearity of the proposed scheme was 107. A new chaotic sine map was designed by [17] to generate a highly nonlinear S-box. The author used an optimization model to enhance the nonlinearity of the S-box, but still, the average nonlinearity of the scheme was 110.25. An optimized S-box generator was designed by [18] based on elliptic curves with nonlinearity in the range 95–106. [19] introduced a new approach to designing robust S-box based on linear fractional transformation and a multi-layer perceptron architecture. They introduced a novel approach to enhance the nonlinearity of the initial S-box. A new approach based on a 2D hyperchaotic map was introduced by [20] to design S-boxes. They used affine transformations and boolean functions to design an S-box and then three possible weaknesses were removed by cryptanalyzing the dynamic approach. There are also existing schemes in literature that describe the techniques for safe storage, privacy, and integrity of data in cloud platforms ([21,22,23,24,25,26,27]).

The methods and techniques for building S-boxes that are described in the literature are either difficult and repetitive, or they are practical for static S-boxes. Due to their inherent flaws, static S-boxes may compromise the security of the cipher. Static S-boxes might aid an attacker in deciphering the intercepted ciphertext using cryptanalysis. Furthermore, the algorithms that create dynamic and key-dependent S-boxes are less effective and confusing. These methods also do not generate a large number of S-boxes with nonlinearity 112 and 4 differential uniformity. So, there is a continuous need for simple, efficient methods that can produce millions of S-boxes with nonlinearity 112 and differential uniformity 4.

1.2 Motivations and contributions

In this study, we have presented an efficient approach to generate a large number of S-boxes using the composition of an automorphism of a finite field of order 256 and a linear fractional transformation. The S-box created in this way has a high level of security and closely resembles the ideal values specified by the conventional S-box. The security strength of the proposed S-box is thoroughly tested and compared with other S-boxes, confirming its high level of security. We explore the complex world of finite fields, investigate the mathematics underlying Mobius transformations, and examine the characteristics that set apart the S-boxes produced by various classes of polynomials. The motivations of the proposed scheme are as follows;

• 1. Assessing the higher degree polynomials for generation of S-boxes.

• 2. Finding new nonlinear bijections of the Galois field with the lowest possible differential uniformity.

• 3. Proposing S-box generator scheme that can produce optimal S-boxes of high nonlinearity.

• 4. Analyzing the chaotic maps for generation of S-boxes.

The following are the contributions of said scheme;

• 1. We introduced another 4 differential uniformity permutation of $GF(2^{8})$ by composing Frobenius automorphism and Mobius transformation.

• 2. Every S-box generated by this scheme has nonlinearity 112.

• 3. This scheme can produce 33553920 S-boxes with fixed irreducible polynomial and thus $30\times 33553920$ total S-boxes.

• 4. A robust dynamic S-box generator is designed by modifying the control parameters in the generation formula using the chaotic logistic map. The suggested approach may effectively guarantee dynamic S-box diversity by exploiting the chaotic map’s complexity and ergodicity.

• 5. For a fixed irreducible polynomial and fixed parameters of Mobius transformation, we can construct similar nonlinear permutations that generate optimal S-boxes of the same strength.

1.3 Structure of the article

The rest of the article is divided into seven sections. Section 2 provides an overview of the basic definition related to the Galois field and a list of irreducible polynomials. The algorithm for creating S-boxes is described in Sect. 3. The proposed S-boxes are analyzed in Sect. 4 for nonlinearity, strict avalanche criteria (SAC), bit independence criteria (BIC), probability of linear approximation (LP), probability of differential approximation (DP), fixed point analysis, and algebraic degree and compared to other S-boxes that are currently in use. Section 5 explains the algorithm of image encryption that employs the proposed S-box and provides the results of the majority logic criteria (MLC). We compared the results of our scheme in Sect. 6. Finally, Sect. 7 presents the conclusion of the study.

2 Preliminaries

In this section, we will present some basic definitions related to the Galois field and a list of all irreducible polynomials of degree 8.

2.1 Ideal

A non-empty subset I of a ring R is called an ideal of R if for every $a\in R, \forall h,k \in I, h-k, ah,ha\in I$.

2.2 Irreducible polynomial

If $(\mathbb {F},+,.)$ is a field then a polynomial $p(x) \in \mathbb {F}[x]$ is called irreducible in $\mathbb {F}[x]$ if whenever $p(x)=q(x)r(x)$ for some $q(x), r(x) \in \mathbb {F}[x]$ then either q(x) or r(x) is a constant polynomial.

2.3 Maximal ideal

Let M be an ideal of R and $M \ne R$ then M is called maximal if no proper ideal of R contains M.

2.4 Galois field

For a prime number p and for an irreducible polynomial f(x) of degree m in $\mathbb {Z}_{p}[x]$ the quotient ring $\dfrac{\mathbb {Z}_{p}[x]}{<f(x)>}=\{\sum _{k=0}^{m-1} a_{k}t^{k} | a_{k}\in \mathbb {Z}_{p} \ \ \forall \ 0\le k\le m-1 \}$ is a finite field of order $p^{m}$ called Galois field and denoted by $GF(p^{m})$, where t is a particular root of f(x).

2.5 Primitive irreducible polynomial

A polynomial f(x) of degree m over $\mathbb {Z}_{p}[x]$ is called primitive if x is the generator of cyclic group $(GF(p^{m}))^{*}$ otherwise f(x) is called non-primitive. The following are primitive irreducible polynomials of degree 8 over $\mathbb {Z}_{2}[x]$;

• 1. $y^{8}+y^{4}+y^{3}+y^{2}+1 \ (285)$

• 2. $y^{8}+y^{5}+y^{3}+y+1 \ (299)$

• 3. $y^{8}+y^{5}+y^{3}+y^{2}+1 \ (301)$

• 4. $y^{8}+y^{6}+y^{3}+y^{2}+1 \ (333)$

• 5. $y^{8}+y^{6}+y^{4}+y^{3}+y^{2}+y+1 \ (351)$

• 6. $y^{8}+y^{6}+y^{5}+y+1 \ ( 355)$

• 7. $y^{8}+y^{6}+y^{5}+y^{2}+1 \ (357)$

• 8. $y^{8}+y^{6}+y^{5}+y^{3}+1 \ (361)$

• 9. $y^{8}+y^{6}+y^{5}+y^{4}+1 \ (369)$

• 10. $y^{8}+y^{7}+y^{2}+y+1 \ (391)$

• 11. $y^{8}+y^{7}+y^{3}+y^{2}+1 \ (397)$

• 12. $y^{8}+y^{7}+y^{5}+y^{3}+1 \ (425)$

• 13. $y^{8}+y^{7}+y^{6}+y^{5}+y^{2}+y+1 \ (487)$

• 14. $y^{8}+y^{7}+y^{6}+y^{3}+y^{2}+y+1 (463)$

• 15. $y^{8}+y^{7}+y^{6}+y^{5}+y^{4}+y^{2}+1 (501)$

• 16. $y^{8}+y^{7}+y^{6}+y+1 \ (451)$

while the non-primitive irreducible polynomials are

• 1. $y^{8}+y^{4}+y^{3}+y+1 \ (283)$

• 2. $y^{8}+y^{7}+y^{6}+y^{5}+y^{4}+y+1 \ (499)$

• 3. $y^{8}+y^{5}+y^{4}+y^{3}+1 \ (313)$

• 4. $y^{8}+y^{7}+y^{5}+y^{4}+y^{3}+y^{2}+1 \ (445)$

• 5. $y^{8}+y^{6}+y^{5}+y^{4}+y^{3}+y+1 \ (379)$

• 6. $y^{8}+y^{7}+y^{3}+y+1 \ (395)$

• 7. $y^{8}+y^{7}+y^{6}+y^{5}+y^{4}+y^{3}+1 \ (505)$

• 8. $y^{8}+y^{7}+y^{6}+y^{4}+y^{2}+y+1 \ (471)$

• 9. $y^{8}+y^{7}+y^{6}+y^{4}+y^{3}+y^{2}+1 \ (477)$

• 10. $y^{8}+y^{7}+y^{5}+y+1 \ (419)$

• 11. $y^{8}+y^{7}+y^{5}+y^{4}+1 \ (433)$

• 12. $y^{8}+y^{6}+y^{5}+y^{4}+y^{2}+y+1 \ (375)$

• 13. $y^{8}+y^{5}+y^{4}+y^{3}+y^{2}+y+1 \ (319)$

• 14. $y^{8}+y^{7}+y^{4}+y^{3}+y^{2}+y+1 \ (415)$

3 Proposed scheme

In this section, we will formulate the proposed mathematical model for S-box generation.

Theorem 3.1

The map $\psi :GF(2^{8}) \rightarrow GF(2^{8})$ defined by

$$\begin{aligned} \psi (z)= {\left\{ \begin{array}{ll} \dfrac{az+b}{cz+d} &{}: z\ne \dfrac{d}{c}\\ \dfrac{a}{c} &{}: z=\dfrac{d}{c}\\ \end{array}\right. } \end{aligned}$$

$\forall \ a,b,c,d,z\in GF(2^{8})$ with $ad-bc\ne 0$ is a bijection on $GF(2^{8})$.

Proof

In order to prove that $\psi$ is one-one, we suppose that there are some $x,y \in GF(2^{8})$ such that

$$\begin{aligned} \psi (x) = \psi (y). \end{aligned}$$

(3.1)

Case -I If $x=y=\dfrac{d}{c}$ then we are done.

Case - II If $x\ne \dfrac{d}{c}, y\ne \dfrac{d}{c}$ then from 3.1, we have $\dfrac{ax+b}{cx+d}=\dfrac{ay+b}{cy+d}$ that yields to $(ad-bc)(x-y)=0$. Since $GF(2^{8})$ is an integral domain and $ad-bc\ne 0$, therefore we must have $x=y$.

Case III If $x \ne \dfrac{d}{c}, y= \dfrac{d}{c}$ then from 3.1, we have $\dfrac{ax+b}{cx+d}=\dfrac{a}{c}$ which leads to the contradiction that $ad-bc=0$. Similarly, we can conclude that it is not possible that $x= \dfrac{d}{c}, y \ne \dfrac{d}{c}$.

Since $GF(2^{8})$ is finite, therefore, being the $1-1$ function, $\psi : GF(2^{8}) \rightarrow GF(2^{8})$ is a bijection.

Theorem 3.2

The Frobenius map $F: GF(2^{8}) \rightarrow GF(2^{8})$ defined by $F(x)=x^2; \hspace{0.3cm} \forall x \in GF(2^{8})$ is an automorphism.

Proof

To show F is an automorphism, we need to show that F is a bijection and preserves the operations of $GF(2^{8})$. Firstly, we will show that F is a bijection. Let $x_{1}, x_{2} \in GF(2^{8})$ such that

$$\begin{aligned} F(x_{1}) = F(x_{2}). \end{aligned}$$

(3.2)

Case-I If one of x and y is zero. Without loss of generality, we assume that $x=0$ then 3.3 implies that $y=0$ and we are done.

Case-II If $x \ne 0 \ \& y \ \ne 0$ then from 3.3 we have $x^2=y^2$ which implies that $x^{2}-y^{2}=0$ and $(x-y)^{2}=0$ which shows that $x=y$. As F is one-to-one it is a bijection being a one-to-one function between two same finite sets.

Now $F(x+y)=(x+y)^{2}=x^{2}+y^{2}+2xy=x^{2}+y^{2}=F(x)+F(y)$ and $F(xy)=(xy)^{2}=x^{2}y^{2}=F(x)F(y)$

Theorem 3.3

The functions $\psi , \zeta \!: GF(2^{8}) \!\rightarrow \! GF(2^{8})$ defined by $\psi (t)= {\left\{ \begin{array}{ll} \dfrac{ax^{2}+b}{cx^{2}+d} &{}: x \ne (\dfrac{d}{c})^{2^{-1}} \\ \dfrac{a}{c} &{}: x = (\dfrac{d}{c})^{2^{-1}} \end{array}\right. }$ and $\zeta (t)= {\left\{ \begin{array}{ll} (\dfrac{ax+b}{cx+d})^{2} &{}: x \ne (\dfrac{d}{c})^{2^{-1}} \\ (\dfrac{a}{c})^{2} &{}: x = (\dfrac{d}{c})^{2^{-1}} \end{array}\right. }$ are the bijections on $GF(2^{8})$.

Proof

We know that the Mobius transformation $f:GF(2^{8}) \rightarrow GF(2^{8})$ defined by $f(t)= {\left\{ \begin{array}{ll} \dfrac{at+b}{ct+d} &{}: t\ne \dfrac{d}{c}\\ \dfrac{a}{c} &{}: t= \dfrac{d}{c}\\ \end{array}\right. }$ is a bijection, where $a,b,c,d \in GF(2^{8})$ and $ad-bc \ne 0$. As the map $F(t)=t^{2}$ is an automorphism of $GF(2^{8})$ so the functions $\psi (t)= (f \circ F)(t)$ and $\zeta (t)=(F \circ f)(t)$ are the bijections being the composition of bijective maps.

Note We can again compose the functions $\psi , \zeta$ with Frobenius automorphism to design new bijections.

Table 1 S-box $\psi$

Table 2 S-box $\zeta$

3.1 Algorithm for construction of S-box

We used the chaotic logistic map as the starter of our proposed scheme. To choose irreducible polynomials and parameters of maps $\psi$ and $\zeta$, we iterate the logistic map. The procedure is described in the following steps;

Step 1: Set initial value $x_{0} \in (0,1)$ and parameter $r=3.9999$ in

$$\begin{aligned} x(i+1)=rx(i)(1-x(i)). \end{aligned}$$

(3.3)

Iterate Eq. 3.3 for $K+5$ times and discard the first K values, where K is a positive integer in the range 1000–2000.

Step 2: The index of irreducible polynomial is calculated using the formula:

$$\begin{aligned} \text {Index} = \mod (\lfloor x(K+1) \cdot 2^{10} \rfloor , 30) + 1 \end{aligned}$$

In this way, we will get the value of the index in the range 1–30. while the values of parameters a, b, c, d are selected in the following way,

$$\begin{aligned} \begin{aligned} a&= \mod (\lfloor x(K+2) \cdot 10^{13} \rfloor , 255) + 1, \\ b&= \mod (\lfloor x(K+3) \cdot 10^{14} \rfloor , 255) + 1, \\ c&= \mod (\lfloor x(K+4) \cdot 10^{15} \rfloor , 255) + 1, \\ d&= \mod (\lfloor x(K+5) \cdot 10^{16} \rfloor , 255) + 1. \end{aligned} \end{aligned}$$

and we get the values a, b, c, d in range 1–255.

Step 3: Choose the degree of the irreducible polynomial and based on the index of the irreducible polynomial, calculate $ad-bc$ in the Galois field generated by the polynomial. If $ad-bc =0$ then go to step 1 otherwise calculate the outputs of $\psi$ and $\zeta$.

Step 4; To generate dynamic S-boxes, include steps 1–3 in a for loop.

Two sample S-boxes are presented in Tables 1 and 2.

4 Security analysis of S-box

In this segment, we present the analysis of dynamic S-box generators against the cryptographic attacks. To ensure strong cryptographic resilience, the S-box needs to fulfill some prerequisites. The commonly employed criteria for evaluating the S-box typically include nonlinearity, strict avalanche criteria, bit independence criteria, linear approximation probability, differential approximation probability, fixed point analysis, and algebraic degree. The efficiency of the evaluations was then assessed by comparing the results to the standard S-boxes.

4.1 Bijectiveness and balanacedness

An S-box must ensure that each input value has a unique and exclusive output value, with each output value deriving from a separate input value, to satisfy the conditions of bijectivity. The decryption process in cryptographic algorithms requires the use of the inverse of the S-box, highlighting the significance of a bijective S-box in such algorithms.

If the same number of zeros and ones appear in the truth table of a boolean function then the S-box is considered to be balanced. An S-box is said to be balanced if and only if each of its component boolean functions exhibits equilibrium. If an S-box is unbalanced, favoring particular bit values for some or all of the input values, the security of cryptographic techniques may be compromised.

The S-boxes presented in Tables 1 and 2 are bijective, and satisfy the balance property.

4.2 Nonlinearity (NL)

An important factor in assessing the effectiveness of the S-box is the measurement of its unpredictability and nonlinearity (NL) is seen to be a key factor in this evaluation. The degree to which an S-box deviates from connecting its input and output bits in terms of their magnitudes linearly is referred to as its nonlinearity. Strong nonlinearity is necessary for an S-box used in cryptography because it increases system security by prohibiting attackers from inferring input bits from output bits.

4.3 Strict avalanche criteria (SAC)

The SAC (Strict Avalanche Criterion) predicts how an S-box will behave when its input is subjected to slight alterations, [34]. To pass the security criteria, an S-box must adhere to the strict avalanche criterion, which mandates that each output bit has an average probability of 0.5 of changing when a single bit is flipped in the input. With the use of this feature, attackers will have a difficult time extracting the original input data from the generated output.

4.4 Bit independence criteria (BIC)

The set of properties that make up the criterion for bit independence determines how statistically uncorrelated the input and output bits of an S-box are. The criteria specify the requirements that the S-box must fulfill for the output bits to show statistical independence from the input bits. We compute the BIC-Nonlinearity and BIC-SAC to assess the BIC performance of the S-box.

4.5 Linear approximation probability (LAP)

The likelihood that a linear function may resemble an S-box is measured by the Linear Approximation Probability (LAP). A measure of the S-box’s fortitude or resistance to linear assaults is the linear approximation probability (LAP). The S-box’s security strength increases as the LAP value decreases.

4.6 Differential approximation probability (DAP)

When all possible input differences are taken into account, the differential uniformity (DU) of an S-box is the maximum variation in frequency found between two distinct input differences that produce a specific output difference. This metric measures the largest probability difference between two input variations leading to a particular output variation. The differential approximation probability of an S-box is determined by dividing its differential uniformity by 256.

4.7 Fixed point analysis (FPA)

An S-box’s design objective is to avoid having fixed points, which implies that no input value will map to itself as a result of the S-box transformation. Cryptographers rely on this study to evaluate the strength and resilience of cryptographic algorithms that use S-boxes against different types of cryptographic assaults, which is essential for understanding the security characteristics, weaknesses, and overall efficacy of these algorithms.

4.8 Algebraic degree (AD)

It is defined as the longest term in the algebraic normal form of an S-box. A stronger S-box can fend off higher-order differential attacks, hence higher algebraic degree is preferable. Based on the coordinate function $g_{i}$, the algebraic degree of an S-box S is determined.

$$\begin{aligned} AD(S)=max\{deg(g_{i}) | i=1,2,3,,,8\} \end{aligned}$$

Table 3 Comparative analysis of sample S-boxes $\psi$ and $\zeta$

5 Applications in image encryption

The majority logic criteria (MLC) can be used to evaluate the encryption capabilities of S-boxes. MLC consists of several studies, including mean absolute deviation (MAD), contrast, energy, homogeneity, entropy, and correlation, which are used to determine the randomness in an encrypted image.

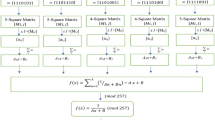
The properties of an encrypted image can be ascertained by an examination of homogeneity and energy. The correlation test looks for similarities or resemblances between encrypted images and plain images. The lower correlation value indicates a higher distortion brought on by encryption. The brightness loss of the original image is approximated by contrast. A more effective encryption method is one with a greater contrast score. The difference between the encrypted image and the original is measured using the MAD analysis. The quality of the S-box is determined by statistical characteristics, which are based on the distortions caused by the encryption process. We demonstrate the use of our dynamic S-boxes by using it in the proposed image encryption scheme presented by authors in [10]. The proposed scheme uses the CBC mode of AES for encryption of digital images. We used four-color images of Baboon, Cornfield, X-ray, and Pepper. The plain images with separate components are displayed in Figs. 1, 2, 3, 4, while the encrypted image and color components are presented in Figs. 5, 6, 7, 8. The decryption is just the reverse of these steps of AES CBC mode operation.

Algorithm 1

Encryption Algorithm for RGB Image

Algorithm 2

Decryption Algorithm for RGB Image

Fig. 1

Plain image of Baboon and histogram of its channels

Fig. 2

Plain image of Cornfield and histogram of its channels

Fig. 3

Plain image of Pepper and histogram of its channels

Fig. 4

Plain image of X-Ray and histogram of its channels

Fig. 5

Cipher image of Baboon and histogram of its channels

Fig. 6

Cipher image of Cornfield and histogram of its channels

Fig. 7

Cipher image of Pepper and histogram of its channels

Fig. 8

Cipher image of X-Ray and histogram of its channels

5.1 Key space analysis

Keyspace analysis establishes the number of distinct keys that may be developed and employed. A larger key space is preferred since it increases the number of keys that an attacker must attempt in a brute-force attack to successfully decrypt data. Brute force attacks consist of repeatedly trying every key until the right one is discovered. This increases the safety of the encryption technique since a wider key space makes brute force attacks more computationally expensive and time-consuming. An image encryption scheme can withstand brute force attacks if its key space is at least $2^{100}$. The key space of our used scheme is $2^{256}$ with an extra layer of security by a 128 bit random vector.

5.2 Key sensitivity analysis

Key sensitivity analysis is a procedure used to assess how slight changes in the encryption key may affect the safety and effectiveness of the algorithm. The encryption key is subjected to minor modifications or disturbances. Individual bits may be changed, a minor value may be added or subtracted, or certain key generation settings may be altered. The same input image is then subjected to the image encryption process with the changed encryption keys being used in place of the original ones. As a result, various encrypted versions of the same image are produced. Images that were encrypted using the modified keys and the images that were encrypted using the original, unmodified key are contrasted. Considerations like image quality, security, resilience to attacks, and processing efficiency are evaluated during the comparison. Key sensitivity analysis is used to determine how resilient an image encryption technique is to changes in the encryption key. We used a gray image for the encryption process with the original key and modified key. The results can be seen in Figs. 9, 10, 11, and Table 10.

Table 4 Comparison of AD and FP of $\psi$, and $\zeta$

Table 5 Experimental results of entropy

Table 6 Experimental results of correlation

Table 7 Experimental results of energy, contrast, homogeneity, MAD

Table 8 Experimental results of differential analysis

Table 9 Comparative analysis of proposed image encryption scheme

Table 10 NPCR and UACI results for key sensitivity analysis

Fig. 9

Encrypted original image

Fig. 10

Encrypted image with modified key

Fig. 11

Difference of images

6 Discussion

The following are the main findings of the scheme

• 1. S-box needs a high value of nonlinearity to fend against linear cryptanalysis. With a nonlinearity value of 112, our suggested sample S-boxes attain the optimal value (Table 3). Each S-box in our proposed scheme has nonlinearity 112, which too good as compared to other existing schemes [5, 6, 9, 10, 12, 15, 18, 31, 32, 35,36,37,38,39,40]. The scheme proposed in [15] has a nonlinearity range in 110–112 with 2584 S-boxes of nonlinearity 110 and 5416 S-boxes with nonlinearity 112. The scheme in [18] has produced S-boxes with a nonlinearity range in 95–106. Our scheme produces better results with average nonlinearity 112 as confirmed by 1000 S-boxes in Fig. 12.

• 2. Regarding the satisfaction avalanche criteria, a SAC score close to the ideal value (0.50) is deemed acceptable. The SAC of our sample S-boxes is 0.5022 and 0.5002 which are very close to the ideal value of 0.5 and better than most of S-boxes as depicted in Table 3. We computed the average value of dependency matrices for each of generated S-box and displayed it in Fig. 13. The dependence matrices’ mean values have upper and lower limits of 0.52 and 0.48, respectively, as can be seen. Since the majority of the dependence matrices’ mean values are concentrated around 0.50, our technique produces S-boxes with excellent stringent avalanche criteria. We can confirm the average deviation of the SAC score of our S-boxes by Fig. 14, as most of the values are very close to 0.

• 3. Under the bits independence requirement, the pair-wise disjoint Boolean functions have shown strong performance for both SAC and nonlinearity scores. The results for BIC Nonlinearity are depicted in Fig. 15 and confirm the efficacy of the proposed scheme as each S-box has BIC Nonlinearity 112, which is not found for each in schemes developed in [6, 10, 15, 18, 31, 32]. The scores of BIC Nonlinearity and BIC SAC for sample S-boxes are presented in Table 3. In Fig. 16, BIC-SAC values of 1000 S-boxes are clustered in the range 0.48–0.52, which is quite near to the optimal value of 0.5 and most values are very close to 0.5. We calculated the deviation of BICSAC from 0.5, which is shown in Fig. 17. As a result, our technique produces S-boxes with excellent BIC-SAC performance. By combining these two assessment metrics, it is possible to determine that the S-box produced by our approach performs well in terms of BIC.

• 4. A lower DU score is indicative of a secure S-box. We can see the results of the DAP of our sample S-boxes in Table 3. We compute the DAP values of resultant S-boxes and display them in Fig. 18 to confirm their resistance to differential assault. The value of DAP is 0.0156 showing equality to AES S-box. The experimental findings demonstrate the remarkable performance of the S-boxes that our technique dynamically generates in withstanding differential assaults.

• 5. The resistance of S-box against linear cryptanalysis is likewise correlated with the likelihood of linear approximation. An S-box is considered more resilient against linear cryptanalysis if its LAP score is lower. Our sample S-boxes have the LAP value of 0.0625, which is quite low as compared to a single S-box presented in [31, 40]. Figure 19 represents the LAP of 1000 S-boxes and this value is the same as of AES S-box and better than [6, 10, 15, 18, 31, 32]. This suggests that our strategy produces S-boxes with strong resistance to linear assaults.

• 6. Our goal is to design S-boxes without any fixed points and our proposed S-boxes presented in Tables 1 and 2 satisfy this criteria as seen in Table 4. Our proposed scheme has the potential to design S-boxes with no fixed points. The sample S-boxes do not have fixed points while the 10000 randomly generated S-boxes have fixed points 0, 1, 2, 3, 4 as displayed in Figs. 20 and 21. The distribution of fixed points is displayed in Figs. 22 and 23. Among 1000 S-boxes, 33.1 % with no fixed points, 48.9 % with 1 fixed points, 17.9 % with 3 fixed points, and 0.1 % with 4 fixed points.

• 7. A higher value of the algebraic degree is needed for a strong S-box. For AES S-box, its value is 7. Our proposed S-boxes have the same value, which shows the efficiency of the proposed scheme. The algebraic degree of randomly generated 1000 S-boxes is calculated and displayed in Fig. 24. The algebraic degree of each S-box is 7, which is the same as of AES S-box.

• 8. Entropy analysis is used to determine the randomness in an encrypted image. We can observe that the entropy of the proposed cipher image is better than [6, 10, 31, 41, 42]. The contrast in an image refers to the variation in brightness. The viewer may discern the underlying information via contrast analysis by seeing items. The contrast of our scheme is better than [5, 31, 35, 40, 42, 43]. Correlation is used to determine how similar pixels are to each other so an encrypted image must have a low value of correlation. The average correlation values for the proposed scheme are $-0.0003,-0.0010,-0.0003$ and better than [5, 31, 35, 40, 42, 43]. We can observe the efficiency of the encryption scheme by uniform histograms of each channel and from the results of MLC as depicted in Tables 5, 6, 8, 7, 9.

• 9. Single-bit variations in plain text should cause a strong cryptosystem to become very sensitive. NPCR and UACI assessments are used to gauge how sensitive the framework is. When a picture is encrypted using the recommended method, the NPCR (Number of Pixel Change Rate) statistic assesses the impact of a single-pixel change on the whole image. It calculates how often a pixel in the encrypted picture changes for every pixel that changes in the original image. The ideal value of NPCR is 99.61, whereas the values in our proposed scheme are in the range 99.57–99.63 as seen in Table 7 and show the strong resistance to differential attacks on the image encryption algorithm. The UACI value indicates the average magnitude of the changes made to the pixel intensities during the encryption process. A lower UACI value indicates a smaller average change, suggesting better preservation of the original pixel intensities. Conversely, a higher UACI value indicates a greater average change, indicating a more significant alteration of the pixel intensities. The ideal value of UACI is 33.45 and our scheme shows great resistance to differential attacks with values in the range of 33.39–33.61 as seen in Table 7.

Fig. 12

Results of nonlinearity of randomly generated 1000 S-boxes

Fig. 13

Results of SAC of 1000 S-boxes generated randomly by proposed scheme

Fig. 14

Deviation of SAC from 0.5

Fig. 15

Results of BIC nonlinearity of 1000 S-boxes generated randomly by the proposed scheme

Fig. 16

Results of BIC SAC of 1000 S-boxes generated randomly by the proposed scheme

Fig. 17

Deviation of BIC SAC from 0.5

Fig. 18

DAP values of 1000 S-boxes

Fig. 19

LAP of 1000 S-boxes

Fig. 20

Fixed points of 1000 S-boxes generated by function psi

Fig. 21

Fixed points of 1000 S-boxes generated by function zeta

Fig. 22

Distribution of fixed points of S-boxes generated by function Psi

Fig. 23

Distribution of fixed points of S-boxes generated by function Zeta

Fig. 24

Algebraic degree

7 Conclusion

This article introduced a new approach to generating S-boxes, based on the Frobenius automorphism of the Galois field and a chaotic logistic map. Our generator is capable of producing S-boxes that are optimized and randomized, with strong cryptographic features such as minimum computing complexity and high nonlinearity. Through the demonstration of a prerequisite for our generator to produce different S-boxes, we were able to mathematically examine the dynamic behavior of our generator. We performed several thorough analyses on the performance of the S-boxes created by our system, looking at both single and batch S-box testing. Our S-box generation approach can effectively generate highly secure S-boxes in a short amount of time, according to the tests we conducted, which makes it a workable option for a variety of apps that need strong encryption infrastructure. By substituting our sample S-box for the scheme designed by [10], we presented the efficiency of our proposed S-box. The results of image encryption using the suggested S-box reveal a high degree of security for the image’s cryptosystem. The proposed S-box generator shows remarkable efficiency by producing a large number of optimal S-boxes of nonlinearity 112, but it has just one limitation which is the term $ad-bc$ in Mobius transformation. Thus Our scheme shows great promise for creating encryption algorithms using dynamic S-boxes and providing various S-boxes for image security.