Temperature modulation effects on chaos and heat transfer in Darcy–Bénard convection using a local thermal non-equilibrium model

Abstract

This article investigates the effect of temperature modulation on convective heat transport in a fluid-saturated porous layer under local thermal non-equilibrium (LTNE) conditions. The boundary temperatures are modulated to have two parts: a steady part and an externally imposed time-dependent oscillatory part. An extended Darcy model with a time derivative term is used for the momentum equation for porous medium. A fifth-order Lorenz model is derived using a truncated Fourier series representation involving only two terms. The resulting heat transfer is calculated in terms of thermal Nusselt number by solving finite-amplitude equations numerically. The influence of the governing physical parameters on heat transport is analyzed and depicted graphically. It has been found that heat transfer can be effectively controlled by appropriately adjusting the external thermal mechanisms of the system. A study of streamlines and isotherms has also been conducted to get an insight of the flow phenomena under LTNE conditions. The plots of bifurcation diagrams and the largest Lyapunov exponent are also reported in the paper to describe the chaotic behavior of the fifth-order, non-autonomous system.

1 Introduction

A medium composed of a solid matrix with interconnected voids is called a porous medium, such as metal foam or rock. The liquid can flow through the pores present in a porous material. Physical quantities have a random trend in pore size and are evaluated macroscopically based on the number of voids. Porous medium has a wide range of applications in various industrial sectors such as electronic equipment cooling, geothermal conditions, petroleum extraction, grain storage, drying processes, heat exchangers, and heat pipes [1, 2]. In addition, the flow theory and heat transfer in these materials have been studied in various fields of engineering such as petroleum engineering, mechanical engineering, environment, and agriculture (for details, see Ingham and Pop [3], Vafai [4], and references therein).

The problem of natural convection in an infinitely extended horizontal dense porous layer saturated with Newtonian fluid heated from below is known as Darcy–Bénard convection (DBC) [5,6,7]. In modeling DBC, most studies assume local thermal equilibrium (LTE) conditions between fluid and solid phases. At any location, temperature gradient between the two phases is negligible. The LTE assumption is not appropriate in many practical applications with high-speed flows or significant temperature differences between the phases. It is, therefore, essential to consider the LTNE effect [8, 9]. As the porous media theory has various applications in simple techniques such as microwave heating, drying and freezing of foods, and many others, so, it is believed that the idea of LTNE plays an essential role in future developments [10,11,12,13,14].

LTNE is a specific condition wherein employing a single heat transfer equation becomes inadequate to model infinitesimal heat exchange occurring between the fluid and solid phases. In such scenarios, a dual-heat transfer approach is adopted, entailing the use of separate heat transfer equations for each phase, and the system is closed by adding a source/sink term proportional to the temperature difference between the phases. The early studies by Anzelius [15] and Schumann [16] represent pioneering works that employed two distinct temperature fields to investigate LTNE phenomena. Notably, Banu and Rees [8] used LTNE model to show that Lapwood’s result, originally applicable to LTE model, could be retrieved by approaching the LTE limit through parameter variations in the non-equilibrium analysis. Subsequently, several studies [17,18,19] considered LTNE effect in a porous medium, contributing to the understanding of this complex thermal phenomenon.

Over the past few decades, in a system with the time oscillating boundary conditions, natural convection has garnered a lot of attention [20,21,22,23]. The basic temperature gradient within the fluid layer should exhibit both space and time-dependent. It can be constructively used to control convection through external interventions and adjustments. Firstly, Venezian [24] analyzed Rayleigh-Bénard convection (RBC) for free-free surfaces linearly for small-amplitude temperature modulation. The author employed a perturbation method to determine the shift in the critical Rayleigh number. The results of the author’s work demonstrated that by appropriately adjusting the modulation frequency, it is possible to either destabilize or stabilize the system. Caltagirone [25] conducted a study exploring the impact of thermal modulation on the onset of Darcy convection within a porous medium saturated with fluid. The author linearly analyzed the system using the Galerkin technique. Stability analysis in a fluid-saturated porous media with a non-zero mean value of time-periodic temperature modulation on the boundaries is performed by Chhuon and Caltagirone [26]. Later, many authors such as Gershuni and Zhukhovitskii [27], Rosenblat and Tanaka [28], Rosenblat and Herbert [29], Bhadauria and Bhatia [30], and Malashetty and Swamy [31] studied similar problems with various configurations.

The studies reviewed so far have primarily focused on the linear stability analysis of thermal systems within porous media in the presence of gravity or temperature modulation, thus addressing only the issues related to the onset of convection. However, for a comprehensive understanding of systems’ dynamic behavior, encompassing aspects like chaotic motion, heat transfer within porous media, linear stability analysis proves inadequate, making nonlinear stability analysis imperative. Roppo et al. [32] first studied the non linear realm of thermal instability under temperature modulation. Siddheshwar et al. [33] adopted a weakly nonlinear study to analyze the conductive fluid layer’s magnetic convection under the influence of gravity and temperature modulation. Bhadauria et al. [34] also contributed by conducting a weakly nonlinear stability analysis to study the effects of time-periodic gravity and temperature modulation on thermal instability within a fluid-saturated, rotating porous layer. The authors used stationary convection modes to study the individual impacts of gravity and temperature modulation on heat transport. Furthermore, Siddheshwar et al. [35] delved into the nonlinear analysis of two-component convection within a porous medium, exploring the effects of gravity and temperature modulation. Their work involved deriving a non-autonomous Ginzburg-Landau equation, allowing them to study heat and mass transfer in stationary convection. Siddheshwar et al. [36] investigated the influence of asynchronous and synchronous boundary temperature modulation on Darcy–Bénard convection (DBC) using a new approach to determine the impact of phase angle and frequency on the mean Nusselt number. Later, several authors [37,38,39,40,41] also examined the effect of external modulation on heat transfer in a horizontal fluid-saturated porous layer.

Lorenz [42] conducted a nonlinear stability analysis of RBC within a fluid layer, using a truncated Fourier series representation with only two terms. This model effectively describes the qualitative dynamics of the entire system. The author found chaos in a relatively simple system comprising three autonomous ordinary differential equations (ODEs), using only second-order non-linearities to describe a simplified RBC problem. For low and moderate Prandtl numbers, Vadasz and Olek [43, 44] studied chaotic convection in a porous layer using LTE model. Vadasz [45,46,47,48,49] has also shown that a truncated Galerkin expansion may be used to recover the transition from rigid behavior to chaotic convection in porous media. Siddheshwar et al. [50] used the energy-conserving Lorenz model to investigate the impact of boundary conditions on the onset of chaos in RBC. Following Lorenz’s research, chaotic systems have been actively employed to investigate various thermal convection problems [51,52,53,54,55,56] under LTE conditions. By employing LTNE model, Sheu [57] analyzed how inter-phase heat transfer changes the route toward chaos and how using the LTNE model may stabilize steady convection. Later, several authors [58,59,60] studied chaotic convection in a porous medium under LTNE conditions.

As can be observed from the above literature review, the works on thermal instability discussed earlier with heat transport are in the absence of a time-dependent temperature field under LTNE conditions. The LTNE model with temperature modulation has practical applications in diverse fields. In biomedical applications, it improves thermal therapies with tissue temperature modulation. In microelectronics, such as integrated circuits (ICs) or microprocessors, where heat generation is significant, managing temperature distribution is important for reliability and optimal performance of devices. Considering LTNE conditions with temperature modulation can help in design of heat sinks or cooling systems and engineers can enhance heat dissipation efficiency and prevent localized overheating, thus improving the overall reliability and lifespan of electronic devices. In industrial processes involving heating or cooling, such as chemical reactors, food processing, or metal casting, precise control over temperature distribution and heat transfer rates is essential for product quality and process efficiency. By incorporating LTNE with thermal modulation into process design and equipment operation, engineers can optimize thermal management strategies to improve process performance and energy efficiency.

A linear analysis investigating the effect of thermal modulation on DBC using an LTNE model was recently studied by Bansal and Suthar [61]. To the best of our knowledge, no study dealing with non-linear analysis has been available that investigates the effect of temperature modulation under LTNE conditions. A linear stability analysis is sufficient to obtain the stability condition and the corresponding eigenfunctions of the static solution. It qualitatively describes the convection but cannot provide information about its amplitude or heat transfer rate. We perform a weakly nonlinear analysis under LTNE conditions with these motives, considering the temperature modulation at both boundaries. This helps to understand the physical mechanism with minimal mathematical analysis and represents a step towards understanding a complete nonlinear problem. A fifth-order Lorenz model is derived using a truncated two-term Fourier series representation. The objective of present study aims to address the following questions:

• 1. In both the solid and fluid phases, how do the governing parameters affect the heat transfer in the system?

• 2. What is the impact of LTNE parameters on the flow pattern?

• 3. How do modulation and LTNE parameters affect the chaotic motion within the system?

The answer to the first question is addressed in terms of the Nusselt number in Sect. 4.1. Further, the nature of flow patterns and temperature distribution in the form of streamlines and isotherms has also been investigated in Sect. 4.2. For the third question, the influence of various modulation parameters, i.e., amplitude and frequency of modulation, and LTNE parameters, i.e., inter-phase heat transfer coefficient and porosity-modified conductivity ratio, on chaotic motion is explained using plots of the bifurcation diagrams and largest Lyapunov exponent in Sect. 4.3.

2 Mathematical formulation

We assumed (x, y, z) as the coordinate frame in this study so that the z-axis is vertically upward and the origin is on the lower plane. A horizontal porous layer saturated with Newtonian fluid is considered, which is bounded between two infinitely extended parallel planes at $z = 0$ and $z = d$ and is time-periodically heated from below and cooled from above. The gravity acts in the vertical downward direction. The fluid and porous matrix are assumed to be out of thermal equilibrium; hence, a two-field temperature model is adopted. The system of equations that govern the fluid motion for analyzing DBC in a porous medium using an LTNE model [8] is:

$$\begin{aligned}{} & {} \nabla \cdot \textbf{u}=0, \end{aligned}$$

(2.1)

$$\begin{aligned}{} & {} \dfrac{\rho _{0f}}{\delta } \dfrac{\partial \textbf{u}}{\partial t} = -\nabla p - \dfrac{\mu }{K} \textbf{u} + \rho _{f}(T_{f}){\textbf {g}}, \end{aligned}$$

(2.2)

$$\begin{aligned}{} & {} \delta (\rho _{0} c)_{f} \dfrac{\partial T_{f}}{\partial t} + (\rho _{0} c)_{f} \textbf{u}\cdot \nabla T_{f} = \delta k_{f} \nabla ^{2} T_{f} \nonumber \\{} & {} \qquad + h(T_{s}-T_{f}), \end{aligned}$$

(2.3a)

$$\begin{aligned}{} & {} (1- \delta ) (\rho _{0} c)_{s} \dfrac{\partial T_{s}}{\partial t} = (1- \delta ) k_{s} \nabla ^{2} T_{s} - h(T_{s}-T_{f}), \nonumber \\ \end{aligned}$$

(2.3b)

where $\rho (T_{f})$ is given by

$$\begin{aligned} \rho _{f}(T_{f}) = \rho _{0f}[1- \beta (T_{f}-T_{0})], \end{aligned}$$

(2.4)

so that the reference density, $\rho _{0f} = \rho _{f}(T_{0})$. Furthermore, we adopt the modulated boundary temperatures as described by Venezian [24].

$$\begin{aligned}{} & {} T_{f} = T_{s} \nonumber \\{} & {} \quad = {\left\{ \begin{array}{ll} T_{0} + \frac{1}{2} \Delta T [1+ \epsilon \cos (\omega t)] &{} ~~~~ \text { at}~~~~ z=0,\\ T_{0} - \frac{1}{2} \Delta T [1- \epsilon \cos (\omega t + \phi )] &{} ~~~~\text {at}~~~~z=d, \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.5)

Fig. 1

Physical configuration

We must note that since LTNE includes both the solid and fluid phases, selecting appropriate thermal boundary conditions at the boundaries is difficult. The assumption in the Eq. (2.5) that the modulated temperatures of the two phases are the same at the boundary surfaces helps to relieve this difficulty and to obtain an analytical expression for the basic state of the system. Furthermore, assuming that thermally induced instabilities predominate over hydrodynamic instabilities, we neglect the convective acceleration term $\left( (\textbf{u} \cdot \nabla ) \textbf{u}\right)$, which represents the inertial effects within the system, in comparison to heat advection term $\left( (\textbf{u} \cdot \nabla ) T_f\right)$. In the Eqs. (2.1)–(2.5) mentioned above, several symbols are employed to represent various physical parameters. Specifically, $\textbf{u} = (u, v)$ signifies the velocity vector, while p represents pressure. The symbols $\beta$, $k_f$, and $\mu$ denote the fluid’s thermal expansion coefficient, thermal conductivity, and viscosity, respectively. Furthermore, the ratio of the voids in the porous medium to its total volume, i.e. porosity, is denoted by $\delta$, and K denotes the permeability that indicates ease of flow through the medium. $(\rho _0 c)_s$ and $(\rho _0 c)_f$ are used to signify the volumetric heat capacity of the solid and the fluid, respectively. Additionally, the symbol h stands for the inter-phase heat transfer coefficient and $k_s$ represents the thermal conductivity of the solid phase. The temperature variables in the system include $T_0$ as a reference temperature for the fluid, $T_f$ for the fluid-phase temperature, and $T_s$ for the solid-phase temperature. The parameter $\phi$ signifies the phase angle, while $\epsilon$ and $\omega$ represent the amplitude and frequency of modulation, respectively. Please refer to Fig. 1 for a schematic of the system’s physical configuration. To render the governing system of equations dimensionless, we employ the following transformations:

$$\begin{aligned}{} & {} (x_{*}, y_{*}, z_{*}) = \dfrac{ (x, y, z)}{d}, ~~~~ \mathbf {u_{*}} = \dfrac{(\rho _{0} c)_{f} d}{\delta k_{f}} \textbf{u}, \\{} & {} \quad t_{*} = \dfrac{k_{f}}{(\rho _{0} c)_{f}d^2} t,~~~~ p_{*} = \dfrac{(\rho _{0} c)_{f} K}{\delta \mu k_{f}} p,\\{} & {} \omega _{*} = \dfrac{(\rho _{0} c)_{f}}{k_{f}} d^2\omega ,~~~~ \rho _{*} = \dfrac{\rho - \rho _{0f}}{\rho _{0f}},\\{} & {} \quad \theta _{f}^{*} = \dfrac{T_{f} - T_{0}}{\Delta T}, ~~~~ \theta _{s}^{*} = \dfrac{T_{s} - T_{0}}{\Delta T}, \end{aligned}$$

where, non-dimensional quantities are represented with asterisks ($*$). After eliminating the pressure term in Eq. (2.2) and introducing the stream function $\psi$ such that $u = \psi _{z}$ and $v = -\psi _{x}$, the resulting non-dimensional equations governing the motion (with the asterisks dropped) can be expressed as follows:

$$\begin{aligned}{} & {} \left( 1+\frac{1}{\text {Va}} \dfrac{\partial }{\partial t} \right) \nabla ^{2} \psi = - \text {Ra} \dfrac{\partial \theta _{f}}{\partial x}, \end{aligned}$$

(2.6)

$$\begin{aligned}{} & {} \dfrac{\partial \theta _{f}}{\partial t} -\nabla ^{2} \theta _{f} - H (\theta _{s} - \theta _{f}) = \dfrac{\partial (\psi ,\theta _{f})}{\partial (x,z)}, \end{aligned}$$

(2.7)

$$\begin{aligned}{} & {} \alpha \dfrac{\partial \theta _{s}}{\partial t} -\nabla ^{2} \theta _{s} + \gamma H (\theta _{s} - \theta _{f}) = 0, \end{aligned}$$

(2.8)

and the corresponding non-dimensionalized boundary conditions are

$$\begin{aligned} \theta _{f} = \theta _{s} = {\left\{ \begin{array}{ll} \frac{1}{2} \left[ 1+ \epsilon \cos (\omega t)\right] &{} ~~~~ \text { at}~~~~ z=0,\\ - \frac{1}{2} \left[ 1- \epsilon \cos (\omega t + \phi )\right] &{} ~~~~\text {at}~~~~z=1, \end{array}\right. } \end{aligned}$$

(2.9)

where $\nabla ^{2} \equiv \dfrac{\partial ^{2}}{\partial x^{2}} + \dfrac{\partial ^{2}}{\partial z^{2}}$ and the non-dimensional parameters

$$\begin{aligned} \text {Pr}= & {} \dfrac{\mu }{\rho _{0} k_{f}},\quad \text {Da} = \dfrac{K}{d^{2}},\quad \text {Va} = \dfrac{\delta \text {Pr}}{\text {Da}},\\ {}{} & {} \text {Ra} = \dfrac{\rho g \beta \Delta T K d }{\delta \mu \kappa _{f}},\quad \\ H= & {} \dfrac{h d^{2}}{\delta k_{f}},\quad \alpha = \dfrac{(\rho _{0} c)_{s}}{(\rho _{0} c)_{f}}\dfrac{k_{f}}{k_{s}},\quad \gamma = \dfrac{\delta k_{f}}{(1-\delta )k_{s}}, \end{aligned}$$

are Prandtl number, Darcy number, Vadasz number, Darcy–Rayleigh number, scaled inter-phase heat transfer coefficient, diffusivity ratio, porosity-modified conductivity ratio, respectively. It’s important to note that the non-dimensionalized parameters mentioned above are valid within the constraint of $0< \delta < 1$.

The quantities associated with the quiescent basic state are expressed as follows:

$$\begin{aligned} \psi _{b} = 0, \,\,\,\,\,\ \theta _{f} = \theta _{fb}(z,t), \,\,\,\,\,\ \theta _{s} = \theta _{sb}(z,t), \end{aligned}$$

where the basic state quantities are denoted with the subscript b.

To obtain the temperature field $\theta _{fb}$, we consider a composition of two components: a steady temperature field and an unsteady oscillating part $\epsilon F(z,t)$. Under the boundary conditions described in (2.9), we derive the basic state solution as follows

$$\begin{aligned} \theta _{fb}(z,t) = \frac{1}{2}(1-2z) +\epsilon F(z,t), \end{aligned}$$

(2.10)

and

$$\begin{aligned} \theta _{sb}(z,t) = \frac{1}{2}(1-2z) +\epsilon G(z,t), \end{aligned}$$

(2.11)

where

$$\begin{aligned} F(z,t) = \frac{1}{2}\left[ f(z) e^{i \omega t} + \bar{f}(z) e^{-i \omega t}\right] , \end{aligned}$$

(2.12)

and

$$\begin{aligned}{} & {} G(z,t) \nonumber \\ {}{} & {} = \frac{1}{2}\left[ \left( 1+ \dfrac{i \omega }{H}\right) f(z) e^{i \omega t} + \left( 1- \dfrac{i \omega }{H}\right) \bar{f}(z) e^{-i \omega t}\right] \nonumber \\{} & {} -\frac{1}{2 H}\left[ g(z) e^{i \omega t} + \bar{g}(z) e^{-i \omega t}\right] ,\nonumber \\ \end{aligned}$$

(2.13)

with

$$\begin{aligned} f(z)= & {} A(\lambda _{1},\lambda _{2},z) +A(\lambda _{2},\lambda _{1},z), \end{aligned}$$

(2.14)

$$\begin{aligned} g(z)= & {} \lambda _{1}^2 A(\lambda _{1},\lambda _{2},z) +\lambda _{2}^2 A(\lambda _{2},\lambda _{1},z),\nonumber \\ \end{aligned}$$

(2.15)

$$\begin{aligned} A(\lambda _{1},\lambda _{2},z)= & {} \dfrac{1}{2 \sinh (\lambda _{1})}\dfrac{(\lambda _{2}^{2} + i \omega )}{(\lambda _{2}^{2} - \lambda _{1}^{2})} \nonumber \\{} & {} \left[ e^{- i \phi } \sinh (\lambda _{1} z) + \sinh (\lambda _{1}(1-z))\right] ,\nonumber \\ \end{aligned}$$

(2.16)

$$\begin{aligned} \lambda _{1}^{2}= & {} \frac{-X - \sqrt{X^{2} +4(i \omega H(\alpha + \gamma ) + \alpha \omega ^{2} )}}{2},\nonumber \\ \end{aligned}$$

(2.17a)

$$\begin{aligned} \lambda _{2}^{2}= & {} \frac{-X+ \sqrt{X^{2} +4(i \omega H(\alpha + \gamma ) + \alpha \omega ^{2} )}}{2},\nonumber \\ \end{aligned}$$

(2.17b)

and

$$\begin{aligned} X=-(1+\gamma )H + i \omega (1+\alpha ). \end{aligned}$$

(2.17c)

A finite amplitude perturbation is assumed on the quiescent basic state, which can be expressed in the following manner:

$$\begin{aligned} \psi = 0 + \psi ^{'},~~~~~~\theta _{f} = \theta _{fb} + \theta _{f}^{'},~~~~~~\theta _{s}=\theta _{sb} + \theta _{s}^{'}, \end{aligned}$$

(2.18)

where the prime notation is used to denote infinitesimal perturbed quantities. By substituting Eq. (2.18) into Eqs. (2.6)–(2.8), we arrive at the following expressions

$$\begin{aligned}{} & {} \left( 1 {+}\frac{1}{\text {Va}}\frac{\partial }{\partial t}\right) \nabla ^{2} \psi ^{'} {+} \text {Ra} \frac{\partial \theta _{f}^{'}}{\partial x} {=} 0 , \nonumber \\ \end{aligned}$$

(2.19a)

$$\begin{aligned}{} & {} \left( \frac{\partial }{\partial t} {-} \nabla ^{2} {+} H\right) \theta _{f}^{'} {-} H \theta _{s}^{'} {-} \frac{\partial \psi ^{'}}{\partial x}\frac{\partial \theta _{fb}}{\partial z} {-} \frac{\partial (\psi ^{'}, \theta _{f}^{'} )}{\partial (x,z)}{=} 0 , \nonumber \\ \end{aligned}$$

(2.19b)

$$\begin{aligned}{} & {} \left( \alpha \frac{\partial }{\partial t} {-} \nabla ^{2} {+} H \gamma \right) \theta _{s}^{'} {-}H \gamma \theta _{f}^{'}{=}0 ,\nonumber \\ \end{aligned}$$

(2.19c)

and the following perturbed boundary conditions are

$$\begin{aligned} \psi ^{'} = 0,~~~~~~ \theta _{f}^{'} = 0,~~~~~~ \theta _{s}^{'} = 0~~~~~~ \text {at }z = 0,1. \end{aligned}$$

3 Weakly nonlinear analysis

To conduct a nonlinear analysis, we employ a truncated Fourier series representation, wherein the series coefficients are solely dependent on time. In Fourier representation for stream function, like Lorenz’s formulation, only one term is retained. However, to maintain some portion of the non-linearities in Eqs. (2.19a)–(2.19c), two terms in the temperatures’ expressions are needed. Thus, we represent $\psi ^{'}$, $\theta ^{'}_{f}$, and $\theta ^{'}_{s}$ in their respective forms

$$\begin{aligned} \begin{aligned} \psi ^{'}(x,z,t)&= -\dfrac{\sqrt{2} ~\Gamma ^2}{a \pi }A(t) \sin (a x) \sin (\pi z),\\ \theta ^{'}_{f}(x,z,t)&= \dfrac{\sqrt{2} }{\text {r} \pi } B_{1}(t) \cos (a x) \sin (\pi z) \\ {}&-\dfrac{1}{\text {r} \pi } B_{2}(t) \sin (2 \pi z),\\ \theta ^{'}_{s}(x,z,t)&= \dfrac{\sqrt{2} }{\text {r} \pi } C_{1}(t) \cos (a x) \sin (\pi z)\\ {}&- \dfrac{1}{\text {r} \pi } C_{2}(t) \sin (2 \pi z), \end{aligned} \end{aligned}$$

(3.1)

where $\Gamma ^2 = \pi ^2 +a^2$, r $= \dfrac{a^2 \text {Ra}}{\Gamma ^4}$ and A is the amplitude of velocity convection, $B_{1}$ and $B_{2}$ are the amplitudes of fluid phase temperature, $C_{1}$ and $C_{2}$ are the amplitudes of solid phase temperature and these amplitudes are to be determined from the systems’ dynamics. On substituting Eq. (3.1) into Eqs. (2.19a)–(2.19c) and employing the orthogonality condition with the eigenfunctions as per Eq. (3.1), along with spatial domain integration, we obtain a system of five ODEs governing the time evolution of the amplitudes in the following manner:

$$\begin{aligned}{} & {} \dfrac{dA(t)}{d \tau } {=} {-}\text {Va}^* \left( A(t) {-} B_{1}(t) \right) , \end{aligned}$$

(3.2a)

$$\begin{aligned}{} & {} \dfrac{dB_{1}(t)}{d \tau } {=} {-}(1 {+} H^*)B_{1}(t) {+} H^* C_{1}(t) {-} A(t)B_{2}(t) \nonumber \\{} & {} \qquad {-}\text {r} A(t) I(t), \end{aligned}$$

(3.2b)

$$\begin{aligned}{} & {} \dfrac{dB_{2}(t)}{d \tau } {=} {-}( B^*{+}H^*) B_{2}(t) {+} H^* C_{2}(t) {+} A(t) B_{1}(t),\nonumber \\ \end{aligned}$$

(3.2c)

$$\begin{aligned}{} & {} \alpha \dfrac{dC_{1}(t)}{d \tau } {=} \gamma H^* B_{1}(t) - (1{+}\gamma H^* )C_{1}(t), \end{aligned}$$

(3.2d)

$$\begin{aligned}{} & {} \alpha \dfrac{dC_{2}(t)}{d \tau } {=} \gamma H^* B_{2}(t) {-} ( B^*{+} \gamma H^*) C_{2}(t), \end{aligned}$$

(3.2e)

where $I(t) =\int _{0}^{1} \left[ \dfrac{\partial \theta _{fb}(z,t)}{\partial z} \sin ^2 (\pi z)\right] dz$, $\tau = \Gamma ^2 t$, $\text {Va}^* = \dfrac{\text {Va}}{\Gamma ^2}$, $H^* = \dfrac{H}{\Gamma ^2}$, and $B^* = \dfrac{4 \pi ^2}{\Gamma ^2}$.

The fifth-order generalized Lorenz system described by Eqs. (3.2a)–(3.2e) maintains uniform boundedness over time and encapsulates several essential characteristics of the complete problem. Moreover, it is noteworthy that the phase-space volume consistently undergoes uniform contraction.

$$\begin{aligned} \begin{aligned}&\dfrac{\partial }{\partial A} \left( \dfrac{dA(t)}{d \tau } \right) + \dfrac{\partial }{\partial B_1} \left( \dfrac{dB_{1}(t)}{d \tau } \right) + \dfrac{\partial }{\partial B_2} \left( \dfrac{dB_{2}(t)}{d \tau }\right) \\&\qquad + \dfrac{\partial }{\partial C_1} \left( \dfrac{dC_{1}(t)}{d \tau }\right) + \dfrac{\partial }{\partial C2} \left( \dfrac{dC_{2}(t)}{d \tau }\right) \\&\quad =- \left( \text {Va}^* +1+ B^* +2 H^* + \dfrac{1 + B^* + 2 \gamma H^*}{\alpha }\right) . \end{aligned} \end{aligned}$$

(3.3)

This negativity of the rate implies that the system is both bounded and dissipative in this case. Consequently, the trajectories within the system are subsequently drawn toward a set of measure zero within the phase space. Specifically, these trajectories may converge to a fixed point, a limit cycle, or even a strange attractor. We have a well-established theory for Lorenz systems of third order, as documented in references [6, 42, 62,63,64]. However, for higher-dimensional Lorenz systems or Lorenz-like systems, one has to resort to computational analysis.

From Eq. (3.3), we can deduce that if we have an initial set of points in phase space occupying a region V(0) at time $\tau = 0$, then after a certain time, the endpoints of the corresponding trajectories will encompass a volume $V(\tau )$, given as

$$\begin{aligned} V(\tau )= & {} V(0) \exp \left[ - \left( \text {Va}^* +1+ B^* +2 H^* \right. \right. \nonumber \\{} & {} \left. \left. + \dfrac{1 + B^* + 2 \gamma H^*}{\alpha }\right) \right] . \end{aligned}$$

(3.4)

For general time-dependent variables, the above non-autonomous nonlinear ODE system is unsuitable for analytical treatment. Therefore it must be solved numerically. The horizontally averaged thermal Nusselt number for the fluid-phase $(\text {Nu}_{f})$, for the stationary convection is defined as

$$\begin{aligned} \text {Nu}_{f}(\tau ) = 1+ \left[ \dfrac{\int _{0}^{2\pi /a}\left( \frac{\partial \theta ^{'}_{f}}{\partial z}\right) dx}{\int _{0}^{2\pi /a}\left( \frac{\partial \theta _{fb}}{\partial z}\right) dx}\right] _{z=0}. \end{aligned}$$

(3.5)

On substituting expression for $\theta ^{'}_{f}$ in the above equation, we get

$$\begin{aligned} \text {Nu}_{f}(\tau ) = 1 + \dfrac{2}{\text {r}} B_{2}(\tau ). \end{aligned}$$

(3.6)

Similarly, for solid-phase, Nusselt number $(\text {Nu}_{s})$ is given by

$$\begin{aligned} \text {Nu}_{s}(\tau ) = 1 +\dfrac{2}{\text {r}} C_{2}(\tau ). \end{aligned}$$

(3.7)

Fig. 2

Effect of $\alpha$, $\gamma$, H, Va, $\epsilon$, and $\omega$ on $\text {Nu}_{f}$ and $\text {Nu}_{s}$ with $\tau$ in case of synchronous modulation

3.1 Largest lyapunov exponent

Lyapunov characteristic exponents (LCE) is used in chaos theory to measure the rate of convergence or divergence of nearby trajectories in a dynamical system, i.e., it helps to determine how sensitive the system is to initial conditions. A positive LCE indicates chaotic behavior, suggesting that small changes in initial conditions lead to significantly different outcomes over time. This concept is widely used in various fields such as biology, physics, and engineering, to study the predictability and stability of complex systems.

For n-dimensional non-autonomous dynamical system, we will not explicitly consider it as $\dot{ \textbf{X}} = \textbf{F}(\textbf{X}, \tau )$, but for our purpose, it will be sufficient to treat $\tau$ as an independent variable with the trivial evolution equation $\dot{\tau } =1$. In other words, we will rewrite the non-autonomous system as an autonomous system $\dot{ \textbf{X}} = \textbf{F}(\textbf{X}, \tau )$, $\dot{\tau } =1$ at the expense of increasing the dimension by one. Lyapunov exponent are calculated as

$$\begin{aligned} \zeta _i = \lim _{\tau \rightarrow \infty } \left[ \dfrac{1}{\tau } \textrm{ln} \left( \dfrac{|\Delta X_i (\tau )|}{|\Delta X_i (0)|}\right) \right] , \end{aligned}$$

(3.8)

such that $\Delta X_i (\tau )$ satisfy the variational equation

$$\begin{aligned} \dfrac{d (\Delta \textbf{X})}{ d \tau } = \textit{J} \Delta \textbf{X}, \end{aligned}$$

(3.9)

where $J_{ij} = \partial F_i/ \partial X_j$. Here, the number of exponents is one more than the dimension of the system. The greatest exponent is indicated by the symbol $\zeta ^{\text {Max}}$, and the exponents are listed in descending order. One can describe the behavior of the system using the value of $\zeta ^{\text {Max}}$. The state is regular if $\zeta ^{\text {Max}}<0$, but the state is chaotic if $\zeta ^{\text {Max}}>0$. The periodic or quasi-periodic condition is represented by the marginal case of $\zeta ^{\text {Max}} =0$. It takes the entire Lyapunov spectrum to fully understand the periodicity’s nature.

A bifurcation diagram is an additional tool that can be used to characterize the dynamical state. When there is a continuous stream of points in the variable in the bifurcation diagram, the behavior is either quasi-periodic or chaotic. On the other hand, when there is only one point in the variable, the state is either stationary or periodic with a period of one.

Fig. 3

Effect of $\alpha$, $\gamma$, H, Va, $\epsilon$, and $\omega$ on $\text {Nu}_{f}$ and $\text {Nu}_{s}$ with $\tau$ in case of asynchronous modulation

4 Results and discussion

This article investigates the effects of time-periodic boundary temperatures on the thermal instability in a Newtonian fluid-saturated Darcy porous layer using the LTNE model. A nonlinear analysis is performed assuming Boussinesq approximation and small-scale convective motions. A fifth-order Lorenz model is derived using a truncated two terms Fourier series representation. For the effect of thermal modulation on the system, two modulations are considered at the boundaries: synchronous (when $\phi = 0$) and asynchronous (when $\phi \ne 0$). Since our main aim is to understand the effect of thermal modulation under LTNE, thus the main governing parameters are $\gamma$ and H, along with $\epsilon$, $\phi$ and $\omega$.

We assume modulation to be of order $\delta$, meaning only a small modulation amplitude has been considered. To study the effect of the following system parameters diffusivity ratio ($\alpha$), porosity-modified conductivity ratio ($\gamma$), inter-phase heat transfer coefficient (H), Vadasz number (Va), modulation amplitude ($\epsilon$), and modulation frequency ($\omega$) on the convective heat transport, we report the variation of Nusselt numbers to time in Figs. 2–3. Taking into account the experimentally possible values of the parameters, we choose $\epsilon = 0.05$, $\gamma = 1$, $\alpha = 0.5$, $\text {Va} = 100$, $H = 50$, $\omega = 20$, and $\text {r}= 20$ as constant fixed values of these parameters. Unless otherwise mentioned, the parametric values below are those mentioned above. From these figures, it can be observed that $\text {Nu}$ initially starts with 1, which exhibits a conduction state. This means that when $\tau$ is small, heat transfer through the porous layer is only by conduction. It can also be concluded that for intermediate values of $\tau$, the $\text {Nu}$ value increases and often oscillates, indicating unsteady heat transfer between the phases. However, over time, the amount of heat transferred reaches a nearly constant value, representing a fully developed convective flow.

Fig. 4

Variation in streamlines and isotherms(fluid) for different values of $\gamma$ and H

4.1 Effect of physical parameters on Nusselt number

First, we discuss the results on heat transfer in both solid and fluid phases corresponding to the synchronous temperature modulation as illustrated in Fig. 2, in which we plotted the thermal Nusselt number ($\text {Nu}_{s}$) for solid phase and ($\text {Nu}_{f}$) for fluid phase, with respect to the slow time ($\tau$) for various values of system parameters. From Fig. 2a, it is noted that there is no significant effect of $\alpha$ in fluid phase but in solid phase, the heat transfer decreases with increasing $\alpha$. Increasing the value of $\alpha$ leads to a decrease in the heat conductions’ contribution of the solid phase and thus, decreases the heat transfer at the lower boundary in solid phase. In Fig. 2b, we observe that both $\text {Nu}_{f}$ and $\text {Nu}_{s}$ increases with the increasing $\gamma$. Smaller values of $\gamma$ correspond to a dense porous media leading to flow restriction. In contrast, a large value of $\gamma$ reduces the non-equilibrium state between the saturating fluid and porous matrix. It corresponds to fluids’ high thermal conductivity relative to that of solid. Therefore, both in solid and fluid, heat transfer increases with an increase in $\gamma$. Figure 2c presents the effect of H on $\text {Nu}_{f}$ and $\text {Nu}_{s}$. It is observed that heat transfer in fluid decreases with increasing H while an opposite effect is observed in solid phase. We recollect that for extremely small H-values, there is almost no interaction between solid and fluid phases, i.e., they act independently, and the heat transfer between the phases is nearly zero. Therefore, when limit $H \rightarrow 0$, the fluid properties dominate the flow development and solid-phase temperature no longer affects the fluid-phase temperature (and vice-versa). Hence, heat transfer in solid phase is insignificant for small H-values. On the other hand, for moderate H-values, the temperatures of both solid and fluid phases are different, as the properties of the solid also contribute to the system’s stability. As a result, it is expected (and shown in Fig. 2c) that heat transfer in the fluid will lessen, and the system will become more unstable on increasing H. However, when $H \rightarrow \infty$, the temperature of both phases becomes indistinguishable, and they act as a single phase fluid leading to the system being in LTE.

The effect of Va on $\text {Nu}_{f}$ and $\text {Nu}_{s}$ is shown in Fig. 2d. It is observed that on increasing Va, the heat transfer also increases. As Va governs the effect of porosity on the flow in a porous medium and with a densely packed porous medium, inertial effects are less important. Thus, the destabilizing effect is also lower compared to the Venezian’s [24] clear liquid problem. On further increasing the time, its effect on heat transfer diminishes. The effect of $\epsilon$ and $\omega$ on $\text {Nu}_{f}$ and $\text {Nu}_{s}$ is presented in Fig. 2e and f, respectively. It shows that in the case of synchronous modulation, these parameters do not affect the heat transfer at the lower boundary. This is because the boundary temperature does not significantly change the temperature gradient across the layer. Therefore, no significant effect of modulation on heat transfer is observed in this case.

Fig. 5

Variation in streamlines and isotherms (solid) for different values of $\gamma$ and H

Figure 3 shows the effect of asynchronous temperature modulation (corresponding to $\phi = \pi$) on heat transport in both solid and fluid phases. The impact of $\alpha$, $\gamma$, H, and Va on $\text {Nu}_{f}$ and $\text {Nu}_{s}$ is observed in Fig. 3a–d, respectively. It is observed that these parameters affect heat transfer in the same way as they do under synchronous modulation, but for large t, the behavior is sinusoidal in fluid phase, i.e., $\text {Nu}_{f}$ doesn’t achieve a constant value. The effect of $\epsilon$ on $\text {Nu}_{f}$ and $\text {Nu}_{s}$ is shown in Fig. 3e. It is found that increasing $\epsilon$ increases the magnitude of $\text {Nu}_{f}$, improves heat transfer, and promotes the onset of convection. An increase in $\epsilon$ leads to larger area where the fluid and solid temperature difference is different. This benefits the enhancement of heat transfer between solid and fluid phases. In Fig. 3f, it is observed that the heat transport amplitude decreases, and the wavelength of oscillation shortens as $\omega$ increases. As for low values of $\omega$, a modulating effect on the temperature field is felt across the fluid layer. Therefore, convective waves propagate through the fluid layer for asynchronous modulation, preventing instability and the convection occurs at higher Rayleigh numbers than predicted by linear theory with a steady temperature gradient. However, the effect of thermal modulation diminished as the $\omega$ increased, and finally, the impact of modulation completely disappeared when $\omega$ was very large, confirming the Venezian [24] results.

A comparative analysis of the values of thermal Nusselt numbers for fluid and solid phases (reported in Figs. 2–3) reveals that Nu is larger for the fluid phase than for the solid phase. It indicates that the amount of heat transfer is higher in fluid compared to the solid phase. Another important observation one should make here is that the effect of modulation is prominent when asynchronous modulation is considered. Keeping these observations in mind, we plot in Figs. 4–5, the streamlines and isotherms for the fluid and solid phases in the case of asynchronous temperature modulation ($\phi = \pi$).

Fig. 6

Largest Lyapunov exponent and bifurcation diagrams as a function of r for LTE and LTNE cases, with and without modulation effect

Fig. 7

Largest Lyapunov exponent and bifurcation diagrams as a function of r for LTE and LTNE cases, with and without modulation effect

4.2 Effect of $\gamma$ and H on streamlines and isotherms

The plots in Figs. 4–5 are aimed at analyzing the flow pattern and temperature distribution within the porous medium under local thermal non-equilibrium. Hence, we consider a variation in the values of $\gamma$ and H. The standard natural convection pattern is visible in these plots as assumed through normal mode expansion. In the streamline plots, the sense of movement in subsequent cells is alternately identical with and opposite to the adjacent cell. The streamlines are colored according to the velocity magnitude at different cell points to visualize the change in velocity magnitudes. The color legends at the top correspond to velocity magnitude. We observe that the fluid velocity is prominent in the middle and outer portion of a cell, whereas it is small in the center and edges of a cell (see Figs. 4–5).

We first report the observation regarding the flow pattern by analyzing the streamlines. First, one should note that the streamlines plotted in Figs. 4 and 5 are identical and show that the velocity magnitude remains same when the porosity-modified conductivity ratio $\gamma$ increases for small H value. This result is evident as higher $\gamma$ corresponds to a fluid with higher thermal conductivity resulting in a stable layer. Moreover, it is apparent from the figures that the cells also become slightly broader (c.f. [8]) on increasing $\gamma$. These figures also show that the flow velocity is higher for $H= 10$ than for $H = 50$ throughout the cell when the time $\tau$ is small (see the subplot corresponding to $\tau = 0.1$). The difference between the velocity magnitudes increases as time progresses. This phenomenon occurs because large values of H correspond to better heat transfer between the phases, enhancing heat diffusion as time progresses. Thus, the convective flow slows down, resulting in a decreased velocity. We also note that the cell size increases with H, as reported by Banu and Rees [8].

Assessing fluid-isotherms plotted as the background in Fig. 4a (for $\gamma = 0.1$), we observe that initially, the temperature is higher at the center due to higher fluid velocity. But, as time progresses, the temperature spreads quickly across the porous layer but returns to its earlier state as fluid velocity increases. However, due to the large value considered for $\gamma$ (greater than 1), we observe in Fig. 4b (for $\gamma = 1$) that the temperature diffusion is higher even with a lower fluid velocity at all times. The isotherms for fluid phase in Fig. 4b and c reflect that heat diffusion is faster for higher values of H as the higher temperature region in the center of the cell is narrower for $H = 50$. A similar observation regarding higher heat exchange between the phases can be made for Fig. 5b and c that the isotherms for solid are almost invariant for a small value of H. Whereas, for large H, the isotherms display heat diffusion induced by the convective flow. Therefore, the center of the cell (see Fig. 5c) is a slightly higher temperature region when compared to the isotherms in Fig. 5b. Thus, we can conclude that the inter-phase heat transfer coefficient’s role is vital in setting up the convective currents and the heat transfer process.

On the same reasoning, we may proceed to interpret the result depicted in Fig. 5a–b. We observe that the isotherms of the solid phase are substantially affected by a change in $\gamma$. For large values of $\gamma$, the fluid properties dominate the flow development and increase the heat transfer in the solid phase through convection.

4.3 Effect of modulation on bifurcation and Chaos

We computed the Lyapunov exponents following the algorithm suggested by Wolf et al. [65], with a particular focus on the largest exponent, denoted as $\zeta ^{\text {Max}}$. Using a constant time step of $\Delta \tau = 0.005$ and a set of randomly chosen fixed initial conditions: $(A, B_1, B_2, C_1, C_2, \tau ) = (0.58923, 0.61950, 0.39968, 0.28658, 0.16479, 0),$ we conducted our simulations employing the conventional fourth-order Runge–Kutta technique. To plot bifurcation diagram, we need to take into account the time series of $B_2(t)$ and identified its local maximum values within a time interval between 0 and 1000.

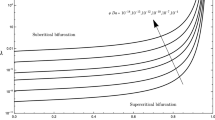
Figures 6 and 7 visually depict the largest Lyapunov exponent (LLE), $\zeta ^{\text {Max}}$ and the bifurcation diagram of $B_2^{\text {Max}}$ as functions of r for non-modulated and modulated LTE and LTNE cases. These figures provide insights into the presence of windows containing periodic points or intervals and reveal regions characterized by chaotic dynamics. It’s worth noting that prior to the existence of a window of periodic points, there exist certain points where LLE is close to zero ($\zeta ^{\text {Max}} \approx 0$). This is something that can be seen before the creation of the window of periodic points. These points do not exhibit clear periodic or chaotic behavior, and we categorize them as nearly periodic or chaotic. The Hopf–Darcy–Rayleigh number ($r_h$) signifies the critical value of r marking the transition from regular convective motion to chaotic motion in the system.

Fig. 8

Phase portraits in ($A, B_1, B_2$) - space at r = 110

Table 1 Value of $r_h$ at which chaotic motion starts for LTE and LTNE cases, with and without modulation effect

Table 2 Lyapunov spectrum at different values of r for LTE and LTNE cases, with modulation effect ($\omega = 20$)

By carefully examining Figs. 6 and 7, one can find several important and interesting physical phenomena. In Fig. 6a, for $\gamma =1$ and small value of H, i.e., $H = 0.01$ (which indicates weak inter-phase heat transfer between the solid and fluid phase), the bifurcation from regular convection to chaos is observed in the neighborhood of $r_h$, i.e., r-value at which the first transition to chaotic motion occurred, for all modulated and non-modulated cases. It is also observed that in non-modulated case, there are more possible periodic windows, around r $\approx 55, 75, 90, 103$ and a transition to a wide periodic window regime in the range r $\approx 81-90$ and above r $\approx 105$ as compared to the modulated cases. For $\omega =2$, the possible periodic window is around r $\approx 82.6$. A wide periodic window is also observed above r $\approx 121$, while for $\omega = 20$, the possible periodic windows are around r $\approx$ 90–92, 106, 115–120, 138, 141–142, and many more. Still, no such wide periodic window is observed, as observed in other cases. LLE and the bifurcation scenarios characterized by the parameters $\gamma = 1, H= 10$ (LTNE) are illustrated in Fig. 6b, respectively, for the interval $0 \leqslant$r $\leqslant 150$. When H is increased to 10, some more periodic windows appear around r $\approx 43, 44, 48, 49, 50$, after the onset of chaos, $r_h \approx 42.6$ for the modulated case with $\omega = 20$ as compared to other modulated and non-modulated cases. In this case, the route to chaos differs from the case when $H = 0.01$, i.e. gets delayed. The wide period windows for both modulated, $\omega =2$ and non-modulated cases also get delayed, i.e., r $\approx 138$ and r $\approx 128$, respectively.

The bifurcation diagram and LLE are shown in Fig. 7a for $\gamma = 10$ and $H = 10$. Here, we observed that a sudden transition from regular convection to chaos occurred earlier than when $\gamma =1$ (Fig. 6b) for all modulated and non-modulated cases. No periodic windows just after the onset of chaos are observed for the modulated case when $\omega = 20$, as observed in Fig. 6b. However, the detailed scenarios of the route to chaos for modulated case, $\omega =2$ and non-modulated case are similar to the case when $\gamma =1$ (Fig. 6b). Figure 7b shows the bifurcation diagram and LLE as a function of r for $\gamma =10^2$ and $H = 10^4$, i.e., LTE case ($\gamma H \rightarrow \infty$). Here, the detailed scenarios of the route to chaos for all modulated and non-modulated cases are similar to the case with $\gamma =1$ and $H = 0.01$, as observed in Fig. 6a.

A comparison of the results between modulated and non-modulated scenarios in both LTE and LTNE cases reveals a notable observation. In the non-modulated LTE case, numerous nearly periodic or mildly chaotic points appear compared to that of LTNE cases, highlighting the inherent unpredictability in the dynamics associated with LTE. When $\gamma$ is small and H is moderate, an abrupt chaotic transition is observed for modulated cases with moderate modulation frequency. We also remark here that the bifurcation diagrams reiterate the results obtained using LLE.

Figure 8 shows the phase portraits for all modulated and non-modulated LTE and LTNE cases at r $= 110$. Period-2 is observed for non-modulated LTE (limiting case) and LTE cases, while period-4 is observed for both non-modulated LTNE cases at r $= 110$. However, we observe chaotic motion at r $= 110$ for all modulated LTE and LTNE cases. Extensive computational analysis further reveals that the trajectories do not exhibit attraction towards a strange attractor; instead, they are drawn towards limit cycles.

From Table 1, considering LTE (limiting case), we observe that $r_h$ value is larger for $\omega = 2$, while for $\omega =20$, its value is less than as observed in non-modulated case. However, for small modulation frequency, i.e., $\omega = 2$, $r_h$ value increases with an increase in modulation amplitude, $\epsilon$. In contrast, its value remains the same while considering a moderate value of $\omega$, i.e., $\omega = 20$. A similar effect is observed for the LTE case, i.e., $\gamma H \rightarrow \infty$. In this case, for $\omega = 20$, there is a decrease in the $r_h$ value with an increase in modulation amplitude. In LTNE case, when $\gamma = 1$ and $H = 10$, we observe that for modulated cases, the chaotic motion sets in earlier than in the non-modulated case. However, in modulated cases, with an increase in modulation amplitude, there is a decrease in the $r_h$ value for both the considered modulation frequencies. Also, in LTNE case, it should be noted that on increasing porosity modified conductivity ratio, i.e., $\gamma =10$ for the same H value, there is a decrease in the $r_h$ value as compared to the case when $\gamma = 1$, since smaller values of $\gamma$ correspond to a dense porous medium leading to the inhibition of flow in the medium and delay the onset of chaos. As a result, chaotic motion sets in earlier for larger $\gamma$ values. In this case, we also observe that for modulation frequency $\omega = 2$, there is a delay in the onset of chaos, i.e., $r_h$ value is greater. In contrast, for $\omega = 20$, its value is less than the non-modulated case. Next, we report the conclusions drawn from this investigation.

Table 2 reports numerical values of the Lyapunov exponents (LEs) $\zeta _i$ calculated for the time series obtained for the amplitudes $A, B_1, B_2, C_1$ and $C_2$ for different values of the bifurcation parameter r. The Lyapunov exponent of the auxiliary equation is always zero and, hence, isn’t included in the table. The LE for the stream function amplitude equation is always the largest and changes significantly with a change in r. This observation is analogous to the results concerning the classical Lorenz model. The values of r, for which tabulated values are given, were chosen on the criteria that r $> r_h$ and the variation in the LLE is maximum at these points compared to the neighboring points. This table again implies that moderate-frequency temperature modulation can suppress chaotic motions in porous mediums with LTE/LTNE conditions for specific values of r.

5 Conclusions

Temperature modulations’ effect on heat transport in DBC is investigated by considering an LTNE model. An equivalent Lorenz model is derived using a truncated two terms Fourier series representation. Also, with the help of finite-amplitude equations, we have obtained the Nusselt number. The effect of modulation parameters and LTNE parameters on heat transfer and chaotic motion using plots of the largest Lyapunov exponent and bifurcation diagrams has been found, and the following conclusions have been drawn:

• 1. In the case of synchronous temperature modulation, when time is small, the value of Nusselt number is found to be oscillatory. However, it attains an almost constant value when time is large.

• 2. In the case of asynchronous temperature modulation, the value of the Nusselt number is large than that of synchronous temperature modulation.

• 3. In the case of asynchronous temperature modulation, modulation amplitude enhances heat transfer.

• 4. Effect of diffusivity ratio decreases the heat transport for both types of modulations in the solid phases.

• 5. The effect of porosity-modified conductivity ratio and the Vadasz number enhances heat transport for both types of modulations in the fluid and solid phases.

• 6. In fluid phase, the effect of inter-phase heat transfer coefficient is to suppress heat transport. Whereas, in solid phase, its effect enhances heat transport as expected.

• 7. Onset of chaos for small modulation frequency get delayed as compared to non-modulated case.

• 8. Increasing modulation frequency sets-in the onset of chaos earlier.

• 9. For small $\gamma$-value and moderate H-values, an abrupt transition to chaos is observed for large modulation frequency case.