Bogdanov–Takens bifurcation of an enzyme-catalyzed reaction model

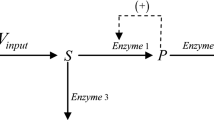
Abstract

Enzyme-catalyzed reactions are frequently observed in the chemical process, and could be described by the mathematical model, such as the Gray–Scott model with Langmuir–Hinshelwood mechanism. The complex dynamical behaviors are analyzed in this work, including the existence and their stability of equilibrium points and the bifurcations of the model. By using stability theory, normal form technique and bifurcation analysis, the stability and the saddle-node bifurcation, Hopf bifurcation and Bogdanov–Takens bifurcation are explored in detail. Numerical simulations are also carried out to verify the validity of theoretical results.

1 Introduction

In the early 20th century, scientists began to study some phenomena, such as catalytic reactions and cell division in living organisms, and found the involved changes of matters in space and time. Reaction-diffusion equations, which describe nonlinear interactions between diffusion and reaction terms, were developed to explain self-organizing phenomena in chemical and biological processes. As the result of the nonlinear interaction between diffusion and reaction terms, self-organizing patterns will emerge, forming various type of patterns, when some specific parameter conditions are satisfied. Turing initiated the research of such self-organizing patterns in 1952 [1], which is now often referred to as the Turing pattern.

Among the various autocatalytic reaction models, Gray–Scott model is one of popular models, which was proposed by Gray and Scott [2,3,4], when they considered the autocatalytic process in a continuous stirred tank reactor and studied the interaction between the chemical and the catalyst. They found that the system could exhibit different self-organizing phenomena, s uch as multistability, hysteresis, extinction, ignition and self sustained oscillations. The model takes the following dimensionless form

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}= -uv^2+a(1-u)+D_u \frac{\partial ^2 u}{\partial x^{2} },\\ \frac{\partial v}{\partial t}=uv^2-(a+b)v+D_v \frac{\partial ^2 v}{\partial x^{2} }, \end{array}\right. } \end{aligned}$$

(1)

where the state variables u(x, t) and v(x, t) respectively represent the concentrations of reactants and autocatalysts, a is the dimensionless feed rate, b is the dimensionless rate constant of the second reaction, and $D_u$ and $D_v$ represent the diffusion coefficients of the reactant and autocatalyst, respectively. In practice, this is also the model of chemical substances in a gel reactor, where the rate a can be relatively easily modified, while b depends on the system temperature.

The enzyme-catalyzed reaction model not only provides new ideas and methods to study self-organization phenomena in chemical reactions, but also has been widely applied in other fields such as biology, physics, and geology. Chen et al. [5] investigated a general reaction-diffusion model with non-local activators and inhibitors and applied the results to Klausmeier–Gray–Scott water-plant model and Holling-Tanner predator–prey model. In [6], Dong et al. proposed a new method for identifying the Gray–Scott model through deterministic learning and interpolation, which is based on local identification results and uses interpolation to achieve global identification. Gandhi et al. [7] considered the spatially localized structures in the Gray–Scott model and focused on the regime in diffusivities by using a combination of numerical continuation technique and weakly nonlinear theory. Saadi et al. [8] discussed a homotopy, which took a Schnakenberg-like glycolysis model to the Gray–Scott model. Several distinct codimension-two bifurcations were discovered by numerical continuation. Kuznetsov et al. [9] studied the homoclinic orbits of the second-order Gray–Scott model and gave the standard form of the Bogdanov–Takens bifurcation of the system.

The Bogdanov–Takens bifurcation is an important research topic in bifurcation theory. Many scholars have applied it to other models and obtained various research results. Yuan et al. [10] studied the bifurcations analysis in a generalist predator–prey model with stage structure. They showed saddle-node bifurcation of codimension 1 and 2, Hopf bifurcation, Bogdanov–Takens bifurcation, and bifurcations of nilpotent singularities of elliptic and focus type of codimension 3. And they also found that the nilpotent focus of codimension 4 serves as an organizing center to connect all the codimension 3 bifurcations in the two-dimensional center manifold of the system, and the bifurcations are also associated with a third order cubic Li$\acute{e}$nard system. In [11], Xiang et al. considered the Holling–Tanner model with constant-yield prey harvesting. They gave the analysis of the nilpotent cusp of codimension 4 and the Bogdanov–Takens bifurcation of codimension 4. And they also showed the situation that Hopf bifurcation of codimension 3 occurs. Jiao et al. [12] considered a delayed predator–prey system with double Allee effect in prey and presented the detailed bifurcation situation. Su et al. [13] studied a dynamic model of the initial lung infection response of the innate immune system, which has a high-dimensional bifurcation, including the Bogdanov–Takens bifurcation of codimension 3 and the Hopf bifurcation of 2 codimension.

In the heterogeneous catalysis, for the vast majority of surface catalytic reactions the Langmuir–Hinshelwood mechanism is preferred [14] to describe the kinetics of enzyme-catalyzed surface reactions. For the enzyme-catalyzed reaction model, we will introduce the Langmuir–Hinshelwood mechanism, which is similar to the Michaelis-Menten type functional reaction function. Moreover, if the concentration of substance v represented by $\frac{v}{1+mv}$, then v will reach saturation during the reaction as v is sufficiently large, i.e. $\lim _{v \rightarrow \infty }\frac{v}{1+mv} =\frac{1}{m}$. Therefore, from the perspective of controllability of chemical reactions, considering the Langmuir–Hinshelwood reaction mechanism may be more practical. So we will consider the impact on the dynamics of local system and find that the model could exhibit the stability, instability and bifurcation.

The paper is organized as follows. The enzyme-catalyzed reaction model with Langmuir–Hinshelwood mechanism is first formulated. The existence and their stability of equilibrium points are given in Sect. 2. In Sect. 3, specific bifurcations are presented, including saddle-node bifurcation, Hopf bifurcation, and Bogdanov–Takens bifurcation. Numerical simulations are given to validate theoretical results in Sect. 4. Some conclusions are drawn in Sect. 5.

2 Existence and stability of equilibria

With the Langmuir–Hinshelwood mechanism the enzyme-catalyzed reaction model takes the form as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}= -u+\frac{ u^{2}v }{1+mv},\\ \frac{\partial v}{\partial t}=b-dv-\frac{ u^{2}v }{1+mv}. \end{array}\right. } \end{aligned}$$

(2)

where the state variables u(x, t) and v(x, t) respectively represent the concentration of autocatalyst and reactant, where b, d, and m are positive constants. Let $f(u,v)=-u+\frac{ u^{2}v }{1+mv}$ and $g(u,v)=b-dv-\frac{ u^{2}v }{1+mv}$, solving the $f(u,v)=0$ and getting that $u=0$ or $u=\frac{mv+1}{v}$. Now, we consider these two cases respectively.

At the boundary equilibrium $E_0(u_0,v_0)=(0,\frac{b}{d})$, the Jacobian matrix is

$$\begin{aligned} J_{E_0}=\begin{bmatrix} -1 &{} 0\\ 0 &{}-d \end{bmatrix}. \end{aligned}$$

The eigenvalues of $J_{E_0}$ are $\lambda _{1}=-1<0$, $\lambda _{2}=-d<0$. So $E_0$ is a stable node of the system (2).

Then we discuss the case of positive equilibrium. From $f(u,v)=0$, we have $u=\frac{mv+1}{v}$, substituting it into $g(u,v)=0$, one has the following equation

$$\begin{aligned} h(v)\overset{\triangle }{=}dv^2-bv+mv+1=0. \end{aligned}$$

The discriminant of h(v) can be obtained as

$$\begin{aligned} \Delta =(m-b)^2-4d. \end{aligned}$$

According to the discriminant, when $d=\frac{(m-b)^2}{4}$, h(v) has a unique solution

$$\begin{aligned} v_1=\frac{b-m}{2d}. \end{aligned}$$

When $d<\frac{(m-b)^2}{4}$, there are two distinct roots

$$\begin{aligned} v_2=\frac{b-m+\sqrt{\Delta }}{2d},\quad v_3=\frac{b-m-\sqrt{\Delta }}{2d}. \end{aligned}$$

In order to ensure that the obtained roots are positive, here we assume that $b-m>0$.

Therefore, we have the following result.

Theorem 1

Assume that $b-m>0$, system (2) has only one boundary equilibrium $E_{0}\left( 0,v_{0} \right) =\left( 0,\frac{b}{d} \right)$, and

• (i) if $d>\frac{(m-b)^2}{4}$, then there are no real equilibria, therefore no positive equilibria;

• (ii) If $d=\frac{(m-b)^2}{4}$, then there is a unique positive equilibrium $E_{1}\left( u_{1},v_{1} \right) =\left( \frac{b+m}{2},\frac{2}{b-m}\right)$;

• (iii) If $d<\frac{(m-b)^2}{4}$, then there are two positive equilibria $E_{2}\left( u_{2},v_{2} \right) =\left( \frac{m\sqrt{\Delta }+bm-m^2+2d }{b-m+\sqrt{\Delta }}\right. ,$ $\left. \frac{b-m+\sqrt{\Delta }}{2d} \right)$ and $E_{3}\left( u_{3},v_{3} \right) =\left( \frac{m\sqrt{\Delta }-bm+m^2-2d }{m-b+\sqrt{\Delta }}, \frac{b-m-\sqrt{\Delta }}{2d} \right)$.

Next, we will present the stability analysis of the equilibrium points $E_1$, $E_2$ and $E_3$. As for $E_1$, we have the following statements.

Theorem 2

The following statements about $E_1$ are true.

• (i) If $d=\frac{1}{2}$, then $E_{1}$ is a cusp of codimension two;

• (ii) If $d<\frac{1}{2}$, then $E_{1}$ is a saddle-node with an unstable parabolic sector;

• (iii) If $d>\frac{1}{2}$, then $E_{1}$ is a saddle-node with a stable parabolic sector.

Proof

Since the Jacobian matrix of system (2) at equilibrium $E_{1}$ is

$$\begin{aligned} J_{E_{1} }= \begin{pmatrix} 1&{}d \\ -2&{}-2d \end{pmatrix}, \end{aligned}$$

we have

$$\begin{aligned} tr J_{E_{1} }=1-2d, \;\;det J_{E_{1} }=0. \end{aligned}$$

Now we translate $E_{1}(u_1,v_1)=(\frac{bm-m^2+2d}{b-m},\frac{b-m}{2d} )$ to the origin with $(u,v)=(U+u_1,V+v_1)$, then system (2) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{U}=a_{10}U+a_{01}V+a_{20}U^{2} +a_{11}UV+a_{02}V^{2}\\ \qquad \ +a_{21}U^{2}V+a_{12}UV^{2}+a_{03}V^{3}+P \left( U,V \right) , \\ \dot{V}=b_{10}U+b_{01}V+b_{20}U^{2}+b_{11}UV+b_{02}V^{2}\\ \qquad \ +b_{21}U^{2}V+b_{12}UV^{2}+b_{03}V^{3}+Q \left( U,V \right) , \end{array}\right. } \end{aligned}$$

(3)

where

$$\begin{aligned}&a_{10}=1,\quad a_{01}=d,\quad a_{20}=\frac{b-m}{bm-m^2+2d},\\&a_{11}=\frac{8d^2}{(b-m)(bm-m^2+2d)},\\&a_{02}=-\frac{2d^2m}{bm-m^2+2d},\quad a_{21}=\frac{4d^2}{(bm-m^2+2d)^2},\\&a_{12}=-\frac{16d^3m}{(b-m)(bm-m^2+2d)^2},\\&a_{03}=\frac{4d^3m^2}{(bm-m^2+2d)^2},\quad b_{10}=-2,\quad b_{01}=-2d,\\&b_{20}=-\frac{b-m}{bm-m^2+2d},\\&b_{11}=-\frac{8d^2}{(b-m)(bm-m^2+2d)},\\&b_{02}=\frac{2d^2m}{bm-m^2+2d},\\&b_{21}=-\frac{4d^2}{(bm-m^2+2d)^2},\\&b_{12}=\frac{16d^3m}{(b-m)(bm-m^2+2d)^2},\\&b_{03}=-\frac{4d^3m^2}{(bm-m^2+2d)^2}, \end{aligned}$$

and P(U, V), Q(U, V) are terms of at least order four in U and V.

When $d=\frac{1}{2}$, we find that both the trace and determinant of $J_{E_1}$ are equal to zero, indicating that both of eigenvalues of $J_{E_1}$ are also equal to zero. After a transformation to (3) by letting $(U,V)=(x,2x+2y)$, then we get the following form

$$\begin{aligned} {\left\{ \begin{array}{ll}\frac{dx}{dt} =y+c_{20}x^2+c_{11}xy+c_{02}y^2+c_{30}x^3+c_{21}x^2y\\ \qquad \ +c_{12}xy^2+c_{03}y^3+P_1(x,y), \\ \frac{dy}{dt} = d_{20}x^2+d_{11}xy+d_{02}y^2+d_{30}x^3+d_{21}x^2y\\ \qquad \ +d_{12}xy^2+d_{03}y^3+Q_1(x,y), \end{array}\right. } \end{aligned}$$

(4)

where

$$\begin{aligned}&c_{20}= \frac{b^2-4mb+3m^2-4}{(b-m)(mb-m^2+1)},\quad c_{11}= \frac{4}{b-m},\\&c_{02}= -\frac{2m}{mb-m^2+1},\\&c_{30}= -\frac{2(2m^2b-2m^3+b+3m)}{(b-m)(mb-m^2+1)^2}, \\&c_{21}= \frac{2(6m^2b-6m^3+b+7m)}{(b-m)(mb-m^2+1)^2},\\&c_{12}= -\frac{12m(mb-m^2+\frac{2}{3}) }{(b-m)(mb-m^2+1)^2},\\&c_{03}= \frac{4m^2}{(mb-m^2+1)^2},\\&d_{20}= \frac{b^2-4mb+3m^2-4}{2(b-m)(mb-m^2+1)},\\&d_{11}= \frac{2}{b-m},\quad d_{02}= -\frac{m}{mb-m^2+1}, \\&d_{30}= -\frac{2m^2b-2m^3+b+3m}{(b-m)(mb-m^2+1)^2},\\&d_{21}= \frac{(6m^2b-6m^3+b+7m)}{(b-m)(mb-m^2+1)^2},\\&d_{12}= -\frac{6m(mb-m^2+\frac{2}{3}) }{(b-m)(mb-m^2+1)^2},\\&d_{03}= \frac{2m^2}{(mb-m^2+1)^2}, \end{aligned}$$

and $P_1(x,y)$, $Q_1(x,y)$ are terms of at least order four in x and y.

To facilitate further calculation, we apply the change $(x,y)=(x_1,y_1+d_{02}x_1y_1-c_{02}y_1^{2})$ to system (4) to eliminate the $y^2$ term and rewrite system (4) as

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_1 = y_1+e_{20}x_1^2+e_{11}x_1y_1+e_{30}x_1^3+e_{21}x_1^2y_1\\ \qquad \ +e_{12}x_1y_1^2+e_{03}y_1^3+P_2(x_1,y_1), \\ \dot{y}_1 = f_{20}x_1^2+f_{11}x_1y_1+f_{30}x_1^3+f_{21}x_1^2y_1\\ \qquad \ +f_{12}x_1y_1^2+f_{03}y_1^3+Q_2(x_1,y_1), \end{array}\right. } \end{aligned}$$

(5)

where

$$\begin{aligned}&e_{20}=c_{20},\quad e_{11}=d_{02}+c_{11},\quad e_{30}=c_{30}, \\&e_{21}= c_{21}+c_{11}d_{02},\\&e_{12}=c_{12}-c_{02}c_{11}+2c_{02}d_{02},\quad e_{03}=c_{03}-2c_{02}^2,\\&f_{20}=d_{20},\quad f_{11}=d_{11},\quad f_{30}=d_{30},\\&f_{21}=d_{21}-c_{20}d_{02}+2c_{02}d_{20}, \\&f_{12}=d_{12}+d_{02}^2+c_{02}d_{11}-c_{11}d_{02}, \\&f_{03}=d_{03}-2c_{02}d_{02}, \end{aligned}$$

and $P_2(x_1,y_1)$, $Q_2(x_1,y_1)$ are terms of at least order four in $x_1$ and $y_1$.

Further, we reduce (5) into the following form by the transformation $(x_2,y_2)=(x_1,y_1+$ $e_{20}x_1^2+e_{11}x_1y_1+M(x_1,y_1))$. Here the $M(x_1,y_1)$ is the term of at least order three in $x_1$ and $y_1$.

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_2=y_2, \\ \dot{y}_2=g_{20}x_2^{2}+g_{11}x_2y_2+g_{02}y_{2}^{2}+ g_{30}x_{2}^{3}+g_{21}x_2^2y_2\\ \qquad \ +g_{12}x_2y_2^2+g_{03}y_{2}^3+Q_2(x_2,y_2), \end{array}\right. } \end{aligned}$$

(6)

where

$$\begin{aligned} \begin{aligned}&g_{20}=f_{20},\quad g_{11}=f_{11}+2e_{20},\quad g_{02}=e_{11}, \\&g_{30}=f_{30}+e_{11}f_{20}-e_{20}f_{11},\\&g_{21}=f_{21}-e_{11}e_{20},\quad g_{12}=f_{12}-e_{11}^2, \\&g_{03}=f_{03}, \end{aligned} \end{aligned}$$

and $Q_2(x_2,y_2)$ is the term of at least order four in $x_2$ and $y_2$.

Then to eliminate the $y_2^2$ term in system (6), we first apply the scaling transformation $dt=(1-g_{02}x_2)d\tau$ to it and obtain the system as

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dx_2}{d\tau }=(1-g_{02}x_2){y}_2,\\ \frac{dy_2}{d\tau }=(1-g_{02}x_2)(g_{20}x_2^2+g_{11}x_2y_2+g_{02}y_2^2+g_{30}x_{2}^{3}\\ \quad \qquad +g_{21}x_2^2y_2+g_{12}x_2y_2^2+g_{03}y_{2}^3+Q_2(x_2,y_2)). \end{array}\right. } \end{aligned}$$

(7)

Further transformation $(x_3,y_3){=}(x_2,(1-g_{02}x_2)y_2)$ for system (7) yields the following result

$$\begin{aligned} {\left\{ \begin{array}{ll}\frac{dx_3}{d\tau }=y_3, \\ \frac{dy_3}{d\tau }=g_{20}x_3^2+g_{11}x_3y_3+Q_3(x_3,y_3), \end{array}\right. } \end{aligned}$$

(8)

where

$$\begin{aligned} \begin{aligned}&g_{20}=\frac{b^2-4bm+3m^2-4}{2(b-m)(bm-m^2+1)}, \\&g_{11}=\frac{2b^2-6bm+4m^2-6}{(b-m)(bm-m^2+1)}, \end{aligned} \end{aligned}$$

and $Q_3(x_3,y_3)$ is the term of at least order three in $x_3$ and $y_3$.

Simple calculation gives

$$\begin{aligned}&g_{20}g_{11}=\frac{(b^2-4bm+3m^2-4)(b^2-3bm+2m^2-3)}{(b-m)^2(bm-m^2+1)^2}. \end{aligned}$$

If $b=2m\pm \sqrt{m^2+4}$ or $b=\frac{3\,m}{2}\pm \frac{\sqrt{m^2+12} }{2}$, then $g_{20}g_{11}=0$. However, note that $b-m>0$, $d=\frac{1}{2}$ and $\Delta =(m-b)^2-4d=0$, then one has that $b=m+ \sqrt{2}$. So it follows that $g_{20}g_{11} \ne 0$ and $E_1(u_1,v_1)$ is a cusp of codimension two.

Next, for the situation $d\ne \frac{1}{2}$, we apply the transformation $(U,V)=(-dx-\frac{y}{2},x+y)$ to system (3) and obtain the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\bar{x}}=\bar{c}_{20}\bar{x}^2+\bar{c}_{11}\bar{x}\bar{y}+\bar{c}_{02}\bar{y}^2+P_4(\bar{x},\bar{y}), \\ \dot{\bar{y}}=\bar{d}_{01}\bar{y}+\bar{d}_{20}\bar{x}^2+\bar{d}_{11}\bar{x}\bar{y}+\bar{d}_{02}\bar{y}^2+Q_4(\bar{x},\bar{y}), \end{array}\right. } \end{aligned}$$

(9)

where

$$\begin{aligned}&\bar{c}_{20}{=}-\frac{d(b^3-3bm^2+(3m^2-8d)b-m^3)}{4(2d-1)(bm-m^2+2d)},\\&\bar{c}_{11}{=}-\frac{-m^3{+}3bm^2{+}(-3b^2{-}8d^2{+}4d)m{+}b(b^2{-}8d^2{-}4d)}{4(2d-1)(bm-m^2+2d)},\\&\bar{c}_{02}{=}-\frac{32d^3m-b^3+3b^2m+16d^2b-3bm^2-16d^2m+m^3}{16d(2d-1)(bm-m^2+2d)},\\&\bar{d}_{01}{=}1-2d,\\&\bar{d}_{20}{=}-\frac{d(b^3-3b^2m+(3m^2-8d)b-m^3)(d-1)}{4(2d-1)(bm-m^2+2d)},\\&\bar{d}_{11}{=}-\frac{((-8b-8m)d^2+(4m-4b)d+(b-m)^3)(d-1)}{4(2d-1)(bm-m^2+2d)},\\&\bar{d}_{02}{=}-\frac{(-m^3{+}3b^2m{+}(-32d^3{-}3b^2{+}16d^2)m{+}b^3{-}16d^2b)(d{-}1)}{16d(d-\frac{1}{2} )(bm-m^2+2d)},\\ \end{aligned}$$

and$P_4(\bar{x},\bar{y}))$ and $Q_4(\bar{x},\bar{y}))$ are the terms of at least order three in $\bar{x}$ and $\bar{y}$.

After introduction of a new time variable $\tau =(1-2d)t$ to system (9), the we arrive at the following form

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\textrm{d} \bar{x}}{\textrm{d} \tau }=\bar{e}_{20}\bar{x}^2+\bar{e}_{11}\bar{x}\bar{y}+\bar{e}_{02}\bar{y}^2+P_5(\bar{x},\bar{y})), \\ \frac{\textrm{d} \bar{y}}{\textrm{d} \tau }=\bar{y}+\bar{f}_{20}\bar{x}^2+\bar{f}_{11}\bar{x}\bar{y}+\bar{f}_{02}\bar{y}^2+Q_5(\bar{x},\bar{y})), \end{array}\right. } \end{aligned}$$

(10)

where $\bar{e}_{ij}=\frac{\bar{c}_{ij}}{1-2d}$, $\bar{f}_{ij}=\frac{\bar{d}_{ij}}{1-2d}(i+j\le 2,0\le i,j\le 2)$, $P_5(\bar{x},\bar{y}))=\frac{P_4(\bar{x},\bar{y}))}{1-2d}$ and $Q_5(\bar{x},\bar{y}))=\frac{Q_4(\bar{x},\bar{y}))}{1-2d}$.

By calculation, it can be obtained that $\bar{e}_{20}=\frac{d(b^3-3b^2\,m+(3\,m^2-8d)b-m^3)}{4(1-2d)^2(bm-m^2+2d)}\ne 0$. From Theorem 7.1 in [15], the origin is always a saddle-node. When $d<\frac{1}{2}$, $E_1$ is a saddle-node with an unstable parabolic sector, and it is a saddle-node with a stable parabolic sector when $d>\frac{1}{2}$.

The proof is completed. $\square$

If $\Delta >0$, then h(u) has two solutions $E_2(u_2,v_2)$ and $E_3(u_3,v_3)$. Now, we intend to give their stability results.

Theorem 3

$E_2$ is a saddle and $E_3$ is

• (i) a source when $trJ_{ E_3}>0$, i.e. $d{>}\frac{(b-m+1)(b-m-1)}{(b-m)^2}$;

• (ii) a center or a fine focus when $trJ_{ E_3}=0$, i.e. $d=\frac{(b-m+1)(b-m-1)}{(b-m)^2}$;

• (iii) a sink when $trJ_{ E_3}<0$, i.e. $d<\frac{(b-m+1)(b-m-1)}{(b-m)^2}$.

Proof

The Jacobian matrix at $E_2(u_2,v_2)$ and $E_3(u_3,v_3)$ are

$$\begin{aligned} J_{E_{2,3}}=\begin{pmatrix} 1&{} -2 \\ \frac{1}{v^2_{2,3}}&{}-\frac{dv^2_{2,3}+1}{v^2_{2,3}} \end{pmatrix}. \end{aligned}$$

The determinants of $J_{E_{2}}$ and $J_{E_{3}}$ are, respectively.

$$\begin{aligned} {\text {det}} J_{E_{2}} =-\frac{2d\sqrt{\Delta }(b-m+\sqrt{\Delta })}{(b-m+\sqrt{\Delta })^2 }<0, \end{aligned}$$

and

$$\begin{aligned} {\text {det}} J_{E_{3}} =\frac{2d\sqrt{\Delta }(b-m-\sqrt{\Delta })}{(b-m-\sqrt{\Delta })^2 }>0. \end{aligned}$$

So $E_2$ is a saddle and the stability of $E_3$ is up to the sign of the trace

$$\begin{aligned} tr J_{E_{3}}{=} \frac{2(d{-}1)(b{-}m)\sqrt{\Delta }(2{-}2d)(b^2{+}m^2){+}4m(d{-}1)b{-}4d}{(b-m-\sqrt{\Delta })^2 }. \end{aligned}$$

It follows that $E_3$ is a source when $d>\frac{(b-m+1)(b-m-1)}{(b-m)^2}$; it is a center or a fine focus when $d=$ $\frac{(b-m+1)(b-m-1)}{(b-m)^2}$ and is a sink when $d<\frac{(b-m+1)(b-m-1)}{(b-m)^2}$. $\square$

3 Bifurcation analysis

3.1 Saddle-node bifurcation

After checking the existence of equilibrium points, we find that the number of equilibria changes with respect to the parameter d. Specifically, when $d=\frac{(m-b)^2}{4}$, the saddle-node bifurcation may occur. In the following discussion, we will investigate the saddle-node bifurcation around $E_1$.

Theorem 4

When bifurcation parameter $d\equiv d_{SN}=\frac{(m-b)^2}{4}$, system (2) will experience the saddle-node bifurcation around $E_1$.

Proof

By applying Sotomayor’s theorem [16], we need to verify the transversality condition around $d\equiv d_{SN}$. The Jacobian matrix at $E_{1}$ is given by

$$\begin{aligned} J_{E_{1}}=\begin{pmatrix} 1 &{} d\\ -2 &{}-2d \end{pmatrix} \end{aligned}$$

Let M and N represent the eigenvectors of the eigenvalue $\lambda _1$ of $J_{E_{1}}$ and $J_{E_{1}}^T$, respectively. To be specific, we have

$$\begin{aligned} M=\begin{pmatrix}M_{1} \\ M_{2} \end{pmatrix}=\begin{pmatrix}-d \\ 1 \end{pmatrix},\qquad N=\begin{pmatrix}N_{1} \\ N_2 \end{pmatrix}=\begin{pmatrix} 2 \\ 1 \end{pmatrix}. \end{aligned}$$

Moreover, we have

$$\begin{aligned} F_{d}(E_1,d_{SN})=\begin{pmatrix}0 \\ \frac{2}{m-b} \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned}{} & {} D^2F(E_1,d_{SN})(M,M)\\{} & {} \quad =\begin{pmatrix}\frac{\partial ^2f}{\partial u^2}M_1^2 +2\frac{\partial ^2f}{\partial u\partial v}M_1M_2+\frac{\partial ^2f}{\partial v^2}M_2^2\\ \frac{\partial ^2g}{\partial u^2}M_1^2 +2\frac{\partial ^2f}{\partial u\partial v}M_1M_2+\frac{\partial ^2f}{\partial v^2}M_2^2 \end{pmatrix}_{(E_1,d_{SN})}\\{} & {} \quad = \begin{pmatrix}-\frac{(b-m)^3}{4}\\ \frac{(b-m)^3}{4} \end{pmatrix}. \end{aligned}$$

Hence, M and N satisfy the transversality conditions, which are given by

$$\begin{aligned} N^{T}F_{d}(E_1,d_{SN})= -\frac{2}{b-m}\ne 0, \end{aligned}$$

and

$$\begin{aligned} N^{T} [D^2F(E_1,d_{SN})(M,M)]=\frac{(b-m)^3}{4}\ne 0. \end{aligned}$$

Therefore, the system (2) exhibits the saddle-node bifurcation around $E_1$. $\square$

3.2 Hopf bifurcation

From Theorem 3, we find that when $d{=}\frac{(b-m+1)(b-m-1)}{(b-m)^2}$, $E_3$ becomes a center or a fine focus, indicating that the Hopf bifurcation may happen. Next, we will explore whether or not the Hopf bifurcation around $E_3$ exists.

According to the Hopf theorem [17], we need to verify the transversal condition

$$\begin{aligned}&\frac{\textrm{d} tr J_{E_{2}} }{\textrm{d} d}\bigg |_{d = c} \\&\quad =(4((-b^4+4b^3m+(1-6m^2)b^2+(4m^3-2m)\\&\qquad \times b-m^4+m^2-1)\sqrt{\frac{(b^2-2bm+m^2-2)^2}{(b-m)^2}}\\&\qquad +(b^4-4b^3m+(6m^2-3)b^2\\&\qquad +(6m-4m^3)b+m^4-3m^2+3)(b-m) ))\\&\qquad / (\sqrt{\frac{(b^2-2bm+m^2-2)^2}{(b-m)^2}}(b-m\\&\qquad -\sqrt{ \frac{(b^2-2bm+m^2-2)^2}{(b-m)^2}})^3(b-m) )\ne 0. \end{aligned}$$

Hence the Hopf bifurcation happens at $E_3$ in system (2).

Then we want to give the direction of the Hopf bifurcation. Translating $E_3(u_3,v_3)$ into (0, 0) with $(\hat{u},\hat{v})=(u-u_3,v-v_3)$, system (2) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\tilde{u} }=\tilde{a}_{10}\tilde{u}+\tilde{a}_{01}\tilde{v}+\tilde{a}_{20}\tilde{u}^2 +\tilde{a}_{11}\tilde{u}\tilde{v}+\tilde{a}_{02}\tilde{v}^2\\ \qquad +\tilde{P}(\tilde{u},\tilde{v}),\\ \dot{\tilde{v} }=\tilde{b}_{10}\tilde{u}+\tilde{b}_{01}\tilde{v}+\tilde{b}_{20}\tilde{u}^2 +\tilde{b}_{11}\tilde{u}\tilde{v}+\tilde{b}_{02}\tilde{v}^2\\ \qquad +\tilde{Q}(\tilde{u},\tilde{v}), \end{array}\right. } \end{aligned}$$

(11)

where

$$\begin{aligned} \begin{aligned}&\tilde{a}_{10}=1,\qquad \tilde{a}_{01}=\frac{1}{v_3^2},\qquad \tilde{a}_{20}=\frac{v_3}{mv_3+1}, \\&\tilde{a}_{11}=\frac{2}{v_3(mv_3+1)},\\&\tilde{a}_{02}=-\frac{m}{v_3^2(mv_3+1)},\qquad \tilde{b}_{10}=-2,\\&\tilde{b}_{01}=\frac{-d^*v_3^2-1}{v_3^2},\qquad \tilde{b}_{20}=-\frac{v_3}{mv_3+1},\\&\tilde{b}_{11}=-\frac{2}{v_3(mv_3+1)},\qquad \tilde{b}_{02}=\frac{m}{v_3^2(mv_3+1)},\qquad \end{aligned} \end{aligned}$$

and $\tilde{P}(\tilde{u},\tilde{v})$, $\tilde{Q}(\tilde{u},\tilde{v})$ are the terms of at least order three in $\tilde{u}$ and $\tilde{v}$.

We continue to change the system (11) by the transformation

$$\begin{aligned} \tilde{x} =-\tilde{u},\qquad \tilde{y}=\frac{1}{\sqrt{S} }(\tilde{a}_{10}\tilde{u}+\tilde{a}_{01} \tilde{v}),\qquad d\tau =\sqrt{S}dt, \end{aligned}$$

where $S=\tilde{a}_{10}\tilde{b}_{01}-\tilde{a}_{01}\tilde{b}_{10}=\frac{-d^*v_3^2+1}{v_3^2}$. Then we obtain the following form

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{\tilde{x} }=-\tilde{y}+\tilde{f}(\tilde{x},\tilde{y}), \\ \dot{\tilde{y} }=\tilde{x}+\tilde{g}(\tilde{x},\tilde{y}). \end{array}\right. } \end{aligned}$$

(12)

where

$$\begin{aligned} {\left\{ \begin{array}{ll}\tilde{f}(\tilde{x},\tilde{y})= \tilde{c}_{20}\tilde{x}^2+\tilde{c}_{11}\tilde{x}\tilde{y}+\tilde{c}_{02}\tilde{y}^2+\tilde{P}_1(\tilde{x},\tilde{y}), \\ \tilde{g}(\tilde{x},\tilde{y})= \tilde{d}_{20}\tilde{x}^2+\tilde{d}_{11}\tilde{x}\tilde{y}+\tilde{d}_{02}\tilde{y}^2+\tilde{Q}_1(\tilde{x},\tilde{y}), \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \tilde{c}_{20}&=-\frac{\tilde{a}_{02}\tilde{a}_{10}^2}{\sqrt{-\tilde{a}_{01}\tilde{b}_{10}+\tilde{a}_{10}\tilde{b}_{01}} \tilde{a}_{01}^2}\\&\quad + \frac{\tilde{a}_{11}\tilde{a}_{10}}{\sqrt{-\tilde{a}_{01}\tilde{b}_{10} +\tilde{a}_{10}\tilde{b}_{01}} \tilde{a}_{01}}\\&\quad -\frac{\tilde{a}_{20}}{\sqrt{-\tilde{a}_{01}\tilde{b}_{10}+\tilde{a}_{10}\tilde{b}_{01}} },\\ \tilde{c}_{11}&=-\frac{2\tilde{a}_{02}\tilde{a}_{10}}{\tilde{a}_{01}^2} +\frac{\tilde{a}_{11}}{\tilde{a}_{01}},\\ \tilde{c}_{02}&= \frac{\tilde{a}_{02}\tilde{b}_{10}}{\sqrt{-\tilde{a}_{01}\tilde{b}_{10} +\tilde{a}_{10}\tilde{b}_{01}} \tilde{a}_{01}} \\&- \frac{\tilde{a}_{02}\tilde{a}_{10}\tilde{b}_{01}}{\sqrt{-\tilde{a}_{01}\tilde{b}_{10} +\tilde{a}_{10}\tilde{b}_{01}} \tilde{a}_{01}^2},\\ \tilde{d}_{20}&=\frac{\tilde{b}_{02}\tilde{a}_{10}^2}{(-\tilde{a}_{01}\tilde{b}_{10} +\tilde{a}_{10}\tilde{b}_{01})\tilde{a}_{10}}-\frac{\tilde{b}_{11}\tilde{a}_{10}}{S} +\frac{\tilde{a}_{01}\tilde{b}_{20}}{S}\\&\quad +\frac{\tilde{a}_{02}\tilde{a}_{10}^2}{S\tilde{a}_{01}^2} -\frac{\tilde{a}_{11}\tilde{a}_{10}}{S\tilde{a}_{01}}+\frac{\tilde{a}_{20}}{S},\\ \tilde{d}_{11}&=\frac{2\tilde{b}_{02}\tilde{a}_{10}}{S\tilde{a}_{01}}-\frac{\tilde{b}_{11}}{\sqrt{S} } +\frac{2\tilde{a}_{02}\tilde{a}_{10}}{\sqrt{S}\tilde{a}_{01}^2} -\frac{\tilde{a}_{11}}{\sqrt{S}\tilde{a}_{01}},\\ \tilde{d}_{02}&=-\frac{\tilde{b}_{02}\tilde{b}_{10}}{S} +\frac{\tilde{b}_{02}\tilde{a}_{10}\tilde{b}_{01}}{S\tilde{a}_{01}} -\frac{\tilde{a}_{02}\tilde{b}_{10}}{S\tilde{a}_{01}}+\frac{\tilde{a}_{02}\tilde{a}_{10} \tilde{b}_{01}}{S\tilde{a}_{01}^2}, \end{aligned}$$

and $\tilde{P}_1(\tilde{x},\tilde{y})$, $\tilde{Q}_1(\tilde{x},\tilde{y})$ are the terms of at least order three in $\tilde{x}$ and $\tilde{y}$.

We can get the first-order Lyapunov number of the system by using MATLAB, which is

$$\begin{aligned} \begin{aligned}&\sigma = \frac{1}{16}[\tilde{f}_{\tilde{x}\tilde{x}\tilde{x} }+\tilde{f}_{\tilde{x}\tilde{y}\tilde{y} } +\tilde{g}_{\tilde{x}\tilde{x}\tilde{y} }+\tilde{g}_{\tilde{y}\tilde{y}\tilde{y} }]\\&\quad +\frac{1}{16} [\tilde{f}_{\tilde{x}\tilde{y}}(\tilde{f}_{\tilde{x}\tilde{x}}+\tilde{f}_{\tilde{y}\tilde{y}})-\tilde{g}_{\tilde{x}\tilde{y}} (\tilde{g}_{\tilde{x}\tilde{x}}+\tilde{g}_{\tilde{y}\tilde{y}})\\&\quad -\tilde{f}_{\tilde{x}\tilde{x}}\tilde{g}_{\tilde{x}\tilde{x}}+\tilde{f}_{\tilde{y}\tilde{y}}\tilde{g}_{\tilde{y}\tilde{y}}]\\&=-\frac{1}{8S^{\frac{3}{2}}a_{01}^4 }[-2b_{20}(a_{20}\frac{b_{11}}{2})a_{01}^5 ]\\&\quad +[(2a_{11}b_{20}+2a_{20}b_{11}+2b_{02}b_{20}+b_{11}^2)a_{10}\\&\quad -a_{11}b_{20}-2a_{20}^2-a_{20}b_{11}]a_{01}^4+... \end{aligned} \end{aligned}$$

And if $\sigma <0$, then the Hopf bifurcation is supercritical; if $\sigma >0$, then it’s subcritical [18].

Theorem 5

When $\Delta =(b-m)^2-4d>0$ and $d=\frac{(b-m+1)(b-m-1)}{(b-m)^2}>0$, system (2) experiences the Hopf bifurcation around $E_3$.

Remark 1

1. When $m=0$, i.e. the system (2) does not have the Langmuir–Hinshelwood mechanism, the first Lyapunov coefficient is $l_1'=-\frac{6v_3(v_3^2+\frac{1}{2})\pi }{(1-dv_3^2)^{\frac{3}{2}}}<0$. Here, $1-dv_3^2>0$ and $d=\frac{b^2-1}{b^2}>0$ needs to be satisfied. Therefore, when $m=0$, $b^2-4d>0$, $1-dv_3^2>0$, and $d=\frac{b^2-1}{b^2}>0$, it has a supercritical Hopf bifurcation occurs around $E_3$.

2. In Ref. [19], the phase portraits and bifurcation diagrams were present for the Gray–Scott model, that is, the model (2) with $m=0$, but no result about the Hopf bifurcation or the Bogdanov–Takens bifurcation.

3.3 Bogdanov–Takens bifurcation

From Theorems 1 and 2, the system has a positive equilibrium point $E_1(u_1,v_1)$ when $\Delta =(m-b)^2-4d=0$ and $b>m$. Furthermore, when $m=m_1\equiv b-\sqrt{2}$ and $d\equiv d_1=\frac{1}{2}$, we find that $tr J_{E_1} = det J_{E_1} = 0$ and $E_1$ is a cusp of codimension 2. Therefore, the Bogdanov–Takens bifurcation will appear around $E_1$ in the system. Now select m and b as the bifurcation parameters to give the detailed analysis.

Theorem 6

When bifurcation parameters $m=m_1$ and $d=d_1$, the Bogdanov–Takens bifurcation occurs in the small neighborhood of $E_1$ in system (2).

Proof

Replacing m and d with $m_1+\varepsilon _1$ and $d_1+\varepsilon _2$ respectively in system (2), one has

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{u}=-u+\frac{u^2v}{1+(m_1+\varepsilon _1)v},\\ \dot{v}=b-(d_1+\varepsilon _2)v-\frac{u^2v}{1+(m_1+\varepsilon _1)v}. \end{array}\right. } \end{aligned}$$

(13)

Using the transformation $(x,y)=(u-u_1,v-v_1)$, we expand system (13) at the origin and obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}=a_{00}(\varepsilon )+a_{10}(\varepsilon )x+a_{01}(\varepsilon )y +a_{20}(\varepsilon )x^2\\ \qquad +a_{11}(\varepsilon )xy+a_{02}(\varepsilon )y^2+M_0(x,y,\varepsilon ),\\ \dot{y}=b_{00}(\varepsilon )+b_{10}(\varepsilon )x+b_{01}(\varepsilon )y+b_{20}(\varepsilon )x^2\\ \qquad +b_{11}(\varepsilon )xy +b_{02}(\varepsilon )y^2+N_0(x,y,\varepsilon ), \end{array}\right. } \end{aligned}$$

(14)

where

$$\begin{aligned}{} & {} \begin{aligned}&a_{00}(\varepsilon )=-\frac{(m_1v_1+1)\varepsilon _1}{1+(m_1+\varepsilon _1)v_1},\quad b_{00}(\varepsilon )=b-(d_1\varepsilon _2)v_1-\frac{(m_1v_1+1)^2}{v_1(1+(m_1+\varepsilon _1)v_1)},\quad a_{10}(\varepsilon )=\frac{1+(m_1-\varepsilon _1)v_1}{1+(m_1+\varepsilon _1)v_1},\\&a_{01}(\varepsilon )=\frac{(m_1v_1+1)^2}{v_1^2(1+(m_1+\varepsilon _1)v_1)^2},\quad a_{20}(\varepsilon )=\frac{v_1}{1+(m_1+\varepsilon _1)v_1},\quad a_{11}(\varepsilon )=\frac{2m_1v_1+2}{v_1(1+(m_1+\varepsilon _1)v_1)^2},\\&a_{02}(\varepsilon )=-\frac{(m_1v_1+1)^2(m_1+\varepsilon _1)}{v_1^2(1+(m_1+\varepsilon _1)v_1)^3},\quad b_{10}(\varepsilon )=\frac{-2m_1v_1-2}{1+(m_1+\varepsilon _1)v_1}, \end{aligned} \\{} & {} \begin{aligned}&b_{01}(\varepsilon )=\frac{-1-(m_1+\varepsilon _1)^2(d_1+\varepsilon _2)v_1^4-2(m_1+\varepsilon _1)(d_1+\varepsilon _2)v_1^3 +(-m_1^2-d_1-\varepsilon _2)v_1^2-2m_1v_1}{v_1^2(1+(m_1+\varepsilon _1)v_1)^2},\\&b_{20}(\varepsilon )=-\frac{v_1}{1+(m_1+\varepsilon _1)v_1}, \quad b_{11}(\varepsilon )=\frac{-2m_1v_1-2}{v_1(1+(m_1+\varepsilon _1)v_1)^2},\quad b_{02}(\varepsilon )=\frac{(m_1v_1+1)^2(m_1+\varepsilon _1)}{v_1^2(1+(m_1+\varepsilon _1)v_1)^3}, \end{aligned} \end{aligned}$$

and $M_0(x,y,\varepsilon )$, $N_0(x,y,\varepsilon )$ are the terms of at least order three in x and y.

In order to obtain the universal unfolding of the system, it is necessary to eliminate the $y^2$-term in system (14). To this end, by the transformation $(x,y)=(x_1+\frac{a_{02}(\varepsilon )}{a_{01}(\varepsilon )}x_1y_1,y_1+\frac{b_{02} (\varepsilon )}{a_{01}(\varepsilon )}x_1y_1)$, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x_1}=c_{00}(\varepsilon )+c_{10}(\varepsilon )x_1+c_{01}(\varepsilon )y_1+c_{20}(\varepsilon )x_1^2\\ \qquad +c_{11}(\varepsilon )x_1y_1+M_1(x_1,y_1,\varepsilon ),\\ \dot{y_1}=d_{00}(\varepsilon )+d_{10}(\varepsilon )x_1+d_{01}(\varepsilon )y_1+d_{20}(\varepsilon )x_1^2\\ \qquad +d_{11} (\varepsilon )x_1y_1+N_1(x_1,y_1,\varepsilon ), \end{array}\right. } \end{aligned}$$

(15)

where

$$\begin{aligned} \begin{aligned}&c_{00}(\varepsilon )=a_{00}(\varepsilon ),\quad c_{10}(\varepsilon )=a_{10}(\varepsilon )-\frac{a_{02}(\varepsilon )b_{00}(\varepsilon )}{a_{01}(\varepsilon )},\\&c_{01}(\varepsilon )=a_{01}(\varepsilon )-\frac{a_{00}(\varepsilon )a_{02}(\varepsilon )}{a_{01}(\varepsilon )},\\&c_{20}(\varepsilon )=a_{20}(\varepsilon )-\frac{a_{02}(\varepsilon )b_{10}(\varepsilon )}{a_{01}(\varepsilon )},\\&c_{11}(\varepsilon )=a_{11}(\varepsilon )+b_{02}(\varepsilon )-\frac{a_{02}(\varepsilon )b_{01}(\varepsilon )}{a_{01}(\varepsilon )},\\&d_{00}(\varepsilon )=b_{00}(\varepsilon ),\quad d_{10}(\varepsilon )=b_{10}(\varepsilon )-\frac{b_{00}(\varepsilon )b_{02}(\varepsilon )}{a_{01}(\varepsilon )},\\&d_{01}(\varepsilon )=b_{10}(\varepsilon )-\frac{a_{00}(\varepsilon )b_{02}(\varepsilon )}{a_{01}(\varepsilon )},\\&d_{20}(\varepsilon )=b_{20}(\varepsilon )-\frac{b_{10}(\varepsilon )b_{02}(\varepsilon )}{a_{01}(\varepsilon )},\\&d_{11}(\varepsilon )=b_{11}(\varepsilon )-\frac{a_{10}(\varepsilon )b_{02}(\varepsilon )}{a_{01}(\varepsilon )}+\frac{a_{02} (\varepsilon )b_{10}(\varepsilon )}{a_{01}(\varepsilon )},\\ \end{aligned} \end{aligned}$$

and $M_1(x_1,y_1,\varepsilon )$, $N_1(x_1,y_1,\varepsilon )$ are the terms of at least order three in $x_1$ and $y_1$.

Through the $C^\infty$ change of variables $(x_2,y_2)=(x_1,c_{00}+c_{10}x_1+c_{01}y_1+c_{20}x_1^2+c_{11}x_1y_1+...)$, system (15) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_2=y_2,\\ \dot{y}_2=e_{00}(\varepsilon )+e_{10}(\varepsilon )x_2+e_{01}(\varepsilon )y_2+e_{20}(\varepsilon )x_2^2\\ \qquad +e_{11}(\varepsilon )x_2y_2 +e_{02}(\varepsilon )y_2^2+N_2(x_2,y_2,\varepsilon ), \end{array}\right. } \end{aligned}$$

(16)

where

$$\begin{aligned} e_{00}(\varepsilon )=&c_{01}(\varepsilon )d_{00}(\varepsilon )-c_{00}(\varepsilon )d_{01}(\varepsilon ),\\ e_{01}(\varepsilon )=&c_{10}(\varepsilon )+d_{01}(\varepsilon )-\frac{c_{11}(\varepsilon )c_{00}(\varepsilon )}{c_{01}(\varepsilon )},\\ e_{10}(\varepsilon )=&-c_{00}(\varepsilon )d_{11}(\varepsilon )-c_{10}(\varepsilon )d_{01}(\varepsilon )\\&+d_{00}(\varepsilon )c_{11} (\varepsilon )+c_{01}(\varepsilon )d_{10}(\varepsilon ),\\ e_{01}(\varepsilon )=&c_{10}(\varepsilon )+d_{01}(\varepsilon )-\frac{c_{11}(\varepsilon )c_{00}(\varepsilon )}{c_{01}(\varepsilon )},\\ e_{11}(\varepsilon ) =&d_{11}(\varepsilon )-\frac{c_{11}(\varepsilon )c_{10}(\varepsilon )}{c_{01}(\varepsilon )}+\frac{c_{11}^2 (\varepsilon )c_{00}(\varepsilon )}{c_{01}^2(\varepsilon )}\\&+2c_{20}(\varepsilon ),\\ e_{20}(\varepsilon )=&-d_{11}(\varepsilon )c_{10}(\varepsilon )-d_{01}(\varepsilon )c_{20}(\varepsilon )\\&+c_{11} (\varepsilon )d_{10}(\varepsilon )+c_{01}(\varepsilon )d_{20}(\varepsilon ),\\ e_{02}(\varepsilon )=&\frac{c_{11}(\varepsilon )}{c_{01}(\varepsilon )}, \end{aligned}$$

and $N_2(x_2,y_2,\varepsilon )$ is the term of at least order three in $x_2$ and $y_2$.

Next, introduce a new time variable $dt=(1-e_{02}(\varepsilon )x_2)d\tau$ and we still denote t as $\tau$

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_2= (1-e_{02}(\varepsilon )x_2)y_2,\\ \dot{y}_2= [e_{00}(\varepsilon )+e_{10}(\varepsilon )x_2+e_{01}(\varepsilon )y_2+e_{20}(\varepsilon )x_2^2\\ \qquad \ +e_{11}(\varepsilon )x_2y_2+e_{02}(\varepsilon )y_2^2+N_2(x_2,y_2,\varepsilon )]\\ \qquad \ \times (1-e_{02}(\varepsilon )x_2). \end{array}\right. } \end{aligned}$$

(17)

Again by the transformation $(x_3,y_3)=(x_2,y_2(1-e_{02}(\varepsilon )x_2))$, one has

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_3=y_3, \\ \dot{y}_3=f_{00}(\varepsilon )+f_{10}(\varepsilon )x_3+f_{01}(\varepsilon )y_3+f_{20}(\varepsilon )x_3^2\\ \qquad +f_{11} (\varepsilon )x_3y_3+N_3(x_3,y_3,\varepsilon ), \end{array}\right. } \end{aligned}$$

(18)

where

$$\begin{aligned} \begin{aligned}&f_{00}(\varepsilon )= e_{00}(\varepsilon ),\quad f_{10}(\varepsilon )=e_{10}(\varepsilon )-2e_{00}(\varepsilon )e_{02}(\varepsilon ),\\&f_{01}(\varepsilon )=e_{01}(\varepsilon ),\\&f_{20}(\varepsilon )=e_{20}(\varepsilon )-2e_{02}(\varepsilon )e_{10}(\varepsilon )+e_{00}(\varepsilon )e_{02}^2(\varepsilon ),\\&f_{11}(\varepsilon )=e_{11}(\varepsilon )-e_{01}(\varepsilon )e_{02}(\varepsilon ), \end{aligned} \end{aligned}$$

and $N_3(x_3,y_3,\varepsilon )$ is the term of at least order three in $x_3$ and $y_3$.

Next, there will be some classification discussions about $f_{20}(\varepsilon )$.

(a) If $f_{20}(\varepsilon )<0$, then the transformation is $(x_4,y_4)=(x_3,\frac{y_3}{\sqrt{-f_{20}(\varepsilon ) } })$ and $\tau = \sqrt{-f_{20}(\varepsilon ) }t$, which will lead to

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_{4}=y_4, \\ \dot{y}_{4}=g_{00}(\varepsilon )+ g_{10}(\varepsilon )x_4+g_{01}(\varepsilon )y_4-x_4^2\\ \qquad \ +g_{11}(\varepsilon )x_4y_4+N_4(x_4,y_4,\varepsilon ), \end{array}\right. } \end{aligned}$$

(19)

where

$$\begin{aligned} \begin{aligned}&g_{00}(\varepsilon )=-\frac{f_{00}(\varepsilon )}{f_{20}(\varepsilon )},\quad g_{10}(\varepsilon )=-\frac{f_{10}(\varepsilon )}{f_{20}(\varepsilon )},\\&g_{01}(\varepsilon )=-\frac{f_{01}(\varepsilon )}{\sqrt{-f_{20}(\varepsilon )} },\quad g_{11}(\varepsilon )=-\frac{f_{11}(\varepsilon )}{\sqrt{-f_{20}(\varepsilon )}}, \end{aligned} \end{aligned}$$

and $N_4(x_4,y_4,\varepsilon )$ is the term of at least order three in $x_4$ and $y_4$.

Let $(x_5,y_5)=(x_4-\frac{g_{10}(\varepsilon ) }{2}, y_4)$, then system (19) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_{5}=y_5,\\ \dot{y}_{5}=h_{00}(\varepsilon )+h_{01}(\varepsilon )y_5-x_5^2+h_{11}(\varepsilon )x_5y_5\\ \qquad \ +N_5(x_5,y_5,\varepsilon ), \end{array}\right. } \end{aligned}$$

(20)

where

$$\begin{aligned} \begin{aligned}&h_{00}(\varepsilon )=g_{00}(\varepsilon )+\frac{g_{10}^2(\varepsilon ) }{4},\\&h_{01}(\varepsilon )=g_{01}(\varepsilon )+\frac{g_{10}(\varepsilon )g_{11}(\varepsilon )}{2 },\quad h_{11}(\varepsilon )=g_{11}(\varepsilon ), \end{aligned} \end{aligned}$$

and $N_5(x_5,y_5,\varepsilon )$ is the term of at least order three in $x_5$ and $y_5$.

Here we suppose $f_{11}(\varepsilon )\ne 0$, then $h_{11}(\varepsilon )=g_{11}(\varepsilon ) =\frac{f_{11}(\varepsilon )}{\sqrt{-f_{20}(\varepsilon )} } \ne 0$. Further, we apply the transformation $(x_6,y_6)=(h_{11}^2(\varepsilon )x_5,-h_{11}^3(\varepsilon )y_5)$ and $\tau =-\frac{1}{h_{11}(\varepsilon )}t$ to system (20) and obtain

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_6=y_6, \\ \dot{y}_6=i_1(\varepsilon )+i_2(\varepsilon )y_6-x_6^2+x_6y_6+N_6(x_6,y_6,\varepsilon ), \end{array}\right. } \end{aligned}$$

(21)

where

$$\begin{aligned} \begin{aligned} i_1(\varepsilon )=-h_{00}(\varepsilon )h_{11}^4(\varepsilon ),\qquad i_2(\varepsilon )=-h_{01}(\varepsilon )h_{11}(\varepsilon ), \end{aligned} \end{aligned}$$

and $N_6(x_6,y_6,\varepsilon )$ is the term of at least order three in $x_6$ and $y_6$.

(b) If $f_{20}(\varepsilon )>0$, then the transformation is $(x_7,y_7)=(x_3,\frac{y_3}{\sqrt{f_{20}(\varepsilon )} } )$, and $\tau =\sqrt{f_{20}(\varepsilon )}t$, which will give

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_{7}=y_7, \\ \dot{y}_{7}=\bar{g}_{00}(\varepsilon )+ \bar{g}_{10}(\varepsilon )x_7+\bar{g}_{01}(\varepsilon )y_7-x_7^2\\ \qquad \ +\bar{g}_{11}(\varepsilon )x_7y_7+N_7(x_7,y_7,\varepsilon ), \end{array}\right. } \end{aligned}$$

(22)

where

$$\begin{aligned} \begin{aligned}&\bar{g}_{00}=-\frac{f_{00}(\varepsilon )}{f_{20}(\varepsilon )},\quad \bar{g}_{10}=-\frac{f_{10}(\varepsilon )}{f_{20}(\varepsilon )},\\&\bar{g}_{01}=-\frac{f_{01}(\varepsilon )}{\sqrt{f_{20}(\varepsilon )} },\quad \bar{g}_{11}=-\frac{f_{11}(\varepsilon )}{\sqrt{f_{20}(\varepsilon )}}, \end{aligned} \end{aligned}$$

and $N_7(x_7,y_7,\varepsilon )$ is the term of at least order three in $x_7$ and $y_7$.

Furthermore, by the transformation $(x_8,y_8)=(x_7+\frac{\bar{g}_{10}(\varepsilon ) }{2}, y_7)$, one gets

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_{8}=y_8, \\ \dot{y}_{8}=\bar{h}_{00}(\varepsilon )+\bar{h}_{01}(\varepsilon )y_8+x_8^2+\bar{h}_{11}(\varepsilon )x_8y_8\\ \qquad \ +N_8(x_8,y_8,\varepsilon ), \end{array}\right. } \end{aligned}$$

(23)

where

$$\begin{aligned} \begin{aligned}&\bar{h}_{00}(\varepsilon )=\bar{g}_{00}(\varepsilon )-\frac{\bar{g}_{10}^2(\varepsilon ) }{4},\\&\bar{h}_{01}(\varepsilon )=\bar{g}_{01}(\varepsilon )-\frac{\bar{g}_{10}(\varepsilon )\bar{g}_{11}(\varepsilon )}{2 },\quad \bar{h}_{11}(\varepsilon )=\bar{g}_{11}(\varepsilon ), \end{aligned} \end{aligned}$$

and $N_8(x_8,y_8,\varepsilon )$ is the term of at least order three in $x_8$ and $y_8$.

Similarly, supposing $f_{11}(\varepsilon )\ne 0$, then $\bar{h}_{11}(\varepsilon )=\bar{g}_{11}(\varepsilon ) =\frac{f_{11}(\varepsilon )}{\sqrt{f_{20}(\varepsilon )} }\ne 0$. Applying transformation $(x_9,y_9)=(\bar{h}_{11}^2(\varepsilon )x_8,\bar{h}_{11}^3(\varepsilon )y_8)$ and $\tau =\frac{1}{\bar{h}_{11}(\varepsilon )}t$ to (23), one obtains

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_9=y_9,\\ \dot{y}_9=\bar{i}_1(\varepsilon )+\bar{i}_2(\varepsilon )y_9+x^2+xy+N_9(x_9,y_9,\varepsilon ), \end{array}\right. } \end{aligned}$$

(24)

where

$$\begin{aligned} \begin{aligned} \bar{i}_1(\varepsilon )=\bar{h}_{00}(\varepsilon )\bar{h}_{11}^4(\varepsilon ), \qquad \bar{i}_2(\varepsilon )=\bar{h}_{01}(\varepsilon )\bar{h}_{11}(\varepsilon ), \end{aligned} \end{aligned}$$

and $N_9(x_9,y_9,\varepsilon )$ is the term of at least order three in $x_9$ and $y_9$.

In order to simplify the discussions, we still denote $\bar{i}_1(\varepsilon )$ and $\bar{i}_2(\varepsilon )$ as $i_1(\varepsilon )$ and $i_2(\varepsilon )$. Here with the help of the MATLAB, we have

$$\begin{aligned} \left| \frac{\partial (i_1(\varepsilon ),i_2(\varepsilon ))}{\partial (\varepsilon _1,\varepsilon _2)} \right| _{\varepsilon _1=\varepsilon _2=0} \ne 0. \end{aligned}$$

So $i_1(\varepsilon )$ and $i_2(\varepsilon )$ are dependent. Then we could give the local representations of the bifurcation curves up to second-order approximation in the following (“+”for $f_{20}(\varepsilon )>0$, “-”for $f_{20}(\varepsilon )<0$):

(1) The saddle-node bifurcation curve $SN=\{(\varepsilon _{1},\varepsilon _{2}): g_{1}(\varepsilon _{1},\varepsilon _{2})=0, g_{2}(\varepsilon _{1},\varepsilon _{2})\ne 0\}$;

(2) The Hopf bifurcation curve $H=\{(\varepsilon _{1},\varepsilon _{2}): g_{2}(\varepsilon _{1},\varepsilon _{2})=\pm \sqrt{-g_{1}(\varepsilon _{1},\varepsilon _{2})}, g_{1}(\varepsilon _{1},\varepsilon _{2})<0\}$;

(3) The homoclinic bifurcation curve $HL=\{(\varepsilon _{1},\varepsilon _{2}): g_{2}(\varepsilon _{1},\varepsilon _{2})=\pm \frac{5}{7}\sqrt{-g_{1}(\varepsilon _{1},\varepsilon _{2})}, g_{1}(\varepsilon _{1},\varepsilon _{2})<0\}$. $\square$

4 Numerical simulation

In this section, we would like to demonstrate the complex dynamical behaviors through numerical simulation. Effectiveness of the theoretical analysis presented above could be confirmed through the phase portraits by using MATLAB. Here, m, b and d are parameters of system (2).

Example 1

Figure 1 shows the dynamical behavior of system (2) with given parameters $m=0.3$ and $b=0.3+\sqrt{2}$. In this case, $d_{SN}=\frac{(m-b)^2}{4}=0.5$. As shown in Fig. 1a, when $d=0.6>d_{SN}$, the system only has one boundary equilibrium $E_0=(0,1.0071)$. In Fig. 1b, when $d=0.5=d_{SN}$, the system has a boundary equilibrium $E_0=(0,3.4284)$ and a positive equilibrium $E_1=(1.0071,1.4142)$, which is a cusp. Saddle-node bifurcation may occur around $E_1$. In Fig. 1c, when $d<d_{SN}$, the system has a boundary equilibrium point $E_0=(0,4.2855)$ and two positive equilibrium $E_2=(0.6909,2.5583)$ and $E_3=(1.3233,0.9772)$.

Fig. 1

Dynamics of system (2) with parameters $m=0.3$ and $b=0.3+\sqrt{2}$. a $d=0.6$; b $d=0.5$; c $d=0.4$

Fig. 2

Dynamics of system (2) with parameters $m=0.3$. a $b=0.3+\sqrt{2.4}$, $d=0.6$; b $b=0.3+\sqrt{1.6}$, $d=0.4$

Example 2

Figure 2 shows the dynamical behavior of system (2) with given parameter $m=0.3$. In Fig. 2a, taking $b=0.3+\sqrt{2.4}$ and $d=0.6$, the system has a unique positive equilibrium $E_1=(1.0746,1.2910)$, which is a saddle node with a stable parabolic sector. In Fig. 2b, taking $b=0.3+\sqrt{1.6}$ and $d=0.4$, the system has a unique positive equilibrium point $E_1=(0.9325,1.5811)$, which is a saddle node with an unstable parabolic sector. As shown in Fig. 1b, with $b=0.3+\sqrt{2}$ and $d=0.5$, the positive equilibrium point $E_1=(1.0071,1.4142)$ is a cusp of codimension 2. Therefore, the Bogdanov–Takens bifurcation may occur around $E_1$.

Example 3

Figure 3 shows the phase portrait of system (2) with parameters $m=0.09$ and $b=1.39$. At this point, $d_{H}=\frac{(b-m+1)(b-m-1)}{(b-m)^2}=0.69/1.69$. In Fig. 3a, where $d=d_{H}$, the system has a boundary equilibrium and two positive equilibrium points $E_2=(0.6208,1.8841)$ and $E_3=(0.8592,1.3000)$. $E_2$ is a saddle point, while $E_3$ is a fine focus. In Fig. 3b, where $d=0.2<d_{H}$, the system has a boundary equilibrium and two positive equilibrium points $E_2=(0.2683,5.6085)$ and $E_3=(1.2117,0.8915)$. $E_2$ is a saddle point, while $E_3$ is a sink. In Fig. 3c, where $d=0.4>d_{H}$, the point $E_3(0.89,1.25)$ is a source. So the system may undergo the Hopf bifurcation near $E_3$.

Fig. 3

Phase portraits

Example 4

Take parameters $m=0.3, b=0.3+\sqrt{2}, d=0.5$, then the Bogdanov–Takens bifurcation occurs around $E_1$. The bifurcation thresholds are $m_1=m$ and $d_1=d$. Then we have

$$\begin{aligned} \left| \frac{\partial (i_1(\varepsilon ),i_2(\varepsilon ))}{\partial (\varepsilon _1,\varepsilon _2)} \right| _{\varepsilon _1=\varepsilon _2=0}=-16.5324 \ne 0. \end{aligned}$$

Therefore the rank of matrix $\left| \frac{\partial (i_1(\varepsilon ),i_2(\varepsilon ))}{\partial (\varepsilon _1,\varepsilon _2)} \right| _{\varepsilon _1=\varepsilon _2=0}$ is 2. For sufficiently small $\varepsilon _i$ $(i=1,2)$, the local representation of the bifurcation curves could be approximated as follows:

$$\begin{aligned} \begin{aligned} SN&=\{(\varepsilon _{1},\varepsilon _{2}):- 17.3481\varepsilon _1^2 - 75.8515\varepsilon _1\varepsilon _2 \\&\quad + 4.7011\varepsilon _1 - 82.9553\varepsilon _2^2 + 9.9123\varepsilon _2=0,\\&\quad \varepsilon _{2}\ne 0\},\\ H&=\{(\varepsilon _{1},\varepsilon _{2}):- 14.4343\varepsilon 1^2 - 53.4060\varepsilon _1\varepsilon _2 \\&+ 4.3203\varepsilon _1 - 36.1388\varepsilon _2^2 + 8.1175\varepsilon _2=0, \varepsilon _{2}<0\},\\ HL&=\{(\varepsilon _{1},\varepsilon _{2}):- 5.9373\varepsilon _1^2- 16.2542\varepsilon _1\varepsilon _2 \\&+ 2.0177\varepsilon _1 + 4.4923\varepsilon _2^2 + 3.2624\varepsilon _2=0,\varepsilon _{2}<0\}. \end{aligned} \end{aligned}$$

Fig. 4

a The subcritical Bogdanov–Takens bifurcation diagram of system (13); b When $(\varepsilon _1,\varepsilon _2) =(0.1, -0.0033)$, the system has no positive equilibrium point in region I; c When $(\varepsilon _1,\varepsilon _2)=(0.064, -0.048)$, the system has an unstable focus in region II; d When $(\varepsilon _1,\varepsilon _2)=(0.064, -0.05)$, the system has an unstable limit cycle in region III; e When $(\varepsilon _1,\varepsilon _2)=(0.064, -0.05280294849)$, the system has an unstable homoclinic orbit on curve HL; f When $(\varepsilon _1,\varepsilon _2)=(0.064, -0.1)$, the system has a stable focus in region IV

Figure 4 shows the subcritical Bogdanov–Takens bifurcation diagram and phase portraits of system (13). The conclusions are as follows.

• (a) The bifurcation curves SN, H and HL divide the $(\varepsilon _1,\varepsilon _2)$-plane into four regions, which rotate clockwise around the critical parameter values of the Bogdanov–Takens bifurcation $(\varepsilon _1,\varepsilon _2)=(0,0)$, as shown in Fig. 4a.

• (b) In Fig. 4b, when the parameters are in region I, the system has no positive equilibrium point.

• (c) When the parameter is on the curve SN, the system has a positive equilibrium point, which is a saddle node.

• (d) When the parameter crosses the curve SN and enters region II, passing through the saddle-node bifurcation, the system has two positive equilibrium points, one unstable focus and the other a saddle point (See Fig. 4c).

• (e) When the parameter is on the curve H, there are two positive equilibrium points, one unstable fine focus and the other a saddle point.

• (f) When the parameter crosses the curve H and enters region III, passing through the subcritical Hopf bifurcation, an unstable limit cycle appears, with the focus being stable (See Fig. 4d).

• (g) When the parameter crosses region III and is on the curve HL, passing through the homoclinic bifurcation, an unstable homoclinic orbit containing a stable focus appears (See Fig. 4e).

• (h) When the parameter crosses the curve HL and enters region IV, the homoclinic orbit breaks and a stable focus and a saddle point appear (See Fig. 4f).

5 Conclusion

An enzyme-catalyzed reaction model is formulated in this work. Existence and their stability of equilibrium points, and the bifurcations, including the saddle-node bifurcation, the Hopf bifurcation and the Bogdanov–Takens bifurcation of codimension 2, in the system are presented. By using the stability theory, the existence and stability of equilibrium points of system (2) are provided. Moreover, the detailed bifurcation behaviors of the model are discussed through bifurcation theory, which includes the Sotomayor’s theorem, Hopf analysis and perturbed theory. Numerical simulations are used to validate the results obtained. Specifically, compared to the original temporal Gray–Scott model, the system (2) exhibits richer dynamic behaviors. Effects of the diffusion on the model will be still interesting and could be further explored.